My interest is in the future because I am going to spend the rest of my life there
Charles F. Kettering, inventor
The eminent Canadian psychologist Janet Bavelas once asked a group of students to imagine that one of their professors was going to take a sabbatical in Europe next year.1 She then told them to predict in writing what the professor would do during his year abroad. A second group of students was also asked to think about the same professor. But this time, Bavelas told them he’d just returned from a sabbatical in Europe, and she instructed them to write down what they thought the professor had done during the last year.
You’d be forgiven for thinking the results would be very similar. These were two perfectly representative groups of students asked to perform more or less the same task. But it turned out that the accounts of the imaginary past were richly detailed, while the stories about the future were sketchy and vague. This experiment and many others prove that it’s somehow easier to imagine what someone has done, as opposed to what they’re going to do.
The case of Janet Bavelas’s students captures a central theme of this chapter: the asymmetry between our ability to explain the past and our capacity for predicting the future. Once an event – even a highly unusual event – has occurred we humans find it blissfully easy to provide plausible explanations. The tragedy of 9/11 or the train bombings in Madrid and London are so well known that we’re all sure we understand why they came about. And yet, even the day before these disasters occurred, we had no idea what was about to happen. If someone had come up with all the reasons we now invoke for the tragedies, we would have dismissed them as crazy. After all, there’s always some screwball on a street corner announcing that the end of the world is nigh.
In psychology our know-it-all attitude to the past is known as “hindsight” bias. In the States, it’s also called the “Monday morning quarterback” phenomenon, but it’s pretty universal really. The financial media is rife with after-the-event experts, who are always available to explain changes in a company’s stock price over the last week. Ask them to predict what will happen next week, though, and they won’t sound quite as convincing. Anyone can fit past events into a rational-sounding sequence. But no one can explain, not to mention predict, the future in advance.
This chapter also has a second – more personal – theme that puzzled one of the authors from the age of nine well into his late forties. Why did his music teacher, Miss Johnstone, insist that he join the school choir, when she patently knew he was a lousy singer?
Before solving the enduring mystery of Miss Johnstone’s choir, let’s explore the question of past–future asymmetry further, using another painfully personal example that we alluded to briefly in the preface to this book.
As an expert in statistics, working in a business school during the 1970s, one of the authors (who also, as it happens, can’t sing a note) couldn’t fail to notice that executives were deeply preoccupied with forecasting. Their main interest lay in various types of business and economic data: the sales of their firm, its profits, exports, exchange rates, house prices, industrial output . . . and a host of other figures. It bugged the professor greatly that practitioners were making these predictions without recourse to the latest, most theoretically sophisticated methods developed by statisticians like himself. Instead, they preferred simpler techniques which – they said – allowed them to explain their forecasts more easily to senior management. The outraged author decided to teach them a lesson. He embarked on a research project that would demonstrate the superiority of the latest statistical techniques. Even if he couldn’t persuade business people to adopt such methods, at least he’d be able to prove the precise cost of their attempts to please the boss.
Every decent statistician knows the value of good research, so the professor and his research assistant collected many sets of economic and business data over time from a wide range of economic and business sources. In fact they hunted down 111 different time series which they analyzed and used to make forecasts – a pretty impressive achievement given the computational requirements of the task back in the days when computers were no faster than today’s calculators. They decided to use their trawl of data to mimic, as far as possible, the real process of forecasting. To do so, each series was split into two parts: earlier data and later data. The researchers pretended that the later part hadn’t happened yet and proceeded to fit various statistical techniques, both simple and statistically sophisticated, to the earlier data. Treating this earlier data as “the past,” they then used each of the techniques to predict “the future,” whereupon they sat back and started to compare their “predictions” with what had actually happened.
Horror of horrors, the practitioners’ simple, boss-pleasing techniques turned out to be more accurate than the statisticians’ clever, statistically sophisticated methods. To be honest, neither was particularly accurate, but there was no doubt that the statisticians had served themselves a large portion of humble pie.
One of the simplest methods, known as “single exponential smoothing,” in fact appeared to be one of the most accurate. Indeed, for 61.8% of the time it was more accurate than the so-called Box–Jenkins technique, which represented the pinnacle of theoretically based statistical forecasting technology back in the 1970s. The academic journals of the day had proven that the Box–Jenkins method was more accurate than large econometric models where predictions were based on hundreds of equations and impressive volumes of data. So, by extension, single exponential smoothing was also more accurate than the grand-scale econometric models that cost hundreds of thousands of dollars to develop and use!
At first, the professor and his assistant were so taken aback by their results that they suspected they’d made a mistake. They made extensive checks on their own calculations but could find no errors at all. The initial shock now over, they began to cheer up. If there’s one thing that makes up for an academic proving himself wrong, it’s the opportunity to show that other eminent authorities are wrong too. So the professor submitted a paper on his surprising and important findings to a prestigious learned journal and waited for the plaudits to start rolling in. This in itself turned out to be another forecasting error. The paper was rejected on the grounds that the results didn’t square with statistical theory! Fortunately, another reputable academic journal did decide to publish the paper, but they insisted on including comments from the leading statisticians of the day. The experts were not impressed. Among the many criticisms was a suggestion that the poor performance of the sophisticated methods was due to the inability of the author to apply them properly.2
Undaunted, the valiant statistician and his faithful assistant set out to prove their critics wrong. This time around they collected and made forecasts for even more sets of data (1,001 in total, as computers were much faster by this time), from the worlds of business, economics, and finance. As before, the series were separated into two parts: the first used to develop forecasting models and make predictions; and the second used to measure the accuracy of the various methods. But there was a new and cunning plan. Instead of doing all the work himself, the author asked the most renowned experts in their fields – both academics and practitioners – to forecast the 1,001 series. All in all, fourteen experts participated and compared the accuracy of seventeen methods.
This time, there were no bad surprises for the professor. The findings were exactly the same as in his previous research. Simpler methods were at least as accurate as their complex and statistically sophisticated cousins. The only difference was that there were no experts to criticize, as most of the world’s leading authorities had taken part.
That was way back in 1982. Since then, the author has organized two further forecasting “competitions” to keep pace with new developments and eliminate the new criticisms that academics have ingeniously managed to concoct. The latest findings, published in 2000,3 consisted of 3,003 economic series, an expanding range of statistical methods, and a growing army of experts. However, the basic conclusion – supported by many other academic studies over the past three decades – remains steadfast. That is, when forecasting, always use the KISS principle: Keep It Simple, Statistician.
Although pleased to be vindicated, the statistician couldn’t help feeling a little disillusioned. If statistical forecasting models had such poor powers of prediction, maybe it would be better to rely on human intuition – the simplest method of them all. That was when he got talking to his colleague, a tone-deaf cognitive psychologist. It was the beginning of a beautiful working relationship, but the eventual co-author wasn’t very encouraging at the time. “I’ve got bad news for you,” he said. “Empirical findings in my field show that human judgment is even less accurate at predicting than statistical models.”
The empirical findings he was referring to were those of the psychologist Paul Meehl and others. Meehl had applied his research to people of his own kind, turning psychology on the psychologists. He was particularly intrigued by the methods of diagnosis and decision-making used in clinical psychology. Traditionally, psychologists make their predictions about what’s wrong with a patient based on a tiny sample of immediately available data, together with their own subjective judgments. Meehl asked whether they might be better off taking the time to collect quantitative data about their clients and then draw some statistically sound conclusions from it. He reviewed some twenty studies and discovered that the “statistical” method of diagnosis was superior to the traditional “clinical” approach.
When Meehl published a small book about his research in 1954,4 it was greeted with the same kind of outrage as the statistician’s paper on forecasting methods. Clinical psychologists all over the world felt professionally diminished and dismissed their colleague’s findings. It didn’t seem to matter that he was suggesting a way to make more accurate, more efficient, and more cost-effective clinical judgments. Although many subsequent studies have reinforced Meehl’s original findings,5 his suggestions have not yet been adopted by his own profession.
He may not have been greeted as a prophet in his own land, but Meehl’s observations have been vindicated in other fields. Those in the business of lending money, for example, no longer rely on “clini-cal” procedures such as interviews with a bank manager to decide if you’re worthy of credit. Instead, they make extensive use of computerized credit-scoring. In other words, they use simple statistical models with a select handful of variables to check whether you’re a good risk. Similarly, graduate recruiters who take on fresh, young talent each year in large numbers increasingly depend on computers to profile applicants, before embarking on the expensive (and notoriously unreliable) process of face-to-face interviewing.
After his brief excursion into psychology, the statistician was back to square one. As statisticians do, he sought comfort in further calculations based on his original data. He discovered that the most reliable predictions of all were achieved by taking the average of the results from a number of different forecasting methods. This worked even better than the most accurate statistical methods, including single exponential smoothing. And this incredible power of averaging has remained constant in each of the forecasting “competitions” over the years, not to mention many other areas and scientific fields.6
If you can improve forecasting accuracy by averaging predictions made by different models, can you do the same for predictions by people? The simple answer is “yes,” a finding that has been rediscovered several times over the last century – and recently documented by James Surowiecki in his excellent book, The Wisdom of Crowds.7 Surowiecki recounts the story of Francis Galton, the famous late-Victorian social scientist, who visited a county fair in Plymouth in his native England early in the twentieth century. There Galton observed a contest that involved guessing the net weight of an ox (after it was slaughtered and its skin removed). The person who provided the most accurate estimate would be declared the winner. Galton was an elitist who didn’t have much time for the opinions of ordinary people, so he thought it would be interesting to investigate the levels of inaccuracy to which they would descend.
He set about obtaining all the legible predictions – 787 in total. Some of them really were way out. But the average of all the guesses was 1,197 pounds (543 kg) – and the weight of the ox, after it had been slaughtered and prepared, was 1,198 pounds. In other words, the average of all the predictions – bad and good – was almost perfect. What’s more, it was much more accurate than the guess of the eventual winner. Galton, the elitist, was left to ponder his own discovery that the average prediction of few hundred ignorant yokels was highly accurate. Like the statistician some three-quarters of a century later, he’d glimpsed the incredible power of averaging.
In The Wisdom of Crowds, Surowiecki goes on to describe many other situations where simple averages of people’s judgments provide surprisingly accurate estimates. And everyday life throws up many more examples. Internet sites like www.intrade.com, where the general public bet on who’ll win the next elections, are better at predicting the winner than individual political experts with huge reputations and huge egos. This phenomenon runs contrary to the theories of statistical science, which advocate the existence of a so-called “optimal” model that, once appropriately identified and correctly used, provides more accurate predictions than alternative models. It also runs contrary to our very human need to believe in experts. Not only, it turns out, is an expert’s judgment less accurate than the simple number crunching of a computer, but it’s also less reliable than the average forecast of a bunch of nobodies.
Why is it so easy to explain the past and yet so difficult to predict the future? Why do simple statistical methods forecast events at least as accurately as complex, sophisticated ones? Why do people make worse judgments than mechanical models based on samples of data? Why does averaging, whether of models or people, work better than anything else, including the so-called “optimal” model and the best experts, when it comes to predictions?
To answer these questions let’s go back to basics. The process of forecasting, whether carried out by people or models, is to identify some pattern or relation among the relevant variables and then extrapolate from there. Identifying patterns intuitively is something that human beings do constantly and in many – but not all – cases we are quite good at it. Imagine, for example, how easy it is to predict the trajectory of a ball thrown into the air, the position of another car on the road, or the way someone else’s spoken sentence will end. Most of the members of Miss Johnstone’s school choir were also pretty good at predicting the last note of a good tune. Indeed, psychologists have been fascinated by the human ability to infer pattern in music and see it as a model for other kinds of reasoning. The late Herbert Simon, who was an all-round social scientist and Nobel prize-winner for economics, wrote extensively on the subject.
Patterns, temporal as well as spatial, occur in many spheres of life besides music. People appear to have strong propensities, whether innate or learned, to discover patterns in temporal sequences presented by the environment, and to use these evidences of pattern for prediction. The ability and desire to discover temporal patterns has had great value for the survival of Man: in predicting the seasons, for example, or the weather. The urge to find pattern extends even to phenomena where one may well doubt whether pattern exists (e.g. in movements of the stock market).8
Models do formally – and systematically – what humans do intuitively. They analyze the past and find an underlying pattern or relation between variables. Two factors, however, complicate the task of forecasting. First, the future is rarely a straightforward extrapolation of the past. That’s because environmental, economic, market, and competitive conditions can change in unforeseen ways. Second, we rarely observe a pattern in its pure form. Instead, patterns are typically intermixed with “noise,” that is chance fluctuations that have no discernable cause.
Let’s take the slightly depressing example of climate change. Despite the slow, general trend that is global warming, the summer of 2007 brought unseasonably cold, wet weather to northern Europe and an extreme heat wave to eastern Europe. It’s tempting to conclude that global warming never existed or is speeding up, depending on where you live. But the truth is that there have always been freak-weather years. More prosaically, any seasoned sales manager can recount tales of inexplicably bad or good months that stick out like a very sore thumb from the overall trend. In these and many other situations, what we observe is both the pattern and the noise together. So the first task in identifying the underlying pattern is to filter out the noise. It’s a bit like having an intimate conversation in a loud, trendy restaurant, or blocking out the sound of our children fighting when we’re trying to listen to a favorite CD. Of course, something unexpected could happen in the future that will defy the pattern altogether, but if we don’t identify its shape correctly in the first place, we have no hope at all of making a prediction based on past events.
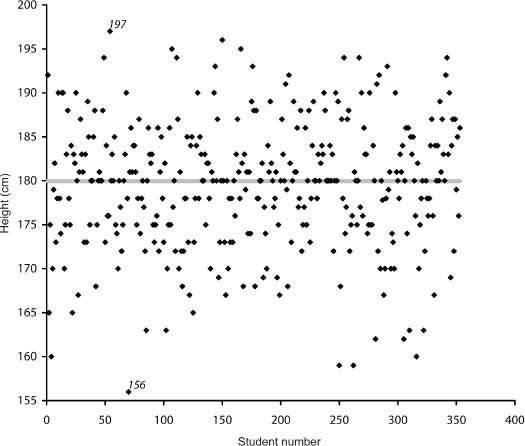
At this point, it’s time to meet the third author of this book (who likes to sing, but only in the shower). Some people collect stamps or antiques, which is strange enough, but he collects data on the heights of male MBA students at INSEAD, the international business school with campuses in France, Singapore and Abu Dhabi. In his defense, it must be stressed that he uses this unusual collection to illustrate the notions of pattern and noise in his decision science classes. Figure 11 shows the heights of the 353 men in a recent MBA intake, displayed in random order. Each dot represents the height of a student. Clearly, there is a great deal of variation in size – between the shortest guy at 156 cm (5 feet 1 inch) and the tallest at 197 cm (6 feet 6 inches). Perhaps if we had some other information, such as the heights of each individual’s parents, we could explain some of this dispersion either side of the average, which is represented by the solid line through the middle of the graph. But this is all the data we have. So, if someone asked you to predict the height of a single student from this intake (without looking at him), your best chance of getting closest would be to suggest the average: 180 cm to be precise. As it happens, not only are most of the dots on the graph close to this line, but there are more dots actually on it (49 of them) than any other horizontal line you could plot. Another way of thinking about this is that the line representing the average is the pattern, while the heights – both above and below – are the noise.
Figure 11 Heights of 353 male MBA students
As it happens, the professor of decision sciences has been collecting the heights of male MBA students at INSEAD for quite some time. He now knows that the average changes very little from year to year. It’s always pretty close to 180 cm, which we can use as a good approximation to the overall average. Suppose you’re now asked to predict the height of a man in next year’s class. You don’t know anything about him that might possibly help you – for example, his nationality or favorite sport. So your best bet will definitely be 180 cm. In making this prediction, you know you’ll probably be wrong. In fact, looking at the amount of “noise” in the past gives you an idea just how wrong you can be. But if you make this same prediction for each of the students in next year’s intake, your average error will be smaller than if you repeatedly made any other estimate.
Let’s complicate matters now. Figure 12 shows the sales figures of a company – we’ll call it Acme, as in the best cartoons – over the last twelve months. We ask you to take a look at it and forecast sales for the next three months.
Figure 12 Sales of Acme
What have you concluded? First of all, it’s clear that this graph is very different from the previous one. Second, we have so little information that it’s hard – if not impossible – to distinguish pattern from noise. Perhaps the company sells ski-wear, accounting for its increasing sales from March to December. Or maybe it launched a new gadget in September, which has had great reviews and is going to turn Acme into the next Apple. Alternatively, it’s possible that Acme is in one of those niche markets, where it’s quite hard to find any kind of pattern and sales tend to fluctuate radically just by chance. Third, we have no idea what’s going on in Acme’s market as a whole. It could be that a competitor contributed to the ups and downs on the graph or even that there was some entirely external problem beyond anyone’s control, like a worldwide widget shortage. All in all, predicting Acme’s sales for the next three months is nowhere near as simple as predicting the height of an INSEAD MBA student.
The problem – as Herbert Simon taught us on page 197 – is that we humans are “programmed” to see patterns and, although this is a highly functional skill, it can also be dysfunctional if we see a pattern where there isn’t one. Psychologists call this “illusory correlation” and it’s amplified by human frailties, such as wishful thinking (or self-promotion). Product managers, for instance, want their sales to increase, so are susceptible to seeing illusory growth trends (or pretending that they can). But – once again – there’s a second kind of error too, namely, not being able to see a pattern that does exist. This can be just as serious as the first.
To illustrate, consider two purely statistical types of pattern that we could plausibly find in Acme’s sales chart. The first pattern is one of continued growth in sales starting from March. The second shows a flat level of sales across time. Both patterns are shown in figure 13 – along with their implied forecasts for the next three months.
The difference between the forecasts is enormous. Predicted sales for next March are 1,296,303 units based on the exponentially increasing pattern and 439,250 based on the flat, average pattern. This huge difference illustrates the significant challenges facing forecasters – and the senior executives to whom product managers report. Fortunately, in most situations there would be a few more clues than we’ve given you here. Meanwhile, in the case of Acme, it might be safer not to conclude anything for now.
Figure 13 Sales of Acme (with trend lines)
Identifying and extrapolating a relation between two variables is much like finding patterns in sets of data. If we want to figure out the relation between the demand for a product and its price, we need to be able to observe how demand changes under different price levels. However, what we observe also includes “noise,” which we have to isolate before we can identify a causal relation. For example, we might reduce the price and sales might increase for several months in a row. But how do we know this is really due to the reduction? The increased sales could be the result of seasonal fluctuations or, worse, chance factors that we can’t identify at all: in other words, noise. The challenge is to isolate the noise and identify the true relation – without falling prey to false optimism.
As with predicting patterns, it turns out that simple methods of identifying and estimating relations between variables are at least as accurate as large, complex models. Indeed, extensive empirical research has shown that – just like human beings – statistically sophisticated methods find illusory patterns or relations that don’t exist. Returning to Acme’s sales projections for the next three months and figure 13, our more complex forecast shows phenomenal growth. The flat line of the average, however, doesn’t extrapolate any pattern and just steers a non-committal conservative course. But maybe the latter is a little too simple. A slightly more elaborate method is “single exponential smoothing.” (If you remember, it’s the simple statistical tool that did so well in the author’s forecasting competitions.) We needn’t be concerned with exactly how it works, but figure 14 shows the result it gives for Acme’s next three months of sales (alongside the other two forecasts).
Figure 14 Sales of Acme (with single exponential smoothing)
Although single exponential smoothing recognizes that sales vary a great deal over time, it also acknowledges that part of such variability is noise and should be ignored. Thus, the pattern it identifies is close to the average and less likely to make a large error if the increase in sales over the last few months was due to chance. On the other hand, single exponential smoothing also suggests there’ll be a slow increase in the sales pattern over the next few months. So, if the last three months weren’t a freak occurrence after all and sales were indeed increasing in a systematic way, the company would be prepared and have enough stock. Everyone’s a winner this way. The product manager and salespeople keep their self-esteem intact and senior management can be cautiously optimistic. If the increase turns out to be greater than expected, it’s a nice surprise all round. But if things take a turn for the worse and sales start to slump, at least there’s not too much excess stock hanging around in the warehouse.
Søren Kierkegaard, the Danish philosopher, once wisely said, “Life can only be understood backwards; but it must be lived forwards.” Like it or not, this sums up a key element of the human condition. What we achieve in the future depends on decisions that we take in the present. And the only basis we have for making those decisions is what happened in the past. This throws up two key problems – and it’s worth looking at them separately. First, is our understanding of the past correct? Second, what assurance can we have that the future will be like the past? Let’s use two examples to examine both questions: one fictional story from the world of business and the other from real-life meteorology.
Megabucks Retail Inc has collected a vast array of data on its past performance over many years. The company’s executives have thus established three empirical regularities. One, sales are 15% higher on Saturdays than the average weekday. Two, sales have grown at a rate of 5.5% a year for the last five years. And three, the Christmas season accounts for 18% of annual sales. It seems reasonable to assume that managers can extrapolate from these data to predict sales for next Saturday, next Christmas, and the whole of next year. As well as finding these patterns, the executives have gone one step further. They’ve experimented for a long time with their pricing strategies and found some interesting relations between the variables of price and demand. On one product range, for example, they’ve noted that if the price decreases by 5%, demand increases, on average, by 7.5%. Having established this relation, the statistically savvy execs can then manipulate demand by increasing or decreasing the price.
Has the Megabucks management understood the past correctly? Well, their accounts of the past certainly seem to make sense. Best of all, they’ve kept it simple (perhaps for the benefit of their bosses) and not tried to go into too much detail. However, most people prefer a story that explains 80% of what happened in the past, as opposed to 50%. The 80% version of events will be much more interesting and comprehensive as stories go, with intricate patterns of interwoven causes and effects. The problem is that the 80% will almost inevitably include noise, as well as the pattern. So the story won’t be as accurate a predictor of the future as the simpler account. In other words our natural tendency to seek a “complete” explanation for past events can blind us to what’s really important: namely, how well our explanation forecasts the future.
Now let’s imagine that a global business magazine commissions a hot-shot financial journalist to write a feature on Megabucks. She sets to work in December, notes that sales have been falling over the last nine months, and starts to dig a little deeper. All that stuff about the Christmas period is well known, but – frankly – who wants to read about that? So instead the journalist concocts an epic saga of boardroom tensions, supply-chain fiascos, and exchange-rate time-bombs. The editor likes the piece so much that he puts it on the cover and goes to print in January trumpeting the company’s impending fall from grace. Unknown to the publishers, Megabucks decides to release its final quarter’s results a week early. The news of their 15% upturn in sales compared to the same period last year breaks the day before the magazine comes out. The editor loses his job and the journalist’s reputation is ruined to the point that she’s forced to take a job in corporate communications. It’s no consolation that all the stories in the article were true and that they had indeed helped to account for lower than expected sales during much of the year. But fortunately for Megabucks, they’d sorted out the problems and got themselves back on track for a better Christmas than ever.
Statistics is strangely like story-telling. Statistical forecasting methods analyze available data to identify established patterns or relations. This is analogous to someone like a financial journalist coming up with a great story to explain past economic events. Our empirical research, which has covered thousands of data sets over the last three decades, shows that the more sophisticated the statistical method, the better it fits with past data. By contrast, simpler methods don’t do so well and fail to account for up to 50% of the data. However – and here’s the important point – there is no correlation between how well methods explain the past and how accurately they predict the future. Past patterns and relations change continually – sometimes temporarily, sometimes for good. In addition, new events occur and new conditions arise to shape a future that’s very different from the past.
To illustrate, let’s move on to our second example: weather forecasting. Thanks to satellite imaging, meteorologists can easily identify weather patterns by comparing photos taken over time. Typically they might track a low-pressure system bringing rain from, say, the south and calculate that it will arrive in your town in two days’ time. So why did it turn out to be a blazing hot, sunny day? The problem is that weather systems don’t always stay on the same course. A new high-pressure system can develop and stop, cancel, or modify the progress of the low-pressure one. That’s why, no matter how expert they are and how many supercomputers they use, meteorologists can never be sure what the weather will do. The future isn’t always a continuation of the past, no matter how well we’ve understood it.
To sum up, the more complicated an explanation, the less likely it is to replicate itself in the future. Simpler accounts have the advantage of staying closer to the average, underlying pattern or relation. They don’t miss the wood by obsessing about the trees. Similarly, complex statistical forecasting methods “overfit” the available data and find pattern where there’s actually noise. But that’s not the only problem. Søren Kierkegaard and the world’s best meteorologists all show us that the future is hardly ever just like the past.
As we’ve seen, averaging the predictions of several people or models results in more accurate forecasts than if we relied on a single person (even an expert) or method (even the most statistically dazzling). This is a well-established empirical fact.9 And the explanation is straightforward. The data we observe consist of a combination of underlying patterns plus noise. The big contribution of averaging is to cancel out the noise. Whereas some noise distorts the pattern in one direction, other noise distorts in other directions. In the process of averaging, the distortions cancel each other out and reveal the underlying shape. Figure 11 (the graph of students’ heights) is a good illustration of how averaging filters out the “noise” (that is, extreme variations in heights) to reveal the underlying “tune” (the straight horizontal line that most usefully represents the observed data).
To demonstrate further how averaging eliminates noise, imagine playing a game that involves estimating the value of a jar full of pennies. This is the modern equivalent of Galton’s fairground ox, updated to avoid any cruelty to animals or messy slaughtering and skinning. It’s a great favorite at school fetes, along with raffles, cake stalls, and performances of choirs like Miss Johnstone’s. According to the rules of the game, you’re allowed to take a good look at the jar before estimating how much money it contains. Just as in Galton’s original game, the closest guess to the actual amount in the jar wins the game. Now, if each player assesses the value of the jar independently of the rest (that is, no one is influenced by anyone else’s guess), it is highly likely that some will underestimate, while others will overestimate. Many of these guesses will be wildly out, and thus constitute the noise, while others will be much closer to the real amount in the jar, forming a distinct pattern either side of it. By taking the average of all the guesses we get quite close to the true value, because the wild guesses – and even some of the more reasonable ones – will cancel each other out.
Time and time again, it’s the crowd who really wins guessing games like these. In fact, the average estimate is nearly always more accurate than the single guess that wins the prize. The crowd is so reliable that several companies have started to use the average opinion of their employees to predict the sales of new products and services. This innovative approach is known as “Prediction Markets” and has worked well for the likes of Google, Yahoo, and other high tech firms. The difficulty, however, is that it’s difficult to keep employees’ judgments independent of each other as they talk and interact with each other.
The importance of independence suddenly becomes clear when we change the rules of the pennies-in-the-jar game. If we start showing some players the results of all previous guesses, the average estimate will wander further and further from the actual sum in the jar. For averaging to retain its power, it’s important that the different errors of prediction are entirely unrelated. In technical jargon, this is known as the “independence assumption.” As an extreme example, imagine three financial analysts at the same investment bank, who study the same company. They base their opinions on the same information provided by the company, analyze the same data about past earnings per share, read the same industry reports, drink water from the same fountain and wine from the same bar. Given that they frequently pick each other’s brains and say more than they meant to, it’s highly unlikely that they’ll come up with independent estimates of future earnings per share. If one of them overestimates, it’s likely the others will too – which means that the average will also be an overestimate.
On the other hand, consider three doctors examining the same patient. They’re all different ages, have trained in different medical schools, and use different procedures. Though they work in the same city, attend the same cocktail parties, and happen to share a passion for ballroom dancing, they’re bound by an ethical code of patient confidentiality. The errors in these physicians’ judgments are likely to be independent. The “average” of their opinions is likely to be close to the truth. Now you know why, in chapter 3, we were so insistent on getting a second – or even third – opinion.
Fortunately, the number of people or models required to improve a forecast doesn’t have to be large. Five to seven people, and an even smaller number of between two and four models, are typically enough to block out the noise and come close to the underlying pattern or relation. Better still, it’s possible to combine the forecasts of human judgment and statistical prediction, to generate a “super-average” that exploits the advantages of both while minimizing their drawbacks. But it remains critical that the inputs of these people and models are as independent of each other as possible.
So is averaging the goose that lays the golden eggs of prediction, the fairytale ending we’ve been searching for? Sadly, no. Averaging improves the accuracy of forecasts but it offers no guarantees. Alas, you cannot get rid of the inherently unpredictable nature of the future. Your only option, we remind you, is to embrace the uncertainties it holds.
How much would you be willing to pay for a tulip bulb? Would you be willing to exchange a medium-sized house for one? Although the last question seems crazy, it was actually taken seriously in the Netherlands 370 years ago, during the great tulip mania. In 1636, at the height of the frenzy, some rare bulbs were valued at astronomical prices, in some cases costing more than houses in the center of Amsterdam. During the mania, many people made huge fortunes buying and selling tulip bulbs. Within a period of less than a year, bulbs originally worth only a few guilders soared in value, as demand skyrocketed and supply failed to keep up. Finally, when the bubble burst and prices returned to pre-mania levels, there were a handful of big winners – the people who had got out in time – and many, many losers. Those who’d bought bulbs, often selling or mortgaging their property in the belief that prices could only go up, found themselves financially ruined. All they had left was a worthless bunch of tulip bulbs that nobody wanted.
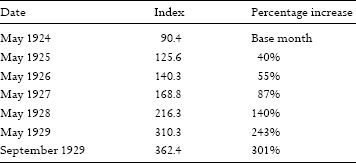
The tulip mania wasn’t a one-off event. There have been many similar incidents throughout history and throughout the world. Nor is the phenomenon confined to the distant past. In May 1924, the value of the DJIA (Dow Jones Industrial Average) index was 90.4 points. Three months later, it had increased by 15%. From May 1924, values and yearly increases for the next five years were as shown in table 12.
These figures tell the story of a growing collective madness every bit as insane as in seventeenth-century Amsterdam. As we saw in chapter 4, the inevitable crash began in September 1929. The DJIA plunged from its peak of 362.4 to 64.1 in April 1932, less than three years later, losing 82.3% of its value. If you’d invested $10,000 across DJIA companies in September 1929, you’d only have had $1,770 to show for it at the lowest point of the Great Depression.
Table 12 Evolution of DJIA: May 1924 to September 1929
If the Great Depression still seems too much like history, take note that the infant twenty-first century has blown two small bubbles that have already burst. The NASDAQ crash of early 2000 turned dotcoms into the tulip bulbs of the present day. The really spooky thing is that the rise and fall of the NASDAQ in the 1990s and 2000s followed a remarkably similar pattern, over the same number of months, to the DJIA back in the 1920s and 1930s. Using almost none of the statistical trickery at our disposal, we’ve plotted the two indexes very simply in figure 15.
This is one pattern that would be nice to dismiss as noise. It suggests some kind of innate tendency to self-destruction that makes human beings the financial equivalent of lemmings. Fortunately for us, however, there was a lot less of our global wealth tied up in the NASDAQ of 2000 than in Wall Street seventy years earlier. Even more fortunately, figure 15 reveals that, once the bubbles broke, both the DJIA and NASDAQ indexes returned to their previous levels – it’s as if nothing had happened. Indeed, if you’d been marooned on a desert island from 1924 to 1932 or meditating in a Tibetan monastery from 1994 to 2002, you would have noticed no great change in the various stock market values on your return to so-called civilization.
Figure 15 DJIA and NASDAQ: relative monthly values starting May 1924 and October 1994
Just as we thought it was safe to go to press with our historical examples, the “subprime” and credit crisis broke and we got that déjà vu feeling again. A story that began with a bunch of low-earning borrowers in the US finished up rocking the entire world’s financial markets. If the story has slipped your memory already, because some new investment scandal has usurped it, we’ll remind you. Rising US house prices fueled a boom in “subprime” mortgage lending, which is another way of saying that high-risk borrowers started to get loans that banks should never have given them. The various financial institutions and investment banks repackaged those loans several times over and sold them on to other financial organizations and investment banks. The bonds that the dodgy loans morphed into didn’t look particularly risky once the financial wizards had worked their magic – and indeed they were as safe as houses so long as property prices kept on rising and the new homeowners were making their repayments. But of course, there’s no such thing as big gains without big risk. When the borrowers started to default, houses were no longer safe. Property prices plummeted, major banks and financial institutions fell, and tremors were felt all over the world as investors feared that the entire financial system was going to collapse. Another bubble had burst with catastrophic negative consequences in terms of financial and job losses. Well, the crisis will pass and calm will eventually return. The problem is that no one can tell how long it will take to return to normality. And worse, we don’t know when the next financial crisis will hit, because – despite the overhaul of the financial system announced by different governments – further similar crises will still occur.
So much then for the great power of averaging. Where money is concerned, the wisdom of crowds turns into madness time and time again. But why does averaging fail in the case of bubbles? Again the answer is simple, but this time it’s rooted in evolutionary psychology, rather than statistics. Of course, it’s true that human beings like to be unique. Some men own drawers full of novelty ties, while many women possess hundreds of pairs of designer shoes. For these people it can be a disaster to show up at a party where some other guest is wearing the same kipper tie or identical stiletto mules (and much worse if the same person is wearing both). But even individuals who like to be different have a conformist side. Novelty-tie man wants other people to get the joke. And designer-shoe woman is determined to be in fashion. Deep down within us there is a herd instinct, based on a time when togetherness was essential for survival in an environment full of physical threats. Even today, it helps us with team work and provides a valuable sense of community.
Uniqueness boosts independence and promotes variety. Herd behavior demands conformity, generates similarity, and kills diversity. Whatever its benefits – historical or current – the pack instinct defeats the power of averaging. In the case of Galton’s ox, no guess was influenced by any other. But the responses of the vast numbers of people who found out from the TV and newspapers that the NASDAQ was doubling, tripling, and then quadrupling in value were anything but independent. Many people felt left out of the big game that was making everyone else get rich quick. Finally, after the market had been increasing for many years, they felt safe to join in . . . and ended up getting poor quicker.
You can’t blame them, though. Such a response is part of the natural herd instinct we all share. It’s when independence ends and pack behavior starts. It fuels irrational bubbles and ultimately leads to prices so unsustainable that the only rational option is to deflate them.10 The trouble is that the herd instinct kicks in again, turning rapidly to a stampede. Rather than gently deflating, the bubble bursts with a loud pop that echoes throughout the world’s economies. It’s a sound as unwelcome as a certain author trying to sing.
Can you discern that precise moment when independence ends and herd thinking begins? If so, you can exploit the pros of both while steering clear of their cons. We wish we could tell you how to do it. But, to hark back to chapters 4 and 5, it’s impossible to get your timing perfect and sell at the top (except by luck or illegal practices). The intellectual difficulties are compounded by the emotional. Greed may interact with the hope that the bubble can last longer and the fear of losing out by selling too early.
However, we’re beginning to get ahead of ourselves here. For now, we’ll go back instead to a possible course of action that we mentioned briefly in chapter 5: the “contrarian” strategy, which involves doing the exact opposite of the herd. Many stock market gurus have built their reputations in this way. They do brilliantly when bubbles burst – in fact that’s when most self-styled contrarians come out of the woodwork. Assuming they were already contrarians when the bubble was building up, it’s not surprising that we heard nothing from them, as they would have been losing money surely and steadily. If the strategy is applied consistently, it works well when the market is doing badly, and badly when the market is doing well. Ultimately, it’s bound to lose over time, because – as we’ve seen before – the market is headed upwards in the long run. Worse still, there’s nothing independent, big, or clever about contrarianism. Because it’s all about systematically doing the exact opposite of the herd, contrarians are absolutely reliant on what everyone else is doing. Whether they like it or not, their behavior is intimately related to that of the pack – albeit in an inverse manner.
We don’t deny that some people or funds that are quite contrary have gardens that grow abundantly. It’s true that they do better than the market on occasion. But as a consistent, long-term solution to financial bubbles, it’s definitely not an option.
In this chapter, we’ve continued to stress how both statistical models and human judgments have limited ability to predict future events. Even when we correctly manage to discern patterns and relations in past events, there’s no guarantee that the future will be the same as the past. In those cases where past and future are symmetrical, averaging and other simple kinds of modeling help – up to a point – as they cancel out “noise.” But in many real-life situations (like investing) it’s almost impossible to achieve the independent thinking required for averaging to work.
Having said all that, some events in the domain of social sciences are surprisingly predictable – even if they’re not always the most interesting ones! For example, we can forecast with amazing accuracy how many people will travel on the London Underground during weekday rush hours, how many cars will cross the George Washington Bridge to enter Manhattan on a Monday morning, and how many people in France will be eligible to receive a pension five or ten years from now. In other words, when forecasting concerns a large number of events (such as people’s actions) and the patterns or relations that link them don’t change across time, predictions can be accurate. Under these conditions, the accuracy of socio-economic forecasting is similar to that of the “hard” sciences.
Unfortunately, the fact remains we can’t predict most events of interest (and potential profit). In this book we’ve focused on medicine, investments, and management, but there are many other areas where accurate forecasting is nigh on impossible. Even hard science sometimes fails. Despite vast arrays of satellite images and supercomputers, meteorologists can’t tell you if it’s going to rain in a week’s time with any certainty. The big question is therefore: how can we take important decisions when we know that we cannot forecast the future accurately?
The next chapter looks more closely at the nature of uncertainty and offers practical advice on how to assess it more realistically. We also, uncharacteristically, reveal a golden rule for predictions. Don’t expect any huge surprises, however. So often in life the answers to our questions have been staring us in the face for a very long time. Indeed, several decades after being coerced into the school choir by the redoubtable Miss Johnstone, it suddenly dawned on the author who (still) can’t sing why she was so keen for him to join in. As it happens, he wasn’t the only kid with a lousy voice – far from it – but the choir sounded really quite good. Even he could hear that. You see, as a musician, Miss Johnstone instinctively understood the power of averaging. As long as the main tune (or pattern) was not too difficult, she knew that the bad voices (or noise) would cancel each other out. The small boy with freckles in the back row, on the other hand, would need years of study and specialization in decision sciences to discover the music of noise.