
A blocker in volleyball needs to be able to perform a large number of repeated vertical jumps without tiring. How can we determine whether training improves the jump height-to-energy cost ratio?

By the end of this chapter you should be able to:
•Define and calculate the quantities of work, power and energy
•Explain the concept of efficiency, with examples from sport
•Develop tests to measure work, power, energy and efficiency and use these to optimise athletic performance
Work
To jump, a volleyballer must apply a force against the ground. This force is applied while the feet are in contact with the ground as the body is raised against gravity. The amount of work done is equal to the average force that is applied (F) multiplied by the distance over which it is applied (d) (see Figure 9.1). Work (W) = F·d. You might normally use the word ‘work’ in the context of working in the garden or doing homework (so you might feel pain at the sight of the word) but in mechanics ‘work’ has a specific meaning: it is often called ‘mechanical work’, to differentiate it from other forms.
Several forces might act at any one time. If two equal but opposite forces are applied to a stationary body, no work is done because the sum of forces is zero (that is, if ΣF = 0 then W = 0, since W = F·d). If one force is greater than the other, then the work done is equal to the total (i.e., the resultant) force multiplied by the distance over which work is done. If there is no movement, no work has been done.
FIG. 9.1 The work done during a vertical jump is equal to the average force multiplied by the distance (dCM) over which the body’s centre of mass moved. Note, however, that there is no force applied while the jumper is airborne, so no work is done by the jumper even though the centre of mass is moving (work is, of course, done by gravity while the jumper is airborne because the gravitational force is applied while the jumper moves over a distance).
You can calculate, for example, the work done by a weightlifter lifting a weight from the floor to a standing position (deadlift), as in Figure 9.2. Notice that the units are not newton-metres (Nm) as you might expect from the equation but joules (J) – 1 Nm equals 1 J. This is helpful because torque is measured in Nm and it could get a bit confusing. In case you’re interested, the unit is named after James Prescott Joule (1818–1869), an English physicist and brewer who, without a formal education or academic position, completed pioneering works on the work–heat relationship (mechanical equivalence of heat; remember from Chapter 4 that the unit name is not capitalised even though the person’s name is).
FIG. 9.2 The work done during a lift is equal to the work done to lift the bar plus the work done to lift the body. If we assume that both the bar and centre of mass of the lifter moved 40 cm (0.4 m) and that the average force measured via a force platform was 800 N, then we can calculate the work done:
W = F·d
= 800 N × 0.4 m
= 320 N·m, or 320 J
The concept of work is important in sport because we often need to manipulate it. For example, rugby players might apply a large force over a great distance to push an opposing player backwards during a ruck or tackle. Rowers apply a force against the oar over a large distance in each stroke and swimmers apply forces over a large distance during their stroke. The greater the total work done the better will be the performance. Muscles also perform work, because they apply a force as they shorten (or lengthen) over a given distance.
In the ‘clean’ movement in weightlifting (Figure 9.3), the lifter has to pull the bar rapidly upwards and then, at some predefined moment, drop quickly under the bar to allow a second lift while the bar is resting across the shoulders. If the lifter performed work in the first part of the lift but the bar velocity was zero at the end of it, then the bar would fall towards the ground as soon as the lifter stopped doing work on the bar. If the lifter is to have time to get under the bar, the bar needs to keep moving upwards after the work is done. As you saw in Chapter 3, the higher the bar velocity, the longer it will take for gravity to slow it and then re-accelerate it in the negative, or downward, direction.
FIG. 9.3 In order to increase the upward speed of the bar to have more time to drop under it during the clean movement, a lifter has to apply a force that results in a large power output. Power can be calculated if force and velocity are measured, or if work (force and distance) and time are measured. For example, if the average force was 1500 N, and the bar was lifted 0.5 m in 0.2 s (i.e. velocity = 2.5 m·s-1):
Power = F·v Power = F·d/t
= 1500 N × 2.5 m·s-1 = 1500 N × 0.5 m/0.2 m·s-1
= 3750 W = 3750 W
If we apply a force (F) to a bar that attains a velocity (v), the bar has power (P); P = F·v. At any instant, the greater the force, or the faster the velocity, the greater the power. You know that velocity is equal to distance divided by time (v = d/t), so we can say that power (P) = F·d/t. Remember that F·d is work, so power is the amount of work performed in a given time, or the rate of doing work. You might also notice that we need to apply a greater force to accelerate the bar to a greater velocity, so work (F·d) is also increased; it is, however, not increased in the same ratio as power. Power is increased when we do a given amount of work in less time or we do more work in a given time. Increasing power results in an increase in the velocity of an object, as long as its mass remains constant. This is important for weightlifters, as it is for a volleyballer trying to attain a high velocity to jump into the air.
Notice that in Figure 9.3 the units of power are not Nm·s-1, which might have been confused with an angular quantity – that is, torque/time, Nm/s – but are watts (W). A watt is equivalent to the production of one joule of energy per second, and is named after James Watt (1736–1819), who was a Scottish inventor and engineer best known for his work on improving the steam engine, which was a key innovation allowing for the industrial revolution.
Energy
To jump high, the volleyballer has to perform a greater amount of work, or attain a higher power output, but they need to repeat such jumps many times in a match. That is, he or she needs to perform a lot of work with little energy cost. How can we quantify that?
Two forms of energy are important here: mechanical energy and metabolic energy. Mechanical energy is the energy associated either with an object’s movement (kinetic energy) or its position (potential energy). Kinetic energy (KE) is the energy associated with motion, so in a linear sense an object with a greater mass or velocity has a greater energy: KE = ½ mv2, where m is the object’s mass and v is its velocity. You can see that an increase in mass has less effect than an increase in velocity (i.e. the v is squared), so faster-moving objects have a far greater kinetic energy. If we produce a greater power and therefore an object or body attains a higher velocity, it will have more kinetic energy. Kinetic energy can be calculated as shown in Figure 9.4. The units of energy are joules (J): that’s right, the units are the same as for work, and you’ll see why a little later.

FIG. 9.4 When the shot-putter released the 7.26 kg shot, it had a velocity of 18 m·s-1.
= ½ mv2
= 0.5 × 7.26 × 182
= 1176.1 J
If the mass of the shot was reduced by 10% (to 6.53 kg) but was thrown with the same velocity, the KE would be 1057.9 J, which is 118.2 J or 10% less.
If the mass of the shot was not changed, but the shot was thrown 10% slower (16.2 m·s-1), the KE would be 952.7 J, which is 223.4 J or 19% less. So altering the velocity has the greatest impact on KE.
The other form of mechanical energy is potential energy (PE), which is the energy associated with position. Think of a rock at the top of a cliff (Figure 9.5); if it were to roll off the cliff it would fall with a velocity, that is, it would have kinetic energy. While it is stationary at the top of the cliff, it has the potential to gain kinetic energy. The distance over which gravity has the chance to accelerate it dictates the velocity the rock will attain if it falls. The higher the cliff, the greater the velocity the rock would attain before it hits the ground, that is, the greater the kinetic energy it would have. So its potential energy is also greater. PE = mgh, where m is the object’s mass, g is the acceleration due to gravity and h is the height of the object at any given time. A falling object has both kinetic and potential energy at the same time (see Figure 9.5), so its total energy is equal to the kinetic energy plus the potential energy (Etotal = KE + PE).
|
Height |
PE = mgh |
KE = ½mv2 |
TE = PE + KE |
3 m |
29.4 J |
0 J |
29.4 J |
|
2 m |
19.6 J |
9.8 J |
29.4 J |
|
1 m |
9.8 J |
19.6 J |
29.4 J |
|
0 m |
0 J |
29.4 J |
29.4 J |
FIG. 9.5 When it falls, a rock that was sitting at the top of a cliff has potential energy. It gains kinetic energy as it falls but loses potential energy. The total energy of the system stays constant (KE + PE = c, where c is a constant). This is called the law of conservation of energy. In this example, a 1 kg rock falls 3 m.
Kinetic energy (KE) = ½ mv2
Potential energy (PE) = mgh
Total energy (Etotal) = KE + PE
You might have used this idea of increasing potential energy to crush a drink can or box. To crush an object, we need to transfer energy to it. If we jump in the air we increase our potential energy. When we land on the can or box, we will have a greater kinetic energy. We transfer this energy rapidly (with high power) to the can or box to crush it. There are many sporting uses too.
Efficiency is the ratio of energy output to input, for any system. To improve jumping efficiency, not just jump height, we need to increase the output (kinetic energy, resulting in greater jump height) while decreasing the input (the energy required to jump). The power that we used to jump comes from muscle contraction. Muscles consume energy through a series of metabolic processes (metabolic processes are those that occur in a cell or organism that are necessary for life). This energy is therefore called ‘metabolic energy’. The efficiency of a jumper will be increased if they produce a greater kinetic energy output for a smaller metabolic energy input. How do we measure these energies?
Efficiency is improved when the energy output increases relative to the energy input
One way to measure the energy of a jump is to measure the work put into it. It’s difficult to measure work but we can measure the jumper’s mass and their velocity at take-off in the jump ... see if you can follow the next passage to see why this is helpful.
Remember, from Chapter 3, that v2 = u2 + 2as. In a vertical jump, the velocity after we lower our body but before we start to jump upwards is zero (since u2 = 0), so v2 = 2as and therefore a = v2/2s. You might also remember that F = ma, so if we put in our other version of a (that is, v2/2s) we get F = mv2/2s. We multiply each side of the equation by s to give Fs = mv2/2, or Fd = ½ mv2.
F·d = work, so the left side of the equation is ‘work’; ½ mv2 is kinetic energy. That’s right, effectively work = kinetic energy, or we can say that a moving object’s energy is equivalent to the work done on it. It now hopefully makes sense as to why work and energy are both measured in joules! This is often referred to as the work–energy relationship.
To measure the energy of a volleyballer, we need only measure their work, which means measuring the forces and the distance over which the forces are applied. If we had an expensive force platform this would be easy. Can we measure it another way?
If we use a standard video camera or a jump (timing) mat to measure the flight time of the volleyballer, we can measure their jump height and/or take-off velocity. If we have their velocity and we know their mass, we will know their kinetic energy at take-off for each jump. We can use v = u + at (since v = 0 at the top of the jump, u = -at, where t is the time to reach the top of the jump, or half of the total flight time as you might measure it) to estimate the velocity at take-off. You can measure the volleyballer’s mass using ordinary bathroom scales (mass is measured in kilograms) and therefore calculate their kinetic energy. Because you want to calculate the average kinetic energy in a number of jumps, you might want to set up a spreadsheet that calculates kinetic energy from body mass and flight time to make things easier.
You might be thinking: ‘I’ll never be able to work the maths to find these things!!!’ Don’t worry. As long as you understand the principles, you will be able to play around with the maths later. Those of you who have learned a foreign language will know that you need a lot of time and practice before you can easily re-arrange the first phrases you learned to express other ideas and thoughts. It’s no different with the language of mathematics.
Measuring metabolic energy
Measuring kinetic energy is easy enough. How about metabolic energy? Cells that convert energy use oxygen, so the more oxygen we use the more metabolic energy we must be producing. We can measure oxygen consumption in a physiology laboratory relatively easily using a gas (oxygen and carbon dioxide) analyser but what if we don’t have one? Happily, there is a reasonably strong relationship between heart rate and oxygen consumption; the more oxygen we use, the faster the heart rate. This is because we need to take more oxygen to the cells, so we need to pump more blood. The only problem is that everyone has a different heart rate response to exercise, so the only real way to know the relationship is to test it in a laboratory. However, there is a strong relationship between oxygen consumption and the heart rate reserve (HRR) or at least, between the reserve to supply more oxygen (called the VO2max reserve, which is the difference between current oxygen consumption and the volume of oxygen consumption at maximum) (Swain & Leutholtz, 1997).
To measure HRR, first determine the resting heart rate, such as after sitting quietly for ten minutes or on first waking in the morning. Then determine the heart rate after maximum exercise exertion, such as after running as fast as possible for 20 s four times with 20 s of recovery between each repetition. Finally, calculate the current (exercise) heart rate, as a percentage of the difference between the resting and maximum heart rates:
%HRR = (HRcurrent – HRresting) / (HRmax – HRresting) × 100
If a volleyballer had a heart rate of 140 beats per minute (bpm) after a series of twenty maximum vertical jumps (HRcurrent), a resting heart rate of 60 bpm (HRresting) and a maximum heart rate of 180 bpm (HRmax), their %HRR would be:
%HRR = (140 – 60) / (180 – 60) × 100 = 67.7%
This suggests that they are using oxygen at about 68% of their maximum ability.
THE ANSWER
Kinetic energy is the energy associated with velocity of our body and can be measured from video or by using a timing mat. The heart rate reserve tells us a lot about how much oxygen we are using. We can therefore examine the KE:%HRR ratio to see if we have been able to increase jump performance while minimising energy cost (that is, maximising efficiency). This is shown in Figure 9.6. If you change the volleyballer’s technique to improve efficiency or give them a period of physical training to increase their fitness, they might perform the twenty jumps with the same average kinetic energy but at a lower %HRR. In that case, the athlete would be more efficient. At best, you would want the athlete to jump higher (that is, move at a higher velocity and therefore attain a higher KE) and have a lower %HRR after the jump series. That would mean the athlete was both functionally better and more efficient. So the ratio of KE:%HRR is a good performance indicator.
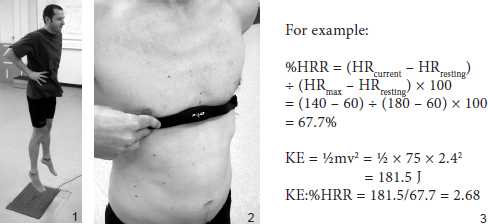
FIG. 9.6 Calculation of the efficiency of a jumper. (1) Measure kinetic energy during a series of vertical jumps. (2) Measure heart rate during the jumps, and measure both the resting and maximum (e.g. obtained during a repeated maximal sprint test) heart rates of the jumper. (3) Calculate the heart rate reserve (HRR) and then the jumper’s kinetic energy as a percentage of HRR.
HOW ELSE CAN WE USE THIS INFORMATION?
You could use this information for any athlete who performs repeated jumps, such as a basketball player or a netball player. However you could also calculate the average kinetic energy of a runner over a given distance (for example a 60 kg runner running 5 km at an average speed of 14 km·h-1 (3.89 m·s-1): KE = ½ mv2 = 30 × 3.892 = 454 J) and measure their %HRR at the end of the run (for example 78%), giving a ratio of 454/78 = 5.8 J per %HRR.
Most importantly, you should consider how an understanding of work, power, energy and efficiency could help you improve performance in many different sports. During lifting, throwing or kicking you might want to increase power output at the expense of efficiency. However, swimmers and rowers, for example, will aim to increase their power output while improving efficiency.
Useful Equations
speed = ∆d/∆t
velocity (v) = ∆s/∆t (rω for a spinning object)
acceleration (a) = ∆v/∆t
torque (moment of force) (τ) = F × d, where d is the moment arm of force
Also τ = Iα
work (W) = F × d
power (P) = F × v or W/t
kinetic energy (KE) = ½ mv2
potential energy (PE) = m × g × h
total energy (Etot) = KE + PE (plus rotational energy if present)
Reference
Swain, D.P. & Leutholtz, B.C. (1997). ‘Heart rate reserve is equivalent to %VO2 reserve, not to %VO2max’. Medicine and Science in Sports and Exercise, 29(3): 410–14.
Related Websites
ZonaLand: National Science Teachers Association (http://zonalandeducation.com/mstm/physics/mechanics/mechanics.html). Clear descriptions and animations of the basic principles of mechanics.
The Physics Classroom – Tutorials (http://www.physicsclassroom.com/Class/). Lessons on basic physics concepts.
The Physics Classroom – Multimedia tools (http://www.physicsclassroom.com/mmedia/). Interactive tools and movies depicting basic physics concepts.
The Physics of Sports (http://www.topendsports.com/biomechanics/physics.htm). Website investigating the applications of physics in sports.
INTERVIEW WITH THE EXPERTS
Steve Backley wins his fourth consecutive European Championships gold medal in Munich, 2002.
Biomechanist:
Name: Calvin Morriss
Nationality: British
Born: 26 July 1969
Athlete Biography:
Name: Steve Backley
Nationality: British
Born: 12 February 1969
Major Achievements:
•Four times world record holder, javelin
•First British athlete to win consecutive medals at three Olympic games in any athletic event (two silver, one bronze, 1992–2000)
•Four consecutive European gold medals
•Personal best 91.46 m
When and how did you use biomechanical analyses or theories to optimise Steve’s training? What were the results of the changes made based on these analyses or theories?
I worked with Steve from 1990 to 2004 and, as one would expect, the nature of the biomechanics support changed during this time. In the early years, we mainly completed 3-D analyses in a competitive setting. The idea was to establish exactly how Steve threw when under competitive pressure, and to develop an understanding of how he applied force to the javelin with his particular throwing technique. With regard to specific examples of how biomechanical analyses shaped the support offered to Steve, here are three:
•Steve picked up two serious injuries in 1992, a shoulder and right thigh adductor injury. These problems meant that Steve had to adapt the way he threw to remain competitive in 1993–94. By 1995, however, he was throwing poorly and in a different manner than before his injury in 1992. By comparing the results of biomechanical analyses that we had conducted prior to 1992 to those through 1993–95, we were able to develop a very clear understanding of the problem. From this, the support team were able to plan a course of technical change through the off-season in 1996. Steve won a silver medal in the Olympic Games in 1996, and his throwing technique, we were able to establish, had returned to what it had been pre-injury in 1996. It was a very successful intervention.
•Steve had exploratory surgery on an Achilles tendon problem. I spoke with the surgeon and explained that during his final foot plant, the angle at the ankle was approximately 135° (i.e. plantar flexed). The surgeon was able to place Steve’s left ankle in this position under anaesthetic, and in this position, a heel spur that encroached on the Achilles tendon was identified. It was removed and rehabilitation was successful.
•A detailed analysis of Steve’s technique demonstrated that shoulder adduction, medial rotation and elbow extension were all key contributors to the achievement of high release speeds. This information was critical in designing bespoke conditioning programmes for him.
How do you think Steve’s career might have been different had you not changed his training/technique?
I think Steve will have been successful regardless of the support he was offered due to his excellent ability to manage himself, and his competitive abilities. That said, the biomechanics support enabled him to make considered and very definite decisions about his throwing technique and his training. I think that it is as important for an athlete to believe in their training as it is to actually do the training. The biomechanical analysis undoubtedly helped develop this confidence and belief. I also think the analysis demonstrated what Steve’s throwing action required from his body, which certainly helped to direct his conditioning programmes. Steve had a particularly long throwing career and I believe that some of this was due to the way in which he trained for his event.
What were the strong points (both personally and intellectually) of the best biomechanists you worked with?
The best biomechanists that I worked with all had a very strong grounding in mechanics – there was never an element of doubt in what they reported, and they never expanded beyond what their data told them. Dr James Hay was a shining example of this type of successful biomechanist. The best support biomechanists that I worked with also had very strong work ethics. It takes time and energy to provide athletes and coaches with good data to work with, and much of the work must be done in unsociable hours.
Overall, how important do you feel a good understanding of biomechanics is to a coach or sports scientist?
Quite simply, I think it helps coaches and athletes to make informed and definite decisions about their training methods. A biomechanics understanding of movement helps to separate fact from what sometimes people would like to believe is true.