
How do we produce forces sufficient to jump to heights greater than our standing height? What factors do we have to optimise to maximise jump height?

By the end of this chapter you should be able to:
•Recite Newton’s laws of motion and use them to explain force production during a variety of sporting movements
•Determine the optimum force magnitude and direction combinations for different sporting tasks, including jumping
•Explain the effect of body mass on jumping performance
•Show an understanding of scientific notation
The Ancient Greeks were a very inquisitive bunch, whose philosophy led them to spend time observing, thinking and discussing, rather than experimenting. Aristotle, when he asked himself ‘what is the natural state of an object, if left to itself?’, postulated a simple answer: since every object he observed generally came to rest, every object’s natural state was to be at rest. More recently, about 400 years ago, Galileo asked himself the same question. But remember from Chapter 3 that he tried systematically to prove or disprove his hypotheses by experiment. Through careful experiments, Galileo found that objects with a very low air resistance continued to move almost indefinitely when on almost-frictionless surfaces. He realised that if the objects could move in conditions where there was no air resistance or friction, they would never stop! So every object’s natural state was ... to be. If an object were moving it would continue to move and if it were stationary it would stay, unless of course a force acted upon it to change that state (see Figure 4.1).
FIG. 4.1 Newton’s First Law. This tennis ball, when travelling through space with no air resistance or friction acting on it, will continue with the same velocity (speed and direction) until acted upon by another force. This propensity is called inertia (I).
Unfortunately, Galileo’s experiments were constrained only to movements on horizontal surfaces. In the seventeenth century, Newton generalised the results to all motions in all planes. From his work, he formulated three laws of motion.
Newton’s First Law states:
An object will remain at rest or continue to move with constant velocity as long as the net force equals zero
The propensity for an object to remain in its present state is called inertia: this law is therefore often referred to as Newton’s Law of Inertia. All objects with a mass have inertia, and the larger the mass the more difficult it is to change the object’s state of motion; I α m, or inertia (I) is proportional to (α) mass (m). For example, a large truck has large inertia because it has a large mass, so it is more difficult to speed up, slow down or change its direction. An important thing to remember about this law is that it uses the term ‘velocity’, not ‘speed’. So objects not only continue at their present speed but also in the same direction (the velocity is zero if the object is stationary).
So, if we want to jump higher, we need to work out how to change our state from rest (or in the case of a high jump, from a constant horizontal running velocity) to vertical motion. The first clue is given by Newton’s Second Law:
The acceleration of an object is proportional to the net force acting on it and inversely proportional to the mass of the object: F = ma
If we want to change the state of motion of an object, we need to apply a force. (Force is measured in newtons (N), in his honour; notice though that the unit does not have the ‘n’ capitalised but the unit abbreviation does? This is standard for all units that are named after a person.) Since mass is measured in kilograms and the acceleration due to gravity is equal to 9.81 m·s-2, the force on a 1 kg ball would be 9.81 N (or approximately 10 N) since F = 1 kg × 9.81m·s-2. We call this the weight of the ball (mass is the amount of matter in an object; weight is the effect of gravity on that matter). On Earth, as a rule of thumb, you can estimate an object’s mass by dividing its weight by 10; an 800 N person would have a mass of about 80 kg. On the moon, where gravity is about 1/6 of that on Earth (1.6 m·s-2), the 80 kg person would have a weight of 128 N.
What does the formula F = ma really tell us? It tells us that the lighter the object is the faster it will accelerate when a force is applied, or that less force will be needed to cause a given acceleration. The lighter a person is, the more they can accelerate their body under a given force, which is very helpful in activities involving running and jumping where the body is projected upwards against gravity. F = ma also tells us that to accelerate an object faster we need to apply a bigger force to it. How can we apply this force to ourselves? Do we ask someone else to apply it for us? The answer is in Newton’s Third Law:
For every action, there is an equal and opposite reaction
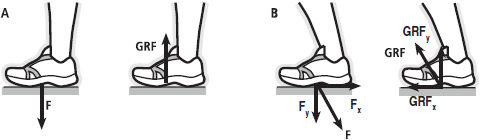
FIG. 4.2 Newton’s Third Law. A vertical (downward) force is applied when the foot contacts the ground (A). The ground exerts an equal and opposite reaction force, in this instance called the ground reaction force (GRF), which stops the foot sinking into the Earth.
During running and jumping, we apply a force with both vertical (Fy, force in the y-direction) and horizontal (Fx, force in the x-direction) components (B). The ground exerts an equal and opposite GRF, which can accelerate us forwards if the force is large enough to overcome our inertia. (Be aware: some people assign these Fy for horizontal and Fz for vertical.)
Notice the arrows indicate the magnitude (length of arrow) and direction (direction of arrow) of the force vectors, as you learned in Chapter 2.
When you fire a gun, the bullet is projected forwards and the gun is thrown backwards with an equal and opposite force – it is said to ‘kick’. For us, this law means that if we apply a force against something that doesn’t move (that is, the force isn’t strong enough to overcome its inertia), the object will exert an equal and opposite reaction force against us. This reaction force is important for two reasons. First, to have the greatest force applied to us, we need to apply the greatest possible force against that object. Second, if we need the force to accelerate us in a specific direction, we need to produce it in a very specific, and opposite, direction.
One question we need to answer is: against what do we apply our large and well-directed force during a jump? In general, we would apply it against the Earth (Figure 4.2). Provided that the Earth’s surface is solid and doesn’t flex under our force, it exerts an equal and opposite force every time we exert a force against it. Since F = ma, our mass (m) is accelerated (a) at a rate proportional to the force – but so is the Earth. Every time you push against it to jump, you change its orbit slightly!
By how much does it move and why don’t we notice it? The mass of the Earth is about 6 × 1024 (6 000 000 000 000 000 000 000 000) kg. (If you’re unfamiliar with scientific notation, see Box 4.1.) If you could produce a force equal to 2000 N (about 200 kg force), which is about as much as a grown adult would produce if they performed a two-legged vertical jump, you would accelerate the Earth by 0.000 000 000 000 000 000 000 33 (3.3 × 10-22) m·s-2, which is imperceptible. You might want to stick to trying to move mountains!
We kick the Earth and it kicks back; but because we are so small, we are the ones who go flying through the air. To be kicked doesn’t sound like fun but that’s how we move. When we walk, run or jump, we apply a force against a relatively immovable Earth but it applies an equal and opposite force to move us.
There’s one more thing we need to realise in order to optimise jump height. The lighter you are, the more you would accelerate for a given force (F = ma). This is even more important when we move vertically, because we are affected by gravity. In addition to his three Laws of Motion, Newton also posited a Law of Gravitation:
All bodies are attracted to each other with a force proportional to the product of the two masses and inversely proportional to the square of the distance between them:
F = Gm1m2 /r 2
where G is a constant (6.67 × 10-11 N·m2·kg-2), m1 and m2 are the masses of two objects and r is the distance between the two objects (that is, radius)
And no, Newton didn’t come up with his Law of Gravitation after being hit on the head by an apple, but he did remark that his idea ‘was occasioned by the fall of an apple’. It was another Briton, Robert Hooke (regarded as the greatest experimental scientist of the 1700s, because of his huge contribution to fields of science from meteorology to mechanics – Newton has been charged with taking many of Hooke’s ideas for his own!), who first suggested that the planets might be attracted to the sun with a strength proportional to their masses and inversely proportional to the square of their distances but he never applied his idea to objects on Earth.
The law of gravitation is useful, because it shows us that gravity will have less influence if the product of two masses is smaller. The mass of the Earth is unchanging, so if we reduce the mass of a body, it will be influenced less. That is, the gravitational force is less when we are lighter. The net force causing acceleration in the upward direction is equal to the upward reaction force plus the downward gravitational force: remember, the downward force would be assigned a negative value because it acts downwards (see Chapters 1 and 2). As you can see in Figure 4.3, if the force of gravity is smaller, then the net force will be greater.
FIG. 4.3 Effect of mass on acceleration against gravity. These two cannons both release a mass of air with a constant force (Fair) of 2000 N. The cannon on the left shot a ball weighing 70 kg so the gravitational force (Fg) equals 683.9 N. The total force then is 2000 + -683.9 = 1316.1 N and the ball therefore accelerates at 18.8 m·s-2 (a = F/m). The ball shot from the cannon on the right hand side is 80 kg, encounters a force of gravity equal to 781.6 N, a total force of 1218.4 N and accelerates at 15.2 m·s-2. The lighter shot accelerates 23.7% faster than the heavier shot. Note: the force of 2000 N is similar to the peak forces reached during a vertical jump, and the masses are common for humans.
Figure 4.3 shows balls being fired vertically from two cannons, which apply a constant force of 2000 N (conveniently, this is roughly the force exerted during a vertical jump). The cannon on the left shot a ball weighing 70 kg (conveniently, this is approximately the average mass of a person). Gravity exerted a force equal to:
Gm1m2/r2 = 6.67 × 10-11 · 70 · 6.0 × 1024/(6.4 × 106)2
= 2.8 × 1016/4.1 × 1013
= 683.9 N
where G is a constant, m1 is the mass of the ball, m2 is the mass of the Earth and r is the radius of the Earth – we assume this is constant while the ball is so close to the Earth’s surface, because a movement of a few metres is nothing compared to the radius of the Earth. The gravitational force is therefore 683.9 N. The total force on the cannonball is 2000 + -683.9 = 1316.1 N and the ball therefore accelerates at:
a = F/m
= 1316.1/70
= 18.8 m·s-2
The ball shot from the cannon on the right hand side is 80 kg (about the size of a slightly larger man) and encounters a force of gravity equal to 781.6 N, a total force of 1218.4 N and accelerates at 15.2 m·s-2.
Assuming the cannon were able to apply its 2000 N force for one second, the lighter and heavier balls would be at speeds of 18.8 and 15.2 m·s-1 (v = a × t), respectively. (Question for you: How long would it have taken for the winner to travel 1 m?). The lighter shot accelerates 23.7% faster than the heavier shot. For comparison, the balls would accelerate at 28.6 and 25.0 m·s-2 if shot horizontally (I’ll leave you to check this), so the lighter shot would accelerate 14.4% faster. The additive effect of a heavy mass moving against gravity is substantial. So by being lighter, we end up with a greater net force accelerating us upwards!
We encountered a similar problem as we raised the projection angle of our shot in Chapter 3. We should remember that the mass of an object is also important in horizontal motion. An object’s inertia is proportional to its mass, so heavier objects require a large force to accelerate. However, the effect is amplified when an object moves vertically because of the effects of gravity. In the sporting context, we need to be more mindful of mass when moving vertically. Since we also project ourselves into the air when we run, we could also say it is important to be light. In endurance running events, when there are a large number of steps taken and we project ourselves slightly vertically each time, we use a lot of energy just getting ourselves airborne. So endurance runners would also benefit significantly from having a lighter body mass.
THE ANSWER
In summary, we’ve learned that to jump to greater height, we need to overcome our inertia (Newton’s First Law) by having a force applied against us (Newton’s Second Law, F = ma). To do this, we apply a large and well-directed force against the Earth, which applies an equal and opposite reaction force back against us (Newton’s Third Law). Since the sum of forces dictates our acceleration and the force of gravity acts downwards (Newton’s Law of Gravitation), it is very important to produce large vertical forces, or have a lower body mass, to jump very high. Optimising each of these components is important for obtaining maximum jump height; although we will learn a little more in the following chapters.
HOW ELSE CAN WE USE THIS INFORMATION?
While it might seem a simple concept that producing forces in a specific direction is important for sporting success, too few athletes and coaches consider how to optimise force production. Foremost in your mind must be the questions: how do we produce our forces and in what direction should we apply these forces for acceleration in the direction desired?
BOX 4.1 LARGE AND SMALL NUMBERS
The Universe is an amazing place. Some objects are so small that we can’t see them even with the most powerful microscopes and some are so big that we can’t see to their ends with the largest telescopes.
It is easy to say something is 1 m long but how do we describe the size of the Milky Way? It is approximately 946 000 000 000 000 000 km in diameter. It can be very difficult to comprehend such numbers. So we use scientific notation for these very large and very small numbers, whereby the diameter of the Milky Way is 9.46 × 1017 km.
Every number has a base and an exponential component. The exponential is always in superscript, for example the number ‘17’ above. The base number is always between 0 and 10, for example 9.46. Essentially, the base gives quantity and the exponent tells us how many zeros (multiples of ten) would be written after the base if we wrote the number out in full. This is much easier both to write and to understand the magnitude of. Clearly, a number with 17 zeros is very large indeed.
The same notation is used for very small numbers, except that the exponential tells us the place of the first part of the base number after the decimal place (in other words, how many zeros there are between the decimal point and that number). The thickness of a human hair is about 2 × 10-8 m or 0.00000002 m (the ‘2’ is the eighth number after the decimal place). Here are some other examples:
Mass of a hydrogen atom = 0.000 000 000 000 000 000 000 000 001 673 (1.673 × 10-27) kg
Mass of a dust particle = 0.000 000 000 753 (7.53 × 10-10) kg
Diameter of a golf ball = 0.042 (4.2 × 10-2) m (that is, 4.2 cm)
Mass of an African Elephant = 7000 (7 × 103) kg
Number of stars in the Milky Way = 300 000 000 000 (3 × 1011)
Mass of the Earth = 6 000 000 000 000 000 000 000 000 (6 × 1024) kg
Occasionally, numbers are written as 4.2 × 10^2 or 4.2E2. The ^ symbol (or exponentiation symbol) means ‘raise the base number to the power of x’ and is the same as writing the number in superscript – so 10^2 is the same as 102. (This notation comes from the early days of computer programming languages.) ‘E’ means the same thing: ‘multiply by 10 to the power of x’ – so 4.2E2 is the same as 4.2 × 102.
You might consider, for example, that in swimming we need to produce some downward force to lift the body slightly in the water (we’ll discuss this in more depth in Chapter 15) while maximising horizontal force production. In rugby we often pass the ball with horizontal force to project it, but also with spin to improve its aerodynamics (you’ll learn about this in Chapter 16). In tennis we often spin the ball to change its trajectory (see Chapter 16), so we must consider the need for horizontal ball velocity and the need to place spin on it. A final example is that in sports such as golf, cricket, baseball or softball and field or ice hockey, we hit balls using a technique in which the body rotates as we swing (we’ll learn more about this in Chapter 17) even though we need to impart a forward, linear velocity on the ball or puck. How do we optimise rotation of the body but maintain a forward motion to optimise horizontal ball/puck speed and improve accuracy? The answer is that we need to test ball or puck accuracy and velocity as we ask the athlete to manipulate the relative amounts of rotational and forward velocity until he or she reaches an optimum. In this sense, the job of the coach or biomechanist is to determine each player’s optimum technique.
Useful Equations
speed = ∆d/∆t
velocity (v) = ∆s/∆t (rω for a spinning object)
acceleration (a) = ∆v/∆t
inertia = mass
convert m·s-1 to km·h-1: x m·s-1 /1000 × 3600
convert km·h-1 to m·s-1: x km·h-1 × 1000/3600
Related Websites
ZonaLand: National Science Teachers Association (http://zonalandeducation.com/mstm/physics/mechanics/mechanics.html). Clear descriptions and animations of the basic principles of mechanics.
The Physics Classroom – Tutorials (http://www.physicsclassroom.com/Class/). Lessons on basic physics concepts.
The Physics Classroom – Multimedia tools (http://www.physicsclassroom.com/mmedia/). Interactive tools and movies depicting basic physics concepts.
Newton’s Laws of Motion (http://www.mcasco.com/Physics-1/p1nlm.html). Complete and interactive website exploring Newton’s laws.
The Physics of Sports (http://www.topendsports.com/biomechanics/physics.htm). Website investigating the applications of physics in sports.