
If, after making the changes shown in Chapter 14, we find that swimming time improves but is still not as good as those of other swimmers, can we improve our swimmer’s propulsion as well?

By the end of this chapter you should be able to:
•Explain the importance of drag and lift forces in swimming propulsion
•Describe the theoretically optimum propulsive technique with respect to the production of drag and lift
•Explain how lift is generated in swimming (and on other objects in sport) with reference to Newton’s laws and the Bernoulli effect
Swimming performance is dictated both by the forces resisting motion (drag) and those assisting motion (propulsion). In this chapter, we will learn about the forces assisting motion to see if we can further improve swimming technique.
Force production in swimming
According to Newton’s Third Law (action–reaction), to move forwards in the water we need to apply a backward force to it, so we could describe swimming in terms of an action force and a reaction force. However, as the aim of swimming is to move through the water more quickly, it is actually the amount of force per unit of time – power – that is important, so we should probably discuss swimming in terms of an action power and a reaction power. Unfortunately, the ‘reaction power’ is not quite the equal and opposite of the ‘action power’ in swimming. Why?
Water is not a solid, so it moves when we apply a force against it. Therefore, some of the power is used to induce movement in the water rather than to propel a swimmer forwards. The trick to swimming propulsion is to increase the amount of reaction power for a given action power; this is called ‘propulsive efficiency’. In good human swimmers, propulsive efficiency is about 80%; that is, 80% of the power or energy goes into moving the swimmer and 20% to moving the water. There are several ways we can manipulate a swimmer’s stroke to improve propulsive efficiency but first we have to understand how we propel ourselves.
Drag effects
Over half a century ago, swimmers were taught to keep their arms straight during the propulsion phase in front crawl swimming. The predominant theory of the 1960s was that an opposing drag force acting on the hand and arm was the major force of propulsion. The drag on the hand and arm opposed their movement through the water and provided the swimmer with a forward-directed (anterior) force (Figure 15.1). Thus, the drag force acted like a handle on which the swimmer could pull. If we could follow the tip of the fingers through the propulsive phase of the stroke, they would almost draw an ‘I’ shape, so this type of stroke is very similar to what we now refer to as the ‘I-shaped’ stroke. In fact, such a stroke also causes small circulations of water (vortices) to develop around the hand and arm, and their rotational speed (i.e. angular momentum) and position around the hand and arm impact on the drag forces produced.
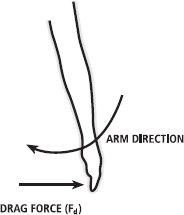
FIG. 15.1 A drag force acts on the hand in the direction opposite to the arm movement.
To increase drag, swimmers need to increase the surface area of their hand and arm. This is accomplished partly through the use of a relatively straight hand and arm path and is improved by slightly spreading the fingers. As fast-moving water flows into the hand, some will pass around it, while some will attempt to pass between the slightly spaced fingers. When the volume of water moving through the fingers reaches a critical level, its flow is impeded. (Imagine a large number of people trying to get through a door at the same time.) Since the water is effectively ‘stuck’ between the fingers, the total surface area of the ‘fluid-stopping’ hand is increased. The greater surface area causes an increase in drag and improves propulsion. Taller swimmers, who might also have longer arms and larger hands, would be able to create greater drag forces, which perhaps is of benefit to them.
Lift effects
There is little debate that a significant drag force acts on the hand and arm but visual inspection of the hand and arm paths of top swimmers of the 1960s revealed a significant ‘S’ (sigmoidal) shape, as shown in Figure 15.2 (Brown & Counsilman, 1971; Counsilman, 1971). Such a movement is called ‘sculling’, and this swimming technique is often called the ‘S-shaped’ stroke. While the benefit of sculling was difficult to explain at first, it was eventually hypothesised that this propulsion method allowed the generation of a lift force that could improve swimming propulsion; this lift force is affected by the development of vortices around the hand and arm, although we won’t delve into the physics of vortices here. Importantly, as the hand moves laterally through the water, its slight tilt or pitch towards the oncoming water causes it to act like an aerofoil or aeroplane wing (Figure 15.2). The lateral movement of the hand creates lift on the palm of the hand, on which the hand can ‘pull’. Also, the phase of the stroke during which the hand changes direction, for example from out-sweep led by the small finger to in-sweep led by the thumb, contributes to the increase in lift force generation (largely due to its effects on vortices, e.g. see Takagi et al., 2016). So the ‘S’ shape provides conditions in which lift forces can contribute additionally to the drag forces to generate propulsive force. Coaches now often teach swimmers to use a more curved hand path. The amount of lift is increased as the size of the hand increases, so swimmers with larger hands (usually taller swimmers) and those who use a slight spacing of the fingers are able to produce greater lift forces.
FIG. 15.2 The hand moving laterally through the water acts much like an aerofoil, creating a lift force directed upwards into the hand (A). The lateral movement of the hand occurs when a swimmer uses a sculling arm action (B). This is done as the outstretched propulsion arm is brought first towards the midline of the body (medial movement) as the hand and arm swings down through the stroke, and is then brought away from the midline (lateral movement) later in the stroke.
To understand how lift is generated, see ‘Special Topic: The Development of Lift in Fluid Environments’. Since many explanations of lift are wrong, this section is worthy of a close read. Understanding lift could help you improve performance in a variety of other sports. However, for now, we will move on and consider more theories of swimming propulsion.
A re-analysis of the hand path: drag forces are more important?
The hypothesis that both lift and drag forces produced through a curved hand path accounted for the propulsive power in (crawl stroke) swimming was prominent until perhaps the early 1990s. However, there seemed to be a discrepancy between the impulses predicted from models of lift and drag and those measured during swimming. Complicated biomechanical analyses of the top swimmers in the early 1990s (e.g. Cappaert, 1993; Cappaert and Rushall, 1994) also seemed to show that these swimmers adopted a straighter hand path than expected and that drag forces contributed much more than lift forces to swimming propulsion (except in the breaststroke). In fact, the hands of good swimmers tended to ‘scull’ relative to the body because the body rolls a little during the stroke, but the hand path through the water was in fact relatively straight. That is, if we watched only the swimmer’s hand relative to the pool surrounds, it would move essentially in a straight line.
This makes sense given that the large surface area of the hand is ideally suited to produce drag forces and also that any lateral movement of the hand to generate lift forces will also create a drag force that’s perpendicular (90°) to the hand direction, thus wasting energy. It also makes sense from a basic efficiency point of view because, in order to reduce the energy cost of movement, we normally want to increase the proportion of the total force that moves us in the desired direction and decrease the proportion that would move us otherwise. When watching the best (i.e. most efficient) crawl stroke swimmers, you will notice that their hand moves largely in a straight line through the water with little lateral or other movement, although there is still clearly a slight ‘S’ shape. That is, they try to ‘catch’ or ‘grab’ the water and then move their body in a straight line past the hand with only small re-orientations of the hand relative to the water during the stroke.
This straighter hand path has another benefit. As the forward propulsive force in crawl stroke swimming actually comes from the water reaction force (remember Newton’s laws, where our backwards force causes a forwards, propulsive, reaction force), a torque is developed at the shoulder joint that we must overcome. To overcome this torque, we use muscle forces. However, an increase in muscle force production will also cause more fatigue. Therefore, we have to consider how to reduce the shoulder torque while still applying a large force to the water.
The best way to do this is to reduce the moment arm of this torque (remember, torque = force × moment arm). In this case, the moment arm is approximately the distance between the hand (assuming most force is produced here) and the shoulder joint. By keeping the hand closer to the shoulder we reduce this distance, and thus reduce the shoulder joint torque for a given hand force. By moving the hand approximately in a straight line, we not only produce forces that are directed in the more appropriate direction for forward swimming propulsion but we also ensure that the hand stays closer to our body (and shoulder) rather than moving deeper into the water during the stroke, and thus further from the shoulder. Compare the hand and arm position, and the elbow angle used to attain it, in Figure 15.3, to the diagram in Figure 15.2 to see how to keep the hand closer to the shoulder (i.e. to reduce the moment arm). This is sometimes referred to as the ‘high elbow’ technique. Importantly, the hand still moves in a slight ‘S’ shape, so it is still referred to as the S-shaped stroke, but the lateral movement of the hand is relatively minor. This S-shaped technique, with only small lateral hand movement, is considered the most efficient method of crawl stroke swimming.
Fig 15.3 During propulsion in crawl stroke swimming the distance between the hand and shoulder (moment arm) can be reduced by flexing at the elbow. This also ensures that the hand travels in a straighter path from in front to behind the body, and that the water reaction force is directed forwards in the direction of travel.
The Bernoulli effect – benefits to faster swimming?
While the bent-arm, S-shaped technique (but with hand moving in a relatively straight line) is used most commonly during swimming, crawl stroke swimmers hoping to accelerate rapidly or swim at fast speeds (e.g. in sprint swimming races or in water polo) tend to choose a ‘straight arm’ technique where the tips of the fingers move straight through the water when viewed from above; the I-shaped stroke. This technique may not be as energy efficient, but may produce greater propulsive forces and thus swimming speeds. Why might it be adopted?
One theory is based on a very simple experiment, performed by Toussaint and colleagues (2002), which demonstrated the potential for the drag and lift forces to be increased through the Bernoulli effect when using this technique. Daniel Bernoulli was born in Groningen, in the Netherlands, in 1700. He was the first scientist to describe the relationship between fluid pressure and velocity. Bernoulli discovered that areas of high-speed fluid flow were associated with lower fluid pressure. The understandable assumption that faster-moving fluids develop higher pressure is not the case.
Think of a pipe with water flowing through it (Figure 15.4). As a mass of water moves through the pipe at slow speed, the moving molecules interact with the pipe’s surface. This interaction creates a pressure (that is, a force over a given area), because each molecule exerts a force when it collides with the pipe. The water speeds up as the pipe narrows, because the same mass of water must flow through this section of the pipe but less water can fit in at any one time (conservation of momentum). If the energy of the fluid is constant, its kinetic energy, and therefore velocity, must also be constant. The molecules therefore flow more in the direction of the pipe and have less opportunity to make contact with the pipe itself. Since there are fewer interactions, the molecules apply less force to the pipe wall. You could also visualise children running about in a large room, bumping their shoulders on the walls, and then running down a narrow hall; they will have less chance to bump into walls if they are concentrating on running quickly down the hall.
FIG. 15.4 Since the same quantity of water must flow at each point in the pipe, water flow at point A is slower than at point B. This allows the molecules to interact with the pipe and thus create a pressure. When the water moves faster, more of the speed of the water is directed along the pipe, so less interaction is possible and pressure is lower.
Bernoulli’s theory is based on the idea that the energy of a fluid is non-changing; its total energy is proportional to its kinetic energy, its potential energy and its pressure (see Figure 15.5). If its kinetic energy is increased (that is, its velocity increases) then its pressure must decrease, unless its potential energy is reduced, for example by the fluid running downhill. Bernoulli never stated that the faster flow causes the lower pressure, only that they tend to co-exist. For example, a drop in pressure at one end of the pipe would cause the water to speed up; either factor can cause the other.
FIG. 15.5 Bernoulli’s equation, where p is the fluid pressure, ρ (rho) is the fluid density, v is the fluid volume, and g and h are the gravitational constant (9.81 m·s-2) and height of the fluid, respectively.
The Bernoulli effect and swimming performance
As the hand moves through water, there is a collision of the water with the palm (ventral side) of the hand and therefore a force is directed into the hand; the pressure on the ventral side is therefore relatively high. A ‘hole’, or area of lower pressure, would normally form behind the hand. Since fluids will always flow from a region of high pressure to one of low pressure there should be a circulation of water from the ventral (palm) to the dorsal (back) side of the hand. In this case, there would be relatively high pressure on the ventral side of the hand and relatively low pressure on the dorsal side (see Figure 15.6).
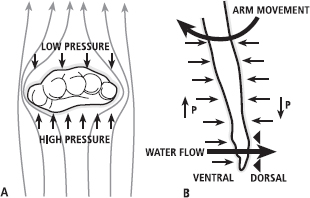
FIG. 15.6 As the hand moves through the water, a region of high pressure is created as water collides with the ventral (palm) side of the hand and arm while a region of low pressure forms on the dorsal (back) side (A). Water therefore flows rapidly to the back of the hand along the pressure gradient, although the rapid movement is associated with a further reduction in pressure, as predicted by Bernoulli’s theorem (B).
The same circulation of water should also occur around the arm but because the proximal part of the arm moves relatively more slowly (remember v = rω; see Chapter 2) the water moves around the arm more slowly and the pressure difference wouldn’t be as great. Therefore, there should be higher pressure on the dorsal side proximally at the arm compared to distally at the hand and the water will flow towards the hand along the pressure gradient (see Figure 15.7). This mass of faster-moving water should further reduce the dorsal pressure and allow greater lift (and drag) forces to be produced. So, the Bernoulli effect should theoretically aid swimming propulsion. Does this really happen?
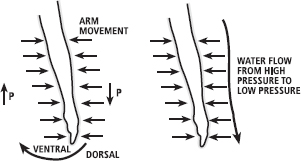
FIG. 15.7 As the pressure on the dorsal surface of the hand decreases more than that at the upper arm, water will flow from the top of the arm towards the hand along the pressure gradient. This further reduces dorsal pressures, increases the ventral–dorsal pressure difference, and increases the magnitude of the lift force.
The first, ingenious, way this was shown to occur was to place tufts of string on the arm of a swimmer and record the motion of the string (Toussaint et al., 2002). As the arm moves through the water – and the water therefore moves past the arm – the string on the back of the arm might be expected to stream away from the arm, as shown in Figure 15.8 (A). However, Toussaint found that the string was actually forced down on to the arm, as water flowed proximo-distally (from upper to lower) along the arm (Figure 15.8 (B))!
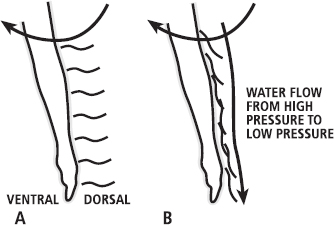
FIG. 15.8 As the arm moves through the water, string attached to the dorsal side might be expected to stream away from the arm, as it would if a wind rushed past the arm (A). However, because of water flow down the dorsal aspect of the arm, the string is forced down on to it (B).
Follow-up experiments corroborated these findings and revealed the magnitude of the pressure changes. They showed that even though the peak pressures of the ventral and dorsal sides of the arm decreased as swimming speed increased (this is to be expected, because water flows across both surfaces, so pressure will decrease as it flows faster), the ventral-to-dorsal pressure difference became greater as a result of the faster-moving water (Figure 15.9). This meant that there was relatively more pressure on the ventral side than the dorsal side, even though the pressure on each surface decreased. The swimmers weren’t swimming faster by applying more force with the front of their hands but by reducing the force produced at the back of them!
The use of a slightly straighter arm during swimming, which maximises the velocity difference between the upper and lower arms, causes a greater water shift down the arm and ultimately for greater drag and lift forces to be developed probably through a greater angular momentum in the vortices created around the hand and arm. Many swimmers use a straighter arm technique during fast front crawl swimming. Because the arm travels straighter through the water, the stroke is referred to as the ‘I’ stroke and it is considered to allow the fastest swimming speeds using the crawl stroke (for review, see Takagi et al., 2016).
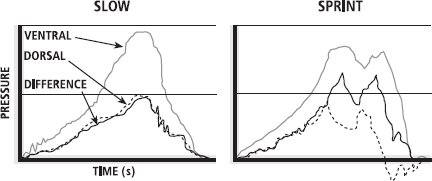
FIG. 15.9 Pressures measured on the ventral (palm) and dorsal (back) surfaces of the hand decrease as swimming speed increases from a slow speed (left) to maximal sprinting (right). However, the difference in pressure between ventral and dorsal surfaces (solid line) increases substantially as swimming speed increases. The resultant force is therefore directed into the ventral surface of the hand, effectively creating a ‘handle’ on which the swimmer can pull.
Use of other knowledge to improve swimming propulsion
Principles we learn in one context can often be applied in others. We have seen that minimising drag and improving propulsion can be achieved through modification of swimming technique but do we know how we can apply the propulsive forces more appropriately?
The swimmer will always produce some downward force, so we should consider that every time we apply a downward force to the side of the midline the body will tend to roll in the opposite direction. This is because we apply that downward force at a distance from the rotation axis of our body, creating a torque. Some body roll may be considered useful (see Chapter 14) but our ability to generate propulsion is lessened as we roll away from the hand. How can we apply an opposing force to minimise the rotation?
Probably the easiest way is to kick downwards, with an amplitude slightly greater than normal with the opposite (or the contralateral) leg, just as the arm begins its propulsive phase. The downward movement of the leg will tend to rotate the body in the opposite direction to the propulsion arm and minimise body roll. Then, instead of the propulsion force causing body roll, it can be used to accelerate the body upwards and forwards. A kick of larger amplitude will affect the drag force, as you learned in Chapter 14, so only the kick that is executed at the onset of the propulsive phase should have such a greater amplitude. The technique is probably most useful in sprint events where small energy losses are a reasonable trade-off for greater propulsive power, although it could also be used at the end (sprint phase) of longer events such as the 400, 800 and 1500 m. Of course, during ‘efficient’ (slower) swimming one uses a hand path with less downwards motion and more elbow flexion (high elbow technique), so there is less need for a large kick to balance to body.
One final point is that the forward acceleration of the body is proportional to the impulse provided, not the peak forces achieved. Longer strokes, which increase the time of force application, might thus be beneficial (∆Ft = ∆mv; see Chapter 5). In this sense, taller swimmers with longer arms might have an advantage, but stroke length can be improved by ensuring that the propulsive stroke begins with the arm well outstretched and ends with the hand leaving the water close to the hip (moving the hand further than this does not seem to aid swimming propulsion). Swimmers of all sizes should adopt this strategy, although it should be remembered that very long strokes (as well as very short ones) tend to be less efficient. For a good swimmer travelling just under 2 m·s-1 the optimum stroke appears to take about 1.3 s to complete (Takagi et al., 2016); testing of each individual is important to determine the optimum stroke length-stroke rate combination.
THE ANSWER
From a propulsion point of view, how can we improve the swimming time of a swimmer? It is important to note that there is no ideal swimming stroke that can be used for everyone; individual testing is needed to determine each swimmer’s optimum technique. However, there are several techniques that could improve swim time:
•The fingers of the hand should be slightly spaced, to increase the effective surface area of the hand and thus increase both drag and lift forces during propulsion.
•During the propulsive phase of swimming, when efficiency is important, the elbow may be flexed just after the commencement of the ‘pull’ in order to allow the hand to travel backwards in a relatively straight path. A small sculling motion of the hand is common (S-shaped stroke), and may increase the contribution of lift forces to propulsion or enable to hand to find still water.
•During high-speed swimming (such as that at the end of our swimmer’s 400 m race), swimmers may keep their elbow (and arm) straighter in order to increase the velocity of the hand relative to the shoulder (I-shaped stroke). This will increase fluid flow down the back of the arm and hand and increase the ventral-to-dorsal pressure differential. An increase in this differential will increase the force applied.
•During high-speed swimming, it might be useful to use a large single kick of the contralateral leg just after the start of the propulsive phase (before continuing the normal kick for the rest of the stroke) to prevent excessive body roll and allow effective force production. In slower, ‘efficient’ swimming the large kick is not as necessary because there is less downward movement of the hand and arm, and therefore less body roll to counteract. Also, wave drag is reduced at slower speeds, so the benefit of kicking from a wave minimisation point of view (see Chapter 14) is less.
•The stroke length of the swimmer is important, since the acceleration of the body in the water is proportional to the impulse provided. A longer stroke allows a greater time of force application and therefore greater impulse.
Optimising these techniques, along with those discussed in Chapter 14, should ensure significant improvements in swimming time.
HOW ELSE CAN WE USE THIS INFORMATION?
Much of what you’ve learned in this chapter can be applied to the performance of butterfly, breaststroke and backstroke. It can also be used to develop better methods for treading water in sports such as water polo, or to improve treading ability in lifesavers. The principles are widely used in the design of water craft; the keels of yachts and the underbellies of boats are designed for optimum lift and minimal drag. Furthermore, the principles of lift described in the Special Topic: The Development of Lift in Fluid Environments are applied to all manner of racing vehicles that use upside-down aerofoils to create a downward force and stability at high speeds and around corners (did you know that a Formula 1 racing car could drive upside-down at 160 km·h-1?).
Once you’ve read the Special Topic you’ll also understand better why there is an optimum tilt angle for implements such as the discus. Because the discus is essentially a flat plate, lift can be generated if it flies at an appropriate angle into oncoming air. You might think you should throw it so that it is inclined at an angle to the oncoming wind, at a positive angle of attack, but this is not the case. Remember, if you spin the discus about its longitudinal axis (like spinning it while it sits on a table) it will be more likely to remain stable in flight (see Chapter 13). We therefore project it into the oncoming air at an angle that will be maintained through the duration of the flight, so we choose a specific optimum angle.* With a positive angle of attack, the discus will create lift early in the flight but by mid-flight there will be a great deal of drag, which will reduce horizontal velocity (and, therefore, lift) and the discus will stall; that is, the lift force will tend to push the discus back towards you. This can be seen in Figure 15.10. If we orient the discus perfectly with the oncoming air, it will fly with little drag but also little lift until it reaches the top of its trajectory, at which time it will encounter significant drag.
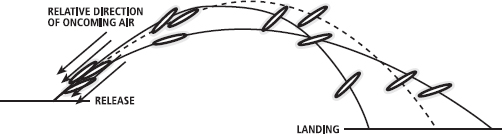
FIG. 15.10 Effect of angle of attack on discus flight distance. The discus with a negative angle of attack (lowest line) travels the greatest distance because this orientation maximises lift and decreases drag through the entire trajectory. Throws with a positive angle of attack (dotted line) may ‘stall’ as the drag force increases significantly in the downward phase of the trajectory.
The final option is to throw the discus with a negative angle of attack. Early in the flight there is some negative lift and a small amount of drag. However, the discus will then create lift as it approaches the top of its trajectory. On its way down, drag forces are smaller than in the other two conditions and some lift is still generated. Given that throwers propel the discus with a positive height of release, the object spends more time in the downward phase, so optimising this phase is more important. The idea that a negative angle of attack is best is corroborated by biomechanical analyses showing that elite throwers often use a negative angle of attack of between 10° and 20° (Terauds, 1978).
SPECIAL TOPIC: THE DEVELOPMENT OF LIFT IN FLUID ENVIRONMENTS
The principle of lift is used in many sports. It is important in swimming and other aquatic sports but also in the flight of projectiles such as the javelin, discus and rugby/American footballs.
How is lift created? There are generally two ways to understand it: (1) by considering Newton’s Third Law (action–reaction) and (2) by considering Bernoulli’s principle. Let’s start with Newton.
Newton did not describe the lift generated by an aerofoil, but his mathematics have been used to explain it. As air passes over an object capable of generating lift, such as the aerofoil (aeroplane wing) in Figure 15.11, the direction of the air is changed: it is said to be ‘turned’. Essentially, the angled aerofoil deflects a mass of air downwards. The air has changed velocity – it is accelerated. (Remember, velocity change occurs when either the speed or direction of an object is changed; in this case both the velocity and direction are changed). The movement of air downwards indicates that a downward force must have been acting, since F = ma. So, according to Newton’s Third Law, there must be an equal and opposite force simultaneously created. This is the lift force.
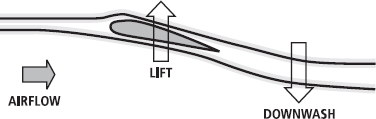
FIG. 15.11 An aerofoil ‘turns’ the air. Since a mass of air is accelerated downwards by the wing (i.e. a force acts: F = ma) there must be an equal and opposite force acting upwards on the aerofoil, according to Newton’s Third Law.
Advocates of this theory point to the existence of a large downwash of air seen behind the wings of aircraft in flight. The phenomenon can be described also from a conservation of momentum point of view; a mass of air is moved downwards so another mass must also be moved upwards to conserve momentum.
Bernoulli didn’t try to explain lift either but we can use his theories of pressure and velocity to explain the lift created by an aerofoil. As the air passes over the aerofoil, the air on the top surface accelerates, while the air on the bottom travels at a relatively slower speed (Figure 15.12). Since the area of fast-moving flow is associated with lower pressure, the region on the top of the aerofoil has lower pressure than the region on the bottom. The resultant pressure pushes the aerofoil upwards, i.e. a lift force is generated. Measurements of both the velocity of air and pressure distributions across a wing are in good agreement with this theory. However, some scientists warn that it is the low pressure caused by the turning of the air or the formation of vortices at the rear side of the wing (see below) that accelerates the air on top of the wing and not that an increased velocity causes a drop in pressure.
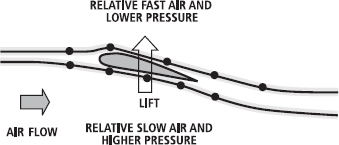
FIG. 15.12 Acceleration of the air on the top surface of the wing is associated with a lower pressure than the slower-moving air under the bottom surface; dots on the airflow lines show the paths of two particles that meet the aerofoil simultaneously. The pressure difference causes a resultant upward pressure, or force, called lift.
One question remains: how does the air on the top of the wing accelerate? There is still a lot that we don’t know about lift but one theory, well backed by experimental data, is that the tail (sharp) edge of the wing would normally hold a vortex or spinning mass of air as the air is turned by the wing (Figure 15.13). At the centre of the vortex is a region of low pressure into which air accelerates. Once the airspeed increases, the vortex is shed off the back of the wing and air flow becomes relatively stable. Of course, according to Newton, if there is a mass of air spinning in one direction there must be another mass of air spinning in the opposite direction. This is seen when air flow is measured around a wing.
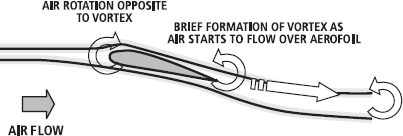
FIG. 15.13 As air starts to flow over an aerofoil, a vortex forms at the trailing edge. Air is accelerated to its centre, which is of lower pressure. The vortex is subsequently shed as the air rushes towards it. An opposite flow of air forms at the leading edge of the aerofoil to conserve angular momentum. The acceleration of air on the top surface is associated with lower pressure, which creates lift.
Both theories of lift are correct, because both explanations are essentially the same. Using Newton’s theories, an upward force is created when the wing turns the air downwards (i.e. a downward force is applied). Using Bernoulli’s theories, the wing turns the air to change its velocity to create regions of varying pressure resulting in an upward force. Both rely on changes in air velocity or a ‘turning’ of the air, either causing, or being caused by, a change in pressure. Essentially, lift is created when the air (or any fluid) is turned.
You may have seen or heard other explanations for the generation of lift and are wondering how those theories differ from the explanations above. There are three theories that are not completely correct (or not correct at all).
Incorrect Theory 1: Skipping stone theory
One theory is that the air touching the under-surface of an aerofoil creates an upward force creating lift (Figure 15.14). Since this is much like the force exerted by the water surface on the underside of a flat rock that is skipped across it, it is often called the ‘skipping stone’ theory.
Unfortunately, this theory neglects the fact that the air moving over the top surface contributes significantly to lift. It predicts that the shape of the top surface wouldn’t affect lift at all, which is incorrect; many aeroplane wings use spoilers to disrupt the air flow over the top surface of the wing to help manoeuvre the aircraft. It also doesn’t predict the lift encountered by symmetrical objects such as a flat plate (or spinning cylinders or balls that encounter an airflow equally on both top and bottom sides, as we’ll see in Chapter 16). While there might be some additional upward force provided by this mechanism, it is incorrect to assume that it explains the majority of the lift force.
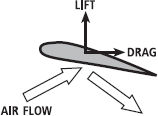
FIG. 15.14 It is incorrect that the main cause of lift is the Newtonian force generated by air hitting the underside of an aerofoil.
Incorrect Theory 2: Air accelerates over the top of the wing as the area for flow decreases
In this theory, movement of air well above an aerofoil is thought to act as a lid or immovable layer (Figure 15.15). Air passing just over the wing is forced through an area with a smaller diameter and must therefore speed up so that the same volume of air can pass. The increase in speed results in a decrease of pressure on top of the wing to create lift.
This theory is wrong on several counts. It neglects the fact that the underside of the wing contributes significantly to lift. If it were true, we could make the underside of the wing any shape we like without affecting lift. However, the shape of the underside significantly affects lift. It is also not true that air flow well above the aerofoil acts like a lid. If it did, then lift would be created if we oriented the aerofoil with a negative angle of attack, since this too would force air to move through a smaller area (Figure 15.15). If we did this we would actually create negative lift; that is, the wing would be forced down. Finally, it requires that the top side of the aerofoil is curved to decrease the area available for flow; however, lift can be generated well with a flat plate or with the flat wings of a paper aeroplane!
Incorrect Theory 3: Air accelerates as it takes a longer path across the top of the aerofoil
This theory is similar to Theory 2, except that the only requirement is that two particles starting at the front edge of the aerofoil but travelling along different path have to reach the back edge simultaneously (Figure 15.16). Since the particle travelling over the wing travels a greater distance when the top surface is curved, it must travel faster and pressure must decrease, according to Bernoulli’s principle.
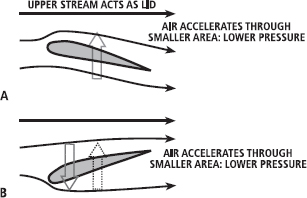
FIG. 15.15 It is incorrect that an upper air flow acts as a lid to reduce the area for flow over the aerofoil, which would increase its velocity and reduce its pressure (A). The easiest way to disprove it is to invert the aerofoil (B); there would still be a constriction that would increase the air velocity and create lift (dotted arrow) but, in fact, this orientation creates negative lift (solid arrow). In either of these two diagrams, the air could theoretically have formed a lid on the opposite surface of the aerofoil.
This theory again neglects the importance of the under-surface and requires that the top surface is longer than the bottom surface. These are clearly false. As you saw in Figure 15.12, the air travelling over the top surface actually reaches the trailing edge earlier. While the theory does explain that air moving faster over the top surface would generate lift, the mechanism by which it is proposed to occur is incorrect.
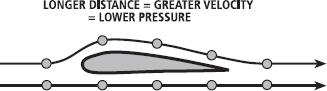
FIG. 15.16 It is incorrect to assume that two air particles that part at the front edge of an aerofoil travel to the trailing edge in the same time. As shown previously in Figure 15.12, air on the top surface reaches the trailing edge earlier.
Useful Equations
force of drag (form) (Fd) = kAv2 (or Fd = CdρAv2)
impulse (J) = F × t or ∆mv
References
Brown, R.M. & Counsilman, J.E. (1971). ‘The role of lift in propelling swimmers’. In: J.M. Cooper (Ed.), Biomechanics, Chicago, Illinois: Athletic Institute, 179–88.
Cappaert, J. (1993). ‘1992 Olympic Report’. Limited circulation communication to all FINA Federations. United States Swimming, Colorado Springs, Colorado.
Cappaert, J., & Rushall, B.S. (1994). Biomechanical Analyses of Champion Swimmers. Spring Valley, California: Sports Science Associates.
Counsilman, J.E. (1971). ‘The application of Bernoulli’s Principle to human propulsion in water’. In: L. Lewillie and J. Clarys (Eds), First International Symposium on Biomechanics of Swimming, Université Libre de Bruxelles, Brussels, Belgium, 59–71.
Takagi, H., Nakashima, M., Sato, Y., Matsuuchi, K. & Sanders, R.H. (2016). Numerical and experimental investigations of human swimming motions. Journal of Sports Sciences, 34: 1564–8.
Terauds, J. (1978). ‘Computerized biomechanical cinematography analysis of discus throwing at the Montreal Olympiad’. Track and Field Quarterly Review, 78: 25–8.
Toussaint, H.M., Van den Berg, C. & Beek, W.J. (2002). ‘“Pumped-Up Propulsion” during front crawl swimming’. Medicine and Science in Sports and Exercise, 34(2): 314–19.
Related Websites
USA Swimming website (http://www.usaswimming.org/USASWeb/DesktopDefault.aspx?TabId=1092&Alias=rainbow&Lang=en). Comprehensive swimming website with links to swimming biomechanics articles.
‘Lift or Drag? Let’s Get Skeptical About Freestyle Propulsion’, BioMech (http://sportsci.org/news/biomech/skeptic.html). Overview of the arguments surrounding lift versus drag as the predominant forces in swimming propulsion, by Ross Sanders.
National Aeronautics and Space Administration (http://www.grc.nasa.gov/WWW/K-12/airplane/bga.html). Well-written introduction to aerodynamics.
NASA Advanced Supercomputing Division, Aerodynamics of car racing (http://www.nas.nasa.gov/About/Education/Racecar/). Complete website exploring the aerodynamics of car racing.
INTERVIEW WITH THE EXPERTS
A successful Felicity Galvez, member of the Australian swimming team, using the Wetplate technology to improve start and turn times to optimise swimming performance.
Australian Institute of Sport on the training of swimming
Coach:
Nationality: Australian
Biomechanists:
Name: Bruce R. Mason
Nationality: Australian
Name: Danielle P. Formosa
Nationality: Australian
Athlete Biography:
Name: Felicity Galvez
Nationality: Australian
Australian Institute of Sport swimming scholarship holder and member of the National Swim Team
Major Achievements:
•Olympic gold medal 4×200 m freestyle relay (heats), August 2008
•Olympic gold medal 4×100 m medley relay (heats), August 2008
•World champion and world record 100 m butterfly short course, 55.89 s, April 2008
•World champion and world record 50 m butterfly short course, 25.32 s, April 2008
•World record 100 m butterfly short course, 55.46 s, November 2009
•World Championships gold medal 4×100 m medley relay (heats), July 2005
•World Championships bronze medal 4×100 m freestyle relay, July 2009
•Commonwealth Games silver medal 200 m butterfly, March 2006
•World short course bronze medal 4×100 m medley relay, April 2008
When and how did you use biomechanical analyses or theories to optimise the athlete’s training?
During the 2008 Olympic Games preparation, the Australian Institute of Sport (AIS) swim programme extensively utilised biomechanics for both skill (starts and turns) development and skill tracking. The aim of the programme was to maximise performance execution at the Games and develop racing skills that would be sustainable under pressure. It was a long-term development process focused on achieving real performance outcomes through identified cross bridges in biomechanics, skill acquisition and psychology. For Felicity, the goal was to achieve best times and performances at the World Championships and the short course meets in 2009. This integrated approach resulted in an average individual improvement of -1.31 seconds (including relay changeovers) or -0.97 seconds (excluding relay changeovers) in start, turn and finish times between the Australian Olympic Selection Trials in March 2008 and the Beijing Olympic Games in August 2008 (see Table 1A and Table 1B). Felicity improved greatly, winning a World Championship bronze medal in the 4×100 m freestyle relay and then breaking the world short course record in the 100 m butterfly; the short course record is substantial because the greater number of turns means that improving this aspect of performance is vital.
|
|
Olympic Trials |
Olympic Games |
Difference |
|
Swimmer 1 |
200 m Freestyle |
35.74 |
34.12 |
-1.62 |
|
Swimmer 1 |
100 m Butterfly |
18.58 |
17.04 |
-1.54 |
|
Swimmer 2 |
200 m Freestyle |
34.99 |
34.45 |
-0.54 |
|
Swimmer 3 |
200 m IM |
39.55 |
38.01 |
-1.54 |
|
Average |
|
32.22 |
30.91 |
-1.31 |
|
TABLE 1A Start, turn and finish total time individual improvements: Olympic Trials to Olympic Games including relay changeovers.
|
|
Olympic Trials |
Olympic Games |
Difference |
|
Swimmer 1 |
200 m Freestyle |
35.74 |
34.12 |
-1.62 |
|
Swimmer 1 |
100 m Butterfly |
11.91 |
11.19 |
-0.72 |
|
Swimmer 2 |
200 m Freestyle |
28.21 |
28.21 |
0.00 |
|
Swimmer 3 |
200 m IM |
39.55 |
38.01 |
-1.54 |
|
Average |
|
28.85 |
27.78 |
-0.97 |
|
TABLE 1B Start, turn and finish total time individual improvements: Olympic Trials to Olympic Games not including relay changeovers.
The primary biomechanical analysis system utilised by the elite swimming programme at the AIS is called Wetplate. The Wetplate analysis provides immediate biomechanical feedback that quantifies the parameters associated with performance in competitive swim start and turn technique. The Wetplate hardware and its computer programme only provide the parameters associated with performance rather than act as a prescriptive tool designed to inform the user of changes that should be made. It is up to the coach or biomechanist to interpret the Wetplate information and provide advice to the swimmer.
The Wetplate biomechanical information is provided in conjunction with high-speed visual images from four machine vision cameras which capture the activity over an interval of 15 m to and from the starting block or turning wall. The Wetplate system utilises an instrumented force platform starting block and force platform turning wall that provide parameters about the forces and timing of those forces associated with starts and wall contact during the turn. Magnetic timing gates are used to calculate the swimmer’s interval and accumulative time at 5 m, 7.5 m, 10 m, 15 m for the start and at 5 m in and 10 m out from the wall during a turn. The parameters examined are extensive and include the force and power profiles while in contact with the starting block or turning wall, as well as the magnitude of the forces and power in the form of a graph. In addition, the Wetplate programme provides the time of wall contact, the depth of foot placement at maximum force and the interval times of the swimmer in and out from the wall during a turn.
How did you change your training/techniques based on this?
Swimmers such as Felicity can perform a turn and have the results available for the coach to interpret on the pool deck within minutes after the skill is completed. This allows the coach to provide an analysis of the activity based on quantitative biomechanical measurements, enabling coach–athlete intervention to eradicate inefficiencies or to improve the mechanics within the turning technique. To help identify inefficiencies or areas that may be improved, the Wetplate programme provides a comparison mode whereby one performance can be visually and biomechanically compared to another. This enables the coach to identify differences within and between individuals and to emphasise these differences using moving visual images at 1/100th second intervals, which are time synchronised to wall contact, as well as force and power profiles of the performances.
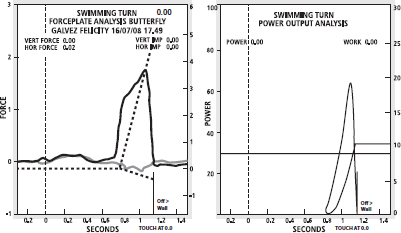
How do these analyses influence the chances of success of the athlete/team?
Competition analysis is utilised to extract each athlete’s start, turn and finish times. These parameters can then be incorporated into Wetplate testing sessions assessing starting and turning technique so that inefficiencies in the technique may be readily eradicated or that improved mechanics may be incorporated back into the athlete’s competitive performance. Without the objective and quantitative analysis information, problems in technique may continue over an extended period without being easily or correctly identified. Even when inefficiencies are rectified swimmers may slip back or relapse into the poor technique habits in time. This may be avoided with the regular use of the Wetplate analysis.
What were the strong points (both personally and intellectually) of the best biomechanists you worked with?
Consistency of language and feedback is vital in skill development. It is essential that everyone giving feedback to the athlete understands the immediate goal and the strategies incorporated for best communicating this feedback to the athlete. The immediate goal is the primary technical element being developed, even though other elements may exist as part of the total performance. During a typical Wetplate testing session there are the biomechanics team of testers, one coach and one athlete present. Over 100 quantitative parameters are measured during a start analysis. There is the potential for confusion unless this information can be refined and communicated effectively. The coach and biomechanists must decide who is going to give the feedback, what the immediate goal is and how to best communicate this information to the athlete in order to make an actual and sustainable change. During Wetplate testing sessions the coach predominantly gives the feedback to the athletes on one or two technical elements using cues. These cues are then utilised by the coach during regular training and competition in order to maintain feedback consistency. The best biomechanists work together with the coach and are able to simplify information in order to achieve real performance outcomes.
Overall, how important do you feel a good understanding of biomechanics is to a coach or sports scientist?
Without quantitative measurement a coach can only surmise if one performance is better than another, unless the two performances are visually significantly different. Unless the coach has a biomechanical knowledge, any difference in the magnitude of a parameter cannot be fully appreciated nor understood. A good example of this is the understanding of the differences between a force and power profile. The Wetplate system displays force and power relative to an individual’s mass, therefore highlighting strengths and weaknesses of the performer that can be readily compared to that of another swimmer. The Wetplate system, due to its immediate feedback ability, provides the opportunity for a test, intervention and retest protocol to identify changes that are made in the performance, thereby enhancing skill learning at an accelerated rate. As the coach is the primary interpreter of the analysis, the reinforcement of skill changes, identified through the Wetplate programme, also occur within the regular training environment.
* The spin can also tilt the discus because one side of the discus is spinning into the oncoming air while the other side is spinning away from it. Therefore, the relative speed of the air is greater on one side than the other and lift is therefore greater. This imbalance of lift causes the discus to tilt. Another force, the Coriolis force, is sometimes thought to act on the discus, but its effects are probably very small. Although the consequences of this tilt are not as significant as the benefits to the discus’s stability, placing too much spin on the discus might be problematic.