
THE IMPULSE–MOMENTUM RELATIONSHIP
A runner can strike the ground with variable foot placement and produce forces of different durations in various directions. What strategy of force application is optimum for those athletes who need to run at high speeds?

By the end of this chapter you should be able to:
•Explain the physical concepts of impulse and momentum and how they relate to the performance of sporting movements
•Explain how alterations in the magnitude and timing of forces affect rates of acceleration of objects or implements
•Use these concepts to qualitatively (that is, without numbers being expressed) describe how to improve sporting performance by altering force production patterns
We learned in Chapter 4 that we need to exert a force on an object to change its velocity; that is, to overcome its inertia. If the force is sufficiently large or the object’s mass is sufficiently small and the force is directed appropriately, it will be accelerated in the desired direction, but is this all we need to know to optimise sporting techniques? Not quite.
In Chapter 4, a force was described as having a continuous action that doesn’t increase or decrease over time, but that usually isn’t the case. Look at the graph of the ground reaction forces measured from two runners using a force platform mounted in the ground (Figure 5.1). A force platform contains a number of force-sensitive instruments (piezoelectric crystals, strain gauges and others) and relays forces measured at the ground to a computer for recording. These forces are commonly measured to help us understand how we stand, walk, run and jump. Notice that the graph of a rear-foot striker first rises (the impact peak), then dips slightly and rises again (the propulsive peak) before falling. The fore-foot/mid-foot striker has only a single rise and fall in force. Therefore, force is not consistent through the ground contact phase of running (or most other movements). The aim of this chapter is to discover how manipulation of these forces might help us improve performance.
FIG. 5.1 When we strike the ground during running the Earth provides a reaction force, measured here using a force platform. The above graph shows the form of the vertical component of the reaction force, called the vertical ground reaction force, for a runner who strikes with the heel of their foot first (rear-foot striker) and a runner who makes contact with a flatter foot (mid-foot striker). There is a larger impact peak (point A) for the rear-foot striker, followed by a slight decrease (B) then a propulsive peak (C). Force varies through the duration of foot–ground contact.
First, you need to understand the concept of momentum. Think of a big bus moving quickly, as in Figure 5.2. It has a large mass (and therefore has a large inertia) and is moving at high velocity. The bus has a lot of momentum. A snail has very little mass and moves very slowly, so it has very little momentum. Essentially, momentum is the product of mass and velocity: momentum (p) = mass (m) × velocity (v) and is measured in kg·m·s-1. (‘p’ for momentum? You could use ‘M’, which is common in many texts but you might confuse that with ‘m’ for mass.)
FIG. 5.2 A large bus moving quickly has a large momentum. It would take a large force produced over a significant time period to stop it.
If we want to move an object of constant mass a bit more quickly, we need to increase its velocity and therefore its momentum. You might be thinking that inertia and momentum are similar and you’d be nearly right. One way to think about the difference is to consider that a stationary object has no momentum, because it has no velocity, but it still has inertia. That is, you still have to apply a force to change its state of motion; the same object doesn’t have a greater inertia when moving, so it will still take the same force to change its velocity by a certain amount (i.e. to accelerate it.).
In sport, we often want to change an object’s momentum, which we do by applying a force. The larger the force, the greater will be the change in momentum. We could also apply the same force for longer. Think of what might happen if you tried to push your car from a stationary position to a reasonable speed when you need to jump-start it after your battery goes flat. You apply the largest force you can but it still takes some time to get the car up to speed. To change the velocity of the car or to change its momentum, you need to apply a big force for a long time. The term that describes the product of force (F) and time (t) is impulse (J). (You will also see Ft used in many texts.)
Essentially, the greater the impulse (J), the greater will be the change in momentum (p), so J = ∆p (remember ∆ means ‘change in’), or ∆Ft = ∆mv. This is the impulse–momentum relationship and gives a hint as to how best to accelerate our body. When we hit the ground with our foot, we need to apply the largest force possible for the longest time possible. The greater the impulse, the greater the change in momentum; since our mass won’t change, our velocity must. You can see how impulse is calculated from a force–time curve in Box 5.1.
BOX 5.1 CALCULATION OF IMPULSE FROM A FORCE–TIME CURVE
Impulse is the product of force and time but how do we calculate it? Below is a force–time curve (FIG. 1). It shows the force produced over a period of time. Strain gauges, force platforms and various other tools can be used to measure forces such as these. Impulse is equal to the area under the curve.
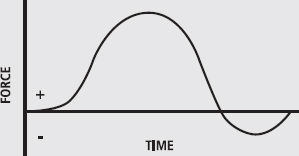
FIG. 1
The easiest way to calculate the area under the curve is to break it up into rectangular columns (FIG. 2). Each column has a known width (time) and a known height (force). The area of a rectangle is given by its height multiplied by its width; that is, force × time.
The height of the column is the distance from the baseline (zero force) to the curve, such that the middle of the column intersects with the curve. The width is equal to any time period we choose. Obviously the smaller the time period, the more accurate we will be, because the top of the column is a straight line whereas the curve is rounded, and so we reduce inaccuracies if we use thinner columns.
Generally, data such as these are collected by a computer that takes a reading at fixed time intervals. We might, for example, collect 100 data points in a second, in which case it is easiest to build columns 1/100 s wide. Each column is therefore the force measured at that data point multiplied by 0.01 s.
Once we have the area of each column, we sum them to get the total area under the curve – the impulse (impulse equals the sum of each force data point multiplied by the time interval). The negative areas are calculated in the same way, remembering that the forces are negative so the impulses are also negative. The total impulse is the positive impulse plus the negative impulse.
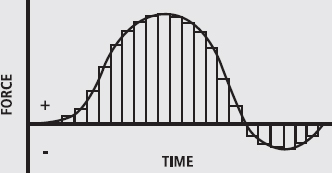
FIG. 2
Remember that velocity has both a magnitude and a direction, so applying this impulse might change direction rather than speed, which is very useful in evasive sports. If we direct the impulse in the opposite direction to which we are moving, it will also slow us down. How is impulse applied during running? You have seen the vertical impulse trace in Figure 5.1 but what about horizontal forces? If we want to run horizontally, we need to apply horizontal forces!
Figure 5.3 shows a typical horizontal force trace measured using a force platform. Notice that we first apply a force or impulse in a forward direction, so the ground reaction force is backward, or negative. That would slow us down! Only later, in the stance phase, do we actually apply a backward force to elicit a reaction force to accelerate us forwards. We call these the braking and propulsive impulses. Since the total impulse is equal to the braking (assigned a negative value) plus propulsive (assigned a positive value) impulses, we need to reduce the braking and increase the propulsive forces in order to accelerate.
FIG. 5.3 Horizontal ground reaction force trace for a runner. A forward force exerted by the runner elicits a backward or braking reaction force (negative; A). Since the force is applied over time, the area under the curve (force × time) is the braking impulse. As the foot passes under the body, the runner pushes backwards to elicit a forward or propulsive reaction force (positive; B). Since the force is also applied over time, there is a propulsive impulse.
How are braking forces produced? If we assume there is a low air resistance then we can assume that the body is travelling at a horizontal velocity dictated by the previous propulsive impulses. In the following step, we attempt to accelerate our leg/foot backwards and downwards towards the ground to apply another impulse. If we don’t accelerate the foot to the same speed that the ground is rushing towards us, the foot will still be travelling slightly forwards relative to the ground, although it is travelling backwards relative to us ... and yes, this is the idea of relative velocity developed in Einstein’s Theory of Relativity. So, the foot hits the ground while still travelling relatively forwards and therefore applies a braking impulse.
Later in the step, we are able to accelerate the foot enough that it would be travelling faster than the ground, if we weren’t connected to it, and we are able to produce a propulsive impulse (see Figure 5.4). This extra acceleration comes largely from the recoil of elastic tissues such as our tendons, which are first stretched when our legs are compressed by the vertical and braking forces (as discussed in Chapter 17). So while we want to minimise the braking force, a small force plays a large role in the ability to run at high speeds. In sprinting, the braking impulse is usually greater when the foot lands further in front of the body (Figure 5.5); there is a trade-off where a small braking force is useful but a large force, generated when the foot lands well in front of the body’s centre of mass, is detrimental. Of course, braking and sideways (medio-lateral) impulses are important for athletes who need to slow down or change direction quickly.
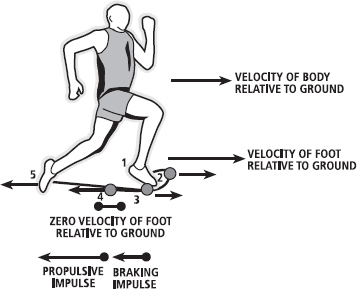
FIG. 5.4 During running, the leg is relocated from behind the body to the front (1). At this point, the foot is travelling forwards relative to both the body and the ground. At (2) the foot is stationary relative to the body, but because the body is still moving forwards the foot is also moving forwards relative to the ground. Immediately prior to foot–ground contact (3), the foot is moving backwards relative to the body, but is still moving slightly forwards relative to the ground. Therefore, at foot contact there is a forward force applied to the ground. The ground exerts an equal and opposite braking force against the runner. The magnitude and duration of this force determines the braking impulse. At (4), the foot is no longer applying a forward force, and at (5) the foot is able to produce a backward force. The resulting forward-directed ground reaction force, applied over time, provides the propulsive impulse. Both minimising the braking impulse and maximising the propulsive impulse are keys to fast running.
FIG. 5.5 When the foot lands at a greater angle in front of the body (left diagram) the braking impulse (measured by the force platform under the foot) is large. The total positive impulse (braking + propulsive) is therefore smaller so acceleration is lesser.
When the foot lands at a smaller angle and further under the body (right diagram) the braking impulse is smaller, although the vertical impulse might be bigger. The total positive impulse, however, is likely to be larger. Elite sprinters land with their foot about 6 cm in front of the body whereas novice sprinters might land with their foot about twice that distance in front.
As for the propulsive impulse, sprinters have traditionally been taught to spend as little time on the ground as possible. Research in the 1970s showed that the faster sprinters in a group had smaller hip angles at take-off (Kunz & Kaufmann, 1981). Essentially, this means that the foot would not travel as far under the body. Top sprinters tend to extend their hip significantly. Figure 5.6 shows a diagram of an elite sprinter. Notice that his foot travels a long way past his body in the propulsive phase. This allows him to produce his propulsive force over a long time and therefore attain a greater propulsive impulse. This is common among top sprinters (although there is a limit – if a runner attempts to push too far then their performance will be affected, but the complexity of this debate is outside the scope of this book). How do they keep their ground contact times so short (less than 0.1 s)? They are able to attain such high forward speeds that their body travels past the foot very quickly. Remember, time is equal to displacement divided by velocity (t =s/v; Chapter 1). If the body needs to travel a certain distance over the foot but travels there at a high velocity, the time taken will be small. So the short contact times of elite sprinters are largely a result of their fast running speed, rather than being a cause of them. If they landed with their foot far out in front of their body, which you already know is not useful since it increases the braking impulse, their contact time would also be greater. So, part of their short contact time can also be attributed to the feet not landing too far in front of their body.
FIG. 5.6 Diagram of foot–ground contact phase of an elite sprinter. His significant hip extension allows the foot to travel far past the body. This provides a greater time for force application, which results in a greater propulsive impulse. His short contact times (~0.10 s) result from the high speed of his body over the foot and the placement of his foot only slightly in front of his body at foot–ground contact.
To improve running performance it is absolutely essential to determine the optimum impulse direction. If the body needs to be accelerated vertically, we need larger vertical impulses; if we need to move sideways, we need to apply larger sideways impulses (we call these mediolateral impulses, because they are directed from medial (towards the midline of the body) to lateral (towards the outside of the body) or vice versa; see Boxes 2.1 and 2.2). To run quickly, we need some vertical impulse to propel us into the air but we also need very large horizontal propulsive impulses with smaller horizontal braking impulses so that our forward velocity is maximised. A greater impulse results from the development of high forces on the ground over a considerable stride length (or time), since impulse is a function of force and time. Generally, rotational impulses applied to the ground provide little benefit and should be minimised.
HOW ELSE CAN WE USE THIS INFORMATION?
In the last chapter we considered how to optimise the direction of force application, but we also need to consider the length of time of force application. One of the benefits of the rotational technique used by many shot putters, for example, is that the force accelerating the shot might be applied over a slightly longer time, allowing a greater velocity to be attained. In swimming and rowing we use long strokes to increase the time available for force application (to increase the impulse). In rugby, or American football, we can perform a longer pass by moving the hands and body through a greater range of motion.
In many sports there is a limited time in which to apply forces to an object, such as a serve in tennis, ground contact during running, or in some hitting sports such as field or ice hockey. In these sports there is a need to increase the force applied to the ball, ground or puck by producing large impulses to create a high velocity of racket, foot or stick, as you saw in Chapters 1 and 2. The problem in other sports is that there is often a need to produce these high movement speeds in a very short time, for example in baseball or softball where there is a short time between the initiation of a swing and striking the ball. This is often referred to as the need for bat ‘quickness’ rather than just bat ‘speed’. Obviously, we need to apply the greatest impulses in very short times by increasing the forces, so that accelerations are greater over short time intervals (remember F = ma). The training required for these different sports will therefore be very specific to their impulse requirements.
momentum (p) = m × v
Reference
Kunz, H. & Kaufmann, D.A. (1981). ‘Biomechanical analysis of sprinting: decathletes versus champions’. British Journal of Sports Medicine, 15(3): 177–81.
Related Websites
ZonaLand: National Science Teachers Association (http://zonalandeducation.com/mstm/physics/mechanics/mechanics.html). Clear descriptions and animations of the basic principles of mechanics.
The Physics Classroom – Tutorials (http://www.physicsclassroom.com/Class/). Lessons on basic physics concepts.
The Physics Classroom – Multimedia tools (http://www.physicsclassroom.com/mmedia/). Interactive tools and movies depicting basic physics concepts.
The Physics of Sports (http://www.topendsports.com/biomechanics/physics.htm). Website investigating the applications of physics in sports.
INTERVIEW WITH THE EXPERTS
Nelli Cooman at the University of Leuven (Belgium) with Herman van Coppenolle and Christoph Delecluse
Coach:
Name: Henk Kraaijenhof
Nationality: Dutch
Born: 5 October 1955
Athlete Biography:
Name: Nelli Cooman
Nationality: Dutch
Born: 6 June 1964
Major Achievements:
• World record 60 m (1986): 7.00 s
• Two-time world champion 60 m indoors (1987 and 1989)
• Five-time European indoor champion at 60 m
• Personal best 100 m: 11.08 s (1986 and 1988)
When and how did you use biomechanical analyses or theories to optimise Nelli’s training? What were the results of the changes made based on these analyses or theories?
At that time there was no organised biomechanics support for athletes in the Netherlands so the only way to access it was to allow Nelli to take part in experiments. So our method of obtaining biomechanics support was slightly unusual. From this participation we learned about Nelli’s specific individual characteristics and gained new ideas on how to improve her performance. One problem was, though, that the results of the research usually sparked as many questions as they provided answers (and in fact we had other questions to start with that we were not able to answer), so a longer and more consistent relationship with a biomechanics support team would have been of great benefit.
The research that Nelli participated in was performed somewhere in the middle of her (long) career, where the demand for more knowledge and new opportunities met. The outcomes were: (1) we were able to examine some interesting aspects with regards to the setting of the starting blocks, (2) there was a starting point for looking into the relationship between her performance in different jump tests and performance in the different phases of the 100 m sprint, and (3) there were interesting data about the functioning of the hamstrings while running at full speed.
This led to some significant changes in the approach to training but also to a better understanding of the sprinting movement in general, and a shift in approach to technique exercises! The results of these changes are always hard to quantify in the complex dynamics of training, but they certainly contributed in a positive way to the improvement of performance. In elite sprinters any improvement, even 10 milliseconds, is respected. Certainly, by changing Nelli’s hamstring exercises as a result of some of the research we were able to significantly reduce the incidence of hamstring injury.
What were the strong points (both personally and intellectually) of the best biomechanists you worked with?
Personally we established a good, even though temporary, relationship with the biomechanists. I seldom experienced the ‘gap’ between science and practice. Because the ultimate goal of a biomechanist is to do research and publish, and as soon as the project is over and the publication done the interest of the biomechanists might change to a completely different research subject, long-term cooperation is difficult. I think a good biomechanics support team needs to provide ongoing support, and work closely with the athlete and coach.
The only problem with some scientists is that most of the time they only consider their field as being predominant in the training process and rarely consider, for example, physiological factors, psychological factors, etc., although I think this is a result of the need for specialism in modern science. One exercise might be superior to another one in respect to optimising muscle contraction timing, for example, but one has to consider the long-term and accumulating effects of this exercise on the athlete as a whole. A practical example is that plyometrics training might be superior to other methods of enhancing explosive performance in the short term, but in the longer term it may lead to a higher incidence of injuries, especially if performed inappropriately. A team approach to testing and training is far more ideal.
Overall, how important do you feel a good understanding of biomechanics is to a coach or sports scientist?
Well, I think it is as important as a good understanding of physiology, nutrition, tactics, psychology, etc. There is no point having the right nutrition and psychology if the athlete is not moving optimally. In the total performance chain there should be no weak link in knowledge of the coach. So, I think it is very important, unless one coaches chess players!

Nelli Cooman at the Toppidrettsentret in Oslo, Norway with Leif Olav Alnes.