
ANGULAR POSITION, VELOCITY AND ACCELERATION
What influence does arm length have on the distance a discus is thrown? Is it more or less important than the angular velocity of the arm in determining the release speed?

By the end of this chapter you should be able to:
•Define the terms angular position, angular velocity and angular acceleration and state their units of measurement
•Describe the relationship between the rotational speed of an object and the linear speed of a point on it
•Develop a simple model to determine the impact of factors affecting discus release speed
To answer these questions, we first have to work out how to predict the release speed of the discus (the speed at which it leaves the hand of the thrower). The release speed is equal to the speed of the discus immediately before release. The thrower creates a high discus speed by spinning about their vertical axis with their arm outstretched (Boxes 2.1 and 2.2 have more about how we describe the planes, axes and relative locations of parts of the body). The faster the angular velocity of the body, the faster the discus will be moving. The angular velocity is simply the rate of change in angle of the thrower. It is quite obvious that the faster the thrower spins (that is, the higher their angular velocity), the faster the discus will be moving.
What is ‘angular velocity’ and how might we calculate it?
BOX 2.1 PRINCIPAL PLANES AND AXES OF THE BODY
It is often useful to describe the axis about which a person (or any other object) rotates, moves, is pushed or pulled, and so on. Typically, the human body is divided into three planes and rotates about three axes. Describing movements in these planes and about these axes reduces the need for complicated descriptions of how we move.
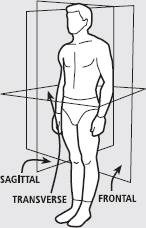
Fig. 1
Three planes, the ‘cardinal planes’, notionally divide the body in three dimensions. The frontal (or coronal) plane cuts the body into front and back halves, the sagittal plane cuts the body into left and right halves and the transverse plane cuts the body into top and bottom halves.
The body can rotate about these planes. For example, if you do a cartwheel you rotate about the frontal plane (that is, you are always facing forwards), if you do a forward somersault you rotate about the sagittal plane (your head drops forwards as you rotate) and if you do a pirouette you rotate about the transverse plane.
Alternatively, we can say you spun about each of three axes of rotation. During a cartwheel you spin about the anteroposterior axis (literally you spin about a line drawn from front (anterior) to back (posterior)), during the forward somersault you spin about the mediolateral axis (about a line drawn from the middle (medial) to the outside (lateral) of your body) and during a pirouette you spin about the longitudinal axis (that is, a line drawn from your head to your feet).
In the photograph of the rugby player (below), you can see the legs and arms swing in the sagittal plane and rotate about the mediolateral axis, the head has turned in the transverse plane about the longitudinal axis but no part of the body has moved in the frontal plane (rotated about the anteroposterior axis) to any significant degree.
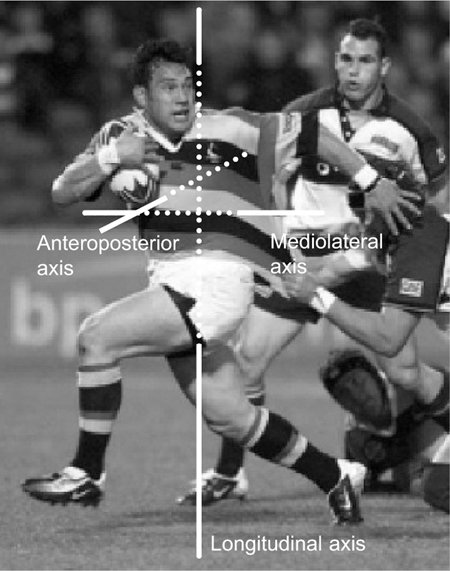
Fig. 2
If you look at Figure 2.1 (below) you can imagine that the line in A is a simple representation of a line drawn from the left to the right shoulder of a discus thrower. As the thrower rotates, the angle of the line changes, relative to its starting position. In B, we can see the line has rotated by 15°; that is, it has changed angular position, or displaced, by 15°. Therefore, its angular displacement is 15°. This is very similar to the linear dimensions I described in Chapter 1, as can be seen in Table 2.1.
FIG. 2.1 Angular position and displacement. The line in A is an imaginary line joining the left and right shoulders of a thrower. In B, the shoulders have rotated by 15°.
If we obtained this information from a video recording and we knew the time between each frame of the film, we could calculate the angular velocity of the shoulders. The frame rate of film is generally 25 frames per second (30 fps in North America, Japan and some South American and Asian countries), so the time between frames would be 1/25 = 0.04 s. This calculation is almost the same as was demonstrated in Chapter 1 for the calculation of linear velocity (s·t-1), except we use the angular equivalents. Angular velocity (ω) = θ·t-1 (θ is the symbol for angular displacement, 15° in this example). So, ω in this case is 15°/0.04 s = 375°·s-1. If we spin around in a circle we move through 360°, so at 375°·s-1 we would spin around a little more than once a second.
Linear dimension |
SI Unit |
Angular dimension |
SI Unit |
Position |
Dimensionless or scaled co-ordinates |
Angle |
radians (rad) relative to a point or line (Figure 2.2) |
Displacement |
metres (m) |
Angular displacement |
radians (rad) |
Velocity |
metres per second (m·s-1) |
Angular velocity |
radians per second (rad·s-1) |
Acceleration |
metres per second per second (m·s-2) |
Angular acceleration |
radians per second per second (rad·s-2) |
TABLE 2.1 Angular equivalents of linear dimensions.
The right units of measurement
The answer is not quite complete. In science, there is a prescribed system of units: the Système International (SI). Using the correct SI units is important, because many of the equations we use in biomechanics will give wrong answers if we don’t use the correct units (I’ll show you this later). We have expressed our answer in the units of °·s-1 (degrees per second) but the SI unit for angle is the radian. A radian is equal to the angle formed when a line joining the centre of a circle to the perimeter is rotated by the length of one radius, that is, the distance from the centre to the perimeter, as shown in Figure 2.2. The perimeter of a circle is 2π times the radius, so there are 2π radians in a circle. Therefore 2π radians = 360° and π radians = 180°. Knowing this allows us to convert from degrees to radians easily: radians = degrees /180/π. You should memorise this conversion, mark this page for future use or remember that 180/π = 57.3 (so radians = degrees/57.3 and degrees = radians × 57.3). In our example, the angular velocity of the thrower in radians is 375°·s-1/57.3 = 6.54 rad·s-1.
FIG. 2.2 A radian is equal to the angle formed when a line joining the centre of a circle to the perimeter is rotated by one radius.
BOX 2.2 OTHER ANATOMICAL REFERENCES
We need to describe how one body part relates to another. For example, the hand is further down the arm than the shoulder; how can we describe that more simply? We could say that the hand is distal to the shoulder. We could also say that our shoulder is proximal to our hand. These anatomical designations are shown in Figure 1.
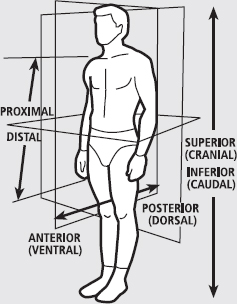
Fig. 1
Some important distinctions are:
1.any body part closer to the head is ‘cranial’ (or ‘rostral’);
2.body parts closer to the feet are ‘caudal’;
3.any body part closer to the front, regardless of the body’s orientation, is ‘anterior’ and anything to the back is ‘posterior’ (so if you lie on your stomach your head is cranial and anterior);
4.the chest (front) surface is ‘ventral’;
5.the back is ‘dorsal’ (so if you lie on your stomach the ventral surface is inferior to the dorsal surface);
6.the chest is anterior to the back (but if you were lying down the head would be anterior to the feet so we would designate the chest as the ventral surface and the back as the dorsal surface);
7.because the hand can be oriented in many directions, the palm side is always the ventral surface and the back side is the dorsal surface, although depending on the orientation of the hand, the ventral and dorsal surfaces might be anterior, posterior, superior or inferior. If the hand is rotated so the palm is facing behind you it is ‘prone’, but if it is rotated so the palm is facing forwards it is ‘supine’.
Developing a model to answer the question
Now that we know how to calculate angular velocity and convert it into radians, we can set about answering our question. We have a thrower who is rotating and an arm that is swinging, or rotating, about their body. To calculate the release speed of the discus we need to know two values: (1) the angular velocity of the arm and (2) the length of the arm.
We know that the faster the arm swings the faster the discus must move. Increasing the distance of the centre, or axis, of rotation also increases its speed, as shown in the example in Figure 2.3. The linear velocity (v) of the discus is a function of the length of the arm (r) and its angular velocity (ω). (The word ‘function’ means that one number is altered in some proportion to another number, but can often be read as ‘to multiply’, so if linear velocity is a function of arm length and angular velocity, then v = rω.) Using video, we might find that the angular velocity of the arm of the thrower is 21 rad·s-1 and we could measure the arm as 0.7 m long, so the linear velocity of the discus would be approximately 0.7 × 21 = 14.7 m·s-1. (This shows why we use SI units: you could substitute 21 rad·s-1 for 1203°·s-1, which will give you a highly unrealistic answer of 842.3 m·s-1 (3032 km·h-1). You must convert all measures to SI units to use these mathematical equations.)
Given this information, how can we determine the relative importance of each factor? In Chapter 1 we created a model of the times taken to complete the acceleration, maximum speed and deceleration phases of a sprint run and showed how it could be improved by 3%, which we considered reasonable. We could do something similar here. However, it might not be ideal to just increase arm length or angular velocity by 3%, so we might find data suggesting that discus throwers typically have an arm angular velocity of between 18 and 26 rad·s-1 and arm lengths between 0.60 and 0.85 m. You can see that the ranges have different magnitudes, so it wouldn’t make sense to just assume a similar percentage variation in both.
FIG. 2.3 Calculation of the linear velocity of an object that rotates. If you were sitting on this softball bat when it was swung about its axis of rotation, you would have travelled further if you sat at point B than if you sat at point A. Since linear velocity (v) is equal to the distance travelled per unit of time, it is greater at point B. Since the linear distance is a function of the angle through which the bat is swung (θ) and the radius of the swing circle (r), the distance is equal to θ · r (or just θr). The velocity is therefore θ · r / t, where t = time. Since θ/t = ω (angular velocity), we often write v = rω.
Assuming that the arm’s angular velocity ranges between 18 and 26 rad·s-1 and arm length varies between 0.6 and 0.85 m, to determine the effects of these variations we use the equation v = rω with this range of values.
Assuming arm length = 0.6 m:
Smallest value (v) = 18 × 0.6 = 10.8 m·s-1
Largest value (v) = 26 × 0.6 = 15.6 m·s-1
Assuming arm length = 0.85 m:
Smallest value (v) = 18 × 0.85 = 15.3 m·s-1
Largest value (v) = 26 × 0.85 = 22.1 m·s-1
So, altering the angular velocity within predicted limits varies the discus velocity between 4.8 m·s-1 (that is, 15.6 – 10.8 m·s-1 for arm length of 0.6 m) and 6.8 m·s-1 (that is, 22.1 – 15.3 m·s-1 for arm length of 0.85 m), which is 44.4% (4.8/10.8 × 100 and 6.8/15.3 × 100).
However, altering the angular velocity varies discus velocity by between 4.5 m·s-1 (that is, 15.3 – 10.8 m·s-1 for angular velocity of 18 rad·s-1) and 6.5 rad·s-1 (that is, 22.1 – 15.6 m·s-1, for angular velocity of 26 rad·s-1), which is 41.7%.
From this model, we can tell that increasing either arm length or the arm angular velocity will affect release velocity by something over 40% and is similar for long and short armed throwers. However, since individuals with the longest arms have a greater release velocity (15.3–22.1 m·s-1) compared to those with shorter arms (10.8–15.6 m·s-1), the approximately 40% increase is of greater absolute magnitude in long armed throwers, with discus velocity increasing by 6.5 m·s-1. Therefore, increasing the angular velocity has more of an effect in throwers who have longer arms, so we can conclude that arm length is very important for a discus thrower.
Our finding is in agreement with published data (for example, Gregor et al., 1985), which shows that most elite throwers are quite tall (men taller than 1.86 m, and women over 1.70 m) and would thus have long arms. Of course, as you’ll learn in Chapter 7, increasing arm length might also reduce the speed at which the thrower can swing their arm so there is probably a limit to the length of arm that can allow fast discus release velocities. Nonetheless, these modelling techniques can be very useful for biomechanists and coaches in predicting the importance of factors that might affect athletic performance.
Interestingly, the world’s best discus throwers achieve release velocities of greater than 25 m·s-1 (Gregor et al., 1985). For a thrower with a 0.75 m arm length we would predict an arm angular velocity of more than 33 rad·s-1 (1890°·s-1), which seems highly unlikely. One explanation is that our arm moves with a whip-like action, where our tendons are first stretched and then recoil at high speeds. Thus the hand, and therefore the discus, reaches much higher speeds than might be achieved from using the arm as a rigid bar, where muscle contraction is the only contributor to the movement. A second explanation is that the hand and wrist also contribute strongly at the point of discus release, so the velocity of the fingers, and therefore the discus, is much faster than that of the whole arm. These movement principles are explored more fully in Chapter 17. These are important considerations for biomechanists, who often use simple models to assess the impact of complex factors.
HOW ELSE CAN WE USE THIS INFORMATION?
It is immediately apparent that if we play a sport where we swing a bat or racket that we will obtain a higher velocity if we swing with our arms outstretched, as long as reaching out doesn’t slow our movement down; you will see this in Chapter 7. So, we need to adopt techniques that allow us to ‘free our arms’. If you were, for example, a pitcher in baseball or softball, you would use this information to ‘cramp up’ your opponent, meaning to make the batter swing with their arms slightly bent by pitching the ball as close to their body as possible. In tennis, a serve that is directed towards the body can prevent a good returner from making an optimum swing.
This information also allows us to determine that if two athletes swing their legs with the same angular velocity, the one with longer legs will have a faster linear foot speed and therefore can run faster. So, as long as you can swing your legs quickly, having longer legs can benefit top speed walking and running. This appears to be a major factor allowing Usain Bolt to run remarkably quickly in sprint running events (Krysztof & Mero, 2013). Those of us with shorter limbs will have to focus more on strategies to increase limb speed, while those with longer limbs will have to concentrate more on developing the force capability to accelerate their longer, and heavier, limbs. Chapters 7 and 8 show why more force is required to swing long limbs quickly.
Useful Equations
angular velocity (ω) = ∆θ/∆t
angular acceleration (α) = ∆ω/∆t
degrees-to-radians (rad) = xº/(180/π) or xº/57.3
radians-to-degrees (deg, º) = xº × (180/π) or xº × 57.3
Reference
Gregor, R.J., Whiting, W.C. & McCoy, R.W. (1985). ‘Kinematic Analysis of Olympic Discus Throwers’. International Journal of Sports Biomechanics, 1(2): 131–8.
Krzysztof, M. & Mero, A. (2013). ‘A Kinematics Analysis of Three Best 100m Performances Ever.’ Journal of Human Kinetics, 36: 149–60.
Hyperphysics (http://hyperphysics.phy-astr.gsu.edu/hbase/rotq.html). Basic and advanced discussions on angular motion, including maths simulations and calculations.
Circular Motion and Rotational Kinematics, by Sunil Singh, Connexions (http://cnx.org/content/m14014/latest/). In-depth descriptions of angular motion with interactive tools and quizzes.
ZonaLand: National Science Teachers Association (http://zonalandeducation.com/mstm/physics/mechanics/mechanics.html). Clear descriptions and animations of the basic principles of mechanics.
The Physics Classroom – Tutorials (http://www.physicsclassroom.com/Class/). Lessons on basic physics concepts.
The Physics Classroom – Multimedia tools (http://www.physicsclassroom.com/mmedia/). Interactive tools and movies depicting basic physics concepts.
The Physics of Sports (http://www.topendsports.com/biomechanics/physics.htm).Website investigating the applications of physics in sports.