Sports Biomechanics

What is the optimum method of cycling the legs in running? How can we increase the speed of the legs to increase maximum running speed?

By the end of this chapter you should be able to:

•Define the terms moment of inertia , radius of gyration and angular momentum

•Explain the parallel axes theorem and discuss its implications for movement speed and efficiency

•Show how changes in the mass , or mass distribution, of a body or object affect its moment of inertia and angular momentum

•Explain how we can modify sporting techniques to influence these parameters and therefore improve performance

•Describe the optimum leg action in sprint running with reference to the moment of inertia and angular momentum

We are able to run forwards because we apply a backward force again st the ground. The leg swings backwards, from the front of the body to the back, and the foot strikes the ground in the process. We then move the leg to the front of the body and repeat. The speed at which we run is limited by the amount of force (more correctly, the impulse) we can produce and the frequency with which we can apply it (i.e. stride frequency). Therefore, to improve running speed we need to understand how to swing our legs more quickly.

Moment of inertia

To move the leg backwards from the front of the body (called the ‘swing phase’ of running) we need to overcome the inertia of the leg. Since the leg swings with the hip as the centre of rotation (pivot point) we use the term moment of inertia. (Remember, from Chapter 6, that the word ‘moment’ describes anything where a quantity is multiplied by a distance.) We use moment of inertia because we are describing the propensity for masses (that is, objects with inertia), which are at a distance from a centre of rotation, to resist changes in their state of motion.

You might remember from Chapter 5 that, because of inertia, objects tend to remain in whatever state of motion they are in unless acted upon by an external force (Newton’s First Law). This is the same in the rotational sense, so we can say:

An object will remain at rest or continue to move with constant angular velocity as long as the net forces causing rotation equal zero

When we talk about an object moving in a straight line, we know that mass and inertia are basically the same; bigger objects have greater inertia. In the rotational sense, inertia (I) is a product of the mass of the object (m) and the square of the distance of that mass from the centre of rotation (r²): I = mr². All objects can be thought to be made of very small particles and the total moment of inertia is the sum of the masses of all these particles multiplied by the distance of each of those particles from the centre of rotation (see Figure 7.1). We can write: I = Σmr²^{(Σ means ‘sum of’).}

FIG. 7.1 The moment of inertia of the softball bat (A) is the sum of the moments of inertia of all of the particles in the bat. In the diagram, the bat is divided into 28 sections (in reality, the bat is the conglomeration of billions of particles). The total moment of inertia is equal to the sum (Σ) of each mass multiplied by the square of its distance from the point of rotation (the handle, near particle 1). Thus, I = Σmr². When a weight (m_weight) is added to the bat (m_bat) the moment of inertia is altered (B and C). The moment of inertia is greatest when the weight is moved further from the centre of rotation (i.e. greater d). So using the same bat weight, a player can manipulate the moment of inertia of the bat during warm-up by altering its distance from the handle.

The more particles that are further from the pivot, the larger is the moment of inertia. For example, if a baseball bat has a weight added to it, rather like the bat weights used by batters in warm-up, we can change the inertia of the bat by changing the placement of the weight (see Figure 7.1). Have you noticed younger cricketers or baseball and softball players holding their bat further down the handle? This reduces the distance from the hands – the centre of rotation – to the main mass of the bat and therefore reduces the bat’s moment of inertia. We use the same technique to swing a hammer or pick when we’re tired.

It is obviously impossible to measure the moment of inertia of every particle in an object. Instead, we calculate the radius of gyration (k) and multiply the square of this by the whole mass of the object. The radius of gyration describes the distribution of the mass relative to the centre of rotation. It is very different from the centre of mass, because particles further away from the pivot point have a greater influence, since the radius of gyration is squared (that is, I = mk²) and it changes as the centre of rotation changes.

The radius of gyration can be mathematically determined for many regular objects and used to calculate the moment of inertia, as shown in Table 7.1. We could, for example, pretend that a human is made of basic shapes such as rods or spheres (Figure 7.2) and then guess the moments of inertia. However, for less regular objects, such as human limbs, bats, clubs or rackets, the radius of gyration can be experimentally determined. One way of doing this is described in Box 7.1, although it is often easier to obtain the radius of gyration from an equipment manufacturer, from published tables or from research articles.

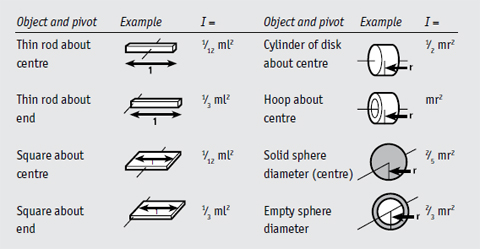
TABLE 7.1 Moments of inertia for regular objects (of uniform density).

FIG. 7.2 Most objects can be modelled as a series of common geometric shapes. This human is ‘built’ out of basic shapes of which the radii of gyration s can be relatively easily determined.

Many coaches and sport scientists do not need actual values for moment of inertia but only need to understand the principle to optimise sporting techniques; for them, values for radius of gyration are relatively unimportant. What is important is to understand that the moment of inertia (I) is a function of the mass of the object (m) and the square of its radius of gyration (k): I = mk². Since k is squared, it becomes very important. For instance, if the mass of an object were doubled then its moment of inertia would be doubled, but if the radius of gyration were doubled then the moment of inertia would be quadrupled (that is, 2² = 4). So, we still need to apply a force that causes rotation of the leg but it seems that changes in the radius of gyration of an object have a great effect on its moment of inertia and therefore the ease with which we can change its angular velocity.

BOX 7.1 CALCULATING THE MOMENT OF INERTIA OF OBJECTS BY THE COMPOUND PENDULUM METHOD

An object can swing freely if we suspend it by its centre of rotation. The radius of gyration can be measured about this point by examining the time it takes to swing. Short and light pendulums swing quickly, whereas long and heavy pendulums swing much slower. We can use this to measure the moment of inertia of an object suspended from a given point.

For example, consider a swinging cricket bat: a long bat will swing slower than a shorter one. We can determine the moment of inertia of the bats using the formula:

I = mgT²/4π²

You can see that the inertia of the bat increases when either the mass (m) or the period of swing (T) (the time that it takes for them to complete one full swing from the centre, to the side, back to the centre, to the other side, then to the centre again) increases. You know that I = mk², so if you know the mass of the bat you could then work out the radius of gyration.

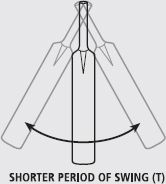
FIG. 1

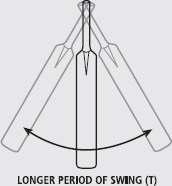
FIG. 2

Moment of force (torque)

Remember from Chapter 6 that the magnitude of the force causing rotation of the leg is defined as the moment of force; more simply, torque. The idea that torque can alter the rotation of an object with a given moment of inertia is similar to the idea that a linear force can alter the movement of a mass (Newton’s Second Law; F = ma). Therefore, we can say that:

The angular acceleration of an object is proportional to the net torque acting on it and inversely proportional to the inertia of the object: τ = Iα

Remember, I stands for inertia and the α stands for angular acceleration. You could re-write this equation α = τ/I, which shows that the angular acceleration of an object will be greater if the torque is increased or the moment of inertia is decreased. At the hip joint, strong muscles, including the gluteus maximus and hamstrings, produce forces at a distance from the hip joint (that is, a torque). The distance between the muscle and the joint centre is called the moment arm; obviously the bigger this is the more torque can be generated about the joint for a given level of muscle force (Figure 7.3). Adults usually have larger moment arms than children, so the adult will be stronger even if they have the same size muscles as the children. The moment arm is not affected by training: we can’t change it but we can improve the muscle forces. In our running example, we can definitely say that increasing the torque we apply will increase the angular velocity of the leg and therefore the linear speed of the foot since v = rω (as you saw in Chapter 2).

FIG. 7.3 The torque generated about a joint is the sum of all of the forces acting across their moment arms. In this example, the biceps brachii (upper arm flexor) is acting with a given line of force (F_muscle). The moment arm is the perpendicular distance from the centre of rotation of the joint to the line of muscle force. Increasing either the muscle force or the moment arm will increase the joint torque.

Calculating torque in a dynamic system (without equilibrium)

Previously you learned that we can calculate torque using the force and moment arm. In that case we can estimate the force of a muscle, such as that holding the arm steady in Figure 7.3, by determining the muscle force that provides a joint torque exactly equal and opposite to the torque created by the weight of the arm (i.e. torque generated by muscle = torque generated by weight of arm). Another way of putting it is that the sum of all the joint torques (or joint moments) is equal to zero (Στ = 0), and the system is in equilibrium.

This works perfectly well in a static situation or in a dynamic situation when the arm moves at constant angular velocity (i.e. no force is accelerating the arm). However, you now know that there is a relationship between torque, moment of inertia and angular acceleration. So if the arm were accelerating about the elbow, then clearly the muscle force must have been higher than in the case of static equilibrium. In this case, the torque created by the muscle must be equal and opposite to the torque created by the weight of the arm plus the torque required to accelerate the arm. So:

Στ = τ_muscle + τ_arm – Iα = 0

And therefore τ_muscle = -τ_arm + Iα

From these equations it can be seen that the torque created by the muscle (where a positive torque is in the anti-clockwise direction) must balance torque created by the arm weight (i.e. the arm weight is negative) and the torque accelerating the arm about the elbow (if the joint is flexing then the torque is positive, but if the joint is extending then we ‘add’ a ‘negative’ number and the torque is negative). Of course, in a more complex system you may need to calculate all the forces and all the torques in all directions, so you’ll have to use the equations you already know (e.g. F = ma)!

Angular momentum

But we have diverged slightly from the goal of answering our question, so I have another thing to discuss – what about the time? Surely we can change the momentum of an object more if we apply a force over a longer time? If we want to increase the velocity of a mass (that is, change its momentum) we could make use of the impulse–momentum relationship that we learned in Chapter 5. We now have a mass moving at an angular velocity, so it has angular momentum, H (although you might also see it as L in physics texts), and so we also have to apply an angular impulse (torque × time, τ·t).

Linear dimension	SI Unit	Angular dimension	SI Unit
Displacement	m	Angular displacement	rad
Velocity	m·s^–¹	Angular velocity	rad·s^-1
Acceleration	m·s^–²	Angular acceleration	rad·s^-2
Force	N	Moment of force or torque	N·m
Inertia	Equivalent to mass	Moment of inertia	kg·m²
Momentum	kg·m·s^–¹	Angular momentum	kg·m²·s^-1
Impulse	N·s	Angular impulse	N·m·s

TABLE 7.2 Angular equivalents of linear dimensions.

Everything in a linear sense has an angular equivalent. You can see this clearly in Table 7.2. The angular impulse–angular momentum relationship would be: τ·t = Iω, where a certain impulse creates a change in angular velocity of a certain amount in an object with a given moment of inertia.

We can examine the idea of angular momentum a little further. As you already know, any mass moving at a velocity has momentum (remember the big bus in Chapter 4). Our leg rotates or moves through an angle and therefore has angular momentum. Just like linear momentum, angular momentum is a function of mass and velocity, except in this case the velocity is angular (ω) and the mass is at a distance; that is, it has a moment of inertia (mk²). Angular momentum is actually a function of the moment of inertia and the angular velocity, H = Iω or H = mk²ω.

The reason it helps to write the mathematical formula is that we can see the effect of each part of the equation. For example, you can see that if the angular momentum (H) remains the same but the moment of inertia (I) is increased, then the angular velocity (ω) must have decreased (H =↑I × ↓ω). In the case of sprinting, this would not be beneficial. Where we want the leg to rotate quickly we would rather the moment of inertia decreased. Since we know that I = mk², we know we have to either reduce the mass of the leg (↓m) or keep the mass closer to the centre of rotation (↓k). Since k is squared, it is more important to keep the mass located close to the centre of rotation.

FIG. 7.4 In order to reduce the moment of inertia of the lower limbs, the fastest humans tend to have their leg mass distributed close to their hip (A). Their calf muscles (circled) are relatively small and their footwear is lightweight. Other animals such as the antelope (B) and cheetah (C) also have muscles that are high in the leg (large circle) with relatively little muscle mass placed lower down (small circle).

With respect to the swing phase in running, what can we take from this? We know we need a relatively straight leg when we land on the ground. This is because the linear velocity of the foot is greatest when it is further away from the hip (v = rω). We can’t bend at our joints to keep the mass closer to the hip joint but we can ensure that we don’t build up the distal muscles in the legs to a significant degree with strength training (for example, have small calf muscles; Figure 7.4) and we can wear light shoes. In this way, both the mass and radius of gyration are reduced and therefore the moment of inertia is smaller. If the angular momentum of the leg is the same, the angular velocity must increase.

Since the change in angular momentum of the leg is greater when the joint torque is produced over a longer period of time, increasing either the muscle force or the time over which it is developed would allow higher velocities to be achieved. Unfortunately, to increase the time of force application, we’d have to move the leg through a much larger range of motion. This would take longer, even if the velocity were higher. So the only practical thing to do is to improve the force developed by the muscles acting at the hip. This is where specific strengthening of the hip muscles would be beneficial.

THE ANSWER

We can now conclude that to move forwards more quickly we have to swing the leg backwards more quickly, so we need to increase the torque developed by the hip muscles, decrease the mass of the leg and ensure that the remaining mass is located as close to the hip joint as practically possible. Having a low leg mass, with that mass distributed proximally towards the hip rather than distally towards the foot, is typical of many of the fastest humans and is also common among animals that need high running speeds to hunt effectively or reduce the likelihood of being caught by others (Figure 7.4). But in running, we also have to get the leg to the front of the body again. How can we optimise that?

The recovery phase

The motion of moving the leg from in front to behind the body is the ‘swing phase’; the motion of moving it to the front again is the ‘recovery phase’. There is no point completing the swing phase quickly if we don’t complete the recovery quickly too, so what is the best way to do that? We know that we can increase the torque developed by the muscles but since the muscles that provide this torque are relatively small (compared to the large gluteal and hamstring muscles), we need to come up with another strategy. The leg’s angular velocity can be greater if the limb is lighter and the mass is closer to the hip joint. We have already sought to reduce the mass of the leg to improve the swing phase but in recovery we can also bend the leg up (flex it) underneath the body, as in Figure 7.5. Elite sprinters, and endurance runners for that matter, are able to bend their leg very effectively so that their moment of inertia is minimised and the angular velocity increased. Such a strategy is common in sports. As shown in Figure 7.5 (B), divers and gymnasts tuck their bodies very tightly when performing somersaults. Also, figure skaters start with their arms extended so that their spins are slow but then bring their arms close to their bodies so that the speed of spin increases. Athletes who change direction keep the arms and legs close to the body (often done by shortening the stride length), which is very important as the body rotates towards the new direction of movement.

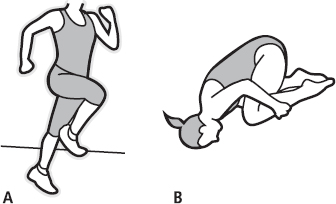
FIG. 7.5 Sprint (and endurance) runners flex their leg during the recovery phase to minimise the moment of inertia (A). Divers and gymnasts tuck their bodies to reduce their moment of inertia and therefore increase their angular velocity (rotation speed) (B).

The parallel axes theorem: a mathematical proof of the answer

While the answer is just about complete, there is one more thing that you should know. Any object that rotates has a moment of inertia: a leg swinging about the hip joint has a moment of inertia, as does any body segment that spins about its own axis. That means it is possible for a body segment to have two lots of moments of inertia. The thigh, for example, not only spins about the hip but also about its own axis (Figure 7.6). The axes about which the thigh spins are ‘parallel axes’, so the total moment of inertia of an object (or limb in our case) is equal to the two lots of moments of inertia.

FIG. 7.6 During running, the thigh not only rotates about the hip axis (left, white arrow), which is also called the remote axis, but also about its own local axis (right, grey arrow). The total moment of inertia is the sum of the moments of inertia about both the remote and local axes .

The moment of inertia of a body rotating about its centre of mass (I_CM) is usually known and is referred to as the ‘local’ term. The moment of inertia of a body rotating about its external pivot is equal to the product of mass and distance squared (mk²) and is called the ‘remote’ term. The total inertia (I_tot) = I_CM + mk². This is the parallel axes theorem.

There are a few questions left to answer. Does it matter whether the local term is included in the equation? How much of an effect does it have? We’ve also stated that reducing the mass of the limb and ensuring this mass is not distributed too distally (i.e. towards the foot) is important but how much of a difference can it actually make? How much does bending the leg in the recovery phase matter? We now have the tools to answer these questions, and the modelling approach we learned in Chapter 3 can help us.

•Step 1: As in Chapter 3, the easiest way to determine the effects of these things is to use dummy data to solve a problem and then alter each part of the problem separately to see what effect it has. In this example, we know that the angular momentum of the leg (the angular impulse provided by the muscle torque being developed over a period of time) is equal to the moment of inertia multiplied by the angular velocity (H = Iω). If we assume the muscles are working as hard as they can and therefore the angular momentum (H) remains constant, we can manipulate the moment of inertia (I) to see its effects on angular velocity (ω). The moment of inertia of the whole leg (I_leg) is equal to the sum of the moments of inertia of the foot, shank (lower leg) and thigh and the moment of inertia of each of these is equal to I_CM + mk². So we need values for the local and remote moments of inertia of each of these parts.

	I_CM	Mass (80 kg)	d_CM	d_CM-end	d_hip
Foot	0.0038	0.015 × mass = 1.2 kg	44.9%	0.127 m	0.90 m
Shank	0.0504	0.043 × mass = 3.44 kg	41.8%	0.188 m	0.60 m
Thigh	0.1052	0.103 × mass = 8.24 kg	40.0%	0.180 m	0.25 m

I_CM: moment of inertia of the segment measured about its own centre of mass (that is, local term). Measured in kg·m².

Mass: mass of segment assuming the mass of the runner was 80 kg.

d_CM: proportional distance from the top end of the segment to the centre of mass of it.

d_CM_-_end: distance in real-world units from the top end of the segment to the centre of mass of it.

d_hip: distance from the hip to the centre of mass of the segment, measured from the video analysis.

Note: Moment of inertia data from Whitsett, C.E. (1963). Some dynamic response characteristics of weightless man, AMRL Technical Documentary Report 63–70, Wright-Pearson Air Force Base, Ohio: AMRL, 11.

TABLE 1

To get realistic data, I carried out a simple video analysis, as shown in Chapter 3. I measured the angular velocity of the limb and the distances of the centres of mass of each segment from the hip joint, according to the data in Table 6.1 (I put markers on the athlete’s leg so I knew where these were when I watched the video). I took local moments of inertia from a published table (see I_CM Table 1) and used the mass proportions you saw in Table 6.2 (the athlete has a mass of 80 kg).

From the video, I also found that the angular velocity of the leg, measured at the thigh, was 460°·s^-1 or about 8 rad·s^-1, immediately before the foot hit the ground. The angles of the other joints can be assumed to be constant over this small part of the stride (that is, the leg is relatively straight and moves as a single object) so each of them is also swinging around the hip joint and their own centre of mass at 8 rad·s^-1.

• Step 2: Draw a diagram to visualise the problem.

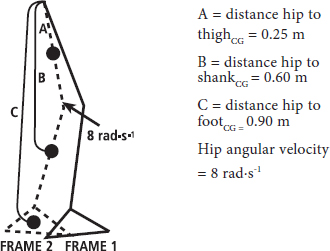
FIG. 7.7

•Step 3: Calculate the angular momentum. To keep it clear, I’ve written the mathematics in full in the following table:

	Local term H = I_CMω↑(kg·m²·s^-1)	Remote term H = mk²ω (kg·m²·s^-1)	Total (Local + Remote) (kg·m²·s^-1)
L_foot	0.0038 × 8 = 0.03	1.20 × 0.9² × 8 = 7.78	7.81
L_shank	0.0504 × 8 = 0.40	3.44 × 0.6² × 8 = 9.91	10.31
L_thigh	0.1052 × 8 = 0.84	8.24 × 0.25² × 8 = 4.12	4.96
Total	1.28	21.80	23.08
%	5.5%	94.5%	100%

TABLE 2

At present, the numbers 1.28, 21.80 and 23.08 kg·m²·s^-1 probably don’t mean too much to you but they will make a little more sense when we re-do the calculation for the leg swinging in the recovery phase, because you’ll have something to compare against.

This solution provides a starting point from which to manipulate masses and distances to see how much they affect limb velocity.

Effect of reducin g limb mass

With these masses and distances and an angular momentum of 23.08 kg·m²·s^-1, the limb was moving at 8 rad·s^-1 (which is very, very fast – if the leg were to keep moving through a complete circle, it would go around 1.3 times in a second!). It also shows us that, for the leg, the local terms contribute only 5.5% to the overall angular momentum (and moment of inertia), so they are relatively less important. In a limb where the segments are lighter or of different length (for example the arm), the remote to local ratio would be different. You shouldn’t assume that the local term is insignificant in all cases.

What we really want to know is what effect losing a few kilograms of body mass might have. Let’s say our sprinter lost 5% of their body mass proportionally over the body. Their mass is now 76 kg (5% of 80 kg = 4 kg) and the masses of the limbs will be altered: the masses of the foot, shank and thigh will be 1.14, 3.27 and 7.83 kg, respectively. If we take account of these new masses, the total moment of inertia will be lowered (we’ll assume the local moment of inertia will stay the same), as shown in I_CM Table 3.

Of course, our hip muscles can still provide the same torque over the same time period (that is, impart the same momentum), so we could move the leg at a higher angular velocity (remember H = Iω, so if I is less, ω increases). To get our angular momentum from 21.92 to 23.08 kg·m²·s^-1, we’d need to increase the angular velocity by 5% ((23.08 – 21.92)/23.08 ×↑100% = 5.0%).

	Local term H = I_CMω (kg·m²·s^-1)	Remote term H = mk²ω (kg·m²·s^-1)	Total (Local + Remote) (kg·m²·s^-1)
L_foot	0.0038 × 8 = 0.03	1.14 × 0.9² × 8 = 7.39	7.42
L_shank	0.0504 × 8 = 0.40	3.27 × 0.6² × 8 = 9.42	9.82
L_thigh	0.1052 × 8 = 0.84	7.83 × 0.25² × 8 = 3.92	4.68
Total	1.28	20.73	21.92
%	5.8%	94.2%	100%

TABLE 3

As the mass of the limb is reduced by 5%, the angular velocity increases by 5%. Five per cent of 8 rad·s^–¹ is 0.4 rad·s^–¹, so if the angular momentum stays the same but the body mass, and therefore inertia, is reduced by 5%, the angular velocity of the limb will increase to 8.4 rad·s^–¹. If the limb was about 1 m long (from the hip joint to ball of foot), then the linear velocity of the foot (rω) would increase from 8 m·s^–¹ to 8.4 m·s^–¹.

Is this enough to make a difference? You could also say that if you held this speed for the final 60 m of a 100 m race and the backward speed of the foot was translated exactly into forward speed of the body, you’d improve that part of the race by 0.36 s, which is very significant (you can do the mathematics on your own). Theoretically, decreasing body mass , or more importantly decreasing limb mass, can improve running performance significantly. You should remember that a sprinter also needs to be able to generate high forces, which requires significant muscle mass: there is a trade-off to be considered here.

Effect of altering mass distribution

What if we were able to move the masses up the leg a little? Relocating the mass slightly closer to the centre in a segment won’t change the local moment of inertia considerably (think of it as taking a small mass located at a distance from the local axis and placing it on the other side of the axis but at the same distance: the same mass is still placed the same distance from the axis). So we will keep this the same but assume that we could move the centre of mass of the thigh and shank segments about 2 cm (0.02 m) up the leg.

	Local term H = I_CMω (kg·m²·s^–¹)	Remote term H = mk²ω (kg·m²·s^–¹)	Total (Local + Remote) (kg·m²·s^–¹)
L_foot	0.0038 × 8 = 0.03	1.20 × 0.9² × 8 = 7.78	7.81
L_shank	0.0504 × 8 = 0.40	3.44 × 0.58² × 8 = 9.26	9.66
L_thigh	0.1052 × 8 = 0.84	8.24 × 0.23² × 8 = 3.49	4.83
Total	1.28	20.53	22.30
%	7.9%	92.1%	100%

TABLE 4

As shown in I_CM Table 4, the angular momentum is now 22.30 kg·m²·s^-1. If we were to keep the angular momentum the same, we’d need to increase the velocity by 3.4% (23.08–22.30)/23.08 × 100 = 3.4). If you had two identical runners but one had the centre of mass of their thigh and shank segments just 2 cm closer to the top, we estimate that they would run about 3.4% faster, which at top speed over 60 m would reduce running time by 0.25 s. This is a great deal, considering an Olympic medal might be decided by 0.01 s!

This highlights the importance of mass being distributed higher up the limbs. Kumagai and colleagues (2000) used ultrasound imaging of the thigh muscles of sprinters to show that their muscle mass is larger towards the top of the thigh than the bottom, compared to untrained individuals. Some of the difference between these two populations could be attributed to the genes of the individuals concerned; however, it has previously been shown that muscle mass gains from strength training do not occur evenly throughout the muscles. Both Häkkinen and colleagues (2001) and Narici and colleagues (1996) found that hypertrophy of the lateral thigh muscle was greatest in distal regions (further down the thigh) after strength training. Others (for example, Housh and colleagues (1992) and Blazevich and colleagues (2003)), found that middle and proximal sites showed greater hypertrophy. The extent to which muscle mass distribution can be altered is still not known, nor is it known how muscle distribution is altered by different forms of training. However, some evidence indicates that training type might influence it, with training at longer thigh muscle lengths eliciting different adaptations than training at shorter muscle lengths (e.g. Noorkoiv et al., 2014) and training at higher movement speeds eliciting different adaptations to training at slower speeds (Earp et al., 2015). Either way, physical training does seem to influence it, so there is a need to monitor the effects of training on muscle mass distribution.

Effect of leg flexion in the recovery phase

Finally, we wanted to know how much of a difference it would make to flex the leg in the recovery phase. The legs have to move through the same range of motion in the same amount of time, so if the swing leg was moving at 8 rad·s^-1 then the recovery leg must be moving at -8 rad·s^-1 (we might just call it 8 rad·s^-1 but remember it is going the other way). From the video, I extracted the information shown in Figure 7.8 and did the calculations below (I_CM Table 5).

	Local term H = I_CMω (kg·m²·s^–¹)	Remote term H = mk²ω↑(kg·m².s^–¹)	Total (Local + Remote) (kg·m²·s^–¹)
L_foot	0.0038 × 8 = 0.03	1.20 × 0.35²× 8 = 1.18	1.21
L_shank	0.0504 × 8 = 0.40	3.44 × 0.35² × 8 = 3.37	3.77
L_thigh	0.1052 × 8 = 0.84	8.24 × 0.25² × 8 = 4.12	4.96
Total	1.28	8.67	9.94
%	12.8%	87.2%	100%

TABLE 5

FIG. 7.8

Because the in ertia of the leg has decreased so much, the angular momentum at 8 rad·s^-1 would only be 9.94 kg·m²·s^-1. Since the angular momentum of the leg is proportional to the angular impulse (impulse–momentum relationship) and the time over which the torque is applied is the same as for the swing leg, the torque generated at the hip on the recovery leg must be only 56.9% ((23.08/9.94)/23.08 × 100% = 56.9%) of that provided to the swing leg. This makes sense, given that the muscles that pull the leg forwards (the hip flexors) are much smaller than the larger gluteal and hamstrings muscles that propel the leg backwards. So, the moment of inertia is substantially reduced by flexing the leg during recovery. This allows the smaller hip muscles to move the leg forwards at the same velocity as the swing leg is moved backwards.

Once again, we have used mathematical modelling to see how important each factor is to our ability to move. We know that reducing limb inertia is important. This can be done either by reducing the mass of the limb or moving the mass closer to the hip (that is, moving it up each segment of the leg), both of which have relatively similar effects. Flexing the leg in the recovery phase also seems important, to reduce limb inertia and therefore increase angular velocity, given that the smaller muscles that perform this action are less able to generate torque.

It must be remembered that increasing the angular impulse (τ·t) is also important to accelerate the leg. The moment arm across which the muscles of the hip move cannot be changed and we would rather not increase the time over which torque is produced (because the limbs would have to move through a larger range, which is counter-productive) but we can use strength and speed training techniques to increase the muscles’ force-generating capacities. These factors should all be considered together when searching for a biomechanically optimum running technique.

HOW ELSE CAN WE USE THIS INFORMATION?

In Chapter 3, we found that longer legs should allow a greater foot speed during running and walking if the hip angular velocity remained the same, but now you know that it requires more force to accelerate a longer leg since not only would it weigh more but much of the mass would be distributed away from the hip joint. So athletes with longer legs probably have a greater need to develop their ability to generate high forces through, for example, weight training. Runners and walkers with shorter limbs require less force to increase their angular velocity but their foot speed for a given angular velocity would be less, so they should focus largely on training with exercises that increase the absolute speed of movement.

Knowledge of these principles can help us to teach children, or those with lesser strength, to learn skills involving implements. By holding the implement further from the end of its handle the radius of gyration is reduced and therefore the moment of inertia of the implement decreases. This means that less force is required to swing it and the child can more easily practise an appropriate technique. We can also use this information to determine that it might be easier to bend the recovery arm during crawl (freestyle) swimming; to bring the arms close to the body during diving, gymnastics and other acrobatic sports to reduce the body’s moment of inertia and thus increase rotation al velocity; or to rapidly shorten the non-throwing arm immediately prior to release of objects such as the discus and shot and ball hitting in tennis. Alternatively, we can stop the rotation of the upper body during kicking by rapidly extending the arms as the leg swings through during kicking movements in rugby and football (soccer) or to stop rotations during acrobatic sports. Learning to manipulate our body segments during sports provides the possibility to rotate or create stability of our body or its segments at any point during the execution of a movement.

Finally, we should answer the question posed in Chapter 1 regarding slower athletes evading faster athletes with a well-timed swerve. This can be done, because the slower athlete will have a lower moment of inertia as they swerve about a central point (think of the runner being a mass rotating about a centre of rotation). It will require less of an angular impulse to accelerate in a curve or they will accelerate more for a given angular impulse (remember that a change of direction holding constant speed is an acceleration , because velocity changes when direction changes; this angular acceleration while speed is constant is often called centrifugal acceleration). The faster runner will have a higher angular momentum and require a much greater angular impulse, or they will not be able to change direction (that is, accelerate) as quickly. If the slower runner waits until the faster runner is about to catch them before swerving, the faster runner will more than likely run past them. In evasion sports, this technique is very effective. The same technique has been seen in animals evading capture.

Useful Equations

torque (moment of force) (τ) = F × d, where d is the moment arm of force

also, τ =Iα

sum of moments or sum of torques (ΣM or Στ) τ_t = τ₁ + τ₂ + τ₃_...

sum of moments or sum of torques in dynamic system Στ = 0 and Στ – Iα = 0

angular momentum (H or L) = Iω or mk²ω

angular impulse–momentum relationship, τ·t = Iω

impulse (J) = F × t or ∆mv

moment of inertia (I) = Σmr² or mk²

total moment of inertia (parallel axes theorem) (I_tot) = I_CM + md²

References

Blazevich, A.J., Gill, N.D., Bronks, R., Newton, R.U. (2003). ‘Training-specific muscle architecture adaptation after 5-wk training in athletes’. Medicine and Science in Sports and Exercise, 35: 2013–22.

Earp, J.E., Newton, R.U., Cormie, P., Blazevich, A.J. (2015). ‘Inhomogeneous quadriceps femoris hypertrophy in response to strength and power training’. Medicine and Science in Sports and Exercise, 47: 2389–97.

Häkkinen, K., Pakarinen, A., Kraemer, W.J., Häkkinen, A., Valkeinen, H., Alen, M. (2001). ‘Selective muscle hypertrophy, changes in EMG and force and serum hormones during strength training in older women’. Journal of Applied Physiology, 91: 569–80.

Housh, D.J., Housh, T.J., Johnson, G.O., Chu, W-K. (1992). ‘Hypertrophic response to unilateral concentric isokinetic resistance training’. Journal of Applied Physiology, 73: 65–70.

Kumagai, K., Abe, T., Brechue, W.F., Ryushi, T., Takano, S., Mizuno, M. (2000). ‘Sprint performance is related to muscle fascicle length in male 100 m sprinters’. Journal of Applied Physiology, 88(3): 811–16.

Narici, M.V., Binzoni, T., Hiltbrand, E., Fasel, J., Tettier, F., Cerretelli, P. (1996). ‘Changes in human gastrocnemius architecture with joint angle, at rest and with isometric contraction, evaluated in vivo’. Journal of Physiology (London), 496: 287–97.

Noorkoiv, M., Nosaka, K., Blazevich, A.J. (2014). ‘Neuromuscular adaptations associated with knee joint angle-specific force change’. Medicine and Science in Sports and Exercise. 46: 1525–1537.

Related Websites

The Physics of Sports (http://www.topendsports.com/biomechanics/physics.htm). Website investigating the applications of physics in sports.

Hyperphysics (http://hyperphysics.phy-astr.gsu.edu/hbase/mi.html; http://hyperphysics.phy-astr.gsu.edu/hbase/amom.html). Basic and advanced discussions on angular momentum and moment of inertia, including maths simulations and calculations.

Momentum Machine, Exploratorium.edu (http://www.exploratorium.edu/snacks/momentum_machine; http://www.exploratorium.edu/snacks/bicycle_wheel_gyro.html). A series of websites linked from the Exploratorium website that demonstrates principles of angular kinetics through experimentation. Searches for other principles are also possible.

ZonaLand: National Science Teachers Association (http://zonalandeducation.com/mstm/physics/mechanics/mechanics.html). Clear descriptions and animations of the basic principles of mechanics.

The Physics Classroom – Tutorials (http://www.physicsclassroom.com/Class/). Lessons on basic physics concepts.

The Physics Classroom – Multimedia tools (http://www.physicsclassroom.com/mmedia/). Interactive tools and movies depicting basic physics concepts.