
What is the optimum angle of trajectory or flight path (that is, the angle thrown relative to the ground) for a shot-putter aiming to throw the maximum distance? (Hint: not 45°.) What factors affect maximum throwing distance and to what degree?

By the end of this chapter you should be able to:
•List the factors that influence an object’s trajectory
•Use the equations of projectile motion to calculate flight times, ranges and projection angles of projectiles
•Design a simple model to determine the influence of factors affecting projection range
•Create a spreadsheet to speed up calculations to optimise athletic throwing performance
•Complete a video analysis of a throw to optimise performance
Projectile motion refers to the motion of an object (for example a shot, ball or human body) projected at an angle into the air. Gravity and air resistance affect such objects, although in many cases air resistance is considered to be so small that it can be disregarded. A projected object can move at any angle between horizontal (0°) and vertical (90°) but gravity only acts on bodies moving with some vertical motion.
Trajectory is influenced by the projection speed, the projection angle and the relative height of projection (that is, the vertical distance between the landing and release points; for example, in a baseball throw that lands on the ground, the vertical distance is the height above the ground from which the ball was released).
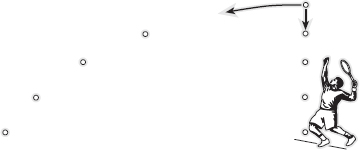
FIG. 3.1 Tennis ball trajectory. Gravity accelerates the ball towards the ground at the same rate regardless of whether the tennis player leaves the ball to fall freely or hits it perfectly horizontally. However, the trajectory of the ball is different in these two circumstances.
Projection speed
The distance a projectile covers, its range, is chiefly influenced by its projection speed. The faster the projection speed, the further the object will go. If an object is thrown through the air, the distance it travels before hitting the ground (its range) will be a function of horizontal velocity and flight time (that is, velocity × time, as you saw in Chapter 1). In Figure 3.1, you can see that a ball thrown in the air by a tennis player will hit the ground at the same time regardless of whether it is hit horizontally by the player or allowed to fall freely but the trajectory of the ball is different.
If the projectile moves only vertically (for example, a ball thrown straight upwards), its projection speed will determine the height it reaches before gravity accelerates it back towards the Earth. If we don’t take air resistance into account, gravity accelerates all objects at the same rate: 9.81 m·s-2 barring some regional variations around the planet*. This is about the same acceleration a lion can achieve or twice the acceleration of the fastest humans. To get an idea of how fast it is, drop a small ball from a height of a few metres and watch it accelerate as it falls.
What might position (displacement), velocity and acceleration graphs look like for a ball thrown vertically?
Projection angle
The angle of projection is also an important factor affecting projectile range. If an object is projected vertically, it will land back at its starting point, after gravity has pulled it back to Earth (remember, the object is accelerated positively the whole way if ‘down’ is assigned the positive direction). So, its range is zero. If the object is projected horizontally from ground level, it will not get airborne, so again its range is zero. It can also be projected at angles between 0° and 90°, where it will travel both vertically and horizontally. At a projection angle of 45° the object will have an equal magnitude of vertical and horizontal velocity and its range will be maximised, as you can see in Figure 3.2. However, we need to take into account other factors that influence projectile range in order to answer our question.
FIG. 3.2 The maximum range of a projectile is determined partly by its angle of projection. When the angle is greater (e.g. 90° and 70° in this example), the object attains a great vertical height but lesser range. When the angle of projection is small (e.g. 30° in this example) the object doesn’t have sufficient vertical velocity to attain a significant range. At a projection angle of 45° there is an equal magnitude of vertical and horizontal velocity, and range is maximised.
Relative height of projection
The relative height of projection is the vertical distance between the projection point of an object and the point at which it lands. If the projection point is higher than the surface on which the object lands, the relative height is positive. If the projection point is lower than the surface on which the object lands, the relative height is negative. You can see the importance of relative height in Figure 3.3; the optimum angle decreases as the relative height becomes more positive but the optimum angle increases as relative height becomes more negative. One way to think of this is that if we are projecting an object from a position below where it will land, we have to give the object some extra flight time, so we increase the vertical velocity and therefore the angle of projection. If we project an object from a point higher than where it will land, the object already has some extra flight time. Instead of giving the object maximum vertical velocity, we can give it a little more horizontal velocity (so the angle decreases). So, if you want to throw this book off a cliff, you should send it horizontally!
FIG. 3.3 Effect of the relative release height on optimum projection angle. When the relative height is positive (A), the optimum angle is less than 45°. When the relative height is negative (B), the optimum angle is greater than 45°.
If a shot-putter released the shot from about two metres above the ground, the relative release height would be +2.0 m and the optimum release angle would be less than 45°. How do we know what the optimum angle is? First, we need to understand the equations of projectile motion, or the equations of uniform acceleration as Galileo originally formulated them nearly four hundred years ago (in 1638).
The equations of projectile motion
Legend has it that Galileo proved that gravity accelerates all objects at the same rate regardless of their mass by dropping two differently-sized cannon balls from the Leaning Tower of Pisa, in Italy. To me, this sounds like fun, much like blowing things up or turning rusty iron into gold. Unfortunately it’s completely untrue: Galileo performed a much more boring experiment in which he rolled balls of different masses down a ramp. He noticed that they all got faster as they rolled and that the increase in speed was dependent on the square of time (t2) but not on the mass of the ball. Galileo had read the work of Niccolo Tartaglia, who had drawn the motions of a projected object and realised they followed a curved path – which the Greeks called a parabola – and was able to use this information to determine equations to predict the flight of objects. We now use the equations to help us understand how all objects move under constant acceleration such as when an object is under the influence of gravity, i.e. in projectile motion.
It is perhaps important to note that Galileo was one of the first to perform well thought-out experiments to prove/disprove hypotheses, when most before him had used theoretical reasoning before checking if the mathematics backed up their thoughts. In this regard, Galileo was one of the first true scientists, whereas many before him were purely philosophers.
The three equations you should know – and memorise – are:
• v = u + at
Final velocity (v) = initial velocity (u) plus acceleration multiplied by time (at).
•v2 = u2 + 2as
Final velocity squared (v2) = initial velocity squared (u2) plus two times acceleration multiplied by displacement (2as).
•s = ut + ½ at2
Displacement (s) = initial velocity (u) multiplied by time (t) plus half of acceleration multiplied by the square of time (½ at2).
BOX 3.1 USE OF OTHER SYMBOLS IN PROJECTILE MOTION EQUATIONS
Unfortunately symbols that denote scientific quantities vary between different countries. In many cases you’ll probably see these three equations written as:
vf = vi + at
vf2 = vi2 + 2as
s = vit + ½ at2
where v is the velocity and the subscripts f and i refer to ‘final’ and ‘initial’, respectively. Check with your teacher to find out which symbols you should use.
Let’s look at an example of the use of the first equation. A batter hits a ball straight up in the air. It takes the fielder a moment to gauge the trajectory of the ball and so he or she doesn’t start to run towards the ball until it is at the top of its trajectory. When a ball is at the top of its trajectory, its vertical velocity is briefly zero and so we can say its ‘initial velocity’ is zero before it begins to fall. If 2.2 s elapse before the fielder finally gets their hands to the ball, what will its vertical velocity be when it’s caught? (Figure 3.4 shows the problem schematically.) We can simply plug the numbers into the equation to see that:
v = u + at
then v = 0 + -9.81 × 2.2
= -21.6 m·s-1 or -77.6 km·h-1
You could find v, u or t by re-arranging the equation appropriately (see Appendix B if you are unsure how to do this).
As an example of the use of the second equation, I might ask how far off the ground the ball was at the top of its trajectory, given that it hit the hands at 21.6 m·s-1 (assuming that the fielder caught the ball only millimetres above the ground):
v2 = u2 + 2as
If we know v, u and a (using the standard Earth value of 9.81 m·s-2) we can re-arrange the equation thus:
v2 – u2 = 2as
u2 was added to 2as, so in moving it to the other side of the equation it becomes a subtraction. However, we need s on its own, so we re-arrange again to:
(v2 – u2) /2a = s
2a was multiplied by s; in moving it to the other side of the equation it becomes a divider. So:
s = (v2 – u2) /2a
s = (466.6 - 0)/19.6
= 23.8 m
If the ball fell 23.8 m into the hands, and the hands were effectively on the ground, the ball must have gone 23.8 m high.
Finally, we have the equation s = ut + ½ at2. If I told you that a 10 m platform diver initiated a dive from a handstand position with an initial vertical velocity of zero (that is, they fell straight down, although they would have had some horizontal velocity as well), how long would they take to hit the water? We could re-arrange the equation as we did above, but in this case the initial vertical velocity is zero, so ut equals zero (any number multiplied by zero equals zero). So:
s = ½ at2
t2 = s/½ a
t2 = 10/4.9 = 2.0 s
This gives us t2, so we can find its square root to get t:
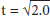
= 1.4 s
This assumes that the centre of mass of the diver’s body actually falls 10 m in 1.4 s: the actual time for the hands to enter the water might vary a little. But it still isn’t very long to complete a triple somersault with a few twists!
FIG. 3.4 When the batter hits the ball in the air, the ball has both vertical (vv) and horizontal (vh) velocity. The vertical velocity decreases as the ball reaches the top of its trajectory until it momentarily reaches zero velocity. We use this as the initial velocity (u) to help solve the problem. Acceleration due to gravity is always 9.81 m·s-2, so we can write that down immediately. The time taken to hit the hands (tdown) is 2.2 s. Drawing a schematic helps us to understand the problem. We can now use equations of projectile motion to solve the problem.
THE ANSWER
So you can see that we can use these equations to understand vertical motion (that is, under the constant acceleration of gravity) just as we used the equations of linear motion from Chapter 1 to understand motion without constant acceleration. Where does this leave us with our original question? Let’s use these new equations to find the answer. Follow the process below slowly, and think about what is accomplished in each step.
•Step 1: To know how a variable affects an outcome, it is useful first to put in some dummy (fictional) data and solve the problem using that. We can then see what happens if we change some of the numbers. So, we might put in some dummy data for angle, velocity and relative height, and so on, and then find the range. Then we can change the angle to see if range increases or decreases. At some point, we’ll know at which angle the range was greatest. This is another type of modelling, which is different from the modelling we used in Chapters 1 and 2.
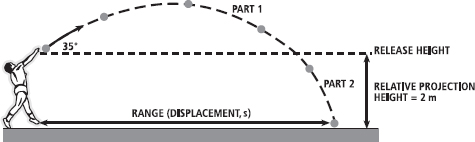
We will assume an initial projection velocity of 14 m·s-1, which is about right for a good thrower, and a release angle of 35°, which is reasonably common (remember, we know the answer must be less than 45°). We will also assume that the shot was released from a height of 2 m above the ground (that is, a positive relative height of release).
We know that: (1) v = u + at, (2) v2 = u2 + 2as, and (3) s = ut + ½ at2 and also that without acceleration, v = s·t-1. It is important to remind ourselves of these.
•Step 2: Draw a diagram to visualise the problem. I shall divide the problem into two parts: Part 1 to calculate the range as if the shot landed with a relative projection height of zero and Part 2 to calculate the ‘extra’ range.
•Step 3: Determine a plan of attack. In simple problems, you might determine which equation to use by looking at what you know and what you’re trying to find out. In this case, we know that v = s·t-1, so s = v × t. So, if we know the horizontal velocity and the time of flight, we can calculate the range.
•Step 4: Calculate the initial horizontal velocity (uh). (If necessary, refer to the cos, sin and tan rules in Box 1.1 or Appendix C.) So we can work out the horizontal velocity thus:
cos 35° = adjacent/hypotenuse = uh/14 m·s-1
uh = cos 35° × 14 = 11.47 m·s-1 or approximately 11.5 m·s-1
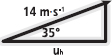
FIG. 3.6
•Step 5: Calculate the flight time. This needs to be done in two parts. First, we calculate the time for the shot to rise to its peak height and back to the starting (release) height; second, we calculate the time to fall the further 2 m to the ground.
•Part 1: There are two things to remember always: (1) the flight time of an object equals time up plus time down, so if it starts and finishes at the same vertical height the total time equals time up multiplied by two, and (2) the vertical velocity or final velocity of an object moving upwards is always zero because it stops briefly at the top of its trajectory before falling back down, so we know that the final velocity, v, also equals zero. Just as we calculated the initial horizontal velocity above, we can calculate the initial vertical velocity using the sin rule. For this calculation, we can use either v = u + at or t = (v – u)/a.
uv (initial vertical velocity) = sin 35° × 14 m·s-1
= 8.03 m·s-1
So t = (0 – 8.03)/-9.81 = 0.82 s
and the total time (time up plus time down) = 1.64 s
•Part 2: We know the initial vertical velocity of the shot is 8.03 m·s-1, because if it leaves the hand with this vertical velocity it must attain it again as it falls back past the level of the hand, but we don’t know the final velocity as it is about to hit the ground. We could use the equation s = ut + ½ at2 but this requires us to understand how to solve a quadratic equation. If you want to try, have a look at Box 3.2. Fortunately, there is another way: we can use the equation v2 = u2 + 2as to find the final vertical velocity and then use v = u + at to find the time. (I worked out this method by looking at the equations and thinking about what I already knew. I then realised that if I had v the problem would be easy, so I sought a way to do that. The two-step process isn’t as hard as it might look at first.) Either way:
v2 = u2 + 2as
v2 = -8.032 + 2 × -9.81 × 2 = 103.7
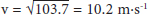
We then use the equation ‘v = u + at’ to find that time = 0.22 s.
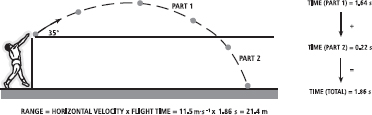
So now we know that the time for Part 1 was 1.64 s and the time for Part 2 was 0.22 s, so the total flight time was 1.86 s. If the initial horizontal velocity was 11.5 m·s-1 and the range = horizontal velocity × flight time, then the range = 11.5 × 1.86 = 21.4 m. Not a bad throw! But is it the best possible?
We now need to take the range and release velocities (vertical and horizontal) and everything else we know and recalculate with lots of different release angles. When the distance is greatest, we’ll have the optimum. Doing this by hand could take a long time, but we can speed things up by using a spreadsheet, such as Microsoft Excel™.
If you don’t know how to write formulae in spreadsheets, don’t worry, just type everything exactly as you see below and it will work (including the ‘=’ signs). You might consider learning how to do these things if you are serious about optimising athletic techniques and you certainly should if you are studying biomechanics at university. Type the equations below into the cells of the spreadsheet (don’t put anything into the cells labelled ‘Blank’):


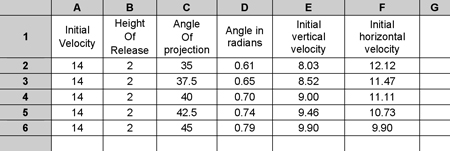
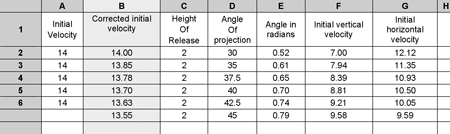
If you type the numbers 14, 2 and 35 into row 2 of columns A, B and C of the spreadsheet it should then look like this (format the cells to display to only two decimal places to make it easier to read):


The answer (column K) differs slightly from the worked answer (21.29 in the table, 21.4 in the worked answer) because we rounded out the numbers in the hand calculation. For example, we used 11.5 m·s-1 instead of 11.47 m·s-1 for the initial horizontal velocity.
If you now copy and paste the formulae in each cell into the cells in the rows below, you can enter different numbers for projection angle and see how this affects throw distance (or just type a new number into the ‘Angle of projection’ cell (C2) and see what happens to the throw distance). With some new figures entered, the spreadsheet looks like this:
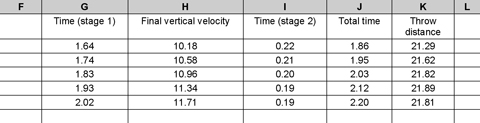
You’ll notice that the distance at 45° (row 6) was less than the distance at 42.5°; the throw is longer if the projection angle is a little less than 45°. This makes sense, given that earlier we found that if an object lands vertically below its release point (that is, it has a positive relative height), the optimum angle is less than 45°. Using the spreadsheet, we can see the optimum is around 42.5°. If we had entered more data points (angles of release of, for example, 40, 40.5, 41, 41.5°) we could have an even more accurate record. Lichtenberg & Wills (1978) showed that the optimum for their ‘thrower’ was about 42.3° but this varies as release speeds and release heights are changed. You can see this for yourself: put some fictional numbers into the ‘Initial velocity’ and ‘Height of release’ columns and see how this affects throw distance and the optimum angle of projection. How do these theoretical figures compare with real data: the known release angles of elite shot-putters?
Interestingly, they don’t compare well. Is the theory or the shot-putter wrong? Elite throwers project the shot at angles much less than 42.5°; typically 36° to 37° (Hubbard, 1989). There are two possible reasons for this: first, the more vertically the shot is thrown, the more the shot-putter is working against gravity to accelerate it, so the projection (release) velocity of the shot will be less. The flatter they throw it, the less they have to push against gravity and so can accelerate it to a higher velocity. (Release velocity is very important, as you know if you manipulate it in your spreadsheet, so throwing at a flatter angle is important.) Second, because of how the chest and shoulder muscles work together in the throw, we can produce more force if we push outwards in front than if we push upwards. For example, most people can bench-press a greater weight than they can press above their shoulders. If we produce more force, we can accelerate the shot to a greater velocity. So it seems a lower angle is optimum because the release velocity is greater.
Can we factor the effect of projection angle on projection velocity into our spreadsheet? Yes: you could perform a simple analysis of a number of video-recorded throws, to determine how release speed is affected by release angle (see Special Topic: Basic video analysis). Data from Hubbard et al. (2001) shows that release velocity decreases by about 1.7 m·s-1 for every increase in angle of 1 rad (57.3°) above horizontal. The increase in release height that might come from having the arm raised to increase the angle makes very little difference (De Luca, 2005), so we don’t have to factor this into our work. (I’m disregarding the fact that the release point is more in front of the body when the angle is less, where the shot would start a few centimetres further out.) We can put all of this information into our spreadsheet thus:


You’ll notice I have inserted a new column B. Cell B2 is a copy of the value entered in A2, whereas cell B3 starts to calculate the difference in initial velocity. (In Excel, the $ symbol means ‘fix this reference’; in this example, the formula will always be calculated using the value in cell D2.) We are calculating how different the new release angle is from the smallest and correcting by 1.7 m·s-1 for every radian (or 57.3°).
Notice also that I’ve had to change every other cell, since each value is now in a different column. You should re-check your spreadsheet to make sure it’s calculating correctly. If it is, you should get the values shown below. I’ve started from an angle of projection of 30° in this example:
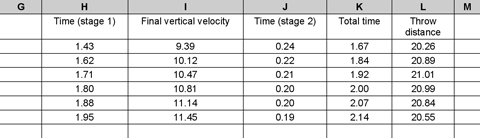
So, it looks as if the optimum angle for our shot-putter is about 37.5°. This is much more in line with the practice of the world’s elite throwers (approximately 36°–37° (Hubbard, 1989)). Again, it would be more accurate if we used more data with projection angles that differed by only half a degree or so. Either way, we can see it makes a big difference to think about the problem more broadly and include the effect on release velocity of trying to throw at greater angles as well as only considering how projectiles move once they are released. To demonstrate the difference more effectively, I constructed a scatterchart of the data as shown in Figure 3.8. (Use the graphing wizard in Excel to create a scatterchart, choose the appropriate x and y columns and add a line of best fit. Choose a second order polynomial, or quadratic, curve.)
BOX 3.2 THE QUADRATIC FORMULA
We often want to put data into equations and to find out something that we don’t know. Sometimes, there are two unknowns in one equation, for example when you are trying to find a value for time (t) using the equation s = ut + ½ at2. We could arrange the formula so it is in quadratic form like this: ½ at2 + ut – s = 0 and solve using the quadratic formula:
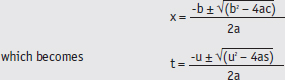
Where acceleration (a) is ‘a’, initial velocity (u) is ‘b’ and displacement or height of release (s) is ‘c’.
If we put in data of a = 9.81 m·s-2, u = 8.03 m·s-1 and s = 2 m, we get answers of +0.22 s and -1.86 s. This literally means that in parabolic flight, the object would have passed the 0 m point at both 0.22 s after release (which seems appropriate) and 1.86 s before release (which is not possible).
Sometimes, having two answers makes good sense. For example, if we wanted to know when an object in parabolic flight passed a point 2 m above the ground, we might find answers of 2.1 s and 6.8 s, which would be about right in the example in Figure 1. Either way, we know that 0.22 seconds is fair and we would use that.
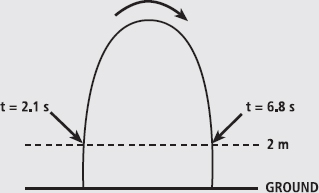
FIG. 1
FIG. 3.8 Graph of throw distance versus angle of release with (dark diamonds, bottom curve) and without (open squares, top curve) correcting for the effects of angle of release (x-axis) on release velocity (y-axis). The optimum angle is lower when the correction is made.
To summarise, we have seen that: 1) using just a few equations we can work out how an object will behave when it becomes a projectile; 2) a projectile’s motion is influenced by its projection speed, projection angle and the relative height of release as well as by how much force we can apply to it when trying to move something at a given angle; 3) the significance of each of these factors can be determined using a model: having solved a problem, you can manipulate parts of your problem to see how they would affect the answer; 4) it is often easiest to use spreadsheets to easily calculate the effects of altering these parts; and 5) optimum projection angles are often not 45°, partly because objects in sport are often released from a point above or below the point where they land and partly because projection speed is often less when we try to attain a high angle of release.
HOW ELSE CAN WE USE THIS INFORMATION?
It might not have been easy getting to the answer but what an amazing thing to be able to do! After doing some basic analyses (see Special Topic below), you could find the theoretical optimum projection angle for any throw in any sport: baseball, softball, cricket and so on. Scientists have used these theories to show that the optimum angle to throw a soccer ball (for example a throw-in after the ball is kicked out) is about 30° (Linthorne & Everett, 2006), although this varies for individuals of different height (because of the different release height) and ability to produce forces (that is, some might be able to throw at higher angles at high speeds than others). You’d be able to tell your players not to throw in at 45° but each person would have a different optimum. In the long jump, the body projection angle should also not be 45°, because we lose velocity as we try to jump upwards. Elite jumpers jump at about 17° to 22° (Hay & Miller, 1985) and take-off angles in the triple jump are even lower.
We must be careful in using these techniques in sports such as the javelin and discus, because the implements have flight properties and so are not subject to the normal laws of projectile motion (see Chapter 15). Believe it or not, rugby or American/Australian footballs and spinning soccer balls also exhibit flight properties, so we can’t model them in this way either (see Chapter 16). Neither can we use them to determine optima for release angles in netball or basketball, because these sports need greater angles of projection to improve shooting accuracy: the ball is much more likely to fall through the ring/basket if it falls vertically than when it skims across the top.
In the end, it is probably necessary to run biomechanical tests to determine the optimum trajectory for whatever object you need to throw, based on the athlete who is actually going to throw or kick it.
SPECIAL TOPIC: BASIC VIDEO ANALYSIS
We can use relatively simple tools to uncover a lot of information about a person’s performances. Video analysis is one such method.
In this chapter we learned how to use information such as an object’s release angle and speed to optimise performance but we need to find methods of obtaining this information easily. If you don’t have a suite of biomechanical analysis tools, you can use a standard video camera, a television, a sheet of plastic and a marker pen. You’ll also need a protractor (or another instrument to measure angles) and a ruler. You will be recording the athlete from the side, so that you can record the angle and speed of a shot as it is put. Set your camera on a tripod a good distance away from the athlete (at least 6–8 m if possible but the further the better) and side on (that is, perpendicular to the line of the throw) as shown in Figure 3.9.

FIG. 3.9 Set-up for video analysis. The camera is placed to view the thrower side-on (i.e. perpendicular to the line of throw) and at a considerable distance. A rod/line of known length is placed in the direction of the throw near the feet of the thrower.
Objects change their size and shape as they move across or towards/away from the camera, which can cause errors in calculations. The two main errors are: perspective error, which occurs as objects seem to get bigger or smaller as they move towards or away from the camera, and parallax error, which occurs as an object’s size and shape seem to change as it moves across the camera (think of a person at left of camera where you can see their front, then moving to centre stage where you see them side on ... when you see that same person a long way away, you will always see them from side on). You can all but eliminate these errors if you have the camera a good distance from the athlete. You can then zoom the camera so that the athlete fills the screen sufficiently.
Next, place a rod or draw a straight line on the ground in the direction of the forthcoming throw from a point near where the thrower’s feet will be at the time of release. This will allow you to measure the angle of trajectory against a known horizontal line. Measure the rod – if you know its exact length, you can use it to work out how big the objects are or the distances thrown when they are on the television screen. This process is called calibration.
Take video recordings of several throws, capturing the point of release and the first part of the flight of the shot. Only throws where the shot travelled perpendicular to the camera can be used, because if the shot travels towards or away from the camera you will get perspective errors.
Once you have taken the video footage, play the first throw on the television and pause it at the point the shot leaves the hand. Stick the clear plastic sheet on the television and mark the athlete’s toe, hand (to determine the height of release) and the horizontal line or rod that was placed on the ground (as shown in Figure 3.10). Last, mark the point of the shot. Then move the video one frame forwards and remark the shot (you now have four points and one horizontal line).
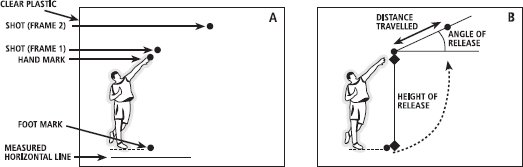
FIG. 3.10 Determining the angle of trajectory, height of release and speed of release (calculated from the distance travelled by the shot in one frame of video) can be done using a basic video camera and television set-up. First, the important landmarks are located and drawn on a clear plastic sheet (A) and then angles and distances can be measured (B). See text for more detail of the procedures.
Now take your measurements. The angle between the line on the ground and a line joining the marks of the shot is the angle of trajectory. The distance between the shot marks gives the displacement of the shot after release. From the frame rate of the camera, you can work out the time between the two points (for PAL systems this is 0.04 s and for NTSC it is 0.033 s; see Chapter 2) and then find the velocity of the shot using v = s·t-1 (that is, distance divided by time).
Before you can use the displacement of the shot, you have to know how far it travelled in the real world, not the distance on the television screen. Divide the length of the line or rod as measured on the television screen by its real length, to get a ‘scaling factor’. For example, if its length on the television was 0.3 m (30 cm) and its actual length was 2 m the scaling factor would be 0.3/2 = 0.15. This process is called calibration. If the shot travelled 0.084 m (8.4 cm) across the television, 0.084/0.15 gives you the real distance travelled (0.56 m). Therefore the velocity was 0.56/0.04 = 14 m·s-1.
So now you have the angle of projection and know the projectile velocity was 14 m·s-1. If you think you’ll use this process often, you might like to look at freely available software such as Kinovea (http://www.kinovea.org/) or Video4Coach (http://video4coach.com/) to help analyse your data. Software packages such as this make the process of analysing data much easier, and allows for a lot of analysis to be done without needing to do all the hard work. Once you choose your method you can do this for any number of throws, but how do we find the relationship between projectile velocity and angle of projection?
After analysing a number of throws at different release angles, you can put your data into a spreadsheet: the data might look something like the spreadsheet in Figure 3.11.
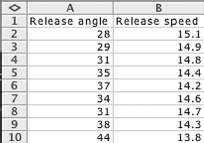
FIG. 3.11 Release angle and release speed entered into a spreadsheet programme.
You can then create a scatterchart and add a linear regression trend-line (the slope of this line tells you the relationship between the two variables). The slope of the line shown in Figure 3.12 is –0.0853; the equation (at the top of the graph) is in the form y = ax + b, where y is a value on the y-axis (that is, what we’re trying to find), x is a point on the x-axis (that is, what we measured) and 17.412 is the value that the line would cross the y-axis if it continued.

FIG. 3.12 Graph of projection velocity against projection angle. The velocity decreases as the angle increases. The equation to the line (at top) shows that the velocity decreases by 0.0853 m·s-1 for every degree increase in projection angle. This would be 0.0853 × 57.3 = 4.89 m·s-1 per radian.
To find y, you simply put in a value of x. For example, the projection velocity at an angle of 35° would be approximately –0.0853 × 35 + 17.412 = 14.9 m·s-1. The number –0.0853 implies that velocity decreases by this much for every degree increase in angle. In the spreadsheet you created earlier, the units were radians (1.7 m·s-1 per radian). You can therefore multiply this figure by 57.3 to find the change in velocity for a whole radian: 4.89 m·s-1, which is significantly larger than the 1.7 m·s-1 you used earlier. For some reason, our shotputter loses much more velocity as the angle increases. (You can enter 4.89 in cell B3 of your spreadsheet to see how this affects the optimum projection angle for this shotputter.)
For the new thrower, what is the optimum angle of release? How do the original velocity and the relative height of projection affect the results? How might you coach this athlete differently to the shotputter described earlier in the chapter?
Useful Equations
convert degrees-to-radians (rad) = x°/(180/π) or x°/57.3
convert radians-to-degrees (deg,°) = x° × (180/π) or x° × 57.3
projectile motion equations
v = u + at
v2 = u2 + 2as
s = ut + ½ at2
sine rule: sin θ = opposite/hypotenuse
cosine rule: cos θ = adjacent/hypotenuse
tan rule: tan θ = opposite/adjacent
time per frame (video) = 1/frame rate
scaling factor: apparent length/true length
Hints for using projectile motion equations
•Always write down what you know, what you’re trying to find, and any equation that might be useful.
•Always draw a diagram of the problem so you can ‘see’ what you’re trying to find.
•If the projectile lands at a different vertical height from which it was thrown, you will have to break the problem into two separate problems.
•If the take-off and landing are from the same vertical height, then the time the projectile takes to get to the top of its trajectory is the same as it takes to get down; therefore total flight time = tup + tdown.
•Acceleration due to gravity is always 9.81 m·s-2, so even if you’re not given this in the problem, you can write it down (unless you have reason to believe that the acceleration was not 9.81 m·s-2).
•At the top of its trajectory, the vertical velocity of a projectile is briefly zero; you can use this as a quantity for v or u, depending on which part of the trajectory you are investigating, even if you’re not explicitly told it.
De Luca, R. (2005). ‘Shot-put kinematics’. European Journal of Physics, 26: 1031–6.
Hay, J.G. & Miller, J.A. (1985). ‘Techniques used in the transition from approach to takeoff in the long jump’. International Journal of Sports Biomechanics, 1(2): 174–84.
Hubbard, M. (1989). ‘The throwing events in track and field’. In: Vaughan, C.L (Ed). Biomechanics of Sport, Boca Raton, Florida: CRC Press inc.
Lichtenberg, D.B. & Wills, J.G. (1978). ‘Maximising the range of the shot put’. American Journal of Physics, 46:546–19.
Linthorne, N.P. & Everett, D.J. (2006). ‘Release angle for attaining maximum distance in the soccer throw-in’. Sports Biomechanics, 5(2): 243–60.
Related Websites
Projectile Motion (http://www.walter-fendt.de/ph14e/projectile.htm). Interactive demonstration of projectile motion that allows the user to set parameters and observe their influence on a projectile.
Lessons on Projectile Motion (http://www.sciencejoywagon.com/physicszone/01projectile-motion/). Movies, animations, descriptions and interactive demonstrations on projectile motion.
Top end sports: The sport and science resource (http://www.topendsports.com/biomechanics/physics.htm ). Website investigating the applications of physics in sports.
ZonaLand: National Science Teachers Association (http://zonalandeducation.com/mstm/physics/mechanics/mechanics.html). Clear descriptions and animations of the basic principles of mechanics.
The Physics Classroom – Tutorials (http://www.physicsclassroom.com/Class/). Lessons on basic physics concepts.
The Physics Classroom – Multimedia tools (http://www.physicsclassroom.com/mmedia/). Interactive tools and movies depicting basic physics concepts.
The Physics of Sports (http://www.topendsports.com/biomechanics/physics.htm). Website investigating the applications of physics in sports.
* The acceleration of an object due to gravity is different at different places on the Earth. The Earth’s radius is slightly greater at the equator, since its shape is distorted by its spin, so acceleration due to gravity is slightly less (9.78 m·s-2) than it is at the poles (9.83 m·s-2). Gravity is lower at the top of mountains (around 0.2% lower at the top of Mount Everest). Many record performances were made at the 1968 Olympic Games in Mexico City, where, due to its altitude and near-equatorial location, gravity is somewhat lesser than at other points on the Earth (air resistance is also less at altitude). You could experiment by performing your calculations with other values for the acceleration due to gravity.