
After you hit it, a golf ball starts off travelling straight but eventually curves to the right. How does it do this? How can you get the ball to travel straight?

By the end of this chapter you should be able to:
•Describe how a lift force is produced by a spinning object with reference to Newton’s laws and the Bernoulli effect
•Explain the effects of relative wind speed and object spin speed on the magnitude of the Magnus force
•Give examples of how the Magnus effect can negatively affect sporting performance
•Give examples of how the Magnus effect can be used to improve sporting performance
If a ball flies off to one side after being hit, the first thought might be that you applied a force to the ball that wasn’t in the desired direction; that is, you hit the ball at an angle. However, in the example above the ball started off straight then started to swerve or swing. So it’s probably not that you’re hitting the ball in the wrong direction. Another force must be acting to make the ball swing after you’ve hit it.
To understand what is going on and how to fix this problem you may need to remind yourself of the concept of lift described in Chapter 15. If an object, such as a golf ball, is moving in a straight line but then one side of the ball encounters a higher pressure than the other side (akin to the pressures around an aerofoil) it will start to swerve or swing. How are these unequal pressures generated?
There has been long debate over the exact mechanism responsible for the development of the lift force on spherical objects such as the golf ball. In 1672, Isaac Newton first noted how a tennis ball’s flight was affected by spin (this was real, or royal, tennis, not modern lawn tennis). Seventy years later (1742), Benjamin Robins showed that a rotating sphere, such as a ball, was associated with a sideways (transverse) force. However, the first explanation of the lateral movement of a spinning ball is attributed to H.G. Magnus who, in 1852, showed that the sideways force was proportional to the speed of the air over the ball and the speed of the spin of the ball. Magnus was actually tasked to understand why artillery shells and cannonballs tended to swerve under some conditions, but also had a keen interest in table tennis and noticed that the ball could swing or dip if appropriate spin was placed on it. The most common explanation is that a spinning ball ‘grabs’ the air that flows past it because of the friction between the air and the ball, so these air particles start to spin with the ball (i.e. the boundary layer of air spins). As you can see in Figure 16.1, the collision between the oncoming air and the ball or air spinning with it causes air on one side of the ball to slow down. On the other side of the ball, the air moves past relatively unimpeded. The speed of air on one side of the ball is thus less than the speed on the other side. As you know (from Chapter 15), slow-moving air is associated with higher pressure whereas faster-moving air is associated with lower pressure, according to Bernoulli’s theorem. Thus, we have a pressure differential.
FIG. 16.1 The spinning ball drags a boundary layer of air with it. On the left side of the ball the air spinning with the ball collides with oncoming air and slows down (left diagram). The slower velocity air is associated with high relative pressure (right diagram). The opposite occurs on the right side of the ball creating a ‘pressure differential’ directed from left to right. Hence the ball starts to swing to the right (curved arrow).
If you’ve hit the ball such that your force is directed in the correct line but you’ve drawn, or pulled, the clubface across the ball slightly, then you have probably spun the ball. You can see this in Figure 16.2. (Re-read Chapter 3 if you’re unsure of how to calculate resultant forces.) The spin you put on it will eventually cause a pressure differential and the ball will start to swerve. This is the Magnus effect (after H.G. Magnus) and the force that is created by the unequal pressures is the Magnus force.
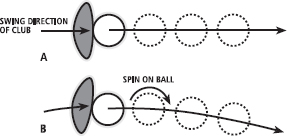
FIG. 16.2 In (A), the club hits the ball straight with an appropriately oriented club face. The ball is hit without side spin and travels straight off the clubface. In (B), the clubface is angled slightly, which puts spin on the ball. Because the angle at which the ball was struck was also altered slightly, the ball started straight, but then swerved in the air due to the Magnus effect.
Life is never quite that simple. More recent studies have shown that only the air that is very close to the ball is dragged around by its spin, so the layer of air trapped against the ball and moving with it (the boundary layer) is also very small; so many believe that the explanations based on the Bernoulli effect are not accurate. However, the collision between the slow-moving air on one side of the ball and the oncoming air causes the air to deflect off the ball sooner, as shown in Figure 16.3. That is, ‘boundary layer separation’, or the separation of the boundary layer from the ball, occurs earlier. The air on the other side of the ball deflects much later and rushes towards the lower pressure area behind the ball. According to Newton’s Third Law, since these masses of air changed their velocities (both magnitude and direction) a force must have been applied. There must therefore be an equal and opposite force, which pushes the ball in the opposite direction (i.e. downwards in Figure 16.3). So the lift force on a spinning ball can be well explained using Newton’s laws.
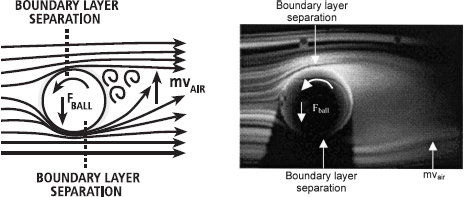
FIG. 16.3 The spin of the ball causes the boundary layer on the top surface to separate earlier and move away from the ball. At the bottom, the boundary layer separates later and air is dragged up the back of the ball. Thus, there is a mass of air with velocity moving upwards behind the ball. That is, the air has momentum (mvair, where m = mass and v = velocity). The upward air movement causes a force in the opposite direction as air above the ball moves down to conserve momentum (Fball).
We could also say that the air has a mass and velocity and therefore a momentum. The law of conservation of momentum means there must be a momentum in the other direction; in other words, the ball has to move in the other direction. These arguments are very similar to those on lift force generation, discussed in Chapter 15. In the end, both the ‘Bernoulli’ and ‘Newton’ explanations are essentially the same, although you should be able to understand both of them. You don’t need to be able to calculate these forces (and the maths is complicated) but you should read Box 16.1.
THE ANSWER
Regardless of the explanation for the forces created around a spinning object, the problem facing golfers is that spin is imparted on the ball by the club, even though the ball was hit in the right direction. The ball starts off straight but the spin creates a sideways lift force that takes the ball off-line. Depending of the direction of swing, the movement of the ball is called a slice (if it swings to the right for a right-handed golfer) or a hook (if it swings to the left). Golfers have to understand how to manipulate their technique to ensure that spin is not imparted to the ball, unless they deliberately want to swing the ball around an obstacle.
BOX 16.1 THE MATHEMATICS OF THE MAGNUS EFFECT
The mechanisms contributing to the Magnus effect are complex and it would take a massive mathematical effort to predict the effects of changes in ball speed, wind speed or rotation speed on the amount of curve of a ball.
Broadly, the faster a ball travels or spins, the greater will be the Magnus force. Therefore, if the ball is travelling into the wind (i.e. the relative speed of ball and air is greater), the ball will swerve more for less imparted spin. So, in tennis, it might be good to hit into the wind because you can hit with greater horizontal speed and need worry less about trying to apply topspin. But if you were an inexperienced soccer player trying to kick the ball straight, it might be better to kick with the wind, since even a small amount of rotation on the ball will cause it to swerve and miss its target.
Unfortunately, the trajectories of balls are far more complex. For example, you saw in Chapter 13 that drag forces on an object were velocity-dependent, in that drag generally increased with the square of velocity but that at a critical velocity there was a marked reduction. This highlights the fact that the speed of air flow around a ball and the formation and stability of the boundary layer also vary with ball speed. Some examples of how ball speeds influence the movement of balls in sport are briefly described below…
Golf balls: as we have just learned, a spinning golf ball will swerve off-line. In fact, the flight path of a spinning ball is that of a parabola (see Figure 1), so the swerve in the first half of the flight is far less than in the second half. This gives the impression that the ball started travelling straight and then swerved later. As expected, the swerve of the ball is greater for faster spin rates and the magnitude of swerve will increase with ball velocity; however, there is some data showing that the amount of swerve per travel distance is greater for a slower golf ball (Bearman & Harvey, 1976).
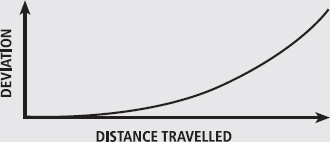
FIG. 1 The sideways deviation of a golf ball influenced by the Magnus force is parabolic.
Baseballs: the curveball is pitched with side spin on the ball so that a sideways Magnus force is generated. A faster spin rate or pitch speed causes a greater sideways movement. In fastball pitches, backspin is placed on the ball. This creates an upward Magnus force which, if of sufficient spin speed, is thought to be responsible for the ball tending to rise as it nears the batter (the so-called rising fastball). In fact, research has shown that the upward force is probably only about half that required to overcome the weight of the ball so, while the pitch may not dip as far as expected, it does not actually rise (Alaways, 1998). For all pitches the seams on the ball increase the Magnus force because the roughened surface reduces the velocity at which the boundary layer is tripped towards turbulence. Pitchers may throw the ball such that either two or four seams tend to rotate to the front of the ball; the four-seam pitches produce more dramatic changes in trajectory although this is probably less pronounced at higher ball spin rates.
Soccer (football) balls and volleyballs: clearly, imparting spin on these balls will cause a Magnus effect. But, in fact, slower-moving balls have been shown to produce greater swerve (Asai et al., 2007). So curvature of a ball may increase later in the ball flight when the effects of drag slow the ball. Asai and colleagues also showed the drag increased when the spin rate of the ball was increased. An interesting flight path can be obtained with soccer balls and volleyballs because the panels that comprise the ball ensure that the surface roughness varies as the ball rotates during flight. This allows the so-called ‘floater’ to be produced, whereby projecting the ball without spin can cause unpredictable swerving that varies during flight. As the ball is first projected the uneven surface causes flow variations that cause swerve. The surface friction variability also causes the ball to rotate slightly and for a different region of the ball to face the oncoming air. This will cause a new swerve of the ball, dependent on the variability in roughness, and a further rotation of the ball. This continuing effect through the flight path causes the inconsistency in flight. Another important phenomenon is the ability to project these balls at speeds faster than the critical speed, where the coefficient of drag (and therefore the drag force) decreases rapidly (see Box 13.1 again). In this case the ball continues to move very rapidly through the air without slowing substantially. The ability to hit or kick a ball fast enough, especially without spin where the flight path is unpredictable, is a good one to have.
Cricket balls: while spin bowlers can see significant swerve as the ball travels down the pitch, the greatest swerve (or swing as it is called in cricket) occurs when fast bowlers bowl the ball with its seam appropriately angled. When a ball is new it can swing if the seam remains perfectly upright during ball travel. This is because irregularities on the ball (usually the manufacturer’s printed logo) cause a greater roughness on one side and thus an imbalance in air pressures (the ball swings towards the rough side). Because there is little roughness, swing is obtained only by the fastest bowlers because the aerodynamic effects are amplified at high speeds. As the ball becomes rougher during play it becomes more likely to swing at slower speeds, as long as one side remains smoother than the other. This type of swing is often referred to as ‘contrast swing’.
It is also possible to increase the swing by bowling the ball with the seam pointed about 20° to one side. The seam acts to trip the boundary layer towards turbulence, thus reducing air pressure on that side. The ball swings to the side that the seam was pointing (what is called ‘traditional swing’). Bowlers often impart a backspin on the ball as it’s bowled. This would not only stabilise the orientation of the ball in flight (as described in Chapter 13) but also increase the magnitude of the effect: swing is greater when backspin is placed on the ball (Mehta, 2005). As the ball gets even rougher the boundary layer is tripped more easily. The roughest side can then cause enough turbulence that drag is reduced (much like the dimples on a golf ball); in this case the drag on the smooth side is actually greater than the drag on the rough side. At fast ball speeds, an effect can be created where the ball swings away from the rough side. To increase the amount of the smooth side facing the oncoming air, the ball is often bowled with the seam angled (much like ‘traditional swing’); however, instead of the ball swinging towards the angled seam the ball swings away from it, towards the smooth side of the ball. This unexpected direction of swing is often referred to as ‘reverse swing’. Despite some anecdotal accounts, it is not necessary to wet the rougher side of the ball to obtain this effect. Another point of interest is that sometimes the ball appears to swing late. This might happen in some instances when the slowing of the ball is associated with a greater swing (e.g. traditional swing); however, the decrease in ball velocity is not great enough to have a large effect. More likely, the observation simply reflects the typical parabolic trajectory of the swinging ball, as shown in Figure 1.
HOW ELSE CAN WE USE THIS INFORMATION?
As Newton first noted the effect on a tennis ball, we’ll follow his great example. Let’s assume that you wanted to hit the ball as fast as you could from your side of the tennis court to the other. If you hit the ball very hard in an upward direction, to get it over the net, it would travel a long way before gravity finally pulled it down to Earth: it would go well over the baseline and you’d lose the point. For gravity to bring the ball down inside the baseline, you could hit the ball with less horizontal force and thus with less horizontal velocity but then your opponent might have time to get to it.
According to the Magnus effect, you know that if you put spin on the ball, where the top of the ball spins over the bottom of the ball (i.e. topspin), the air on top would slow down and the air underneath would move relatively quicker (as in Figure 16.1). Therefore, the pressure on top of the ball would be higher; a Magnus force would be directed down towards the ground and the ball would dip. The alternative explanation is that the boundary layer would separate earlier on the top of the ball, because of the collision of the air travelling around the ball with the oncoming air, whereas on the bottom it would separate later, so some of the air from the underside of the ball would be dragged upwards behind the ball. Therefore, the air above the ball, and the ball itself, would be forced down in accordance with Newton’s Third Law (and conservation of momentum). Either way, putting topspin on the ball allows us to hit the ball with a high horizontal velocity and still get it to land inside the baseline.
By understanding the benefits of spin, performance in numerous other sports can also be improved. Soccer players kick across the ball to put spin on it to curve it around a wall of players at a free kick and goalkeepers hoping to kick the ball a long way kick the ball with backspin so that they can apply a large horizontal force (and therefore velocity) while the lift created increases the ball’s flight time. Golf drivers are designed with a backwards-angled club face, to impart a backward spin on the ball to increase hitting distance. Also, longer hits in baseball tend to occur when the ball has been pitched with topspin so it rebounds off the bat with backspin, rather than when the ball is pitched at maximum speed but without topspin (see Rex, 1985). In cricket, if a spin bowler puts a lot of spin on the ball, it will swerve in the air as it drops. The more it swerves, the more spin must have been on it. The bowler might try to trick a batsman by spinning the ball in the other direction, in which case the swerve will also be in the opposite direction. In fielding in cricket, baseball or softball, a ball hit in the air will often curve on its way down to the ground, according to the spin put on it. If the fielder knows what spin was placed on the ball, he or she will be better able to predict its flight in the air. Alternatively, by watching its movement in the air, the fielder might also be able to predict which way the ball might spin after it hits the ground.
Useful Equations
Bernoulli’s equation: p + ½ ρv2 + ρgh = constant
conservation of momentum: m1v1 = m2v2
References
Alaways, L.W. (1998). ‘Aerodynamics of the curve-ball: An investigation of the effects of angular velocity on baseball trajectories’. PhD dissertation, University of California, Davis.
Asai, T., Seo, K., Kobayashi, O. & Sakashita, R. (2007). ‘Fundamental aerodynamics of the soccer ball’. Sports Engineering, 10: 101–110.
Bearman, P.W. & Harvey, J.K. (1976). ‘Golf ball aerodynamics’. Aeronautical Quarterly, 27: 112-22.
Mehta, R.D. (2005). ‘An overview of cricket ball swing’. Sports Engineering, 8(4): 181-192.
Rex, A.F. (1985). ‘The effect of spin on the flight of batted baseballs’. American Journal of Physics, 53: 1073–75.
Related Websites
NASA, Glenn Research Centre website (https://www.grc.nasa.gov/www/k-12/airplane/bball.html). Website explaining the flow around a spinning ball.
The Physics of Sports (http://www.topendsports.com/biomechanics/physics.htm).Website investigating the applications of physics in sports. More specifically, visit http://www.real-world-physics-problems.com/physics-of-soccer.html to learn about the soccer (football) kick.