
We know that aerodynamics is very important in cycling but how can we determine the optimum aerodynamic body position on a bike?

By the end of this chapter you should be able to:
•Explain the concept of drag and differentiate between different types of drag
•Describe the factors influencing drag and how we might manipulate them to improve sporting performance
•Design experiments to assess the impact of body position or equipment modifications on drag and subsequent performance
We need to find out what factors affect drag so that we can highlight a number of probable ‘best aerodynamic positions’, then test them.
Factors affecting drag
We’ve all noticed that it is harder to run, ride or project an implement such as a football into a strong wind. The reason is that in these circumstances the drag force is increased. Drag occurs when molecules of a fluid (‘fluid’ refers to any moveable medium, including air) collide with an object and take energy away from it. As you learned in Chapter 9, all moving objects have kinetic energy. If energy is taken from them their mass or velocity must decrease. It is rare for mass to be reduced so normally an object loses velocity.
The loss of energy from the object to the fluid can be visualised in two ways. The theoretically correct way is to assume that the fluid moving towards an object is ordered into smooth, parallel layers, that is, it is not being mixed around. This is laminar flow, as shown in Figure 13.1. The fluid has a certain amount of energy, which remains constant. But as it passes an object, the fluid changes direction and therefore velocity (remember, velocity is a vector quantity, so it changes if either the speed or the direction is altered) and so gains energy. The energy gained by the fluid is always equal to the energy lost from the object because (as you already know) energy cannot be created or destroyed. This non-laminar flow is also called turbulent flow (you might have come across the word ‘turbulence’ before, especially if you are afraid of flying!). As a fluid such as air or water is forced from laminar to turbulent flow, its energy increases and the object loses energy.
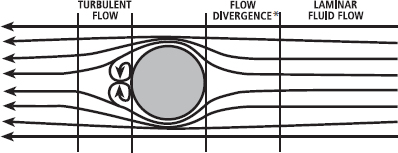
FIG. 13.1 A fluid approaching the object exhibits little mixing. This type of fluid is called laminar because it essentially travels in layers. As it approaches an object, the layers diverge (*this flow divergence is sometimes also referred to as ‘flow separation’, although this can be confusing, as we will see later). At some point, the fluid flow may become turbulent as the fluid rushes towards areas of low pressure. This turbulent flow takes energy away from the object.
Another way to visualise it is to consider that the fluid applies a force to the object during the collision, while the object exerts a force on the fluid (Figure 13.2). The more fluid there is, or the greater the area of contact with the object, the more force is applied. Since the object and fluid exert their forces in opposite directions, their velocities are affected; the air gets deflected from the object (it changes direction violently, because of its very small mass and consequently small momentum) while the object is slowed (it doesn’t observably change direction, because of its large mass and momentum).
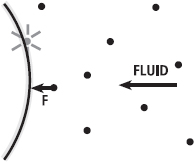
FIG. 13.2 A drag force can be conceptualised by imagining each particle of a fluid applying a force against an object as they collide. The larger the number of collisions (i.e. greater surface area of the object, faster flow of the fluid or a greater density of the fluid) the greater the rate of collisions and therefore the greater the force exerted by the fluid.
Whichever way you choose to model it, you can see that the movement of an object within a fluid will tend to slow the object. This is undesirable in many sports, so we have to minimise it.
As I hinted above, one way to minimise drag is to reduce the area of the object that touches the fluid. This will reduce the amount of fluid that has its velocity changed in the collision with the object (or in a collision with other fluid molecules that have been deflected) and therefore reduce the energy lost from the object. In this sense, we need to find a body position on the bike that has the smallest possible frontal surface area, so that collisions are minimised. This is one benefit of the ‘tuck’ position, which is shown in the photograph at the start of this chapter.
A second factor that influences drag is the shape of the object, because this affects how much the laminar flow will become turbulent. If the leading edge of an object is pointed, the direction of the fluid hitting the object will be changed more slowly than if the fluid hits the object abruptly (see Figure 13.3 (A)). Remember from Chapter 11 that when a ball collides with a bat with a larger angle of incidence (that is, more parallel to the bat) the coefficient of restitution is increased? Similarly, if the fluid hits the object at a larger angle of incidence, less energy will be lost from the object.
FIG. 13.3 A. By shaping objects with a longer leading edge, fluid particles diverge earlier and strike the object’s surface at a larger angle of incidence. This minimises the ability of the fluid to exert a force on the object and reduces drag. B. The flat front end on some buses, trucks and trains traps air molecules to allow an accumulation of air at the front of the vehicle. This mass of air forces oncoming air molecules to diverge from laminar flow earlier (solid line) to reduce drag compared to when air diverges nearer the vehicle surface or after a collision with it (dashed line).
However, this effect can be achieved almost as well in objects with a flat front end. As air hits the face of the object, it is bounced straight back towards the oncoming air. Because the object is moving in the same direction as the reflected air, the air moves with the object and forms a boundary layer, which forms rapidly at the front of the object. This boundary layer helps deflect the oncoming air away, much like a pointed object (Figure 13.3 (B)). This may not be as effective as pointing the front end, but it’s also not as problematic as one might think.
The shape of the tail end of the object is also important. As the object collides with the fluid, it moves the fluid away to the side. The object then fills the space that was once occupied by the fluid (Figure 13.4 (A)). As the object continues to move through the fluid, a ‘hole’, or region of low pressure, will be left behind the object. Air will always move from an area of high pressure to an area of low pressure, so it will rush in behind the object to fill the hole. You can see this for yourself if you move your hand quickly through still water next time you are doing the washing up or having a bath. However, this flow increases turbulence and so takes energy away from the object. Minimising turbulent flow is achieved by tapering the object at its tail, as shown in Figure 13.4 (B). This helps to maintain laminar flow and therefore moves the point at which flow separates from the object further back (or prevents flow separation completely). This is why objects such as cycling helmets are tapered. This advanced aerodynamic shaping allows a peregrine falcon to dive at speeds of over 350 km·h-1 when its wings are swept back!
An object’s size and shape describe its ‘form’. These two factors influence the form drag on an object. The other factor that affects form drag is the relative speed of the object and fluid; drag increases with the square of speed:
Fd = kAv2
where Fd is the force of drag (drag force), k is the coefficient of the shape of the object (measured in a specific fluid), A is the frontal surface area of the object and v is the relative velocity of the object with respect to the fluid. You can see that the velocity of the object and fluid are the most important considerations; relatively small increases in velocity can bring about relatively large increases in drag. We are aiming to increase the cyclist’s speed, so we have to reduce drag by manipulating the coefficient of drag (k; related to our body position) and the frontal surface area. One body position used in downhill skiing and (when permitted by the rules) in cycling is the bullet position, where an athlete in a typical tuck position stretches their arms in front of their body, almost in a Superman pose.
Of course, we can measure drag in many different fluids, so in fact it is more appropriate to use the equation:
Fd = CdρAv2
where Cd is the coefficient of drag and the symbol ρ (rho, pronounced ‘row’) is the density of the fluid in which the Cd was measured. By measuring the Cd instead of the k, we can adjust our drag force when we move an object to a different fluid (e.g. air to water) without having to remeasure the drag coefficient. This second equation looks more complicated, but it’s not really. For the rest of the chapter we’ll stick with k rather than Cdρ because we’re only concerned with one fluid – air.
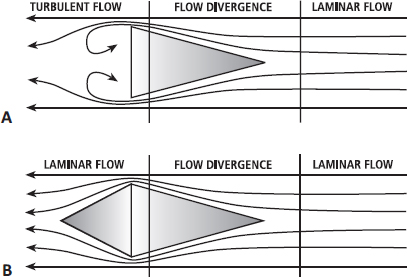
FIG. 13.4 Adding a tapered tail to an object (B) promotes laminar flow across the object when compared to an object without a tail (A). This is because the separation of the fluid from the object (flow seperation) occurs later, or is prevented entirely, which minimises turbulence. This shape is commonly used in sports where aerodynamic configurations are important for enhanced performance.
BOX 13.1 WHY DO GOLF BALLS HAVE DIMPLES?
As shown in Figure 13.1 (and Figure 1A below), as a ball passes through the air there is a turbulent zone behind the ball because the laminar air flow moves over the front surface of the ball but then rushes in behind it, where the pressure is lower. As the speed of the ball increases, this effect becomes more prominent, the air at the front of the ball is deflected (flow seperation) sooner and the turbulent zone increases (see Figure 1B); this results in increased drag, i.e. drag increases with velocity (squared). However, at very fast speeds significant turbulence develops at the front of the ball. In an extreme case, the lower pressure associated with the turbulence allows oncoming air to ‘stick’ to the ball (this phenomenon is explained in detail in Chapter 15), or pass close to it and the separation of this air then occurs later (Figure 1C). Effectively, at some critical speed the formation of a turbulent boundary layer allows for more laminar flow around the object and the object experiences less drag. Many years ago it was recognised that golf balls with roughened surfaces flew further than new, smoother golf balls. Many pundits therefore refrained from buying new balls and opted to find the oldest balls they could. It was soon realised that the roughened surface increased the rate at which the turbulent boundary layer formed, and thus reduced the ball speed needed to reach the critical level where drag actually decreased.
FIG. 1 A turbulent zone appears around a ball moving through air (A). As the air speed increases relative to the ball the laminar air flow separates from the back of the ball earlier and there is more turbulence, increasing drag (B). At a critical speed, however, the turbulence of the boundary layer increases to a point where the air flows close to the ball and remains more or less laminar (C). Dimples on a golf ball increase the boundary layer turbulence to ensure that this phenomenon occurs at slower velocities, thus decreasing drag and increasing flight distance.
It didn’t take long for ball manufacturers to get hold of this idea and manufacture balls with a roughened surface to ‘trip’ the boundary layer. Today we can see the dimpling on the balls, which helps the turbulent boundary layer to form and the balls to fly further. In fact, strict regulations are now in place to limit design alterations that would make balls fly even further than they do today. We sometimes see the same effect when a football (soccer ball) is kicked at a very high speed; the ball seems not to decelerate during its flight path as much as expected, which is due to it being kicked fast enough to be above the critical speed where the drag force drops significantly. This isn’t great news for the goalkeepers, although they seem to have already figured out the phenomenon for themselves and time their saves appropriately. Of course, it’s not the case that the faster a ball flies the less drag it will experience. Once this critical speed is attained where there is a dramatic drop in the drag force, further increases in speed are again associated with gradual increases in drag (see Figure 2).
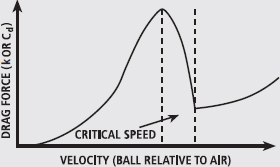
FIG. 2 At lower speeds, the drag force increases with velocity. However, at a critical speed the drag force is dramatically reduced. Thereafter, the drag force again increases with velocity. Dimples on a golf ball reduce the speed at which the drag force is reduced, allowing the ball to travel further.
There is another type of drag that we can manipulate: surface drag. While form drag is affected by the gross shape of our body, surface drag is affected by the roughness of our surfaces (that is, skin and clothing). As a fluid makes contact with our surface, small pockets or ridges in our skin and clothing catch the fluid, thus allowing a force to be applied and energy to be transferred (Figure 13.5). Essentially, this is a friction force, so this type of drag is also referred to as friction drag. As with form drag, the surface drag force increases to the square of velocity, so its effects increase four-fold for a doubling of relative velocity and therefore its effects can be significant in fast-moving objects. Wearing synthetic materials, which are non-porous and allow fluids to travel over their surface easily, is better than wearing natural materials such as cotton, which are porous and catch fluids. The effects of surface drag are not as significant as those of form drag but reductions in surface drag can have measurable effects on performance.
Wave drag
Although it won’t help us improve the aerodynamics of the cyclist, there is one final type of drag: wave drag. This is a drag force that occurs when an object moves at the interface of two fluids with different densities. A good example is the wave created in front of a swimmer as their body moves at the interface of the water and air. The wave applies an opposing force to the swimmer, as you can see in Figure 13.6, and the turbulence created takes energy away from the swimmer. Wave drag has a significant effect on the overall drag in swimming, so we will examine it in more depth (sorry, no pun intended) in Chapter 14.
FIG. 13.5 Rougher surfaces can allow particles of fluid to become trapped, or engage with the object’s surface (A). This increases drag by allowing the molecules to exert a significant force against the object. Smoothing of a surface minimises particle trapping and causes particles to move away from the surface (B). In this case, particles have little time to exert a force on the object, and drag is reduced.

FIG. 13.6 A wave is created as an object (in this case a swimmer) moves at the interface of two fluids of different density (in this case air and water). The wave opposes forward motion. Wave drag is significant in swimming.
Measuring the effects of drag
We now know there are three main forms of drag and that form drag (as opposed to surface and wave drag) will have the greatest effect. We know that form drag is affected by the frontal surface area and the shape of an object and that its effects are increased dramatically as speed increases. We therefore have to use a ‘tapered’ shape on the bike to reduce it but how can we measure the effects of changing body position to reduce drag?
The best way to measure drag is to use a wind tunnel. In a wind tunnel, air of a known velocity is passed over a cyclist sitting on their bike. The bike is attached to a load cell that measures the force exerted by the wind on the bike and rider combination. You will remember that Fd = kAv2, so we can calculate k (the coefficient of drag) if we measure the surface area of the bike and rider combination after re-arranging the equation to be k = Fd/Av2 (or we just measure the drag force, Fd, which is the most important factor). Unfortunately, unless we have a wind tunnel at our disposal, we will need another way to measure the drag force. Fortunately, we can re-use an equation we first saw in Chapter 5: Ft = ∆mv. By dividing both sides of the equation by t, the formula can be re-arranged to find F = ∆mv/t. The mass of the bike and rider is unchanging and can be measured on standard scales, so if we measure the change in velocity of our rider over a known time we can calculate the force that must have caused the change: F = m∆v/t.
The two main factors that will cause this change in velocity are drag (form and surface drag) and the friction between the tyres and the road and in the ball bearings of the wheels. So, if on a completely windless day we measure the change in speed of a bike and rider over a given time period, we can work out the effects of friction and drag. If we change the rider’s position on the bike, drag will change but friction will remain the same, so any difference in the velocity change must be due to the change in drag!
This is a reasonably easy concept. We can use a standard bicycle computer to measure the time it takes to roll 100 m after the rider accelerates to a known speed; the faster the better, because velocity greatly affects drag; small changes in drag will be amplified if we ride at fast speeds, say 60 km·h-1. We can look at the speed of the bike at the 0 m and 100 m points and use these speeds to determine the change in velocity of the bike. An example might look like this:
Mass of rider + bike = 100 kg
Velocity at 0 m = 60 km·h-1 (16.67 m·s-1)
Velocity at 100 m = 41 km·h-1 (11.39 m·s-1)
Change in velocity = 5.28 m·s-1
Measured average velocity over 100 m = 50.5 km·h-1 = 14.028 m·s-1 (you could use (60+41)/2 as a good estimate if you haven’t measured it precisely)
So the time taken = s/v = 100/14.028 = 7.129 s.
Ft = m∆v (remember, m won’t change)
F = m∆v/t
= 100 kg × 5.28 m·s-1/7.129 s
= 74.1 N
So the force of drag plus friction = 74.1 N when rolling at this average velocity. You should re-read the maths slowly if you didn’t quite follow it the first time!
But how much of this force can be attributed to rolling friction? You can read Box 13.2 to find out.
BOX 13.2 FINDING THE SMALL EFFECT OF FRICTION
There are a few questions to be answered. First, how much of this force results from rolling friction and how much from drag? Drag will change as the velocity changes but friction will remain relatively constant. If we measure the rider a few times at different velocities, we might obtain a graph that looks something like this:
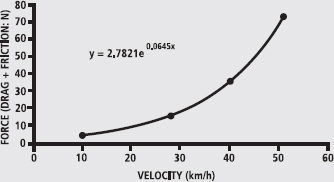
FIG. 1
By putting a line of best fit, or regression line, over the data (an ‘exponential’ curve was the best to use – as opposed to, for example, a straight line) it becomes apparent that there would still have been a small force present if we had been able to test at zero velocity. This force is due only to friction, since drag is zero at zero velocity.
An equation to the line was also calculated. We don’t have time for a full discussion on regression lines and equations but you can find out about them on many websites or in basic mathematics textbooks. Any graph-creating programme can also give you this information. The equation y = 2.7821e0.0645x tells us that we can find any value of y (that is, a number on the vertical axis; Force in this case) if we know a value for x (that is, a value on the horizontal axis; Velocity in this case). The e symbol is an abbreviation for ‘exponential’, which means ‘raise to the power of’.
For example, if we wanted to know the force at an average velocity of 35 km·h-1 (9.72 m·s-1), we would use the equation in this way:
y = 2.7821 e0.0645x
y = 2.7821 e0.0645x35
y = 2.7821 e2.2575
y = 26.59 N
At 35 km·h-1, our cyclist, sitting in his specific riding position, would have experienced friction and drag forces totalling 26.59 N. You might realise that many scientific calculators can’t be used to enter exponentials that have decimal places in them. I used Excel to do the calculation by typing the following formula into a cell in a spreadsheet:
=2.7821*exp(2.2575)
You can use this formula as well but change it depending on the exact numbers you need. We can also use this formula to find the force when velocity is zero by changing the equation to:
=2.7821*exp(0)
This gives us 2.7821 N. So at zero velocity there is a force due to friction of 2.7821 N. If we now subtract that number from any of the values calculated above, we can obtain the force that is solely attributable to drag. Remember that these numbers were obtained under experimental conditions, so you can’t use them as a common rule. You’ll have to do an experiment yourself for your own rider in their positions and with their bike.
THE ANSWER
So, we can now find out how much drag there is while riding in one position at any velocity and we can find out how much of the force is explained by friction and how much by drag alone. This brings me to another question. How much of an effect will a change in riding position, for example from one where the rider adopts a standard cycling position to one in the tuck position (see Figure 13.7), have on drag? We can determine this by measuring the rider in the two positions. We’ve already tested one position – the standard position – so we can now test the other one. Here are the results placed side-by-side:
Standard |
Forward lean with arms stretched |
Mass of rider + bike = 100 kg |
Mass of rider + bike = 100 kg |
Velocity at 0 m = 60 km·h-1 (16.67 m·s-1) |
Velocity at 0 m = 60 km·h-1 (16.67 m·s-1) |
Velocity at 100 m = 41 km·h-1 (11.39 m·s-1) |
Velocity at 100 m = 45 km·h-1 (12.5 m·s-1) |
Change in velocity = 5.28 m·s-1 |
Change in velocity = 4.17 m·s-1 |
Measured average velocity over |
Measured average velocity over |
100 m = 50.5 km·h-1 = 14.028 m·s-1 |
100 m = 53.5 km·h-1 = 14.86 m·s-1 |
Time taken = s/v = 100/14.028 = 7.129 s |
Time taken = s/v = 100/14.86 = 6.729 s |
Ft = m∆ v |
Ft = m∆v |
F = m∆v/t |
F = m∆v/t |
= 100 kg × 5.28 m·s-1 / 7.129 |
= 100 kg × 4.166 m·s-1 / 6.729 s |
= 74.06 N |
= 61.91 N |

FIG. 13.7 We can compare the drag forces when cycling in two positions, A: standard cycling position, and B: ‘tuck’ aerodynamic position.
So, the force exerted on the rider was less in the tuck position. We could, of course, subtract 2.7821 N from these scores to remove the effect of friction, as calculated in Box 13.2, but this will make only a small difference. Clearly, adopting the tuck position reduced the force considerably and this is reflected in the slightly higher average velocity over the 100 m.
However, I’d like to know how much difference this might make to competitive performance. One way to determine this is to examine how different the times would be in a race of a known distance if there was no wind (that is, no drag). We can do it as shown below for a 1000 m time trial with a flying start taking 60 s at an average velocity of 60 km·h-1(16.7 m·s-1):
Step description |
Standard |
Forward lean with arms stretched |
Force of drag (or drag + friction) |
74.06 N |
61.91 N |
Time |
60 s |
60 s |
Mass |
100 kg |
100 kg |
Velocity reduction if force acted over 60 s: |
v = Ft/m = 74.06 × 60 / 100 = 44.44 m·s-1 |
61.91 × 60 / 100 = 37.15 m·s-1 |
Without wind, the final speed would have been (actual final speed 16.7m·s-1 plus speed without wind) |
16.7 + 44.43 = 61.14 m·s-1 |
16.7 + 37.15 = 53.85 m·s-1 |
Average speed would be (assuming a linear speed decline: [start speed + end speed]/2) |
(16.7 + 61.14)/2 = 38.92 |
(16.7 + 37.15)/2 = 35.27 |
Time with no wind (t = d/v) |
1000 m / 38.92 m·s-1 = 25.70 s |
1000 m / 35.27 m·s-1 = 28.35 s |
Time lost attributable to drag |
60 s – 25.70 s = 34.30 s |
60 s – 28.35 s = 31.65 s |
So we can see that 34.30 s of the 60 s time was attributable to the effects of drag for the standard riding position but for the more aerodynamic position it was only 31.65 s. The aerodynamic position is essentially 2.65 s faster! To obtain the same 60 s time, the rider in the aerodynamic position could produce less power, so they would be more efficient. This assumes that using the better aerodynamic position doesn’t then compromise force generation or endurance potential. You could test a number of positions in this way to find the best.
HOW ELSE CAN WE USE THIS INFORMATION?
We now understand a lot about drag in fluids and can do tests to determine the effects of changing body positions or clothing materials but where else can we use this? Aero- and hydrodynamic drag are important in any sport where we, or our implements, move at high velocities. A good example is in rugby and American football, where players often use a ‘torpedo’ kick or pass to achieve a greater distance. A torpedo kick/pass is one where the ball flies with its long axis pointing in the direction of flight, as shown in Figure 13.8. In this position, the ball has the best aerodynamic shape, so form drag is reduced. It is also important that the javelin and discus fly in an appropriate plane (you will learn more about this in Chapter 15). We normally spin such objects to keep them oriented correctly; see Box 13.3. Ultimately, performance enhancement can be made in most sports where individuals or machines move at reasonable speeds, as long as you use this knowledge to minimise drag.
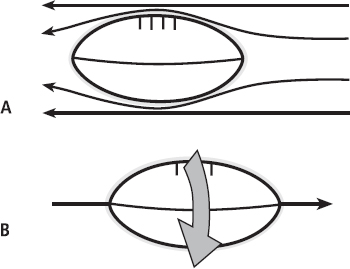
FIG. 13.8 A rugby ball is most aerodynamic when it travels with its axis parallel to the direction of travel (and therefore of the oncoming air flow) as shown in A. In order to keep the ball stable in flight a good player will spin the ball to create a torque vector through the axis of the ball as shown in B (see Box 13.3 below).
BOX 13.3 THE OPTIMUM FLIGHT OF A RUGBY BALL, JAVELIN OR DISCUS
Figure 13.8 shows that the best flight position of these objects is with the long axis aligned with the direction of travel. The question is how can we keep them in this plane? A very slight rotational force or a slight change in the angle of the oncoming air could affect the flight position and stop the object travelling with its axis aligned with the direction of flight. Yet we very rarely see this happen, because good athletes spin the objects to keep them in the correct plane.
Spinning the object gives it an angular momentum, which doesn’t change unless it is acted on by a force. If the object has little (or no) spin, a small force can cause a large change in its rotation but if it has a larger angular momentum, a large force is required to affect its rotation significantly.
The alternative wording for this explanation is that every spinning object creates its own torque vector directed perpendicular to the axis of rotation. This torque vector stabilises the object. While it is beyond the scope of this book to go into detail with respect to the mathematics of these explanations, they are basically the same.
You can see this phenomenon in action: you will have noticed that it is relatively easy to ride a bicycle without your hands on the handlebars when it is moving (that is, when the rotating wheels have angular momentum), but it is nearly impossible to balance on a stationary bicycle, even with your hands on the handlebars. You will have also seen this effect when you throw a Frisbee. The spinning of the Frisbee allows it to keep a horizontal plane and to let its shape create lift to keep it flying (lift is explained in Chapter 15). Since the stability is affected by both the object’s speed of rotation and its mass (and its distribution), there is less need to spin heavy objects as quickly to create stability.
This is the same principle behind rifling of gun barrels. This practice was first used in the cannon barrels of French naval ships many centuries ago and is used in nearly all guns today. The spherical bullets of cannons (and early guns) didn’t travel in a straight line, because slight imperfections affected the air flow around them and caused pressure differences. Pointed bullets are more aerodynamic, so they travel further, faster and in a straight line (as long as they are aligned in the direction of travel). Rifling is the engraving of spiral grooves on the inside surface of the barrel of a gun or cannon. This causes the bullet to spin as it passes along the barrel. A spinning bullet is very stable and therefore it remains a highly aerodynamic projectile as it travels.
When rugby players and javelin or discus throwers release their implements, they impart spin on them to keep them stable in the air and flying with optimum aerodynamic position. The task for the coach or biomechanist is to discover the optimum amount of spin, because the more force we use to spin the object the less force we are able to apply to project it.
SPECIAL TOPIC: UNDERSTANDING TEST VARIABILITY … WAS THERE REALLY AN EFFECT?
How confident are we that the change wasn’t caused by something else?
One theme of this book is to help you understand how you can test for the effects of changes in certain parameters. That is, does making a biomechanical change according to our theories actually make a change in practice? So, it is probably good to remind you of some of the problems of data collection.
We rarely get identical results in different tests. Results are always affected by numerous factors, most of which we don’t have much control over. For example, what if a small gust of wind came up in one of our trials? We might have seen a difference between two riding positions but only because a slight wind was blowing in one of them.
One way to see how repeatable or ‘reliable’ results are is to calculate another coefficient, the coefficient of variation (CV). This is the standard deviation of the results divided by the mean result. To calculate it, we need to make at least three trials of each of our conditions (for example three for each of the standard and aerodynamic positions) and then use a calculator or spreadsheet programme to calculate mean and standard deviations.
In Excel, you can use the formula ‘=stdev(n1, n2, n3…)’ to calculate a standard deviation (where n1, n2, n3… are your results) and for the mean use ‘=average(n1,n2,n3…)’. You might end up with numbers like these:
Step description |
Standard |
Forward lean with arms stretched |
Results for three trials |
74.06, 72.66, 75.90 N |
61.91, 64.32, 60.11 N |
Standard deviation (SD) |
1.62 |
2.11 |
Mean (M) |
74.21 |
62.11 |
Coefficient of variation (CV) = SD/M × 100% |
2.2% |
3.4% |
In this experiment, there was little variability (2.2% and 3.4%). You can see that the change in the mean value ((74.21 – 62.11)/74.21 × 100%) was 16.3%, which is much greater than our CVs. The variability within each condition is much smaller than the variability between them and we can be confident that this is a real result.
There are a few other, very useful, statistical tests that you can do but these are beyond the scope of the book. I’d suggest you visit a basic statistics website (search for terms such as ‘t-test’, ‘ANOVA’ and ‘regression’ for starters; they might not mean anything to you now but they will once you read about them) or get a standard statistics textbook to help you learn a little about statistics.
It can be difficult to see very small changes in drag using the technique presented above. You should remember that drag increases greatly with velocity, so you can see the effects of small differences in drag if the velocity is high. Also, the longer the time over which you take your measurements, the greater the likelihood that you’ll see a difference. If you were a sprint runner and wanted to examine the effect of one Lycra suit against another, where the difference is likely to be small, you might find a long hill that allows high speeds to be maintained for long periods on a bicycle and adopt a position where you are as upright as possible (or standing on your pedals to mimic a standing position more similar to running). You can time from the top to the bottom of the hill to see if there is any (small) difference in drag when you are moving with your running suit on.
speed = ∆d/∆t
velocity (v) = ∆s/∆t (rω for a spinning object)
acceleration (a) = ∆v/∆t
force of drag (form) (Fd) = kAv2 (or Fd = CdρAv2)
momentum (p) = m × v
conservation of momentum: m1v1 = m2v 2
impulse (J) = F × t or ∆mv
coefficient of variation (CV) = SD/mean × 100%
m·s-1 to km·h-1 = x m·s-1 /1000 × 3600
km·h-1 to m·s-1 = x km·h-1 × 1000/3600
Related Websites
Principles of Aeronautics, Aerodynamics in sports equipment, Aeronautics internet textbook (http://learn.fi.edu/wright/again/wings.avkids.com/wings.avkids.com/). Website detailing the importance of aerodynamics in sports.
Cycling Aerodynamics, Exploratorium.com (http://www.exploratorium.edu/cycling/aerodynamics1.html). Description of the use of aerodynamics in cycling, including drag calculators.
Aerodynamics and Hydrodynamics of the Human Body, Birds and Boeing, The world think tank (http://www.worldthinktank.net/art124.shtml). Interesting observations on aerodynamics in humans and animals with links to several websites examining aerodynamics in sports.
What is Fluid Dynamics? (http://www.livescience.com/47446-fluid-dynamics.html). Basic overview of fluid dynamics with links to further reading.
Understanding the Least-Squares Regression Line with a Visual Model: Measuring Error in a Linear Model, Principles and Standards for School Mathematics (http://standards.nctm.org/document/eexamples/chap7/7.4/). Basic explanation of regression equations, with an example allowing the user to explore three methods for measuring how well a linear regression equation can fit a set of data points.
The Physics of Sports (http://www.topendsports.com/biomechanics/physics.htm). Website investigating the applications of physics in sports.
INTERVIEW WITH THE EXPERTS
Andrew Walshe and Per Ludstam use high-speed video and optical sensor systems to analyse ski performance, Chile 2006.
Andrew Walshe
Specialist:
Name: Andrew Walshe
Nationality: Australian
Athlete Biography:
Name: US Alpine Ski Team
Nationality: American
Major Achievements:
•USA achieved historical best team results in 2005 World Championships in Bormio, Italy; third overall with two gold, one silver and three bronze medals
•Among the world’s top three teams for the four years from 2007
When and how did you use biomechanical analyses or theories to optimise the skiers’ training?
Fundamental sports technical assessments commenced in 2000 in preparation for the 2002 Olympic Winter Games (OWG). Base level analysis included extensive qualitative and quantitative video analysis of the athletes’ technical and tactical performances on all World Cup and OWG venues. This has since been enhanced with high-speed video analysis linked to optical sensors attached to the skis. This adds performance feedback – by increasing the pitch of sound in the skier’s ears as velocity increases – as well as high-level technical analysis of the course/skier in terms of displacement on the snow, velocity acceleration, ski angles, slip (sliding) and numerous other parameters.
How did you change your training/techniques based on this?
Training has been modified in several ways:
•The manner in which tactical choices are relayed back to the athlete; course analysis gives athlete feedback as to the ‘optimum’ line to ski so that performance is maximised.
•Technical feedback as to body position that allows the athletes to modify timing and distribution of pressure on the ski during a turn to increase velocity and hence performance.
How do these analyses influence the chances of success of the skiers?
Video/velocity analysis has become an integral part of World Cup performance – no teams that are not using these techniques have been successful in recent years. However, in a sport with as many influencing variables as skiing, it’s very hard to isolate the impact of one intervention/technique over the others.
What were the strong points (both personally and intellectually) of the best biomechanists you worked with?
The success of the programme has been largely the result of the integration of new technologies and ideas into the practical setting. This level of analysis needs to be rigorously tested and evaluated prior to application. Once a successful test has been achieved, extensive education with the coaching staff as to potential strengths and weaknesses of the system needs to be completed. At this point, a carefully managed programme that provides the coaches/athletes with feedback suited to their level of skill, experience, progression, and is part of a long-term strategic plan, needs to be followed. ‘Too much information too soon’ can severely impact the success of any biomechanical evaluation if it’s to be incorporated into the programme at an elite level.
The staff need to be well educated, but more importantly they must have the personal and practical skills to introduce the information in such a way that it supports the existing programme. Some of the most successful applied biomechanists are not the smartest, but are able to relate their findings in a simple and productive manner to the coaches. Great personal and communication skills are critical in this regard.
Overall, how important do you feel a good understanding of biomechanics is to a coach or sports scientist?
It is very important. A programme’s success is typically a function of the coach’s ability to understand the potential of the programme as well as incorporate the testing results into their coaching plan in a practical and effective manner.