
We have performed a race analysis on a 400 m freestyle (front crawl) swimmer and found that their swim time – the time spent swimming during the race, rather than starting or turning – was slower than their competitors’. How might we improve their movement through the water to increase their swim speed?

By the end of this chapter you should be able to:
•Define the term ‘drag’ and explain how different forms of drag (form, surface and wave) might affect sporting performance
•Describe the factors that influence drag in aquatic environments
•Describe the technique parameters that influence form, surface and wave drag during swimming
The first thing that we should understand is that the word hydrodynamics refers to our movement in water-based environments, from the Greek word for water: hydor (or hudor). Fluid dynamics encapsulates movement through all media, including air and other fluids. In this chapter, we are concerned with how to propel ourselves through water.
The second thing we should understand is what a race analysis is. If we want to improve an athlete’s performance, it is very helpful first to determine their strengths and weaknesses. In this example, we may have timed the turns during the race (time from 5 m out from the wall, through the turn, to 5 m away from the wall), then subtracted these from the total race time to obtain the actual swimming time. We would also have measured the time from the ‘starter’s gun’ to the 15 m point to account for the start time, or omitted the first lap from the analysis.
Swim time = total time – start time – turn time
We might have thus found that the swimmer had turn times as good as, or better than, their competitors but that their swimming time was longer and so their swimming stroke possibly requires improvement. From a biomechanical perspective, we need to consider the factors that influence swimming speed and efficiency and work to improve those, before re-testing to see if our interventions were effective. (Of course, we should be mindful that the slow swim times could be due to psychological or physiological reasons, or that perhaps any deficiencies in technique might have resulted from poor strength or flexibility conditioning.)
The forward speed of the swimmer will be dictated by two factors: (1) forces resisting motion – drag; and (2) forces causing motion – propulsion. Since humans manage maximum swimming speeds of just over 2 m·s-1 (compared to running speeds of around 12 m·s-1 and swimming speeds of some fish of over 25 m·s-1), we can see there is a real need to understand the impact of both of these properties to improve swimming performance. The total average drag force on a male swimmer moving at 2 m·s-1 is a considerable 110 N; compare this to the drag values we obtained in Chapter 13 when considering moving on a bicycle at over 16 m·s-1. In this chapter, we will focus on the forces that resist motion.
Wave drag
You will remember that there are three main types of drag: form, surface and wave. Wave drag is present at the interface of the water and the air, as the swimmer pushes through the water. The wave in front of the swimmer pushes back against them, thus slowing their speed or increasing the energy required to swim at a given speed (Figure 14.1). Other waves that form around the body due to pressure differences also take energy away. Therefore, wave drag is caused by the energy cost of wave production.
In swimming, wave drag has a very significant effect. In fact, in arms-only front crawl swimming, wave drag has been estimated to account for up to 50% of the total drag of the body (Toussaint & Truijens, 2005). Wave drag increases to the cube of velocity, so as swimming speed increases its negative effect increases dramatically, e.g. if swimming speed is doubled, the force of wave drag increases 8 times (2 × 2 × 2)!
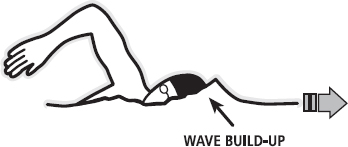
FIG. 14.1 Waves build up at the front of the body during swimming. These waves oppose the forward movement of the swimmer. Other waves also build up around the swimmer according to pressure differentials.
These waves are similar to those that form around ships, and much of what we know about the effects of wave drag comes from our knowledge of ships. Wave length and wave height both increase as the speed of a ship, or a swimmer, increases. The wave system that surrounds a swimmer will travel at the same speed as they do; we ‘carry’ the waves with us, but as we swim more quickly the distance between the first wave (called the bow wave, as in the bow of a ship) and the second wave will increase. At some point, the distance between the waves will be the same as the length of our body and we will effectively be swimming in a hollow (see Figure 14.2). Nearing this point, any attempt to increase speed becomes very energy costly.
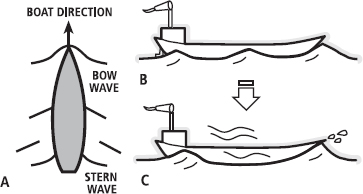
FIG. 14.2 Waves form at consistent intervals along a ship (A). As the boat moves from a slow speed (B) to a fast speed (C) the waves become higher (i.e., greater amplitude) and are spaced further apart. As shown in C, at some point the distance between the bow and stern waves will be the same as the length of the ship. In that case, the ship (or swimmer) will be moving in a ‘hollow’.
If we had a longer body, we could swim faster before this occurred, so in some respects taller swimmers might have a slight advantage. However, the wave-to-wave distance equals the body length at a swim speed of just below 1.8 m·s-1 for a 2 m tall person; competitive swimmers normally swim faster than this anyway, so, at least for this reason, there may not be much of a benefit to being tall. This explains why wave drag makes up such a large proportion of our total drag regardless of body size.
At certain speeds, the bow wave can interfere with a second wave, the stern wave, which is at the back end, or stern, of a ship or swimmer. Although the physics of wave interference is beyond the scope of this book, the phenomenon is shown in Figure 14.3. At some swimming speeds, the stern wave is cancelled or becomes smaller, while at other speeds it is reinforced or becomes bigger (also called ‘wave summation’). As swimming speed increases, there should theoretically be speeds at which there is a slight drop in wave resistance and others where wave drag increases, as shown in Figure 14.4. It is intriguing then to consider that at these speeds we could optimise the efficiency of swimming. However, measurements of active drag during swimming (Toussaint et al., 1988) show that the total drag continues to increase with velocity and is always smaller or equal to the drag arising from the body being pulled passively through the water. This leads to the conclusions that there is no particular speed at which swimmers swim with less wave, or total, drag; that changes in velocity during the stroke will amplify drag; and that swimming technique – possibly including the arm action and body roll – might reduce wave build-up and thus minimise drag.
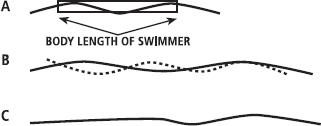
FIG. 14.3 A: At slower speeds, wave formation might look like this. B: At faster speeds, the wave distance increases (solid line) but the first wave would still move backwards similar to the dotted line. C: In this example, the waves cancel where the stern wave would normally have been. This is called cancellation. Wave summation can also occur.
FIG. 14.4 At some speeds during passive swimming (i.e., where the body is dragged through the water), wave cancellation and summation affect wave height and thus wave drag. As such, wave drag does not increase constantly. However, active drag measured during swimming is always lower than, or equal to, drag recorded under passive conditions. It has therefore been suggested that swimming technique strongly influences wave drag.
It has been demonstrated that highly trained swimmers create smaller waves compared to less-skilled swimmers (Takamoto et al., 1985), which strongly suggests that swimming technique might be an important factor influencing wave drag (see Figure 14.5). While it is not clear exactly what techniques influence wave drag the most, one hypothesis is that increasing the effective body length, by stretching the arm in front of the body at the end of the recovery phase (before propulsion), will reduce wave drag since wave drag is greatest when the wave distance equals the body length. The arm might also cause earlier divergence of the oncoming flow, reducing the pressure at the front of the head and therefore minimising wave build-up, a bit like the bulbous front end of a ship minimises wave formation (see Figure 14.6).

FIG. 14.5 Well-trained swimmers exhibit significantly less wave formation. Therefore, resistance due to wave drag is reduced when compared to lesser-trained swimmers (compare to Figure 14.1). Therefore, swimming technique likely has a significant effect on wave drag.
FIG. 14.6 Wave build-up at the nose of a ship increases drag (A). Bulbous front ends reduce wave formation. While there is some contention as to the mechanisms by which they work, the most common theory states that they produce waves that are out of phase with the larger bow wave (B). That is, the trough that normally occurs at the back end of a wave coincides with the peak of the bow wave when the ship is at the appropriate speed. In that case, the trough and wave cancel each other (see Figure 14.3), so a bow wave does not form. Such a mechanism has been variously reported to increase efficiency by 5%–25%.
Nonetheless, the position of the body in the water is probably very significant. It is likely that reducing the up-and-down movement of the body through the water is an important factor, since wave drag is increased with the up-and-down motion of a swimmer. Swimming with the head down (chin tucked slightly towards the chest), rather than with the head up and eyes forward, allows the head to remain further underwater. It has been hypothesised that the lower head position reduces the pressure at the front of the head to minimise wave formation. Finally, body roll may reduce the effective surface area of the body that is perpendicular to the bow wave, so a smaller wave is likely created and the swimmer is more likely to ‘pierce’ the wave that does form. Surf lifesavers at your local beach often use a side-on diving technique through oncoming waves for this reason.
One notable way to reduce wave drag is to swim as much as possible underwater. In fact, some research indicates that drag is reduced as the depth of the swimmer increases, at least until that swimmer is more than 0.5 m below the surface (Mantha et al., 2014), and the best male sprint (50 m) freestyle swimmers may swim 1 m·s-1 faster under the water after the race start than they swim during the race (i.e. on the water). These ‘submarining’ techniques, where swimmers stay well below the waterline so that waves are not created, have been used very effectively to propel the body through water even though a relatively weak ‘dolphin’ kick (wave-like motion of the body) is the only means of propulsion. The International Swimming Federation (FINA) has placed strict limits on the distances that can be swum underwater in most forms of racing (15 m in pool swimming) but if a swimmer fails to swim underwater to the limits of these rules they might be surrendering a competitive advantage.
Form drag
Form drag – drag that is associated with the surface area and shape of the swimmer – is also very significant. To reduce it, we need to minimise the front-facing area of the swimmer as much as possible. This can be done by keeping the head down (that is, not looking forward in the water, which will also reduce wave drag, as discussed above).
The frontal surface area is also increased by the swinging of the legs during flutter-type kicking. At the extreme ranges of the kick (Figure 14.7), the frontal surface area of the body is large. We might therefore choose to keep the amplitude of kicks to a minimum, while making them as powerful as possible. The ideal size of the kick will differ between swimmers with different leg size and length, so we need to test this in training. Having said that, a small leg kick seems to reduce the pressure differential around the leg area of the body, which minimises wave formation and considerably reduces wave drag (van den Hout, 2003). Since the reduction in wave drag is greater than any increase in form drag, a small, continuous kick reduces drag during swimming. Indeed, given the poor capability of swimmers to produce propulsion through the standard flutter kick in crawl swimming, its greatest benefit might be that it reduces drag!
Reducing frontal surface area can also be accomplished by aligning the body as much as possible in the swim direction (see Figure 14.8). Any deviation from this line will increase the frontal surface area of the body. While the body roll that occurs commonly during crawl stroke swimming does not increase frontal surface area, both pitch (rotation about the mediolateral axis) and yaw (rotation about the anteroposterior axis) do. These whole body rotations are therefore detrimental to swimming speed and efficiency. Some major technique factors affect pitch but an understanding of buoyancy and the centre of buoyancy is required; Box 14.1 explores how we can maintain a near-zero pitch angle during crawl swimming.

FIG. 14.7 Since form drag is proportional to the frontal cross-sectional area of the swimmer (remember Fd = kAv2; Chapter 14), kicks with greater amplitude (A) will increase form drag.
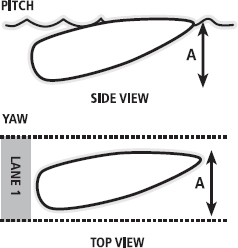
FIG. 14.8 To reduce form drag, an object (e.g. our body) should remain aligned with the direction of travel. In some swimmers, the legs fall below the level of the head (pitch; top diagram), which increases the frontal surface area of the body. Sideways movement of the body can also occur (yaw; bottom diagram), which also increases surface area. Both technical flaws increase form drag and thus reduce swimming performance.
Finally, both wave and form drag can be reduced during turns in pool swimming by staying underwater, perhaps by more than 1 m, after pushing off the wall. The reason for this is relatively simple to understand. A boundary layer of water forms around and trails behind the swimmer as they move through the water, just as air moves with a moving object as described in Chapter 13. At the push-off during a turn in pool swimming, the swimmer accelerates directly into the oncoming water that was moving with, and behind, the swimmer prior to the turn. This means that the velocity of the swimmer relative to the water is high at push-off and, as you know, drag increases substantially with an increase in velocity. By pushing off the wall at a negative angle, deeper into the water, the swimmer avoids much of the fast-moving water and instead travels through the still water at these greater depths. Remarkably, the reduction in drag and consequential increase in velocity more than make up for the loss in swimming time that might be expected by the swimmer travelling further (i.e. the increase in ‘distance’ travelled).
BOX 14.1 OPTIMISING BODY POSITION DURING CRAWL SWIMMING: UNDERSTANDING BUOYANCY
In order to minimise drag during swimming, it’s important to keep the body flat in the water, i.e. minimise the pitch angle. To do this we need to make sure that the forces lifting the body equal the forces pulling the body down, along the entire length of the body. Clearly, the weight force (i.e. gravity) pulls us downwards with the force being proportional to our mass (remember, F = ma). The (vertical) force lifting us in the water is the buoyancy force. The factors that influence the buoyancy force were first described by the Greek mathematician Archimedes (287–212 BC). As legend has it, he was asked by King Hiero II to determine whether his new crown was made of pure gold or was imperfect. Archimedes could not melt the crown and form a new solid where the density could be calculated (remember, density = mass/volume) so he had to come up with another method. While taking a bath he noticed that his body displaced water and he realised that the water displaced was equivalent to his body’s volume. So he could then measure the water displaced by the crown and then weigh it to find the density. This story is probably at least partly fictional, but we will discuss a similar method that is more likely to have been used later.
Archimedes is famous for (among other things) formulating Archimedes’ principle, which states that the magnitude of the buoyant force is equal to the weight of the fluid displaced by a body. Thus, the buoyant force (Fb) can be calculated by measuring the volume of displaced fluid (Vd) and multiplying by the fluid’s specific weight (γ):
Fb = Vd × γ
The specific weight of a fluid is equal to its density (ρ, mass per volume) multiplied by the acceleration due to gravity. For example, the densities of air and water measured at 20°C and at one atmospheric pressure are 1.2 and 998 kg·m3 so their specific weights (i.e. × 9.81) are 11.8 and 9790 N·m-3, respectively. So the buoyancy force on a person with a volume of 0.069 m3 (69 litres) would be:
Fb = 0.069 m3 × 9790 N·m-3
Fb = 675.5 N
Of course, this would increase if the person went deeper in the water because the density of water increases with depth. The centre of volume is the point around which the body’s volume is located. Because, effectively, the buoyancy force is directly related to the volume of the body, the centre of buoyancy is the average point about which all the buoyant forces act. In this way it is similar to the definition of centre of mass, described in Chapter 6.
Of course in order to float we need the buoyancy force to equal the weight force. So for two people with the same volume (i.e. same buoyancy force), a person with lower density, by having either more fat and less muscle or lower bone density, will more likely float. But what does this have to do with body position during swimming?
Well, in swimming we need the body’s pitch angle to be minimal. This means that the buoyancy force-to-body weight ratio must be equal across the body. Because our lungs have a large volume with low density (which helps buoyancy; swimmers often breathe in the upper range of their lung capacity to keep air in their lungs) but our legs are dense, there is a tendency for our legs to sink during crawl stroke swimming. This is because the buoyancy force is less than the weight force at the legs. The result is an increased pitch and thus an increased frontal surface area and form drag.
One way to minimise this effect is to use flotation devices such as wetsuits. There is a large volume of suit around the legs (we have to cover both legs) relative to the leg volume, but it is very light so the buoyant force increases substantially whereas the weight force does not. In the upper body the wetsuit adds a little volume, but it is not as substantial when compared to the volume of the upper body. This extra flotation particularly at the legs can help maintain body position and is one reason why wetsuits help to improve swimming time. A second reason is that the overall increase in buoyancy means that the swimmer can direct more of their effort to creating horizontal propulsion through the water and less to creating vertical propulsion to lift their body in the water.
Another way to minimise the effect is to move the body’s centre of mass forwards in the body, closer to the centre of buoyancy. As shown in Figure 1, a torque is created when the two forces are not in line. Stretching the lead arm above the head shifts the centre of mass and minimises the torque causing pitch. In swimming, having the lead arm remain outstretched for a significant portion of the stroke helps to reduce pitch … of course, it also helps with the minimisation of both form and wave drag as discussed in Chapter 13.
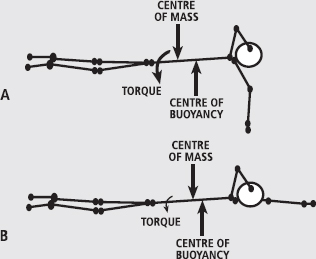
FIG. 1 A swimmer was filmed in the sagittal plane and the body segments digitised using motion analysis software. The estimated centres of mass and buoyancy are shown. In (A), the propulsive stroke occurs while the recovery arm is being brought forwards. This causes the centre of mass to move posteriorly and a torque to be created that increases pitch (and thus drag). In (B), the lead (propulsive) arm is kept in front of the body until the recovery arm is nearly in position for the next stroke. This shifts the centre of mass closer to the centre of buoyancy and minimises the torque and subsequent pitch. As a matter of interest, delaying the propulsive stroke is also thought to make best use of the body’s ability to glide after each propulsive stroke, which also increases movement efficiency.
So can you figure out how Archimedes might have determined whether the crown was pure gold? He knew that he could find enough pure gold to completely balance the crown on a set of scales (i.e. their masses and therefore the weight forces were the same). If they were of the same density then they must also have the same volume. In that case, if he put the scales into water the buoyancy forces would be the same and the scales would remain balanced. However, if the crown was impure and its density less than the pure gold then its volume would be greater than the volume of gold. In water, the buoyancy force would be greater and the scales would tip down towards the gold. The result? The scales tipped, the crown was impure!
You will remember from Chapter 13 that surface drag is caused by the friction of a fluid on the surface of an object. While smaller in magnitude than wave and form drag, the surface drag on a swimmer can significantly affect performance, especially when we consider that races can be decided by differences as small as one-hundredth of a second. Traditional practices aimed at reducing surface drag include minimising the size of swim suits (skin has a lower friction coefficient than Lycra or cotton in water) and shaving the body to remove hair.
In modern times, swimmers have used specially designed suits reported to have much lower drag coefficients (and a small but meaningful buoyancy effect, which we will not discuss here). In suits that were allowed to be used until 2009, design features of the materials caused an increase in surface drag so that water remained attached to the swimmer as a boundary layer, much like the golf ball example from Chapter 13. The hypothesis was that the attached layer reduced pressure differences around the body to minimise both form and wave drag; therefore, changing the surface drag then influenced the other, probably more influential, forms of drag. These suits also compressed body segments, making it easier for swimmers to maintain body alignment and thus to maintain a hydrodynamic body position. The rules have since changed, however, and little research has examined the effects of newer suit designs on drag in swimming. There is therefore not enough data to definitively determine the true effect of wearing the current suits, although speculatively the newer suits are designed within the new rules but using the same principles. Nonetheless, any improvement in swimming performance might be beneficial when a race can be won or lost by 0.01 s, so the emergence of new technologies (and hopefully the research data to verify their benefits) will surely come.
THE ANSWER
Hydrodynamically, how can we improve our swimmer’s 400 m time by improving her swim time (i.e. neglecting start and turn times)? First, it is important to note that there is no ideal body position that can be used for everyone, so individual testing will be needed to determine each swimmer’s optimum. However, we can point to several technique parameters that could be manipulated to improve swimming time by reducing drag:
•The lead arm (recovery arm) should stretch in front of the head/shoulder of the swimmer as the propulsion arm pushes backwards. This should reduce wave formation by increasing the effective body length and reducing pressures at the head that might cause a bow wave build-up. It may also reduce form drag, by allowing water to diverge earlier and travel around the body with less impedance, thus reducing turbulence and energy loss. Importantly, it will also help to balance the buoyancy and weight forces on the body, and therefore help to maintain an optimum pitch angle (Box 14.1).
•The head should be positioned face down in the water to minimise wave and form drag by keeping more of the body under water and increasing the streamlined shape of the body. It can also balance the body better in the water, to reduce the pitch angle and therefore reduce the effective frontal surface area.
•The amplitude of the leg kick should be as small as possible for a given power requirement, since increasing kick amplitude increases frontal surface area and, therefore, form drag. However, a small kick reduces wave (and total) drag and so can be maintained if needed (we’ll discuss the kick more in the next chapter).
•The body must maintain good alignment with the direction of swim; any pitch or yaw of the body will increase the frontal surface area and increase form drag (the effects of body roll are complicated and beyond the scope of this chapter).
•The use of appropriate swimwear might reduce form, wave and surface drag.
The cosmopolitan sailfish (Istiophorus platypterus) is thought to be the fastest fish over short distances. It is very difficult to accurately measure its top speed because it rarely moves in a straight line, but in trials completed at the Long Key Fishing Camp, Florida, USA, a cosmopolitan sailfish took out 91 m of fishing line in just three seconds and so must have been travelling at over 30 m·s-1 or nearly 109 km·h-1! Although the sailfish has a huge propulsive potential, such speeds can only be achieved because of its fantastically low drag. Humans have a long way to go before we fully understand how to minimise hydrodynamic drag to this extent but as biomechanists discover new ways to reduce drag, you can expect swimming world records to continue to fall.
FIG. 14.9 There is significant wave formation at the front of breaststroke swimmers. By staying underwater longer and by keeping the hands in front of the body when surfacing (as shown here), wave drag can be minimised.
HOW ELSE CAN WE USE THIS INFORMATION?
This information is important when developing techniques to optimise other swimming strokes. Breaststroke swimmers commonly propel themselves under water, only surfacing at the end of each stroke to breathe (as the rules state they must); at this point, wave drag is significant (see Figure 14.9) so breaststrokers keep their hands in front of the chest to reduce drag. Butterfly stroke swimmers use similar hydrodynamic techniques for the underwater phase (as well as maximising their use of submarining at each turn) as crawl stroke swimmers. Our increased understanding of hydrodynamic principles has also led to great increases in the speeds of water-based sports craft including speed boats, yachts, Olympic class boats and jet skis.
Useful Equations
force (F) = m × a
force of drag (form) (Fd) = kAv2 (or Fd = CdρAv2)
References
van den Hout, et al., (2003). ‘The influence of the swimmer’s technique on the wave resistance’. In: Werktuigbouwkunde en Maritieme Techniek, Delft, The Netherlands: Delft University of Technology, 107. Cited in: Toussaint, H. & Truijens, M. (2005). ‘Biomechanical aspects of peak performance in human swimming’. Animal Biology, 55(1): 17–40.
Toussaint, H.M., Beelen, A., Rodenburg, A., Sargeant, A.J., de Groot, G., Hollander, A.P. & van Ingen Schenau, G.J. (1988). ‘Propelling efficiency of front crawl swimming’. Journal of Applied Physiology, 65: 2506–12.
Toussaint, H. & Truijens, M. (2005). ‘Biomechanical aspects of peak performance in human swimming’. Animal Biology, 55(1): 17–40.
Takamoto, M., Ohmichi, H. & Miyashita, M. (1985). ‘Wave height in relation to swimming velocity and proficiency in front crawl stroke’. In: D.A. Winter, R.W. Norman, R.P. Wells, K.C. Hayes & A.E. Patla (Eds). Biomechanics IX-B, Champaign, IL, USA: Human Kinetics Publishers, 486–91.
Related Websites
Topend Sports (http://www.topendsports.com/sport/swimming/science-biomechanics.htm).
USA Swimming website (http://www.usaswimming.org/USASWeb/DesktopDefault.aspx?TabId=1092&Alias=rainbow&Lang=en). Comprehensive swimming website with links to swimming biomechanics articles; see especially ‘High Performance Tips’.