CHAPTER 6

TORQUE AND CENTRE OF MASS

Two athletes of the same body stature recorded the same one-leg vertical jump height in a laboratory jump test but one athlete can jump over a higher bar in the high jump. Why might this be so? What techniques can we use to clear obstacles?

By the end of this chapter you should be able to:

 

•Explain the concept of torque and describe the factors that influence it

•Calculate the centre of mass of an athlete or object

•Describe how an athlete can manipulate their body position about their centre of mass to maintain balance or evade objects or opponents

•Explain the optimum technique of the high jump bar clearance in these terms

 

Both athletes are the same height and seem to have identical athletic ability. It is as if one of the athletes can manipulate their body to clear the bar in some way the other athlete can’t. If they went over the bar on their front, perhaps one athlete might have sucked in their stomach? But high jumpers travel over the bar on their backs, using a technique called the Fosbury flop. The Fosbury flop technique of high jump was popularised by Dick Fosbury, who used it to win the gold medal at the 1968 Mexico Olympics while still a college student. Why is it so effective? The idea of sucking in your stomach isn’t too far off the mark.

Bodies are made up of a huge number of particles. The weight (in newtons) of a body is a function of the mass of each particle and their acceleration due to gravity (weight force, F = ma). The point around which all particles of the body are evenly distributed, and therefore the point at which we could place a single weight vector, is the body’s centre of gravity (Figure 6.1). Gravity only applies a force downwards towards the Earth but we could look at the body from any direction. The point at which the mass of the body is evenly distributed in all directions is the centre of mass. Centre of mass and centre of gravity are basically the same, except that centre of gravity is only used to denote the centre of the body in the vertical direction.

FIG. 6.1 A body is made up of a nearly infinite number of particles. The weight of the body is a function of the mass of each particle and their acceleration due to gravity (F = ma). The point around which all of the particles in the body are evenly distributed, and therefore the point at which we could draw a single weight vector (W), is called the centre of gravity (top diagram). If we rotate the object (a, b, c, bottom diagram), there is an equal mass on each side of a line drawn through the centre of mass (m₁ versus m₂). The centre of mass is the point about which the mass of the object is evenly distributed in all directions.

 

To be absolutely correct, we’d need to consider another quantity: torque. The magnitude of the force causing the rotation of an object (or particle in a body) is defined as the moment of force (M; you can now see why it is common to use ‘p’ for momentum instead of ‘M’) or more simply torque (τ; the Greek letter tau, pronounced ‘tor’). The term ‘moment of force’ hints that we are applying a force at a distance from some pivot point, given that the word ‘moment’ is used in physics to describe anything where a quantity is multiplied by a distance. Essentially, torque (τ) is equal to F × d (force × distance). You can see how torque is produced in Figure 6.2. The distance d is always measured perpendicular – that is, at right angles or 90° – to the line of action of the force. In Figure 6.3, the judo player is best advised to apply the forces in the forward–backward direction, to turn their opponent. The body can also be balanced by production of the appropriate torques, as shown by the gymnast in Figure 6.4, where the torque developed by the muscle acting across the joint is influenced by the perpendicular distance from the muscle’s line of action to the joint’s centre of rotation.

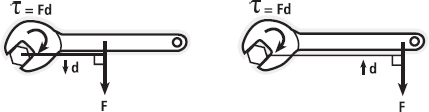
FIG. 6.2 A torque is created when a force (F) is applied at a distance (d) from the centre of rotation of an object (the nut in this instance). Since the torque (τ) is equal to the force multiplied by the distance, an increase in the distance over which force is applied, called the moment arm, will increase distance. In this example, a spanner is used to apply the same force over a greater distance (right diagram versus left diagram), and hence a greater torque. The distance is always measured perpendicular (at right angles, 90º) to the line of force.

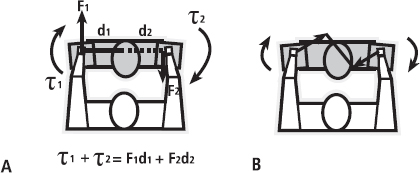
FIG. 6.3 The judo player in A (left) is trying to turn their opponent by applying forces (F₁ and F₂) to the shoulders at distances (d₁ and d₂) from the centre of rotation of the body. The total torque applied is equal to the sum of both of the torques produced (τ₁ and τ₂). In B (right), the forces are not applied in a forward–backward direction so the moment arm, which is always measured perpendicular to the line of force, is smaller. So even though the forces applied are the same, each torque is smaller and therefore the total torque is smaller.

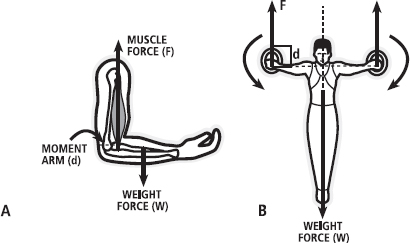
FIG. 6.4 In A (left), the biceps brachii muscle produces a force (F) acting on the bone at a distance (moment arm d) from the centre of rotation of the elbow. In this instance, the arm is stationary, so the torque created by the biceps brachii about the elbow is equal to the torque created by the weight of the forearm and hand (weight force W). In B (right), the muscles acting across the shoulder create a downward force at the hand (F) acting at a distance (d), which is perpendicular to the line of the force. The downward force creates an upward reaction force large enough to prevent the body falling under its own weight (W). The sum of the torques and weight force equal zero, and the body is balanced.

In any object, the downward action of gravity influences every particle. If you look back at Figure 6.1, you can see that this influence of gravity on each particle creates a huge number of individual torques. The centre of gravity is the point about which the sum of all these torques is zero. The centre of mass is therefore the point about which the sum of torques would be zero if the body were re-oriented to be in line with gravity. It might also be important to note that the centre of pressure is the point of contact with a solid object (e.g. the feet on the ground during running or standing; Figure 4.2) through which the centre of gravity or mass acts; it can easily be measured using a force platform (Chapter 5).

THE ANSWER

How does understanding all this allow us to determine why someone might jump higher? When we jump, we apply a force to the ground (F) to accelerate (a) our mass (m) upwards, as you learned in Chapters 4 and 5. The body therefore attains a vertical velocity, with the movement of the body being represented by the movement of the centre of mass. However, we can manipulate the body segments around the centre of mass at the appropriate time to jump a higher bar. Notice in Figure 6.5 (a), the centre of gravity of the jumper is below the level of the bar. This is also true for b, c and d. However, the jumper has manipulated their body so the point that is closest to the bar is always highest. Only one part of the body is higher than the bar at any one time but that’s all there needs to be. Understanding the concept of centre of mass helps us develop strategies to improve athletic performance. The Fosbury flop is a nice example. (Special Topic: Calculation Of An Athlete’s Centre Of Mass – The Segmentation Method (on here) explains how to analyse your own techniques to find where your centre of mass is.)

FIG. 6.5 The Fosbury flop technique. The jumper applies a large force down into the ground in order to attain a high vertical velocity at take-off (A) while the centre of mass of the body is raised (notice the arms and one leg are lifted high). The arms are then moved down the body as the head is extended back over the bar (B) while the centre of mass continues to rise. At the peak of trajectory (C) the centre of mass is slightly below the top of the bar, but the segment of the body crossing the bar is higher; the legs and head remain below the level of the bar. Finally, as the centre of mass falls, the legs are the last to be moved over the bar (D). By manipulating the body about its own centre of mass, a jumper can jump over a bar which is greater than the height of the centre of mass at its highest.

HOW ELSE CAN WE USE THIS INFORMATION?

We can also manipulate our mass in other sports. In evasive sports we try to move our centre of mass around an opponent, but to evade them we only need part of our body to be out of reach at any one point. We might move our arms and legs in one direction, so that our torso or mid-region can be moved in another, out of reach of the outstretched arm of an opponent. In basketball and netball, we might try to ‘hang’ in the air to block a shot or provide upper body stability on which to make a shot of our own. We do this by bringing our legs up under our body after we leave the ground during a jump, as in Figure 6.6. When we would normally be about to fall back down towards the ground under the influence of gravity we rapidly extend our legs downwards and so, to conserve momentum, our upper body moves upwards. In effect, since our body’s centre of mass is moving downwards but, relative to it, our upper body is moving upwards, our upper body momentarily remains stationary or ‘hangs’. In what other sports might we also alter our shape about our centre of mass to good effect?

FIG. 6.6 In many sports it is important to keep the head and eyes still during the execution of a skill. This usually improves the accuracy of our movements. In basketball, athletes can manipulate their body parts while the centre of mass (CM) of the body rises and falls during a jump, according to the law of conservation of momentum. First they bring their legs up under the body, which tends to draw the upper body down relative to the CM, and then rapidly extend their legs to thrust the upper body upwards as the body’s CM falls. Such a technique can be used to project objects in other sports, and by defenders in sports such as basketball, netball and volleyball.

Another important use of this information is in helping athletes (or non-athletes) to obtain balance during a complex skill. In gymnastics, for example, we manipulate our bodies to perform elements requiring balance, as in Figure 6.7. Here, balance is achieved when the body’s centre of mass lies within the base of support, i.e. between the two hands. If the centre of mass moves outside the base of support (that is, the centre of pressure is outside the base of support), either by moving the legs in one direction or by reducing the distance between the hands (i.e. minimising the base of support), balance cannot be achieved. Balance is important in sport, and we often use the term stability to denote that an object such as our body is stable within the base of support.

Of course in some instances it can be useful to allow the body to be unbalanced. When accelerating during running, it helps to allow the centre of mass to move forward of the base of support (i.e. the foot that is contacting the ground) because this will cause a forward rotation of the body. This rotation, which is caused by the force of gravity, provides a forward acceleration that helps us move, that is, it creates mobility. So instead of muscle forces being the sole provider of force, gravity can also provide a force. Leaning towards the direction of acceleration (or away from the direction of deceleration when we stop) can help us move faster and with less muscle force, which also increases our movement efficiency; you will learn more about efficiency in Chapter 9.

FIG. 6.7 The gymnast can balance because the centre of gravity of the body is located directly over the hands (base of support).

SPECIAL TOPIC: CALCULATION OF AN ATHLETE’S CENTRE OF MASS – THE SEGMENTATION METHOD

For a coach, it is often important to be able to determine where the centre of mass of an athlete lies. For a physiotherapist or rehabilitation specialist, it might be important to determine it to aid a rehabilitating patient maintain balance while performing a daily task. Using our understanding of torques, we can determine this relatively simply. The barbell in Figure 6.8 consists of two weights of 250 N and a bar weighing 200 N. Because the barbell is symmetrical, you can see that its centre of mass would be at the midpoint of the bar (at the arrow indicating the weight of the bar – 200 N).

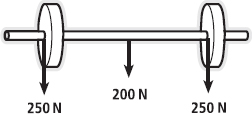
FIG. 6.8

It can also be shown that the sum of the torques created by these masses, when measured from an external point, can be calculated to show the same thing. Look at Figure 6.9, where I’ve arbitrarily placed an external point and shown the distances from this point to each of the masses.

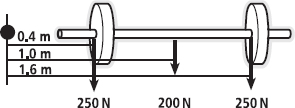
FIG. 6.9

Let’s calculate the sum of these torques:

 

250 N × 0.4 m = 100 Nm

200 N × 1.0 m = 200 Nm

250 N × 1.6 m = 400 Nm

Sum of torques = 700 Nm

 

We assumed that the centre of mass was located at the centre of the bar (1.0 m from my arbitrary point). If the sum of all of the masses is multiplied by this distance, we get:

 

700 N × 1.0 m = 700 Nm

 

The same answer. If we hadn’t known the location of the centre of mass but knew that the total torque was 700 Nm and the total mass was 700 N, we could just divide 700 Nm by 700 N to get a distance of one metre (torque/force = distance). This method of finding the centre of mass is called the segmentation method, because we calculate the influence of each segment to find the centre of mass of a whole object. We can use this idea to find the centre of mass of a high jumper, for example, by following the steps below.

FIG. 6.10

Step 1: Obtain a still image of the athlete with all body parts visible. This can be a difficult task sometimes for a high jumper. I’ve obtained the image here from a video.

Step 2: Draw reference lines for both the x and y directions as shown (Note: in the barbell example, we only calculated the location of the centre of mass in the x, or horizontal, direction).

Step 3: Use the data published by other researchers to estimate the centre of mass locations of each of the body segments. I’ve provided estimates for the general population in Table 6.1.

Segment	Centre of mass location
Head	53.6 (chin–neck intersect to top of head)a
	45.0b
Trunk	56.2 (hip axis to base of neck)
	61.0
Upper arm	50.9 (elbow to shoulder)
	54.2
Forearm	58.2 (wrist axis to elbow)
	56.6
Hand	52.0 (finger tip to wrist)
	53.2
Thigh	60.0 (knee to hip)
	57.2
Calf	58.2 (ankle to knee)
	58.1
Foot	55.1 (tip of longest toe to heel)
	50.0

^a Male data from: Clauser, C.E., McConville, J.T. & Young, J.W. (1969). Weight, volume and center of mass of segments of the human body. AMRL Technical Report 69–70, Wright-Pearson Air Force Base, Ohio: AMRL, 46–55.

^b Plagenhoef, S., Evans, F.G. & Abdelnour, T. (1983). Anatomical data for analyzing human motion. Research Quarterly for Exercise and Sport, 54: 169–78.

TABLE 6.1 Centre of mass locations as percentage (%) distance from one end to the other (as described in the table). The upper number describes the location in men; the lower number describes the location in women.

Step 4: On the diagram, draw the location of these points, using a ruler to measure the lengths of each of the segments.

Step 5: For each segment, measure the distance from both the x- and y-axes to the centre of mass location on each segment. Make a note of these, as shown in Table 6.3. Calculations for the high jumper are very difficult; I’ve had to guess just a little for a few of these.

Segment	Relative mass	Segment	Relative mass
Head	0.073 (male)	Hand	0.007
	0.082 (female)		0.005
Trunk	0.507	Thigh	0.103
	0.452		0.118
Upper arm	0.026	Leg	0.043
	0.029		0.054
Forearm	0.016	Foot	0.015
	0.016		0.013

For data sources, see Table 6.1

TABLE 6.2 Relative mass of body segments (Note: proportion for one limb only).

Step 6: Obtain data published by other researchers to estimate the mass of each body part relative to the mass of the athlete. I’ve provided estimates for the general population in Table 6.2. Notice you now have both the masses and distances, in both the x and y directions.

Step 7: Multiply each mass by its distance from the x- and y-axes and then find the sum of these torques, as shown in Table 6.3.

Segment	Segment mass	Distance from x-axis	Torque in x direction (Nm)	Distance from y-axis	Torque in y direction (Nm)
Head	0.082	1.65	0.135	3.58	0.293
Trunk	0.452	2.94	1.329	4.53	2.046
Upper arm	0.029	2.04	0.059	4.95	0.143
Upper arm	0.029	3.37	0.098	4.05	0.118
Forearm	0.016	2.59	0.041	5.68	0.091
Forearm	0.016	4.20	0.067	5.21	0.083
Hand	0.005	3.10	0.015	6.63	0.033
Hand	0.005	4.51	0.023	6.47	0.032
Thigh	0.118	3.61	0.426	5.79	0.683
Thigh	0.118	5.10	0.602	5.37	0.633
Leg	0.054	4.16	0.224	4.53	0.244
Leg	0.054	6.55	0.354	3.74	0.202
Foot	0.013	4.94	0.064	2.21	0.029
Foot	0.013	6.74	0.088	1.63	0.021
	1.000	Sum of torque x direction	= 3.525	Sum of torque y direction	= 4.653

Note: distance is measured in arbitrary units as shown in diagram. Since the total mass of the subject is 1 (that is, we didn’t multiply each segment mass by the mass of the athlete), the distance from the x- and y-axes equals the torque (for example 4.732 / 1 = 4.732). So the centre of mass is 4.732 and 4.200 units along the axes.

TABLE 6.3 Calculations to determine the location of the centre of mass for a female high jumper.

Step 8: To find the distance, we would normally divide the total torque by the total mass (that is, sum of all the segments or the mass of your subject) but we have kept the masses as a proportion of 1 instead of finding the total masses by multiplying the proportional masses by the athlete’s body mass, so this is not needed. The distances obtained can be measured from the x- and y-axes to the centre of mass of the athlete.

Step 9: Mark this on your diagram.

Step 10: What does this tell you about the technique of the high jumper? How can we use this information to improve jumping technique? (Note: if you’ve been learning how to write formulae in spreadsheets, you could make a spreadsheet of this to speed up your calculations of the athlete at other positions; or for other athletes).

 

By this analysis, the jumper would have knocked the bar. Instead, she has cleared the bar easily by manipulating her body segments at the appropriate time. This example highlights the importance of these analyses to the optimisation of sporting techniques. Such analyses can be used to optimise many other sports such as diving, gymnastics, evasion sports, etc., where manipulation of body segments about the centre of mass is important.

Useful Equations

force (F) = m × a

force of gravity (g) = Gm₁m₂/r², where G = 6.67 × 10^-11 N·m²·kg^-2

torque (moment of force) (τ) = F × d, where d is the moment arm of force

sum of moments or sum of torques (ΣM or Στ) τ_t = τ₁ + τ₂ + τ₃ ...

Related Websites

Hyperphysics (http://hyperphysics.phy-astr.gsu.edu/hbase/torq.html). Basic and advanced discussions on linear motion, including maths simulations and calculations.

Biomechanics of Human Performance, Jesus Dapeña (http://www.indiana.edu/~sportbm/research/hj-animations.html). Website dedicated to biomechanics of athletics, including simulations and animations of the high jump.