
COLLISIONS 2 – THE COEFFICIENT OF RESTITUTION
You need to hit a six (cricket) or a home run (baseball or softball) to win the game. What can you do to increase the distance the ball travels after it collides with your bat?

By the end of this chapter you should be able to:
•Define the term ‘coefficient of restitution’ in terms of energy loss during a collision
•Give examples of factors that influence energy loss during collisions
•Manipulate factors involved in collisions to improve the outcome for a player or athlete
In Chapter 10, you learned that if we know the masses and velocities of two objects before a collision, we can determine what their velocities will be afterwards. Is this completely true? If a ball were to bounce on a concrete floor, its velocity after the collision should theoretically be the same as its velocity before, but this isn’t so. If you drop a ball, it never bounces back to the same height (Figure 11.1), so its velocity after the impact cannot have been as great as it was before.
FIG. 11.1 Due to the energy lost during the collision of the ball with the ground, a ball never bounces to the same height from which it is dropped.
This loss of velocity can be attributed to energy dissipation during the collision. Some kinetic energy will be converted to sound (wave energy), emitted as the ball hits the ground. Heat energy is also produced (you might have noticed that a squash ball becomes warmer when it is hit repeatedly during a game). Energy cannot be destroyed but it can be converted to other forms. In the example in Chapter 10, some energy would be converted to other forms during the collision and the energy of our players involved slightly reduced. We’d see this as a decrease in the total momentum after the collision, but how can we work out the effects of this energy loss?
Coefficient of restitution
The coefficient of restitution describes the proportion of total energy that remains with the colliding objects after the collision. The term is not as abstract as it might at first seem. If you’ve ever seen a slow-motion film of an object colliding with another object, you will have noticed that the objects deform slightly as they collide, as depicted in Figure 11.2. As they rebound, they regain their original shape. This is restitution; we say that the ball is first compressed and then undergoes restitution. The greater the restitution, the less energy must have been lost during the collision. When a ball of dough hits the floor it doesn’t undergo restitution, because all its energy is dissipated. The collision of dough with the floor has a very low coefficient of restitution. When a rubber ball hits the floor it bounces back nearly to the height from which it was dropped; it has a high coefficient of restitution.
FIG. 11.2 During an impact, a ball will first compress, during which time energy is released from the system, and then undergo restitution. The amount of restitution depends on the amount of energy retained after the collision (i.e. its efficiency).
The coefficient of restitution is different for every object–material combination but its magnitude is always expressed as a figure between 0 and 1; where ‘0’ means that all the energy is lost and ‘1’ means it is all retained (such a collision is called ‘perfectly elastic’). For example, the coefficient of restitution for a collision between a softball and a hardwood floor is 0.31, whereas that between a basketball and the same floor is 0.76. This effectively means that only 31 per cent or 76 per cent of the energy was retained after these collisions. Further examples are given in Table 11.1.
Type of ball |
Type of surface |
Coefficient of restitution |
Height bounced (m) |
‘Superball’ |
Hardwood |
0.89 |
1.44 |
Basketball |
Hardwood |
0.76 |
1.06 |
Squash ball (yellow dot) |
Hardwood |
0.41 |
0.42 (from 2.54 m) |
Squash ball (white dot) |
Hardwood |
0.46 |
0.53 (from 2.54 m) |
Squash ball (red dot) |
Hardwood |
0.48 |
0.59 (from 2.54 m) |
Squash ball (blue dot) |
Hardwood |
0.50 |
0.64 (from 2.54 m) |
Tennis ball (new) |
Hardwood |
0.67 |
0.87 |
Tennis ball (worn) |
Hardwood |
0.71 |
0.91 |
Field hockey ball |
Hardwood |
0.50 |
0.46 |
Cricket/softball |
Hardwood |
0.31 |
0.18 |
Volleyball |
Hardwood |
0.74 |
1.01 |
Volleyball |
Concrete |
0.74 |
1.00 |
Volleyball |
Grass |
0.43 |
0.34 |
TABLE 11.1 Coefficients of restitution for different balls bouncing off different surfaces, calculated by measuring the height of rebound from a 1.83 m drop height (except where stated otherwise).
We learned in Chapter 10 that the momentum of a system after a collision must be the same as before it, but now we know that some energy can be lost. If the masses of the two objects remain the same, then the relationship between the velocities of the objects and the coefficient of restitution is:
v1 – v2 = -e(u1 – u2)
Where v1 and v2 are the final velocities of our two objects, u1 and u2 are their initial velocities and e is the coefficient of restitution. If you look at the equation, you can see it simply states that the velocities of the objects after the collision are equal to the velocities before the collision but that we have to take account of the coefficient of restitution. The coefficient, e, will have a greater effect as it gets smaller (that is, it gets closer to zero). So, the coefficient of restitution tells us something about how much energy is retained in a collision and we can ‘correct’ velocity estimates by including it in the equation.
If you don’t happen to have a reference for the exact coefficient you need, you can work out the coefficient of restitution for various objects yourself. We can use the information we learned in Chapter 3 to help us. If we drop an object on to the floor, its velocity immediately before contact can be calculated from the drop height:
v2 = u2 + 2as (remember, v is the final velocity, u is the initial velocity, a is the acceleration due to gravity and s is displacement)
v2 = 0 + 2as
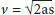
So the final velocity can be found from a (which is a constant 9.81 m·s-2) and displacement (which we can measure).
In exactly the same way, we can determine the velocity with which the ball left the ground if we measure the height to which it bounces. Remember that the coefficient of restitution is proportional to the ratio of the velocities before and after a collision, and since the floor has a velocity of zero we can see that the coefficient for the ball would be: -e = v/u
Instead of measuring v and u, we can use the calculation above so that we can just measure the drop and rebound heights: 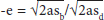
Where sb and sd are the bounce (b) and drop (d) heights. Since the term 2a appears on both sides, we can cancel it out by dividing both sides by 2a, so it might be easier to write: 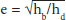
Where hb and hd are the bounce (hb) and drop (hd) heights. (Note that e has no negative sign in the final solution because the rebound velocity would be expressed as negative in the equation above.)
If you set up a simple experiment to measure the drop and bounce heights of a ball off a surface, you could determine its coefficient of restitution (see Figure 11.3). Or you could hold a bat or racket using a strong clamp and bounce balls off it if you wanted to. You can see the results of such experiments in Table 11.1. By the way, you could use a video camera with a scale rod in the background to determine the heights accurately.
FIG. 11.3 In this example, the coefficient of restitution of a rubber ball bouncing off a solid floor can be calculated as:
Drop height (hd) = 0.40 m Bounce height (hb) = 0.34 m
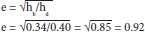
So 8% of the energy of the collision is lost as heat and sound, and 92% is retained and is visible as ball velocity.
(Re-read Chapter 3 if you’ve forgotten how to do this.) Once you can measure these, you can start to work out the factors that affect the speed of a ball off a bat.
If you were to do some of these experiments, you might well find that the coefficient of restitution is affected by temperature. A warm ball will bounce higher than a cold one. Baila (1966) discovered that a baseball bouncing on a solid surface from a height of 1.83 m had a coefficient of restitution of 0.53 (bounce height = 0.51 m). After heating for 15 min at 225°C, this increased to 0.55 (bounce height = 0.55 m) and after cooling for 1 h in a freezer it decreased to 0.50 (bounce height = 0.46 m). If you are a keen golfer, it might be more useful to know that a golf ball had a coefficient of 0.80 (bounce height = 1.17 m) but this decreased to 0.67 (bounce height = 0.82 m) when cooled. So, if you’re playing golf on a cold day, keep your ball in your warm pocket as much as possible rather than leaving it on the cold ground or in your cold club bag! This might also explain why sprint runners feel that they run more quickly on a hot day than on a cold one. It might not just be that their body temperatures are higher, allowing them to generate more muscle power, but also that the hotter track allows a greater coefficient of restitution in the collision with the foot.
The coefficient is also reduced as the velocity of impact increases. Plagenhoef (1971) found that the coefficient was reduced from 0.60 to 0.58 for a golf ball striking a wood floor at 22.4 to 26.8 m·s-1 compared to when it struck at 7 m·s-1. This decrease was far more noticeable for a handball, which had coefficients of 0.8 and 0.5 at the slow and fast velocities. So, it might be easier to hit a fast ball for six in cricket or a home run in baseball but this is because of the greater momentum in the collision, not because of a higher coefficient of restitution. More energy is lost from the collision when the ball comes to you at a higher speed, so, relatively, the velocity of the ball is lower. But you already know this because you have heard that faster collisions are louder, indicating a greater energy loss.
So, we now know that the velocity of a ball after an impact is a function of the momentum of the system before the collision (which is affected by the masses and velocities of the bat and ball) and the energy lost from the system (which is measured by the coefficient of restitution and is affected by temperature and velocity). There is one last consideration, however: the angle of incidence; the angle at which the ball strikes the surface relative to a line drawn perpendicular to that surface (see Figure 11.4).
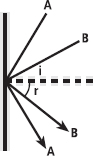
FIG. 11.4 Object B impacted with the surface at an angle of incidence (i) and rebounded with an angle of reflection (r). In collisions where there is a loss of energy, the angle of reflection is always greater than the angle of incidence. In this example, object A struck the surface with a greater angle of incidence and rebounded with a greater angle of reflection than object B.
The mathematics involved in calculating the angle and speed of a ball after it strikes a bat at a given angle of incidence are outside the scope of this chapter, but I will tell you that increasing the angle of incidence allows the ball to leave the collision at a higher velocity. A graph of the relationship, according to Hay (1993), is shown in Figure 11.5. Notice that the angle at which the ball leaves the bat, the angle of reflection, is not exactly equal to the angle of incidence.
FIG. 11.5 As the angle at which the ball meets a bat (angle of incidence) increases, the speed at which it exits the collision increases. This effect, however, is quite small and so is probably not a major concern in most sports. Notice also that the angle of reflection, which is the angle of the ball leaving the bat, is not the same as the angle of incidence. These data were for a collision of a 0.15 kg ball with a 0.85 kg bat with bat and ball speeds of 25 and 15 m·s-1 and a coefficient of restitution (e) of 0.5. Data from Hay (1993).
The factors we need to consider when working out how to hit a ball further can be summarised as follows:
•Increase the speed of the bat: this increases the total momentum of the system but also makes it more likely that the bat will continue to move forwards after the collision while the ball reverses its direction, as you might remember from Chapter 10.
•Increase the mass of the bat: this increases the total momentum of the system, as long as the mass of the bat doesn’t compromise your ability to swing it quickly. You could analyse yourself or other players to determine the mass that optimises momentum.
•Increase the speed of the ball: this increases the total momentum of the system and since the ball is light it does not cause the bat to be moved backwards in the collision.
•Decrease the mass of the ball: this might slightly reduce the total momentum of the system but also ensures the greatest change in ball velocity, so that it rebounds off the bat at high speed; compare the speed at which a light baseball (142–149 g) comes off the bat compared to a heavier softball (177–198 g).
•Increase the angle of incidence: this slightly increases the speed of the ball, as you saw above.
•Increase the coefficient of restitution: this reduces the energy lost in the collision of the bat with the ball; it will be reduced slightly as the ball speed increases (the positive effect of increasing ball speed is greater than its negative effect on the coefficient of restitution) and increased as ball temperature rises.
If you can manipulate some or all of these factors, you should have no problem hitting the ball over the fence or out of the park. In particular, you’ll need to find the bat weight that maximises momentum during the swing, that is, the bat with the greatest mass that still allows a high swing velocity. I’m sure you can use your knowledge of inertia and video analysis to find the perfect sized bat. You should also choose the fastest balls, although we might have to revisit this strategy after Chapter 16. Unfortunately, it might not be possible (or ethical) to manipulate the temperature of the ball.
HOW ELSE CAN WE USE THIS INFORMATION?
As far as performance enhancement is concerned, the bat and ball example above is the best example of how an understanding of impact might influence performance. However, the major application of this knowledge is in the design of safety equipment. Developing equipment with low coefficients of restitution is important, since the dissipation of the energy in collisions reduces the likelihood of impact-related injuries. Everything from body protection equipment, gloves and pads to goalposts are tested to improve their energy dissipation capability.
More important to many coaches is the use of this theory in tactical situations in sports. For example, wet ground is associated not only with a lower coefficient of restitution in collisions with balls but also with collisions of the foot: because more energy is lost at each contact of the foot with the ground, there is a greater energy cost of running; that is, we have to apply more energy to the collision to get the same amount back. In field sports, you might adopt tactics that force the opposition to run more than normal, or reduce the need for you to run.
Useful Equations
speed = ∆d/∆t
velocity (v) = ∆s/∆t
acceleration (a) = ∆v/∆t
projectile motion equations
(1) v = u + at
(2) v2 = u2 + 2as
(3) s = ut + ½ at2
coefficient of restitution 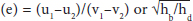
References
Baila, D.L. (1966). ‘Project: Fast ball – Hot or cold?’ Science World, September 16, 10–11.
Hay, J. (1993). The Biomechanics of Sports Techniques (4th ed.). Englewood Cliffs, New Jersey: Prentice Hall, 92.
Plagenhoef, S. (1971). Patterns of human motion: A cinematographic analysis, Englewood Cliffs, New Jersey: Prentice Hall, 82–3.
Related Websites
The Physics of Sports (http://www.topendsports.com/biomechanics/physics.htm). Website investigating the applications of physics in sports.
The Physics Classroom – Tutorials (http://www.physicsclassroom.com/Class/). Lessons on basic physics concepts.
The Physics Classroom – Multimedia tools (http://www.physicsclassroom.com/Physics-Interactives). Interactive tools and movies depicting basic physics concepts.
Introduction to Racquet Science, Racquet Research (http://www.racquetresearch.com). Website exploring the science of tennis rackets, including discussions of the coefficient of restitution.