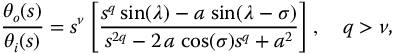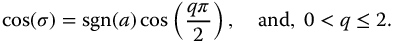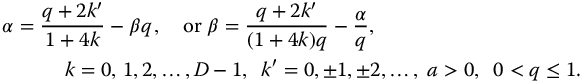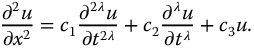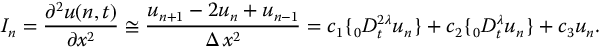Chapter 16
Fractional Oscillators
Oscillators, electrical, mechanical and natural, are found in many applications and situations in the physical world. In the past, analysis of such oscillators has been based on the methods of the integer-order calculus and the application of ordinary differential equations. With the growing number of applications of the fractional calculus and fractional differential equations, there is considerable interest in determining how these new analytical tools will impact the practical and theoretical applications of fractional-order oscillators.
In a series of papers, the dynamics- and energy-based behaviors of fractional oscillators have been studied by Achar et al. [1–4]. Their work has also forwarded a concept of generalized momentum for application to the area and further studies of chained fractional oscillators [4].
Others have studied various aspects concerning fractional oscillators. Practical implementation of fractance-based oscillators and derivation of the Barkhausen conditions has been done by Radwan et al. [111]. The concept of fractional calculus-based oscillators modeled by ensembles of harmonic oscillators has been contributed by Stanislavsky [117]. Gorenflo and Mainardi [39] provide fundamental analysis of fractional oscillations and relaxation. Additional papers on the subject include Koh and Kelly [59], Eab and Lim [32], and Drodzdov [30]. Lorenzo et al. [84] have determined the space of fractional oscillators defined by the fractional trigonometry. This work is the basis of the following section.
16.1 The Space of Linear Fractional Oscillators
A fractional oscillator is a physical system definable by a fractional differential equation and characterized by sustained oscillations after an initial transient. The Laplace transforms of the fractional meta-trigonometric functions when considered as system transfer functions may yield such sustained oscillations, Lorenzo et al. [84]. The objective of this section is to identify the parameters of the fractional trigonometric functions that cause their transfer functions to behave as fractional oscillators. In other words, the goal is to identify the trigonometric-based transfer functions that are oscillatory and are neutrally stable. Because the oscillators are definable as transfer functions, they will also be linear as well as fractional.
Such a transfer function based on the Laplace transform 
is given as
and for the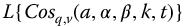 
Here, 
is considered to be a system output variable and 
is a system input variable. Solving for the highest order output term from equation (16.1) gives
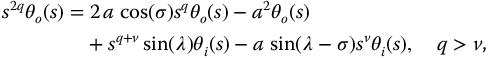
As a practical consideration, because q>v, 
can be computed using only fractional integrations based on equation (16.4). Figure 16.1 shows a fractional integration-based block diagram for a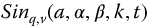 
-based system.
Figure 16.1 Block diagram for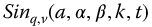 
interpreted as a physical system.
The objective of the following sections is to determine the arguments for the set of fractional meta-trigonometric functions that define the space of linear neutrally stable fractional oscillators for the fractional meta-trigonometry.
16.1.1 Complexity Function-Based Oscillators
The following results are adapted from Lorenzo et al. [84]:
The numerator terms of equations (16.1) and (16.2) do not influence the stability for these transforms, thus the form
with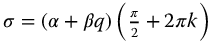 
is applicable to both the fractional sine and cosine transforms. In Chapter 13, the conditions for neutral stability for the complexity functions were determined in Section 13.9.1 and given as equation (13.36), that is,
Now, when a is positive, that is,
,
and when a is negative, that is, 
,
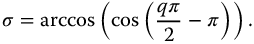
Both cases are captured by the equation
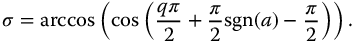
For the complexity-based oscillators (equations (16.5) and (16.6),
, and with
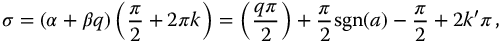
or
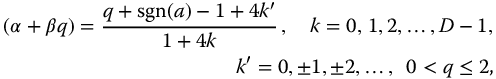
defines the argument relationships for neutrally stable responses and hence defines the space of linear fractional oscillators for the complexity functions. For 
and this simplifies to
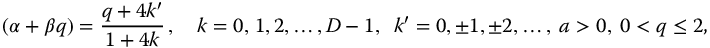
while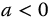 
gives
For convenience, alternative expressions are given. These simplify to
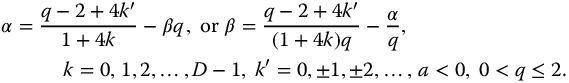
For the principal meta-trigonometric functions k = 0, and when
, these results simplify further.
16.1.2 Parity Function-Based Oscillators
Similar arguments apply to transfer functions of fractional oscillators associated with the parity functions (equations (13.17)–(13.22), also Section 9.2). Here again, the numerator terms of these functions do not influence the stability; thus, for these transforms, we consider the form
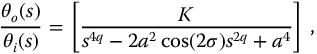
as applicable to all four forms and again where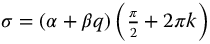 
. In Chapter 13, the conditions for stability for the parity functions were determined in Section 13.9.2 and given as equation (13.41), that is, the parity function-based oscillators will be neutrally stable when
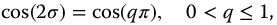
or
Thus,
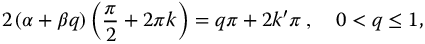
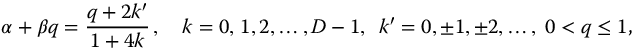
defines the argument relationships for neutrally stable responses and hence defines the space of linear fractional oscillators for the parity functions. Note that the order variable, q, is limited to values between 0 and 1. For convenience, alternative expressions are given:
Figure 16.2 shows selected fractional oscillators based on the results for the complexity function 
. Figure 16.3 presents a set of oscillators using the parity function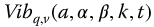 
. The effect of variations in the index variable, k, for a set of fractional oscillators based on the 
-function is presented in Figure 16.4.
Figure 16.2 A set of linear fractional oscillators based on the complexity function 
, with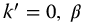 
from equation (16.9), 
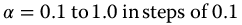, q = 0.5, v = 0, a = 1.0, and k = 0.
Figure 16.3 A set of linear fractional oscillators based on the parity function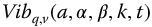 
, with 
from equation (16.14), 
, q = 0.5, v = 0, a = 1.0, 
, and k = 0.
Figure 16.4 Effect of variation of k, for a set of linear fractional oscillators based on the parity function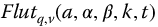 
, with 
from equation (16.14) q = 0.9, v = 0, a = 1.0, 
, 
.
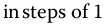16.1.3 Intrinsic Oscillator Damping
The previous sections have studied neutrally stable oscillators; here, we consider briefly damped oscillators. It is interesting to observe that the pseudo (or fractional)-damping of the oscillators associated with the fractional trigonometric functions is fixed when the oscillator parameters are chosen. That is, when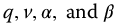 
are selected for any oscillator based on a fractional trigonometric function, the pseudo-damping is determined. To see this, from Chapter 13, the pseudo-damping factor, ζ, for the complexity functions is given by
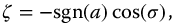
where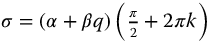 
. For the oscillators associated with the parity functions, we also have from Chapter 13
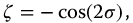
where again 
. The pseudo-damping factor, of course, determines the length of time required for the oscillator to arrive at its long-term amplitude. The reader interested in this area is referred to [119] and the references therein.
16.2 Coupled Fractional Oscillators
Coupled oscillators have found important application in the study of physical systems (cf. Achar [4])]. It is reasonable to expect that coupled fractional oscillators will similarly find important application to systems exhibiting fractional behavior. The coupling of fractional oscillators is considered here by application to the linear commensurate-order time-fractional diffusion–wave equation. Thus, we consider equations of the form
Discretizing in the x dimension (Figure 16.5) will allow this equation to be approximated by a system of (nonpartial) fractional differential equations. Then, the second spatial derivative is approximated by the following second-order central difference approximation:
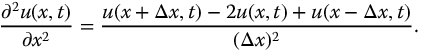
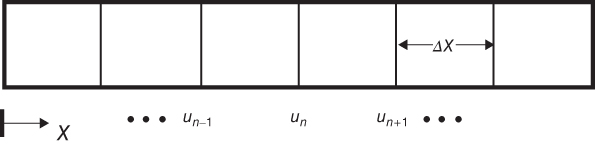
Figure 16.5 Spatial discretization.
For the nth increment, we have
or
In terms of the highest order derivative, we have the system of N fractional differential equations of the form
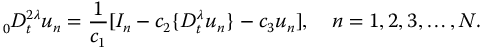
Each of these N equations is, of course, a fractional oscillator of (differential) order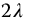 
and of trigonometric order 
.
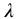The coupling of these equations to approximate the solution of time-fractional diffusion–wave equation is illustrated in Figure 16.6. Note that, for clarity of the figure, the oscillator prefilter shown in Figure 16.2 has been omitted. This figure, of course, illustrates only two oscillators, without consideration of driving forces or boundary and initial conditions. However, as the number of oscillators, N, approaches infinity, the size of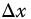 
approaches zero and the approximation approaches the exact solution.
Figure 16.6 Coupled fractional oscillators. Individual oscillators are indicated by dashed boxes.
The transfer function associated with these oscillators is obtained by taking the Laplace transform of equation (16.19), neglecting initialization,
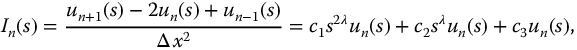
or
These forms are readily analyzed using the fractional meta-trigonometric functions developed in Chapter 12, specifically, equations (12.21), (12.24), (12.27) (12.29) (12.35), (12.38), and (12.40). These results clearly indicate the importance of fractional oscillators and fractional-trigonometric-function-based oscillators in the analysis of physical systems. The results also lead to the expectation that the fractional meta-trigonometric functions will be components of the solution of equations of the form of the time-fractional diffusion–wave equation (16.17).
The question one might ask is: what is the benefit of using a fractional oscillator over using an integer-order sinusoidal oscillator, since the fractional oscillator response is ultimately sinusoidal? The primary answer, of course, is that the local oscillation is fractional, leading to the fractional behavior defined by equation (16.17). However, it may be more important in many applications, such as those discussed in the later chapters, that the transient preceding the sustained oscillation is the focus of interest.