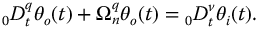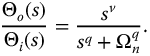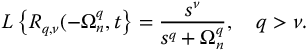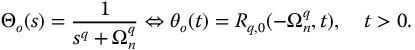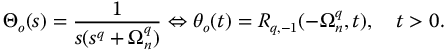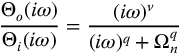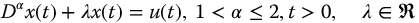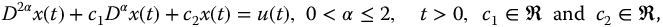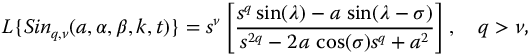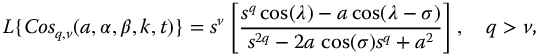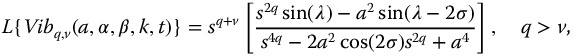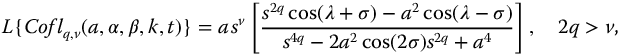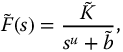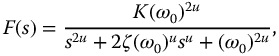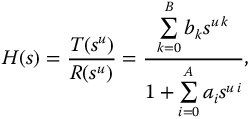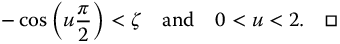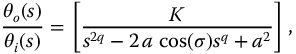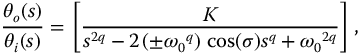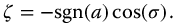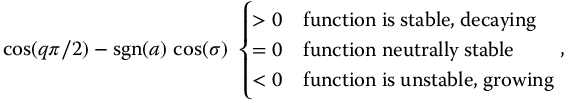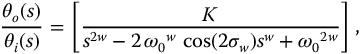Chapter 13
Fractional Trigonometric Systems
This chapter considers the R-function and the fractional trigonometric functions as system impulse responses. That is, the Laplace transforms of the R-function and the trigonometric functions are treated as system transfer functions. The properties of these transfer functions reflect intrinsic characteristics of the underlying trigonometric functions. Specifically, the stability of the fractional trigonometric-based transfer functions indicates the growth/decay properties of the function.
Chapters 6–12 have basically been studies of the R-function,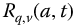 
, with complex parameters for a and t. Here, we study a form of the R-function where a is selected to generalize the time constant and natural frequency of integer-order linear dynamic systems.
13.1 The R-Function as a Linear System
The two building blocks of linear integer-order dynamics are commonly known as first- and second-order systems. A first-order system is defined by the ordinary differential equation:
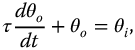
where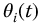 
is the system input, 
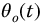is the system output, and 
is known as the system time constant. The Laplace transform of this system, with zero initialization, is
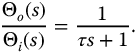
A second-order system is defined by the ordinary differential equation:
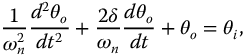
where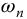 
is the system natural frequency and 
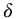is known as the damping ratio. The second-order system is also known as the harmonic oscillator when 
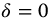. The Laplace transform of a second-order system, with zero initialization, is given by
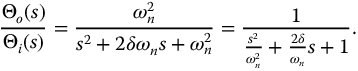
Many properties of these foundation systems have been studied in controls and linear system theory (see, e.g., Kuo [60], Gabel and Roberts [36]) as well as physics textbooks. The fractional calculus allows the following generalization of these fundamental systems. Consider the fractional differential equation
The system transfer function associated with this equation is
The related Laplace transform of the R-function may be written as
Clearly, an undamped second-order system and a first-order system may be represented by equations (13.5)–(13.7). For the first-order system with q = 1 and v = 0, we have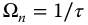 
. For the undamped second-order system with q = 2 and v = 0, we have 
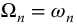as the natural frequency. Thus, 
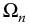is seen as a fundamental property of linear dynamic systems, it has been named the natural quency; see Appendix E. The following sections present typical time and frequency responses associated with these generalized systems.
13.2 R-System Time Responses
Two input time responses are evaluated when the R-function Laplace transform is considered as a physical system transfer function. These are the unit impulse and the unit step function. When the input is a unit impulse function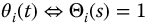 
; thus,
For a unit step function input,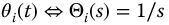 
and
Figure 13.1 shows the system impulse response,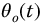 
, for various values of q with 
. The step response over the same range is shown in Figure 13.2.
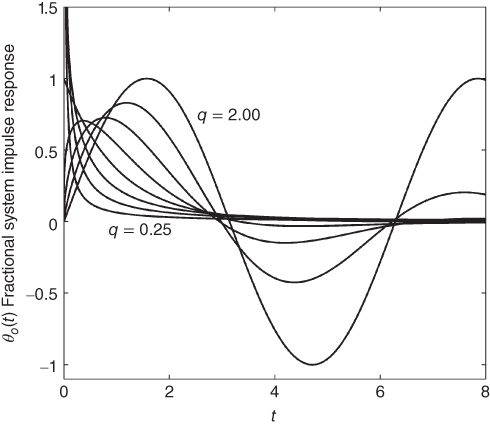
Figure 13.1 System impulse response,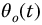 
, equation (13.8), with q = 0.25–2.0 in steps of 0.25, 
.
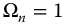Figure 13.2 System step response, 
, equation (13.9), with q = 0.25–2.0 in steps of 0.25, 
.
13.3 R-Function-Based Frequency Responses
The frequency responses associated with the R-function, that is, equations (13.8) and (13.9), are determined by the substitution of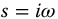 
in equation (13.6)
and then computing the magnitude ratio and phase angle. A low-pass response is shown in Figure 13.3 with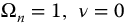 
, and the symmetrical band-pass case is shown in Figure 13.4 with 
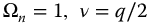. In Figure 13.3a, the asymptotic slope of the high-frequency response is seen to be 20q db/decade, while in Figure 13.3b, the overall phase shift is 90q degrees or 
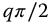rad. The stability properties of the F-function and the Rq,0-function interpreted as system impulse responses have been studied in Chapter 2.
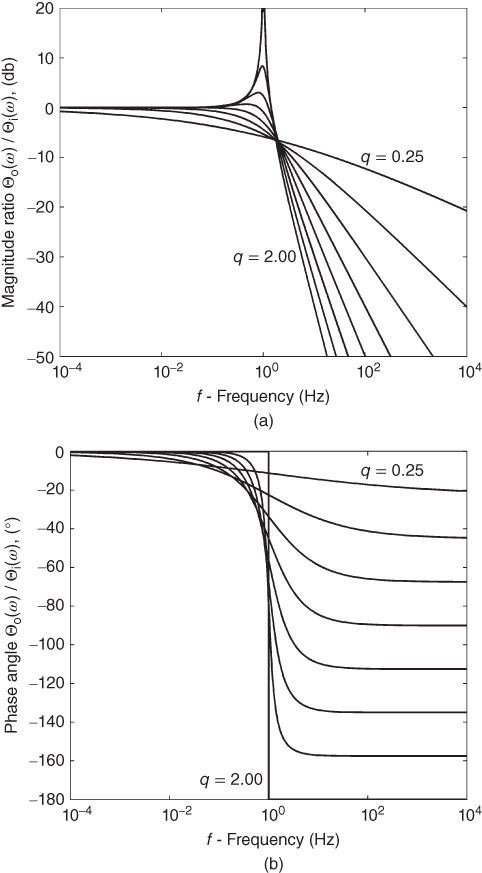
Figure 13.3 System frequency response for equation (13.10) with v = 0, that is 
with q = 0.25–2.0 in steps of 0.25, 
. (a) Magnitude ratio in decibel. (b) Phase angle in degrees.
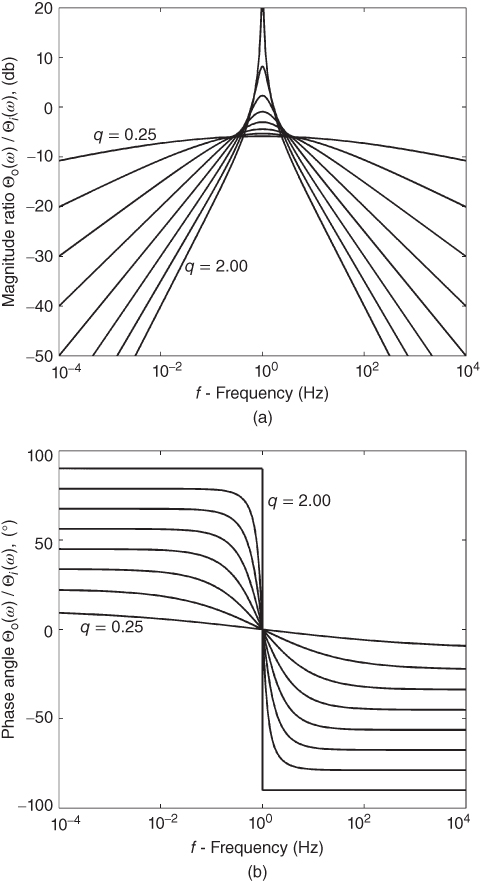
Figure 13.4 System frequency response for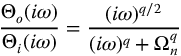 
, with q = 0.25–2.0 in steps of 0.25, 
.
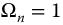13.4 Meta-Trigonometric Function-Based Frequency Responses
In the followings sections, the stability (growth and decay) of the fractional meta-trigonometric functions are studied based on the fractional transfer functions of the second kind and the Laplace transforms of the fractional meta-trigonometric functions. Linear fractional differential equations of the form
can be taken as the basis of fractional oscillation and have been referred to as fractional oscillators. The solutions of this equation may be expressed in terms of R-functions with real arguments. We consider the more general form
which may also have oscillatory solutions. These solutions are based on R-functions with complex arguments, and can also be the basis of fractional oscillation. The fractional trigonometries, defined in previous chapters, define a wide variety of oscillatory fractional functions that, as we have seen in Chapter 12, are the solutions or components of solutions to such linear fractional differential equations.
The character of the frequency responses associated with the fractional meta-sine and meta-cosine functions is best considered based on the behavior of their denominators. Thus, we consider simplified transforms associated with equations (12.21) and (12.24), namely for the fractional meta-cosine
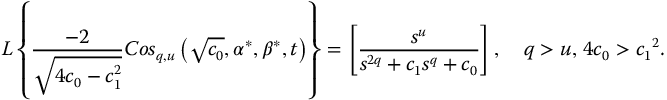
The frequency responses based on the transfer function
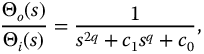
or in terms of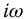 
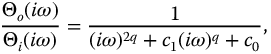
best exposes the frequency domain behavior. Figure 13.5 shows the frequency response for this function with c0 = 1 and c1 = 3.0. Immediately obvious in this plot is the presence of a second resonance at q = 2.0 and the inflection in the magnitude when q = 1.75. Furthermore, because of the order 2q term, the high-frequency amplitude asymptotes fall off at twice the rate as those seen in Figure 13.3a. Also note that the high-frequency asymptotic phase shifts are double those of Figure 13.3b.
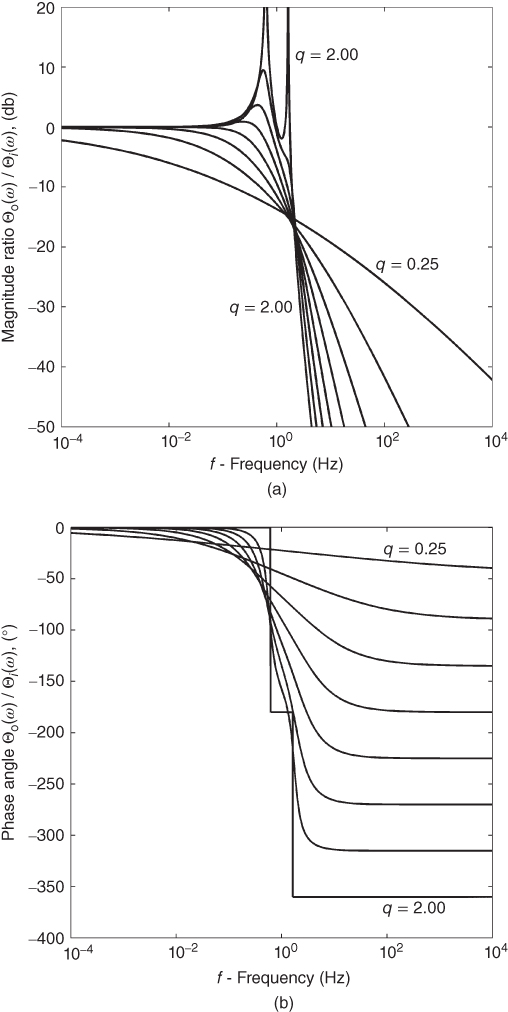
Figure 13.5 System frequency response for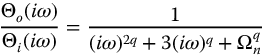 
, with q = 0.25–2.0 in steps of 0.25. (a) Magnitude ratio in decibel. (b) Phase angle in degrees.
This chapter explores the growth and decay of the fractional meta-trigonometric functions based on the stability of their inferred transfer functions. It is noted that Green's functions for equations such as equations (13.11) and (13.12) have also been determined by Podlubny [109].
13.5 Fractional Meta-Trigonometry
The fractional meta-trigonometries are an infinite set of fractional trigonometries and hyperboletries that are based on the R-function, with fully complex arguments, namely
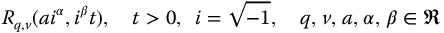
and are based on the definition
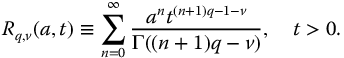
The meta-trigonometric functions based on complexity and parity are defined for t > 0 in Table 9.2. For convenience the Laplace transforms for these functions are repeated here:
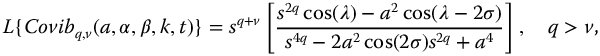
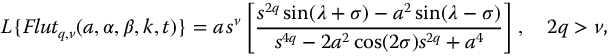
where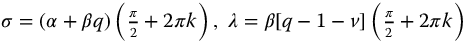 
. In the following sections, these functions are considered as system transfer functions and their stability analyzed.
13.6 Elementary Fractional Transfer Functions
Elementary transfer functions of the first kind, studied in Chapter 2 and by Hartley and Lorenzo [45, 48], and applied in Chapter 12 to the solution of fractional differential equations, are given by
with real-valued coefficients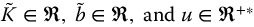 
. Elementary transfer functions of the second kind studied by Malti et al. [90, 91] and Lorenzo et al. [84] are given by
with real-valued coefficients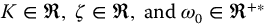 
. The parameter 
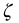does not have the same meaning as in integer-order systems: it is the classical damping factor only if u = 1. It is referred to as a pseudo-damping factor (Malti et al. [91]).
As we have seen in Chapter 12, elementary transfer functions of the first and second types are required to reduce higher-order fractional differential equations to analytically manageable elements. Linear fractional system transfer functions may be represented by
with real-valued coefficients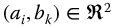 
.
Stability conditions for such fractional transfer functions have been studied by Matignon and independently by Hartley and Lorenzo [45] and in Chapter 2. The following section studies the stability of such transfer functions.
13.7 Stability Theorem
The following theorem originally proved by Matignon [92], and revisited by Malti [91], applies to (13.25). From Malti et al. [91], with permission of Automatica:
“A commensurable transfer function with a commensurable order u, as in (13.25) with T and R two coprime polynomials, is stable if and only if
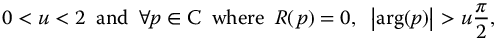
where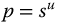 
.□”
Applying the stability theorem to the elementary transfer function of the first kind (equation (13.23) with real-valued coefficients yields the following stability conditions:
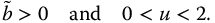
Moreover, the commensurate-order transfer function of the first kind is neutrally stable if
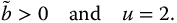
Applying the stability theorem on the elementary transfer function of the second kind (equation (13.24) requires computing both su poles:
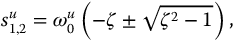
and finding all ζ satisfying the following inequalities:
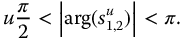
13.8 Stability of Elementary Fractional Transfer Functions
The stability conditions for elementary transfer functions of the second kind in terms of the pseudo-damping factor ζ and the commensurable order u, and are summarized in the following corollary to the Stability theorem. Continuing from Malti et al. [91]:
Elementary transfer functions of the first kind
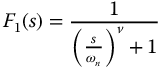
with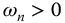 
are stable iff 0 < v < 2.
The transfer function of the second kind (13.6.2) is stable iff:
Refer to Ref. [90] for the proof of this corollary. It is well known from integer-order system theory that the second-order rational transfer function, equation (13.24) with u = 1, is stable if and only if
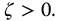
From the preceding development (see also Ref. [84]), it can be seen that the commensurate-order transfer function of the second kind equation (13.24) is neutrally stable for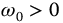 
, if
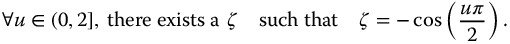
The work of Malti et al. [91] is summarized graphically in Figure 13.6 in which the behavior of fractional elementary transfer functions of the second kind (equation (13.24) are determined for various values of 
. Our particular interest here is the stability of the transfer function; however, the figure also contains information pertaining to the system resonances. Most importantly, the transfer function equation (13.24) is stable for all values of 
above area 4, that is, those values that are greater than the negative cosine function and located in areas 1, 2, and 3, and with 0 < u < 2.
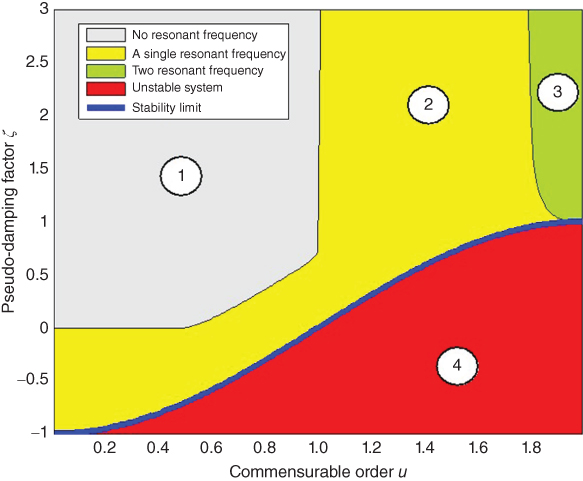
Figure 13.6 Stability and resonance regions of the elementary transfer function of the second kind in the 
versus u plane. Area 1, stable with no resonant frequency; Area 2, stable with a single resonant frequency; Area 3, stable with two resonant frequencies; Area 4, unstable.
Source: Malti, Moreau, and Khemane 2011 [91]. Reproduced with permission of Elsevier. Please see www.wiley.com/go/Lorenzo/Fractional_Trigonometry for a color version of this figure.
The responses for values of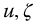 
in the four areas are as follows:
- Area 1, – stable and non-resonant,
- Area 2, – stable with a single resonance,
- Area 3, – stable with two resonances,
- Area 4, – unstable.
The stability results are specialized for application to the Laplace transforms of fractional meta-trigonometric functions in the following section.
13.9 Insights into the Behavior of the Fractional Meta-Trigonometric Functions
The general theoretical results on the stability of fractional transfer functions of the second kind developed in the previous sections can provide insight into the behavior of the fractional meta-trigonometric functions. In this section, these results are applied to the meta-trigonometric Laplace transforms. The complexity functions are considered first.
13.9.1 Complexity Function Stability
The stability of the complexity-based meta-trigonometric functions is determined from their respective Laplace transforms equations (13.17) and (13.18). When expressed in minimum form, only the denominator terms influence the stability for these transforms. The form
where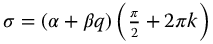 
then applies to both transforms. The substitution of 
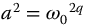yields the mathematical form
which may be compared with equation (13.24). Relating equation (13.34) to equation (13.24), the pseudo-damping factor, ζ, for the complexity functions is found to be
It is seen from Section 13.8 (equation (13.30) that the complexity function will be growing (unstable) when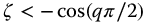 
. From equation (13.35), for the complexity functions, we have that 
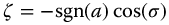. Therefore, the Laplace transform of the fractional complexity meta-trigonometric functions represented by equation (13.33) will be decaying (stable) when 
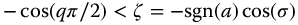or when 
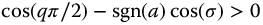and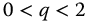 
, giving the general result that
where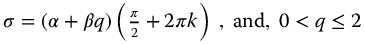 
. Insight into the resonance behavior of the functions in the stable domain is given in Section 13.8 and in considerable detail in Ref. [90].
13.9.2 Parity Function Stability
The Laplace transforms of the parity functions (equations (13.19)–(13.22) may also be considered as system transfer functions and analyzed for their stability. As in the complexity function case, the numerator terms of these functions do not influence the stability. Thus, for these transforms, we consider the form
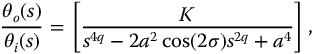
to apply to all four fractional trigonometric functions (equations (13.19)–(13.22). For this equation, we also have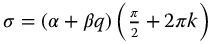 
. For a real, substituting 
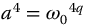, and letting 
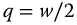gives
with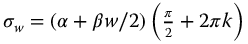 
. This transform now may be directly compared with equation (13.24). Comparing equations (13.38) with (13.24), the pseudo-damping factor, 
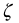, for the parity functions is given by
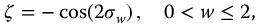
or in terms of q
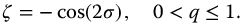
Thus, the pseudo-damping factor for the parity functions is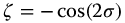 
. Then, the Laplace transform of the fractional parity meta-trigonometric functions represented by equation (13.38) will be stable when 
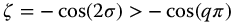and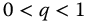 
, or when 
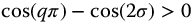and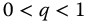 
. This gives the general result for the parity functions:
where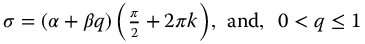 
.
This behavior is validated in Figure 13.7, where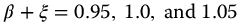 
, for which 
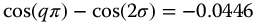, 0.0, and 0.0460, respectively. In turn, this yields unstable, neutrally stable, and stable responses for the Flutter function, respectively.
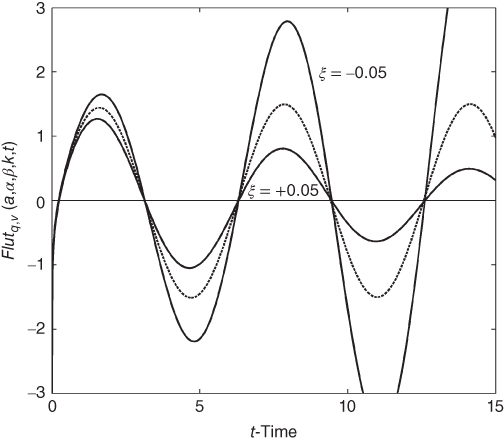
Figure 13.7 Neutrally stable, underdamped stable, and oscillatory unstable transfer functions of the second kind.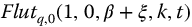 
with q = 1/3, v = 0, a = 1.0, 
, 
.
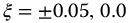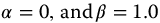These stability results apply to all of the parity functions (equations (13.19)–(13.22).
13.10 Discussion
In this chapter, we have considered the Laplace transforms of the fractional trigonometric functions as impulses responses of transfer functions describing physical systems and have applied linear system theory to help further characterize these functions. This process defines the combinations of variables for which the fractional meta-trigonometric functions will exhibit sustained oscillations (neutrally stable), growing responses (unstable), and decaying response (stable). In Chapter 16, these results will be applied to the study of fractional oscillators.