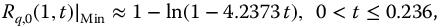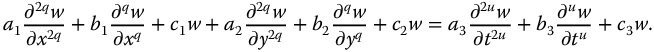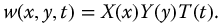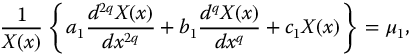Chapter 20
A Look Forward
In an effort such as that leading to this book, many questions and opportunities arise that may not contribute to the main theme, or were too difficult to complete in a timely manner. Some are simple questions, such as what does a half-order triangle look like? Yet, they may not have easy answers. Others might require the development of new theory, for example, fractional orthogonality.
In this final chapter, we attempt to briefly outline areas where further development is needed both in regard to the theoretical aspects of the fractional trigonometric and fractional exponential functions and also relative to application of the theory to scientific problems. It is useful to start by looking backward, that is, by considering the scope of knowledge that has been uncovered relative to the classical exponential and trigonometric functions, which is shown graphically in Figure 20.1.
Figure 20.1 Classical connections.
At the core of the classic theory is the common exponential function. From this, the connection is made to the classic trigonometry via the Euler equation. The exponential function and the trigonometric functions provide solutions to ordinary linear differential equations and are often components in the solution of integer-order partial differential equations. The trigonometric functions are important because the solutions derived from them are real functions that are seen in the physical world as opposed to complex exponential functions.
The development of Fourier series was enabled because of the orthogonal nature of the classical sine and cosine. From the Fourier series, important extensions to Fourier transforms and spectral analysis were possible.
If we now generalize the common exponential function to the F- or R-function, as has been done for the fractional calculus, and further develop a fractional generalization of the trigonometry and hyperboletry, the focus of this book, it is appropriate to consider possible fractional generalizations of the important fruits of the classical trigonometry. As part of the development of the fractional trigonometry, important generalizations of the Euler equation were uncovered.
A key result of the fractional trigonometry has been its use for the solution of linear commensurate-order fractional differential equations (Chapter 12). Relative to generalizing the classical Fourier methods, the central question becomes “can orthogonal subsets of the fractional trigonometric functions other than the classical functions be found or created?” For example, such creation may be possible by multiplication of the functions by appropriate functions to yield a constant envelope. Or, more broadly, is a fractional orthogonality possible that allows the creation of fractional versions of the Fourier series and subsequently fractional-order Fourier transforms and spectral analysis? While some initial effort has been done toward this end (Lorenzo and Hartley [79]), significant challenges and opportunities are found here. Finally, the fractional generalization of the natural logarithm, the inverse fractional exponential, if accomplished may allow generalization of the multiplication operation. This is addressed in more detail in Section 20.2.
20.1 Properties of the R-Function
While numerous properties for the R-function have been developed in Chapters 3 and 4, much more is needed. For example, can simple forms be found for the evaluation of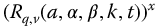 
or 
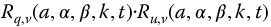, and many more similar operations?
20.2 Inverse Functions
It is easy to numerically obtain a plot for the inverse of the R-function; however, determining the analytical expressions for the fractional inverse turns out to be problematic. The difficulty arises because the inverse is multivalued over some domains. Figure 20.2 shows the R-function plotted as a function of t-time. The same data set is shown in Figure 20.3 but as the inverse function. In the plots, the minimum values of the R-function are approximated numerically. An approximate equation for the locus of minima as seen in Figure 20.2 (black dashed line) is
and for Figure 20.3, this is expressed as
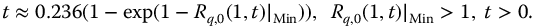
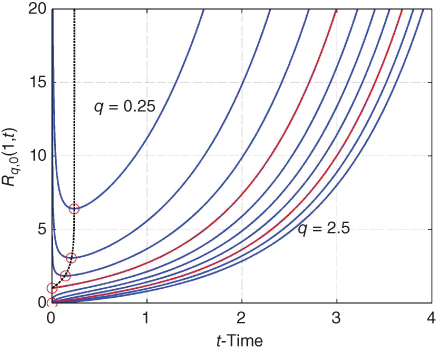
Figure 20.2 R-Function as a function of time with q = 0.25 to 2.5 in steps of 0.25, v = 0, and a = 1. Circles mark the approximate local minima. Please see www.wiley.com/go/Lorenzo/Fractional_Trigonometry for a color version of this figure.
Figure 20.3 Inverse R-Function,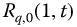 
, with q = 0.25 to 2.5 in steps of 0.25, v = 0, and a = 1. Circles mark the approximate local minima from Figure 20.2. Please see www.wiley.com/go/Lorenzo/Fractional_Trigonometry for a color version of this figure.
Importantly, there are three domains in Figure 20.3 that must be separately analyzed to define the inverse function. Based on the approximate minima equation (20.1), these domains are defined by
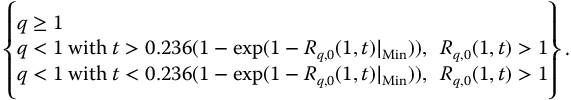
At this time, the inverse function is only analytically known for two values of the q parameter. One of these is for q = 1, of course, where the inverse function is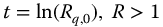 
. The other, for q = 2, is inferred from equation (3.41), that is, 
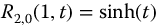. From this, we have 
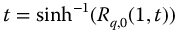. These values are highlighted by dashed curves in the figures. Series expansions are readily available for both functions. The end goal, of course, is the development series expressions that directly define the inverse in each domain defined. Recent progress has been reported on the determination of the inverse for the closely related Mittag-Leffler function by Hanneken and Achar [126]. While those results do not appear to be directly relatable to the R-function, it may be possible that the techniques used there can be applied to the determination of the inverse R-function.
The character of the fractional hyperbolic functions (Chapter 5) is quite similar to that of the R-functions that compose it. Thus, the problem of determining inverse series for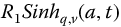 
and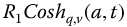 
will be difficult, but important.
Finding direct inverse functions for the fractional trigonometric functions may not be feasible. Importantly, most of the functions are not periodic, and their inverses are multivalued. Furthermore, the number of functions involved is large. From a practical point of view, perhaps the most useful approach is the development of software routines that can be applied to the forward function to determine its inverse. This would be the modern equivalent of the trigonometric tables.
20.3 The Generalized Fractional Trigonometries
The formal definitions of the generalized fractional trigonometries were presented in Chapter 11. The development of this area presents significant challenges that place it beyond the scope of this book. Based on their Laplace transforms, these functions provide the solutions to fractional differential equations of more complexity than those discussed in Chapter 12. Because of this, it is important that the detailed properties of these functions be determined.
20.4 Extensions to Negative Time, Complementary Trigonometries, and Complex Arguments
The meta-trigonometry introduces the possible study of imaginary and complex time as well as imaginary and complex quency; see Chapter 13 and Appendix E. It is expected that such capability will be of interest in physics research. Furthermore, because the fractional trigonometries are based on the R-function, which is defined for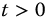 
, it is of some interest to note that for 
, we have the basis 
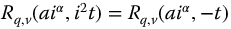. An important question is: can a fractional trigonometry based on 
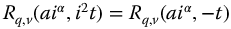extend the fractional trigonometry based on 
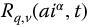into the negative time domain? Or the more general question is: can complementary trigonometries be formed, for example, using the basis pairs 
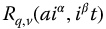and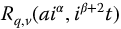 
?
Limited numerical studies have not yet conveyed a clear picture in this regard. It presently appears that, with certain choices of the q, v,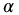 
, and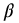 
variables, this may be possible for the fractional trigonometric functions. A particular case is shown in Figure 20.4 where for various values of 
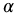the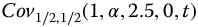 
is interpreted as running backward in negative time and the complementary 
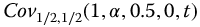is running in forward time. As may be observed from the plot, this interpretation smoothly continues the functions into negative time, that is, the functions have the same values and slopes at the origin. Note, particularly in cases where a singularity exists at t = 0, the results are inconclusive.
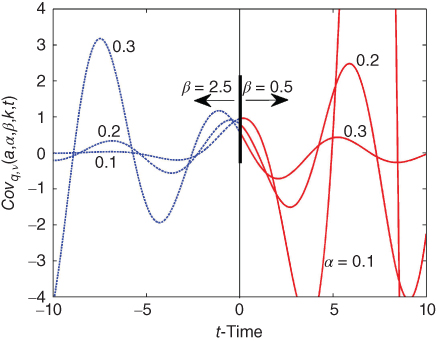
Figure 20.4 Negative time issue. 
versus t-time for a = 1.0, with q = 0.5, v = 0.5, k = 0, 
; 
, and 
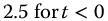. For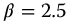 
, the function is interpreted as 
.
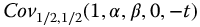Source: Lorenzo 2009b [83]. Reproduced with permission of ASME. Please see www.wiley.com/go/Lorenzo/Fractional_Trigonometry for a color version of this figure.
In forward time, of course, the backward running slopes are the negative of those of the forward interpretation. Furthermore, the functions' apparent stabilities change between the forward and backward interpretations. This explains the observations made in Figures 9.47 and 9.48 where both the Flutter and Coflutter functions each smoothly continue backward in time because of the 1–3 relationships in the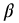 
term.
A second example is shown for the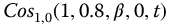 
-function in Figure 20.5. The 
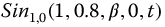-function can also be extended into negative time in a similar manner. It should be noted that this method has not been found to provide extension to negative time for all of the meta-trigonometric functions nor for all selections of the function parameters.
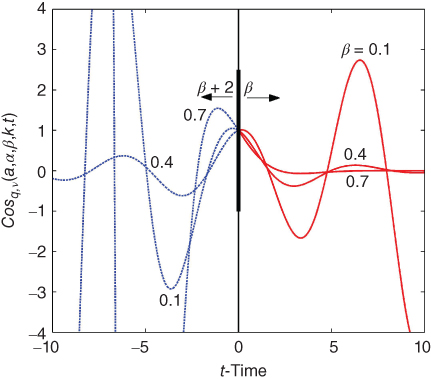
Figure 20.5 Negative time issue.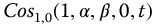 
versus t-time for a = 1.0, with q = 1.0 and v = 0, 
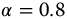, k = 0, 
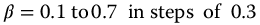. For 
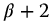, the function is interpreted as 
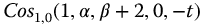. Please see www.wiley.com/go/Lorenzo/Fractional_Trigonometry for a color version of this figure.
The fractional trigonometry brings meaning to the R-function with complex arguments. Clearly, a future development to the effort presented in this book is to determine the properties of the fractional trigonometric functions with complex arguments.
20.5 Applications: Fractional Field Equations
In the second half of this book, considerable effort has been spent to identify potential application areas for the fractional trigonometry. The discovery and identification of the fractional spirals was very helpful in this regard. These spirals, when oscillatory in the time domain, are generalizations of the harmonic oscillator in that they allow both decay and growth.
The occurrence of spiral behavior in nature is very well known (e.g., Hartmann and Mislin [50]). Historically, in most instances, these were thought to be or were at least approximated by logarithmic spirals. The logarithmic spiral, however, is infinite in both directions; that is, it can become infinitely large or infinitely small. The problem encountered in applying the logarithmic spirals is in the small direction, because it does not start its growth at a finite time (or position). This is most clearly apparent in the cases of shell growth and galactic morphology. This issue is alleviated by the application of the barred and apparently unbarred fractional spirals.
In retrospect, it is amazing to observe the broad application of these spirals that were generated by only cross-plotting the raw fractional trigonometric functions, without any cross-coupling or variation in the order variable q. Within the scope of these studies, temporal data have not been easily available to allow determination of fractional field equations that generalize the wave or diffusion equations and yield the fractional spirals in the spatial or temporal variables. For example, it would be of great interest to acquire a fractional field equation that yields the spatial barred spirals used to match the morphology of the spiral galaxies found in Chapter 18. Such an equation may provide a path to evolutionary or trajectory information. Only for the case of growth of the Nautilus was it possible to use some auxiliary data to infer a dynamic equation for growth of the animal (equation (17.15)). However, in this and the other cases, nonpartial fractional differential equations in space have been shown; see equations (17.4), (17.5), (18.5), and (18.6).
So the question becomes: how can we devise a partial fractional field equation where, for example, after an assumed separation of variables, the spatial parts of the equation yield the fractional barred spirals seen in the preceding applications?
Let us consider the following partial fractional differential equation:
Applying the method of separation of variables, we assume a solution of the form
Introducing equation (20.5) into equation (20.4) gives
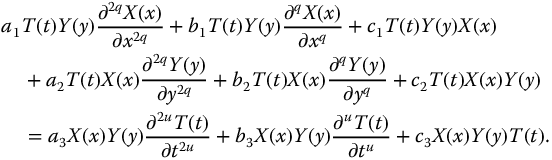
Now, dividing by 
yields
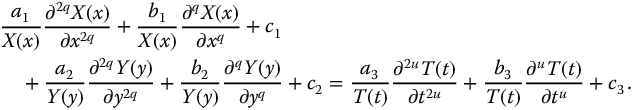
Regrouping the results gives
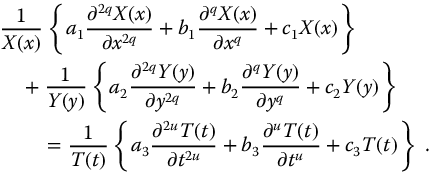
In the two previous equations, each group is independent of the other two, that is, the variables have been separated. Thus, each group may be treated as nonpartial fractional differential equation and can only be equated to a constant, giving the following set:
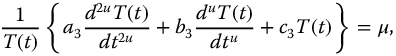
where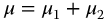 
. Now, each of these equations may be solved individually by applying appropriate boundary and initialization conditions. By selection of appropriate values for 
, 
, 
, 
, 
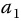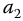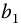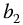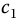, and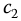 
, equations (20.10) and (20.11) may be Laplace transformed by the methods of Chapter 12 to yield the fractional sines and cosines needed to model various spatial barred and apparently unbarred spirals in the time-sensitive context, as seen in the applications of previous chapters. Selection of 
, 
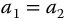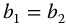, and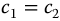 
will yield most of the fractional spirals used in modeling the various physical phenomena in this book.
By proper selection of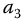 
, 
, 
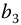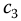, and u, wave or diffusion behavior or some combination may be modeled. Of course, u can also be fractional. Furthermore, as we have seen in the applications, the spatial differential-order can be greater than two. Even more generally, the time derivatives are not necessarily of commensurate order and also may not be limited in order to be less than or equal to two.
Hence, we have apparently achieved our goal in rectangular coordinates. However, to achieve a reasonable statement for the boundary conditions for phenomena such as hurricanes, galactic evolution tornadoes, and the like, equation (20.4) must be converted into cylindrical or in some cases spherical coordinates. This has not yet been done.
20.6 Fractional Spiral and Nonspiral Properties
The studies in Chapter 15 only begin to explore the properties of the fractional spirals and have not considered those trigonometric functions not formally defined as spirals. Further study is needed to determine whether these functions can be further characterized.
Relative to the fractional spirals, for example, the cross-plot of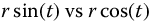 
becomes 
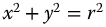in nonparametric, that is, rectangular coordinates. Can simple rectangular forms for some of the fractional spirals be determined? In a similar manner, since the circumference of a circle is well known, can the perimeter of a single rotation of, for example, an R1 spiral be determined as a simple algebraic function of the order, q and the number of rotations of the spiral?
The logarithmic spiral is characterized by a growth rate logarithmically proportional to the angle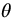 
. The spiral of Archimedes is characterized by growth proportional to the angle 
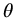. The question becomes: can appropriate characterizations be determined for the various classes of the fractional spirals?
20.7 Numerical Improvements for Evaluation to Larger Values of atq
For the applications we have studied, with values of the trigonometric order q > 1, typically 3 or 4 rotations of the fractional spirals have been adequate to model the physical behavior. This is fortunate because as we have shown in Chapter 14 as atq grows, numerical evaluation becomes problematic. Serious and creative effort is needed to address this issue.
20.8 Epilog
The integer-order trigonometry is typically thought of as a study of triangles and their properties and applications, in spite of the fact that we call the functions the circular functions. It is clear from the new perspective obtained by the development of the fractional trigonometry that the integer-order trigonometry is about circles and that triangles are an analysis tool used to study the properties of the circle.
The fractional trigonometry releases the constant circular radius of the integer-order trigonometry to allow the vast array of spiral and spiral-like functions that we have seen in Chapters 9 and 15. Also, unlike the logarithmic spiral, the fractional spirals have a beginning. Furthermore, as we have seen in Chapter 12, these functions provide the solutions to a broad array of linear fractional differential equations of any real order in terms that can be related to real-world physics.