CHAPTER 6 Powerful Ideas in Mind-Size Bites

“I love your microworlds but is it physics?

I don’t say it is not. But how can I decide?”

—A TEACHER

A COMMON DISTINCTION BETWEEN TWO WAYS OF KNOWING IS OFTEN expressed as “knowing-that” versus “knowing-how” or as “propositional knowledge” versus “procedural knowledge” or again as “facts” versus “skills.” In this chapter we talk about some of the many kinds of knowing that cannot be reduced to either term of this dichotomy. Important examples from everyday life are knowing a person, knowing a place, and knowing one’s own states of mind. In pursuit of our theme of using the computer to understand scientific knowing as rooted in personal knowing, we shall next look at ways in which scientific knowledge is more similar to knowing a person than similar to knowing a fact or having a skill. In this, we shall be doing something similar to how we used the Turtle to build bridges between formal geometry and the body geometry of the child. Here, too, our goal is to design conditions for more syntonic kinds of learning than those favored by the traditional schools. In previous chapters we have explored a paradox: Although most of our society classifies mathematics as the least accessible kind of knowledge, it is, paradoxically, the most accessible to children. In this chapter we shall encounter a similar paradox in the domain of science. We shall look at ways in which the thinking of children has more in common with “real science” than “school science” has with the thinking either of children or of scientists. And once more we shall note a double paradox in the way computers enter into and influence this state of affairs. The introduction of the computer can provide a way out of the paradoxes, but it usually is used in ways that exacerbate them by reinforcing the paradoxical ways of thinking about knowledge, of thinking about “school math” and “school science.”

Mathetically sophisticated adults use certain metaphors to talk about important learning experiences. They talk about getting to know an idea, exploring an area of knowledge, and acquiring sensitivity to distinctions that seemed ungraspably subtle just a little while ago.

I believe that these descriptions apply very accurately to the way children learn. But when I asked students in grade schools to talk about learning, they used a very different kind of language, referring mainly to facts they had learned and skills they had acquired. It seems very clear that school gives students a particular model of learning; I believe it does this not only through its way of talking but also through its practices.

Skills and the discrete facts are easy to give out in controlled doses. They are also easier to measure. And it is certainly easier to enforce the learning of a skill than it is to check whether someone has “gotten to know” an idea. It is not surprising that schools emphasize learning skills and facts and that students pick up an image of learning as “learning that” and “learning how.”

Working in Turtle microworlds is a model for what it is to get to know an idea the way you get to know a person. Students who work in these environments certainly do discover facts, make propositional generalizations, and learn skills. But the primary learning experience is not one of memorizing facts or of practicing skills. Rather, it is getting to know the Turtle, exploring what a Turtle can and cannot do. It is similar to the child’s everyday activities, such as making mudpies and testing the limits of parental authority—all of which have a component of “getting to know.” Teachers often set up situations in which they claim that children are actually getting to know this or that concept even though they might not realize it. Yet the Turtle is different—it allows children to be deliberate and conscious in bringing a kind of learning with which they are comfortable and familiar to bear on math and physics. And, as we have remarked, this is a kind of learning that brings the child closer to the mathetic practice of sophisticated adult learners. The Turtle in all its forms (floor Turtles, screen Turtles, and Dynaturtles) is able to play this role so well because it is both an engaging anthropomorphizable object and a powerful mathematical idea. As a model for what mathematical and scientific learning is about, it stands in sharp contrast to the methodology described by the fifth grader, Bill (mentioned in chapter 3), who told me that he learned math by making his mind a blank and saying it over and over.

For me, getting to know a domain of knowledge (say, Newtonian mechanics or Hegelian philosophy) is much like coming into a new community of people. Sometimes one is initially overwhelmed by a bewildering array of undifferentiated faces. Only gradually do the individuals begin to stand out. On other occasions one is fortunate in quickly getting to know a person or two with whom an important relationship can develop. Such good luck may come from an intuitive sense for picking out the “interesting” people, or it may come from having good introductions. Similarly, when one enters a new domain of knowledge, one initially encounters a crowd of new ideas. Good learners are able to pick out those that are powerful and congenial. Others who are less skillful need help from teachers and friends. But we must not forget that while good teachers play the role of mutual friends who can provide introductions, the actual job of getting to know an idea or a person cannot be done by a third party. Everyone must acquire skill at getting to know and a personal style for doing it.

Here we use an example from physics to focus the image of a domain of knowledge as a community of powerful ideas, and in doing so take a step toward an epistemology of powerful ideas. Turtle microworlds illustrate some general strategies for helping a newcomer begin to make friends in such a community. A first strategy is to ensure that the learner has a model for this kind of learning; working with Turtles is a good one. This strategy does not require that all knowledge be “Turtle-ized” or “reduced” to computational terms. The idea is that early experience with Turtles is a good way to “get to know” what it is like to learn a formal subject by “getting to know” its powerful ideas. I made a similar point in chapter 3 when I suggested that Turtle geometry could be an excellent domain for introducing learners to Polya’s ideas about heuristics. This does not make heuristic thinking dependent on turtles or computers. Once Polya’s ideas are thoroughly “known,” they can be applied to other domains (even arithmetic). Our discussion in chapter 4 suggested that theoretical physics may be a good carrier for an important kind of meta-knowledge. If so, this would have important consequences for our cultural view of its role in the lives of children. We might come to see it as a subject suitable for early acquistion not simply because it explicates the world of things but because it does so in a way that places children in better command of their own learning processes.

For some people, taking physics as a model for how to analyze problems is synonymous with a highly quantitative, formalistic approach. And indeed, the story of what has happened when such disciplines as psychology and sociology have taken physics as a model has often had unhappy endings. But there is a big difference in the kind of physics used. The physics that had a bad influence on social sciences stressed a positivistic philosophy of science. I am talking about a kind of physics that places us in firm and sharp opposition to the positivistic view of science as a set of true assertions of fact and of “law.” The propositional content of science is certainly very important, but it constitutes only a part of a physicist’s body of knowledge. It is not the part that developed first historically, it is not a part that can be understood first in the learning process, and it is, of course, not the part I am proposing here as a model for reflection about our own thinking. We shall be interested in knowledge that is more qualitative, less completely specified, and seldom stated in propositional form. If students are given such equations as f = ma, E = IR, or PV = RT as the primary models of the knowledge that constitutes physics, they are placed in a position where nothing in their own heads is likely to be recognized as “physics.” We have already seen that this is the kind of thing that puts them at very high risk as learners. They are on the road to dissociated learning. They are on the road to classifying themselves as incapable of understanding physics. A different sense of what kind of knowledge constitutes physics is obtained by working with Turtles: Here a child, even a child who possesses only one piece of fragmentary, incompletely specified, qualitative knowledge (such as “these Turtles only understand changing velocities”) can already do something with it. In fact, he or she can start to work through many of the conceptual problems that plague college students. The fragment of knowledge can be used without even knowing how to represent velocities quantitatively! It is of a kind with the intuitive and informal, but often very powerful, ideas that inhabit all of our heads whether we are children or physicists.

This use of the computer to create opportunities for the exercise of qualitative thinking is very different from the use of computers that has become standard in high school physics courses. There it is used to reinforce the quantitative side of physics by allowing more complex calculations. Thus it shares some of the paradox we have already noted in the use of new technologies to reinforce educational methods whose very existence is a reflection of the limitations of the precomputer period. As previously mentioned, the need for drill and practice in arithmetic is a symptom of the absence of conditions for the syntonic learning of mathematics. The proper use of computers is to supply such conditions. When computers are used to cure the immediate symptom of poor scores in arithmetic, they reinforce habits of dissociated learning. And these habits which extend into many areas of life are a much more serious problem than weakness in arithmetic. The cure may be worse than the disease. There is an analogous argument about physics. Traditional physics teaching is forced to overemphasize the quantitative by the accidents of a paper-and-pencil technology which favors work that can produce a definite “answer.” This is reinforced by a teaching system of using “laboratories” where experiments are done to prove, disprove, and “discover” already known propositions. This makes it very difficult for the student to find a way to constructively bring together intuitions and formal methods. Everyone is too busy following the cookbook. Again, as in the case of arithmetic, the computer should be used to remove the fundamental problem. However, as things are today, the established image of school physics as quantitative and the established image of the computer reinforce each other. The computer is used to aggravate the already too-quantitative methodology of the physics classes. As in the case of arithmetic drill and practice, this use of the computer undoubtedly produces local improvements and therefore gets the stamp of approval of the educational testing community and of teachers who have not had the opportunity to see something better. But throughout this book we have been developing the elements of a less quantitative approach to computers in education. Now we directly address the concerns this shift in direction must raise for a serious teacher of physics.

The quotation at the beginning of this chapter was spoken in some anguish by a teacher who manifestly liked working with Turtles but could not reconcile it with what she had come to define as “doing physics.” The situation reflects a permanent dilemma faced by anyone who wishes to produce radical innovation in education. Innovation needs new ideas. I have argued that we should be prepared to undertake far-reaching reconceptualizations of classical domains of knowledge. But how far can this go? Education has a responsibility to tradition. For example, the job of the community of English teachers must be to guide their students to the language and literature as it exists and as it developed historically. They would be failing in their duty if instead they invented a new language, wrote their version of poetry, and passed on to the next generation these fabricated entities in the place of the traditional ones. The concern of the teacher worried about whether working with Turtles is “really learning physics” is very serious.

Is work with Turtles analogous to replacing Shakespeare by “easier,” made-up literature? Does it bring students into contact with the intellectual products of Galileo, Newton, and Einstein or merely with an idiosyncratic invention that is neither marked by greatness nor tested by time? The question raises fundamental problems, among them: What is physics? And what is the potential influence of computation on understanding it?

Most curriculum designers have easy answers to these questions. They define elementary physics as what is taught in schools. Occasionally they move material usually taught in college down to high school, or bring in new topics of the same kind as the old. For example, modern particles are mentioned and the textbooks show schematically how a nuclear reactor works. Even the more visionary curriculum reformers stayed within the conceptual framework defined by equations, quantitative laws, and laboratory experiments. Thus, they could feel secure that they were really “teaching physics.” The possibility opened by the computer of a new kind of activity and of a new relationship to ideas poses problems of responsibility toward the cultural heritage. I take this responsibility seriously but cannot feel that I serve it by taking shelter behind the existing curriculum. One cannot accept this shelter without seriously considering the question of whether school science is not already in the position of the hypothetical English teacher who taught an ersatz form of English because it seemed to be more teachable. I believe that this is the case.

In chapter 5, I suggested that it is “school physics” rather than “Turtle physics” that betrays the spirit of “real physics.” Here I pursue my argument by talking about components of physics that are even further removed than Dynaturtles from the traditional curriculum. These are very general, usually qualitative, intuitive ideas or “frames” used by physicists to think about problems before they can even decide what quantitative principles apply.

I ask readers who may not be familiar with such qualitative thinking in physics to follow a hypothetical conversation between two great physicists.

Many millions of students have grown up believing that Galileo refuted Aristotle’s expectation that the time taken for an object to fall to the ground is proportional to its weight by dropping cannonballs from the tower of Pisa. Galileo’s experiment is supposed to have proved that except for minor perturbations due to air resistance, a heavy and a light cannonball would, if dropped together, reach the ground together. In fact it is extremely unlikely that Galileo performed any such experiment. But whether he did or did not is less interesting than the fact that he would not have had the slightest doubt about the outcome of the experiment. In order to convey a sense of the kind of thinking that could have given him this assurance, we shall go through a hypothetical dialog between two imaginary characters, GAL and ARI.

GAL:

Look, your theory has got to be wrong. Here’s a two-pound and a one-pound ball. The two-pound ball takes two seconds to fall to the ground. Tell me, how long do you think the one-pound ball would need?

ARI:

I suppose it would take four seconds. Anyway, much more than two seconds.

GAL:

I thought you would say that. But now please answer another question. I am about to drop two one-pounders simultaneously. How long will the pair of them take to reach the ground?

ARI:

That’s not another question. I gave my opinion that one-pound balls take four seconds. Two of them must do the same. Each falls independently.

GAL:

You are consistent with yourself if two bodies are two bodies, not one.

ARI:

As they are… of course.

GAL:

But now if I connect them by a gossamer thread… is this now two bodies or one? Will it (or they) take two seconds or four to fall to the ground?

ARI:

I am truly confused. Let me think.… It’s one body, but then it should fall for four seconds before reaching the earth. But then this would mean that a thread finer than silk could slow down a furiously falling ball of iron. It seems impossible. But if I say it is two bodies… I am in deep trouble. What is a body? How do I know when one becomes two? And if I cannot know, then how sure can I be of my laws of falling bodies?

From a strictly logical point of view, GAL’s argument is not absolutely compelling. One can imagine “fixes” for ARI’s theory. For example, he could propose that the time taken might depend on the form as well as the weight of the body. This would allow him the possibility that a two-pound body made of two cannonballs and gossamer threads would fall more slowly than a two-pound sphere of iron. But in fact the kind of argument used by GAL is subversive of the kind of theory expounded by ARI, and historically, it is highly plausible that the great conversion from Aristotelian thinking was fueled by such arguments. No single argument could by itself convert Aristotle, for whom the theory of falling objects was an element in a mutually supporting web. But as GAL’s way of thinking gained currency, the Aristotelian system was eroded. Indeed I contend that arguments of this kind, as opposed to the apparently more compelling arguments from precise facts and equations, play an essential role in the evolution of thinking, both on the historical scale of the evolution of science itself and on the personal scale of the development of the individual learner.

ARI would have been far better able to defend himself had GAL argued from specific facts or calculations, which might allow quibbles about their conditions of applicability and allow themselves to be compartmentalized. The hard punch of GAL’s argument comes from the fact that it mobilizes ARI’s own intuitions about the nature of physical objects and about the continuity of natural effects (thinner than silk versus furiously falling iron). To a logician this argument might seem less compelling. But as empathetic fellow humans we find ourselves squirming in confusion with ARI.

There is a lot to be learned by thinking through the issues raised by this dialogue, simplistic as it is. First we note that GAL is not just being cleverer than ARI: He knows something that ARI seems not to know. In fact, if we look carefully we see that GAL skillfully deploys several powerful ideas. Most striking is his principal idea of looking at a two-pound object as made up of two one-pound objects, seeing the whole as additively made of whatever parts we care to divide it into. Stated abstractly this idea sounds trivial in some contexts and simply false in others: We are used to being reminded that “the whole is more than the sum of its parts.” But we should not treat it as a proposition to be judged by the criterion of truth and falsity. It is an idea, an intellectual tool, and one that has proved itself to be enormously powerful when skillfully used.

GAL’s idea is powerful and is part of the intellectual tool kit of every modern mathematician, physicist, or engineer. It is as important in the history and in the learning of physics as the kind of knowledge that fits into propositions or equations. But one would not know this from looking at textbooks. GAL’s idea is not given a name, it is not attributed to a historical scientist, it is passed over in silence by teachers. Indeed, like most of intuitive physics, this knowledge seems to be acquired by adult physicists through a process of Piagetian learning, without, and often in spite of, deliberate classroom teaching. Of course, my interest in recognizing the existence of these informally learned, powerful intuitive ideas is not to remove them from the scope of Piagetian learning and place them in a curriculum: There are other ways to facilitate their acquisition. By recognizing their existence we should be able to create conditions that will foster their development, and we certainly can do a lot to remove obstacles that block them in many traditional learning environments.

GAL’s dialogue with ARI has something to teach us about one of the most destructive blocks to learning: the use of formal reasoning to put down intuitions.

Everyone knows the unpleasant feeling evoked by running into a counterintuitive phenomenon where we are forced, by observation or by reason, to acknowledge that reality does not fit our expectations. Many people have this feeling when faced with the perpetual motion of a Newtonian particle, with the way a rudder turns a boat, or with the strange behavior of a toy gyroscope. In all these cases intuition seems to betray us. Sometimes there is a simple “fix”; we see that we made a superficial mistake. But the interesting cases are those where the conflict remains obstinately in place however much we ponder the problem. These are the cases where we are tempted to conclude that “intuition cannot be trusted.” In these situations we need to improve our intuition, to debug it, but the pressure on us is to abandon intuition and rely on equations instead. Usually when a student in this plight goes to the physics teacher saying, “I think the gyroscope should fall instead of standing upright,” the teacher responds by writing an equation to prove that the thing stands upright. But that is not what the student needed. He already knew that it would stay upright, and this knowledge hurt by conflicting with intuition. By proving that it will stand upright the teacher rubs salt in the wound but does nothing to heal it. What the student needs is something quite different: better understanding of himself, not of the gyroscope. He wants to know why his intuition gave him a wrong expectation. He needs to know how to work on his intuitions in order to change them. We see from the dialogue that GAL is an expert at how to manipulate intuitions. He does not force ARI into rejecting intuition in favor of calculation. Rather he forces him to confront a very specific aspect of his intuitive thinking: how he thinks about objects. One suspects from the dialogue that GAL is used to understanding objects by thinking of them as composed of parts, or subobjects, while ARI is used to thinking of objects more globally, as undivided wholes with global properties such as shape and weight.

We might seem to have strayed far from our discussion of computers. But the interaction between GAL and ARI is close to an important kind of interaction between children and computers and between children and instructors via computers. GAL tried to make ARI confront and work through his intuitive ways of thinking about objects, and ARI might be skillful enough to do so. But what can children do to confront their intuitions?

Of course the question is rhetorical in that I know that children think a great deal about their thinking. They do worry about their intuitions. They do confront them and they do debug them. If they did not, the idea of making them do so would indeed be utopian. But since they do it already, we can provide materials to help them do it better.

I see the computer as helping in two ways. First, the computer allows, or obliges, the child to externalize intuitive expectations. When the intuition is translated into a program it becomes more obtrusive and more accessible to reflection. Second, computational ideas can be taken up as materials for the work of remodeling intuitive knowledge. The following analysis of a well-known puzzle is used to illustrate how a Turtle model can help bridge the gap between formal knowledge and intuitive understanding. We have seen many examples in incidents where children work with computers. Here I shall convey a sense of what this means by inviting you to work on a situation where your intuitions will come into conflict.

The purpose in working on the problem is not to “get the right answer,” but to look sensitively for conflict between different ways of thinking about the problem: for example, between two intuitive ways of thinking or between an intuitive and a formal analysis. When you recognize conflicts, the next step is to work through them until you feel more comfortable. When I did this, I found that the Turtle model was extremely helpful in resolving some of the conflicts. But my reaction is undoubtedly shaped by my positive feelings about Turtles.

Imagine a string around the circumference of the earth, which for this purpose we shall consider to be a perfectly smooth sphere, four thousand miles in radius. Someone makes a proposal to place the string on six-foot-high poles. Obviously this implies that the string will have to be longer. A discussion arises about how much longer it would have to be. Most people who have been through high school know how to calculate the answer. But before doing so or reading on, try to guess: Is it about one thousand miles longer, about a hundred, or about ten?

Most people who have the discipline to think before calculating—a discipline that forms part of the know-how of debugging one’s intuitions—experience a compelling intuitive sense that “a lot” of extra string is needed. For some the source of this conviction seems to lie in the idea that something is being added all around the twenty-four thousand miles (or so) of the earth’s circumference. Others attach it to more abstract considerations of proportionality. But whatever the source of the conviction may be, it is “incorrect” in anticipating the result of the formal calculation, which turns out to be a little less than forty feet. The conflict between intuition and calculation is so powerful that the problem has become widely known as a teaser. And the conclusion that is often drawn from this conflict is that intuitions are not to be trusted. Instead of drawing this conclusion, we shall attempt to engage the reader in a dialog in order to identify what needs to be done to alter this intuition.

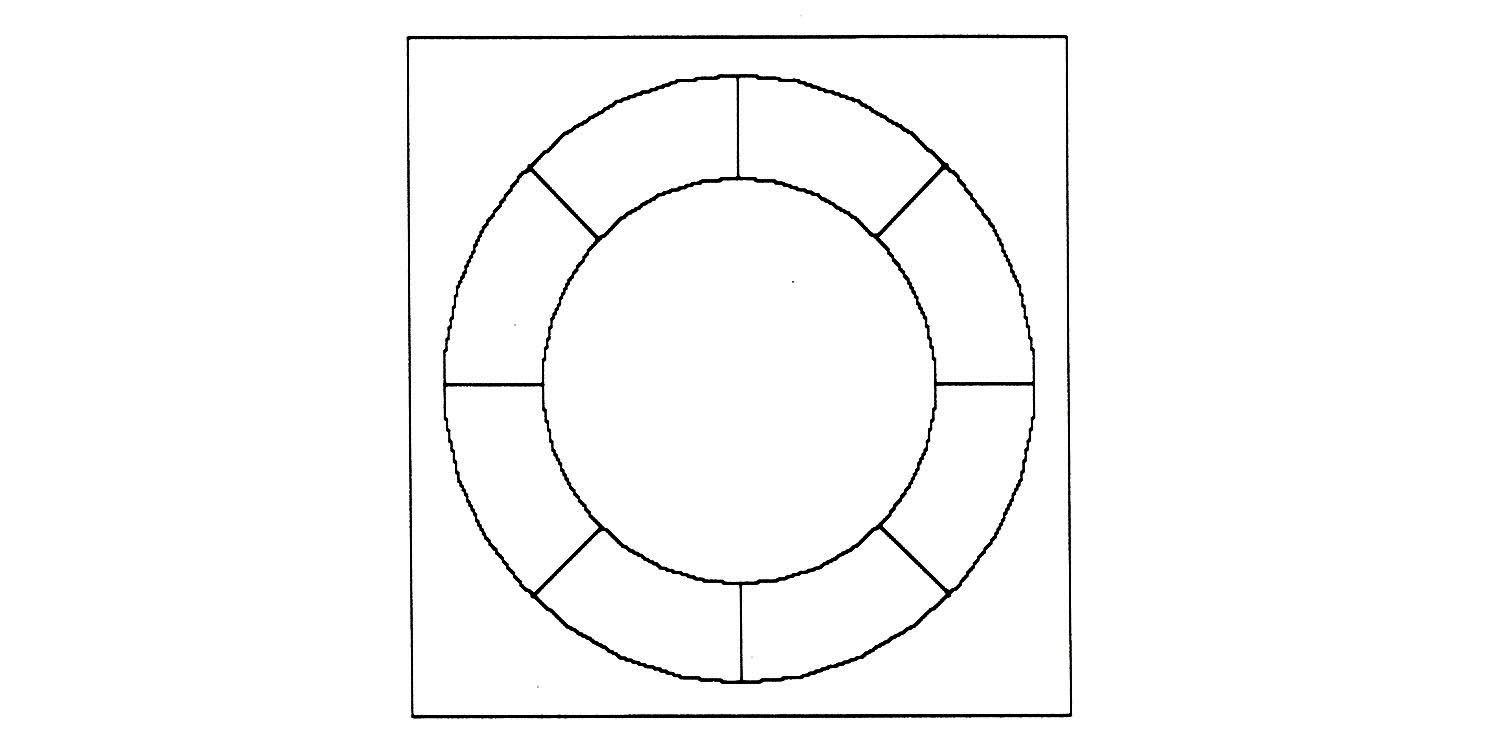
Figure 15

The figure shows a string around the earth supported by poles of greatly exaggerated height. Call the radius of the earth R and the height of the poles h. The problem is to estimate the difference in length between the outer circumference and the true circumference. This is easy to calculate from the formula:

CIRCUMFERENCE = 2π × RADIUS

So the difference must be

2π(R + h) − 2πR

which is simply 2πh.

But the challenge here is to “intuit” an approximate answer rather than to “calculate” an exact one.

As a first step we follow the principle of seeking out a similar problem that might be more tractable. And a good general rule for simplification is to look for a linear version. Thus we pose the same problem on the assumption of a “square earth.”

Figure 16a

The string on poles is assumed to be at distance h from the square. Along the edges the string is straight. As it goes around the corner it follows a circle of radius h. The straight segments of the string have the same length as the edges of the square. The extra length is all at the corners, in the four quarter-circle pie slices. The four quarter circles make a whole circle of radius h. So the “extra string” is the circumference of this circle, that is to say 2πh.

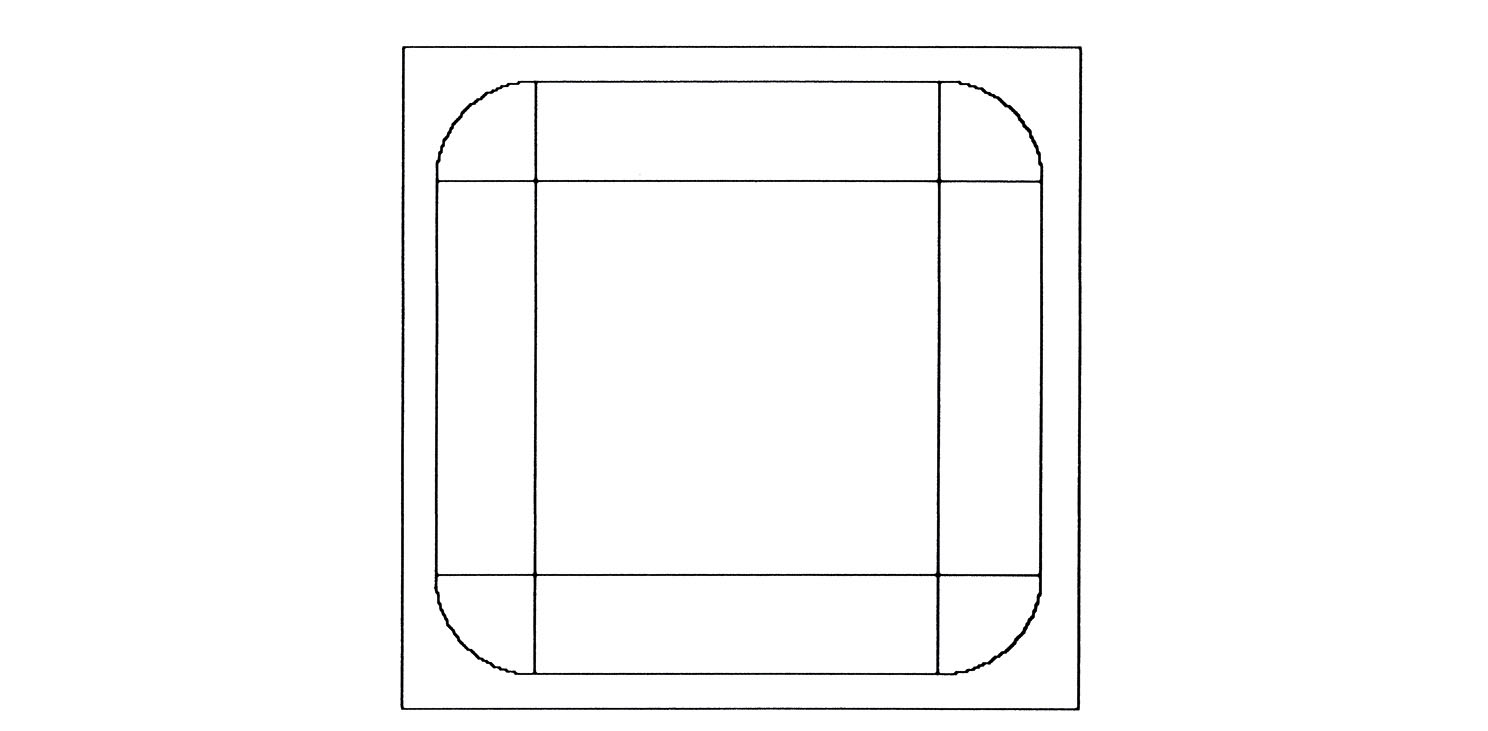
Figure 16b

Increasing the size of the square does not change the quarter-circle pie slices. So the extra string needed to raise a string from the ground to height h is the same for a very small square earth as for a very large one.

The diagram gives us a geometric way to see that the same amount of extra string is needed here as in the case of the circle. This is itself quite startling. But more startling is the fact that we can see so directly that the size of the square makes no difference to how much extra string is needed. We could have calculated this fact by formula. But doing so would have left us in the same difficulty. By “seeing” it geometrically we can bring this case into line with our intuitive principle: Extra string is needed only where the earth curves. Obviously no extra string is needed to raise a straight line from the ground to a six-foot height.

Unfortunately, this way of understanding the square case might seem to undermine our understanding of the circular case. We have completely understood the square but did so by seeing it as being very much different from the circle.

But there is another powerful idea that can come to the rescue. This is the idea of intermediate cases: When there is a conflict between two cases, look for intermediates, as GAL in fact did in constructing a series of intermediate objects between the two one-pound balls and one two-pound ball. But what is intermediate between a square and a circle? Anyone who has studied calculus or Turtle geometry will have an immediate answer: polygons with more and more sides. So we look at Figure 17, which shows strings around a series of polygonal earths. We see that the extra string needed remains the same in all these cases, and, remarkably, we see something that might erode the argument that the circle adds something all around. The 1000-gon adds something at many more places than the square, in fact two hundred fifty times as many places. But it adds less, in fact one two hundred fiftieth at each of them.

Now will your mind take the jump? Like GAL, I have said nothing so far to compel this crucial step by rigorous logic. Nor shall I. But at this point some people begin to waver, and I conjecture that whether they do or not depends on how firm a commitment they have made to the idea of polygonal approximations to a circle. For those who have made the polygonal representation their own, the equivalence of polygon and circle is so immediate that intuition is carried along with it. People who do not yet “own” the equivalence between polygonal representation and circle can work at becoming better acquainted with it, for example, by using it to think through other problems.

Figure 17

In the octagon, too, the “extra string” is all in the pie slices at the corners. If you put them together they form a circle of radius h. As in the case of the square, this circle is the same whether the octagon is small or big. What works for the square (4-gon) and for the octagon (8-gon) works for the 100-gon and for the 1000-gon.

The following problem is taken from Martin Gardner’s book, Mathematical Carnival:

If one penny rolls around another penny without slipping how many times will it rotate in making one revolution? One might guess the answer to be one, since the moving penny rolls along an edge equal to its own circumference, but a quick experiment shows that the answer is two; apparently the complete revolution of the moving penny adds an extra rotation.¹

Again there is a conflict between the intuitive guess (one revolution) and the result of more careful investigation. How can one bring one’s intuition into line?

The same strategy works here as for the string around the earth problem. Roll a penny around a square without slipping. You will notice that it behaves quite differently as it rolls along the sides than when it pivots around the corners. It is easy to see that the total rotation at the four corners combined is 360°. This remains true for any polygon, however many sides it has and however big it is. And once more, the crucial step becomes the passage from the polygon to a Turtle circle to a true circle.

I am not suggesting that one more exercise will change your intuition of circularity. Here too, as in the case of Aristotle’s physics, the particular piece of knowledge is part of a large network of mutually supportive ways of thinking. I am suggesting that you keep this new way of thinking in mind for awhile, looking for opportunities to use it as you might look for opportunities to introduce a new friend to old ones. And even then, I have no way of knowing whether you want to change your intuition of circularity. But if it is to change, I think that the process I am suggesting here is the best, perhaps the only, way whether it is adopted deliberately or simply happens unconsciously.

I want you to go away from this book with a new sense of a child’s value as a thinker, even as an “epistemologist” with a notion of the power of powerful ideas. But I also realize that these images might seem abstract and even irritating to some of you, perhaps especially those of you who teach children.

For example, a third-grade teacher who spends many frustrating hours every day trying to teach thirty-six children to write grammatical sentences and to do arithmetic might view my suggestions about Turtle geometry, physics microworlds, and cybernetics as far removed from reality, as far removed as was Marie Antoinette when she suggested that those who were starving for bread should eat cake. How are the powerful ideas we have discussed related to what most schools see as their bread-and-butter work, that is to say, the basic skills?

A first connection works through the attitude of the learner. You can’t learn bread-and-butter skills if you come to them with fear and the anticipation of hating them. When children who will not let a number into their head fail to learn arithmetic, the remedy must be developing a new relationship with numbers. Achieving this can put children in a positive relationship to anything else that they will recognize as being of the same kind. This can be school mathematics.

Kim was a fifth-grade girl who invariably came out on the bottom on all school arithmetic tests. She hated math. In a LOGO environment she became engrossed in programming. She designed a project that maintained a special database to store information about her family tree. One day a visiting educator remarked to her that “computers made math fun.” Kim looked up from her work and said very angrily: “There ain’t nothin’ fun in math.” The instructor in her class had not thought it advisable to discuss with her whether what she was doing with the computer was “math.” Clearly, anything that was good was definitionally not math. But by the end of the year Kim made the connection herself and decided that mathematics was neither unpleasant nor difficult.

Getting to know (and like) mathematics as you get to know (and like) a person is a very pertinent image of what happened in this case. Computers can also contribute to the learning of bread-and-butter arithmetic by changing our perception of what it is about, of what powerful ideas are most important in it. School arithmetic, generally thought of as a branch of number theory, might better be thought of as a branch of computer science. Difficulties experienced by children are not usually due to deficiencies in their notion of number but in failing to appropriate the relevant algorithms. Learning algorithms can be seen as a process of making, using, and fixing programs. When one adds multidigit numbers, one is in fact acting as a computer in carrying through a procedure something like the program in Figure 18.

1. Set out numbers following conventional format.

2. Focus attention on the rightmost column.

3. Add as for single digit numbers.

4. If result <10 record results.

5. If result in rightmost column was equal to or greater than 10, then record rightmost digit and enter rest in next column to left.

6. Focus attention one column to left.

7. Go to line 3.

Figure 18

To get better at this sort of activity one needs to know more about, and feel more comfortable with, the ways of procedures. And this, of course, is what a good computer experience allows.

These remarks should be put in the context of our earlier discussion about the difference between the New Math curriculum reform of the 1960s and the kind of enrichment the computer culture can bring to mathematics. In chapter 2 we dealt with one important reason for the failure of the New Math: It did not ameliorate our society’s alienated relationship with number. On the contrary, it aggravated it. We now see a second reason for the failure of the New Math. It tried to root the teaching of math in number theory, set theory, or logic instead of facing the conceptual stumbling blocks that children really experience: Their lack of knowledge about programming. Thus the authors of the New Math misunderstood the source of children’s problems. This misunderstanding is harmful in several ways. It is harmful insofar as it seeks to improve the child’s understanding of arithmetic by drill in irrelevant areas of knowledge. It is also harmful insofar as it imparts an inappropriate value system into mathematics education. The pure mathematician sees the idea of number as valuable, powerful, and important. The details of procedure are seen as superficial and uninteresting. Thus the child’s difficulties are referred back to abstract difficulties with the notion of number. The computer scientist takes a more direct approach. Trouble with adding is not seen as symptomatic of something else; it is trouble with the procedure of adding. For the computerist the procedure and the ways it can go wrong are fully as interesting and as conceptual as anything else. Moreover, what went wrong, namely the bugs, are not seen as mistakes to be avoided like the plague, but as an intrinsic part of the learning process.

Ken was a fifth grader who added 35 and 35 and got 610. His bug was showing clearly. Since 32 plus 32 is 64, then 35 plus 35 should be 610. Ken was brought into a better relationship with mathematics when he learned to see his mistake as a trick that mathematical formalisms play on us. The French can say seventy as soixante dix, “sixty-ten,” but although they can write sixty-five as 65, they cannot write sixty-ten as 610. This symbol has been preempted to mean something else.

Ken might superficially appear to have had bad intuitions about numbers. But this is quite wrong as a diagnosis. When asked, “If you had thirty-five dollars and you got thirty-five dollars more, would you have $610.00,” his answer was an emphatic, “No way.” When asked how much he would have, he returned to his paper calculation, crossed off the zero from 610, and came up with the new answer of 61, which intuitively is not so far off. His problem is not bad intuition or notion of number. From a computerist’s point of view one can recognize several difficulties, each of which is understandable and correctable.

First, he dissociates the operation of the procedure from his general store of knowledge. A better procedure would have an “error check” built into it. Since he could recognize the error when prompted, he certainly should have been capable of setting up the procedure to include prompting himself. Second, when he found the error he did not change, or even look at, the procedure, but merely changed the answer. Third, my knowledge of Ken tells me why he did not try to change the procedure. At the time of this incident he did not recognize procedures as entities, as things one could name, manipulate, or change. Thus, fixing his procedures is very far indeed from his awareness. The idea of procedures as things that can be debugged is a powerful, difficult concept for many children, until they have accumulated experience in working with them.

I have seen children like Ken get over this kind of difficulty after some experience writing programs in a LOGO environment. But why don’t children learn a procedural approach from daily life? Everyone works with procedures in everyday life. Playing a game or giving directions to a lost motorist are exercises in procedural thinking. But in everyday life procedures are lived and used, they are not necessarily reflected on. In the LOGO environment, a procedure becomes a thing that is named, manipulated, and recognized as the children come to acquire the idea of procedure. The effect of this for someone like Ken is that everyday-life experience of procedures and programming now becomes a resource for doing formal arithmetic in school. Newton’s laws of motion came alive when we used computational metaphor to tie them to more personal and conceptually powerful things. Geometry came alive when we connected it to its precursors in the most fundamental human experience: the experience of one’s body in space. Similarly, formal arithmetic will come alive when we can develop links for the individual learner with its procedural precursors. And these precursors do exist. The child does have procedural knowledge and he does use it in many aspects of his life, whether in planning strategies for a game of tic-tac-toe or in giving directions to a motorist who has lost his way. But all too often the same child does not use it in school arithmetic.

The situation is exactly like the one we met in the dialog between ARI and GAL and in the use of the Turtle circle model to change the intuition of circularity brought to bear on the string and coin problems. In all these cases, we are interested in how a powerful idea is made part of intuitive thinking. I do not know a recipe for developing a child’s intuition about when and how to use procedural ideas, but I think that the best we can do is what is suggested by the metaphor of getting to know a new person. As educators we can help by creating the conditions for children to use procedural thinking effectively and joyfully. And we can help by giving them access to many concepts related to procedurality. This is achieved through the conceptual content of LOGO environments.

In this book I have clearly been arguing that procedural thinking is a powerful intellectual tool and even suggested analogizing oneself to a computer as a strategy for doing it. People often fear that using computer models for people will lead to mechanical or linear thinking: They worry about people losing respect for their intuitions, sense of values, powers of judgment. They worry about instrumental reason becoming a model for good thinking. I take these fears seriously but do not see them as fears about computers themselves but rather as fears about how culture will assimilate the computer presence. The advice “think like a computer” could be taken to mean always think about everything like a computer. This would be restrictive and narrowing. But the advice could be taken in a much different sense, not precluding anything, but making a powerful addition to a person’s stock of mental tools. Nothing is given up in return. To suggest that one must give up an old method in order to adopt a new one implies a theory of human psychology that strikes me as naive and unsupported. In my view a salient feature of human intelligence is the ability to operate with many ways of knowing, often in parallel, so that something can be understood on many levels. In my experience, the fact that I ask myself to “think like a computer” does not close off other epistemologies. It simply opens new ways for approaching thinking. The cultural assimilation of the computer presence will give rise to a computer literacy. This phrase is often taken as meaning knowing how to program, or knowing about the varied uses made of computers. But true computer literacy is not just knowing how to make use of computers and computational ideas. It is knowing when it is appropriate to do so.

GAL:	Look, your theory has got to be wrong. Here’s a two-pound and a one-pound ball. The two-pound ball takes two seconds to fall to the ground. Tell me, how long do you think the one-pound ball would need?
ARI:	I suppose it would take four seconds. Anyway, much more than two seconds.
GAL:	I thought you would say that. But now please answer another question. I am about to drop two one-pounders simultaneously. How long will the pair of them take to reach the ground?
ARI:	That’s not another question. I gave my opinion that one-pound balls take four seconds. Two of them must do the same. Each falls independently.
GAL:	You are consistent with yourself if two bodies are two bodies, not one.
ARI:	As they are… of course.
GAL:	But now if I connect them by a gossamer thread… is this now two bodies or one? Will it (or they) take two seconds or four to fall to the ground?
ARI:	I am truly confused. Let me think.… It’s one body, but then it should fall for four seconds before reaching the earth. But then this would mean that a thread finer than silk could slow down a furiously falling ball of iron. It seems impossible. But if I say it is two bodies… I am in deep trouble. What is a body? How do I know when one becomes two? And if I cannot know, then how sure can I be of my laws of falling bodies?