For the exponential-type case under consideration here, we can writeWe present here a simplified, not wholly rigorous, argument leading to the asymptotic Type I extreme-value distribution. The reader is referred to Gumbel [1958] for an entire book devoted to the subject of extreme value distributions. Our interest is in underlying distributions FX having an upper tail of the exponential type, Eq. (3.3.47). Yn is the largest of n independent, identically distributed random variables, X1, X2, . . ., Xn.
For convenience, we introduce what is known as the characteristic value un of Yn. It is defined to equal that value x for which FX(x) = 1 – 1/n. For example, the characteristic value of u2 of Y2 is the median of the Xi, while u100, the characteristic value of Y100, is the value which any Xi exceeds with probability For the exponential-type case under consideration here, we can write
Thus
We shall use this result below.
Consider now the distribution of Yn, Eq. (3.3.45):
If n is large, Yn will almost certainly take on values only in the upper tail of the distribution of X. Thus in the region of interest
Introducing a factor equal to unity [Eq. (B.l)],
If y is "not far" from un (and un was seen in Sec. 3.3.3. to be the "most likely" value or mode of Yn), then in the spirit of Sec. 2.4.4 we can replace g(y) by a linear approximation. An expansion of g(y) about y = un gives:
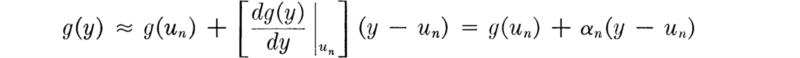
in which αn depends only on n and not on y. Note, for example, that if g(y)= λy, αn is simply λ. Therefore,
Substituting into Eq. (B.2),
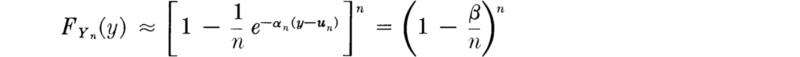
in which β has temporarily replaced 
As n gets large, if g(y) and hence αn are reasonably well-behaved functions,†
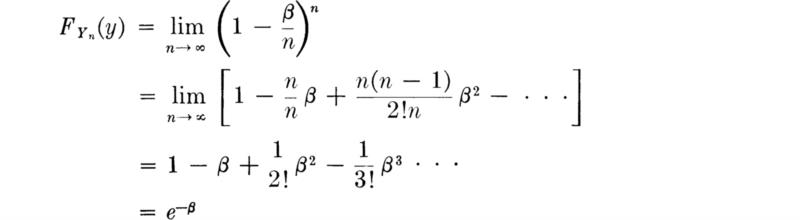
† Rigorously we should formalize the assumption that we are always (i.e., for all n) interested in values of y near to the mode un [in terms of 
which is proportional to 
, Eq. (3.3.52)]. Then β can be considered a “constant” as n grows.
This is the form of the asymptotic Type I extreme-value distribution introduced in Eq. (3.3.48).
Note that α and u depend in general on the number n of variables of which Yn is a maximum. The most likely value of Yn is the mode un. We should expect this to increase as n increases. In the text the subscript n is dropped because its value is usually not known. It is simply assumed that it is large enough that the functional form, Eq. (3.3.48), is an appropriate model for Y, the numerical estimates of α and u being obtained directly from observations of Y.
The dependence of un and αn on n may be important, however. It is used, for example, in the theory of the strength of materials to explain statistical size effect, that is, the physical phenomenon of larger specimens of brittle material failing at smaller stresses than smaller specimens. Here the argument is that the mode of Yn, the largest flaw (which determines the strength of a brittle specimen) grows as the size of the specimen grows (i.e., as the number n of unit volumes of material in which flaws occur grows).
The functional relationship between un and n depends on the functional form of g(x), since, from Eq. (B.1),
or
Thus if g(x)= λx, g-1 (In n) = (1/ λ) In n; while if g(x)= λx2,
Thus from the dependence of the mode of specimen strength on the specimen or sample size n, one can infer the functional form of the upper tail of the distribution of the underlying Xi’s. Consideration of the observed influence of n on the dispersion of Yn can support these studies, particularly in distinguishing between underlying distributions of the exponential type [Eq. (3.3.47)] and that displayed in Eq. (3.3.65). This second type leads to another asymptotic extreme-value form, Eq. (3.3.66), whose central value and dispersion also depend on n, but in a different manner. A derivation parallel to that in this appendix will show these distinctions.
