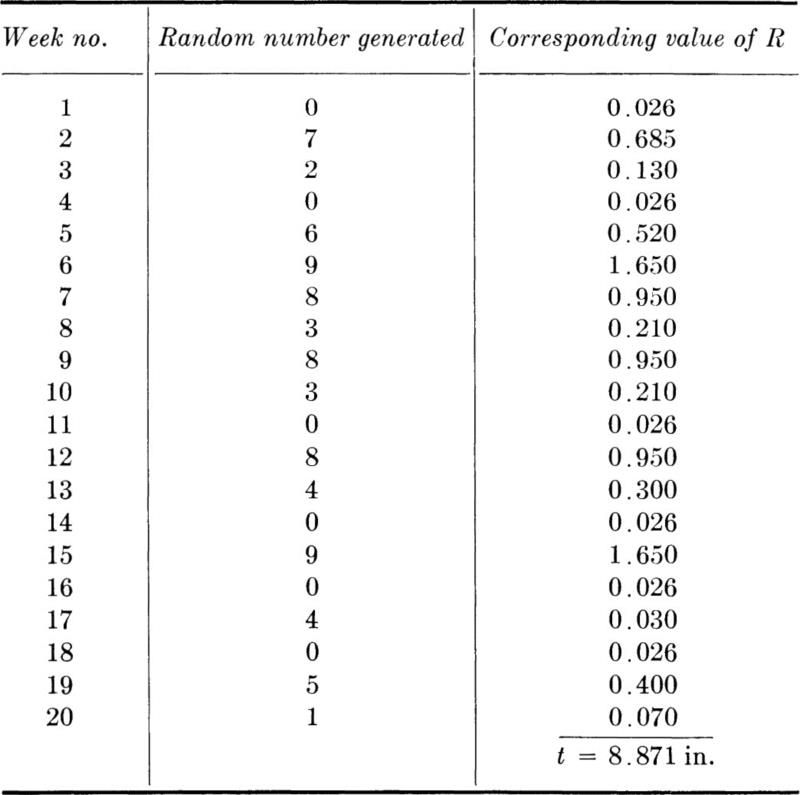
Table 2.3.2 Simulated values of the rainfall in the 20 rainy weeks of 1 year
Fig. 2.3.16 Histograms of several simulation runs reduced to estimated density functions and an estimated cumulative distribution function.
It should be evident even from these simple illustrations that many complex engineering problems can be analyzed by Monte Carlo simulation techniques. The models need not be restricted to functional relationships, but can involve complicated situations in which the distributions of variables depend upon the (random) state of the physical system or in which the whole sequence of steps to be followed may depend upon which particular value of a random variable is observed. Elaborate probabilistic models of many vehicles on complicated networks of streets and intersections have proved most useful to traffic engineers trying to predict the performance of a proposed design. The uncertainty and variation in drivel reaction time, driving habits, and origin-destination demands can all be treated on a probabilistic basis. Long histories of the operation of whole river-basin systems of water-resource controls have been simulated in minutes (Hufschmidt and Fiering [1966]). Rainfall and runoff values form probabilistic inputs to chains of dams and channels (real or designed) whose proposed operating policies (e.g., the degree to which reservoirs should be lowered in anticipation of flood runoffs) are being evaluated for long-term consequences, likelihoods of poor performance, and economics. Simulation, combined with numerical integration of the equations of motion, has been used to obtain approximate distributions of the maximum dynamic response of complex, nonlinear structures to the chaotic, random ground motions during earthquakes (Goldberg et al. [1964]).
The successful application of simulation depends upon the appropriateness of the model and the interpretation of the results as much as on the sophistication of the simulation techniques used. The former problems are the ones the engineer usually faces in using mathematical models of natural phenomena; for the latter problems, those of technique, the engineer can find help and documented experience in a number of references. (See, for example, Tocher [1963] or Hammersley and Hands-comb [1964].) Many methods are available, for example, to generate random numbers, to account for dependence among variables, or to reduce the effort needed to get the desired accuracy.
This section presents methods for deriving the distributions of random variables which are functionally dependent upon random variables whose distributions are known. In general, one should seek the CDF of the dependent random variable Z. For any particular value z, FZ(z) is found by calculating in the sample space of X (or X and Y) the probability of all those events where g(x) [or g(x,y)] is less than or equal to z:
This can be done by enumeration if the distribution of X (or X and Y) is discrete. If the distribution of X is continuous, integration is required. In certain circumstances (monotonic, increasing, one-to-one relationships), this procedure simply reduces to
The density function of Z can be found by differentiation of FZ(z) (assuming that Z is a continuous random variable). In certain cases the differentiation can be carried out explicitly before particular probability laws FX(x) are considered, in which case one can obtain a formula for the PDF of Z directly. The two most important examples are
1. Under monotonic, one-to-one conditions:
2. If Z = X + Y :
Certain computational methods are available for cases where analytical solutions are difficult or impossible. They include
1. Approximating continuous distributions by discrete ones, and solving by enumeration
2. Applying simulation techniques to obtain, by repeated experimentation, observed histograms which approximate desired results.
Because of the very nature of a random variable it is not possible to predict the exact value that it will assume in any particular experiment, but a complete description of its behavior is contained in its probability law, as presented in the CDF (or PMF or PDF, if applicable) of the variable. This complete information can be communicated only by stipulating an entire function, e.g., the PDF. In many situations this much information may not be necessary or available. More concise descriptors, summarizing only the dominant features of the behavior of a random variable, are often sufficient for the engineering purpose at hand. One or more simple numbers are used in place of a whole probability density function. These numbers usually take the form of weighted averages of certain functions of the random variable. The weights used are the PMF or PDF of the variable, and the average is called the expectation of the function.
We will find that, compared with entire probability laws, these expectations are much easier to work with in the analysis of uncertainty, as well as much easier to obtain estimates of from available data. Therefore, in engineering applications, where expedience often dictates that approximate but fast answers are better than none at all, averages and expectations prove invaluable.
Mean Every engineer is familiar with averages of observed numerical data. The sample mean and sample variance (Sec. 1.2) are the most common examples. Although they do not communicate all the available information, they are concise descriptors of the two most significant properties of the batch of observed data, namely, its central value and its scatter or dispersion.
On the other hand, given a solid body, e.g., a rod of nonuniform shape or density, the engineer is accustomed to determining certain numerical descriptions of the body such as the location of its center of mass and a moment of inertia about that point. Not complete in their description, these quantities are nonetheless sufficient to enable the engineer to predict a great deal about the gross static and dynamic behavior of the body.
Both these examples deserve being kept in mind when we define the mean mX or the expected value E[X] of a discrete random variable X as
or, for a continuous random variable, as
In the mean (or mean value) we are condensing the information in the probability distribution function into a single number by summing over all possible values of X the product of the value x and its likelihood pX(x) or fX(x) dx.
Recall from Chap. 1 that the sample mean of n numbers was defined as
If several observations of each value xi are found, this definition can be written
in which r is the total number of distinct values observed, ni is the total number of observations at value xi, and fi = ni/n is the observed frequency of the value xi in the sample.
Notice the close proximity in appearance between the definition of the mean of a (discrete) random variable, Eq. (2.4.1), and the sample mean of a batch of observed numbers, Eq. (2.4.4). This similarity helps make clear the notion of the mean of a random variable (especially when repeated observations of the random variable are anticipated), but the student should be most careful to avoid confusing the two means. The sample mean is computed from given observations, and the mean (or expectation) is computed from the mathematical probability law (e.g., from the PDF, CDF, or PMF) of a random variable. The latter is sometimes called the population mean to distinguish it from the sample mean. Geometrically, it is clear from its definition, Eqs. (2.4.1) or (2.4.2), that the mean defines the center of gravity of the shape defined by the PDF or PMF of a random variable.
In a physical problem, where some phenomenon has been modeled as a random variable, the mean value of that variable is usually the most significant single number the engineer can obtain. It is a measure of the central tendency of the variable, and, often, of the value about which scatter can be expected if repeated observations of the phenomenon are to be made. The sample mean of many such observations will, with high probability, † be very close to the (population) mean of the underlying random variable. For these and other reasons to be seen, when probabilistic model and a deterministic (nonprobabilistic) model of a physical phenomenon are compared, it is usually the mean of the probabilistic model which one compares with the single value of a deterministic model.
The mean of the discrete random variable adopted in Sec. 2.2.1 to model the annual runoff (see Fig. 2.2.3) is computed as follows, using Eq. (2.4.1):
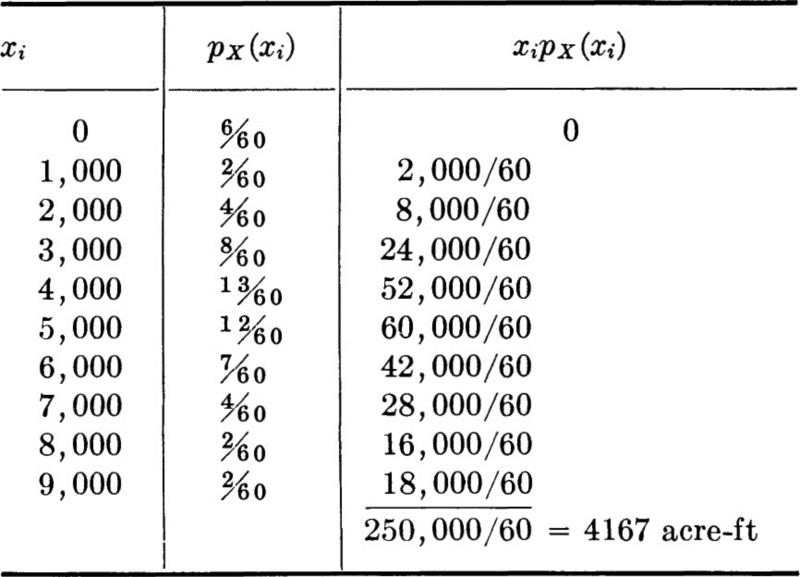
The mean runoff is 4167 acre-ft. This is a central value, a value about which observed values of X will tend in the long run to be scattered. It is probably the number the engineer would use if he were restricted to using only a single number to describe the runoff, that is, if he had to treat runoff deterministically rather than probabilistically in his analysis.
The mean value of the rainfall in a rainy week, the random variable R in the illustration in Sec. 2.3.3, is calculated by integration, after Eq. (2.4.2). Substituting for the PDF the function 2e–2r, r ≥ 0,
If it rains in a week, ½ in. is the mean value or “expected” value of the rainfall. Comparing this value with the density function of R (Fig. 2.3.15), it is apparent that in this case, the mean of R is not central, in that it does not correspond to a peak in the distribution. Nor is the mean the value which will be exceeded half of the time.† (That is, 1 – FR(½ in.) = e–1 = 0.368 ≠ 0.5. Solving 1 – FR(u) = 0.5 yields the median u = 0.346 in.) Nonetheless, even here the mean value yields “order of magnitude” information as to weekly rainfall in rainy weeks, and, if the observed records of many such weeks are averaged, this sample average would almost certainly be very close ‡ to ½ inch (assuming always that the mathematical model is a good representation of the physical phenomenon).
Variance The mean describes the central tendency of a random variable, but it says nothing of that behavior which leads engineers to study probability theory at all, namely, uncertainty or randomness. Here we seek a descriptor, a single number, which will give an indication of the scatter or dispersion, or, loosely, of the “randomness” in the random variable’s behavior.
Several such measures are possible. The range of the random variable is one example, although it is frequently a rather uninformative pair of numbers such as – ∞ to ∞ or 0 to ∞. Even if the range is two finite numbers, say, a to b, it gives no indication of the relative frequency of extreme values as compared with central values. It is desirable therefore to measure the dispersion from a central value, the mean, and to weight all deviations from the mean by their relative likelihoods.
The most common and most useful such measure of the dispersion of a random variable is the variance σX2, or Var [X], It is defined as the weighted average of the squared deviations from the mean:
or
The variance of a random variable bears the same relationship to the sample variance of a set of numbers (Sec. 1.2) as the mean does to the sample mean, and a comparison analogous to that made above between Eqs. (2.4.1) and (2.4.4) could be made with ease. A more meaningful analogy to draw is that between the variance of a random variable and the central moment of inertia of a bar of variable density (and unit mass). The variance σX2 is the second central moment of the area of the PDF or PMF with respect to its center of gravity mX.
In Fig. 2.4.1 are shown probability density functions of the same basic shape. The curves in Figs. 2.4.1a and b differ only in their mean, while the curves in Figs. 2.4.1b and c differ only in their variances. Smaller variances generally imply “tighter” distributions, less widely spread about the mean.
Standard deviation The positive square root of the variance is given the name standard deviation:
The conventional form of the standard notation, σ and σ 2, seems to indicate that in practice the standard deviation is given more importance than the variance. That is, in fact, the case.† The standard deviation has the same units as the variable X itself and can be compared easily and quickly with the mean of the variable to gain some feeling for the degree and gravity of the uncertainty associated with the random variable.
Fig. 2.4.1 Changes in PDF’s with changes in means and standard deviations.
Coefficient of variation A unitless characteristic that formalizes this comparison and that also facilitates comparisons among a number of random variables of different units is the coefficient of variation VX:
The coefficient of variation of the strength of the concrete produced by a given contractor is often assumed to be a constant for all mean strengths and to be a measure of the quality control practiced in his work (see ACI [1965] and Prob. 2.45). Thus a contractor practicing “good” control might produce concrete with a coefficient of variation of 0.10 or 10 percent, implying that concrete of mean strength 4000 psi would have a standard deviation of 400 psi, whereas “5000-psi concrete” would have a standard deviation of 500 psi.
The variance of the discrete runoff random variable can be computed from Eq. (2.4.7) as follows:
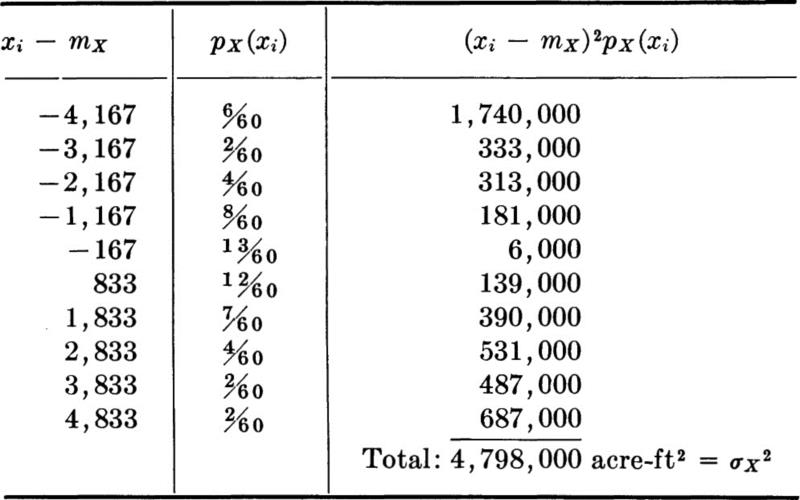
The standard deviation of this variable is
and the coefficient of variation is
The variance of the rainfall variable R is found by applying Eq. (2.4.8):
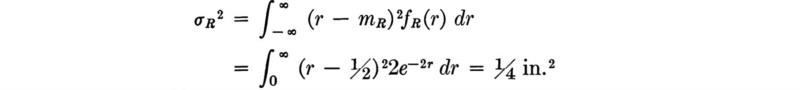
while
and
Illustration: Sigma bounds and the Chebyshev inequality It is common in engineering applications of probability theory to speak of the “one-, two-, and three-sigma” bounds of a random variable. The range between the two-sigma bounds, for example, is the range between mX – 2σX and mX + 2σX. The two-sigma bounds on the runoff variable X are 4167 – 2(2200) and 4167 + 2(2200) or 0 and 8567.† The three sets of bounds for this variable are shown in Fig. 2.4.2.
Fig. 2.4.2 Sigma bounds: runoff model.
In absence of the knowledge of the complete PDF, but knowing mean and variance, it is frequently stated in engineering applications (for reasons that will be clear in Sec. 3.3.1) that the probability that a variable lies within the one-sigma bounds of its mean is approximately 65 percent; within the two-sigma bounds, about 95 percent; and within the three-sigma bounds, about 99.5 percent. That even rough probability figures can be given with so little information is indicative of the value of the standard deviation and the variance as measures of dispersion. In fact, these approximate statements should only be used when it is known that the distribution is roughly bell-shaped.
More formally we can show that the mean and standard deviation alone are sufficient to make certain exact statements on the probability of a random variable lying within given bounds. The Chebyshev inequality ‡ states that
Note that, corresponding to the one-, two-, and three-sigma bounds, h equals 1, 2, and 3.
For example, the runoff variable has mean 4167 and standard deviation 2200. The Chebyshev inequality states
If h = 2
Or, recognizing in this particular case that X, the runoff, is nonnegative,
or, in another form,
The rule of thumb for the two-sigma bounds suggests that the former probability, that is, P[X ≤ 8567], should be about 95 percent, while the exact value, Fig. 2.4.2, is 
.
The Chebyshev inequality does not yield very sharp bounds. [Consider, for example, any value of h less than 1, when the right-hand side of Eq. (2.4.11) is negative.] It has the advantage, however, that it requires no assumption on the part of the engineer regarding the shape of the distribution. Hence the probability statements are totally conservative, within the qualification, of course, that mX and σX are known with certainty. When these parameters’ estimates are based on only a small amount of observed data, they, in fact, are not known with high confidence; this uncertainty is a subject of Chaps. 4 and 6.
A host of less general, but more precise inequalities are available. (See, for example, Parzen [1960], Freeman [1963].) As the engineer makes more and more assumptions regarding the shape of the distribution, such as its being unimodal (single-peaked), having “high-order contact” with the x axis in the extreme tails, † being symmetrical, having known values of higher moments (see Sec. 2.4.2), etc., the sharper his probability statements can be. Finally, of course, if he is willing to stipulate FX(x) itself, he can state exactly the proportion of the probability mass lying inside or outside any interval. This progression is common in applied probability theory; the more the engineer is willing to assume to be known, given, or hypothesized information, the more precise and penetrating can he be in his subsequent probabilistic analysis.
Discussion It should be emphasized that from the point of view of applications, two quite opposite problems have been discussed in this section. The first is that of calculating the mean and variance of a random variable knowing its distribution, and the second is that of making some kind of statement about the behavior of the variable when only the mean and variance are known.
The latter case is frequent. It arises in many situations. Data is often available only as summarized by its sample mean and sample variance, which are the natural estimates of the corresponding two model parameters. Also, in the analysis of complex models, the mean and variance of the dependent random variable are often easily obtainable when the complete story, i.e., the whole distribution, is lost in a maze of intractable integrals (Sec. 2.3). As will be discussed later in this section, we can often determine these two parameters as simple functions of the same two parameters of the independent random variables involved, implying that the engineer may never need to commit himself to unnecessarily detailed models of these variables. As shown in the next section, the mean and variance alone contain a substantial amount of information on which to base engineering decisions. Finally, they represent the first and most important step beyond deterministic engineering models in that they characterize not only the typical value, as the traditional model does, but also the dispersion. Recognition of the existence of the variance indicates that the probabilistic aspects of the engineering problem won’t be ignored. Study of the mean and variance, and their later counterparts, is referred to as a second-order-moment analysis; there will be an emphasis on this notion throughout our study of applied probability and statistics.
Summary In Sec. 2.4.1 we have defined the mean, variance, standard deviation, and coefficient of variation of a random variable. They are defined as sums of the possible values of the random variable or as sums of the squared deviations from the mean, weighted by their probabilities of occurrence. The mean and variance are the center of gravity of the probability mass and its moment of inertia. They can be calculated from given probability distributions, or used alone, without knowledge of the entire distribution, as summaries of the predominant characteristics of central value and dispersion.
In Sec. 2.3 we emphasized the importance in engineering applications of being able to determine the behavior of a (dependent) random variable Y, which is a function g(X) of another (independent) random variable X, whose behavior is known. The computational difficulties involved in actually finding, say, the PDF of Y from the PDF of X have also been encountered. Fortunately, as mentioned above in the justification for a concentrated study of the mean and variance, no such computational complications arise if one seeks only these two moments of Y, given the probability law of the independent variable X. Often even less is needed; for example, often only the mean and variance of X can be used to find corresponding moments of Y.
Expectation of a function If we know the probability law of X and our interest is in Y, where
then the expected value or expectation of Y is, by definition [Eq. (2.4.2)],
The method for computing fY (y) and its attendant difficulties were the subject of Sec. 2.3. It is a fundamental, but difficult to prove, † result of probability theory that this expectation can be evaluated by the much easier computation‡
where the notation E[g(X)] is defined as:
For a discrete variable, § the expectation of g(X) is defined as
It is helpful to see a simple discrete illustration. Suppose a random variable X has PMF as shown in Fig. 2.4.3a. Then the PMF of Y = g(X) = X2 is as shown in Fig. 2.4.3b. This result can be verified by straightforward enumeration in this simple example. The expected value of Y is, by definition, E[Y] = (⅔)(1) + (⅓)(4) = 2. Equation (2.4.14) states, however, that this expected value can also be found without first determining PY(y) Using Eq. (2.4.14),
as before.
Notice that the two quantities defined in Sec. 2.4.1, the mean and variance, can in fact be interpreted as merely special cases of Eq. (2.4.14) with g(X) = X for the mean and g(X) = (X – mX)2 for the variance. This equivalence suggests that two quite different interpretations might be given to Eq. (2.4.14). In some situations one may think of E[g(X)] as representing the mean of a random variable Y = g(X) conveniently calculated by this equation rather than by Eq. (2.4.12). This interpretation is common when interest centers on Y = g(X) as a dependent random variable functionally related to another random variable X (with known distribution function), as, for example, when X is velocity and Y = aX2 is kinetic energy. On the other hand, if interest centers on X itself, then the expectation of g(X) as given by Eq. (2.4.14) is usually interpreted as weighted average of g(X), over X, that is, as the sum of the values of the function of X evaluated at the various possible values of X and weighted by the likelihoods of those values of X. The variance of X, for example, is usually thought of in this light, rather than as the mean of a random variable Y = (X – mX)2. The distinction between these two interpretations is not of fundamental importance, but it may prove helpful when considering the uses to which the material to follow will be put.
Fig. 2.4.3 PMF’s of X and derived Y = X2 (a) Discrete PMF of X; (b) discrete PMF of Y = X2.
Moments In keeping with the latter interpretation of E[g(X)] as a weighting of g(x) by fX(x), we introduce a family of averages of X, called moments, that prove useful as numerical descriptors of the behavior of X. We call
the nth moment of X. Notice that this moment corresponds to the nth moment of the area of the PDF with respect to the origin. If n = 1, when the superscript is usually omitted, we have the mean of the variable.
It is possible, of course, to consider moments of areas about any point. In particular, moments with respect to the mean are called central moments:
Such moments correspond to the familiar moments of areas with respect to their centroids. The most important particular case is for n = 2, when 
the variance. The first central moment is, of course, always zero. If the asymmetry of a distribution is of interest, this property is often quantified or characterized by the third central moment μX(3), or by the corresponding dimensionless coefficient of skewness γ1:
If a distribution is symmetrical, this coefficient is zero (although the converse is not necessarily true). Positive values of γ1 usually correspond to PDF’s with dominant tails on the right; negative values to long tails on the left (see Fig. 2.4.4).
A less common coefficient γ2, the coefficient of kurtosis (flatness), is defined similarly:
It is often compared to a “standard value” of 3.†
Fig. 2.4.4 Variation of shape of PDF with coefficient of skewness γ1. (a) Negative skewness; (b) zero skewness; (c) positive skewness.
For example, the central moments of the rainfall variable R, defined in Sec. 2.3.3, are, in general,
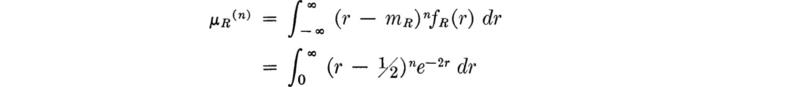
In the previous section, it was found that
Also
and
Hence the skewness and kurtosis coefficients are
indicating a positive skewness or long right-hand tail (see Fig. 2.3.15), and
Properties of expectation No matter which interpretation of the expectation E[g(X)] is involved, several general properties of the operation can be pointed out. For example, the expectation of a constant c is just the constant itself. This fact is easily shown. Simply by writing out the definition, we have
Similarly the following properties can be verified with ease for constants a, b, and c:
The implication of this last equation is that expectation, like differentiation or integration, is a linear operation. This linearity property is very useful computationally. It can be used, for example, to find the following formula for the variance of a random variable in terms of more easily calculated quantities.
Expanding the square,
Each term in the sum can be treated separately as a function of X and, according to Eq. (2.4.23), the expectation of their sum is the sum of their expectations:
Using other properties of expectation [Eqs. (2.4.20) and (2.4.21)],
But E[X] = mX; therefore
In an alternate form, the variance is said to be the “mean square” minus the “squared mean”:
Given the PDF of X, the simplest way to evaluate the variance is usually to calculate 
that is, E[X2], and then to subtract the squared mean.
Note that this last derivation took place without any reference to a particular form of the PDF and even without indication as to whether a discrete or continuous variable was involved. It is this ability to work with expectation without specifying the PDF that often permits us to determine relationships among the moments of two functionally related variables, X and Y = g(X), before specifying or even without knowledge of the PDF of X. For example, in concrete the quadratic relationship
holds between compressive stress Y and unit strain X well beyond the linear elastic range (Hognestad [1951]). If the unit strain applied to a specimen by a testing machine is a random variable, owing, say, to uncertainties in recording, then so is the stress in the concrete. How might the expected or mean stress be determined? If the PDF of X is known, the mean stress mY could be found by using the methods of Sec. 2.3 to find fY(y), and then applying Eq. (2.4.2). Alternatively, E[Y] could be calculated using Eq. 2.4.14, since
But, if the mean and variance of the strain are available, even if the PDF is not, the mean of Y can be found much more directly as simply
Using Eq. (2.4.24),
Therefore
Thus the mean and variance of X are sufficient to determine the mean of Y. An important practical distinction between deterministic and probabilistic analysis is also illustrated by this example. In a deterministic formulation of this problem, one would assume only a single value of strain was possible, say the typical value mX. The predicted stress would then be bmX – cmX2, which does not coincide with the mean value of F, unless, of course, the dispersion in X is truly zero. The greater the uncertainty in the strain, the greater the systematic error in the predicted value of the stress.
Formalizing this observation: in general, we cannot find the expectation of a function of X by substituting in the function E[X] for X, or
For example, the mean of 1/X is not 1/mX.
The linearity property of expectation, which made the previous derivations so direct, does not carry over to variances. The variance of Y = 2X is not two times the variance of X. This fact is easily demonstrated:
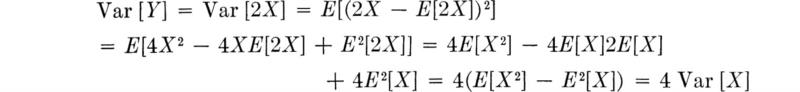
Several useful general properties of variances can be stated (and easily verified) however:
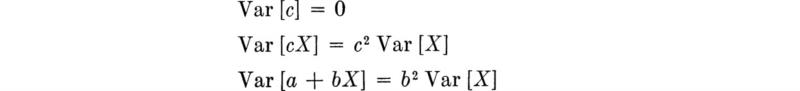
That is, a constant has no variance, and the standard deviation of a linear function of X, a + bX, is just |b|σX A simple example of such a linear function is a problem in which there is a change of units.
Conditional expectation In Sec. 2.2 we discussed briefly the construction of conditional distributions which are formed conditionally on the occurrence of some event. For example, in a design situation we might be interested in the distribution of the demand or load X, given that it is larger than some threshold value x0, say, the nominal design demand. Then, by definition of conditional probabilities,
The conditional PDF is found by differentiation with respect to x:
The conditional distributions satisfy all the necessary conditions to be proper probability distributions, and may be used as such.
It is therefore also meaningful to consider conditional means, conditional variances, and in general any expectation that is conditional on the prescribed event. So the conditional mean of the demand X, given that it is larger than the nominal demand x0, is
and its conditional variance is defined as
In general, for some event A,
Note that there is a trivial case:
A numerical example of the use of conditional distributions and expectations in engineering design will be found in an illustration to follow.
Expected costs and benefits A common use of expectation of a function of a random variable arises from the practice of basing engineering decisions, in situations involving risk, on expected costs. Frequently a portion of the total cost of a proposed design depends upon the more or less uncertain future magnitudes of such phenomena as local rainfall, traffic volume, or unit bid prices. If the engineer describes the uncertainty associated with these variables by treating them as random variables, then, when comparing alternate designs, the question arises of how to combine those portions of the costs or benefits that depend upon these random variables with the other, nonrandom, components of cost. How do you compare a more expensive spillway design with one of smaller initial cost, but of smaller capacity, and hence of greater risk of inadequacy during peak flows?
As demonstrated in previous illustrations (e.g., the industrial park example in Sec. 2.1), the expected cost (or benefit) related to the variable is usually used to obtain a single number; this cost reflects the sum of all possible values of the random cost weighted by the likelihood of their occurrence. The use of expected cost in making decisions is the subject of much experimental as well as theoretical investigation (Fish-burn [1965]), and it will be discussed more fully in Chap. 5. For the time being it can be accepted as an intuitively rational description of the economic consequences associated with the random variable.
In general, every value of the random variable leads to a corresponding cost or benefit. In other words, we can define cost as a function of the variable:
Examples of the shapes of such cost functions are sketched in Fig. 2.4.5.
In many cases the cost function is at least approximately linear. The cost of evacuating 100,000 yd3 of earth, for instance, depends linearly on X, the price bid per cubic yard, Fig. 2.4.5c. Then C(X) is of the form (in Fig. 2.4.5c the constant a is zero)
and the expected cost
That is, in this case the expected cost depends only on the mean of the random variable.
Fig. 2.4.5 Some cost functions, (a) Annual rainfall; (b) maximum load on a concrete beam; (c) unit bid price.
In other situations the cost can be approximated by a quadratic relationship. Figure 2.4.5a is a possible example. In this case the expected cost depends only on the mean and variance of the random variable:
The importance of the first- and second-order moments, i.e., means and variances, of random variables is magnified when it is recognized that frequently the ultimate engineering use of the probabilistic model will be in a decision-making context where a linear or quadratic cost function is a valid approximation. In such cases, the mean and variance are sufficient information on which to base the decision if an expected cost criterion is used.
Illustration: Pump-capacity decision This extended illustration is designed to demonstrate a number of the concepts discussed to this point in the text and to serve as a discussion of others. In particular, a mixed random variable will be encountered, a result here of a function g(X) which takes on the same value for many different values of X.
The demand X during the peak summer hour at a water-pumping station has a triangular distribution given by
and sketched in Fig. 2.4.6a.
The existing pump is adequate for any demand from 0 to 150 cfs. A new pump is to be added; it will be operated only if demand exceeds the capacity of the existing pump. Hence a demand of up to 150 cfs involves no load on the new pump, while a demand of 250 cfs would impose a load of 100 cfs on the new pump. Let Y be a random variable, “the load on the new pump” (i.e., the excess of demand over existing capacity):
This function is shown in Fig. 2.4.6b. It is not a one-to-one function.
Let us review how the distribution of Y can be determined. After Eq. (2.3.16), we have
where Ry is the region in which Y = g(X) ≤ y. Y is clearly never negative, but it is zero when X is less than 150; thus
By the symmetry of fX(x) about 150,
Fig. 2.4.6 Pump-design illustration, (a) Water-demand distribution; (b) load on new pump versus demand; (c) CDF of load on new pump; (d) PDF of load on new pump.
Y is never greater than 250 – 150, or 100, but the probability that Y is less than any value in the range 0 to 100, say, 30, is the probability that X is less than 30 + 150 = 180, or, in general, for 0 ≤ y ≤ 100,
Substituting for fX(x) in the range x = 150 to 250,since FX(150) = ½,
This function is, of course, unity for y > 100 and zero for y < 0, as shown in Fig. 2.4.6c.
The distribution of Y is of the mixed type; that is, there is a finite probability, ½, that Y will be exactly equal to zero, but elsewhere it behaves as a continuous random variable. Strictly, it has neither a PMF nor a PDF,† but a graphical representation of the latter is possible, as shown in Fig. 2.4.6d. The spike at zero represents the finite probability of that value occurring. The area under the “continuous part,” which we will denote as “fY”(y), is, of course, only ½, not unity. This continuous part is given by
It is helpful to recognize that any mixed distribution of practical interest can be represented as the weighted sum of two proper distributions, one discrete and one continuous:
in which 0 ≤ p ≤ 1 and in which 
is associated with the discrete values which Y can take on and 
is associated with the continuous range. In the example here, p = ½,
and
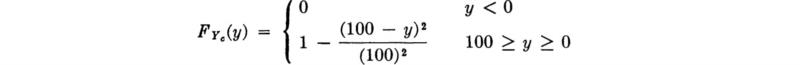
The function denoted “fY(y)” in Eq. (2.4.43) is just 
. The treatment of mixed distributions does not deserve special discussion in this applied text, not because they are not useful, but because their treatment follows in an obvious manner from that of discrete and continuous variables.
Consider now the task of choosing a capacity for the new pump. A “conservative” design would be 100 cfs, the maximum value the pump could possibly be called on to provide. But the occurrence of large values of demand are rare, and so alternate design rules might prove more economical in balance. One such rule might be to match the new pump’s capacity to the expected demand upon the pump, that is, E[Y].
This value can be obtained using the definition of expectation. Here an obvious extension of both Eqs. (2.4.1) and (2.4.2) is needed to provide for the mixed distribution of Y:
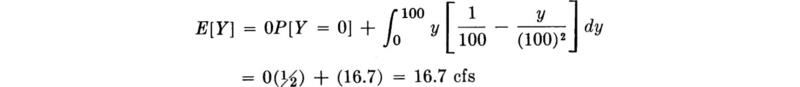
Alternatively, if this expected value were the only objective, we could have obtained it directly using Eq. (2.4.14) without the necessity of finding the probability law of Y. In this case
Substituting first for g1(x) [Eq. (2.4.41)],
and then for fX(x),
This rule suggests a second pump of capacity 16.7 cfs.
An alternate design rule might call for a pump capacity equal to the average of the nonzero demands on the pump, i.e., the expected demand given that the pump must be turned on at all. Formally, this value is the expected value of Y given that Y is greater than zero. The conditional distribution of Y given that Y is strictly greater than zero is, in this case, just the continuous part of its probability law renormalized to unit area or
Hence, the expected value of Y given Y > 0, written E[Y | Y > 0], is
This design rule suggests a pump twice as large as the first rule.
As a less arbitrary and more explicitly cost-oriented approach, the engineer might seek that pump capacity z which promises the lowest expected total cost. Costs (in arbitrary units) are thought to be described by a cost of 100 + 10z (representing a fixed installation cost and the cost of the pump itself) plus a cost associated with failing to meet the peak demand. Determination of this latter factor is complicated by the possibility of large, but off-peak, demands at other times in the same year and by the fact that the system will be in place over a number of years. The engineer might summarize these effects, however, by saying that they are represented in a cost of failing to meet the peak demand in any one arbitrary year given by 10 + (Y – z)2, if Y – z, the amount by which the pump of capacity z fails to meet a random demand of Y, is positive, and zero otherwise. Formally, for a given z > 0, the cost as a function of the random variable Y is
When z = 0, there is no initial cost—only the cost of failing to meet the demand.
For a pump of capacity 0 < z < 100, then, the expected value of the total cost C(z) can be found by using either the probability law of Y with Eq. (2.4.14) [and (2.4.15)] or the probability law of X with Eq. (2.4.31). The former path is taken here:†
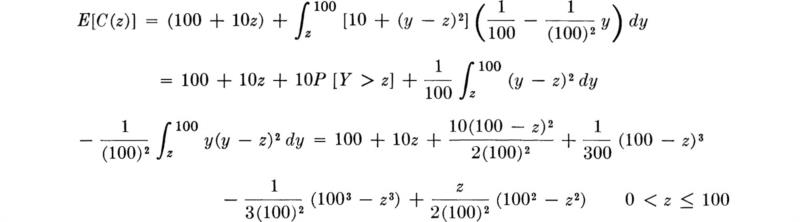
The minimum cost must occur either (1) when no pump is installed, z = 0,
or (2) when the largest peak is matched, z = 100,
or (3) at some intermediate value found by differentiating the expression above, setting it equal to zero, and solving for the optimal value z0,
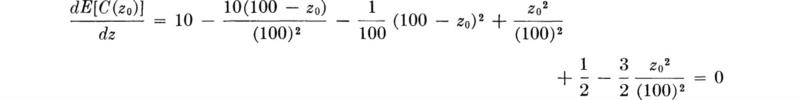
Solving,
The root of interest is
The expected cost at z = 67.5 cfs is about 883 units. (Therefore the extremum found is, in fact, a minimum and not a maximum.) Because this cost is less than the expected cost (3305) associated with the “do-nothing” (z = 0) policy, and less than the expected cost (1100) of the most conservative (z = 100) policy, the best design is to provide a pump with a capacity of 67.5 cfs.
Fig. 2.4.7 Expected cost versus pump capacity.
The other two design rules, suggesting capacities of 16.7 and 33.3 cfs, have, of course, expected costs larger than the optimum value. (In particular, the expected cost of a z = 33.3 cfs capacity decision is 1402 units.) The function E[C(z)] is plotted in Fig. 2.4.7. In words, such small-capacity designs, although cheaper initially, run a large risk of a very high penalty due to insufficient capacity. The high initial cost of a very large pump (say, 100 cfs) is apparently not justified in the light of the small likelihood of its full capacity being needed. The indicated optimum design achieves a balance between these two factors.
When two or more random variables must be dealt with simultaneously, their behavior is described by their joint probability distribution (Sec. 2.2.2). The notions of expectation are also extended easily to this situation. Owing to the difficulty in practice of dealing with entire joint distributions, analysis of the joint behavior of random variables is often restricted to their moments. Therefore this subject will be discussed in some detail.
Expectation of a function Generalizing Eqs. (2.4.13) and (2.4.14), we obtain the expectation of a function Z = g(X, Y) of two jointly distributed random variables as
if X and Y are continuous random variables, and
if they are discrete. As in the previous section it is possible but difficult to show that E[Z] calculated from the appropriate equation above is identical to that which would be obtained if, by the technique of Sec. 2.3.2, the distribution fZ(z) were first derived from that of X and Y and then the mean of Z were obtained by Eq. (2.4.2).
As before, we can distinguish between two interpretations of expectation. One looks upon E[g(X,Y)] as the average of a function of X and Y over all values x and y, weighted everywhere by the probability that X = x and Y = y. Moments fall into this category. The second interpretation sees E[g(X,Y)] as the expected value or mean of a random variable Z = g(X,Y).
Moments We have already seen that moments, examples of the “averaged function of X and Y” interpretation of E[g(X,Y)], facilitate the study of the marginal behavior of individual random variables. We shall find them of even greater value in studying the joint behavior of two random variables. Consider the function of X and Y of this form:
Then its expectation
is called a moment of order l + n of the random variables X and Y. The most important are the two first-order moments: (l = 1, n = 0) and (l = 0, n = 1). In the former case, g(X,Y) = X, and
Here we have simply the mean or expected value of X. Notice that this may be written as
The second integral is simply the marginal distribution fX(x) [Eq. (2.2.43)]; thus
which is the same definition given in Eq. (2.4.2). Thus the expected value of X, Eq. (2.4.53), is the average value of X “without regard for the value of Y.” The definition and meaning of E[Y] are, of course, similar.
It may be helpful for the civil engineer to observe that mX and mY locate the center of mass of a two-dimensional plate of variable density or the horizontal coordinates of the center of mass of the “hill” or terrain whose surface elevations are given by fX,Y(x,y). This follows from the definition of these terms and the fact that the volume under fX,Y(x,y) is unity.
By the same analogy, the second-order moments (l = 2, n = 0), (l = 0, n = 2), and (l = 1, n = 1) correspond respectively to the moment of inertia about the x axis, the moment of inertia about the y axis, and the product moment of inertia with respect to these axes.
Central moments As for a single variable, and as in mechanics, the more useful second (and higher) moments are those with respect to axes passing through the center of mass. Taking g(X,Y) equal to
we find
which is called a central moment of order l + n of the random variables X and Y. The first central moments are, of course, both zero.
The most valuable central moments are the set of second-order moments: (l = 2, n = 0), (l = 0, n = 2), and (l=1, n = 1). The first two cases, as above with the means, reduce to the marginal variances. With (l = 2, n = 0), for example,
The result for Y, (l = 0, n = 2), is similar.
Covariance The new type of second central moment that is found when joint random variables are considered is that involving their product, that is, (l = 1, n = 1). This moment also has a name, the covariance of X and Y: Cov [X,Y] or† σX,Y.
If the variances correspond to the moments of inertia about axes in the x and y direction passing through the centroid of a thin plate of variable density, then the covariance corresponds to its product moment of inertia with respect to these axes.
Correlation coefficient A normalized version of the covariance, called the correlation coefficient ρX,Y,, is found by dividing the covariance of X and Y by the product of their standard deviations:
It can be shown that this coefficient has the interesting property that
Before discussing the interpretations of the covariance and the correlation coefficient (and its bounds, ±1), let us illustrate the computation of these numbers in a simple discrete case. Consider the discrete joint distribution of X and Y sketched in Fig. 2.4.8, where the distribution might represent a discrete model of the maximum annual flows at gauge points in two different, but neighboring, streams. The engineer’s interest in their joint behavior might arise from his concern over flooding of the river which the streams feed or from his desire to estimate flow in one stream by measuring only the flow in the other.
Fig. 2.4.8 Joint PMF of stream flows.
The means and variances are found from the marginal PMF’s, or as follows:
Similarly
The covariance is found using the discrete analog of Eq. (2.4.58) or
which here becomes
The correlation coefficient pX,Y is
Fig. 2.4.9 Joint density-function contours of correlated random variables. (a) Positive correlation ρ > 0; (b) high positive correlation ρ ≈ 1; (c) negative correlation ρ < 0; (d) (e) low correlation ρ ≈ 0; (f) large negative correlation ρ ≈ – 1.
Discussion: Correlation In Fig. 2.4.9 some joint density functions are sketched and the corresponding values of the correlation coefficients are indicated. Note that the marginal distributions of X and Y remain the same from case to case. Comparing these figures with Fig. 2.2.13, it is clear that large values of ρ imply peaked conditional distributions, such as fY|X; the reverse is not necessarily true (e.g., case e). The implication is that if ρ is large, an observation of X will be very useful in refining and in reducing the uncertainty in predicting Y. Prediction will be discussed more thoroughly later (see page 175).
Examples of phenomena with large positive correlation coefficients (positively correlated random variables) include the length and weight of vehicles, and the yield strength and hardness of steels. Negatively correlated random variables include the speed and weight of vehicles, the ultimate compressive stress and ultimate compressive strain of concrete, and the capacity remaining in a dam and rainfall on its watershed for the past month. Random phenomena displaying small or zero correlation coefficients (uncorrelated random variables) are successive annual maximum floods at a site or the dead and live load on a structure.
Like the mean and variance, the correlation coefficient is often available when the complete probability law is not. This situation may result from the intractability of complete distribution calculations (Sec. 2.3), or from the lack of complete information about the variables. Rather than a well-defined joint probability law, we may have reliable estimates of only the first- and second-order moments. In this case, for example, pairs of observations from two variables may have yielded a scattering of points and an estimate of their correlation coefficient. For the proper interpretation of this number, it is important to know what it says and does not say about the joint behavior of the two variables.
First, from inspection of its definition [Eqs. (2.4.58) or (2.4.67)], the covariance (and hence the correlation coefficient) will be positive if larger than mean values of X are likely to be paired with larger than mean values of Y (and smaller with smaller). In this case the product (x – mX)(y – mY) will be positive where fX,Y(x,y) or pX,Y(x,y) is significantly large. If larger than average values of X usually appear with smaller than average values of Y (and vice versa), the covariance and correlation coefficient will be negative. In either case it can be said that at least some linkage or (stochastic) dependence exists between X and Y. This dependence may not be causal; in metals, greater hardness does not cause greater yield stresses, but the high correlation between the two characteristics is useful. It means that nondestructive hardness tests can be used to predict the strength of a piece of metal with a certain, but imperfect, reliability.
Secondly, if the two variables are independent, their covariance and correlation coefficient are zero. To verify this statement consider Eq. (2.4.58). Independence implies that fX,Y(x,y) factors into fX(x)fY(y); the integral becomes simply the product E[X – mX]E[Y – mY], both factors of which are zero. In words, if the variables are unrelated, their correlation coefficient is zero.
Unfortunately, in practice the error is often made of adopting the converse to this last statement; the third and most neglected fact about the correlation coefficient is that a small value does not imply that the X and Y are independent. Stochastic dependence (as reflected, say, by the sharpening of conditional distributions relative to marginals, Sec. 2.2.2) may be high even if ρ is zero or near zero.
More specifically, the correlation coefficient is a measure of the linear dependence between two random variables, in the following sense. An extreme value of ρ (±1) obtains if and only if there is a linear functional relationship† between X and Y, that is, if and only if Y = a + bX. Hence, if ρ is one in absolute value, an observation of X, for example, will permit a perfect prediction of Y; that is, the stochastic dependence is “perfect”—the conditional distribution of Y given X = x is simply a unit spike at y = a + bx. However, as will be demonstrated in an illustration to come, such perfect (or functional) dependence may exist, but, being nonlinear (for example, Y = aX2) may yield a small correlation coefficient. Less than functional dependence but a close (nonlinear) relationship such as indicated in Fig. 2.4.9e, can also yield a small or zero correlation coefficient. Stochastic dependence in such a case is clearly large; given a value of X = x, the conditional distribution of Y will greatly differ from its marginal distribution. But if one mistakenly concludes a lack of strong stochastic dependence from a small value of the correlation coefficient, he will not reach the proper conclusion in such cases.
In summary, given only the value of the correlation coefficient, one can conclude from a high value that the stochastic dependence is high and furthermore that X and Y have a joint linear tendency, whereas a small value implies only the weakness of a linear trend and not necessarily a weakness in stochastic dependence.
The definitions of moments may be generalized in a straightforward manner to more than two jointly distributed random variables, but the use of higher than second-order moments is seldom encountered in practice. Further discussion of moments will be postponed until they are needed.
Properties of expectation As suggested, Eq. (2.4.50) provides a more efficient way of computing the expected value of a random variable, Z = g(X,Y), than that of first finding its probability law and then finding its expectation. That is, if, in the discrete example of stream flows above, the mean of the total at the maximum flows ‡ Z = X +Y, is desired, it could be found by finding pZ (z) and then averaging. Alternatively and more simply, using Eq. (2.4.50), E[Z]
Even more simply we can make use of the easily verified linearity property of expectation
For example, in this special case,
The linearity property can be used, as in the preceeding section, to find relationships among expectations which simplify computations, or which, because they are independent of the underlying distributions, are valuable when only these expectations are known.
For example, the following relationship often simplifies covariance computation
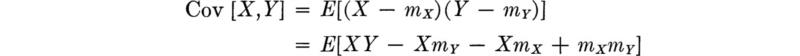
which, using the linearity property, reduces to
Illustration: Correlated demand and capacity We illustrate the use of the linearity property in situations where moments are known, but distributions are not, by the following example. If the capacity C of an engineering system and the demand upon it D are random variables, the margin M = C – D is a measure of the performance of the system, whether it be inadequate, M < 0, or “over-designed,” M large. Even if the joint distribution of C and D is unknown, the mean and variance of M can be found from first and second moments of X and Y:
which, using the linearity property, is
The variance, on the other hand, is
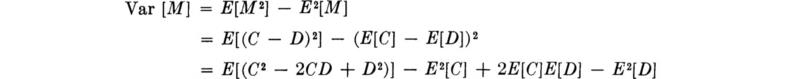
Applying the linearity property to the first term and then grouping as
we recognize that
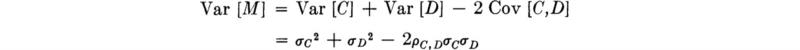
Demand and capacity may frequently be correlated. Both depend, for example, upon the average travel velocity of a highway system. Notice that if the correlation is positive, i.e., if higher than expected demand tends to occur with higher than expected capacity (as may be the case of a highway system where the better the system performs the more it is used), the variance of M is reduced from the sum of the variances. This latter value, the sum, obtains, of course, only if C and D are uncorrelated, or, in particular, if they are independent. If ρC,D = 0:
Notice that the variance of the difference between (independent) C and D is not the difference of their variances, but the sum. The uncertainty in both variables “contributes” to the dispersion in their difference.
Even though their joint distribution is not known, the second-order moments of C and D are sufficient to obtain a lower bound on the system reliability, the probability that the capacity exceeds the demand. Clearly
The probability of “failure” of the system, P[M < 0], has an upper bound given by the Chebyshev inequality [Eq. (2.4.11)] as
Hence the system reliability is at least 1 – VM2 where VM, the coefficient of variation of M, is
For example, a highway engineer, who estimates that the demand on his system 10 years hence will have a mean 1200 vehicles per hour (vph) and a standard deviation of 400 vph, might consider a design with an expected capacity of 2200 vph and standard deviation 300 vph. Assume that the correlation coefficient in such situations has been measured to be +10 percent; then
The likelihood that the capacity will exceed the demand is at least
It is assumed here that the engineer knows the moments exactly. If they are the result of estimates from small samples, there arises another order of uncertainty, that is, statistical uncertainty (Chap. 4).
Moments of linear functions The linearity property, Eq. (2.4.71), can also be employed to derive some general results for the very important case when a linear relationship among two or more jointly distributed random variables is involved. Interest lies in the variable Y, where
The expectation of Y is
The result is valid whether or not the Xi are independent. In words, the equation states that “the mean of the sum is the sum of the means.”
An analogous statement does not hold for variances unless the random variables are all uncorrelated. In general,† by carrying out the now familiar steps, we can show that
which reduces for uncorrelated random variables to, simply,
The special case for n = 2 is worth displaying if only because it appears so frequently in practice. If Z = aX + bY, then, according to the previous equation,
This equation can be verified in a manner parallel to the technique used in determining the variance of M = C – D. In fact, notice that that illustration was a special case of the result above with a = 1 and b = – 1.
Illustration: Total capacity of a system of components Some of the implications of Eq. (2.4.82) are best understood by example. Consider the relative variability and hence relative reliability of two contending systems: the first consists of two elements, the sum of whose capacities or strengths, X and Y, determines the capacity of the system; the second consists of a single element of capacity Z. A simple example is the situation where two smaller bars of ductile steel or one larger bar will be used to provide the tensile capacity of a reinforced concrete beam. Other examples include simple pipe or transportation networks. Assume that mean system capacities are, by design, equal (that is, E[Z] = E[X] + E[Y] = m) and that the mean small-element capacities are equal (E[X] = E[Y] = ½m). How do the dispersions in the two systems’ capacities compare if the coefficients of variation of X, Y, and Z are equal †? In the latter case,
while in the case of the two-element system,
Notice that if X and Y are perfectly positively correlated, ρ = 1, the variability of the system capacity is equal to that in the one element case. But under any other conditions, the two- (parallel-) element system has less variance and generally higher reliability than the system with one larger element. In particular, if X and Y are independent, the variance of X + Y is ½ of that of Z. (There is evidence that two bars from the same batch of steel may have a ρ as large as 98 percent.)
Moments of a product The general properties of expectation in one final common case deserve mention, for it is one of the few functions outside of the linear ones considered above which lends itself to such simple treatment. If Z = XY, then, from Eq. (2.4.72),
If and only if the variables are uncorrelated, the expectation of the product is the product of the expectations
If X and Y are independent, expansion will show that
and that
Illustration: Correlation versus functional dependence The correlation coefficient alone is frequently used to make deductions about the joint behavior of random variables. In many fields, particularly the biological and social sciences, where basic laws are difficult to derive otherwise, it is common to measure repeatedly two variables which are suspected or hypothesized to be related and then to estimate † their correlation coefficient. If the coefficient is near unity in absolute value, strong dependence is assumed verified; if the coefficient is low, it is concluded that one variable has little or no effect on the other.
Such techniques of verification or determination of suspected relationships are becoming more and more common in civil engineering, where many of our common materials—e.g., concrete and soil—and many of our systems—e.g., watersheds and traffic—are so complex that relationships among variables can only be determined empirically. To use such an approach correctly, it is necessary to have a sound understanding of its implications and its potential errors. The following extended illustration is designed both as an exercise in using expectation operations and as an aid to understanding the effects on the correlation coefficient caused by such factors as the character of the functional relationship and the presence of other causes of variation. It is important to appreciate the fact that the conclusions deduced from this study do not depend on the shape of the joint probability distribution. This fact demonstrates the power and generality of working with means, variances, and correlations, without detailed probability law specifications.
Suppose that an engineer is investigating the possible relationship between density of a particular highway subbase material and the road’s performance. In each of a number of segments of a road of nominally uniform design, he measures both the density of the subbase material (found in a core drilled through the pavement) and the value of some index of the segment’s performance, namely, the smoothness of the ride provided to passing vehicles. ‡ Let the random variable Y be the “ridability” or performance index and let X be the deviation of the subbase density from the specified (say, the mean) density. §
The engineer could estimate from the data the correlation coefficient, ρX,Y. Generally, a low value of this coefficient would lead him to conclude that performance (ridability) is virtually independent of subbase density. A relatively high value of ρX,Y, on the other hand, would normally cause the conclusion that subbase density strongly affects performance (and hence, perhaps, must be well controlled in future jobs, if high performance is to be obtained).
In order to understand the general validity of such conclusions, we want to presume that, in fact, a physical law or function (unknown to the engineer, of course) governs the relationship between performance Y and subbase density X. The law we shall assume is of the form
in which a, b, and c are constants and in which W is a random variable with mean zero, stochastically independent of X, and W represents the variation in Y attributable to factors other than the subbase density X. These might include such factors as settlement of the soil fill below the subbase or variations in pavement placement. Assuming the average effect of these factors is accounted for in the constant a, W need only represent the effect on Y of the random variations about the mean values of these factors. Thus the mean zero assumption is reasonable.
Calculation of the Correlation Coefficient First, as an exercise in dealing with expectation we seek the correlation coefficient ρX,Y given that Eq. (2.4.89) defines the relationship between Y, X, and the other factors. From Eq. (2.4.72),
Evaluating the first term with the use of the linearity property,
Owing to the assumed independence of W and X, E[WX] = E[W]E[X]. Since E[W] was assumed to be zero, the last term is zero. Assuming that X, the deviation from the specified subbase density, is symmetrically distributed about zero,† E[X] = 0, E[X3] = 0 and Var [X] = E[X2]. Thus
The sign of the covariance in this example depends only on the sign of b.
To find the correlation coefficient, we need the standard deviations of X and Y:
Owing to the assumptions above, many terms drop from this expression. Combining these results and grouping terms,
Simply to shorten the expression, we substitute† Var [X2] for E[X4] – E2[X2]:
Finally,
Let us concentrate on ρ 2, since it is simpler in form than ρ. Of course ρ = 0 implies ρ2 = 0 and ρ = ±1 implies ρ2 = 1; hence the same implications regarding presence or lack of dependence follow from ρ2 exactly as from ρ. Simplifying,
Note that no use has been made of integration or density functions in obtaining these results.
Values of ρ Implied by the Form of the True Law We are now prepared to use this equation to demonstrate how various conditions in the true underlying law, Eq. (2.4.89), affect the value of the correlation coefficient and hence the validity of conclusions drawn from its value. The joint density functions implied by each case are sketched in Fig. 2.4.10.
Case 1: Y = a + bX Notice first that the only way a value of ρ (or ρ2) equal to unity will be found is if b is not equal to zero but both c and σW2 are, that is, if a linear functional relationship, ‡ Y = a + bX, and hence perfect stochastic dependence, exists. Values of ρ2 less than 1 will be found in all other situations.
Case 2: Y = a + bX + W Let us look next at the case when c = 0, that is, when a linear relationship between X and Y exists, but other sources of randomness Y are present:
Then
In this case, if the variance of the other contributions to the variation in Y is relatively small, the correlation coefficient will be very nearly unity. The engineer’s conclusions, based on observing ρ ≈ 1, that strong stochastic dependence (almost a simple functional dependence) exists between X and Y would be valid. If, however, the contributions to the scatter in Y come predominantly from other factors, and/or if the functional dependence between X and Y is weak (b is small), then 
As a result the correlation coefficient will be very small. A conclusion (based on observing a small value of ρ) that there is no relationship between X and Y would not be valid, as a linear relationship does exist. But ρ does remain a good indicator of the stochastic dependence between X and Y, for this will be small too; the conditional distribution of Y given X = x will have variance σw2, very nearly as large as that of marginal distribution of Y, which is b2σX2 + σw2. In this case the random variation W, which is the result of other factors, masks the linear Y verses X relationship. The implication for field practice and betterment of performance is simply that, even though there may be a functional relationship between performance and subbase density, it is so weak or the variance of subbase density is so small that, compared with the influence of the other factors, the deviations in subbase density contribute little to the variations in performance. Hence the conclusion, based on observation of a small value of ρ2, that for nominally similar designs (i.e., same mean density) there is little effect of subgrade density on performance may be a valid one operationally.
Fig. 2.4.10 Joint density-function contours fX,Y(x,y) for various cases of a physical law governing Y and X. In cases 1 and 3, the PDF’s degenerate into “walls” which are only suggested graphically.
Case 3: Y = a + bX + cX2 Next we look at another limiting case, namely when σw2 = 0, that is, when the variation in other factors is negligible or at least has negligible effect upon performance. Now a functional relationship between X and Y exists:
and so does perfect stochastic dependence; i.e., the conditional distribution of Y given X = x is a spike of unit mass at the value a + bx + cx2. But the correlation coefficient may well prove misleading:
If the squared term dominates over the linear one, that is, if 
the correlation coefficient will be small even though dependence is perfect. In this situation an engineer’s conclusion, based on an observed small value of ρ2, that subgrade density does not significantly affect performance, would be incorrect. Subsequent action based on neglecting the existing dependence could lead to relaxing of quality control standards on subgrade construction and consequent deterioration in performance (assuming b and c are negative). In this case a plot of the data points will usually exhibit the strong functional relationship which the correlation coefficient fails to suggest. Note, on the other hand, that if the linear term predominates, i.e., if 
, the correlation will be high (but never unity) and will properly indicate strong dependence. This illustrates why it was stated that the correlation coefficient should properly be called a measure of linear dependence.† It must be pointed out that these last conclusions from the illustration depend on the assumption that E[X3] =0.† If this condition does not hold, the correlation coefficient is generally enhanced as a measure of dependence. No matter what the relative values of c and b, if additional sources of variation W also exist, they will tend to decrease ρ2 [Eq. (2.4.94)] and mask further the functional relationship between X and Y.
Spurious Correlation It is important, too, to point out another potential source of misinterpretation associated with the use of correlation studies. The discussion above revealed that small correlation does not necessarily imply weak dependence, and it is also true that spurious correlation may invite unwarranted conclusions of a cause and effect relationship between variables when, in fact, none exists. In the example here, for instance, some other variable factor, such as moisture content of the soil or volume of heavy trucks, might cause variation in both subbase density and performance. Hence higher-than-average values of density might, in fact, usually be paired with higher-than-average performance (and low with low), yielding a positive correlation that is not a result of subbase density’s beneficial effect on performance but is rather a result of both factors being increased (or decreased) by presence of the high (or low) value of the third factor. This fact does not, however, reduce the value of using an observation of one variable to help predict the other, as long as the factor causing the correlation is not altered.
Benson [1965] reported on spurious correlation and on its potential and actual presence in many civil-engineering investigations, even those which are deterministic rather than probabilistic in formulation. He cites as a particularly common source of spurious correlation that introduced by the engineer who seeks to normalize his data by dividing it by a factor which is itself a random variable. For example, correlation between X, accidents, and Y, out-of-town drivers, is not necessarily implied by correlation (observed in a number of cities) between X/Z, the number of accidents per registered vehicle, and Y/Z, the number of commuters per registered vehicle. Formally, X and Y may be independent, but X/Z and Y/Z are not, and high correlation between the latter pair does not imply correlation between the former pair. Similarly, correlation between live load per square foot and cost per square foot in structures need not imply that cost and load are dependent, because both may depend upon the normalizing factor, that is, total floor area.
Summary The correlation coefficient provides a very useful measure of dependence between variables, but the engineer must be careful in its interpretation. Large values of p2 imply strong stochastic dependence and a near-linear functional relationship, but not necessarily a cause-and-effect relationship. Small values may result from the predominance of other sources of variation (and hence low stochastic dependence), or, if a functional relationship exists, from its lack of strong linearity.
Conditional expectation and prediction† As with single random variables there is often advantage in working with expected values conditioned on some event A. In general we have
in which fX,Y|[A](x,y) is the joint conditional distribution of X and Y given the event A [for example, Eq. (2.2.58)].
The single most important application of conditional expectation is in prediction. If Y is a maximum stream flow or the peak afternoon traffic demand on a bridge, the engineer may be asked to “predict what Y will be.” To “predict Y” is to state a single number, which, in some sense, is the best prediction of what value the random variable Y will take on. Without additional information, the (marginal) mean of Y, or mY, is conventionally used to predict Y. Intuitively it is a reasonable choice. More formally it is the predictor of Y which has a minimum expected squared error (or “mean square error”). The error in predicting Y by mY is simply Y – mY. Its expected square is
or the (marginal) variance of Y. No other predictor will give a smaller mean square error. † It should be emphasized that the mean square error criterion for evaluating a predictor is simply a mathematically convenient engineering convention. More generally the engineer should use a predictor which minimizes the expected cost, the cost being some function of the error. If this cost is approximately proportional to the square of the error, whether positive or negative, then the mean square error criterion is also a minimum expected cost criterion and the mean is the best predictor. If, on the other hand, there are larger costs associated with underestimating Y than with overestimating it, the minimum cost predictor will be greater than the mean. Such economic questions are more properly treated in Chaps. 5 and 6; we restrict attention here to the conventional mean square error criterion.
Suppose now that the engineer learns that another random variable X has been observed to be some particular value, say x. The hydraulic engineer may have learned the maximum flow in a neighboring river or at an upstream point, or the traffic engineer may have learned that the morning peak flow was x = 1000 cars per hour. Conditional on this new information, what value should the engineer use to predict Y? Applying the same argument used above to the conditional distribution of Y given that X = x, one concludes that the “best” predictor of F is the conditional mean, or mY|X.
Fig. 2.4.11 Illustration of conditional means and variances of Y given X.
Note that in general this conditional mean † depends on the value x. This predictor has a mean square error equal to the conditional variance of Y given X = x:
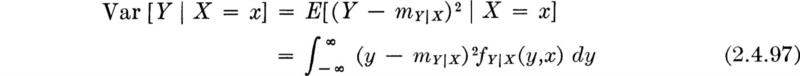
This variance is also a function of x, in general. These relationships are sketched in Fig. 2.4.11, where the square root of the mean square error (or rms) is indicated rather than the mean square error itself.
In Sec. 3.6.2 we will discuss in detail an illustration of conditional prediction applied to a particular, commonly adopted, joint distribution of X and Y. In that case we will find, upon carrying out the integrations indicated above, that
and that
We note in this special application that the predictor mY|X is linear in x and that the mean square error is a constant, independent of x. The importance, once again, of the correlation coefficient ρ is observed. For this particular joint distribution, † given X = x, the amount the conditional predictor mY|X will be altered from the (marginal) predictor mY is directly proportional to ρ. Also, the uncertainty in predicting Y given X = x (as measured by the mean square error or conditional variance) is smaller than the marginal uncertainty σY2 by an amount proportional to the square of ρ.
Illustration: Sum of a random number of random variables Conditional expectation is also valuable when studying probability models. Often moments of important variables may be difficult to determine unless one takes advantage of conditional arguments.
For example, recall that in Sec. 2.3.3 we assumed that T, the total rainfall on a watershed, was the sum of the (independent, identically distributed) random rainfalls, R1, R2, . . ., in N “rainy” weeks, where the number of rainy weeks is itself random (and independent of the Ri’s):
The estimation of the distribution of T by simulation was found to be a long numerical task. In addition, it required complete knowledge of the distribution of N and Ri. Having knowledge only of the means and variances of N and Ri, it would be desirable to be able to calculate explicitly the mean and variance of T. They are
and
The randomness in N makes a direct attack on this problem troublesome. But, given the number of rainy weeks (that is, conditional on N = n), we can apply familiar formulas [Eqs. (2.4.81a) and (2.4.81b)] for the sum of a known number of (independent) random variables:
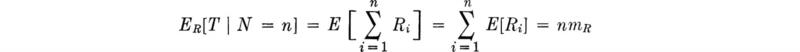
and
in which σR2 and mR are the variance and mean of any Ri. The subscript R on the expectation symbol is simply a reminder that this expectation is with respect to the R’s. Now, recognizing that N is in fact random, we have two simple functions of the random variable N:
To find E[T] and E[T2], we need simply take expectation of g1(N) and g2(N) with respect to N:
and
This implies
In words, the expected value of the sum of a random number of random variables is just the mean number times the mean of each variable. The variance of the sum is, however, larger than the mean number times the variance of each variable (as it would be if N were not random but known to equal its mean). The additional term is just the variance of the mean of each variable times N; that is,
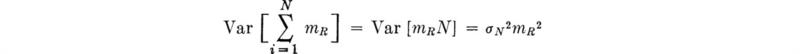
In short,
This result is intuitively satisfying but hardly easy to anticipate. It shows clearly the potential danger (or error) in oversimplifying probabilistic models. If the engineer had tried, in this case, to simplify his model either by replacing the number of rainy weeks by their average number or by replacing the rainfall in a rainy week by its mean value, he would have underestimated the uncertainty (variance) in the total rainfall. If, however, either σN2 or σR2 were small enough, the error induced by the corresponding simplification would not be significant.
It is important to appreciate that again we have been able to analyze a probability model using only means and variances. No assumptions were made in this example about the shapes of the distributions of R and N. Expectations alone were used, and this was done symbolically (or operationally) without resort to formal integration.
Approximate solutions to the problem of determining the behavior of dependent random variables are usually possible. The approximations have the advantage of always giving moments of dependent variables only in terms of functions of moments of the independent variables. As stressed before, these moments may be all that are available or all that are necessary for the engineer’s purposes. Simple approximations to the distribution of dependent random variables are also possible.
Approximate moments: Y = g(X) If the relationship Y = g(X) is sufficiently well behaved, and if the coefficient of variation of X is not large, ‡ the following approximations are valid
or
where dg(x)/dx|mx signifies the derivative of g(x) with respect to x, evaluated at mX.
If, for example, Y = a + bX + cX2, then the approximations state that
or
That the approximations are not exact can be observed by looking at the last term in Eq. (2.4.109) which should be cE[X2] or c(mX2 + σX2) or cmX2(l + VX2). Clearly if the coefficient of variation of X is less than 10 percent, the error involved in this approximation is less than 1 percent.
The justification for these approximations lies in the observation that if VX is small, X is very likely to lie close to mX and hence a Taylor-series expansion of g(X) about mX is suggested:
Keeping only the first two terms in the expansion and taking the expectation of both sides, we obtain the stated approximation for E[g(X)], since E[X – mX] = 0. Similarly, keeping the same terms and finding the variance of both sides yields the approximation in Eq. (2.4.107), since
and
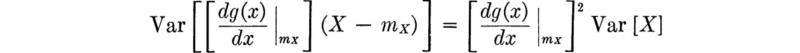
It is of course possible to increase accuracy by keeping additional terms in the expansion and by involving higher moments in the approximations. The mean is better approximated in general by using three terms of the expansion when taking expectations yields
Notice that in the quadratic case, Y = a + bX + cX2, this “approximation” is exact:
This is true, of course, because the higher-order derivatives and hence the higher-order terms of the Taylor-series expansion are all zero. In practice this second-order approximation of the mean [Eq. (2.4.113)] and the first-order approximation of the variance and standard deviation [Eqs. (2.4.107) and (2.4.108)] are commonly used, since they depend upon only the mean and variance of X.
Approximate distribution: Y = g(X) Similar reasoning can be used to find an approximate distribution for Y (at least in the region of the mean) from the Taylor expansion of Y = g(X). Keeping only the first two or the linear terms in X, we can write
which is of the linear form
Applying Eq. (2.3.15), for a continuous distribution of X,
The implication is that the approximate fY(y) has the same shape as fX(x), only stretched and shifted. In essence the technique replaces the true relationship between X and Y by the linear one associated with the tangent to g(X) at mX. Consequently one can expect that the approximate distribution will be reasonably close to the exact one at those values of y where the tangent provides a reasonable approximation to g(X). If, owing to the shape of fX(x), X is confined to lie in this same region (at least with high likelihood), the indicated distribution of Y will be a good approximation to the true fY(y) almost everywhere. A quick sketch of fX(x) and g(X) should determine if these conditions hold.
For illustration assume that Y = X2 and find the approximate distribution of fY(y) when X has the distribution
with mX = 5, by inspection. Then
and
and
Notice that the limits on the definition also must come from the approximate relationship, e.g., from y ≥ –25 + 10(4) = 15, not from y ≥ 42 = 16 to guarantee that the resulting distribution is a proper one. The true distribution, using Eq. (2.3.4), † is
This situation is sketched in Fig. 2.4.12, in a manner analogous to that used for Fig. 2.3.4. There is also shown in the figure the case where fX(x) is 
in the region 0 ≤ x ≤ 2, a region in which the nonlinearity of g(x) is more severe and where the approximate distribution is therefore less precise.
Fig. 2.4.12 Approximate distributions
Multivariate approximations Similar approximations can be made in multivariate situations. Now a multidimensional Taylor-series expansion is necessary before expectations are taken.
The second-order approximation to the expected value of
is
in which (∂2g/∂xi ∂xj)|m is the mixed second partial derivative of g(x1,x2, . . . ,xn) with respect to xi and xj evaluated at 
. The second term (which reduces to one-half the sum of the variances times the second derivatives if the Xi are uncorrelated) is negligible if the coefficients of variations of the Xi and the nonlinearity in the function are not large.
The first-order approximation to the variance of Y is
which, if the Xi are uncorrelated, is simply
Notice the form of this equation. It may be interpreted as meaning that each of the n random variables Xi contributes to the dispersion of Y in a manner proportional to its own variance Var [Xi] and proportional to a factor [(∂g/∂xi) |m]2, which is related to the sensitivity of changes in Y to changes in X. We can use this interpretation to evaluate quantitatively the common practice of using engineering judgement to simplify problems. In many cases it is sufficiently accurate to treat some of the independent variables as deterministic rather than as stochastic. This formula indicates that the effect of this action is to neglect a contribution to the variance of Y and that the simplification is a justified approximation if either the variance or the “sensitivity” factor of that variable is small enough that their product is negligible compared to the contributions of other variables in the problem. In the study of the variance of the ultimate moment capacity of reinforced-concrete beams, for example, it is found that the “most uncertain” independent variable,† namely, the ultimate concrete strength, can in practice be treated as a constant because, owing to a small “sensitivity” factor, it contributes relatively little to the variance of the ultimate moment. For similar reasons it is reasonable to treat the width of the beam as deterministic, whereas the depth to the steel reinforcement makes a major contribution to variation in the ultimate moment.
To complete the spectrum of second-order moment approximations we need the covariance between two functions, Y1 and Y2, of the X’s:
In this case,
It should be pointed out that, again, first- and second-order moments are sufficient to provide at least approximations of the same moments of functionally dependent random variables.
For example, if X1 through Xn are mutually independent, we have, generalizing Eq. (2.4.86), product
The answer based on the approximation technique is the same. Exact expressions for variances are more cumbersome (although possible), but the approximate result is simply
For n = 2,
Compare this result with the exact result, Eq. (2.4.87), which has an added term 
, which is relatively small if the coefficients of variation are small. Notice that, approximately,
This useful result, true in general for two or more variables, says that the square of the coefficient of variation of the product of uncorrelated random variables is approximately equal to the sum of the squares of the coefficients of variation of the variables. Compare this with the analogous statement for the variance of the sum of uncorrelated random variables [Eq. (2.4.81c)].
The previous results state, for illustration, that the mean force F on a body submerged in a moving fluid (a truss bar in the wind or a grillage in a stream of water, for example) is
when F = RCAS2. Here R is the density of the fluid, S is the velocity of the fluid, C is the body’s shape-dependent, empirical drag coefficient, A is its exposed area, and the variables are assumed mutually independent. The coefficient of variation of the force is approximately
The coefficient of variation of the square of S is, by definition,
which, in the light of Eqs. (2.4.106) and (2.4.108), is, approximately,
In practice, one or more of these coefficients might be sufficiently small that the corresponding variable could be treated as a deterministic constant rather than as a random variable.
Approximate distributions of functions of jointly distributed random variables can also often be found more easily than the exact distribution by using the linear part of a Taylor-series expansion and the relatively simple relationships † for the distributions of linear functions of random variables. The procedure is straightforward; no further discussion will be given here.
This section presents in detail methods of analysis of probabilistic models based on moments rather than on entire distributions. Defining the expectation E[g(X)] of a function g(X) of a random variable X as a weighted average, that is,
we recognize that the two most important cases are first and second moments, the mean of a random variable
and the variance
The standard deviation σx is the positive square root of the variance, and the coefficient of variation VX is the ratio σX/mX.
These formulas show that these expectations can be calculated by integration (or summation) if the probability law ƒx(x) is known. More important is the fact that even without knowledge of complete distributions, useful practical analysis of engineering problems can be carried out with expectations alone. Certain rules of thumb and inequalities permit probabilities to be related to these moments. Economic analyses can be based on expected costs. Owing primarily to the linearity property of the expectations operation,
moment analysis of models can often be completed with relative ease and without explicit use of integration.
In particular, this property leads to important formulas for the mean and variance of a sum of random variables. For two variables,
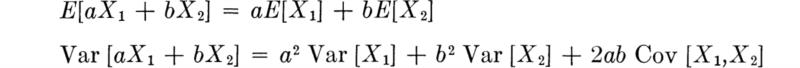
The covariance is defined as
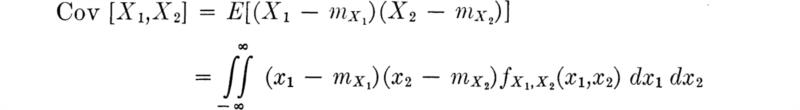
The correlation coefficient ρ is defined as
The latter coefficient is bounded between –1 and +1 and is a useful measure of linear dependence when properly interpreted.
The concept of conditional expectation and the availability of approximate expressions for moments (Sec. 2.4.4) extend the range of probabilistic models to which moment analysis can be applied without complete distribution information.
In Chap. 2 we have presented all the basic theory necessary to accomplish meaningful probabilistic analyses of engineering problems. We have defined, interpreted, and operated on the following important factors: sample spaces, events, probabilities (marginal and conditional), random variables (simple and joint), probability distributions (discrete, continuous, and mixed; marginal, joint, and conditional), random variables which are functions of random variables [Y = g(X)], expectation, and moments (marginal, joint, and conditional).
These represent the fundamental tools for construction and analysis of stochastic models. The next chapter will present a number of the most frequently encountered models. It is emphasized throughout Chap. 3 that we are merely applying there the methods of this chapter in conjunction with various sets of assumptions. These assumptions represent the engineer’s model of the physical phenomenon.
In Chap. 4 we discuss the problem of estimating the parameters of these models when presented with a limited quantity of real data. We shall find that again we are only applying the methods of Chap. 2 to a particular class of random variables called statistics. Having analyzed the probabilistic behavior (mean, variance, distribution) of a statistic, we attempt to quantify the confidence we can place on inferences about the model that are drawn from an observed value of the statistic.
Chapters 5 and 6 again apply the tools of this chapter to a particular class of problems, namely, decision making in the face of uncertainty.
Feller, W. [1957]: “An Introduction to Probability Theory and Its Applications,” vol. I, 2d ed., John Wiley & Sons, Inc., New York.
Freeman, H. [1963]: “Introduction to Statistical Inference,” Addison-Wesley Publishing Company, Inc., Reading, Mass.
Hahn, G. J. and S. S. Shapiro [1967]: “Statistical Models in Engineering,” John Wiley & Sons, Inc., New York.
Hald, A. [1952]: “Statistical Theory with Engineering Applications,” John Wiley & Sons, Inc., New York.
Hammersley, J. M. and D. C. Handscomb [1964]: “Monte Carlo Methods,” Methuen & Co., Ltd., London.
Parzen, E. [1960]: “Modern Probability Theory and Its Applications,” John Wiley & Sons, Inc., New York.
Tocher, K. D. [1963]: “The Art of Simulation,” D. Van Nostrand Company, Inc., Princeton, New Jersey.
Tribus, M. [1969]: “Rational Descriptions, Decisions, and Designs,” Pergamon Press, New York.
Von Mises, R. [1957]: “Probability, Statistics, and Truth,” 2d ed., The Macmillan Company, New York.
Wadsworth, G. P. and J. G. Bryan [I960]: “Introduction to Probability and Random Variables,” McGraw-Hill Book Company, New York.
ACI Standard Recommended Practice for Evaluation of Compression Test Results of Field Concrete (ACI Standard 214–65) [1965], American Concrete Institute, Detroit, Michigan.
Benson, M. A. [1965]: Spurious Correlation in Hydraulics and Hydrology, ASCE Proc, J. Hydraulics Div., vol. 91, no. HY4, July.
Blum, A. M. [1964]: Digital Simulation of Urban Traffic, IBM Systems J., vol. 3, no. 1, p. 41.
Esteva, L. and E. Rosenblueth [1964]: Espectros de Temblores a Distancias Moderadas y Grandes, Bol. Soc. Mex. Ing. Sismica, vol. 2, no. 1, March.
Fishburn, P. C. [1964]: “Decision and Value Theory,” John Wiley & Sons, Inc., New York.
Goldberg, J. E., J. L. Bogdanoff, and D. R. Sharpe [1964]: Response of Simple Nonlinear Systems to a Random Disturbance of the Earthquake Type, Bull Seismol. Soc. Am., vol. 54, no. 1, pp. 263–276, February.
Hognestad, E. [1951]: A Study of Combined Bending and Axial Load in Reinforced Concrete Members, Eng. Exptl. Sta. Bull., no. 399, University of Illinois.
Hufschmidt, M. and M. B. Fiering [1966]: “Simulation Techniques for Design of Water Resource Systems,” Harvard University Press, Cambridge, Miss.
Hutchinson, B. G. [1965]: The Evaluation of Pavement Structural Performance, Ph. D. thesis, Department of Civil Engineering, University of Waterloo, Waterloo, Ontario.
Rosenblueth, E. [1964]: Probabilistic Design to Resist Earthquakes, J. Eng. Mech. Div., ASCE Proc, vol. 90, paper 4090, October.
2.1. An engineer is designing a large culvert to carry the runoff from two separate areas. The quantity of water from area A may be 0, 10, 20, 30 cfs and that from B may be 0, 20, 40, 60 cfs. Sketch the sample spaces for A and B jointly and for A and B separately. Define the following events graphically on the sketches.
2.2. A warehouse floor system is to be designed to support cartons filled with canned food. The cartons are cubic in shape, 1 ft on a side and weigh 100 lb each. Consider that the cartons may be stacked to a height of 8 ft.
(a) Sketch the sample space for total weight on a square foot of floor area assuming that it is loaded by one stack of boxes. How would this sample space be changed if the area in question can be loaded by half the weight of each of two stacks of boxes?
(b) Sketch the sample space for total load on two adjacent floor areas each 1 by 1 ft, assuming that each such area supports a single stack of boxes.
(c) Define the following events on the sketches.
2.3. (a) Sketch a sample space for the following experiment. The number of vehicles on a bridge at a particular instant is going to be counted and weighed; only the total number and total weight of the vehicles are to be recorded (observed). The maximum number of vehicles which can be found is five; the maximum weight of a single vehicle is 5 tons and the minimum weight is 2 tons.
(b) Indicate on the sketch the regions corresponding to each of the following events:
2.4. (a) Sketch a sample space for the following experiment: A timber pile will be chosen from a supply of assorted lengths L, the longest of which is 60 ft. The pile will be driven into the ground in an area where the solid-rock-bearing stratum is at a variable depth D, the maximum being 60 ft.
(b) On a sequence of such sketches shade the following events:
2.5. A question of the acceptability of an existing concrete culvert to carry an anticipated flow has arisen. Records are sketchy, and the engineer assigns estimates of annual maximum flow rates and their likelihoods of occurrence (assuming that a maximum of 12 cfs is possible) as follows:
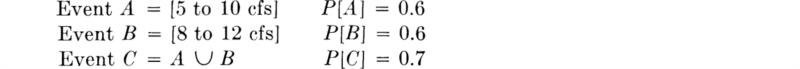
(a) Construct the sample space. Indicate events A, B, C, A ∩ C, A ∩ B, and Ac ∩Bc on the sample space.
2.6. (a) An engineer has observed that two of the designers in his office work at different rates and have a different frequency of making errors. If designer A will take 6, 7, or 8 hr to do a particular job with the possibility of 0, 1, 2 errors, sketch the sample space associated with this designer. Designer B is faster but more prone to errors. He will require 5, 6, or 7 hr and may make 0, 1, 2, 3 errors. Sketch the sample space for designer B.
If designer A is equally likely to have any one of the nine possible combinations occur, sketch the probability attributes on the sample space for A.
If designer B is twice as likely to make 1 error as either 0, 2, or 3 errors and twice as likely to require 6 hr as either 5 or 7 hr, sketch the probability attributes on the sample space for designer B. Assume independence.
(b) Sketch following events for designer A and determine probabilities.
(c) Indicate the following events for designer B on sample space and determine probabilities.
(d) Compare the probabilities of various job times for the two designers (sketch).
(e) If both designers are working at the same time on the same kind of task, can the probabilities of two 7-hr times be added to determine the probability of a 14-hr total? Why?
(f) Determine the probabilities of various total time requirements in (e) if the designers work independently. Repeat for total number of errors.
2.7. If the occurrences of earthquakes and high winds are unrelated, and if, at a particular location, the probability of a “high” wind occurring throughout any single minute is 10-5 and the probability of a “moderate” earthquake during any single minute is 10–8:
(a) Find the probability of the joint occurrence of the two events during any minute. Building codes do not require the engineer to design the building for the combined effects of these loads. Is this reasonable?
(b) Find the probability of the occurrence of one or the other or both during any minute. For rare events, i.e., events with small probabilities of occurrence, the engineer frequently assumes
Comment.
(c) If the events in succeeding minutes are mutually independent, what is the probability that there will be no moderate earthquakes in a year near this location? In 10 years? Approximate answers are acceptable.
2.8. Revise the water-supply situation (page 52) for a lateral with four tributary sites. Determine probabilities of various water demand levels. What is the optimum design size if capacity costs are linear at $500 per unit provided and enlarging costs are $1000 per unit provided? Formulate a solution for arbitrary costs if enlarging costs are double initial capacity costs and both are linear with quantity.
2.9. Find the probability that a pile will reach bedrock n ft below without hitting a rock if the probability is p that such a rock will be struck in any foot and the occurrences of rocks in different 1-ft levels are mutually independent events.
Evaluate this probability for 
and n = 10 and 20 feet, and for 
and n = 10 and 20 ft. Notice that even in the last case it is not certain that a rock will be struck.
2.10. Consider the possible failure of a water supply system to meet the demand during any given summer day.
(a) Use the equation of total probability [Eq. (2.1.12)] to determine the probability that the supply will be insufficient if the probabilities shown in the table are known.
(b) Find the probability that a demand level of 150,000 gal/day was the “cause” of the system’s failure to meet demand if an inadequate supply was observed. (Clearly the word “cause” is not appropriate in such a situation, but this interpretation of Bayes theorem is often adopted. It should be used with caution.)
(c) The likelihood of a pump failing and causing the system to fail is 0.02 regardless of the demand level. What does the equation of total probabilities reduce to in this case, that of independence?
(d) The system may fail in one and only one of three possible modes: M1, inadequate supply; M2, a pump failure; or M3, overload of the purification plant. We have the following information:
(The other probabilities are as given above.) Find the probabilities of each of the various possible causes (modes) if a system failure takes place when the demand level is 150,000 gal/day. Hint: Modify Bayes theorem [Eq. (2.1.13)] to read P[A | Bt n
in which here the Bi’s are the modes of failure, the Ci is the demand level, and A is the event a failure took place. Verify this “conditional” Bayes theorem. It can be interpreted as a Bayes-theorem application in the conditional sample space (i.e., given Ci).
(e) What are the probabilities of the various causes (modes) if the demand level at failure was 100,000 gal/day? In general, what does Bayes theorem reduce to if A can occur if and only if Bi occurs? Recognize that within the familiar deterministic, one-cause-one-effect view of phenomena, the determination of cause by observation of effect can be interpreted as just such a special case of the application of Bayes theorem.
2.11. An engineer concerned with providing a continuous water supply to a critical operation is considering installing a second “backup” pump to take the place of the primary pump in the event of its failure. Let F1 be the event that the primary pump fails once during a given period. (The likelihood of two or more such failures is negligible). Let F2 be the event that the second pump fails to function if it is switched on.
(a) What is the relationship between these events and the event F0 that the system fails to provide continuous service during the period?
(b) What is the reliability of the system 
in terms of the reliabilities of the individual pumps 
if the events F1 and F2 are independent? How does this answer compare with the reliability of a series-type system in which both components must operate simultaneously for the system to function?
(c) What is P[F0] if P[F1] = P[F2] = 10–1 and the conditions in (b) hold?
(d) If the failure of one component in a redundant system is caused by an overload, the failure of the stand-by unit will probably not be independent of the failure of the first. Generally, P[F2 | F1]> P[F2]. Find the reliability of the system above if P[F2| F1]= 2 X 10–1.
The system described here is an example of a parallel-type system, in which redundant elements are provided to reduce the likelihood of a system failure.
2.12. In the study of a storage-dam design, it is assumed that quantities can be measured sufficiently accurately in units of ¼ of the dam’s capacity. It is known from past studies that at the beginning of the first (fiscal) year the dam will be either full, ¾ full, ½ full, or ¼ full, with probabilities ⅓, ⅓, 
, and 
, respectively. During each year water is released. The amount released is ½ the capacity if at least this much is available; it is all that remains if this is less than ½ the capacity. After release, the inflow from the surrounding watershed is obtained. It is either ½ or ¼ of the dam’s capacity with probabilities ⅔ and ⅓, respectively. Inflow causing a total in excess of the capacity is spilled. Assuming independence of annual inflows, what is the probability distribution of the total amount of water at the beginning of the third year?
2.13. A large dam is being planned, and the engineer is interested in the source of fine aggregate for the concrete. A likely source near the site is rather difficult to survey accurately. From surface indications and a single test pit, the engineer believes that the magnitude of the source has the possible descriptions: 50 percent of adequate; adequate; or 150 percent of possible demand. He assigns the following probabilities of these states.
Prior to ordering a second test pit, the engineer decides that the various likelihoods of the sample’s possible indications (Z1 Z2, Z3) depend upon the (unknown) true state as follows:
What are the probabilities of observing the various events Z1, Z2, and Z3?
The second test pit is dug and the source appears adequate from this pit. Compute the posterior probabilities of state. If another test pit gives the same result, calculate the second set of posterior state probabilities. Compare prior and posterior state probabilities.
2.14. The following “urn model” has been proposed to model the occurrence (black ball) or nonoccurrence (red ball) of rainfall on successive days. There are three urns: the “initial urn” containing n1 black and m1 red balls, the “dry urn” containing n2 black and m2 red balls, and the “rainy urn” containing n3 black and m3 red balls. To simulate (sample) a sequence, one draws a ball from the initial urn, its color indicating occurrence or not of rain on the first day. The weather on the second day is found by sampling from the rainy or dry urn depending on the outcome of the first trial. Subsequent draws are made from the rainy or dry urn depending on the weather on the immediate past day. The ball is returned to its appropriate urn after each draw. The model is devised to simulate the persistence of rainy or dry spells. This is an example of what we will come to know as a Markov chain (Sec. 3.7).
Assume that all the balls in any urn are equally likely to be drawn and n1 = n2 = n3 = 10 and m1 = 70, m2 = 90, and m3 = 40.
(a) What is the probability that the first four days in a row will be observed to be rainy?
(b) What is the probability that at least three dry days will follow a rainy day? Source: E. H. Wiser [1965], Modified Markov Probability Models of Sequences of Precipitation Events, Monthly Weather Review, vol. 93, pp. 511–516. This reference contains many suggested urn models of more complicated varieties.
2.15. At a traffic signal, the number N of cars that arrive during the red-green cycle on the northbound leg has a PMF of px(n), n = 0, 1, 2, ... . At most three cars can pass through the intersection in a cycle. The engineer is disturbed by his choice of cycle times any time there is a car left at the end of the green phase.
(a) What is the probability that the engineer is disturbed with any particular cycle if at the end of the previous green phase no cars are present?
(b) What is the probability that he is “disturbed” at least twice in succession? (Assume the same zero starting conditions as in (a) at the beginning of the first of these two cycles.)
(c) Evaluate (a) and (b) if
(See Table A.2.)
2.16. A quality-control plan for the concrete in a nuclear reactor containment vessel calls for casting 6 cylinders for each batch of 10 yd3 poured and testing them as follows:
1 at 7 days
1 at 14 days
2 at 28 days
2 more at 28 days if any of first four cylinders is “inadequate”
The required strength is a function of age.
If the cylinder to be tested is chosen at random from those remaining (i. e., with equal likelihoods):
(a) What is the probability that all six will be tested if in fact one inadequate cylinder exists in the six?
(b) If the batch will be “rejected” if two or more inadequate cylinders are found, what is the likelihood that it will not be rejected given that exactly two are in fact inadequate? (Rejection will lead to more expensive coring and testing of concrete in place.)
(c). A “satisfactory” concrete batch gives rise to an inadequate cylinder with probability p = 0.1. (This value is consistent with present recommended practice.) What is the probability that there will be one or more inadequate cylinders in the six when the batch is “satisfactory”? (Assume independence of the quality of the individual cylinders.)
(d) Given that the batch is satisfactory (p = 0.1), what is the probability that the batch will be rejected? What is the probability that an unsatisfactory batch (in particular, say, p = 0.3) will not be rejected? Clearly a quality control plan wants to keep both these probabilities low, while also keeping the cost of testing small.
2.17 new transportation system has three kinds of vehicles with seating capacities 2, 4, and 8. They become available to the dispatcher at a terminal in mixed trains having from one to four cars. If each of the possible train lengths is equally likely and if the three vehicles appear independently and in equal relative frequencies, what is the probability that exactly 10 seats will be available for dispatch in an arbitrary train?
2.18. Pairwise independence does not imply mutual independence. Assume that the particular scales used in dry-batching a concrete mix are such that both aggregate and cement weights are subject to error. The two weights are measured independently. The aggregate is equally likely to be measured exactly correct or 20 pounds too large. The cement is equally likely to be measured exactly correct or 20 pounds too small. The total weight of aggregate and cement is desired. Let event A be no error in aggregate weight measurement, event B be no error in cement weight, and event C be no error in total weight.
(a) Show that the pairs of events A and B, A and C, and B and C are independent.
(b) Use (a) as a counterexample to show that pairwise independence does not imply mutual independence.
(c) Is the inverse statement true?
2.19. A major city transports water from its storage reservoir to the city via three large tunnels. During an arbitrary summer week there is a probability q that the reservoir level will be low. Owing to the occasional call to repair a tunnel or its control valves, etc., there are probabilities pi(i = 1, 2, 3) that tunnel i will be out of service during any particular week. These calls to repair particular tunnels are independent of each other and of the reservoir level.
The “safety performance” of the system (in terms of its potential ability to meet heavy emergency fire demands) in any week will be satisfactory if the reservoir level is high and if all tunnels are functioning; the performance will be poor if more than one tunnel is out of service or if the reservoir is low and any tunnel is out of service; the performance will be marginal otherwise.
(a) Define the events of interest. In particular, what events are associated with marginal performance?
(b) What is the probability that exactly one tunnel fails?
(c) What is the probability of marginal performance?
(d) What is the probability that any particular week of marginal performance will be caused by a low reservoir level rather than by a tunnel being out of service?
2.20. At a certain intersection, of all cars traveling north, the relative frequency of cars continuing in the same direction is p. The relative frequency of those turning east is q; all others turn west.
Assume that drivers behave independently of one another. A small group of n cars enters the intersection. For this group
(a) What is the marginal distribution of Y, the number of cars turning west? Find the conditional distribution of X, the number of cars turning east, given that Y equals y. Hint: what is the probability that any car not turning west will turn east?
(b) Find the joint distribution of X and Y. Be careful with the limits of validity.
(X, Y, and Z, the number going straight, have a joint “multinomial” distribution which is studied in Sec. 3.6.1.)
2.21. Two kinds of failure of reinforced-concrete beams concern the engineer: one, “the under-reinforced moment” failure, is preceded by large deflections which give warning of its imminence; the other, the “diagonal-tension or shear” failure, occurs suddenly and without warning, not permitting persons to remove the cause of the overload or to evacuate the structure.
A structural consultant has been retained to observe a suspect beam in a building. From the engineer’s experience he estimates that about 5 percent of all beams proportioned according to the building code in use at the time the building was designed will fail owing to a weakness in the shear manner, if tested to failure, while the others will fail in the moment manner. From laboratory experience, however, the engineer knows that at some load prior to failure 8 of 10 beams destined to fail in the shear manner will exhibit small characteristic diagonal cracks near their ends. On the other hand, only 1 of 10 beams which would finally fail in the moment manner shows similar cracks prior to failure.
Suppose that the relative consequences of the sudden shear failure versus warning-giving moment type of failure are such that the expensive replacement of the beam is justified only if a sudden failure is more likely than a moment failure. Then, if upon inspecting the beam, the engineer observes these characteristic diagonal cracks, should he demand the repairs or conclude that the risk is too small to justify the repairs (without further study)?
2.22. A preliminary investigation of a site leads an engineer to state that the relative weights are 3 to 5 to 2 (respectively) that the unconfined compressive strength of the soil below is 1200, 1000, or 800 psf (the only three values considered possible, for simplicity). “Undisturbed” samples of the soil will be obtained by boring and tested to gain further information. Owing to the difficulties in obtaining such samples and owing to testing inaccuracies, the following frequencies of indicated strengths are considered applicable for each specimen:
P [indicated strength | state]
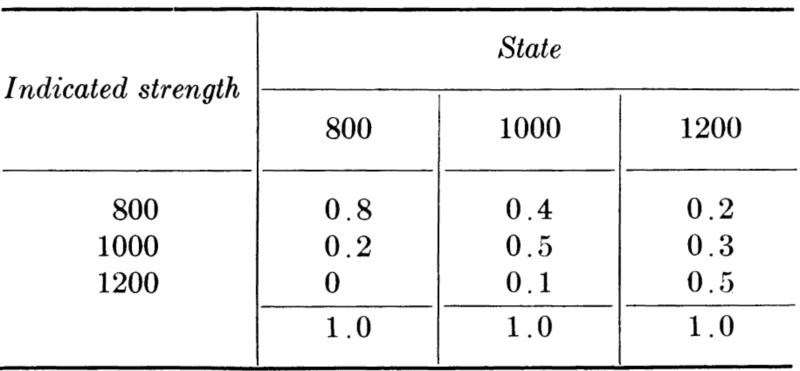
The engineer calls for a sampling plan of two independent specimens.
(a) Find the conditional probabilities of each of the possible outcomes of this sample of size two given that the true strength is 1200 psf.
(b) If the results of the sampling were one specimen indicating 1000 and one indicating 800 psf, find the engineer’s posterior probabilities of the strength.
(c) Suppose that after these two specimens the engineer continued sampling and found an uninterrupted sequence of specimens indicating 1200 psf. After how many could he stop:
(i) Confident that the strength was not actually 800?
(ii) At least “90 percent confident” that the strength was actually 1200?
2.23. Consider the following problem associated with synchronizing traffic lights. A particular traffic light has a cycle as follows:
Red = 1 min
Green = 1.5 min
Yellow =0.5 min
Some distance before this light—light 1—is another light—light 2. Owing to varying drivers and conditions, the travel time between the two varies from vehicle to vehicle. Data suggest that 40 percent of all cars leaving the location of light 2 at a time when light 1 is red are not delayed by light 1 when they reach it, 80 percent of all cars leaving light 2 during a green cycle of light 1 are not delayed, and 20 percent of all cars leaving during a yellow cycle are not delayed.
Given that a car was delayed by light 1, what is the probability that it left light 2 while light 1 was red? green? yellow?
2.24. A machine to detect improper welds in a fabricating shop detects 80 percent of all improper welds, but it also incorrectly indicates an improper weld on 5 percent of all satisfactory welds. Past experience indicates that 10 percent of all welds are improper. What is the probability that a weld which the machine indicates to be defective is in fact satisfactory?
2.25. The cost of running an engineering office is a function of office size X. Assume that an engineer is trying to make a projection of cost for the next year’s operations. He believes the demand will require an X of from 1 to 6.
(a) Cost varies with X according to:
The first term represents space and salary expense while the second term represents overhead. Find the PMF of Y.
(b) The gross income to the owner Z is jointly distributed with X:
Find the PMF of the net income:
2.26. Show that the function below is the PDF of R, the distance between the epicenter of an earthquake and the site of a dam, when the epicenter is equally likely to be at any location along a neighboring fault. You may restrict your attention to a length of the fault l that is within a distance r0 of the site because earthquakes at greater distances will have negligible effect at the site.
Sketch this function.
Fig. P2.26
2.27. A system has a certain capacity R and must meet a maximum demand L; both can be treated as nonnegative, continuous random variables, with joint density fR,L(r,l).
Write an integral expression in terms of f R,L(r,l) for the probability of failure, PF = P[R < L]. A sketch of the sample space will help. Evaluate the integral if
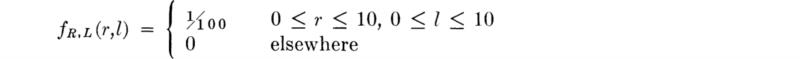
2.28. It has been found that the risk of an accident (in terms of expected number per 100 million vehicle miles) depends on the speed at which a vehicle travels. This risk is a minimum if one travels at 10 mph above the average speed a of all vehicles on the highway. In general, the risk for a vehicle traveling at a “constant” speed v is approximately
Assume that any vehicle in a particular class of vehicles (say certain commercial vehicles) travels at a “constant” speed V, which has the probability distribution (over all the vehicles in this class):
Sketch this relationship and this distribution. Find the PDF of R, the risk experienced by a vehicle from this class.
2.29. Owing to variations in raw materials, preparation, etc., the quality Y of concrete varies from batch to batch. For a batch of concrete of given quality (Y = y), a specimen taken from the batch and tested by a standard procedure (itself subject to variation) will indicate “O.K.” with probability py, some increasing function of the quality. Thus this probability P varies from batch to batch.
Assume that P has been found to have a quadratic distribution for a particular set of production and testing conditions
(a) What is the distribution of the number N of O.K. specimens in a sample of three (independent) specimens, if the quality is exactly equal to the desired quality y0 (with its associated probability p0)?
(b) Express the joint distribution of N and P.
(c) What is the distribution of the number of O.K. specimens in an arbitrary batch?
(d) What is the probability that the quality of a particular batch is less than the desired quality given that two out of three specimens were found to be O.K.?
(e) A desirable property of a quality-control plan is that it not “indicate” good quality when quality is in fact low [e.g., part (d) above]. State and demonstrate, qualitatively, ways in which this probability can be reduced, using this example. Consider both the reliability of the testing procedure and the number of specimens per sample.
2.30. Earthquakes of many sizes (magnitudes) occur. The density function of magnitudes is known to be
The design for a nuclear power plant near an active source of earthquakes will be based on the assumption that an earthquake of magnitude x0 will occur, where x0 is chosen such that P[X ≥ x0]= p. If this magnitude (x0) occurs, the structure will be designed so that uninterrupted operation will continue. To avoid a nuclear incident, however, the designer wants to design to resist collapse of the structure if some larger earthquake occurs. He wants to choose this other value x1 such that, given that an earthquake larger than x0 occurs, the probability that it will exceed x1 is again p. Find x1 in terms of x0, λ, and p (or fewer parameters, if possible). (This distribution is considered in detail in Sec. 2.2.2.) Find the conditional distribution of X given that X ≥ x0. Find the conditional mean and variance of X given that X ≥ x0.
2.31. The stress-strain relationship for a certain type of concrete has the form shown in the accompanying diagram, which can be adequately approximated by saying that strain is proportional to the square of the stress. In structural laboratories strains rather than stresses are measured. Many specimens of a structural model were tested to failure, and the strain at failure appeared to have a probability density function of the form
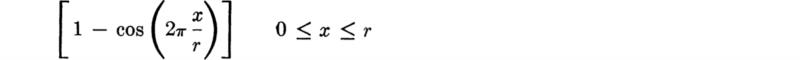
What is the form of the probability density function of the stress at failure?
Fig. P2.31
2.32. The manager of a dam is said to be following a “normal operating policy” if he releases in a year an amount of water Y, which depends on the amount of water available Z, through the relationship shown in the accompanying diagram.† In the figure c is the capacity of the dam and d is the “target outflow,” that is, the amount planned on or expected by users. Slopes are unity. (Other policies, i.e., other functional relationships between y and z, must, of course, lie between the dashed lines to be feasible.)
Fig. P2.32
(a) The amount of water available in any year is a random variable Z with a distribution given by
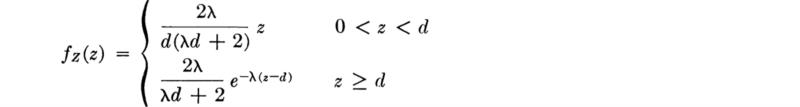
Sketch this function and show that it is a proper probability density function.
(b) Find the cumulative distribution function of Y, the amount of water released in a year, if the “normal operating policy” is followed.
2.33. An engineer states that the error X in a measurement has probability distribution in the shape of a cosine curve:
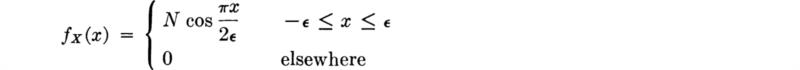
(a) Find the normalizing factor N that will make this a proper probability density function.
(b) Sketch the density function.
(c) Find and sketch FX(x).
(d) What is the probability that X is greater than 
/2?
(e) What is the probability that the error is greater than /2 in absolute magnitude?
(f) Find fX(x) from FX(x).
2.34. Probability integral transformation. Consider a random variable X with cumulative function FX(x), —∞ ≤ x ≤ ∞. Now define a new random variable U to be a particular function of X, namely,
For example, if FX(x) = 1 — e–λx, then U = 1 — e–λx = g(X). Show [at least for reasonably smooth FX(x)] that the random variable U has a constant density function on the interval 0 to 1 and is zero elsewhere. Hint: Convince yourself graphically that g(g–1(u))= u and assume that FX(x) satisfies the conditions needed to apply Eq. (2.3.3).
To illustrate this notion, sketch the FX(x) and 
for several CDF’s, including the case where X is a mixed random variable and the case where FX(x) equals a constant, say 0.5, over an interval. [These cases suggest why the definition of the inverse function 
is better stated as “smallest value of x for which F(x) is greater than or equal to u. With this definition of the inverse function, Eq. (2.3.3) will hold for any practical CDF.]
The practical importance of this, the “probability integral transformation,” lies in the fact that in simulation studies (Sec. 2.3.3) one can sample the variable X by the easier process of first sampling the variable U, finding the value u, and then calculating the corresponding value of X by
If 
cannot be evaluated explicitly, the finding of x given u can always be done graphically on a plot of FX(x) (or in a computer by “table lookup”).
For the example distribution above (with λ = 1), find the values of the random variable X corresponding to the random numbers 0.51, 0.20, and 0.98 drawn from a table. These are observations of U.
2.35. In tests on a model structure, which has been instrumented to find the maximum strain in each member caused by windstorm loadings, a number of data points have been found for X, the wind load strain in the first member. X is judged to have a gamma distribution (Sec. 3.2.3)
with parameters b = 1, c = 2. Assuming a linear model, the total stress Y is the known dead load stress y0 plus the wind load stress rX, where r is the modulus of elasticity of the material:
(a) Find fY(y).
(b) Find E[Y] two ways, using both fY(y) and fX(x).
2.36. (a) The Bernoulli distribution:
for 0 ≤ p ≤ 1. Find the mean and variance of X in terms p. For what value of p is the variance a maximum? Evaluate at p = 0.5 and 0.1.
(b) The Poisson distribution:
for λ > 0. Find the mean and standard deviation of X. Evaluate at λ = 0.5 and 2. Sketch the PMF for these cases.
(c) A triangular distribution:
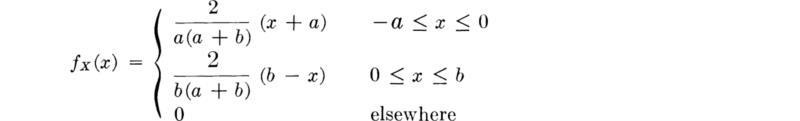
for a and b nonnegative. Find mean and standard deviation of X. It will prove simplest to make use of tables of moments of areas of simple shapes and parallel axes transformation theorems.
2.37. Owing to the gradual accumulation of strain, the likelihood (given that the last earthquake took place in year zero) of a major earthquake on a particular fault in year i grows with i. Specifically, it can perhaps be assumed that
in which a is a constant between 0 and 1.
(a). What is the probability that the first occurrence will take place in year k?
(b). What is the cumulative distribution function of X, the year of the first occurrence?
2.38. Population concentration in cities has been found to obey the law
as a function of radius r from the center. Convert the law to a PDF and find the outermost radius necessary in a public transportation network that will serve 75 percent of the residents.
Find the average distance from the center of the city of
(a) A resident
(b) A resident served by the network above
2.39. In a construction project, units are arriving at an operation which takes time or causes delay. If a unit arrives within b sec of the arrival of the previous unit, departure of the later unit will be delayed until a given time c sec after the arrival of the
Fig. P2.39
preceding object (c > b). If a unit arrives more than b sec after the previous arrival, it will be delayed until d sec (d < c) after its own arrival time. If the distribution of independent interarrival times is uniform
what is the cumulative distribution of X, the length of the interval between the time of the previous unit’s arrival and the time of the later unit’s departure? The stated functional relationship between X and T is sketched in the accompanying diagram.
2.40. Treat the accompanying table of data as the joint probability mass function of wind velocity X, and wind direction Y, at Logan Airport, Boston, Massachusetts. Assume that conditions are similar at a nearby site for a nuclear reactor. For safety studies relating to the area downwind which would be covered by a potential cloud of radioactivity released in the event of an accident and the penetration of the containment vessel, sketch the region on a sample space representation and determine
This data was obtained by observing the wind velocity and direction each hour on the hour for 10 years. Speeds indicated are middle values in recording intervals. Higher speeds than 28 occurred with negligible frequency.
2.41. Trucks of three types are being used for a long haul on a large earth-dam construction project in such proportions that the likelihood that a foreman arriving at the construction site at some arbitrary point in time observes the next arriving truck to be type A is ½, type B, ⅓, and type C, 
.† If the round-trip times for these types are the minimum trip time, 20 min, plus exponentially distributed‡ random additional times with parameters ⅓ min-1, 
min-1, and ⅛ min-1 for types A, B, and C, respectively, what is the probability that the foreman will have to wait more than 10 min beyond the minimum trip time after the first arriving truck until he sees it return a second time? Knowing the planned minimum trip time, an observed trip time exceeding this by 10 min might be a signal in an operation-control plan to start a more careful check to see if there is a systematic slowdown in the operation which needs correcting. The probability found is the likelihood that the “signal” will be made even though the operation is running as planned. Suggestion: Use the theorem of total probability, Eq. (2.1.12).
2.42. Chebyshev inequality. Show that the Chebyshev inequality, Eq. (2.4.11) holds by:
(a) Splitting the integral defining σ2 into three intervals, — ∞ to m — hσ, m — hσ to m + hσ, and m + h∞ to ∞.
(b) Showing that
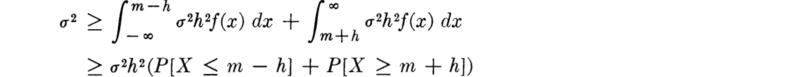
and hence that Eq. (2.4.11) holds.
If a random variable has known m equal to 5000 and known σ2 equal to (1000)2 but with unknown distribution (owing, say, to the intractable mathematics involved in its derivation), find the ranges within which the variable will lie with probabilities at least 0.5, 0.75, 0.90, and 0.99.
2.43. Law of large numbers. Find the mean and standard deviation of the random variable
when the random variables X1, X2, . . ., Xn are mutually independent, have the same means m, and the same variances a2. Notice that if the Xi represent n independent samples from the same distribution, then Y is the random variable which is the average of the observed random variables. The variance of the random variable Y decreases as n (the size of the sample) increases. Hence Y can be expected (or proved, by Chebyshev’s inequality) to be very near its mean (and the mean of all the Xi) if n is large (at least with high probability). Y appears to be a good choice as an estimate of m if this parameter is not known.
Thus no matter how small is chosen, given large enough n, the probability that the sample average Y lies within e of the mean of the random variable m can be made arbitrarily close to unity. This statement is one form of the law of large numbers.
2.44. The horizontal distance X from a given structure to the epicenter of the next large earthquake within r0 miles is distributed:
The magnitude Y of large earthquakes is distributed:
Assume that X and Y are independent. What is the probability that the next large earthquake within r0 will have a magnitude greater than 8 and that its epicenter will lie within 
of the structure?
2.45. In designing a concrete mix to meet specified “minimum strength” (ultimate compressive stress) requirements, the American Concrete Institute Code requires that the mix be designed such that the mean strength resulting is 1.5 standard deviations above the specified strength. It has been shown experimentally that the coefficient of variation of concrete strength remains almost constant when the mean is varied by adjusting the proportions—e.g., water-to-content ratio—of the mix design.
Find an expression for the required mean strength (the value the mix designer uses) in terms of the specified strength S and the coefficient of variation V.
The value of the coefficient of variation depends on the material quality, the working conditions, and the contractor’s mixing and pouring policies. All else being equal, it serves as a measure of the latter, i.e., of the contractor’s quality control, and usually remains constant from job to job. V may be as high as 20 percent for some contractors, as low as 10 percent for others. What reduction in (mean) mix design strength—and hence in material costs—can a contractor providing 5000 psi concrete (minimum specified strength) achieve if he is willing to allocate more time and men (to provide better treatment, placing, and curing of the concrete) sufficient to reduce the coefficient of variation from its present value of 15 to 10 percent?
Sketch rough bell-shaped curves for the two conditions.
2.46. The formula for the ultimate moment capacity I of a rectangular (under-reinforced) concrete comes from simple statics; that is,
in which A is the area of the ductile (elastoplastic) reinforcement, FY is the stress at which it yields, D is the depth to the center of gravity of the steel, B is the width of the beam, Fc is the ultimate compressive stress of the concrete, and K is a factor dependent upon the shape of the stress distribution on the concrete portion of the section. All might be treated as independent random variables.
Find the approximate mean and variance of M given:
Which variables “contribute” most significantly to the variance of M? What are the implications to the engineer seeking ecomonical ways to reduce the variance of M ?
2.47. Standardized variables, U = (x — mX)/σX-’
(a) Show that
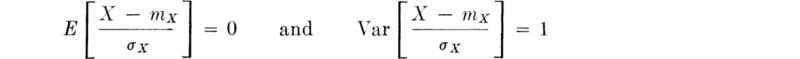
For these reasons the variable U = (X — mx)σx is called the unit, standardized, or normalized variable. Recall that the distribution of U is of exactly the same shape as that of A”. Consequently, it is commonly used to facilitate tabulating distribution functions (see Sec. 3.3.1).
(b) Show that the correlation coefficient between any two random variables A” and Z is the covariance between their corresponding standardized variables
2.48. In the determination of the strength of wooden structural members it has been suggested that the estimated strength of full-size pieces A” can be found as the product of the clear-wood strength of small, standard specimens Y, times a strength ratio R. After inspection of data, Y and R have been modeled as independent (normal, see Sec. 3.3.1) random variables. Find the mean and variance of A in terms of the corresponding moments of R and Y (see Prob. 2.52).
For construction grade Douglas Fir in bending, mR = 0.659, σR = 0.165, my = 7480 psi, and VY = 15 percent. Evaluate m and σx. How many standard deviations below the mean is the present allowable working stress of 1500 psi?
2.49. Uncorrelated variables through a linear transformation (orthogonalization). Consider two random variables X and Y, not necessarily independent.
(a) Find the covariance of Z and W when
in terms of the moments of A and Y.
(b) Find the values of the coefficients a, b, c, and d such that Z and W will be uncorrelated.
(c) If X and Y are the monthly rainfalls at two neighboring locations, then Z and W, with the coefficient properly chosen, can be considered the uncorrelated rainfalls at two “fictitious” locations. When faced with the problem of creating artificial rainfall records for water-resource systems, Hufschmidt and Fiering [1966] have suggested that the (spatially) uncorrelated records Z and W be generated as independent variables† (a relatively easy task) and that these be properly combined to obtain values X and Y for the actual (correlated) stations. What should the constants be in the equations for X and Y,
(in terms of the moments of X and Y)? Hint: find a', b', c', and d' in terms of a, b, c, and d first, by solving the pair of simulateous equations.
(d) Generate, using random numbers and the method above, a year’s record of monthly rainfalls of two stations, each with (for simplicity) independent (in time) monthly flows which have constant means m = 1 and standard deviations a = 0.25. Assume that owing to the stations’ proximity to one another, each pair of monthly rainfalls has a correlation coefficient of 0.7. Assume normal distributions.
Note: The technique is obviously easily extended to n stations. The procedure here is analogous to finding normal modes of vibration.
2.50. The cost of an operation is proportional to the square of the total time required to complete it. Completion time for the first phase is X and the second is Y. X and Y are correlated random variables with moments mX, mY, σX, σY, and ρ X,Y.
Find
2.51. Linear transformation. Sketch an arbitrary density function fX(x) and then sketch density functions for Y = a + bX for the special cases
The first three cases are particularly important; they represent the effect on changing scale or units. Cases (d) and (e) illustrate the effect of the addition of constants. Describe in words the effects on the PDF of changing units or adding constants.
2.52. Distribution and moments of a product of two random variables. The expression relating one random variable Z to two other random variables:
is very common in engineering. For example, let X be the demand and Y be the cost per unit of demand.
(a) If X and Y are independent continuous random variables, show that
and find fz(z) if
(b) Show that the variance of the product of independent random variables is
Hint: Use Eq. (2.4.25): Var [XY]= E[X2Y2]– [E[XY]]2.
(c) Evaluate the variance of Z for the PDF’s given above in two ways, using the equation in b and using the PDF of Z computed in a.
2.53. The following technique (algorithm) can be used to generate a sequence† of (pseudo) random numbers for simulation studies or other purposes.
(a) Pick arbitrarily an initial number M0, which is less than 9999 and not divisible by 2 or 5.
(b) Choose a constant multiplier M of the form
where t is any integer and r is any of the values 3, 11, 13, 19, 21, 29, 37, 53, 59, 61, 67, 69, 77, 83, 91. (A good choice of M is a value around 100.)
(c) Compute the product M1= MM0. The last four digits form the first ‘ ‘random” number.
(d) Determine successive random numbers by forming the product Mi+1 = MMi and retaining the last four digits only.
(i) Generate by hand a sequence of five random numbers and use the numbers to simulate a sequence of tosses of an unbalanced coin with the probability of “heads” equal to 0.7.
(ii) Write a computer subroutine to generate such random numbers.
2.54. The following relationships arise in the study of earthquake-resistant design, where Y is ground-motion intensity at the building site, X is the magnitude of an earthquake, and c is related to the distance between the site and center of the earthquake:
If X is exponentially distributed (Sec. 3.2.2),
Show that the cumulative distribution function of Y, FY(y), is
Sketch this distribution.
2.55. Specifications are set so that all but a fraction p of the tested specimens will be satisfactory. The number of specimens that have to be inspected before an unsatisfactory one is found is X. The additional number before the second is found is Y. Assume that X and Y are independent and geometrically distributed (as will be shown in Sec. 3.1.3):
Find the probability mass function of Z = X + Y. What is Z in words?
2.56. The amount of water lost from a dam due to evaporation during a summer is proportional to the dam’s surface area. The proportionality factor is random, depending as it does on weather conditions. For a particular reservoir with a particular cross section the surface area increases proportionately to the volume of water in storage. The water in storage during the summer (July and August) is the difference between the water made available since the previous September and the water released since that time. Both these volumes are random. Assume that the water released and the water made available during the summer are negligible. Neglecting second-order effects (e.g., the change in surface area due to the evaporation loss), find the mean and variance of the water lost due to evaporation in a summer in terms of the same moments of the various factors mentioned. Assume a lack of correlation among these factors. Define carefully all the variables, constants, moments, relationships, etc., that you use.
2.57. Reconsider the dam-operating-policy problem (Prob. 2.32).
(a) Find the expected value of Z, the water available.
(b Find the expected value of Y = g(Z), the water released.
2.58. Variability in stream flows makes it difficult to properly design the capacity of new dams. Concern is primarily with providing sufficient storage to avoid water shortage. Early studies focused on the range R, the difference between the maximum value of the impounded water and its minimum value over a period of n years, the design life of the dam. Assuming (unrealistically, but as a first approximation) that the annual “impoundments” are independent with common mean m and variance σ2, it has been shown† that (for large n)
(a) Show that the coefficient of variation of R is a constant, independent of the stream characteristics m and σ and of the lifetime n.
(b) A possible dam design rule is to design for a range of value r0 = mR + kσR, where k depends on the risk level adopted. For k = 2 how many times the mean range is the design value? How many of (the infinite number of) moments of the annual impoundment does the design range depend on? Is design for an infinite lifetime possible? How sensitive to the design lifetime is the design range? (For example, if n is doubled from 50 to 100 years, what is the increase in the design range?) Data suggests that the exponent on n for mR should be 0.72, which is presumably an influence of correlation.†
2.59. A proposed set of dam-operating policies ‡ can be characterized by this (continuity) equation relating the reservoir storage at the end of the (i + l)th time interval Si+1 to the storage at the end of the previous interval Si:
in which Xi+1 is the inflow during the (i + l)th interval and d is the “target” draft (the “desired” amount of release) in any interval. The policy parameter a (0 ≤ a ≤ 1) reflects the importance of carrying over water from one interval to the next. If a = 0, Si+1 = 0 and there is no carryover; if a = 1, the policy is the “normal release policy” (Prob. 2.32) (if, as we shall do, one neglects the possibility of the available water in any year being less than d or more than d + c, where c is the dam’s capacity).
Assume that the inflows are uncorrelated with common mean mX and variance 
Our concern is to calculate the corresponding moments of the storage S and the release or draft Y.
(a) Show that the mean and variance of the reservoir storage in any year (along time after the initial year) are
Hint: the Si’s are not independent. Write an expression for Si in terms of the independent Xi’s and take the limit as i becomes large. Check that ms and 
(valid presumably for both Si and Si+1 since the moments prove to be independent of i) satisfy the equations found by taking the expectation and variance, respectively, of both sides of the continuity equation. Discuss the design implication of the variance for the “normal release policy,” a = 1.
(b) Show that the mean and variance of Y, the release in any year (substantially after the first year), are
Hint: Show first that Yi+1 = (1 - a)(Xi+1 + Si) + ad.
Discuss the implications. If my were any other value, what would the implications be? How do you explain the variance under the limiting cases, a = 0 and a = 1?
(c) Show that the coefficient of correlation between Si and Si+1 is a. Discuss this result for the limiting cases, in terms of one’s ability to predict Si+1 given Si.
(d) In the light of our assumption that we neglect the possibility of the available water being very small or very large, discuss the conditions of target draft and dam capacity for which the results above are valid. Qualitatively, for a = 1, how would you expect these results to change if either or both restrictions were dropped? Hint: See the sketch in Prob. 2.32. You can easily prove to yourself that the continuity equation we have adopted implies (for a = 1) that our operating policy is y = d for all z, which may not be feasible.
2.60. The relationship below is often used in water-resources projects to relate short-term benefits U to the amount of water released in any year F.† (d is the announced or “target” release; see Prob. 2.32.)
(a) Find the annual expected benefits if the annual release Y has a uniform distribution on the interval d/2 to 2d.
(b) Find the annual expected benefits when the annual release Y is related to the available water Z by the “normal operating policy,” and when Z has the distribution given in Prob. 2.32. Hint: If you do not have available the distribution of Y (asked for in part (b) of Prob. 2.32) instead construct first a functional relationship between U and Z.
Fig. P2.60
2.61. For a given target release d, the short-term benefits U of a dam release Y are shown in the sketch with Prob. 2.60. If the planned or target release were increased, however, long-term benefits associated with increased downstream development (more irrigation, etc.) could accrue. In other words, the value v associated with a release equal to the target value (see sketch in Prob. 2.60) is itself an increasing function of d, the target release. The combined result can be shown as indicated for two particular target values d1 and d2.
Fig. P2.61
For a given capacity dam, assume that the distribution of F, the annual release, is independent of d, the target release. The designer’s problem is to choose that target release 
. Show that the value of d that maximizes the expected annual benefits is that value 
such that†
In short, the optimal target value 
is the value that divides the density function of Y into two areas (f – h)/(g – h) to the left and (g – f)/(g – h) to the right.
2.62. Moment generating and characteristic functions. The expectations of two particular functions g(X) of random variables are of great value. They are
and
in which i is the imaginary number 
. The expectations of these functions have special names and properties. The moment generating junction (mgf) is defined, here for continuous variables, as
and the characteristic function (cf) as
(a) Show that these functions (integral transforms) can be used as “moment generators.” In particular, show that
(b) Show that
(c) Show that for independent random variables X1 and X2 the moment generating function and characteristic function of Y = X1 + X2 are
These simple relationships among mgf and cf of independent random variables and their sums explains these functions’ great utility in modern probability theory and mathematical statistics.
Although often difficult in practice, it is theoretically possible to transform 
back into fY(y). At a minimum the moments of Y are easily made available through 
Hint: Because of the assumptions on convergence, the operations of differentiation and expectation (integration) can be interchanged quite freely.
The student familiar with transform techniques in applied mathematics will recognize these transforms and their relationships when he recalls Eq. (2.3.43). We will not explore these transforms as they might be in the remainder of the text, since most students are not familiar with their use.
(d) Find the moment generating function and characteristic function of the random variable R in the illustration in Sec. 2.3.3:
Use these functions to find four moments of the variable. Hint: In performing the integrations, one can assume u < 2. Since after differentiation the functions will only be evaluated at u = 0, there is no problem with convergence of the integrals.
2.63. You are performing some computations on the computer which involve a Monte Carlo evaluation of a particular integral. From experience you know that the running time for evaluation of the integral with a variety of data can be described by the negative exponential distribution
Total running time of the program can be estimated from the relation
(a) If λ = 3, what is the density function describing the behavior of program running time?
(b) Set up at least two expressions for the expected value of the program running time. At least three are possible.
(c) Use the more convenient expression to evaluate the expected value.
2.64. In the very preliminary planning of some harbor island developments, there was discussion regarding the cost estimates of building four bridges. There had as yet not been a preliminary soil survey in the harbor area, and it was recognized that the bridge costs are highly dependent on soil conditions. Therefore there was great uncertainty in the preliminary cost estimates. A spokesman, however, made this statement; “I recognize the uncertainty in the cost estimate of any bridge. But I am much more confident of our estimate for the total cost of all four bridges because of the likelihood that a high estimate on one will be balanced by a low estimate on another”
Discuss this statement. Use your knowledge, simply, of the means and variances of sums of random variables to support your comments. If your initial intuition lies with that of the spokesman, be sure you resolve in your own mind why it is inconsistent. Compare both the variance and the coefficients of variation of the total cost versus those of an individual cost.
If the four bridge sites are relatively close to one another, soil conditions, although unknown, are probably similar. What implications does this observation have for your analysis?
2.65 A total cost of earthwork on a road construction project will be the total number of cubic yards excavated Y times the contractor’s unit bid price P. If the mean and variance of the former are 100,000 yd3 and 10 X 106 (yd3)2, and the mean and variance of P are 6 $/yd3 and 0.25 ($/yd3)2, respectively, find the expected value and variance of the total cost, assuming that Y and P are independent. Compare with the approximate values in Sec. 2.4.4. See Prob. 2.52.
2.66. System reliability. A major application of probability has been in the determination of the reliability of systems made up of components whose reliabilities are known. (This reliability of a component is the probability that it will function properly throughout the period of interest.) Simple block diagrams are helpful in demonstrating how system performance depends on component performance.
(a) Series system. For example, if a system will perform only if each and every component proves reliable, then the block diagram will be chainlike:
Fig. P2.66a
If the events Ci = [component i performs satisfactorily] are independent, show in terms of relationships among the events Ci that
if pi is the probability of 
and (1 – ps) is the reliability of the total system.
(b) Parallel redundant system. If the system will perform satisfactorily if any one of the components “survives,” the block diagram is
Fig. P2.66b
For independent events Ci, show that the system reliability is
(c) Mixed systems. For a system indicated thus:
Fig. P2.66c
show that the system reliability, 1 – ps, is
for independent events Ci. Note that at the cost of an additional redundant component, number 3, this system is more reliable than this simpler one.
Fig. P2.66d
(d) Examples. Nuclear power plants, which depend on the functioning of many components, are designed with numerous redundancies. Assume, for simplicity, that during a particular, major, design level of earthquake intensity, the controlled shutdown of the reactor depends on the proper functioning of the control system, the cooling system, and the primary containment vessel. Assume that there are three redundant control systems, two redundant cooling systems, and a single, steel primary containment with two critical necessary components A and B. Block model the system and calculate the system reliability with respect to shutdown, in terms of component reliabilities. Assume independence of component performances (at the given earthquake level).
There will be no major accident if either the shutdown is controlled or the reinforced-concrete secondary containment vessel performs properly. Model the total system with respect to major accident reliability.
(e) Component dependence. Recalculate the system reliability in part (c) if the conditional probability of satisfactory performance of component 3 given failure of component 2 is only 
.
Dependence of component performance events is often introduced by the systems environment or demand. If a large, random demand on the system is the cause of the failure of component 2, it is likely to cause failure of component 3 also.
Reconsider, for example, part (d), assuming now that the level of the earthquake intensity is uncertain [not a given level as it was in (d)]. Then, given an earthquake occurrence of uncertain level, the reliability of, say, the secondary containment given failure of the primary vessel may be substantially smaller than the (marginal) reliability of the secondary containment. In the marginal analysis a whole spectrum of possible earthquakes intensities had to be incorporated in the analysis. Failure of the primary vessel suggests that a large intensity has probably occurred. Conditional on this information, the reliability of the secondary containment must be smaller.
2.67. In evaluating the consolidation settlement of the foundations of new buildings, it is necessary to predict the sustained column loads that are transmitted to the footing. We consider here only the sustained live loads.
Let the load on a particular column due to floor i be:
and that due to floor j be :
in which a is the tributary area. B is a random variable with a mean mB that is equal to the average unit load over all buildings of this prescribed type of use (e.g., offices), and a variance 
, that is equal to the variance of mean (over the building) building loads from building to building. Si and Sj are random variables with zero mean representing the spatial variation of load within a given building. They both have variance 
. B and the S’s are uncorrelated.
(a) What are the mean and variance of the total (sustained live) load transmitted to a footing by a column supporting n such floors?
(b) For σB = 2σS and for σB = ½σs, sketch a plot of the coefficient of variation of this total load versus n.
(c) What is the correlation coefficient between Lt- and Lj?
(d) What is the “partial correlation coefficient between Li and Lj, given that B = b0? This coefficient is defined in the usual way, except that the expectations are conditional on B = bQ. This coefficient appears again in Sec. 4.3.1.
2.68. A storage reservoir is supplied with water at a constant rate k for a period of time Y. Then water is drawn from it at the same rate for a period of time X. X and Y are independent, with distributions
(Assume that the reservoir is infinitely large and contains an infinite amount of water so that it cannot run dry or overflow.)
What are the probability density functions of Z = Y – X and of W = k(Y – X), the change of the amount of water in the reservoir after one such cycle of inflow and outflow?
2.69. Hazard functions. If an engineering system is subjected to a random environment, its reliability can be defined in terms of the random variable T, the time to failure, since the reliability of the system during a planned lifetime of t0 is simply
Reliability (t0) = P[no failure before t0] = P[T > t0] = 1 – F(t0)
The hazard function h(t) is defined such that h(t) dt is the probability that the failure will occur in the time interval t to t + dt given that no failure occurred prior to time t.
(a) Show that
Its shape determines, for example, whether a system deteriorates with age or wear (i.e., if h(t) grows with time).
(b) Show that the probability distribution of T, given a (“well-behaved,” continuous) hazard function h(t), is
in which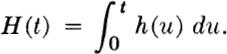 
(c) Show that if the time to failure has an exponential distribution,
then the hazard function is a constant. In Sec. 3.2 we will call such conditions “random” or Poisson failure events, and ν is their average rate of arrival. It is a commonly adopted assumption in reliability analysis.
(d) Find the distribution of the time to failure T of a system which is exposed to two independent kinds of hazard, one due to random occurrences of “rare events” (e.g., earthquakes) and one due to wearout or deterioration (e.g., fatigue). The rare events occur with average annual rate v. The hazard due to wearout is negligible at time zero, but it grows linearly with time. At time t = 10 years it is equal to that due to rare events. Justify why the total hazard function is just the sum of the two hazard functions. What is the reliability of the system if it is desired that it operate for 20 years?
2.70. In simple frame structures (with rigid floors) such as the one shown in the diagram, the total deformation of the top story Y is simply the sum of the deformations of the individual stories X1 and X2, acting independently. These variables are uncorrelated and have mean and variance m1 and 
, m2 and 
, respectively.
(a). Find the mean and variance of Y.
(b). Find the correlation coefficient between Y and X2. Discuss the results in terms of very large relative values of the moments (m1, m2, σ1, and σ2), for example, σ2 much larger than σ1, and vice versa.
Fig. P2.70
(c) Find the correlation coefficient between Y and X2 if X1 and X2 are not uncorrelated, but have a positive correlation coefficient p, owing, say, to the common source of material and common constructor.
2.71. Tests on full-scale reinforced-concrete-bearing walls indicate that the deflection of such a wall under a given horizontal load is a random variable. The form of the distribution of the variable is
in which c = λk(k – 1)! for k integer. It has mean k/λ and variance k/λ2. Different wall dimensions and different concrete properties will change the values of the parameters k and λ.
In a small two-story building the deflection Y of the roof will be the sum of the deflection of the first-story wall X and the deflection of the second-story wall X2. X1 and X2 are assumed to be independent. Find the probability density function of Y if
2.72. A harbor breakwater is made of massive tanks which are floated into place over a shallow trench scraped out of the harbor floor and then filled with sand. There is concern over the possibility of breakwater sliding under the lateral pressure of a large wave in a major storm. It is difficult to predict the lateral sliding capacity of such a system. What is the reliability (the probability of satisfactory performance) of this system with respect to sliding if the engineer judges the following?
(a) That the sliding resistance has a value 100, 120, or 140 units, with the middle value twice as likely as the low value and twice as likely as the high value.
(b) That the lateral force under the largest wave in the economic lifetime of the breakwater X, has an exponential distribution with parameter λ = 0.02; that is,
The units of sliding resistance and lateral force are the same. Resistance and force are independent.
2.73. In planning a building, the number of elevators is chosen on a basis of balancing initial costs versus the expected delay times of the users. These delays are closely related to the number of stops the elevator makes on a trip. If an elevator runs full (n people) and there are k floors, we want to find the expected number of stops R the elevator makes on any trip. Assuming that the passengers act independently and that any passenger chooses a floor with equal probability 1/k, show that
Hint: It is often useful to define “indicator random variables” as follows. Let Xi = 1 if the elevator stops at floor i, and 0 if it does not. Then observe that k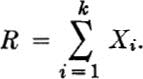 
Find the expected value of Xi after finding first the probability that
2.74. The peak annual wind velocity Xi in any year i at a certain site is often assumed to have a distribution of the form
Peak annual wind velocities in different years are independent.
The pseudostatic force on an object subjected to the wind is proportional to the square of the wind velocity: force = c(velocity)2. Find the probability density function of Y, the maximum force on an object over a period of n years.
2.75. The flooding (peak-flow) potential of a rain storm (defined here to be a ½-day period with more than 2 hr of rainfall) depends on both the total rainfall Y and the duration X. Available data in a particular region suggests that the PDF of X is approximately:
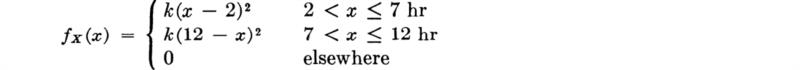
(a) Find k and sketch this PDF.
(b) The conditional distribution of the total rainfall F, given that the duration X equals x hr, is uniformly distributed on the interval ½x – 1 to ½x + 2 in.:
What is the joint distribution of X and Y? Sketch it.
(c) “High” flow rates will occur if the rate of rainfall during the total storm exceeds ⅔ in./hr. What fraction of storms cause “high” flow rates?
† If A is the certain event, i.e., if A is the collection of all sample points in the sample space S, the complement Ac of event A will be the null event; i.e., it will contain no sample points.
‡ The square brackets [ ] should be read “the event that.”
† P[A] is read “the probability of the event A.”
‡ Upon returning in Sec. 2.2 to continuous sample spaces, where the number of sample points is infinite, we shall not assign probabilities to specific points but to small lengths or areas. Then the integral (sum) over all these regions in the sample space must be unity.
† Such figures, which exploit the analogy between the algebra of events and the areas in a plane, are called Venn diagrams. They can be most helpful in visualizing event relationships, but it is important to realize that these diagrams cannot illustrate relationships among numbers, that is, the probabilities of events.
† Notice that the calculation of P[W2 | E10] on page 48, which is based on the client’s four probability estimates, contradicts this assumption, for P[W2 | E10] = 0.86 does not equal P[W2] = 0.8. Hence, using the client’s probabilities, the events are not independent. The engineer, on the other hand, has assumed independence, and has estimated only P[E5] and P[W1], and calculates the remaining probabilities of interest. The assumption of independence reduces the number of numerical estimates necessary to describe the phenomenon completely.
† In that chapter we shall find that, in general, decisions should be based on utilities, which may or may not coincide with dollars.
† This and subsequent sections and illustrations marked with a dagger may be omitted at first reading since they are of a more advanced nature.
‡ This example is based on the treatment developed in M. A. Benson and N. C. Matalas [1965], The Effects of Floods and Obsolescence on Bridge Life, Proc. ASCE, J. Highway Div., HW1, vol. 91, January.
† The engineering reader should take special care to read these equations in terms of their event definitions. The following equation, for example, states that the probability of neither a critical flood nor obsolescence in the first year is the probability that no flood occurs multiplied by the probability that no obsolescence occurs. In the more involved equations to follow, understanding will usually come more quickly in this way than through abstract symbols.
† This concept is discussed in detail in Sec. 3.1.
† Note that P[Ai | B400] is undefined, since P[B400] = 0 [see Eq (2.1.4a)].
† Since concrete strength increases with time, a strength of, say, 3500 psi now suggests that the 28-day strength (which is used as a design standard) was probably about 3000 psi.
† Unless, of course, the engineer excluded their possibility at the outset by setting their prior probabilities to zero.
† More precisely, a random variable is a function denned on the sample space of the experiment. It assigns a numerical value to every possible outcome. (See, for example, Parzen [I960].)
‡ In general a capital letter will be used for a random variable, and the same letter, in lowercase, will represent the values which it may take on.
† Two alternate ways of specifying a probability law—moment-generating and characteristic functions—are discussed in Prob. 2.62, but will not be used in this text.
† As will be seen, this does not imply that the random variable must take on values over the entire axis. Intervals, such as the negative range, for example, can be excluded (i.e., assigned zero probability).
† This line will usually be omitted, the PDF (or PMF or CDF) being tacitly defined as equal to zero in regions where it is not specifically defined (except that the CDF is 1 for values of the argument larger than the indicated range).
† These functions are zero everywhere except at a single point where they are infinite, although the integral under the “curve” is finite. They are analogous to the concentrated load, pure impulse, or infinite source employed elsewhere in civil engineering.
‡ Notice that in general some care must be taken with the inequalities. If a jump does not occur in FX(x) at x, then the inequalities (≤ and ≥) and strict inequalities (< and >) may be interchanged freely without altering the value of the right-hand side of the equation. This is always the case if X is a continuous random variable.
† Additional comment is made in Secs. 2.3.3, 3.3.1, and 3.5.3 on this particular runoff problem.
† A more commonly adopted distribution for maximum wind velocities will be discussed in Sec. 3.3.3.
† Note that for continuous random variables, GX(x) = P[X ≥ x] and for discrete random variables, GX(x) = P[X > x].
† As mentioned in Sec. 2.2.1, the reader should remember that the engineer’s mathematical model is conceptually different in kind from observed data, histograms, scattergrams, observed relative frequencies, and the like. In situations such as this, however, it may be quite reasonable simply to adopt a model with probability assignments equal in numerical value to previously observed relative frequencies.
† The theoretical difficulties here revolve around the fact that the probability that Y takes on any specific value is zero. See, for example, Parzen [I960].
† Only continuous random variables are illustrated here, but in fact continuous, discrete, and mixed random variables might well appear simultaneously as jointly distributed random variables.
‡ Although rare in practice, the reader should be aware that pairwise independence of random variables (for example, X and Y, X and Z, and Y and Z) does not necessarily imply mutual independence (X, Y, and Z). Problem 2.18 demonstrates the parallel fact for events.
† It is important not to confuse the notions of functional dependence (the more familiar) and stochastic or probabilistic dependence (Secs. 2.1.3 and 2.2.2). The first implies the second, but the converse is not true. In fact, functional dependence can be thought of as “perfect” stochastic dependence. If Y is functionally related to X by the equation Y = g(X), the conditional distribution of Y given that X = x is a unit mass at y = g(x) and zero elsewhere (assuming g(x) is single valued). That is, if there is functional dependence, the joint probability density contours (Fig. 2.2.13) “squeeze” together and merge into the line y= g(x).
† Such a function is said to be a “monotonically increasing” function.
‡ Such a function is said to express a “one-to-one” transformation between the variables x and y. Note, for example, that the relationship between X and Y in the preceding dispatching example is not one-to-one. Y = 2 could result from X equal to either 4 or 5.
† This is a confusing, but standard, notation consistent with sin–1 (u) for the arcsine or inverse sine function. In general, g–1(u) does not equal 1/g(u).
‡ An additional restriction, continuity of y = g(x), is also necessary for this next step.
† This result is true on the average. In fact, for any given time T = t, the population Q may better be considered a random variable. Such a model is an example of a random function of t or a “stochastic process.’’ Note that the population size, actually an integer number, is being treated for convenience as a continuous variable, since it is a large number.
† For example, this is a common engineering assumption in the case where X and Y represent the largest river flows in each of 2 successive years.
† For a discussion of this question see, for example, Rosenblueth [1964].
‡ This problem is considered in Esteva and Rosenblueth [1964]. For Southern California it has been found empirically that c1 = ln 280/ln 2, c2 = 1/ln 2, and c3 = 1.7/ln 2 with R in kilometers. This empirical relationship is not valid for small values of r (less than about 40 km), but it will be retained here for simplicity.
† The reader is referred, however, to any of several texts (e.g., Freeman [1963], page 82) for a particularly efficient technique for obtaining the joint PDF of n random variables which are (simultaneous) functions of n other jointly distributed random variables whose PDF is known; the method applies to the case where the functional relationship is one-to-one and continuous. It is sometimes called the method of Jacobeans. Equation (2.3.12) is a special case when n = 1.
‡ This section can be omitted at first reading.
§ It should be noted that probabilistic Monte Carlo methods are also used to evaluate multidimensional integrals which arise from problems which are not probabilistic at all. (See Hammersly and Hanscomb [I960].)
¶ There is a negligible error here; as described, 
pN(n) does not equal 1 unless n = 1, 2, . . ., ∞. See Sec. 3.2, where the distribution will be introduced as the “Poisson distribution.” The total probability mass of the neglected terms is small in this case.
† One of many schemes is described in Prob. 2.53.
† Or better, some kind of average value, say the centroid of the area under the probability density curve.
† There can be as many intervals as there are members in the set of random numbers from which the generator is selecting, and this number is indefinitely large, since successive one-digit numbers can always be strung together to make higher-order numbers. If decimal fractions between 0 and 1 (obtained by dividing the random number by the total number members in the set) are employed, in the limit one obtains a continuous, uniform distribution of the random numbers on the interval 0 to 1.
† This method implicitly makes use of the so-called “probability integral transform,” Prob. 2.34.
† As we shall see in Chap. 4, the sample mean and sample variance (Sec. 1.2) also have significance with respect to the random variable T. They are estimates of the first two moments (Sec. 2.4.1) of T.
† For a more formal statement of this, the law of large numbers, see Prob. 2.43.
† These two descriptors of a random variable, namely, the “most probable” value, that at the peak of its PDF, and the “midpoint,” the value of x at which the CDF equals ½, are known, respectively, as the mode and the median. They are only seldom used (see Sec. 3.3.2 for one use) and will not be considered further here. Clearly the mean, mode, and median coincide if a distribution has a single peak and is symmetrical. Note, however, that neither mode nor median may have a unique value for some distributions.
‡ This notion can be made more explicit through the law of large numbers, Prob. 2.43.
† In the analysis and development of models, on the contrary, the variance is a more fundamental notion and also is easier to work with, as will be seen in subsequent sections.
† Since negative values are not meaningful in this problem, the lower two-sigma bound on this variable is given as 0 rather than –233.
‡ The proof of this inequality is elementary and is outlined in a hint to Prob. 2.42.
† If only these first two conditions are assumed, for example, h2 can be replaced by 2.25h2 in Eq. (2.4.11) (Freeman [1963]).
† No proof will be attempted here. It is hoped that the student can mentally generalize upon the discrete example which is to follow well enough to convince himself of the plausibility of the result.
‡ The expectation is said to “exist” if and only if the integral in Eq. (2.4.14) is absolutely convergent, that is, if 
§ In this section, subsequent definitions will be stated only in terms of continuous random variables. The extension to the discrete case will be obvious.
† (γ2 – 3) is called the coefficient of excess. The value of 3 is chosen only because it is the value of the kurtosis coefficient of a particular, commonly used distribution (see Sec. 3.3.1).
† This is true unless one employs Dirac delta functions, as suggested in Sec. 2.2.1.
† Despite the superficial appearance of linear and quadratic relationships, g1(X) and g2(y), and the implication that the mean and variance of X would suffice to determine E[C], it should be noted that in fact these functions are not linear or quadratic owing to their varying definitions over various ranges (see Fig. 2.4.6b).
† If X and Y have the same dimensions, the dimensions of σX,Y are the same as those of 
; nonetheless convention dictates the notation σX,Y rather than 
† One side of this contention is easily verified by assuming that Y = a + bX and showing that ρ = 1 for b > 0 and – 1 for b < 0. The other side, that ρ = +1 implies Y = a + bX, is demonstrated in Freeman [1963].
‡ To be conservative, the engineer might assume that the maximum flows always occur simultaneously, when Z = X + Y would be the maximum flow in the confluence of the two streams.
† The variance of Y is the sum of the terms in the n × n array of covariances, but owing to the symmetry, that is, Cov [Xi,Xj] = Cov [Xj,Xi] and to the fact that the diagonal terms are the variances, that is, Cov [Xi,Xj] = Var [Xi], the sum reduces to the form shown.
† The coefficients of variation will be equal in the bar-strength case if each yield force is the product of bar area and yield stress, with all stochastic variation being in the latter. The doubling in mean strength from X to Z is obtained by doubling the bar area, which also doubles the standard deviation.
† Estimation of moments from data is a subject of Chap. 4.
‡ Such indices are normally highly subjective, but more objective techniques, including statistical ones, are possible and are under investigation (see Hutchinson [1965]).
§ This definition of X as the deviation about the mean of the subbase density is for algebraic convenience only. The density is Z = mZ + X. Clearly σZ2 = σX2, and it is easily shown that ρZ,Y= ρX,Y. Later assumptions will be interpreted in terms of Z as well as X.
† This is equivalent to assuming that Z, the subbase density itself, is symmetrically distributed about its mean mZ.
† In terms of 
. Note that Eq. (2.4.92) could have been obtained directly from Eq. (2.4.89) using Eq. (2.4.81c), since, interestingly, X and U = X2 are uncorrected random variables (if E[X] and E[X3] are zero). The reader can verify this in one line.
‡ A linear functional relationship between Y and X implies that a linear form also relates Y and Z; Y = a + bX = a + bmZ + bZ.
† Notice that if c were much greater than b and this strong parabolic relationship were suspected by the engineer, he could estimate the correlation coefficient between Y and U = X2. Then a strong linear dependence between Y and U would exist and a large correlation coefficient ρY,U would be found. Note, however, that 
implying that Y = a + cX2 does not imply that Y = a′ + c′Z2. The latter relationship contains a linear term in X: Y = a′ + c′mz2 + c′2mzX + c′X2.
† That is, μz(3) = 0, which holds if Z is symmetrically distributed.
† This material may be bypassed on first reading. However, it is necessary for a thorough understanding of Secs. 3.6.2 and 4.3.
† Any other predictor, say a, has mean square error:
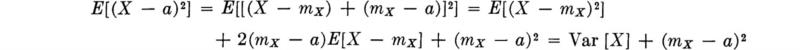
Clearly this is greater than Var [X] for any predictor other than a = mX.
† This conditional mean is also called the “regression of Y on X.”
† We must pass over many interesting topics in prediction, where the role of correlation is central. In particular, if, as is usually done in practice to avoid analytical difficulties, we restrict attention to predictors of Y which are simply linear in the observed value x, it can be shown that the best (linear) predictor of Y is, for any joint distribution, the function given above, Eq. (2.4.98a). This equation is called the linear regression of Y on X. The mean square error of that best linear predictor, when averaged over all values of x, is also for any distribution the same as the function given above, Eq. (2.4.98b). Therefore in linear prediction, second moments alone define all the necessary information. (See, for example, Freeman [1963].)
† Note the subtle change in notation from E[T | N = n] to E[T | N] which accompanies this step.
† Reading of this section is not critical for understanding of subsequent chapters. It may be bypassed on first reading. The material is most important, however, when approximate models and analyses are sufficient for the engineering purpose.
‡ How large the coefficient may be depends upon the degree of nonlinearity of g(X) in the region around mX and upon the degree of acceptable approximation error.
† The transformation is one-to-one only because X is restricted to positive values by the form of fX(x).
† The “most uncertain” variable is that variable with the largest coefficient of variation (see Prob. 2.46).
† See, for example, Freeman [1963] or Wadsworth and Bryan [I960].
† M. B. Fiering [1967], “Streamflow Synthesis,” Harvard University Press, Cambridge, Mass.
† This does not imply that the numbers of trucks are in exactly these proportions; the faster trucks make more trips. For an analysis of this point see F. A. Haight [1963], “Mathematical Theories of Traffic Flow,” Academic Press, Inc., New York.
‡ That is,
where λ is the parameter of the distribution.
More precisely, show, using the Chebyshev inequality, that
† If the variables are assumed jointly normally distributed (Sec. 3.6.2), lack of correlation implies independence.
† This procedure will begin repeating numbers after a sequence of 500. If a different sequence is needed, pick new values of M0 or M. See “Random Number Generation and Testing” [1959], IBM Reference Manual.
† W. Feller [1951], The Asymptotic Distribution of the Range of Sums of Independent Random Variables, Ann. Math. Stat., vol. 22, pp. 427–432, September, as reported by M. B Fiering [1967], “Streamflow Synthesis,” p. 17, Harvard University Press, Cambridge, Mass. (See Prob. 2.59.)
‡ See Prob. 2.32 for a definition of an operating policy. This problem is based on the work of G. T. Bryant [1961], “Stochastic Theory of Queues Applied to Design of Impounding Reservoirs,” Ph.D. dissertation, Harvard University, Cambridge, Mass., as reported by M. B. Fiering [1967], op. cit., p. 17.
† M. B. Fiering [1967], op. tit.; see Prob. 2.32.
† This result is attributed by M. B. Fiering [1967], op. cit., to G. T. Bryant, Prob. 2.59.
