Every engineering problem involves phenomena which exhibit scatter of the type illustrated in the previous chapter. To deal with such situations in a manner which incorporates this variability in his analyses, the engineer makes use of the theory of probability, a branch of mathematics dealing with uncertainty.
A fundamental step in any engineering investigation is the formulation of a set of mathematical models—that is, descriptions of real situations in a simplified, idealized form suitable for computation. In civil engineering, one frequently ignores friction, assumes rigid bodies, or adopts an ideal fluid to arrive at relatively simple mathematical models, which are amenable to analysis by arithmetic or calculus. Frequently these models are deterministic: a single number describes each independent variable, and a formula (a model) predicts a specific value for the dependent variable. When the element of uncertainty, owing to natural variation or incomplete professional knowledge, is to be considered explicitly, the models derived are probabilistic and subject to analysis by the rules of probability theory. Here the values of the independent variables are not known with certainty, and thus the variable related to them through the physical model cannot be precisely predicted. In addition, the physical model may itself contain elements of uncertainty. Many examples of both situations will follow.
This chapter will first formalize some intuitively satisfactory ideas about events and relative likelihoods, introducing and defining a number of words and several very useful notions. The latter part of the chapter is concerned with the definition, the description, and the manipulation of the central character in probability—the random variable.
Uncertainty is introduced into engineering problems through the variation inherent in nature, through man’s lack of understanding of all the causes and effects in physical systems, and through lack of sufficient data. For example, even with a long history of data, one cannot predict the maximum flood that will occur in the next 10 years in a given area. This uncertainty is a product of natural variation. Lacking a full-depth hole, the depth of soil to rock at a building site can only be estimated. This uncertainty is the result of incomplete information. Thus both the depth to rock and the maximum flood are uncertain, and both can be dealt with using the same theory.
As a result of uncertainties like those mentioned above, the future can never be entirely predicted by the engineer. He must, rather, consider the possibility of the occurrence of particular events and then determine the likelihood of their occurrence. This section deals with the logical treatment of uncertain events through probability theory and the application to civil engineering problems.
Experiments, sample spaces, and events The theory of probability is concerned formally with experiments and their outcomes, where the term experiment is used in a most general sense. The collection of all possible outcomes of an experiment is called its sample space. This space consists of a set S of points called sample points, each of which is associated with one and only one distinguishable outcome. The fineness to which one makes these distinctions is a matter of judgment and depends in practice upon the use to which the model will be put.
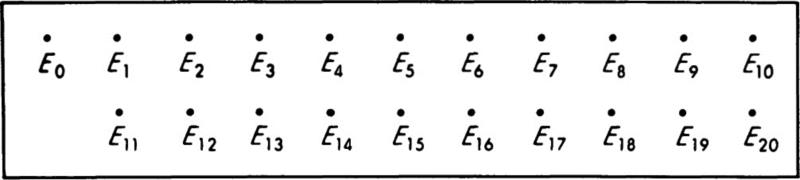
As an example, suppose that a traffic engineer goes to a particular street intersection exactly at noon each weekday and waits until the traffic signal there has gone through one cycle. The engineer records the number of southbound vehicles which had to come to a complete stop before their light turned green. If a minimum vehicle length is 15 ft and the block is 300 ft long, the maximum possible number of cars in the queue is 20. If only the total number of vehicles is of interest, the sample space for this experiment is a set of 21 points labeled, say, E0, E1, . . ., E20, each associated with a particular number of observed vehicles. These might be represented as in Fig. 2.1.1. If the engineer needed other information, he might make a finer distinction, differentiating between trucks and automobiles and recording the number of each stopped. The sample space for the experiment would then be larger, containing an individual sample point Ei,j for each possible combination of i cars and j trucks such that the maximum value of i+j = 20, as in Fig. 2.1.2.
Fig. 2.1.1 An elementary sample space—Ej implies j vehicles observed.
An event A is a collection of sample points in the sample space S of an experiment. Traditionally, events are labeled by letters. If the distinction should be necessary, a simple event is an event consisting of a single sample point, and a compound event is made up of two or more sample points or elementary outcomes of the experiment. The complement A c of an event A consists of all sample points in the sample space of the experiment not included in the event. Therefore, the complement of an event is also an event.†
Fig. 2.1.2 Elementary sample space for cars and trucks. Eij implies i cars and j trucks with a maximum of 20 including both types of vehicles.
In the experiment which involved counting all vehicles without regard for type, the observation of “no stopped vehicles” is a simple event A, and the finding of “more than 10 stopped vehicles” is a compound event B. The complement of the latter is the event Bc, “10 or fewer stopped vehicles were observed.” Events defined on a sample space need not be exclusive; notice that events A and Bc both contain the sample point E0.
In testing the ultimate strength of reinforced-concrete beams described in Sec. 1.2, the load values were read to the nearest 50 lb. The sample space for the experiment consists of a set of points, each associated with an outcome, 0, 50, 100, . . ., or M lb, where M is some indefinitely large number, say, infinity. A set of events of interest might be A0, A1, A2, ..., defined such that A0 contains the sample points associated with loads 0 to 950 lb, A1 contains those associated with 1000 to 1950 lb, and so forth.
In many physical situations, such as this beam-strength experiment, it is more natural and convenient to define a continuous sample space. Thus, as the measuring instrument used becomes more and more precise, it is reasonable to assume that any number greater than zero, not just certain discrete points, will be included among the possible outcomes and hence defined as a sample point. The sample space becomes the real line, 0 to ∞. In other situations, a finite interval is defined as the sample space. For example, when wind directions at an airport site are being observed, the interval 0 to 360° becomes the sample space. In still other situations, when measurement errors are of interest, for example, the line from – ∞ to + ∞ is a logical choice for the sample space. To include an event such as ∞ in the sample space does not necessarily mean the engineer thinks it is a possible outcome of the experiment. The choice of ∞ as an upper limit is simply a convenience; it avoids choosing a specific, arbitrarily large number to limit the sample space.
Events of interest in the beam experiment might be described as follows‡ (when the sample space is defined as continuous):
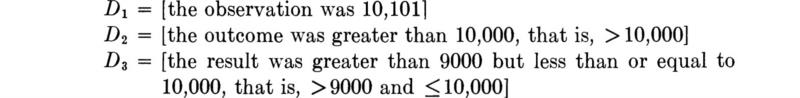
Fig. 2.1.3 Continuous sample space for beam-failure load.
D1 is a simple event; D2 and D3 are compound events. They are shown graphically in the sample space 0 to ∞ in Fig. 2.1.3.
Relationships among events Events in a sample space may be related in a number of ways. Most important, if two events contain no sample points in common, the events are said to be mutually exclusive or disjoint. Two mutually exclusive events—A, “fewer than 6 stopped vehicles were observed” and B, “more than 10 stopped vehicles were observed”—are shown shaded in the sample space of the first vehicle-counting experiment (Fig. 2.1.4). The events D1 and D3 defined above are mutually exclusive. D2 and D3 are also mutually exclusive, owing to the care with which the inequality (≤) and strict inequality (>) have been written at 10,000.
The notion of mutually exclusive events extends in an obvious way to more than two events. By their definition simple events are mutually exclusive.
If a pair of events A and B are not mutually exclusive, the set of points which they have in common is called their intersection, denoted A ∩ B. The intersection of the event A defined in the last paragraph and the event C, “from four to eight stopped vehicles were observed,” is illustrated in Fig. 2.1.5. The intersection of the events D1 and D2 in Fig. 2.1.3 is simply the event D1 itself. If the intersection of two events is equivalent to one of the events, that event is said to be contained in the other. This is written D1 ⊂ D2.
Fig. 2.1.4 Mutually exclusive events. Compound events A and B are mutually exclusive; they have no sample points in common.
Fig. 2.1.5 Intersection A ∩ C, comprising events E4 and E5, is the intersection of compound events A and C.
The union of two events A and C is the event which is the collection of all sample points which occur at least once in either A or C. In Fig. 2.1.5 the union of the events A and C, written A ![]() C, is the event “less than nine stopped vehicles were observed.” The union of the events D2 and D3 in Fig. 2.1.3 is the event that the failure load is greater than 9000 lb. The union of D1 and D2 is simply D2 itself.
C, is the event “less than nine stopped vehicles were observed.” The union of the events D2 and D3 in Fig. 2.1.3 is the event that the failure load is greater than 9000 lb. The union of D1 and D2 is simply D2 itself.
Two-dimensional and conditional sample spaces For purposes of visualization of certain later developments, two other types of sample spaces deserve mention. The first is the two- (or higher) dimensional sample space. The sample space in Fig. 2.1.2 is one such, where the experiment involves observing two numbers, the number of cars and the number of trucks. It might be replotted as shown in Fig. 2.1.6; there each point on the grid represents a possible outcome, a sample point. In the determination of the best orientation of an airport runway, an experiment might involve measuring both wind speed and direction. The continuous sample space would appear as in Fig. 2.1.7, limited in one dimension and unlimited in the other. Any point in the area is a sample point. An experiment involving the measurement of number and average speed of vehicles on a bridge would lead to a discrete-continuous two-dimensional sample space.
The second additional kind of sample space of interest here is a conditional sample space. If the engineer is interested in the possible outcomes of an experiment given that some event A has occurred, the set of events associated with event A can be considered a new, reduced sample space. For, conditional on the occurrence of event A, only the simple events associated with the sample points in that reduced space are possible outcomes of the experiment. For example, given that exactly one truck was observed, the conditional sample space in the traffic-light experiment becomes the set of events E0,1,El,1, . . ., E19,1. Given that two or fewer trucks were observed, the conditional sample space is that illustrated in Fig. 2.1.8. Similarly, the airport engineer might be interested only in higher-velocity winds and hence restrict his attention to the conditional sample space associated with winds greater than 20 mph, leading to the space shown in Fig. 2.1.9. Whether a sample space is the primary or the conditional one is clearly often a matter of the engineer’s definition and convenience, but the notion of the conditional sample space will prove helpful.
Fig. 2.1.6 Discrete two-dimensional sample space. Each sample point represents an observable combination of cars and trucks such that their sum is not greater than 20.
Fig. 2.1.7 Continuous two-dimensional sample space. All possible observable wind speeds and directions at an airport are described.
Fig. 2.1.8 Discrete conditional sample space. Given that two or fewer trucks were observed (see Fig. 2.1.6).
Fig. 2.1.9 Continuous conditional sample space. Describes all possible wind directions and velocities given that the velocity is greater than 20 mph.
For the remainder of Sec. 2.1 we shall restrict our attention to one-dimensional discrete sample spaces, and shall return to the other important cases only after the introduction in Sec. 2.2 of the random variable.
Interpretation of probabilities To each sample point in the sample space of an experiment we are going to assign a number called a probability measure. The mathematical theory of probability is not concerned with where these numbers came from or what they mean; it only tells us how to use them in a consistent manner. The engineer who puts probability to work on his models of real situations must be absolutely sure what the set of numbers he assigns means, for the results of a probabilistic analysis of an engineering problem can be helpful only if this input is meaningful.
An intuitively satisfying explanation of the probability measure assigned to a sample point is that of relative frequencies. If the engineer assigns a probability measure of p to a sample point in a sample space, he is usually willing to say that if he could make repeated trials of the same experiment over and over again, say M times, and count the number of times N that the simple event associated with this sample point was observed, the ratio of N to M would be very nearly p. One frequently hears, for example, that the probability of a tossed coin coming up “heads” is one-half. Experience has shown that this is very nearly the fraction of any series of a large number of tosses of a well-balanced coin that will show a head rather than a tail. This interpretation of the probability measure is commonly adopted in the physical sciences. It is considered quite objectively as a property of certain repetitious phenomena. When formalized through limit theorems, the notion of relative frequency can serve as a basis as well as an interpretation of probability (Von Mises [1957]). Relative frequency, when it applies, is without question a meaningful and useful interpretation of the probability measure.
But what is the engineer to do in a situation where such repetition of the experiment is impossible and meaningless? How does one interpret, for instance, the statement that the probability is 0.25 that the soil 30 ft below a proposed bridge footing is not sand but clay? The soil is not going to be clay on 1 out of every 4 days that it is observed; it is either clay or it is not. The experiment here is related to an unknown condition of nature which later may be directly observed and determined once and for all.
The proved usefulness in bringing probability theory to bear in such situations has necessitated a more liberal interpretation of the expression “the probability of event A is p.” The probabilities assigned by an engineer to the possible outcomes of an experiment can also be thought of as a set of weights which expresses that individual’s measure of the relative likelihoods of the outcomes. That is, the probability of an event might be simply a subjective measure of the degree of belief an engineer has in a judgment or prediction. Colloquially this notion is often expressed as “the odds are 1 to 3 that the soil is clay.” Notice that if repetitions are involved, the notions of relative frequencies and degree of belief should be compatible to a reasonable man. Much more will be said of this “subjective” probability in Chap. 5, which includes methods for aiding the engineer in assessing the numerical values of the probabilities associated with his judgements. This interpretation of probability, as an intellectual concept rather than as a physical property, also can serve as a basis for probability theory. Engineering students will find Tribus’ recent presentation of this position very appealing (Tribus [1969]).
Like its interpretations, the sources of the probability measure to be assigned to the sample points are also varied. The values may actually be the results of frequent observations. After observing the vehicles at the intersection every weekday for a year, the traffic engineer in the example in the previous section might assign the observed relative frequencies of the simple events, “no cars,” “one stopped car,” etc., to the sample points E0, E1 . . ., E20.
Reflecting the second interpretation of probability, the probability measure may be assigned by the engineer in a wholly subjective manner. Calling upon past experience in similar situations, a knowledge of local geology, and the taste of a handful of the material on the surface, a soils engineer might state the odds that each of several types of soil might be found below a particular footing.
Finally, we shall see that through the theory of probability one can derive the probability measure for many experiments of prime interest, starting with assumptions about the physical mechanism generating the observed events. For example, by making certain plausible assumptions about the behavior of vehicles and knowing something about the average flow rate, that is, by modeling the underlying mechanism, the engineer may be able to calculate a probability measure for each sample point in the intersection experiment without ever making an actual observation of the particular intersection. Such observation is impossible, for example, if the intersection is not yet existent, but only under design. As in deterministic problem formulations, subsequent observations may or may not agree with the predictions of the hypothesized mathematical model. In this manner, models (or theories) are confirmed or rejected.
Axioms of probability No matter how the engineer chooses to interpret the meaning of the probability measure and no matter what its source, as long as the assignment of these weights is consistent with three simple axioms, the mathematical validity of any results derived through the correct application of the axiomatic theory of probability is assured. We use the notation† P[A] to denote the probability of an event A, which in the context of probability is frequently called a random event. The following conditions must hold on the probabilities assigned to the events in the sample space:
Axiom I The probability of an event is a number greater than or equal to zero but less than or equal to unity:
![]()
Axiom II The probability of the certain event S is unity:
![]()
where S is the event associated with all the sample points in the sample space.
Axiom III The probability of an event which is the union of two mutually exclusive events is the sum of the probabilities of these two events:
![]()
Since S is the union of all simple events, the third axiom implies that Axiom II could be written:
![]()
in which the Ei are simple events associated with individual sample points.‡
The first two axioms are simply convenient conventions. All probabilities will be positive numbers and their sum over the simple events (or any mutually exclusive, collectively exhaustive set of events) will be normalized to 1. These are natural restrictions on probabilities which arise from observed relative frequencies. If there are k possible outcomes to an experiment and the experiment is performed M times, the observed relative frequencies Fi are

where n1, n2, . . ., nk are the numbers of times each particular outcome was observed. Since n1 + n2 + · · · + nk = M, each frequency satisfies Axiom I and their sum satisfies Axiom II:
![]()
If, alternatively, one prefers to think of probabilities as weights on events indicative of their relative likelihood, then Axioms I and II simply demand that, after assigning to the set of all simple events a set of relative weights, one normalizes these weights by dividing each by the total.
Axiom III is equally acceptable. It requires only that the probabilities are assigned to events in such a way that the probability of any event made up of two mutually exclusive events is equal to the sum of the probabilities of the individual events. If the original assignment of probabilities is made on a set of collectively exhaustive, mutually exclusive events, such as the set of all simple events, there can be no possibility of violating this axiom. If, for example, the source of these assignments is a set of observed relative frequencies, as long as the original set of k outcomes has been properly defined (in particular, not overlapping in any way), the relative frequency of the outcome i or j is
![]()
Similarly, if an engineer assigns relative weights to a set of possible distinct outcomes, he would surely be inconsistent if he felt that the relative likelihood of either of a pair of disjoint outcomes was anything but the sum of their individual likelihoods.
Suppose that the soils engineer in the above example decides that the odds on there being clay soil at a depth of 30 ft are 1 to 3 (or 1 in 4), and sand is just as likely; and if neither of these is present, the material will surely be sound rock. The implication is that he gives clay a relative weight of 1 and the other outcomes a total weight of 3. These possible outcomes include only sand, with a weight 1, and rock, with weight 3 – 1, or 2. To be used as probabilities these weights need normalizing by their sum, 4, to satisfy the first and second axioms of probability. Let the event C be “there is clay 30 ft below the footing” and let the events S and R be associated with the presence of sand and rock, respectively. Then

Notice that the three axioms are satisfied and that
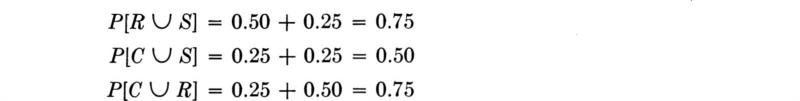
Once measures have been assigned in accord with these three axioms to the points in the sample space, these probabilities may be operated on in the manner to be demonstrated throughout this book. The engineer may be fully confident that his results will be mathematically valid, but it cannot be emphasized too strongly that the physical or practical significance of these results is no better than the “data,” the assigned probabilities, upon which they are based.
Certain relationships among the probabilities of events follow from the relationships among events and from the axioms of probability. Many simple conclusions are self-evident; others require some derivation. Further, some additional relationships between events are defined in terms of relationships between their probabilities. The remainder of this section treats and illustrates these various relationships.
Probability of an event Since, in general, an event is associated with one or more sample points or simple events, and since these simple events are mutually exclusive by the construction of the sample space, the probability of any event is the sum of the probabilities assigned to the sample points with which it is associated. If an event contains all the sample points with nonzero probabilities, its probability is 1 and it is sure to occur. If an event is impossible, that is, if it cannot happen as the result of the experiment, then the probabilities of all the sample points associated with the event are zero.
Fig. 2.1.10 Venn diagram. Illustrates decomposition of two events A and B into mutually exclusive events A0,B0 and A ∩ B.
Probability of union The probability of an event which is the union of two events A and B, disjoint or not, can be derived from the material in the previous sections. The event A can be considered as the union of the intersection A ∩ B and a nonoverlapping set of sample points, say, A0. Similarly, event B is the union of two mutually exclusive events A ∩ B and B0. These events are illustrated in Fig. 2.1.10.† By Axiom III
Now A ![]() B can be divided into three mutually exclusive events, A0, B0, and A ∩ B.
B can be divided into three mutually exclusive events, A0, B0, and A ∩ B.
Therefore, by Axiom III,
Solving Eqs. (2.1.1a) and (2.1.1b) for P[A0] and P[B0] and substituting into Eq. (2.1.2),
Fig. 2.1.11 Illustration of industrial-park utilities.
In words, the probability of the occurrence of either one event or another or both is the sum of their individual probabilities minus the probability of their joint occurrence. This extremely important result is easily verified intuitively. In summing the probabilities of the events A and B to determine the probability of a compound event A ![]() B, one has added the probability measure of the sample points in the event A ∩ B twice. In the case of mutually exclusive events, when the intersection A ∩ B contains no sample points, P[A ∩ B] = 0 and the equation reduces to Axiom III.
B, one has added the probability measure of the sample points in the event A ∩ B twice. In the case of mutually exclusive events, when the intersection A ∩ B contains no sample points, P[A ∩ B] = 0 and the equation reduces to Axiom III.
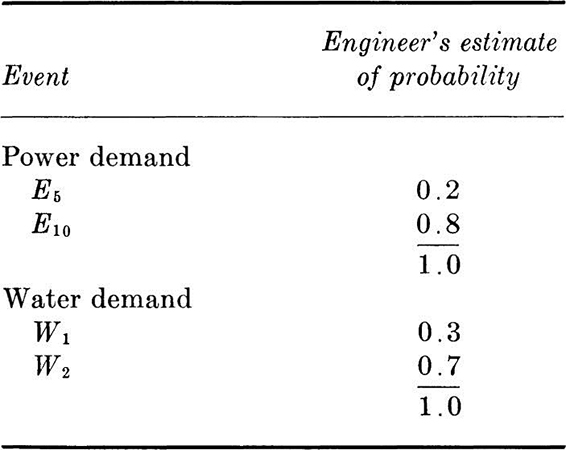
To illustrate this and following concepts, let us consider the design of an underground utilities system for an industrial park containing six similar building sites (Fig. 2.1.11). The sites have not yet been leased, and so the nature of occupancy of each is not known. If the engineer provides water and power capacities in excess of the demand actually encountered, he will have wasted his client’s capital; if, on the other hand, the facilities prove inadequate, expensive changes will be required. For simplicity, consider any particular site and assume that the electric power required by the occupant will be either 5 or 10 units, while the water capacity demanded will be either 1 or 2 units. Then the sample space describing an experiment associated with a single occupant consists of four points, labeled (5,1), (10,1), (5,2), or (10,2), according to the combination of levels of power and water demanded. The space can be illustrated in either of two ways, as shown in Fig. 2.1.12. The client, in an interview with the engineer, makes a series of statements about odds and relative weights from which the engineer calculates the following set of probabilities.
Fig. 2.1.12 Alternate graphical representations of the utilities-demand sample space.
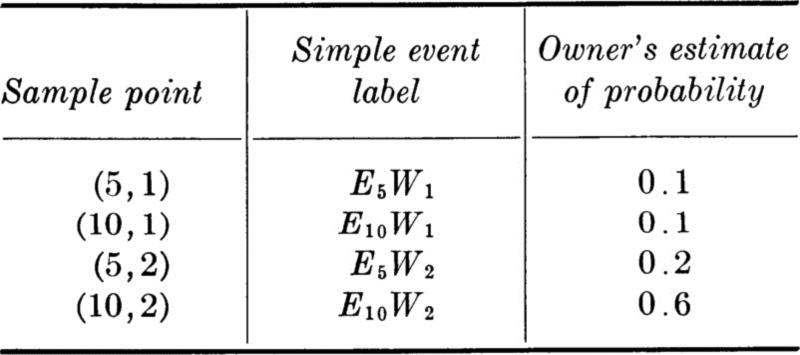
The probability of an event W2, “the water demand is 2 units” is the sum of the probabilities of the corresponding, mutually exclusive, simple events.
![]()
Also, the probability of power demand being 10 units at a particular site is
![]()
The probability that either the water demand is 2 units or the power demand is 10 units may be calculated by Eq. (2.1.3).
![]()
or, since the intersection of events E10 and W2 is the simple event E10W2,
![]()
Notice that the same result is obtained by summing the probabilities of the simple events in which one observes either a water demand of 2 units or a power demand of 10 units or both.
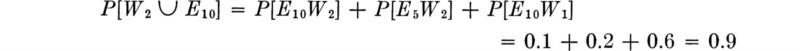
Conditional probability A concept of great practical importance is introduced into the axiomatic theory of probability through the following definition. The conditional probability of the event A given that the event B has occurred, denoted P[A | B], is defined as the ratio of the probability of the intersection of A and B to the probability of the event B.
(If P[B] is zero, the conditional probability P[A | B] is undefined.)
The conditional probability can be interpreted as the probability that A has occurred given the knowledge that B has occurred. The condition that B has occurred restricts the outcome to the set of sample points in B, or the conditional sample space, but should not change the relative likelihoods of the simple events in B. If the probability measure of those points in B that are also in A, P[A ∩ B], is renormalized by the factor 1/P[B] to account for operation within this reduced sample space, the result is the ratio P[A ∩ B]/P[B] for the probability of A given B.
In the preceding illustration the engineer might have need for the probability that a site with a power demand of E10 will also require a water demand W2. In this case
![]()
In applications, P[B] and P[A | B] often come from a study of the problem, whereas actually the joint probability P[A ∩ B] is desired; this is obtained as follows:
Where many events are involved, the following expansion is often helpful:
![]()
Illustrations are given later in the section and in problems.
Independence If two physical events are not related in any way, we would not alter our measure of the probability of one even if we knew that the other had occurred. This intuitive notion leads to the definition of probabilistic (or stochastic) independence. Two events A and B are said to be independent if and only if
From this definition and Eq. (2.1.4a), the independence of events A and B implies that
Any of these equations can, in fact, be used as a definition of independence.
Within the mathematical theory, one can only prove independence of events by obtaining P[A], P[B], and P[A ∩ B] and demonstrating that one of these equations holds. In engineering practice, on the other hand, one normally relies on knowledge of the physical situation to declare that in his model two particular events shall (or shall not) be assumed independent. From the assumption of independence, the engineer can calculate one of the three quantities, say, P[A ∩ B], given the other two.
In general, events A, B, C, . . ., N are mutually independent if and only if
This is the theorem known as the multiplication rule. In words, if events are independent, the probability of their joint occurrence is simply the product of their individual probabilities of occurrence.
Returning to the industrial-park illustration, let us assume that the engineer, not content with the loose manner in which his client assigned probabilities to demands, has sampled a number of firms in similar industrial parks. He has concluded that there is no apparent relationship between their power and water demands. A high power demand, for example, does not seem to be correlated with a high water demand.
Based on information easily obtained from the respective utility companies, the engineer assigns the following probabilities:
Adopting the assumption of stochastic independence of the water and power demands, † the engineer can calculate the following probabilities for the joint occurrences or simple events.
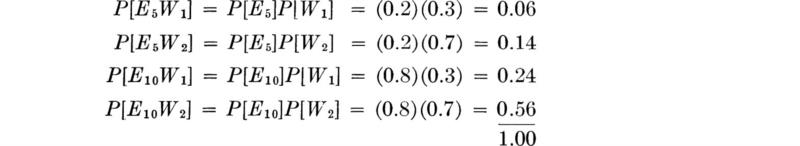
Decisions under uncertainty With no more than the elementary operations introduced up to this point, we can demonstrate the usefulness of probabilistic analysis when the engineer must make economic decisions in the face of uncertainty. We shall present only the rudiments of decision analysis at this point. We chose to continue to use the preceding example to introduce these ideas. For simplicity of numbers, let us concentrate on the water demand only and investigate the design capacity of a secondary main serving a pair of similar sites in the industrial park. The occupancies of the two sites represent two repeated trials of the experiment described above. Denote the event that the demand of each firm is one unit by W1W1 and the event that the demand of the first is one unit and the second is two units by W1W2, and so forth. Assuming stochastic independence of the demands from the two sites, one can easily calculate the probabilities of various combinations of outcomes.
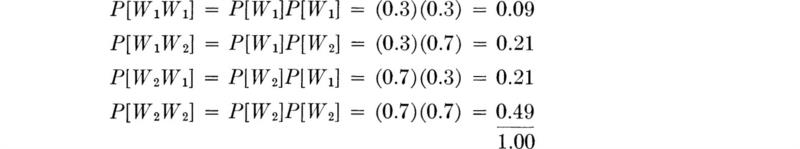
Notice that events W1W2 and W2W1 lead to the same total demand; on the sample space of this two-site experiment, we could define new events D2, D3, and D4 which correspond to total demands of two, three, and four units, respectively (see Fig. 2.1.13). It is most often the case that engineers are interested in outcomes which have associated numerical values. This observation is expanded upon in Sec. 2.2.
The assumption of independence between sites implies that the engineer feels that there would be no reason to alter the probabilities of the demand of the second firm if he knew the demand of the first. That is, knowledge of the demand of the first gives the engineer no new information about the demand of the second. Such might be the case, for example, if the management of the second firm chose its site without regard for the nature of its neighbor. If the demands of all six sites are mutually independent, the probability that all the sites will demand two units of water is:
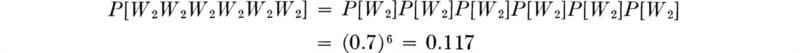
How can such information be put to use to determine the best choice for the capacity of the secondary pipeline? These estimates of the relative likelihoods must in some way be related to the relative costs of the designs and the losses associated with possible inadequacies. Suppose the engineer has compiled the following cost table:
Fig. 2.1.13 Two-site water-demand illustration sample space.
Initial costs:
![]()
Cost associated with possible later enlargement:

A common method used to account for uncertain losses is to weight the possible losses by the probabilities of their occurrences. Thus to the initial cost of a moderate design of capacity three units the engineer might add the weighted loss (0.49) ($1500) = $735, which is associated with a possible need for later enlargement if both firms should demand two units (the event W2W2). If a two-unit capacity is chosen, either of two future events, D3 or D4, will lead to additional cost. The weighted cost of each contributes to the total expected cost of this design alternative. These costs are called “expected costs” for reasons which will be discussed in Sec. 2.4. The validity of their use in making decisions, to be discussed more fully in Chap. 5,† will be accepted here as at least intuitively satisfactory. The following table of expected costs (over the basic initial cost of the two-unit capacity) can be computed for each alternative design.
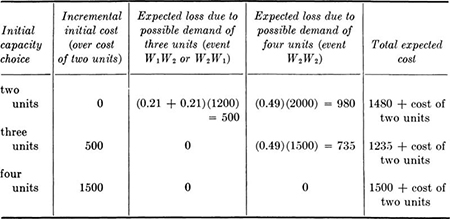
A design providing an initial capacity of three units appears to provide the best compromise between initial cost and possible later expenses. Notice that the common cost of two units does not enter the decision of choosing among the available alternatives.
As modifications lead to future rather than initial expense, the effect of the introduction of interest rates, and hence the time value of money, into the economic analysis would be to increase the relative merit of this strategy (three units) with respect to the large-capacity (four-unit) design while decreasing its relative advantage over the small-capacity (two-unit) system. A high interest rate could make the latter design more economical.
To design the primary water lines feeding all sites in the industrial park, a similar but more complex analysis is required. In dealing with repeated trials of such two-outcome experiments, one is led to the binomial model to be introduced in Sec. 3.1.2. Where more than two demand levels or more than one service type are needed, the multinomial distribution (Sec. 3.6.1) will be found to apply.
In Chaps. 5 and 6 we shall discuss decision making in more detail. The following two illustrations demonstrate further the computations of probabilities of events using the relationships we have discussed up to this point, and the use of expected costs in decisions under uncertainty.
Illustration: Construction scheduling A contractor must select a strategy for a construction job. Two independent operations, I and II, must be performed in succession. Each operation may require 4, 5, or 6 days to complete. A sample space is illustrated in Fig. 2.1.14. M4 is the event that operation I requires 4 days, N4 that II requires 4 days, etc. Each operation can be performed at three different rates, each at a different cost, and each leading to different time requirement likelihoods. In addition, if the job is not completed in 10 days, the contractor must pay a penalty of $2000 per day. The total time required for each combination of time requirements is shown in parentheses in Fig. 2.1.14. For example, M4 ∩ N6 requires a total of 10 days.
Fig. 2.1.14 Sample space for construction-strategy illustration.
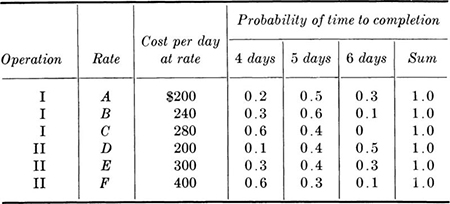
The contractor judges from experience that by working at rate A his probability of completing phase I in 4 days, event M4, is only 0.2, in 5 days (or M5) is 0.5, and in 6 days (M6) is 0.3. Proceeding in this manner, he assigns a complete set of probabilities (Table 2.1.1) to all possibilities, reflecting that he can probably accelerate the job by working at a more costly rate. He assumes that the events M4, M5, and M6 are independent of N4, N5, and N6.
The expected costs E[cost] of construction can now be calculated. For level I at rate A,
![]()
or
![]()
Similarly,
![]()
Similarly, all expected costs of construction are:
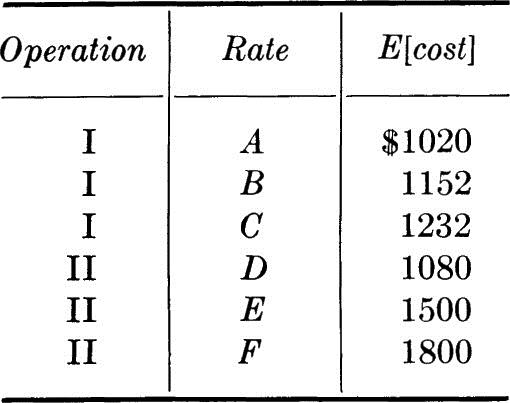
The optimum strategy is rate A for operation I and rate D for II to obtain a minimum expected cost of construction.
The possibility of an overtime penalty must also be included in the total cost. The probability of strategy AD requiring 8 days of time is the probability of (M4 ∩ N4) and, owing to independence, is simply the product of the individual probabilities of each operation requiring 4 days. Assuming independence of the events, under strategy AD,
![]()
A 9-day construction time can occur in two mutually exclusive ways: 4 days required for I and 5 days for II, or 5 days for I and 4 days for II. This event is crosshatched in Fig. 2.1.14.
![]()
Under strategy AD, P[9 days] = (0.2)(0.4) + (0.5)(0.1) = 0.13. Similarly, a 10-day time occurs as shown in Fig. 2.1.14 and, with the probabilities of strategy AD, has probability
![]()
Losses are associated with construction times of 11 or 12 days. Using rates A and D,
![]()
The expected penalty, if strategy AD is adopted, is, then,
![]()
The complete penalty results are shown in Table 2.1.2, and the total expected costs, that is, those due to construction plus those due to possible penalties, are collected in Table 2.1.3.
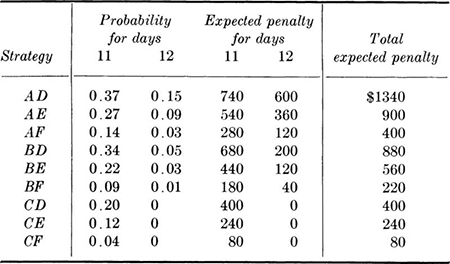
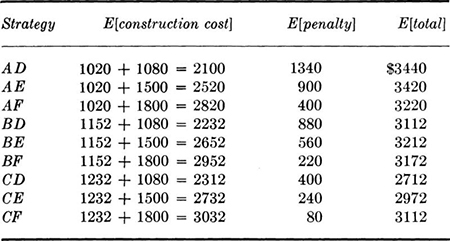
The optimum strategy has a minimum expected total cost and is in fact strategy CD.
Expected costs simply provide a technique for choosing among alternative strategies. The contractor’s cost will not be $2712 if he chooses strategy CD, but rather the cost of either 4, 5, or 6 days with I and with II plus $2000 per actual day of overtime.
Illustration: Analysis of bridge lifetimes† As an example of the construction of a more complex probability model from simple basic assumptions, consider this problem in bridge design. Assume that a bridge or culvert is usually replaced either because a flood exceeding the capacity of the structure has occurred or because it becomes obsolete owing to a widening or rerouting of the highway. The designer is interested in the likelihood that the life of the structure will come to an end in each of the years after construction.‡ Assume that there is a constant probability p that in any year a flow exceeding the capacity of the culvert will take place. Let ri be the probability that the structure will become obsolete in year i given that it has not become obsolete prior to year i. For most situations this probability grows with time. It may well be a reasonable engineering assumption that the effects of floods and obsolescence are unrelated and that the occurrences of critical flood magnitudes from year to year are independent events. Our problem is to determine the probability that the life of the structure comes to an end in year j for the first time.
Each year is a simple experiment with events defined as
![]()
The elementary events in these simple experiments are
![]()
The probability that the structure’s life does not end in the first year is, owing to the assumed independence, †
![]()
Successive years represent repetitions of such experiments. The probability that the life does not end in either of the first two years is, by Eq. (2.1.4a),
![]()
Similarly, the last term on the right-hand side can be written
![]()
This is easily verified by writing out the definitions of the conditional probabilities involved, although a simple reading of the statement suggests why it must be so.
Because of the various assumptions of independence made above,
![]()
Putting these results together,
![]()
Clearly, the probability that the structure survives floods and obsolescence through j years is
![]()
which by simple extension of the argument above is
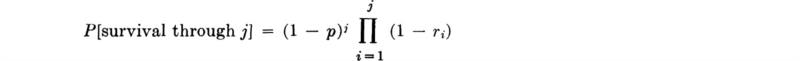
For the structure’s life to first come to end in year j, on the other hand, it must have survived j – 1 years, which will have happened with probability

and must then either have become obsolete or met a critical flood in year j. The latter event, Aj ![]() Bj, has probability, given previous survival, of
Bj, has probability, given previous survival, of
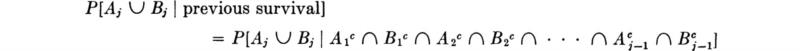
Equation (2.1.3) applies, subject to the conditioning event, previous survival, and
![]()
Owing to the various independences,
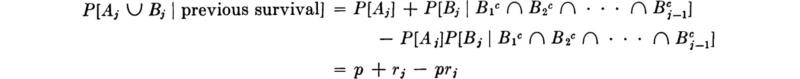
Finally, then,
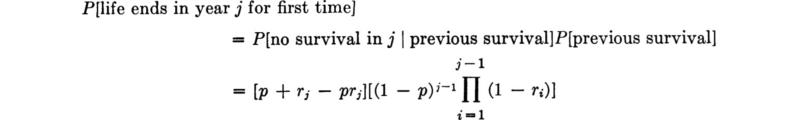
For example, if the structure is designed for the so-called “50-year flood,” † it implies that p = 1/50 = 0.02, and, if ri = 1 – e–0.025i, i = 1, 2, 3, . . ., then
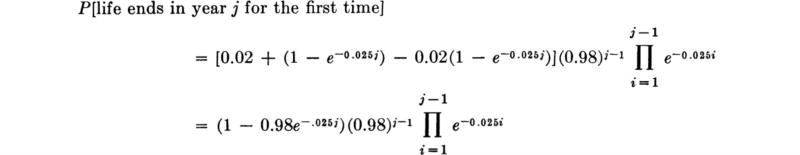
A plot of these probabilities for the years j = 1 to 22 is given in Fig. 2.1.15.
Combined with economic data these probabilities would permit the engineer to calculate an expected present worth of this design, to be compared with those of other alternate designs of different capacities for flow and perhaps with different provisions to reduce the likelihood of obsolescence.
Total probability theorem The equation defining conditional probabilities, Eq. (2.1.4a), can be manipulated to yield another important result in the probability of events. Given a set of mutually exclusive, collectively exhaustive events, B1, B2, . . ., Bn, one can always expand the probability P[A] of another event A in the following manner:
Fig. 2.1.15 Solution to culvert-life example. Probabilities of finding various lengths of life are plotted against length of life.
Figure 2.1.16 illustrates this fact. Each term in the sum can be expanded using Eq. (2.1.4a):
This result is called “the theorem of total probabilities.” It represents the expansion of the probability of an event in terms of its conditional probabilities, conditioned on a set of mutually exclusive, collectively exhaustive events. It is often a useful expansion to consider in problems when it is desired to compute the probability of an event A, since the terms in the sum may be more readily obtainable than the probability A itself.
Fig. 2.1.16 Venn diagram for total probability theorem. Event A intersects mutually exclusive and collectively exhaustive events Bi.
Illustration: Additive random demands on engineering systems Consider the generalized civil-engineering design problem of providing “capacity” for a probabilistic “demand.” Depending on the situation, demand may be a loading, a flood, a peak number of users, etc., while the corresponding capacity may be that of a building, a dam, or a highway. In many examples to follow, the general terminology, that is, demand and capacity, will be used with the express purpose of encouraging the reader to supply his preferred specific application. In this example two possible types (primary and secondary) of capacity at different unit costs are available, and loss is incurred if demand exceeds the total capacity provided or if it requires the use of some secondary capacity. This situation faces every designer, for the peak demand is often uncertain and the design usually cannot economically be made adequate for the maximum possible demand. The engineer seeks a balancing of initial cost and potential future losses.
For example, a building frame should be able to sustain a moderate seismic load without visible damage to the structure. During a rare, major earthquake, however, a properly designed structure will develop secondary resistance involving large plastic deformations and some acceptable level of damage to windows and partitions. Design for zero damage under all possible conditions is impossible or uneconomical. Similar problems arise in design of systems in which provision for future expansion is included. The future demand is unknown, so that the estimation of the optimum funds to be spent now to provide for expansion in the future is a similar type of capacity-demand situation.
Assume, in this example, that demand arises from two additive sources A and B and that the engineer assigns probabilities as shown in Table 2.1.4 to the various levels from source B and conditional probabilities to various levels from source A for each level of source B. The two sources are not independent.
Table 2.1.4 Conditional probabilities of [A, i Bj] and the probabilities of Bj
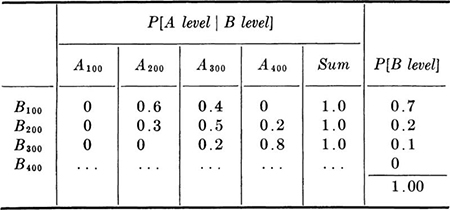
The probabilities of the A levels can be found by applying Eq. (2.1.12) for each level from source A. For example,
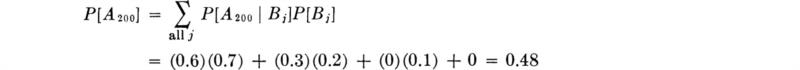
Similarly,

Before proceeding with the analysis, note that the engineer has assigned some zero probabilities.† Two interpretations exist of a zero probability. First, the event may simply be impossible. Second, it may be possible, but its likelihood negligible, and the engineer is willing to effectively exclude this level from the current study (while retaining the option to assign later a nonzero probability).
A two-dimensional sample space for the demand levels appears in Fig. 2.1.17. Any simple event is an intersection Ai ∩ Bj of an A level and B level. The various simple events which lead to the same total demand Dk are also indicated in this figure, the total values being given in parentheses. To determine the probabilities of an event such as D700 = [total demand is 700], we find the probability of this event as the union of mutually exclusive, simple events (and hence as simply the sum of their probabilities). Example:
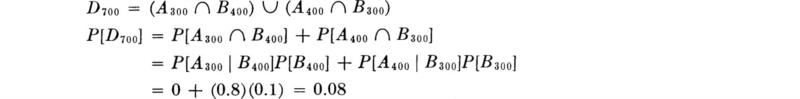
Fig. 2.1.17 Demand-level sample space showing how various total demands may arise.
A similar calculation for D500 involves four terms:
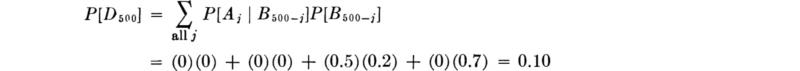
Similarly, we find that the probabilities of various demand levels are:
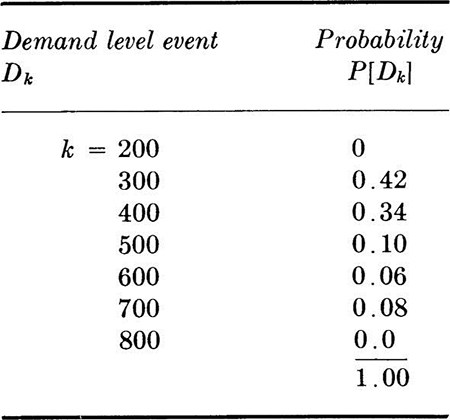
Although questions about the events which lead to particular demand levels are not asked in this decision problem, they might well be of interest in such problems. We ask one such question here to illustrate conditional sample spaces and conditional probabilities. What is the conditional sample space given that the total demand is 600? It is the set of those events which produce such a total demand, namely A200 ∩ B400, A300 ∩ B300, and A400 ∩ B200. This space is illustrated in Fig. 2.1.18. The conditional probabilities of these events, given total demand is 600, are
![]()
Fig. 2.1.18 Conditional sample space for a given total demand of 600.
Table 2.1.5 Example: expected cost calculations for several possible designs
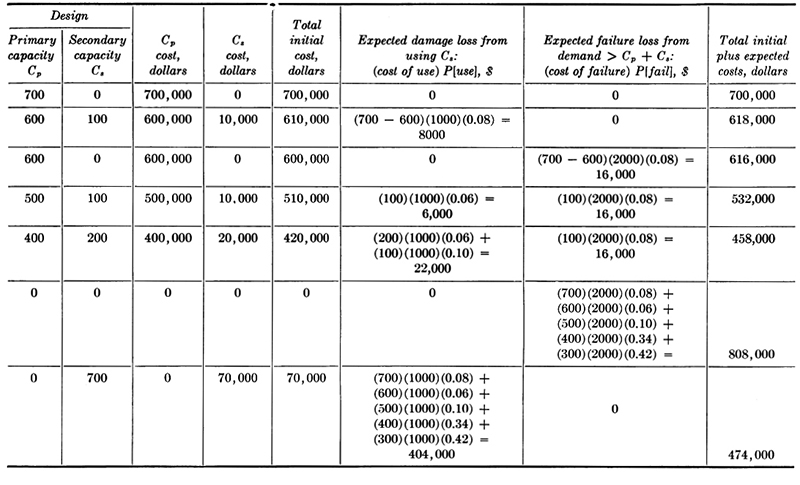
Because D600 includes the event A400 ∩ B200, we get

Notice that the unconditional probabilities of these events are 0.04, 0.02, and 0. These conditional probabilities are just these same relative values normalized to sum to unity.
Assume that primary capacity can be provided at $1000 per unit and that the secondary capacity cost is $100 per unit. If the demand is such that the secondary capacity must be used, the associated (“damage”) loss is $1000 per unit used, and if the demand exceeds total (primary plus secondary) capacity, the (“failure”) loss is $2000 per unit of excess over total capacity. The design alternatives include any combination of 0 to 700 primary capacity and 0 to 700 secondary capacity.
Associated with each design alternative is a primary capacity cost Cp, a secondary capacity cost Cs, and an expected cost associated with potential loss due to excessive demands. The latter cost includes a component due to demand possibly exceeding primary capacity, but not secondary capacity, and a component arising due to demand possibly exceeding the total capacity. {In the latter event, “failure,” no “damage” loss is involved; e.g., if primary capacity is 500, secondary capacity is 100, and a demand of 700 occurs, the loss is 2000[700 – (500 + 100)], not this plus 1000(700 – 500).}
A number of expected cost computations are illustrated in Table 2.1.5. The trend, as capacities are decreased from the most (initially) costly design of 700 units of primary capacity, is toward lowering total cost by accepting higher risks. After a point, the risks become too great relative to the consequences and to the initial costs, and total expected costs rise again.
Bayes’ theorem Continuing the study of the event A and the set of events Bi considered in Eq. 2.1.11 (Fig. 2.1.16), examine the conditional probability of Bj given the event A. By Eq. (2.1.4a), and since, clearly,
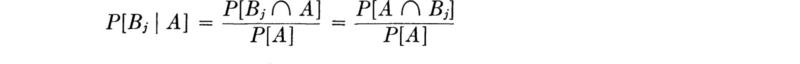
The numerator represents one term in Eq. (2.1.11) and can be replaced as in Eq. (2.1.12) by the product P[A | Bj]P[Bj], and the denominator can be represented by the sum of such terms, Eq. (2.1.12). Substituting,
This result is known as Bayes’ theorem or Bayes’ rule. Its simple derivation belies its fundamental importance in engineering applications. As will best be seen in the illustration to follow, it provides the method for incorporating new information with previous or, so-called prior, probability assessments to yield new values for the engineer’s relative likelihoods of events of interest. These new (conditional) probabilities are called posterior probabilities. Bayes’ theorem will be more fully explained and applied in Chaps. 5 and 6.
Illustration: Imperfect testing Bayes’ theorem can be generalized in application by calling the unknown classification the state, and by considering that some generalized sample has been observed. Symbolically, Eq. (2.1.13) becomes

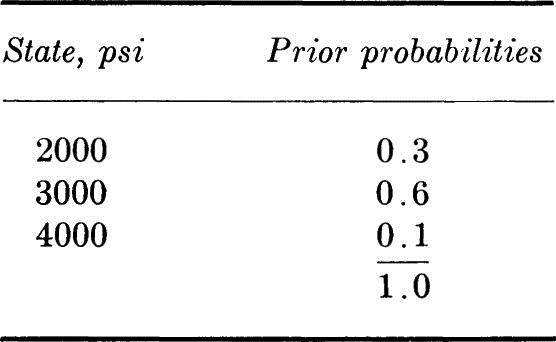
To illustrate the generalization, assume that an existing reinforced concrete building is being surveyed to determine its adequacy for a new future use. The engineer has studied the appearance and past performance of the concrete and, based on professional judgment, decides that the concrete quality can be classified as either 2000, 3000, or 4000 psi (based on the usual 28-day cylinder strength). He also assigns relative likelihoods or probabilities to these states:
Concrete cores are to be cut and tested to help ascertain the true state. The engineer believes that a core gives a reasonably reliable prediction, but that it is not conclusive. He consequently assigns numbers reflecting the reliability of the technique in the form of conditional probability measure on the possible core-strength values z1, z2, or z3 (in this case, core strength† of, say, 2500, 3500, or 4500 psi) as predictors of the unknown state:
P [core strength | state]
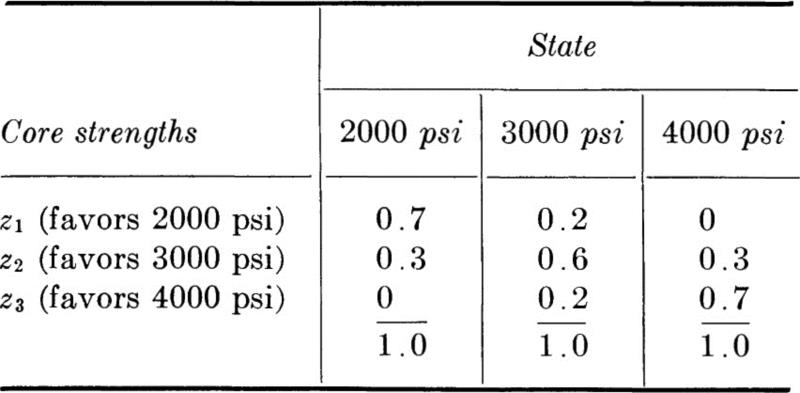
In words, if the true 28-day concrete quality classification is 3000 psi, the technique of taking a core will indicate this only 60 percent of the time. The total error probability is 40 percent, divided between z1 and z3. That is, the technique will significantly overestimate or underestimate the true quality 4 times in 10, on the average. Controlled experiments using the technique on concrete of known strength are used to produce such reliability information.
A core is taken and found to have strength 2500 psi favoring a 28-day strength of 2000 psi; that is, z1 is observed. The conditional probabilities of the true strength are then [Eq. (2.1.13)]
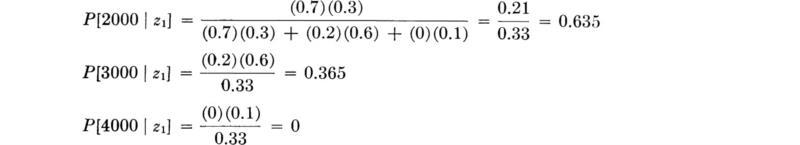
The sample outcome causes the exclusion of 4000 as a possible state and shifts the relative weights more towards the indicated state.
In the light of the test’s limitations, the engineer chooses to take a sample of two independent cores. In this case, it makes no difference if the calculation of posterior probabilities is made for each core in succession or for both cores simultaneously. Consider the latter approach first. Assume that the first core indicated z1 and the second core indicated z2. The probability of finding the sample outcome {z1,z2} if the state is really 2000 (or 3000 or 4000) psi is the product of two conditional probabilities (since the core results are assumed independent). Thus,
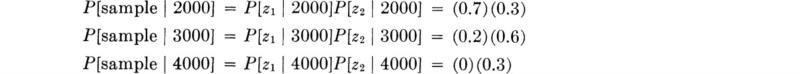
Recall that the probabilities of state prior to this sample of two cores were 0.3, 0.6, and 0.1. The posterior probabilities then become

The role of Bayes’ theorem as an “information processor” is revealed when it is recognized that the engineer might have taken the first core only, found z1 (favoring 2000 psi), computed the posterior probabilities of state as (0.635, 0.365, 0), and only then decided that another core was desirable. At this point his prior probabilities (prior, now, only to the second core) are 0.635, 0.365, 0. The posterior probabilities, given that the second core favored 3000, become

As they must, these probabilities are the same as those computed by considering the two cores as a single sample. If a third core (or several more cores) were taken next, these probabilities 0.47, 0.53, 0 would become the new prior probabilities. Bayes’ theorem will permit the continuous up-dating of the probabilities of state as new information becomes available. The information might next be of some other kind, for example, the uncovering of the lab data obtained from test cylinders cast at the time of construction and tested at 28 days. Such information, of course, would have a different set of conditional probabilities of sample given state (quite possibly, in this case, with somewhat smaller probabilities of “errors,” that is, with smaller probabilities of producing samples favoring a state other than the true one).
This simple example illustrates how all engineering sampling and experimentation can better be viewed in a probabilistic formulation. For reasons of expediency and economy, most testing situations measure a quantity which is only indirectly related to the quantity that is of fundamental engineering interest. In this example, the engineer has measured an extracted core’s ultimate compressive strength in order to estimate the concrete’s 28-day strength, which in turn is known to be correlated with its compressive strength in bending strength, shear (or diagonal tension) strength, corrosion resistance, durability, etc. The soils engineer may measure the density of a compacted fill not because he wishes to estimate its density, but because he wishes to estimate its strength and ultimately the embankment’s stability. Various hardness-testing apparatuses exist because testing for hardness is a simple, nondestructive way to estimate the factor of direct interest, that is, a material’s strength.
Both in the actual making of the measurement and in the assumed relationship between the measurable quantity (sample) and factor of direct interest (state) there may be experimental error and variation, and hence uncertainty. For example, accompanying a hardness-testing procedure is usually a graph, giving a strength corresponding to an observed value of a hardness measurement. But repeated measurements on a specimen may not give the same hardness value, and, when the graph was prepared for a given hardness there may have been some variation in the strength values about the average value through which the graph was drawn. It is this uncertainty which is reflected in the conditional probabilities P[sample | state]. A very special case is that where there is negligible measurement error and where the relationship between the sampled quantity and the factor of interest is exact (for example, if the state can be measured directly). In this case, the engineer will logically assign P[sample | state] = 1 if the sample value indicates (i.e., “favors”) the state, and 0 if it does not. These assignments are implicit in any nonprobabilistic model of testing. With these special conditional probability assignments, inspection of Bayes’ theorem will reveal that the only nonzero term in the denominator is the prior probability of the state favored by the observed sample, while the numerator is the same for this state and zero for all states not favored by the sample. Hence, if the entire sampling procedure is, indeed, perfect, the posterior probabilities of the states are zero except for the state favored or indicated by the sample. This state has probability 1. If, however, there is any uncertainty in the procedure, whether due to experimental error or inexact relationships between predicted quantity and predicting quantity, at least some of the other states will retain nonzero probabilities.† The better the procedure, the more sharply centered will be its conditional probabilities on the sample-favored state and the higher will be the, posterior probability of this state.
This fundamental engineering problem of predicting one quantity given an observation of another related or correlated one will occur throughout this text. In Secs. 2.2.2 and 2.4.3, and in Sec. 3.6.2, the probabilistic aspects of the problem are discussed. In Sec. 4.3 the problem is treated statistically; that is, questions of determining from observed data the “best” way to predict one quantity given another are discussed. In Chaps. 5 and 6, we shall return to the decision aspects of the problem.
In Sec. 2.1 we have presented the basic ideas of the probability of events. After defining events and the among-events relationships of union, intersection, collectively exhaustive, and mutually exclusive, we discussed the assignment of probabilities to events. We found the following:
1. The probability of the union of mutually exclusive events was the sum of their probabilities.
2. The probability of the union of two nonmutually exclusive events was the sum of their probabilities minus the probability of their intersection.
3. The probability of the intersection of two events is the product of their probabilities only if the two events are stochastically independent. In general, a conditional probability must appear in the product.
These basic definitions were manipulated to obtain a formula for the probability of the intersection of several events, the total probability theorem, and Bayes’ theorem.
The use of simple probability notions in engineering decisions was illustrated, using the weighted or expected-cost criterion.
Most civil-engineering problems deal with quantitative measures. Thus in the familiar deterministic formulations of engineering problems, the concepts of mathematical variables and functions of variables have proved to be useful substitutes for less precise qualitative characterizations. Such is also the case in probabilistic models, where the variable is referred to as a random variable. It is a numerical variable whose specific value cannot be predicted with certainty before an experiment. In this section we will first discuss its description for a single variable, and then for two or more variables jointly.
The value assumed by a random variable associated with an experiment depends on the outcome of the experiment. There is a numerical value of the random variable associated with every simple event defined on the sample space, but different simple events may have the same associated value of the random variable.† Every compound event corresponds to one or more or a range of values of the random variable.
In most engineering problems there is seldom any question about how to define the random variable; there is usually some “most natural” way. The traffic engineer in the car-counting illustration (Sec. 2.1.1) would say, “Let X equal the number of cars observed.” In other situations the random variable in question might be Y, the daily discharge of a channel, or Z, stress at yield of a steel tensile specimen. In fact, a random variable is usually the easiest way to describe most engineering experiments. The cumbersome subscripting of events found in previous illustrations could have been avoided by dealing directly with random variables such as demand level, concrete strength, etc., rather than with the events themselves.
The behavior of a random variable is described by its probability law, which in turn may be characterized in a number of ways. The most common way is through the probability distribution of the random variable. In the simplest case this may be no more than a list of the values the variable can take on (i.e., the possible outcomes of an experiment) and their respective probabilities.
Discrete probability mass function (PMF) When the number of values a random variable can take on is restricted to a countable number, the values 1, 2, 3, and 4, say, or perhaps all the positive integers, 0, 1, 2, . . ., the random variable is called discrete, and its probability law is usually presented in the form of a probability mass function, or PMF. This function pX(x) of the random variable X‡ is simply the mathematical form of the list mentioned above:
For example, having defined the random variable X to be the number of vehicles observed stopped at the traffic light, the engineer may have assigned probabilities to the events (Fig. 2.1.1) and corresponding values of X such that
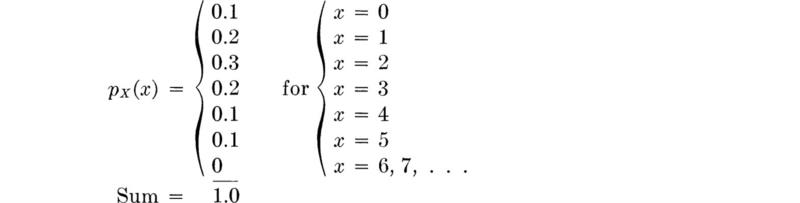
The probability mass function is usually plotted as shown in Fig. 2.2.1a, with each bar or spike being proportional in height to the probability that the random variable takes on that value.
To satisfy the three axioms of probability theory the probability mass function clearly must fulfill three conditions:
The sums in Eqs. (2.2.2b) and (2.2.2c) are, of course, only over those values of x where the probability mass function is defined.
Cumulative distribution function (CDF) An equivalent means† by which to describe the probability distribution of a random variable is through the use of a cumulative distribution function, or CDF. The value of this function FX(x) is simply the probability of the event that the random variable takes on value equal to or less than the argument:
For discrete random variables, i.e., those possessing probability mass functions, this function is simply the sum of the values of the probability mass function over those values less than or equal to x that the random variable X can take on.
Fig. 2.2.1 Probability law for traffic illustration. (a) Probability mass function PMF; (b) cumulative distribution function CDF.
The CDF of the random variable X, the number of stopped cars, with the PMF described on page 73, is a step function:
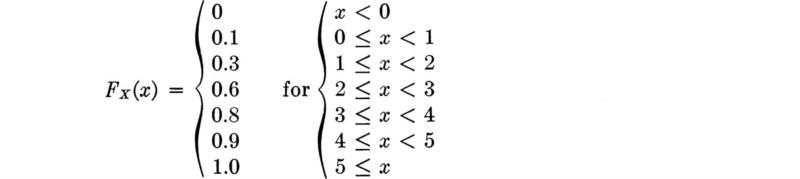
Although clumsy to specify analytically, such functions are easy to visualize. This discontinuous function is graphed in Fig. 2.2.1b. One would read from it, for example, that the probability of finding a line containing two or fewer vehicles is FX(2) = 0.6 [which equals pX(0) + pX(1) + pX(2) = 0.1 + 0.2 + 0.3] or that FX(3) = 0.8 [or FX(2) + pX(3) = 0.6 + 0.2].
The PMF can always be recovered if the CDF is given, since the former simply describes the magnitudes of the individual steps in the CDF. Formally,
![]()
where ![]() is a small positive number.
is a small positive number.
Continuous random variable and the PDF Although the discrete random variable is appropriate in many situations (particularly where items such as vehicles are being counted), the continuous random variable is more frequently adopted as the mathematical model for physical phenomena of interest to civil engineering. Unlike the discrete variable, the continuous random variable is free to take on any value on the real axis.† Strictly speaking, one must be extremely careful in extending the ideas of sample spaces to the continuous case, but conceptually the engineer should find the continuous random variable more natural than the discrete. All the engineer’s physical variables—length, mass, and time—are usually dealt with as continuous quantities. A flow rate might be 1000, 1001, 1001.1, or 1001.12 cfs. Only the inadequacies of particular measuring devices can lead to the rounding off that causes the measured values of such quantities to be limited to a set of discrete values.
The problem of specifying the probability distribution (and hence the probability law) of a continuous random variable X is easily managed. If the x axis is separated into a large enough number of short intervals each of infinitesimal length dx, it seems plausible that we can define a function fX(x) such that the probability that X is in interval x to x + dx is fx(x) dx. Such a function is called the probability density function, or PDF, of a continuous random variable.
Since occurrences in different intervals are mutually exclusive events, it follows that the probability that a random variable takes on a value in an interval of finite length is the “sum” of probabilities or the integral of fX(x) dx over the interval. Thus the area under the PDF in an interval represents the probability that the random variable will take on a value in that interval
The probability that a continuous random variable X takes on a specific value x is zero, since the length of the interval has vanished. The value of fX(x) is not itself a probability; it is only the measure of the density or intensity of probability at the point. It follows that fX(x) need not be restricted to values less than 1, but two conditions must hold:
These properties can be verified by inspection for the following example.
For illustration of the PDF see Fig. 2.2.2a. Here the engineer has called the yield stress of a standard tensile specimen of A36 steel a random variable Y. He has assigned this variable the triangular probability density function. The bases of the assumption of this particular form are observed experimental data and the simplicity of its shape. Its range (35 to 55 ksi) and mode (41 ksi) define a triangular PDF inasmuch as the area must be unity. Although simple in shape, this function is somewhat awkward mathematically
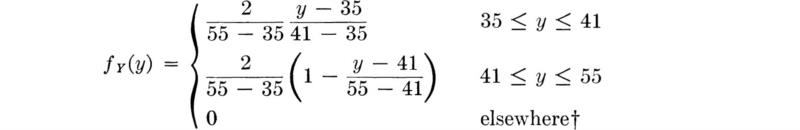
The shaded area between y2 and y3 represents the probability that the yield strength will lie in this range, and the shaded region from y = 35 to y1 is equal in area to the probability that the yield strength is less than y1. For the values of y1, y2, and y3 in the ranges shown in Fig. 2.2.2a,
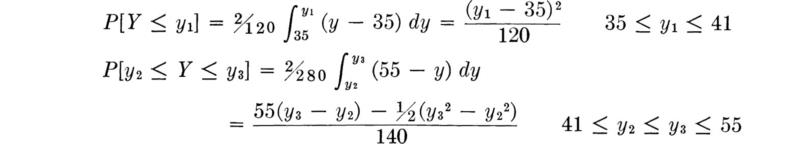
Continuous random variable and the CDF Again the cumulative distribution function, or CDF, is an alternate form by which to describe the probability distribution of a random variable. Its definition is unchanged for a continuous random variable:
The right-hand side of this equation may be written P[– ∞ ≤ X ≤ x] and thus, for continuous random variables [by Eq. (2.2.5)],
where u has been used as the dummy variable of integration to avoid confusion with the limit of integration x [the argument of the function FX(x)]. The CDF of the steel yield stress random variable is shown in Fig. 2.2.2b.
Fig. 2.2.2 Steel-yield-stress illustration, (a) Probability density function; (b) cumulative distribution function.
In addition, the PDF can be determined if the CDF is known, since fX(x) is simply the slope or derivative of FX(x):
It is sometimes desirable to use as models mixed random variables, which are a combination of the continuous and discrete variety. In this case one can always define a meaningful (discontinuous) CDF, but its derivative, a PDF, cannot be found without resort to such artifices as Dirac delta functions.† The mixed random variable will seldom be considered explicitly in this work, since an understanding of the discrete and continuous variables is sufficient to permit the reader to deal with this hybrid form. One use is pictured in Fig. 2.2.5.
The cumulative distribution function of any type of random variable—discrete, continuous, or mixed—has certain easily verified properties which follow from its definition and from the properties of probabilities:‡
Equation 2.2.14 implies that the CDF is a function which is monotonic and nondecreasing (it may be flat in some regions). Cumulative distribution functions for discrete, continuous, and mixed random variables are illustrated in Figs. 2.2.3 to 2.2.5.
Histograms and probability distribution models Although they may be similar in appearance, the distinction between histograms (Chap. 1) and density functions (Chap. 2) and the distinction between cumulative frequency polygons and cumulative distribution functions must be well understood. The figures presented in Chap. 1 are representations of observed empirical data; the functions defined here are descriptions of the probability laws of mathematical variables.
The histogram in Fig. 2.2.6, for example, might represent the observed annual runoff data from the watershed of a particular stream. [The first bar includes six observations (years) in which the runoff was so small as not to be measurable.] In constructing a mathematical model of a river basin, the engineer would have use for the stream information represented here. Letting the random variable X represent the annual runoff of this area, the engineer can construct any number of plausible mathematical models of this phenomenon. In particular, any one of the probability laws pictured in Figs. 2.2.3 to 2.2.5 might be adopted.
Fig. 2.2.3 Discrete random variable model reproducing histogram of Fig. 2.2.6. (a) Probability mass function; (b) cumulative distribution function.
Fig. 2.2.4 Continuous random variable approximately modeling histogram of Fig. 2.2.6. (a) Probability density function; (b) cumulative distribution function.
The first model, Fig. 2.2.3, within the restriction of a discrete random variable, reproduces exactly the frequencies reported in the histogram. The engineer may have no reason to alter his assigned probabilities from the observed relative frequencies, even though another sequence of observations would change these frequencies to some degree. The second model, Fig. 2.2.4, enjoys the computational convenience frequently associated with continuous random variables. In assigning probabilities to the mathematical model, the observed frequencies have been smoothed to a series of straight lines to facilitate their description and use. A third possible model, Fig. 2.2.5, employs, like the second model, a continuous random variable to describe the continuous spectrum of physically possible values of runoff, but also accounts explicitly for the important possibility that the runoff is exactly zero. Over the continuous range the density function has been given a smooth, easily described curve whose general mathematical form may be determined by arguments† about the physical process leading to the runoff.
Unfortunately it is not possible to state in general which is the “best” mathematical model of the physical phenomenon. The questions of constructing models and the relationship of observed data to such models will be discussed throughout this work. Commonly used models will be discussed in Chap. 3. The use of data to estimate the parameters of the model will be considered in Chap. 4, where we also discuss techniques for choosing and evaluating models when sufficient data is available.
Fig. 2.2.5 Mixed random variable approximately modeling characteristics of histogram of Fig. 2.2.6. (a) Graphical description of a mixed probability law; (b) cumulative distribution function.
Fig. 2.2.6 Histogram of observed annual runoff (60-year record).
Often distributions of interest are developed from assumptions about underlying components or “mechanisms” of the phenomenon. Two examples follow. A third illustration draws the PDF from a comparison with data.
Illustration: Load location An engineer concerned with the forces caused by arbitrarily located concentrated loads on floor systems might be interested in the distribution of the distance X from the load to the nearest edge support. He assumes that the load will be located “at random,” implying here that the probability that the load lies in any region of the floor is proportional only to the area of that region. He is considering a square bay 2a by 2a in size.
From this assumption about the location of the load, we can conclude (see Fig. 2.2.7) that
Fig. 2.2.7 Floor-system illustration. Shaded region is area in which distance to nearest edge is equal to or less than x.
which is simply a triangle. That this is a proper probability distribution is verified by noting that at x = 0, FX(0) = 0, and at x = a, FX(a) = 1.
Illustration: Quality control Specification limits on materials (e.g., concrete, asphalt, soil, etc.) are often written recognizing that there is a small, “acceptable” probability p that an individual specimen will fail to meet the limit even though the batch is satisfactory. As a result more than one specimen may be called for when controlling the quality of the material. What is the probability mass function of N, the number of specimens which will fail to meet the specifications in a sample of size three when the material is satisfactory? The probability that any specimen is unsatisfactory is p.
Assuming independence of the specimens,

This last expression follows from the fact that any one of the three sequences {s,s,u}, {s,u,s}, {u,s,s} (where s indicates a satisfactory specimen and u an unsatisfactory one) will lead to a value of N equal to 1, and each sequence has probability of occurrence p(1 – p)2. Similarly,
![]()
These four terms can be expressed as a function:
This function is plotted in Fig. 2.2.8 for several values of the parameter p. (We will study distributions of this general form in Sec. 3.1.2.)
That the PMF is proper for any value of p can be verified by expanding the individual terms and adding them together by like powers of p. The sum is unity.
In quality-control practice, of course, the engineer must make a decision based on an observation of, say, two bad specimens in a sample size of three about whether the material meets specifications or not. If, under the assumption that the material is satisfactory, the likelihood of such an event is, in fact, calculated to be very small, the engineer will usually decide (i.e., act as if) the material is not satisfactory.
Illustration: Annual maximum wind velocity A structural engineer is interested in the design of a tall tower for wind loads. He obtains data for a number of years of the maximum annual wind velocity near the site and finds that when a histogram of the data is plotted, it is satisfactorily modeled from a probability viewpoint by a continuous probability distribution of the negative exponential form.† If X is maximum annual wind velocity, the PDF of X is of the form:
Fig. 2.2.8 Quality-control illustration. Plots of
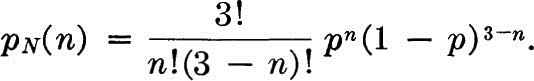
![]()
where k is a constant which can be found by recognizing that the integral of fX(x) over 0 to ∞ must equal unity. Hence
![]()
or
![]()
yielding
The CDF is found by integration:
The record shows that the probability of maximum annual wind velocities less than 70 mph is approximately 0.9. This estimate affords an estimate of the parameter λ. (Other methods for parameter estimation are discussed in Chap. 4.)

Then,
The PDF and CDF of X are shown in Fig. 2.2.9.
One minus FX(x) is important because design decisions are based on the probability of large wind velocities. Define † the complementary distribution function as
GX(x) is the probability of finding the maximum wind velocity in any year greater than x. The probability of a maximum annual wind velocity between 35 and 70 mph is indicated on the PDF of Fig. 2.2.9 along with the probability of a maximum annual wind velocity equal to or greater than 140 mph. Equation (2.2.23) can be used to determine numerical values of these probabilities. Their use in engineering design will be discussed in Secs. 3.1 and 3.3.3.
In Sec. 2.1 we discussed examples, such as counting cars and counting trucks, in which two-dimensional sample spaces are involved. When two or more random variables are being considered simultaneously, their joint behavior is determined by a joint probability law, which can in turn be described by a joint cumulative distribution function. Also, if both random variables are discrete, a joint probability mass function can be used to describe their governing law, and if both variables are continuous, a joint probability density function is applicable. Mixed joint distributions are also encountered in practice, but they require no new techniques.
Fig. 2.2.9 Wind-velocity illustration, (a) PDF of X and (b) CDF of X (X is maximum annual wind velocity).
Joint PMF The joint probability mass function pX,Y(x,y) of two discrete random variables X and Y is defined as
It can be plotted in a three-dimensional form analogous to the two-dimensional PMF of a single random variable. The joint cumulative distribution function is defined as
Consider an example of two discrete variables whose joint behavior must be dealt with. One, X, is the random number of vehicles passing a point in a 30-sec time interval. Variability in traffic flow is the cause of delays and congestion. The other random variable is Y, the number of vehicles in the same 30-sec interval actually recorded by a particular, imperfect traffic counter. This device responds to pressure on a cable placed across one or more traffic lanes, and it records the total number of such pressure applications during successive 30-sec intervals. It is used by the traffic engineer to estimate the number of vehicles which have used the road during given time intervals. Owing, however, to dynamic effects (causing wheels to be off the ground) and to mechanical inability of the counter to respond to all pulses, the actual number of vehicles X and the recorded number of vehicles Y are not always in agreement. Data were gathered in order to determine the nature and magnitude of this lack of reliability in the counter. Simultaneous observations of X and Y in many different 30-sec intervals led to a scattergram (Sec. 1.3). The engineer adopted directly the observed relative frequencies as probability assignments in his mathematical model,† yielding the joint probability mass function graphed in Fig. 2.2.10. Notice by the strong probability masses on the diagonal (0, 0; 1, 1; etc.) that the counter is usually correct. Note too that it is not possible for Y to take on a value greater than X in this example. The joint CDF could also be plotted, appearing always something like an exterior corner of an irregular staircase, but it seldom proves useful to do so.
Fig. 2.2.10 Joint PMF of actual traffic and traffic recorded by counter.
The probability of any event of interest is found by determining the pairs of values of X and Y which lead to this event and then summing over all such pairs. For example, the probability of C, the event that an arbitrary count is not in error, is
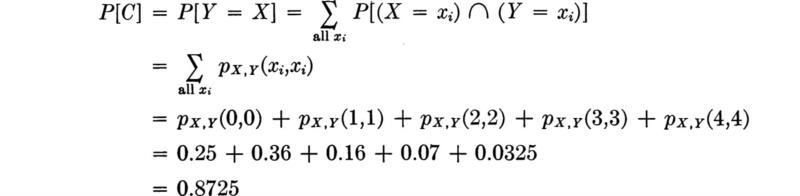
The probability of an error by the counter is
![]()
This probability is most easily calculated as
![]()
Since, to be properly defined,
Marginal PMF A number of functions related to the joint PMF are of value. The behavior of a particular variable irrespective of the other is described by the marginal PMF. It is found by summing over all values of the disregarded variable. Formally,
Similar expressions hold for the marginal distribution of Y.
Fig. 2.2.11 (a) Marginal PMF of actual traffic X and (b) marginal PMF counter response Y.
In the example here the distribution of X, the actual number of cars, is found for each value x by summing all spikes in the y direction. For example,
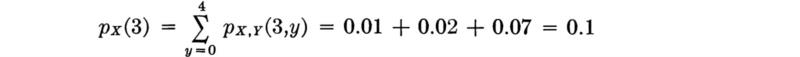
The marginal distributions of X and Y are plotted on Fig. 2.2.11. It should be pointed out that generally the marginal distributions are not sufficient to specify the joint behavior of the random variables. In this example, the joint PMF requires specification of (5)(5) = 25 numbers, while the two marginal distributions contain only 5 + 5 = 10 pieces of information. The conditions under which the marginals are sufficient to define the joint will be discussed shortly.
Conditional PMF A second type of distribution which can be obtained from the joint distribution is also of interest. If the value of one of the variables is known, say Y = y0, the relative likelihoods of the various values of the other variable are given by pX,Y(x,y0). If these values are renormalized so that their sum is unity, they will form a proper distribution function. This distribution is called the conditional probability mass function of X given Y, PX|Y(x,y). The normalization is performed by dividing each of the values by their sum. For Y given equal to any particular value y,
(The function is undefined if pY(y) equals zero.) Notice that the denominator is simply the marginal distribution of Y evaluated at the given value of Y. The conditional PMF of X is a proper distribution function in x, that is,
and
The conditional distribution of Y given X is, of course, defined in a symmetrical way.
It is the relationship between the conditional distribution and the marginal distribution that determines how much an observation of one variable helps in the prediction of the other. In the traffic-counter example, our interest is in X, the actual number of cars which have passed in a particular interval. The marginal distribution of X is initially our best statement regarding the relative likelihoods of the various possible values of X. An observation of Y (the mechanically recorded number) should, however, alter these likelihoods. Suppose the counter reads Y = 1 in a particular interval. The actual number of cars is not known with certainty, but the relative likelihoods of different values are now given by PX,Y(x,1) or 0, 0.36, 0.03, 0.01, and 0 for x equal, to 0, 1, 2, 3, and 4, respectively. Normalized by their sum, these likelihoods become the conditional distribution PX|Y(x,1), which is plotted in Fig. 2.2.12. As expected, the probability is now high that X equals 1, but the imperfect nature of the counter does not permit this statement to be made with absolute certainty. The better the counter, the more peaked it will make this conditional distribution relative to the marginal distribution. In the words of Sec. 2.1, the more closely the measured quantity (here Y) is related or correlated with the quantity of interest (here X), the more “sharply” can we predict X given a measured value F.
Other conditional distributions It is of course true that any number of potentially useful conditional distributions can be constructed from a joint probability law depending on the event conditioned on. Thus one might seek the distribution of X given that Y is greater than y:
Fig. 2.2.12 Conditional PMF of traffic given that the counter reads unity.
or the conditional distribution of Y given that X was in a particular interval:
We will encounter examples of such conditional distributions at various points in this text. Their treatment and meaning, however, is obvious once the notation is defined. In this notational form the fundamental conditional PMF [Eq. (2.2.29)] becomes
![]()
Joint PMF from marginal and conditional probabilities As mentioned before with regard to events, conditional probabilities are often more readily determined in practice than are the joint probabilities. Together with one of the marginal PMF’s a conditional PMF can be used to compute the joint PMF, since, from Eq. (2.2.29),
Illustration: Analytical approach to traffic-counter model We shall illustrate the use of the previous equation by showing that the joint distribution in the traffic-counter example might have been determined without data by constructing a mathematical model of the probabilistic mechanism generating the randomness. A commonly used model of traffic flow (to be discussed in Sec. 3.2.1) suggests that the number of cars passing a fixed point in a given interval of time has a discrete distribution of the mathematical form
where v is the average number of cars in all such intervals. If it is assumed, too, that each vehicle is recorded only with probability p, then in Sec. 3.1.2 we shall learn that the conditional distribution of Y given X = x must be
[The argument is a generalization of that which led to Eq. (2.2.18).] Hence we need data or information sufficient only to estimate v, which is related to the average flow, and p, the unreliability of the counter, rather than all the values in the joint PMF. This is true because the joint PMF follows from the marginal and conditional above:
Without being able to argue through the conditional PMF, it would have been extremely difficult for the engineer to derive this complicated joint PMF directly. For v = 1.3 cars and p = 0.9, its shape is very nearly that given in Fig. 2.2.11, although the sample space now extends beyond 4 to infinity. It is not expected or important at this stage that the reader absorb the details of this model. It is brought up here to illustrate the utility of the conditional distribution and to display the “more mathematical” form of some commonly encountered discrete distributions. It points out that, if the physical process is well understood, the engineer may attempt to construct a reasonable model of the generating mechanism involving only a few parameters (here v and p), rather than rely on observed data to provide estimates of all the probability values of the distribution function.
Joint PDF and CDF The functions associated with jointly distributed continuous random variables are totally analogous with those of discrete variables, but with density functions replacing mass functions. Using the same type of argument employed in Sec. 2.2.1, the probability that X lies in the interval {x, x + dx} and Y lies in the interval {y, y + dy} is fX,Y(x,y) dx dy. This function fX,Y(x,y) is called the joint probability density function.
The probability of the joint occurrence of X and Y in some region in the sample space is determined by integration of the joint PDF over that region. For example,
This is simply the volume under the function fX,Y(x,y) over the region. If the region is not a simple rectangle, the integral may become more difficult to evaluate, but the problem is no longer one of probability but calculus (and all its techniques to simplify integration, such as change of variables, are appropriate).
Clearly the joint PDF must satisfy the conditions
The joint cumulative distribution function is defined as before and can be computed from the density function by applying Eq. (2.2.38). Thus
in which dummy variables of integration, x0 and y0, have been used to emphasize that the arguments of the CDF, x and y, appear in the limits of the integral. The properties of the function are analogous to those given in Eqs. (2.2.11) to (2.2.15) for the CDF of a single variable.
It should not be unexpected that, as in Sec. 2.2.1, the density function is a derivative of the cumulative function, now a partial derivative,
Marginal PDF As with the discrete random variables, one frequently has need for marginal distributions. To eliminate consideration of Y in studying the behavior of X, one need only integrate the joint density function over all values of Y and determine the marginal PDF of X, fX(x):
The marginal cumulative distribution function of X, FX(x), is, consequently,
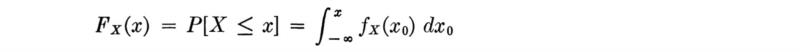
or
which implies
![]()
Symmetrical results hold for the marginal distribution of Y.
Conditional PDF If one is given the value of one variable, Y = y0, say, the relative likelihood of X taking a value in the interval x, x + dx is fX,Y(x,y0) dx. To yield a proper density function (i.e., one whose integral over all values of x is unity) these values must be renormalized by dividing them by their sum, which is
![]()
In this manner we are led, plausibly if not rigorously,† to the definition of the conditional PDF of X given Y as
The conditional cumulative distribution is
As with discrete variables, distributions based on other conditioning events, for example, ![]() may also prove useful. Their definitions and interpretations should be obvious.
may also prove useful. Their definitions and interpretations should be obvious.
Sketches of some joint PDF’s appear in Fig. 2.2.13 in the form of contours of equal values. Graphical interpretations of marginal and conditional density functions also appear there.
Fig. 2.2.13 Three types of joint PDF’s illustrating the relationships between the two random variables, (a) Contours (higher values of X usually occur with lower values of Y); (b) marginal PDF’s (higher values of X occur about equally with higher and lower values of Y); (c) cross sections at y = y0 and y = y1 (higher values of X usually occur with higher values of Y).
As an illustration of joint continuous random variables, consider the flows X and Y in two different streams in the same day. Interest in their joint probabilistic behavior might arise because the streams feed the same reservoir. If, as in the case in Fig. 2.2.13c, high flows in one stream are likely to occur simultaneously with high flows in the other, their joint influence on the reservoir will not be the same as it would if this were not the case. Assume that the joint distribution in this simplified illustration is that shown in Fig. 2.2.14. By inspection, its equation is
Fig. 2.2.14 Joint PDF of two stream flows.
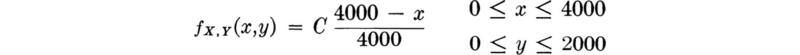
The constant, C = 2.5 × 10–7, was evaluated after the shape was fixed so that the integral over the entire sample space would be unity.
The probability of such events as “the flow X is more than twice as great as the flow Y” can be found by integration over the proper region. The portion of the sample space where this is true is shown shaded in Fig. 2.2.15a. The probability of this event is the volume under the PDF over this region, Fig. 2.2.15b. Formally,
![]()
By carrying out the integrations or by inspection of the volume, knowing it to be (⅓) (area of base) (height):
![]()
The marginal distributions of X and Y are formally
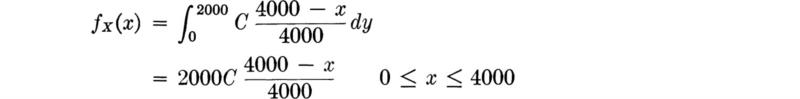
and
![]()
These functions are plotted in Fig. 2.2.16. Their shapes could have been anticipated by inspection of the joint PDF.
Without further information, prediction of the flow X must be based on fX(x). It might be, however, that the engineer has in mind using an observation of Y (the flow in the “smaller” stream) to predict X more “accurately,” just as the traffic engineer used an inexpensive, but unreliable, mechanical counter to provide a sharper knowledge of the number of vehicles which passed. As we have seen, the relationship between the conditional distribution function and the marginal distribution provides a measure of the information about X added by the knowledge of F. The conditional PDF of X given Y is
Fig. 2.2.15 Stream-flow illustration, (a) Sample space showing the event X ≥ 2Y; (b) volume equal to P[X ≥ 2Y]
Fig. 2.2.16 Marginal distributions of stream flow from joint PDF of Fig. 2.2.14. (a) Marginal PDF of X; (b) Marginal PDF of Y.
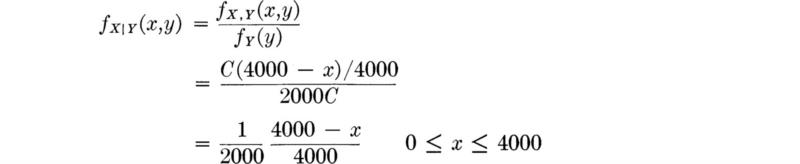
Notice that this is unchanged from the marginal distribution fX(x). The knowledge of Y has not altered the distribution of X and hence has not provided the engineer any new information in his quest to predict or describe the behavior of X. This case is an example of a very important notion.
Independent random variables In general, if the conditional distribution fX|Y(x,y) is identical to the marginal distribution fX(x), X and Y are said to be (stochastically) independent random variables. Similarly, for discrete variables, if, for all values of y
then X and Y are independent. The notion of independence of random variables is directly parallel to that of independence of events, for recall that Eq. (2.2.46) can be written in terms of probabilities of events as
If the random variables X and Y are independent, events related to X are independent of those related to Y. As a result of the definition above, the following statements hold if X and Y are independent and continuous (analogous relationships for discrete or mixed random variables can be derived):
As with events, in engineering practice independence of two or more random variables is usually a property attributed to them by the engineer because he thinks they are unrelated. This assumption permits him to determine joint distribution functions from only the marginals [Eq. (2.2.50)]. In general this is not possible, and both a marginal and a conditional are required.
The concept of probabilistic independence is central to the successful application of probability theory. From a purely practical point of view, the analysis of many probabilistic models would become hopelessly complex if the engineer were unwilling to adopt the assumption of independence of certain random variables in a number of key situations. Many examples of assumed independence of random variables will be found in this text.
Three or more random variables Attention has been focused in this section on cases involving only two random variables but, at least in theory, the extensions of these notions to any number of jointly distributed random variables should not be difficult. In fact, however, the calculus—the partial differentiation and multiple integrations over bounded regions—may become unwieldy. Many new combinations of functions become possible when more variables are considered. A few should be mentioned for illustration. For example, with only three variables X, Y, Z with joint CDF fX,Y,Z(x,y,z) there might be interest in joint marginal CDF’s, such as
as well as in simple marginal CDF’s, such as
Joint probability density functions are, as above, partial derivatives:†
Joint conditional PDF’s are also now possible, and they are defined as might be expected:
The simple conditional PDF follows this pattern:
If the random variables X, Y, and Z are mutually independent,‡
and conditional distributions reduce to marginal or joint PDF’s. For example,
Illustration: Reliability of a system subjected to n random demands In a capacity-demand situation such as those discussed in Sec. 2.1, it is often the case that the system is subjected to a succession of n demands (annual maximum flows, or extreme winds, for example). Assuming that these random variables D1, D2, . . ., Dn are independent and identically distributed, and that the random capacity C is independent of all these demands, we can find the probability of the “failure” event, A = [at least one of the n demands exceeds the capacity], as follows. Assume the random variables are all discrete.
Expanding, using Eq. (2.1.12),
Since capacity C is assumed independent of the Di,
Since the Di are assumed mutually independent,
![]()
and since the Di are assumed identically distributed (say, all distributed like a random variable denoted simply D),
Thus
For example, if the PMF’s of D and C have values at the relative positions shown in Fig. 2.2.17, then
Assuming that np1 and ![]() are small compared with unity,
are small compared with unity,
Assuming that ![]() is small compared with 1,
is small compared with 1, ![]() is small compared to
is small compared to ![]()
Depending on the magnitudes of p1p2, ![]() the last term may or may not be negligible.
the last term may or may not be negligible.
The relative magnitudes and locations of the probability spikes in Fig. 2.2.17 are intended to be suggestive of the common design situation where c3 is the “intended” capacity expected by the designer and ![]() is the anticipated or typical “design” demand. Failure of the system will occur during the design lifetime of n demands if any of the following happens:
is the anticipated or typical “design” demand. Failure of the system will occur during the design lifetime of n demands if any of the following happens:
1. A demand ![]() rare in magnitude or unanticipated in kind, occurs at some time during the lifetime.
rare in magnitude or unanticipated in kind, occurs at some time during the lifetime.
Fig. 2.2.17 Distributions of demand and capacity. Positions of spikes on c axis are relative only.
2. An unusually low capacity c1 is obtained either through construction inadequacy or through a gross misjudgement by the engineer as to the design capacity which would result from his specified design.
3. There exists a combination or joint occurrence of a moderately higher demand ![]() and a capacity of the only moderately lower value c2.
and a capacity of the only moderately lower value c2.
After simplification and approximation these three events make their appearance as the three terms in Eq. (2.2.69).
Notice that in general the probability of a system failure increases with design life n; a system intended to last longer is exposed to a greater risk that one of the higher load values occurs in its lifetime. One term, ![]() , does not grow with n, however, since, if this very low capacity is obtained, the system will fail with certainty under the first demand. If the capacity is not this low, further demands do not increase the likelihood of failure due to such a source.
, does not grow with n, however, since, if this very low capacity is obtained, the system will fail with certainty under the first demand. If the capacity is not this low, further demands do not increase the likelihood of failure due to such a source.
Much of science and engineering is based on functional relationships which predict the value of one (dependent) variable given any value of another (independent) variable. Static pressure is a function of fluid density; yield force, a function of cross-sectional area; and so forth. If, in a probabilistic formulation, the independent variable is considered to be a random variable, this randomness is imparted to those variables which are functionally dependent upon it. The purpose of this section is to develop methods of determining the probability law of functionally dependent random variables when the probability law of the independent † variable is known.
The nature of such problems is best brought out through a simple, discrete example.
Solution by enumeration For several new high-speed ground-transportation systems it has been proposed to utilize small, separate vehicles that can be dispatched from one station to another, not on a fixed schedule, but whenever full. If the number of persons arriving in a specified time period at station A who want to go to station B is a random variable X, then Y, the number of vehicles dispatched from A to B in that period, is also a random variable, functionally related through the vehicles’ capacities to X. For example, if each vehicle carries two persons, then Y = 0 if X = 0 or 1; Y = 1 if X = 2 or 3; Y = 2 if X = 4 or 5, etc. (assuming that no customer is waiting at the beginning of the time period). A graph of this functional relationship is shown in Fig. 2.3.1a.
The probability mass function of Y, pY(y), can be determined from that of X by ennumeration of the values of X which lead to a particular value of Y. For example,
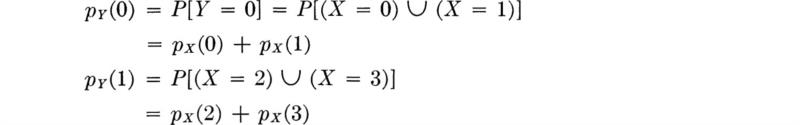
Or, in general,
A numerical example is shown in Fig. 2.3.1b and c.
In this and in all derived distribution problems, it is even easier to obtain the cumulative distribution function FY(y) from that of X. Thus
Fig. 2.3.1 High-speed transportation-system example, (a) Functional relationship between the number of arriving customers X and the number of dispatched vehicles Y; (b) PMF of number of arriving customers; (c) PMF of number of dispatched vehicles.
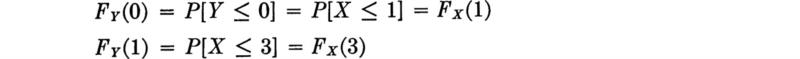
or
(It should be stated that this dispatching policy may not be a totally satisfactory one; it should perhaps be supplemented by a rule that dispatches half-full vehicles if the customer on board has been waiting more than a certain time.)
In this section we shall be concerned, then, with deriving the probability law of a random variable which is directly or functionally related to another random variable whose probability law is known. Owing to their importance in practice and in subsequent chapters, we shall concentrate on analytical solutions to problems involving continuous random variables. Problems involving discrete random variables can always be treated by enumeration as demonstrated above. In practical situations it may also prove advantageous to compute solutions to continuous problems in this same way, after having first approximated continuous random variables by discrete ones (Sec. 2.2.1).
One-to-one transformations For a commonly occurring class of problems it is possible to develop simple, explicit formulas as follows. If the function y = g(x) relating the two random variables is such that it always increases as x increases † and is such that there is only a single value of x for each value of y and vice versa, ‡ then Y is less than or equal to some value y0 if and only if X is less than or equal to some value x0, namely, that value for which y0 = g(x0). (See Fig. 2.3.2.)
Fig. 2.3.2 A monotonically increasing one-to-one function relating Y to X
Fig. 2.3.3 Derived distributions, construction-cost illustration, C = 10,000 + 100H. (a) Functional relationship between cost and time; (b) cumulative distribution function of H, given, and C, derived; (c) probability density function of H, given, and C, derived.
Suppose, for example, that for purposes of developing a bid, the distribution of the total cost C of constructing a retaining wall is desired. Assume that this cost is the cost of materials, which can be accurately predicted to be $10,000, plus the cost of a labor crew at $100/hr. The number of hours H to complete such a job is uncertain. The total cost is functionally related to H:
![]()
The relationship is monotonically increasing and one-to-one (Fig. 2.3.3). The cost is less than any particular value c only if the number of hours is less than a particular value h. This is the key to solving such problems.
Generally we can solve y = g(x) for x to find the inverse function† x = g–1(y), which gives the value of x corresponding to any particular value of y. (See Figs. 2.3.2 and 2.3.3.) For example, if the value of c corresponding to any given h is c = g(h) = 10,000 + 100h, the value of h corresponding to any given c is h = g–1(c) = (c – 10,000)/100. If, as another example, y = g(x) = aebx, then x = g–1(y) = (1/b) ln (y/a), in which ln (u) denotes the natural logarithm of u.
Under these conditions we can solve directly for the CDF of the dependent variable Y, since the probability that Y is less than any value of y is simply the probability that X is less than the corresponding value of x, that is, x = g–1(y). This probability can be obtained from the known CDF of X:

or
Thus, in the construction-cost example,

Suppose, for example, that the CDF of H is the parabolic function shown in Fig. 2.3.3b. Then, in the range of interest, we find FC(c) by simply substituting (c – 10,000)/100 for h in FH(h):
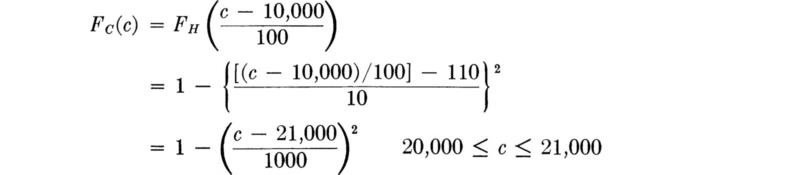
In general, when finding distributions of functionally related random variables, we must work with their CDF’s. To obtain a PDF of Y, the CDF must be found and then differentiated. A major advantage of the class of functional relationships ‡ we are considering, however, is hat we may pass directly from the PDF of one to the PDF of the other. Analytically we simply need to take the derivative of the CDF, Eq. (2.3.3):
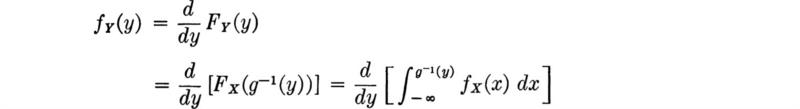
which can be shown to be
or, replacing g–1(y) by x, we obtain the more suggestive forms
or
In words, the likelihood that Y takes on a value in an interval of width dy centered on the value y is equal to the likelihood that X takes on a value in an interval centered on the corresponding value x = g–1(y), but of width dx = dg–1(y). As shown graphically in Fig. 2.3.4, these interval widths are generally not equal, owing to the slope of the function g(x) or g–1(y) at the value of y of interest. This slope and hence the ratio of dx to dy may or may not be the same for all values of y.
In our construction-cost example, the ratio dh/dc is constant because the relationship between C and H is linear (Fig. 2.3.3a):
![]()
Therefore, given the PDF of H, the PDF of C follows directly from Eq. (2.3.4) or Eq. (2.3.5):
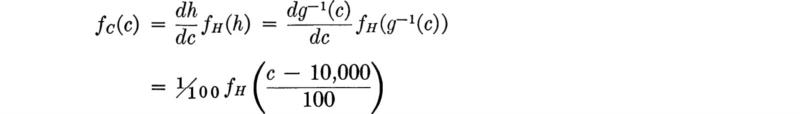
For example, the CDF of H given in Fig. 2.3.3b implies that the PDF of H is triangular (Fig. 2.3.3c):
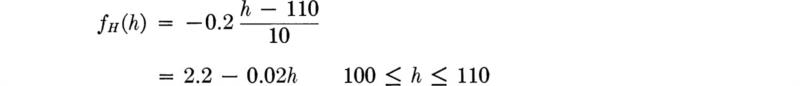
Fig. 2.3.4 Graphical interpretation of Eqs. (2.3.5) and (2.3.12) :fY(y) = |dx/dy|fX(x).
Therefore, substituting g–1(c) = (c – 10,000)/100 for h and multiplying by ![]() give
give

Note that care must be taken to obtain the region on the c axis in which the density function holds. In this case it is found simply by calculating the values of c corresponding to h = 100 and 110, the ends of the region on the h axis. The PDF of C is also shown in Fig. 2.3.3c. In this simple linear case, the shape of the density function has been left unchanged. As is demonstrated in the following illustration this is not generally the case.
Illustration: Bacteria growth for random time We illustrate here separately the two procedures, passing from CDF to CDF and passing from PDF to PDF. Under constant environmental conditions the number of bacteria Q in a tank is known to increase proportionately to eλT, where T is the time, λ is the growth rate, and the proportionality constant k is the population at time T = 0:†
If the time permitted for growth (as determined, say, by the time required for the charge of water in which the bacteria are living to pass through a filter) is a random variable with distribution function FT (t), t ≥ 0, then the final population has distribution function
Here, g–1(q) = (1/λ) ln (q/k).
Now, considering passing from PDF to PDF,
![]()
Note that the derivative of the inverse function is a function of q, not a constant. Then,
Clearly the population Q will be no smaller than the initial population k.
Suppose, as a specific example, that fT(t) is of a decaying type, say,
Then
These two distributions are sketched in Fig. 2.3.5. Note the change in shape in passing from one PDF to the other.
Fig. 2.3.5 Bacteria-growth illustration.
If the relationship between Y and X is one-to-one, but monotonically decreasing, Y will take on values less than any particular value y0 only if X takes on values greater than the corresponding value x0. The implications for the previous derivations can be shown easily by the reader. The final result for the relationship between PDF’s is simply that an absolute value sign needs to be placed about the dx/dy or dg–1(y)/dy in previous equations, yielding the general result:
The simplest and single most important application of this formula is for the case when the relationship between X and Y is linear:
Simple scale changes, such as feet to inches or Fahrenheit to Centigrade, are commonly arising examples. In this case, X = (Y – a)/b and |dx/dy| = |1/b|. Hence,
The effect of such a linear transformation is to retain the basic shape of the function, but to shift it and to expand or contract it.
General transformations Relationships Y = g(X), for which Eq. (2.3.13) holds, are very common in engineering, where an increase in one variable usually means either an increase or decrease in some dependent variable. Nevertheless in many situations a more complicated nonmonotonic or non-one-to-one relationship may be involved. The simple discrete illustration at the beginning of this section is an example. Although the relationship was nondecreasing, it was not one-to-one; values of X of either 0 or 1, for example, led to a single value of Y, namely, 0. In all such problems the reader is urged to deal directly with the cumulative distribution function of Y, as follows.
Mathematically, the problem is to find FY(y) given that Y = g(X) and given that X has CDF FX(x). Conceptually the problem is simple. By definition
![]()
but
where Ry is that region where g(x) is less than or equal to y. In Fig. 2.3.6a a representation of a general function y = g(x) is sketched. Any particular value of y, say y0, is represented by a straight horizontal line. To determine FY(y0) is to determine the probability that the random variable X falls in any of those intervals where the curve g(x) falls below the horizontal line, y = y0 If, for example, X were described by a continuous PDF as shown in Fig. 2.3.6b, FY(y0) would be equal to the crosshatched area under the density function in these intervals. Solution of the problem requires relating these intervals to each and every value y0.
Consider the following example. The kinetic energy K of a moving mass, say a simple structural frame vibrating under a dynamically imposed wind or vehicle load, is proportional to the square of its velocity V:
Fig. 2.3.6 Functions of random variables: general case.
in which m is the known mass of the object. Velocity may, of course, be positive or negative (e.g., right or left, up or down). The relationship is neither monotonic nor one-to-one, as shown in Fig. 2.3.7a. The probability that the kinetic energy will be less than a certain value k0 is evidently
The probability of the complementary event K > k0 is more easily calculated. This is 1 – FK(k):
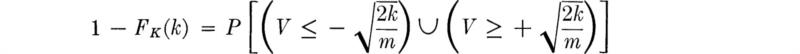
Since these events are mutually exclusive,
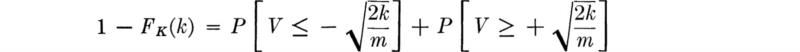
This result is true no matter what the distribution of V. As a specific case, suppose the velocity has been repeatedly measured and the engineer claims that the triangular-shaped distribution shown in Fig. 2.3.7b represents a good model of the random behavior of the velocity at any instant. By the symmetry of the distribution of V,
The limits of the values that K can take on, namely, 0 and ![]() follow from the minimum (0) and maximum (3) values of the absolute magnitude of the velocity. The density function of K can be found by differentiation of the CDF:
follow from the minimum (0) and maximum (3) values of the absolute magnitude of the velocity. The density function of K can be found by differentiation of the CDF:
This density function is shown in Fig. 2.3.7c.
In more complicated cases involving non-one-to-one transformations, required regions of integration may become difficult to determine and sketches of the problem are strongly recommended. If discrete or mixed random variables are involved (see, for example, the pump-selection illustration to follow in Sec. 2.4), sums may have to replace or supplement integration, but the formulation in terms of the cumulative distribution of Y remains unchanged. The determination of the PDF or PMF from the CDF follows by the techniques discussed in Sec. 2.2.
Frequently a quantity of interest to the engineer is a function of two or more variables which have been modeled as random variables. The implication is that the dependent variable is also random. For example, the spatial average velocity V in a channel is the flow rate Q divided by the area A. If Q and A have a given joint probability distribution, the problem becomes to find the probability law of V. The total number of vehicles Z on a particular transportation link may be the sum of those vehicles on two feeder links, X and Y.
Fig. 2.3.7 Energy-velocity illustration, Nonmonotonic Case. (a) Functional relationship between energy and velocity; (b) given PDF of velocity V; (c) derived PDF of kinetic energy K.
Clearly in a discrete case like the latter example we can use enumeration to calculate the PMF or CDF of Z. The probability that Z equals any particular value z, say 4, is the sum of the probabilities of all the pairs of values of X and Y which sum to 4, that is, (0,4), (1,3), (2,2), (3,1), and (4,0). These individual probabilities are given in the known joint PMF of X and Y. Similarly the CDF of Z at value z could be found by summing the probabilities of all pairs (x,y) for which x + y ≤ z. In difficult cases this approach may also prove computationally advantageous when dealing in an approximate way with continuous random variables. In this section we deal, however, with analytical solutions of problems involving continuous random variables.
Two approaches are considered and illustrated. One begins, as is generally appropriate, with the determination of the CDF of the dependent variable; the other makes use of the notions of the conditional distribution (Sec. 2.2.2) to go directly after the PDF of the dependent random variable.
Our problem, in general, is to find FZ(z) when we know Z = g(X,Y) and when the joint probability law of X and Y is also known.
Direct method In Sec. 2.3.1 we found the CDF of the dependent variable Z, say, at any particular value z0 by finding the probability that the independent variable X, say, would take on a value in those intervals of the x axis where g(x) ≤ z0. Now, by extension, since Z is a function of both X and a second variable Y, we must calculate FZ(z0) by finding the probability that X and Y lie in a region where g(x,y) ≤ z0.
An easily visualized example is the following. We wish to determine the CDF of Z, where Z is the larger of X and Y, or
If, for example, X and Y are the magnitudes of two successive floods or of the queue lengths of a two-lane toll station, then primary interest may lie not in X or Y in particular, but in the Z, the greater of the two, whichever that might be. To determine FZ(z) for any value z, it is necessary to integrate the joint PDF of the (assumed continuous) random variables X and Y over the region where the maximum of x and y is less than z. This is the same as the region where both x and y are less than z, that is, the region shown in Fig. 2.3.8.
Fig. 2.3.8 Z = max[X,Y] illustration.
The integral of fX,Y(x,y) over this region is, of course, simply FX,Y(z,z) [Eq. (2.2.41)]. If, as a special case, X and Y are independent and identically distributed† with common CDF FX(r),
In this case it is possible to determine the PDF of Z explicitly by differentiation
In words, this last result can be interpreted as the statement that “the probability that the maximum of two variables is in a small region about z is proportional to the probability that one variable X or Y is less than or equal to z while the other is in a small region about z.” Since this can happen in two mutually exclusive ways, the (equal) probabilities are added. The treatment of the maximum of a set of several random variables will be discussed more fully in Sec. 3.3.3.
If, for example, X and Y are independent and identically distributed annual stream flows, with common distribution,
implying
then the distribution of Z, the larger of the two flows, is
and
These density functions are sketched in Fig. 2.3.9 for ![]() acre-ft.
acre-ft.
Illustration: Distribution of the quotient As a second example, consider the determination of the probability law of Z when
In specific problems Z might be a cost-benefit ratio or a “safety factor,” the ratio of capacity to load. Proceeding as before to find the CDF of Z, assuming that X and Y are jointly distributed,
Fig. 2.3.9 PDF of stream flow of each of two rivers and PDF of largest stream flow, (a) Density function of stream flow, fX(x) = 0.001e–0.001x; (b) density function of largest stream flow.
where Rz is that region of the xy plane, the sample space of X and Y, where x/y is less than z. Such a region is shown shaded in Fig. 2.3.10 for a particular value of z. Other values of z would lead to other lines x/y = z through the origin. The limits of integration are of the same form for any value of z and follow from inspection of this figure:
Fig. 2.3.10 Derived-distribution illustration, Z = X/Y.
To carry out this integration may in fact be a troublesome task, particularly as the joint PDF of X and Y may be defined by different functional forms over different regions of the x and y plane. We shall give complete examples later in this section, but we prefer to avoid further details of calculus at this point as they serve only to confuse the probability theoretic aspects of the problem, which are complete in this statement, Eq. (2.3.31).
In this case we can again find an expression for the PDF of Z by differentiating with respect to z before carrying out the integration. Consider the first term
The second term is similar, lacking the minus sign. The terms may be combined to form
Again for specific functions fX,Y(x,y) the subsequent evaluation of the integral may be tedious, but it is not fundamentally a probability problem.
Distribution of sum X and Y by conditional distributions It is useful to have available the important results for the case when the dependent variable is the sum of two random variables. Sums of variables occur frequently in practice, e.g., sums of loads, of settlements, of lengths, of waiting times, or of travel times. Furthermore, their study is an important part of the theories of probability and mathematical statistics, as we shall see in Chaps. 3 and 4. In determining these results, an alternate, but less general, approach to finding directly the formula for the PDF of a continuous function of continuous random variables will be demonstrated. This method employs conditional probability density functions and a line of argument that often proves enlightening as well as productive.
We wish to determine the density function of
when the joint PDF of X and Y is known. Let us consider first the conditional density function of Z given that Y equals some particular value y. Given that Y = y, Z is
and the (conditional) distribution of X is
The density function of such a linear function of a single random variable (y being treated as a constant for the moment) is given in Eq. (2.3.15). Using the results found there, conditional on Y = y, the conditional PDF of Z is
The joint density function of any two random variables Z and Y can always be found by multiplying the conditional PDF of Z given Y by the marginal PDF of Y [Eq. (2.2.34)]:
Substituting Eq. (2.3.37),
But the right-hand side, being the product of a conditional and a marginal, is only the joint PDF of X and Y evaluated at z – y and y. Thus
In words, this result says, roughly, that the likelihood that Y = y and Z = X + Y = z equals the likelihood that Y = y and X = z – y.
The marginal of Z follows upon integration over all values of y [Eq. (2.2.43)]:
or
For the important special case when X and Y are independent, their joint PDF factors into
By the symmetry of the argument, it follows that it is also true that
or, if X and Y are independent,
Roughly speaking, this last equation states that the probability that Z lies in a small interval around Z is proportional to the probability that X lies in an interval x to x + dx times a factor proportional to the probability that Y lies in a small interval around z – x, the value of Y necessary to make X + Y equal z. This product is then summed over all values that X can take on. [Equation (2.3.45) is the type of integral known as the convolution integral. This form occurs time and time again in engineering, and it will be familiar already to the student who has studied the dynamics of linear structural, hydraulic, mechanical, or electrical systems.]
As mentioned above, equations such as Eqs. (2.3.24), (2.3.33), and (2.3.45) are in fact complete answers to the probability theory part of the problem of finding the distribution of the function of other random variables, but the completion of the problem, that is, carrying out the indicated integrations, may prove challenging, particularly since many practical PDF’s are defined by different functions over different regions. Illustrations follow.
Illustration: Distribution of total waiting time When a transportation system user must travel by two modes, say bus and subway, to reach his destination, a portion of this trip is spent simply waiting at stops or terminals for the arrivals of the two vehicles. Under certain conditions to be discussed in Sec. 3.2, it is reasonable to assume that the individual waiting times X and Y have distributions of this form
![]()
To determine the properties of the total time spent waiting for the vehicles to arrive we must find the PDF of Z = X + Y. Assuming independence of X and Y, we can apply Eq. (2.3.45):
![]()
Substitution of the functions takes some care, since they are, in fact, zero for negative values of their arguments. Since fX(x) is zero for negative values of x:
![]()
Since fY(y) is zero for y negative, fY(z – x) is zero for z – x negative or for x greater than z. Therefore,
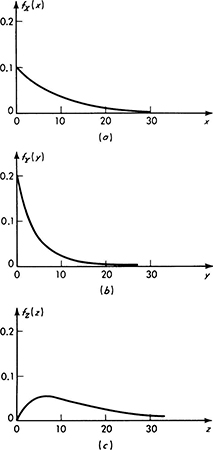
Fig. 2.3.11 Waiting-time illustration with Z = X + Y. (a) Bus waiting time, minutes; (b) subway waiting time, minutes; (c) total waiting time, minutes.
The density functions of X, Y, and Z are sketched in Fig. 2.3.11 for α = 0.1 min–1 and β = 0.2 min–1.
Illustration: Earthquake intensity at a site We are interested as the designers of a dam which is in an earthquake-prone region in studying the intensity of ground motion at the site given that an earthquake occurs somewhere in a circular region of radius r0 surrounding the site. The information about the geology of the region is such that it is reasonable to assume that the location of the source of the disturbance (the epicenter) is equally likely to be anywhere in the region; that is, the engineer assigns an equal probability to equal areas in the region and hence a constant density function over the circle. The constant value is 1/(πr02), yielding a unit volume under the function. The implication is that the density function of R, the radial distance from the site to the epicenter, has a triangular distribution
a fact the reader can verify formally by the techniques of this section.
We shall assume that historical data for the region suggest a density function of the form†
for Y, the Richter magnitudes of earthquakes of significant size to be of concern to the engineer. Magnitudes greater than 9 have not been observed. The equation relating an empirical measure of the intensity X of the ground motion at the site to the magnitude and distance of the earthquake we shall assume to be
reflecting the attenuation of intensity with distance from the epicenter. ‡ The distribution of X is the desired result.
We seek first the CDF of X,
in which Rx is the region in the ry plane where g(y,r) = c1 + c2y – c3 In r is less than x. For a given value of x this region is as shown in Fig. 2.3.12a. For such fixed values of x, it is possible to solve for the equation of the line bounding the region as a function of r:
Fig. 2.3.12 Earthquake-intensity illustration, (a) Rx: the region where g(y,r) = c1 + c2y – c3 ln r ≤ x for a particular value of x; (b) region where fY,R(y,r) is nonzero.

Hence, in general, the CDF of X is (for nonnegative random variables Y and R) found by integrating over this region:
![]()
This completes the formal probability aspects of the problem. The calculus of the integral’s evaluation proves more awkward.
In this particular case the joint density function of Y and R is positive only over the region shown in Fig. 2.3.12b. This causes the limits of the integrals to become far more complicated. As shown in Fig. 2.3.12 three cases, x1, x2, or x3, exist depending on whether the particular value of x creates a bounding curve passing out through the top of the rectangle, through its side, or not at all. In the first situation, where x is larger than x′ = c1 + 9c2 – c3 ln r0,
For x″ ≤ x ≤ x′ complicated forms of FX(x) and fX(x) result. For x ≤ x″, both functions are zero. For the values of the constants appropriate for Southern California (with r0 = 300 km) the CDF and PDF of X, the intensity of the ground motion at a site given that an earthquake of magnitude 5 to 9 occurs within this radius, are plotted in Fig. 2.3.13. Notice that as long as one is interested only in intensities in excess of 7.1 (i.e., in intensities with probability of occurrence, given an earthquake, of less than 2.5 percent) it is possible to deal with the distribution in the region in which its form is simple and tractable. (Other problems will be found throughout this text dealing with this question of seismic risk.)
Fig. 2.3.13 Probability distribution of intensity at site.
A variety of methods and problems in deriving distributions of random variables will go unillustrated here. The awkard analytical aspects far outweigh any new insights they provide into probability theory, †
The probabilistic portion of the derivation of the distributions of a function of one or more random variables may be a rather direct problem. The calculus needed to evaluate the resulting integrals, however, is frequently not tractable. In such circumstances one can often resort to numerical integration or other techniques beyond the interest of this work. One approximate method of solution of derived distribution problems is of immediate interest, however, because it makes direct use of their probabilistic nature§ to obtain artificially the results of many repeated experiments. The histogram of these results will approximate the desired probability distribution. This, the Monte Carlo method, or simulation, is best presented by example.
Simulating a discrete random variable First let us find simply the distribution of the ratio of the number of wet weeks to the number of dry weeks in a year on a given watershed, when N, the total number of rainy weeks with at least a trace of rain, is a random variable with a probability mass function given by¶
We seek the distribution, then, of the ratio of wet to dry, or
We could use, following the methods of Sec. 2.3.1, simple enumeration of all possible values of N and the corresponding values of Y to find the PMF of Y. For illustrative purposes we are going to determine an approximation of the distribution of Y by carrying out a series of experiments, each of which simulates a year or an observation of N. In each experiment we shall artificially sample the distribution of the random variable N to determine a number n, the number of rainy weeks which occurred in that “year.” Then we can calculate y = n/(52 – n) to find the ratio of the number of wet to dry weeks in that “year,” that is, an observation of the random variable Y. A sufficient number of such experiments will yield enough data to draw a histogram (Sec. 1.1), which we can expect to approximate the shape of the mass function pY(y). It remains to be shown how the sampling is actually carried out.
The experimental sampling of mathematically defined random variables is accomplished by selecting a series of random numbers, each of which is associated with a particular value of the random variable of interest. Random numbers are generated in such a manner that each in the set is equally likely to be selected. The numbers 1 to 6 on a perfect die are, for example, a set of random numbers. Divide the circumference of a dial into 10 equal sectors labeled 0 to 9 (or 100 equal sectors labeled 0 to 99, etc.), attach a well-balanced spinner, and you have constructed a mechanical random number generator. Various ingenious electrical and mechanical devices to generate random numbers have been developed, and several tables of such numbers are available (see Table A.8), but most random number generation in practice is accomplished on computers through numerical schemes, †
To relate the value of the random variable of interest N to the value obtained from the random number generator, one must assign a table of relationships (a mapping) which matches probabilities of occurrence. Assume that a random number generator is available which produces any of the numbers 0 to 9999 with equal probability 1/10,000. On the other hand, the probability that N takes any of the various values 0, 1, 2, . . ., 52 can be determined by evaluating its probability mass function. For example,


Then values of the random numbers and the random variable N might be assigned as follows:
If the first random number generated happened to be 4751, the number n of rainy weeks in that simulated year would be taken as 20. Then the corresponding value of Y would be ![]() Repetition of these “experiments,” a process ideally suited for digital computers, will yield y1, y2, y3,, a sample of observed values of Y. A histogram (Sec. 1.1) of these values will approximate the true PMF of Y. For example, the 100 random numbers in Table 2.3.1 lead to the indicated values of N, Y, and the histogram in Fig. 2.3.14. The exact PMF is plotted in the same figure.
Repetition of these “experiments,” a process ideally suited for digital computers, will yield y1, y2, y3,, a sample of observed values of Y. A histogram (Sec. 1.1) of these values will approximate the true PMF of Y. For example, the 100 random numbers in Table 2.3.1 lead to the indicated values of N, Y, and the histogram in Fig. 2.3.14. The exact PMF is plotted in the same figure.
Fig. 2.3.14 Probability mass functions of Y, exact and by simulation.
Note that if another set of 100 values were generated, a histogram similar in shape but different in details is to be expected. In short, the histograms are themselves observations of random phenomena. Practical questions which the simulator must face are, “How much variability is there in such histograms?” “What can I safely conclude about the true PMF from one observed histogram?” “How does the shape of an observed histogram behave probabilistically as the sample size increases?” These and similar questions will be considered in Secs. 4.4 and 4.5.
Illustration: Total annual rainfall Monte Carlo techniques become particularly useful when the relationships among variables are complicated functions, involve many random variables, or, as in the next example, themselves depend upon a random element. In this illustration it is desired to determine the distribution of total annual rainfall T when the rainfall Ri in the ith rainy week is given by
and when the total number of rainy weeks in a year is N, as before, a random variable with the distribution given in Eq. (2.3.52). This problem might be part of a large study of the performance of a proposed irrigation system. The relationship between T, N, and the Ri’s is:
That is, T is the sum of a random number of random variables. (It is assumed, for convenience, that rainfalls in rainy weeks are identically distributed, mutually independent, and independent, too, of the number of rainy weeks in the year.)
In Sec. 2.3.2, we saw that the determination of the sum of even two random variables can be difficult enough. Analytical solutions to the type of problem here, are, in fact, feasible (Sec. 3.5.3), but we propose to determine the distribution of T experimentally by simulating a number of years and producing a sample of values of T. In each year we shall sample the random variable N to determine a particular number of rainy weeks n. Then the random variables Ri will be sampled that number of times and the n values summed to get one observation of T. This total experiment will be repeated as accuracy requires.
The sampling of the discrete variable N has been discussed. Several schemes for relating values of random numbers to values of the continuous random variable Ri can be considered. One approach simply approximates the continuous distribution of Ri by a discrete one. Equal intervals of r, say 0.0 to 0.9, 0.10 to 0.19, etc., might be considered, the probability of Ri taking on a value in each interval evaluated, and a corresponding proportion of the random numbers assigned to be associated with the interval. The middle value† of each interval can then be used as the single representative value of the entire interval. If a random number associated with the interval were drawn, this representative value would be accumulated with others to determine an observed value of T.
Alternatively, a preferable scheme calls for dividing the range of r into intervals of equal probability. The fineness of the intervals chosen depends only on the accuracy desired.† Assume here that 10 intervals are considered sufficient. Then the dividing lines between intervals are 0, r1, r2, . . ., r10 such that

From tables of e–x we obtain intervals:
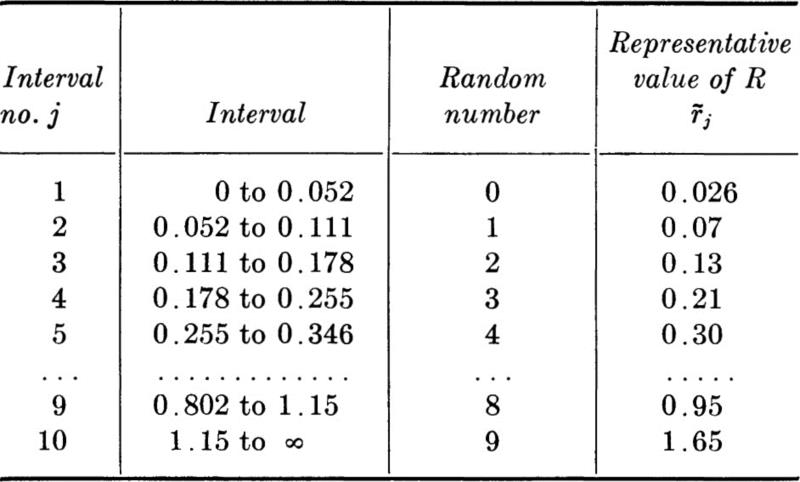
Corresponding values of the random numbers are assigned as shown.
In this case, where the number of intervals is small, the determination of the representative value ![]() for each interval is most important. What, for example, should be used as the representative value of the last interval? The center of gravity is a logical choice. The centroid of the segment of the density function over the last interval is
for each interval is most important. What, for example, should be used as the representative value of the last interval? The center of gravity is a logical choice. The centroid of the segment of the density function over the last interval is

Fig. 2.3.15 Partition of the distribution of rainfall R for simulation. (a) CDF of R; (b) PDF of R.
The use here of these centroids will be justified in the following section, where it will be known as the “conditional mean” of Ri given that 1.15 ≤ Ri ≤ ∞. This and other representative values appear in the previous list, and the dissection of the PDF and CDF of R is illustrated in Fig. 2.3.15a and b.
In computer-aided simulation a large number of intervals are normally used (e.g., 1 million, if six-digit random numbers are generated). In this case it is common to use simply the division values rj as the representative values ![]() A random number is generated on the interval 0 to 1, say 0.540012. The corresponding value r is found by solving F(r) = 0.540012 for r, that is, by finding the inverse of F(r). In this example we have
A random number is generated on the interval 0 to 1, say 0.540012. The corresponding value r is found by solving F(r) = 0.540012 for r, that is, by finding the inverse of F(r). In this example we have
![]()
implying
![]()
This same procedure is valid no matter what the form of the CDF of the random variable, † It is not always feasible, however, to obtain a closed-form analytical expression for the inverse of the CDF of a random variable. In this case one can find the value of x corresponding to the randomly selected value of FX(x) by hand through graphical means or by computer through “table lookup” schemes. Various other techniques are also used to generate sample values of random variables with particular distributions. For example, a sample of a “normally distributed” random variable (Sec. 3.3.1) is usually obtained in computer simulation by adding 12 or more random numbers. The justification for this procedure will become clear in Sec. 3.3.1.
In the first experiment in this example a random number 4751 was generated, and a sample value of N, n = 20, determined. Consequently, to complete this first experiment, 20 random numbers must be generated and the corresponding values of the Ri listed and accumulated to determine a sample value of T. Such a sequence is shown in Table 2.3.2 using the divisions shown in Fig. 2.3.15. The table represents “1 year” of real-time observation.
Again, repetition of such experiments will yield a sample of values of T whose histogram is an approximation of fT(t) and whose frequency polygon † is an approximation to FT(t). Figure 2.3.16 shows the results of such a series of experiments for several sample sizes and two different numbers of histogram intervals of r. Analytical treatment of aspects of this same problem will follow in Sec. 2.4 and Chap. 3.