The first four chapters of this text have been concerned with probability models and statistical analyses of these models. The emphasis has been on finding a realistic description of an unpredictable, natural phenomenon. Although scientific description or explanation may be an intermediate goal, in engineering practice the use of any analysis is ultimately in situations where the engineer must make a decision. This decision might be the choice of: (1) a flood-control channel’s dimensions, when future flood magnitudes are unpredictable; or (2) the decision of whether to install a traffic control at an intersection where the number of long gaps between randomly passing vehicles determines the delays and safety risks to crossing vehicles on an intersecting street; or (3) the choice among alternate pavement designs when the amount of useful aggregate in the available borrow area is not well established. In this chapter and the next we shall deal with the analysis of decision making when unknown or unpredictable elements are involved in decisions.
In Chaps. 2 and 3 there was little discussion of the influence of the particular application and particular engineer on the description of the random variable. There was a tacit assumption that all engineers in all situations would arrive at substantially the same description of the random variable. In Chap. 4 it was recognized, however, that once we had left the world of purely mathematical models and were forced to relate these models to real data or to make elementary decisions about these models, there were no longer hard and fast rules of “correct” analysis. Two or more reasonable models may exist, different rules for choosing parameter estimators are available, and significance-test conclusions depend upon the convention for the choice of acceptable error probabilities. It is clear, then, that the particular engineer and hence the particular situation necessarily influence the results of applied probability and statistics. The discussions of the methods of previous chapters do not go far enough, however, in revealing the central role of engineering decisions and their influences.
In recent years a new philosophy of applied probability and statistics has been under development. This approach recognizes not only that the ultimate use of probabilistic methods is decision making but also that the individual, subjective elements of the analysis are inseparable from the more objective aspects. This new theory, Bayesian statistical decision theory, provides a mathematical model for making engineering decisions in the face of uncertainty. It derives its name from Thomas Bayes, an English mathematician who introduced the equation now used to relate certain probabilities in the decision model.
In this chapter we shall be concerned with situations where the consequences of a decision depend on some factor which is not known with certainty. We call this factor the ‘‘state of nature.” The factor might be the total settlement of the soil below a proposed bridge footing, or the fraction of a suburban population which will use a proposed rapid-transit system, or the average annual maximum daily rainfall in a stream’s watershed, or whether or not a potentially active geological fault exists in the bedrock several hundred feet below the site of a nuclear power plant. Recognizing that the uncertainty of what the true state of nature is can be expressed as probabilities, the engineer can analyze the alternative decisions facing him to determine which is the optimal choice. In this chapter, we present this method of analysis.
When uncertainty exists regarding the true state of nature, it is often feasible, but not necessarily economical, to obtain more information concerning the state. With the problems given above, for example, the engineer may use drill holes to learn the values of certain soil characteristics at a limited number of points below the footing; he may interview a representative group of the suburban population; he may install gauges and wait to collect several observations of the annual maximum daily rainfall; he may drill a pattern of holes hoping to intersect a fault plane and, if found, examine the recovered cores to assess the likelihood that it is potentially active. The data seldom permit a perfectly confident statement to be made about the true state of nature of interest, but they do provide new information.
Two major questions that we consider in this chapter are:
1. How to combine this new data with the previous probability assignments before making the decision analysis
2. Whether (and how) one should obtain more such information before making a final decision
Section 5.1 discusses the analysis of decisions with a given set of information. Sections 5.2 and 5.3 treat the processing of new or potential information. When this incorporation of new data has been completed, the method of analysis of the decision reverts to that given in Sec. 5.1.
In Chap. 6 we shall treat in some detail decision analysis when the consequences depend upon future outcomes of a process which generates a sequence of random variables, such as successive annual maximum floods or a sequence of concrete cylinders. The uncertain state of nature will be defined as the value of the parameters of the process. Information on the value of the parameters is made available through past observations of the sequence.
In this section we treat those situations in which a decision must be made based on the available information about nature. In later sections we treat the questions of, first, deciding whether more information should be obtained and, second, how the new information should be processed.
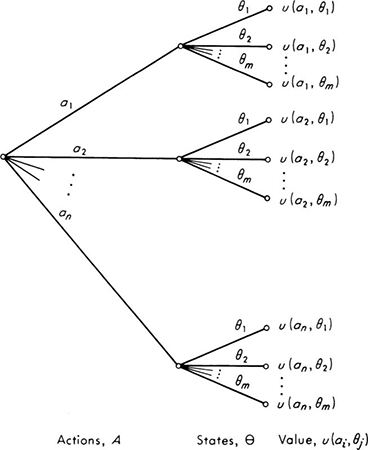
Components of the model Our concern is decision. What course of action should be taken when uncertainty exists regarding the “true state of nature,” i.e., when some aspects of the problem have been treated by the engineer as probabilistic? The decision-making process will be formulated as the process of choosing an action a from among the available alternative actions a1, a2, . . ., an, the members of an action space A. In practice this set or space will have already been reduced to a limited number by the engineer’s exclusion of all but the potentially optimal courses of action. Once the decision has been made, the engineer can only wait to see which state of nature θ in the space of possible states θ is the true one. As a result of having taken action a and having found true state θ, the engineer will receive value u(a, θ), a numerical measure (say, dollars) of the consequences of this action-state pair.
Fig. 5.1.1 Decision tree for discrete-state space.
This formulation is displayed graphically in Fig. 5.1.1 as a decision tree. The process can be viewed as a game: the engineer chooses an action, a state is chosen in a probabilistic manner “by chance,” and the engineer receives a payoff dependent upon his action and the outcome.
Examples The formulation of decision problems will be demonstrated by examples. They include a construction engineer’s problem of selecting a steel pile length when the depth to rock is uncertain. The available actions are driving a 40- or 50-ft pile, and the possible states of nature are a 40- or 50-ft depth to bedrock. The consequences of any action- state pair can be given in a payoff table:
Table 5.1.1 A simple payoff table
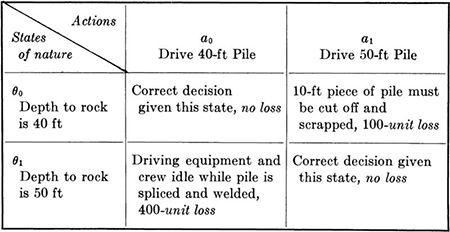
This situation is shown in decision-tree form in Fig. 5.1.2. The losses have been entered as negative values. (In this case they represent the “opportunity loss” associated with not making the best choice of action possible in light of the true state. This is discussed more thoroughly in Prob. 5.7.)
Other examples of decisions under uncertainty include an engineer’s choosing one of four cofferdam designs when the state of nature is the magnitude of next year’s maximum flow. Here the state space θ might logically be treated as continuous, 0 to ∞. The magnitude of that future flow is uncertain to the designer. Value to the engineer results from the initial cost of his design and its performance under the observed flood. The decision tree is shown in Fig. 5.1.3.
Fig. 5.1.2 Decision tree: pile-length choice.
Fig. 5.1.3 Decision tree: cofferdam.
The performance and hence the value of a facility might depend both upon its capacity and upon the demand. If both are uncertain, the possible states are the possible pairs of capacity and demand levels. These pairs can be represented as a two-dimensional state θij, representing the joint occurrence of demand level i and capacity level j. If these levels are discrete, the situation can be indicated by another level of branches in the decision tree, as in Fig. 5.1.4. The probabilities of the capacity levels, and possibly of the demand levels,† will depend upon the action or design chosen.
Another engineer might be responsible for designing a small flood-control channel for a 20-year lifetime. The state of nature could be taken as a set of values, the annual maximum flows in each of the next 20 years; that is, θ is a highly multidimensional continuous-state space. The value received from taking an action and finding a point in this state space will depend on the initial cost and future performance associated with these 20 flows.
When choosing between two types of pavement, an engineer may recognize that the cost and performance of one type will depend on the volume of a convenient aggregate borrow pit. A more expensive or lower-quality aggregate will have to be obtained if the volume in the available pit is inadequate. This quantity, the true state of nature, is uncertain (and, in fact, may never become known unless the designer chooses the pavement type requiring use of the pit). The decision tree might appear as in Fig. 5.1.5. Other examples will be found throughout this chapter.
Fig. 5.1.4 Demand-capacity decision tree.
Fig. 5.1.5 Decision tree: pavement choice.
Our problem now is to analyze such decision problems, that is, to develop a method which makes consistent use of all the engineer’s information: his degrees of belief in the various possible states, his subsequent observed data, and his preferences among the various possible action-state pairs. We shall see that the method suggests the use of relative likelihoods or probabilities—no matter how subjectively defined and evaluated—to express the engineer’s uncertainty, and the use of expected value to rank order the available actions. These concepts, probability and expectation, are not new to us. The validity of the expected-value criterion, however, relies on a properly chosen measure of preference among the outcomes. Hence we require a brief discussion of a new idea: value theory.
Our concern in this section is to demonstrate that if preferences or values of outcomes are properly expressed, then expected value is a logical basis for choosing among alternative actions. As early as Sec. 2.1 this criterion was suggested as reasonable. Here we shall explore its validity. Actually, this discussion is little more than suggestive of the more formal treatment that the subject requires in order that the criterion be firmly based. The reader is referred to other sources† for such discussions. Our purpose here is to suggest their content and necessity.
Consider a simple decision situation where the engineer must choose between actions a1 and a2. Action a1 will lead with certainty to consequences B. Action a2, on the other hand, involves uncertainty. The state of nature may be θ1, in which case the consequences are A, or it may be θ2, in which case C will be the consequences of this action and state. The decision tree is shown in Fig. 5.1.6. A simple example is the choice of pavement type mentioned in the previous section. Another example involves a construction engineer who must decide between a1, paying for insurance against work stoppage due to rain during a critical 1-day erection operation, and a2, buying no such insurance. In the latter case, if the true state of nature is θ1, good weather on that day, the consequences are A, which includes no insurance costs. If, on the other hand, bad weather forces delay (that is, if state of nature proves to be θ2), the consequences include monetary losses (and, possibly, professional embarrassment for having failed to buy the insurance!). Before the true state is known, however, the optimal decision depends upon the likelihood of θ2 and the relative degrees of seriousness of these various consequences.
Fig. 5.1.6 A basic decision process.
Utility function In order to proceed with the decision-making analysis, then, we require a numerical assessment by the designer of his preferences among these outcomes. Let us assume that he would prefer A to B and B to C. (Formally the theory also requires transitivity, i.e., that the decision maker also prefers A to C. We shall not include in our present discussion a number of similar but equally reasonable formal requirements.) This simple preference statement can be expressed numerically by any function u (that is, by any numerical values assigned to A, B, and C) such that
![]()
For example, u(A) = 1.0, u(B) = 0.5, and u(C) = 0; or, alternatively, u(A) = +100, u(B) = 93.6, and u(C) = –106. Our purpose is to find a particular function u, which we will call a utility function, such that it is logically consistent to make the decision between actions a1 and a2 by comparing u(B) and the expected value of the utility of action a2, pu(A) + (1 – p)u(C). Here p is the probability that θ1 is the true state. Actually, there is no need for such a utility function in these simple decision problems, but once we have established expected utility as a valid criterion, we can continue to use it in very complicated problems.
We shall see that the choice of any two values of u may be arbitrary; we may assign the two utilities u(A) and u(C), for example, the values 1 and 0, say, or +10 and –10. It is somewhat advantageous to assign the two arbitrary values to A and C, the most preferable and the least preferable outcomes. All other values of u will thus lie between u(A) and u(C) in numerical value. Assume then that u(A) and u(C) have been given convenient values. What value should be given u(B) to make expected value a valid decision criterion? To answer this, we must return to our decision maker for a more precise preference statement. Notice that if p, the probability of θ1 being the true state, were unity, the engineer would choose action a2 over a1 because he prefers A (now a sure consequence of a2) to B. On the other hand, if p were zero, a1 would be chosen over a2 if the engineer were going to act consistently with his stated preferences. As for other values of p, it can be said that as p grows from zero, a1 will be preferred less and less strongly over a2 until some point p*, after which a2 will be preferred over a1. We assume that by some means of interrogation we can find the crossover value p* between 0 and 1, such that the engineer is indifferent between choosing a1, with its certain consequence B, and choosing action a2, the lottery with chance p* of receiving A and 1 – p* of receiving C.
Validity of expected-value criterion Once we have that value p*, we choose to assign u(B) the value
![]()
(Note, in passing, that for any p* between 0 and 1 the assigned value u(B) will lie between u(A) and u(C) in value; this is consistent with the original preference statements.) By this assignment we have accomplished our intended purpose, that of establishing expected utility value as the consistent criterion by which to choose actions. The decision maker should choose a1 if and only if the expected utility given this action choice, E[u | a1], is greater than E[u | a2]. That this is true is verified by noting that:
1. For all p < p*:
(a) The engineer should, to be consistent with his preferences, as reflected in his p* choice, choose a1 over a2, and it is also true that for these values of p (and only these values of p):
![]()
as can be seen by evaluating the expectations:
![]()
and substituting for u(B) its assigned value
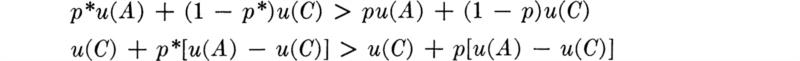
The inequality holds because p* > p and u(A) – u(C) is positive.
2. Similarly, for all p > p*:
(a) The engineer should choose a2 over a1, and also
(b) E[u | a1] < E[u | a2], since
![]()
For example, assume that the engineer was given choices between action a1 and a2 for a selection of values of p until he showed by his choices to be indifferent at p* = 0.3. We arbitrarily let u(A) = 100 and u(C) = 0. Then we should assign
![]()
If the available information suggests that the probability of θ1 is p = 0.4, then the expected utilities of the actions are:
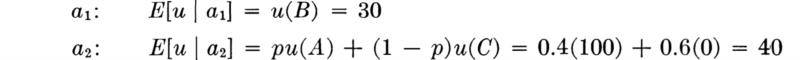
The engineer should choose action a2, since 40 > 30.
In other words, if u(B) is properly assigned to be consistent with the decision maker’s stated preferences (here expressed in the statement A preferred to B preferred to C and in the indifference probability p*), then ranking of the expected values of utility for the actions determines the ranking of the actions which is consistent with those preference statements. The logic may appear circular and unnecessary. It is, however, precisely the circular reasoning which guarantees that the decision criterion remains valid when more complicated model structures make the decision choice far from obvious and the need for a consistent, formal analysis overwhelming.
Linear transformations We note in passing, because it will be useful shortly, the validity of the arbitrary choice of any two values of u. To assign two other values, ū(A) and ū(C), to these two consequences is equivalent to saying ū = c0 + c1u, that is, that a scaling and shifting (or linear transformation) is being made in the utility function. It is trivial to show that our conclusions remain true for a positive linear transformation of the utilities. Let us simply demonstrate this fact through the previous numerical example. Suppose that we assign a new utility function ū = – 1 + 2/100u. Then
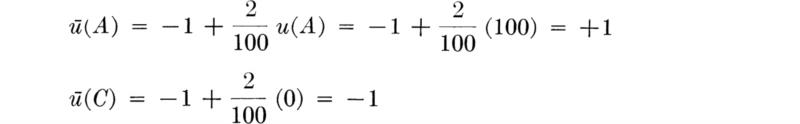
and
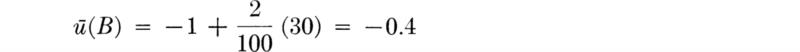
This is the same value for the utility of B that we would have reached had we assigned, initially, A a utility of +1 and C a utility of – 1, since then ū(B) = p* ū(A) + (1 – p*)ū(C) = 0.3(1) +0.7(–l) = –0.4. The decision also remains unchanged, of course. Now we have, with p = 0.4,
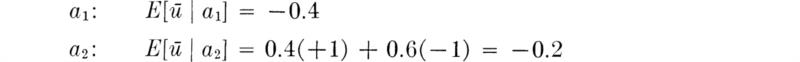
The expected utility of action a2 still exceeds that of action a1.
The freedom in assigning the utility function is analogous to that in assigning a temperature scale. Note that, owing to this degree of arbitrariness, no significance can be attached to the relative magnitude of the expected utility values. In the example above, action a1 cannot be said to be, say |(40 – 30)/40| or “¼ worse” than a2, for with the ū utility function it is |[–0.2 – (–0.4)] / – 0.2| or “100% worse.” It can only be said that “a1 ranks below a2.”
In simple decision situations such as this, nothing is gained by the steps of finding p*, finding u(B), and then finding the expected utilities in order to make a decision. It would be easier in this case simply to find p* and ascertain whether p is greater or less than p*. We shall become interested, however, in more complex decision problems where the latter approach is impossible, but where the determination of expected utilities will require nothing but familiar operations. The analysis of such complex decision situations will find us replacing lotteries (some embedded within others) by their expected utilities, † in order to reduce each action to an associated single number, the expected utility if that action is taken. By extension of the simple case above, we can say that if our utility assignment has been made in the manner outlined above, maximization of expected utility is a criterion of action choice which is consistent with the decision maker’s stated preferences.
Monetary value versus utility; risk aversion It is common in business and engineering practice to express the consequences of decisions and outcomes in monetary terms. It may or may not be appropriate to replace expected utility by expected dollar value as a decision criterion. Let us investigate this problem briefly.
If a decision tree has a number of terminal points, each the consequence of an action-state pair, and if dollar values are attached to these consequences, it is in general necessary to replace each of these dollar values by a proper utility in order to justify the use of the expected-value criterion. If the number of such terminal points is large, it is often easier to attempt to plot a smooth function of utility versus dollars, u(d). Then one may simply read the utility value from this curve for each particular dollar value of a consequence. The determination of this utility function follows the established pattern. Suppose the terminal-point dollar consequences are as shown in Fig. 5.1.7. The most preferable outcome is +$10,000; assign this, arbitrarily, a utility of u($10,000) = 100. The least preferable value is a loss, –$5,000; assign this a utility value of 0, u(– $5,000) = 0. Then to find the utility of any other dollar value, say $0, the engineer must be quizzed to determine at what value of p he would be indifferent between a sure gain of $0 and a lottery in which he would win $10,000 with probability p and lose $5,000 with probability 1 – p. In personal financial matters most individuals would undoubtedly find themselves in the position where a gain of $10,000 would be welcome but a loss of $5,000 would be very serious. For any value of p less than, say, 0.7, they might prefer to take no risk at all, i.e., a sure $0. Above p = 0.7 they might feel that the potential large income was so likely that the small risk of loss was “worth the gamble.” Arriving in this way at a p* of 0.7, $0 is assigned a utility of
Fig. 5.1.7 Terminal-point dollar-value consequences.
Fig. 5.1.8 Utility curves.
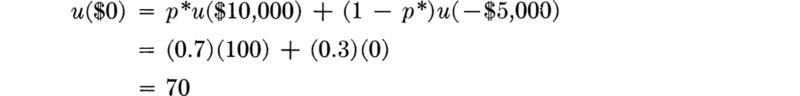
A number of similar processes obtaining preferences for dollar values of, say, –$2,000, +$2,000, and +$6,000 versus lotteries involving a gain of $10,000 and a loss of $5,000 will lead to corresponding values of p*, and thence to the utilities of –$2,000, +$2,000, and +$6,000. For indifference p*’s of 0.5, 0.85, and 0.95, respectively,

A plot of these points and a smooth curve drawn through them is shown as a solid line in Fig. 5.1.8. From this curve utilities can be assigned to all the dollar-valued consequences of the terminal points of the decision tree in Fig. 5.1.7. The utility of +$1,000, for example, is found to be about 75. Given probabilities on θ1, θ2, and θ3, say, 0.4, 0.4, and 0.2, the expected utility of taking action a1 (Fig. 5.1.7) could be evaluated as
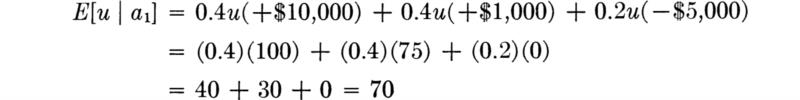
Similar calculations for the other actions would lead to a choice of the action which is optimal in the light of the preferences reflected in the utility curve. We shall discuss these steps in detail in Sec. 5.1.4.
The shape of the solid-line utility curve in Fig. 5.1.8 has been commonly encountered (Grayson [I960]) among individuals making decisions involving dollar values which are large in relation to their working capital. This concave-downward curve reflects the facts that in such situations the utility of a gain of d dollars is less in magnitude than a loss of the same amount, and that, after a gain of d, a gain of d more has, incrementally, a smaller utility. Decision makers with such utility functions are said to be “risk averters.”
In many practical circumstances the decisions may not involve dollar sums which are “large” for the individual or body (corporate or social) involved. For a large professional office, for a major business, or for a large political body the dollar values of +$10,000 and –$5,000 are not large. Many decisions may be made each day involving such numbers. For some individuals the comparable “not large” numbers might be +$10 and –$5. In these cases a strongly curved, concave utility assignment may be too conservative. As individuals we might assign an indifference probability of almost ⅓ to a choice between a sure $0 (no gamble) and a lottery with a chance p of gaining $10 or 1 – p of losing $5. So too, a large firm might assign a breakeven probability of about ⅓ to the earlier situation involving a sure $0 versus a lottery with payoffs +$10,000 or –$5,000. Assigning the largest and smallest dollar-value utilities of 100 and 0, as before, the proper utility assignment to $0 is 33 for the large firm.
This point and others for the same situation of a large firm or political body are shown as crosses in Fig. 5.1.8. The dashed line through them is linear. The implication is that utility can be expressed as u = c1 + c2d or, inversely, that dollars can be expressed as d = c3 + c4u. Since, as we have seen, we retain a valid utility function after any linear transformation, it is clear that under these special circumstances dollars themselves are a valid utility measure. The important consequence is that if utility is linear in dollars, expected monetary value is a valid criterion for choosing among alternative actions. In most examples to follow, we shall assume that this linearity exists and hence that expected dollar values are adequate for decision-making purposes.
Extracting preferences Methods for interrogating individuals to determine their utility assignments can be found in other references (e.g., Schlaifer [1959] or Pratt, Raiffa, and Schlaifer [1965]). They usually involve choices among hypothetical lotteries in search of indifference points. The assessment may in practice prove difficult. Individuals may, for example, respond less favorably to hypothetical risky situations than to real ones. Some consequences (e.g., dam failures, formwork collapses, highway accidents) involve difficult, but fundamentally unavoidable problems in assessing utilities. When a highway planner puts the limited funds available to him into a new, time-saving highway link rather than into accident-reducing modifications at an existing intersection, he has made such an assessment implicitly. Explicit utility assessments could potentially bring more consistency to the decisions that must be made under such difficult circumstances. † Experience comparable to that being gained in major business decision applications (Howard [1966]) is needed in engineering situations.
Discussion A number of comments are in order about the validity of the expected utility decision criterion and about aspects of utility assignment which are peculiar to civil engineering.
It is important to note that for expected (or average) utility to become the valid criterion of choice, there has been no need for the situation to involve repeated trials. The decision may be, as most civil-engineering decisions are, a “one-shot” affair. Nor does the criterion say that one should always prefer a 50–50 lottery with yields $100,000 or $0 to a sure gain of, say, $40,000. For any number of reasons the decision maker may have an aversion to risk taking. The one-shot and risk-aversion elements will be reflected in the utility assignments which express the individual’s preferences among outcomes of the situation at hand. For example, the engineer might feel that in this decision situation p* is 0.7, in which case u($40,000) = 0.7u($100,000) + 0.3u($0) = 0.7, if we set u($100,000) = 1 and u($0) = 0. Then the preferred decision is the sure $40,000, since its expected utility is 0.7, whereas the lottery has an expected utility of only (0.5) (1) + (0.5) (0) = 0.5. Thus, the utility assignment has expressed the engineer’s aversion to risking a sure $40,000 against a possible $100,000. He will accept the risk only if the likelihood of success is sufficiently high, for example, p > 0.7.
It should be clear that the utility assignments to consequences may be highly subjective. Depending on circumstances, such assignments may differ from individual to individual and even from time to time for one individual. They should represent the preferences of the moment of the individual responsible for the decision.
Civil engineers make many professional decisions under conditions of uncertainty about the future. Do these professional decisions bring them value? Can the value accruing from a particular professional decision be directly identified? Or is value only received over a long period of time from many decisions with few apparent direct relationships to the engineer, beyond the generalization that consistently wise decisions are associated with long-term economic gain and increase in professional stature?
In the field of business, where much of applied decision theory has been developed, an executive can often specifically identify value accruing from a specific decision. He is operating for himself or in the name of the concern, and an economic gain or loss is more apparent. The operations of a professional civil-engineering office do parallel ordinary business operations in that a profit or loss is found, but only a small part of the decisions made pertain to the management of the engineering business itself. Most of the decisions of interest are professional in nature. That is, the engineer is acting as an agent for his client, and he has a professional obligation to attempt to make a design with characteristics optimal to the owner. The situation is complicated since some aspects of decisions are predominantly client-related, whereas others are more closely engineer-related. For example, absolute minimum cost to the owner is rarely a goal for the engineer because of other professional factors that must be considered, such as public safety, appearance, etc. The values of these latter factors to the owner may be extremely difficult to ascertain. But the saving of $10,000 in the cost of construction of a building is of immediate importance to the client or owner. How important is this saving to the engineer who must make the critical design decision? Utility to the client is not equivalent to the utility to the engineer. The reverse may be in part true; the saving of $10,000 in construction costs may actually reduce the fee received by the engineer for the job. Another example will follow in a bridge-design illustration in Sec. 5.1.4.
How, in short, should the preferences of the client be reflected or transformed into the preference assessments of the engineer responsible for the decision? These are questions which have received no quantitative answers. But these are not new problems generated by the methodology of statistical decision theory. They are, in fact, only new ways of expressing some of the key issues underlying professionalism. By dealing with them in a more formal, mathematical framework, decision theory may provide a basis for further discussion of them and for a rational, quantitative resolution.
Despite the immediate practical difficulties in assessing utilities, the concept remains fundamental to the understanding of rational decision making under uncertainty.
Closure It should be repeated that our development of the value theory underlying statistical decision theory has been nonrigorous and only suggestive of the basis for the expected utility criterion. Briefly, the use of the criterion is justified by the method of making the utility assignments. The assignments are consistent both with the engineer’s preferences and with the use of the expected utility criterion. In the analysis of decision trees in Sec. 5.1.4, we shall use this fact over and over to replace an array of branches and associated outcomes by a single number—the expected utility.
We next must reconsider briefly the probability assignments on the decision tree. We shall find that some of the earlier statements in Chap. 2 about the degree of belief or operational interpretation of probability can now be made more explicit.
The probability assignments on a decision tree are more familiar than utilities. Their treatment has been the subject of all the preceding chapters. The sources of these probabilities may include observed frequencies, deductions from mathematical models, and, in addition, measures of an engineer’s subjective degree of belief regarding the possible states of nature. The former two sources have been emphasized up to this point, but the broader, subjective interpretation can now be given a firmer basis. As mentioned briefly in Sec. 2.1, such statements as “The odds are 2 to 1 that this job will be completed in 2 months,” “I’ll bet a quarter to your nickel that the depth to bedrock is less than 50 ft,” or “The most likely value of the mean trip time is 8 minutes, but it may be as large as 10 or as small as 7” all represent expressions of the engineer’s judgment about unknown quantities. These quantities may represent repetitive experiments, one-of-a-kind situations, fixed but unknown factors, or even parameters of the distributions of repetitive random variables. The subjective expressions above can all be related to probability distributions assigned to these quantities. An excellent engineering argument for this position is presented by Tribus [1969].
Both observed frequencies and these “more subjective” probability assignments can now be interpreted as those numerical summaries of an individual’s degrees of belief or relative likelihoods upon which that individual is prepared to base his decision. The implication seems to be that another individual might make different probability assignments to the same decision tree. This is true; it is consistent with the observation that different engineers have had different experiences and use different reasoning processes.
This operational interpretation of probability as an individual’s decision-making aid is not, however, inconsistent in practice with the more restricted relative-frequency interpretation; if a large amount of relevant observed data is available, two reasonable individuals will undoubtedly use it in the same way, obtaining the same personal probability of the event. The techniques for determining probability assignments when sufficient data and/or theoretical models are available have been discussed.
In those cases where the probabilities depend strongly upon judgment, however, the extraction of an engineer’s degrees of belief in terms of personal or subjective probabilities may not be an easy task. When accustomed to the idea, an engineer may be able to make direct statements. For example, he might say:
Based on the information available to me at the moment, the probability is 0.3 that the volume of useful aggregate in this borrow pit is about 4000 yd3 and 0.7 that it is about 5000 yd3.
Or, if a continuous-state space is desirable:
There is a 50–50 chance that the volume is less than 4750 yd3. If it proves to be less than 4750 yd3, however, there is a 50–50 chance that it is less than 3800 yd3. Given that it is greater than 4750 yd3, on the other hand, the probability is 50 percent that it is greater than 5000 yd3. There is no significant chance that the volume is less than 3000 yd3 nor more than 5250 yd3.
The points implied by these latter statements and a smooth curve through them yield the CDF in Fig. 5.1.9.
Alternatively, these quantifications of degrees of belief can be extracted in a manner which more strongly reflects the decision situation at hand. The engineer can be asked to state a preference between two lotteries, one artificial, the other involving the state of nature or event under consideration. His preference will indicate a bound on the probability sought. For example, assume that an engineer states a preference for an artificial “lottery,” lottery I, which offers a sure $5, over lottery II, which offers him $0 if the amount of useful aggregate is found to be less than 4500 yd3, and $8 if it is found to be more than 4500 yd3. The implication of this preference statement is that the expected utility of the first lottery is greater than that of the second, or
![]()
in which p = P[volume ≤ 4500]. Assuming, for simplicity, that utility and dollars have been found to be linearly related (Sec. 5.1.2) in this range, and letting u($d) = d, the engineer’s preference implies that
Fig. 5.1.9 Subjective cumulative probability distribution on usable aggregate volume.
![]()
or
![]()
By changing the values of the rewards or the values of the probabilities (or both) in lotteries I and II, one can presumably find a situation where the engineer states that he is indifferent between the two lotteries. In this case the expected utilities can be set equal and the implied value of p solved for. This probability is clearly the one upon which the engineer is prepared to make a decision which rests in part, at least, upon the quantity of aggregate in the borrow pit.
Subjective probabilities have proved (Howard [1966]) a useful way to transmit judgments within an organization where numerous individuals have to contribute to the components of a larger decision. For example, they can help a consulting engineer communicate the uncertainty in his estimate of a factor in his field specialty. A soils consultant, who has pulled together various kinds of data and experience to estimate that the mean shear strength of a particular soil layer is 400 lb/ft2, might go one step further and state that he is “50 percent sure” that the strength is with ± 10 percent of that estimate. The figure 10 percent might have been arrived at by varying that fraction until he was indifferent between lottery I, a coin flip offering $0 or $1, and lottery II, offering $1 if the true mean strength is found to be within +10 percent of his estimate and $0 if it were outside of those limits. By transmitting two numbers—a best estimate 400 and a “probable error” ± 10 percent—rather than only a conservative estimate, say, 350 lb/ft2, this engineering specialist will permit a balanced, economical design decision to be made by those supervising engineers who have gathered all such individual judgments together with the costs and the alternatives. This approach avoids uneconomical compounding of “safety factors” which can arise when each opinion is transmitted simply as a conservative estimate. This is true whether or not a formal decision analysis is made.
We can afford no further discussion on the subject of trying to get probability assessments from individuals, but we refer the reader to other sources (e.g., Schlaifer [1959], Pratt, Raiffa, and Schlaifer [1965], Grayson [1960], and Howard [1966]) for additional discussion. Interesting questions remain concerning the “policing” of inconsistent probability statements and lottery choices, the influence of the hypothetical nature of the lotteries, and the extension of the procedures to small probability values.
Like the procedure for utility assignments, the assessment of judgment-based probabilities utilizes the decision maker’s preferences among simple, obvious lotteries to extract numbers which will become parts of the actual larger, more complicated decision problem. Many of the probabilities in a decision analysis will be determined by the methods developed in earlier chapters, that is, by manipulation of probabilities and random variables in a manner consistent with the rules of probability theory. Nonetheless, all applications rest fundamentally on an individual’s probability assignment, whether it is extracted by preference statements or implied in the adoption of a particular distribution.
In the following section we will put together the pieces of the decision problem and analyze the problem to determine the best decision consistent with the probability and utility assignments.
We have discussed how, in principle, the elements of the decision problem are assembled. These elements are the available actions, the possible states with their assigned probabilities (representing the information available to the decision maker), and the utilities associated with the action-state pairs (representing the decision maker’s preferences). The analysis of the problem determines the optimal action consistent with the individual’s probability and preference assignments.
The criterion of choice among actions is maximum expected utility. That this is a valid criterion has been guaranteed by the method of utility assignment. The analysis of the decision situation reduces then to calculation of expected utilities and selection of the action which shows the largest expected value.
Finding expected values is a familiar process by this time, but we include several examples to illustrate its application in decision analysis. We shall adopt the short-hand notation P[θi] to mean “the probability that the true state of nature is θi.” Notice in the examples that, if it is numerically valued, the state of nature θ will be treated as if it were a random variable. Since there is no opportunity for ambiguity in this chapter, we shall not, however, distinguish by upper and lower case between the random variable and its specific values.
Illustration: Pavement design, discrete-state space As a simple example we shall complete the analysis of the decision between two pavement types, Fig. 5.1.5. Uncertainty exists regarding the amount of aggregate in the available borrow pit. Assuming that it is sufficient to use just a pair of discrete states (θ1 = “large” volume of aggregate, say about 5000 yd3, and θ2 = “small” volume, about 4000 yd3), we shall use probability assignments extracted as in Sec. 5.1.3: 0.7 and 0.3, respectively. The engineer’s utility assignments for the action-state pairs have been assessed to be 60 and 200 and 0 for u(a1), u(a2, θ1), and u(a2, θ2), respectively. The final tree with the numerical assignments indicated appears in Fig. 5.1.10. The expected value promised by choosing a particular action is indicated within a box at the right-hand end of the action branch.
For action a2 it is 140. This expected value can be interpreted, recall, as the certain gain equivalent in value (in the decision maker’s eyes) to the existing a2 “lottery.” In essence this is the “selling price” he would accept for his “ticket” in the lottery. Because 140 is greater than 60, the indication is that a2 is the choice which is consistent with the engineer’s assessment of the preferences and judgments (probabilities). It is important to realize that the value which will be received if a2 is taken will not be 140 but rather either 0 or 200.
Fig. 5.1.10 Pavement-type decision tree.
It is also important to recognize the distinction between a good decision and a good outcome. The analysis suggests that a2 is the better decision, but there is a possibility that the volume will turn out to be inadequate; that is, the outcome may be bad. Such an outcome does not imply that a bad decision was made. At the earlier time when the choice had to be made, the available information did not include the fact that the volume was inadequate. The available information at that time was summarized by the engineer as a probability of only 0.3 that volume was inadequate.
Notice, too, that even if the engineer had judged that the volume was “somewhat more likely than not” to be inadequate, say P[θ1] = 0.4 and P[θ2] = 0.6, action a2 would have remained the better decision; the conclusion is that a decision should not necessarily be based on the “most likely” state, without consideration of the consequences.
Illustration: Pavement design, continuous-state space The engineer may have preferred a more detailed model of the state space in the pavement-choice example, a space which permitted the possibility of any of a range of values. Assume, then, that the state space of aggregate available in the borrow pit is the positive line, 0 to ∞. Assume, too, that utility is linearly related to construction cost dollars. We shall assume arbitrarily a scale of u(–$100,000) = –100,000 and u($0) = 0. In other words, we shall use expected monetary value as a criterion. Pavement type II requires 4750 yd3 of aggregate. If this amount is not available in the borrow pit, the additional material, (4750 – θ) yd3, will have to be hauled a great distance at added cost. Assume, then, that the construction cost of type II is $95,000 if the pit volume exceeds 4750 yd3. But if the volume is less than 4750 yd3, the cost will be $95,000 plus $10 per imported cubic yard, or $95,000 + $10(4750 – θ). Pavement type I has a cost of $100,000. In short, the utility of choosing type I is –$100,000 and the utility of the type II choice is
![]()

Assume that the engineer’s probability assignment on the available volume θ, is the CDF indicated in Fig. 5.1.9. The decision tree can be indicated as shown in Fig. 5.1.11. Since the discrete-state “branches” are no longer appropriate, the value of the tree as a visual aid is weakened when continuous variables are involved. It remains useful conceptually however. The expected values associated with actions a1 and a2 are again shown in boxes.
The determination of the expected value of a2 now requires integration:
This evaluation requires that a PDF be determined from the given CDF and that, analytically or numerically, the integration be accomplished. The approximate result is indicated in Fig. 5.1.11 to be –97,900. Action a2 is preferable. The continuous-state model may be more detailed than the discrete-state representation, but any model which is accurate enough to give the proper action choice is sufficient. In all further examples in this chapter we shall restrict our attention to discrete models.
Fig. 5.1.11 Continuous-state-space model of pavement-type decision.
Recall that the expected utility criterion is sufficient only to obtain a ranking of actions. It should not be concluded, after inspecting the expected values – $100,000 and –$97,900, that a2 is about 2 percent “better” than a1, only that a2 is better. Recall that assignment of a different, linearly transformed utility scale could yield a different proportion between the expected values, but never a different conclusion as to the better decision.
Illustration: John Day River bridge Two spans of a bridge over the John Day River near Rufus, Oregon, failed during the floods of December, 1964. The primary cause was “abnormal” flooding of the river. The foundation of the center pier was undermined by the unusually fast current, and two 200-ft spans collapsed. The bridge was 1 year old and had cost $2,500,000.
The original plans for the bridge called for this pier to bear on bedrock, but after the contractor had excavation difficulties, he was allowed to found the pier on compacted sand and gravel. The outcome was bad, but the decision may not have been. The highway department explained that the change was allowed because the bridge would eventually be in the reservoir formed by the John Day dam, and by then it would not be exposed to fast currents. The change speeded construction and saved $150,000 in construction cost. It is interesting to note that after the failure the decision was publicly called a “clear error in judgment.”
The foundation was “designed” for 37,000 cfs. The river reached 40,000 cfs during the flood. Three older bridges on the same river were undamaged even though some of their piers also bear on gravel; performance under a given “load” cannot be precisely predicted when such a complex process as scour and erosion are involved. The cost of reconstruction was estimated to be $765,000. †
This type of decision situation is very often encountered in civil-engineering practice. It is common to consider design changes when new information is obtained during construction. Reanalysis of this foundation-design decision provides an excellent opportunity to illustrate the use of statistical decision theory. All probability statements and conclusions that follow are entirely fictitious and are designed only to illustrate the methods.
The decision tree is shown in Fig. 5.1.12. The engineer must choose between action a1, requiring strict compliance with original plans, and action a2, accepting the contractor’s proposal to found the pier on sand and gravel at a saving of construction money and time.
Fig. 5.1.12 Decision tree: foundation design.
Based on historical records, the engineer assigns probabilities to the four possible discrete flood states that he thinks are sufficient to describe this aspect of the problem. These must be the probabilities of the largest flow in the time before the foundations are protected by the dam. The states selected are:
Their probabilities are independent of the action taken and are estimated semi-subjectively from available records of past flows (see, for example, Sec. 4.5.2):
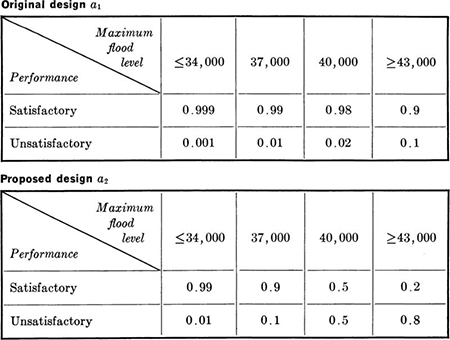
The conditional probabilities of successful or unsuccessful performance of the original design and the proposed design, given the maximum flood level, appear in Table 5.1.2 and in the decision tree. Note, for example, that the (fictitious) engineer has estimated that the probability of the original design’s failing under a peak flow of 37,000 cfs is about 10 percent of that of the revised design. The states are labeled θi1 and θi2 for flood state i and satisfactory or unsatisfactory performance, respectively. Such performance probabilities can only be subjective assignments reflecting the engineer’s judgment about the reliability of these particular designs under these particular conditions. Related experience and professional knowledge represent the only sources of information. Data cannot be obtained before the designs are completed.
Table 5.1.2 Conditional probabilities of performance given the design and the maximum flood level
The gains and losses in dollars are estimated as shown in the decision tree. The cost of poor performance, i.e., foundation and pier failure, will be taken as $765,000; the construction-cost savings associated with the proposed design are $150,000. Failure of a revised design has a net cost of $765,000 – $150,000 or $615,000. Assume that the engineer is making a decision to maximize the expected utility of the people of Oregon and hence that utility to the people and dollars can be assumed to be linearly related.
Analysis of the tree proceeds by finding the expected utilities or monetary values at each branching point. The right-hand-most expected values on the decision tree are the expected values given a particular action and flood level θi. For example, the top boxed value is:
The expected utilities for each action are found in turn by weighting the expected utilities given the flood level by the probabilities of these levels. For example:
The better decision is to choose the proposed revised design because E[u | a2] is greater than E[u | a1].
Several observations are in order. First, the problem could also have been represented by a simple tree with only one set of state branches, as shown in Fig. 5.1.13. There are eight such states, the combinations of four flood levels and two performance levels. Call them ![]() k = 1, 2, 3, . . ., 8. Note that each
k = 1, 2, 3, . . ., 8. Note that each ![]() corresponds to an earlier θi1 or θi2, i = 1, 2, 3, 4. For each action, there is associated with each state its probability of occurrence. Each probability is the product of a probability of flood level and a conditional probability of performance level given that flood level. The products of these eight probabilities and the eight dollar values give the expected monetary value of an action. In symbols, the calculation is
corresponds to an earlier θi1 or θi2, i = 1, 2, 3, 4. For each action, there is associated with each state its probability of occurrence. Each probability is the product of a probability of flood level and a conditional probability of performance level given that flood level. The products of these eight probabilities and the eight dollar values give the expected monetary value of an action. In symbols, the calculation is
Fig. 5.1.13 Alternate decision tree: foundation design.
The reader can quickly convince himself that this is the same number obtained above, where that computation can be shown as:
The equivalence of the two computations implies that the expected utilities in the original tree, Fig. 5.1.12, can be computed either by working to the left with sets of conditional expectations to obtain the expected utility of an action (as done) or by working to the right with sets of conditional probabilities to find the probability of each possible terminal point (and taking expectations only as a final step).
As a third alternative for the decision tree, the engineer might have preferred only two states, those prompted by observing that there is only a pair of utilities appearing in the larger decision trees (Figs. 5.1.12 or 5.1.13). These two states could be called “satisfactory performance” and “unsatisfactory performance.” Their probabilities could be found by adding the probabilities of the mutually exclusive events which make them up. For example, the probability of satisfactory performance is the sum of the probabilities of ![]() in Fig. 5.1.13. The purpose of mentioning this large number of alternative decision trees is simply to make the point that there is no single “proper” formulation. The engineer has freedom in how he chooses to view a problem, and the several possible views will lead to the same action.
in Fig. 5.1.13. The purpose of mentioning this large number of alternative decision trees is simply to make the point that there is no single “proper” formulation. The engineer has freedom in how he chooses to view a problem, and the several possible views will lead to the same action.
A second major observation is that the decision may well have been altered had the engineer assessed his personal preferences in making the utility assignments. For illustration, let us simplify the decision tree to the elementary one shown in Fig. 5.1.14. (Note that the engineer has chosen now to assume that there is no probability of unsatisfactory performance with action a1.) The engineer responsible for the decision might recognize that the consequences to him of each action-state pair are quite complicated. Failure to accept the immediate, sure construction savings (i.e., choosing action a1) might brand him as inflexible and over conservative. If he takes this action, the possible poor performance that might have been (and was!) found under a2 could never take place, and the engineer’s conservatism (appropriate, after the fact) would never be appreciated. If the engineer takes action a2, either he will obtain the benefits for himself and the people which he represents (θ1) or the poor performance will be observed (θ2). In the latter case, the consequences to the engineer will depend in part upon the review of his decision which is likely to follow. If the flood which causes the failure is truly a large one, larger at least than any on record, the engineer may escape personal criticism even though financial losses are quite large.
Viewed in this light, the professional decision situation, like most, is quite personal in nature. The methodology of decision theory remains applicable, however. Only a preference statement on the part of the engineer is needed. Assign, arbitrarily, u(a2, θ1) = 10 and u(a2, θ2) = –10. Then, through interrogation, an indifference probability p* is sought. It is the value at which the engineer has no preference between (1) obtaining the consequences of a1 for sure and (2) being given a chance in a lottery where the consequences of a2 and θ1 will be found with probability p* and the consequences of a2 and θ2 will be his with probability 1 – p*. Then
Fig. 5.1.14 Simplified tree: bridge-foundation design.
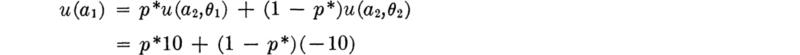
Assume that the engineer’s preference statements imply that p* = 0.98. (That is, 1 – p* is about equal to the likelihood that the engineer can correctly name the top card on a deck of cards.) Then

With these preferences the engineer should still take action a2, since
![]()
while
![]()
As a final observation, notice that the dollar consequences of an action-state pair may also be uncertain. In this case, still another level of branches can be established to represent the various levels of costs associated with a given action and outcome. Conditional probability assignments must be made to each new branch. The first step in the analysis will be to calculate the rightmost expected value, which will now be the conditional expectation of the dollar consequences given the action and outcome. With this value the analysis proceeds exactly as above. In this sense the dollar estimates in the original tree (Fig. 5.1.12) can be thought of as expected dollar consequences given the action and outcome. Notice, however, that this interpretation is valid only if a utility and dollars are linear for the decision maker. If not, the dollar values must all be converted to utilities before taking expected values.
Illustration: General capacity-demand problem The preceding problem can be considered to be a special case of a more general capacity-demand type of problem. The flow rate is a measure of demand; the resistance of the foundation to this flow is a measure of capacity. The relationship between capacity and demand levels determines the performance of the system and hence the payoff or consequences: capacity greater than demand defines a more-or-less satisfactory behavior; demand greater than capacity implies a system failure of some magnitude.
Both capacity and demand may be uncertain. Commonly the probabilities of demand levels are largely independent of the action or design, whereas the specified design level or action determines the most likely capacity as well as the dispersion about that value. Performance and consequences depend upon the action and the value of the two-dimensional state, demand and capacity. If for a given action, 10 discrete demand levels and 10 discrete capacity levels are considered, 100 combinations of levels exist and each must be considered.
As mentioned in the bridge-foundation-design illustration, it may be possible to simplify the decision-tree analysis by lumping many of the demand-capacity pairs into a smaller number of common performance levels. This is possible if the consequences are equivalent for each action-state pair in a particular performance level.
Table 5.1.3 Safety margin levels
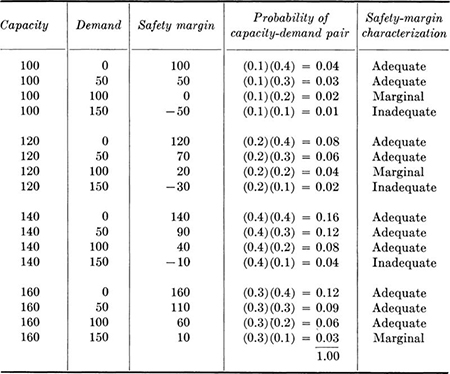
For example, for a particular action, the decision maker may consider the four possible demand levels 0, 50, 100, and 150 and the four possible capacity levels 100, 120, 140, and 160. Assume that the probabilities of the demands are 0.4, 0.3, 0.2, and 0.1, respectively, whereas the probabilities of the capacities are 0.1, 0.2, 0.4, and 0.3. If performance can be related to simply the “safety margin” or the difference between capacity and demand, it is appropriate to calculate the possible values of the safety margin with their likelihoods. Assuming independence of demand and capacity, these values all appear in Table 5.1.3. The performance levels associated with each safety margin are shown. Negative values of the safety margin are termed “inadequate,” non-negative values less than 30 are called “marginal,” and larger values are considered “adequate.” In these terms the probabilities of the three performances are 0.07, 0.09, and 0.84 for the inadequate, marginal, and adequate safety margins. Analysis of the tree could continue based on only these three outcomes, with their respective probabilities and utility values.
The simple decision model consists of a set of possible actions, a1, a2, . . . ., an, and a set of possible states, θ1, θ2, . . ., θm. Decision theory prescribes how one should choose among the actions when the state is uncertain. The prescribed decision criterion is maximization of expected utility.
The criterion is appropriate if the decision maker’s preferences among the various possible action-state pairs are expressed in terms of a particular utility measure u(aj, θi) (or any positive linear transformation of that measure). The proper utility measure may or may not coincide with simple monetary units.
In decision analysis, probability assignments p(θi) are also interpreted with reference to the particular decision maker, and hence they are, in general, subjective quantities rather than, say, physical attributes of the uncertain states.
Analysis of the decisions involves only the computation of expected utilities E[u | aj] and choice of the action with the largest expected utility (or minimum expected loss).
In the previous section we discussed the analysis of a decision tree when the various probability assignments were available. In this section we consider terminal analysis, the analysis of the tree when new information about the states has become available. We shall learn in Sec. 5.2.1 to incorporate the new information with the old to yield new probability assignments. After this has been done, the decision-tree analysis is identical to that discussed in Sec. 5.1.
Our interest turns now to the problem of reassessment of the probabilities of state in the light of new information. No new ideas are involved; we wish only to reconsider some familiar ideas in the context of a decision situation. For clarity we denote our initial or prior probabilities as P'[θi] and our revised or posterior probabilities as Pʺ[θi]. (For notational simplicity we suppress possible dependence of these state probabilities on the action a.)
Calculation of posterior probabilities The prior probabilities of state are known. As the result of an experiment e, † we have observed new information, namely, an outcome zk in the space Z of all possible outcomes of that experiment. The problem is to combine this new information with the prior probabilities of the state P'[θi] to obtain posterior probabilities of state Pʺ[θi]. We do this through Bayes’ rule, Eq. (2.1.13). This rule, recall, is derived as follows. Consider the two alternative products which equal the probability of zk and θi:
![]()
in which an obvious short-hand notation has been adopted, e.g., P[zk | θi] is the probability that the outcome of the experiment would be zk if θi is the true state of nature.
Solving for P[θi | zk] or Pʺ[θi],
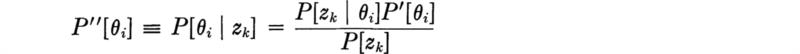
Substituting for P[zk] in the denominator,
Bayes’ rule states that the posterior probability of a state is the product of three factors:
in which
The normalizing factor simply insures that the P”[θi] form a proper set of probabilities. The mixing of new information and old appears through the product of the sample likelihood, P[zk | θi], and the prior probability P'[θi]. The sample likelihood is the probability of obtaining the observed sample as a function of the true state of nature θi. Or (as discussed in Sec. 4.1.4) the sample likelihoods can also be interpreted as the relative likelihoods of the various states given the observation zk. If this likelihood is relatively higher for θi than other states, the posterior probability of this state will be increased over its prior probability. If θi is a relatively unlikely state to be associated with observation zk, Pʺ[θi] will reflect this by being smaller than P'[θi]. If either the sample likelihood or the prior is sharply defined, strongly favoring one or a small group of states, the subsequent posterior probabilities will be predominantly influenced by this function (unless the other is also strongly peaked). (This notion is demonstrated in Chap. 6.)
Once the posterior probabilities have been computed, the decision analysis proceeds exactly as in Sec. 5.1.
A simple example We reconsider the pile decision discussed in Sec. 5.1. A construction engineer must choose a length of steel section to be driven to a firm layer below. The decision elements of that problem are as follows. The engineer has a choice between two actions:
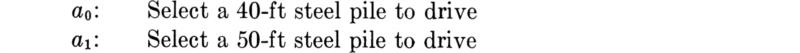
The possible states of nature are assumed to be just two:
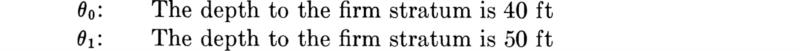
The utilities † are shown in Table 5.1.1 and in the decision tree shown in Fig. 5.2.1.
Fig. 5.2.1 Pile-selection problem.
The prior probabilities of state, representing the engineer’s assessment of such information as large-scale geological maps, depths of piles driven several hundred feet away, etc., are assumed to be

The engineer plans, as the experiment or source of information, to use a simple sonic test to give a depth indication. An instrument records the time required for the sound wave created by a hammer blow on the surface to travel to the firm stratum and return. Owing to soil irregularities, measuring errors, etc., the indicated depth Z is not a wholly reliable estimate of the true depth. Assume that the sample space of possible experimental outcomes is discrete with only three values, 40, 45, and 50 ft. Two of the possible outcomes might be said to favor a particular state of nature, while the third possible outcome, 45 ft, is ambiguous. The engineer summarizes the test’s properties in a table of sample likelihoods or conditional probabilities of observing particular test outcomes given each of the states of nature.
Sample likelihoods P[zk | θi]
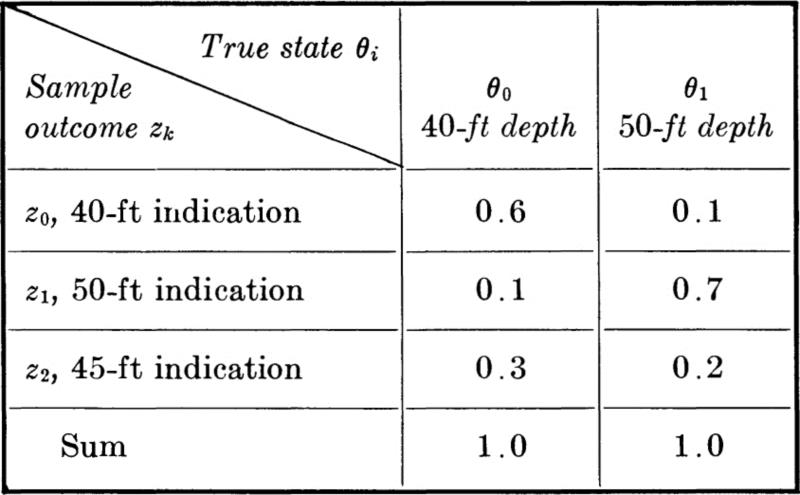
In words, the right-hand column of the table states that if the true depth is 50 ft, the engineer believes that one of the three indications— 40, 45, or 50 ft—will result, with the probabilities shown. Given this true depth and the local conditions, the instrument is 70 percent reliable; it has a 10 percent chance of being flatly wrong (by indicating 40 ft); and it will give an ambiguous 45-ft reading with probability 20 percent. The total is, of course, unity. Comparing the two columns, the instrument is apparently somewhat more likely to give a too-deep indication than a too-shallow indication. These sample likelihoods may be in part subjective, since in addition to the manufacturer’s calibration tests and stated “tolerances,” they may depend on the engineer’s judgment, based on his own previous experience with similar tests on a number of different soil types and depths using the same instrument.
The engineer makes the test and the instrument indicates 45 ft; i.e., z2 is observed. The posterior probabilities of state, given the observation of a 45-ft depth indication, are [Eq. (5.2.1)]:

The true state is either θ0 or θ1; therefore the sum of the posterior probabilities must equal unity. Normalizing these posterior likelihoods by their sum,
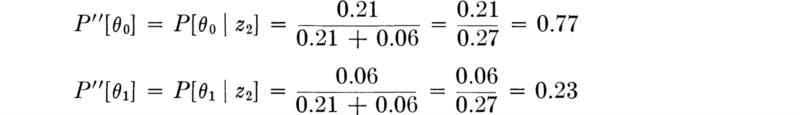
Notice that the ambiguous result has, in fact, altered the probabilities of state, owing to the asymmetry of the “error” probabilities, 0.3 versus 0.2.
The decision analysis uses these posterior probabilities of state as indicated in Fig. 5.2.1. The expected utility of each action is found as the sum of products of utilities and posterior probabilities. (In this problem, state probabilities are independent of the action.) The better decision is a1, i.e., the longer pile. Although the engineer believes that the true state is more likely to be θ0, the shallower one, his prior information and the ambiguous sonic test result do not give sufficient confidence to offset the relatively large loss (– 400) that he will absorb if the action appropriate to θ0 is taken and θ1 is found to be the true state.
Note, in passing, that if the engineer must drive a number of piles in a close area, the choice of piles, after driving the first, can be made without risk since the true state will have been determined. In decision terms, by driving one pile the engineer will have carried out a perfectly reliable experiment for which the conditional probabilities are all zero except two:
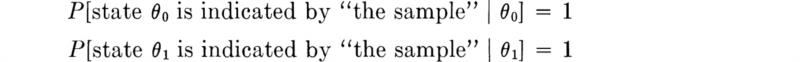
The implication is that Bayes’ rule will lead to a posterior probability of zero for one state and unity for the other, depending on whether the first pile hits a firm stratum at 40 or 50 ft. A more detailed, but similar, illustration appears in Sec. 5.3.1.
Illustration: Remodeling decision with imperfect testing In an illustration of Sec. 2.1 an engineer is concerned with the quality of concrete in an old building which is being considered for a new purpose. The concrete qualities are classed as 2000 psi (θ1), 3000 psi (θ2), or 4000 psi (θ3). The engineer assigns the states prior probabilities of 0.3, 0.6, and 0.1, respectively. His available actions are either to report that the floor slabs of this concrete should be replaced (a1), to restrict the use of the rooms they support to a light office category (a2), or to give permission that the rooms be used for all office-use types including file rooms (a3). The performance of any slab will depend upon its concrete strength, plus a number of other random factors such as the loads to which it is subjected.
The engineer summarizes these factors in the decision tree (Fig. 5.2.2) (perhaps after an analysis of additional branches representing load levels, etc., given each concrete state and action pair).
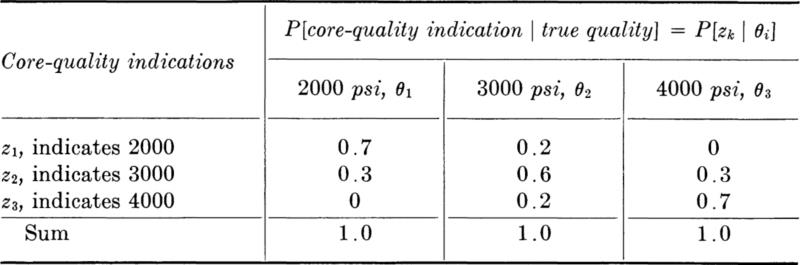
To better his information he has two cores taken and tested. The reliability of any one of these core tests in defining in-place concrete quality is defined by the table of sample likelihoods or conditional probabilities:
Fig. 5.2.2 Remodeling decision.
The two cores are taken, one indicating 2000, one indicating 3000; that is, the outcome is {z1,z2}. As discussed in detail in Sec. 2.1, we can find the posterior probabilities of state in either of two ways: (1) by first finding the conditional probabilities of the {z1,z2} outcome given the various possible states and then finding the posterior probabilities of state; or (2) by first finding the posterior probabilities of the states given the first outcome z1 and then, using these posterior probabilities as priors, finding the posterior probabilities given the second outcome z2. In either case, the results are the same. With the former approach, we find first (assuming independence of the samples) the conditional probabilities or sample likelihoods.
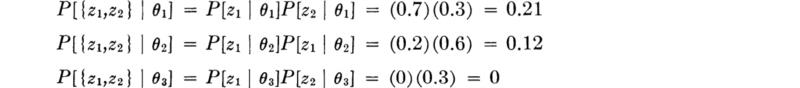
Then the posterior probabilities are
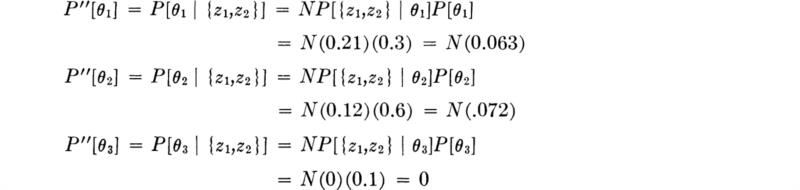
In which N is the normalizing factor needed to make these posterior probabilities sum to 1.
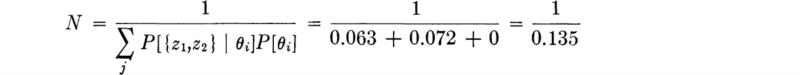
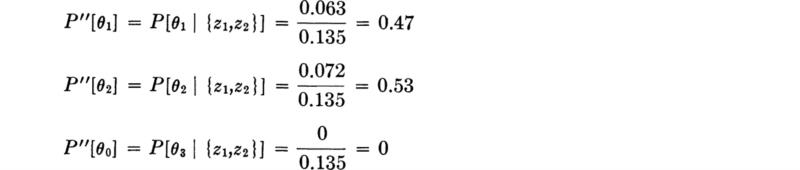
The core outcomes have eliminated the possibility that the concrete is of high strength, and they suggest that the lower-strength state is more likely then the engineer had originally judged.
Using these probabilities in the decision tree, Fig. 5.2.2, the best decision seems to be a2, limiting the use of rooms.
In fact the engineer might reconsider his position, which now finds the concrete quality quite uncertain. He may also recognize that he can, at some expense, carry out further experimentation to gain further information. In this case, he might want to order another or several more cores or even a load test. In Sec. 5.3, we shall treat such questions as, “When should he postpone the decision and pay for more information?” and, “Which experiment should he pay for?”
Illustration: A traffic-sampling problem In a study of the dispersion of traffic throughout a city, one car in every r cars entering the city between 8 and 9 A.M. via a certain route, route A, was stopped and small, easily visible stickers were placed on its bumpers. During the day various points in the city were monitored by men who counted the total number of marked autos passing certain points during a certain time interval. A decision as to whether to restrict a particular street to one-way traffic is going to be based on the total number of cars that enter the city via route A and then use this street during the time interval. The performance of the total traffic system will be improved if the change is made and this number is large. If the decision to restrict the street is made, but the traffic on it from route A is now small, the inconvenience to others will outweigh the gain for route A commuters.
The engineer summarizes these potential consequences in a utility assignment of
![]()
in which a1 is the action to restrict the street to one-way flow. The action will incur cost c1 to others, but it will bring benefits to route A users which the engineer assumes are an increasing function of θ, the total number of cars from route A using the street during the time interval (on the day of the study, for simplicity). To take action a2 is to leave the street as is, with (relative) utility of zero:
![]()
We need information about the state of nature θ. The engineer summarizes the information contained in a number of related, but less specific, past traffic surveys and traffic-assignment analyses by assigning θ a prior distribution, P'[θ], θ = 0, 1, 2 ... . His decision will be determined by an expected utility criterion based on the posterior distribution of θ.
The results of the day’s survey are an observation that z0 cars with stickers used the street during the specified time interval. What is the posterior distribution of θ?
We ask first for the sample likelihood P[Z = z | θ] in which Z is the random number of marked route A cars using the street. The probability that any one of the θ route A cars using the street has a sticker is 1/r. Assuming independence of cars, Z, the total number of marked cars in the total of θ cars, has a binomial distribution:
Thus, given the observation that Z = z0, the likelihood function, a function of θ, is
since any value of θ equal to or larger than z0 could lead to the observation of Z = z0. AS a function now of θ, the likelihood function gives the sample-implied relative likelihoods of the various possible values of the state θ. It should be emphasized that in this case the sample likelihoods were derived from a theoretical analysis of the experiment, not from purely subjective assignments.
The posterior distribution of θ is thus
The interesting part (θ ≥ z0) can be rewritten
in which the new normalizing constant is
It should be expected that the larger the proportion of cars that are stopped for stickers, the “better” the survey. In the limit, if every car is stopped, r = 1, the information on θ is perfect. The likelihood function [Eq. (5.2.6)] becomes simply
![]()
in which z0 might equal, say, 64 cars. In this case Eq. (5.2.7) becomes
![]()
This result is true no matter what the engineer’s prior distribution is (as long as that distribution does not specifically exclude the possibility of θ = 64, that is, as long as P'[64] > 0). The expected costs of the actions are

implying that a1 is the better decision only if the cost of the change c1 is less then 64b1 + 4096b2.
The cost of a survey that stops every car may be high. Had the engineer decided to stop only every other car, the sample likelihood function would, of course, not be concentrated solely at θ = z0. If every other car were stopped (r = 2) and the number of marked cars observed were z0 = 32, the sample-likelihood function [Eq. (5.2.6)] would appear as shown in Fig. 5.2.3. Combined with the prior distribution [through Eq. (5.2.8)], this would yield the posterior distribution Pʺ[θ] and finally E[u(a1)]. The shapes of two posterior distributions are shown in Fig. 5.2.4. In both cases the engineer’s prior distribution was triangular, either increasing from θ = 50 to θ = 90 (Fig. 5.2.4a) or decreasing from θ = 50 to θ = 90 (Fig. 5.2.4b). Compare these with the likelihood function, Fig. 5.2.3. Even for these diverse prior shapes, the posterior distribution and hence the decision are stili influenced predominantly by the shape of the sample-likelihood function, that is, by the information in the experimental results.
Fig. 5.2.3 Selected values of the sample-likelihood function given an observation of 32 marked cars; every second car marked.
Fig. 5.2.4 Posterior distributions based on every second car marked.
If an even smaller proportion of cars were stopped and marked, say one in four, and 16 were observed† on the street, the likelihood function becomes much more diffuse (Fig. 5.2.5), implying that it contains less information about the value of θ. In this case the engineer’s prior information will be of more relative significance. Figure 5.2.6, parts a and b, shows posterior distributions based on the two triangular prior distributions mentioned above. Clearly, these prior distributions have a strong influence on the final shape, and hence potentially on the decision.
The trend is clear. If only every eighth car is marked, we know that unless the value of Z observed is very large or very small, the information to be gained will be of such small value relative to the engineer’s triangular prior distribution as to have little influence on the posterior distribution of θ or the decision. This conclusion is influenced, of course, by the shape of the prior distribution.
Fig. 5.2.5 Selected values of the sample-likelihood function given an observation of 16 marked cars; every fourth car marked.
In Sec. 5.3 we shall investigate the method by which the engineer here could have planned whether to mark every car, every second car, or every rth car, or whether even to dispense with the new survey entirely and base his decision on his prior distribution. We should anticipate that the decision to experiment and the level of experimentation will depend on the nature of the engineer’s prior distribution, the costs of various experiments, and the quality of information we expect to gain from them.
Illustration: A flow-measurement problem In this example we shall illustrate several factors commonly appearing in engineering problems. These include the use of inexact, empirical functional relationships, the observation of an easily measured variable to help predict the state of interest, and the presence of joint state variables, one or more of which may not be of direct interest, but whose influence must be accounted for.
In the decision as to the amount of pollutant that can be safely released into a river in any day, the flow rate θ for that day must be estimated. This flow rate is the integrated effect of the distribution of the downstream component of the velocity across the cross-sectional area of the channel on that day. Owing to the difficulty and expense of making all the velocity and depth measurements necessary to calculate θ, however, it is predicted using only an easily measured depth Z at a convenient reference point.
Fig. 5.2.6 Posterior distributions based on every fourth car marked.
To “calibrate” the measuring procedure, the river was carefully surveyed a number of times under different flow conditions to measure θ, the total flow rate. At the same time the reference depth Z was observed and a reference, midstream, velocity V was measured. A regression analysis (Sec. 4.3) of the observations of θ/V versus Z led to the conclusion that a straight line gave a reasonable fit in the region of interest, but the scatter of the observations about this line was significant. †
The channel conditions are constantly changing. On a particular day, the engineer responsible for the decision on that day interprets historical data, seasonal information, and other indirect information (such as a careful measurement 5 miles upstream made earlier in the summer), by putting a joint prior distribution on θ and V. We shall see that a distribution on θ alone is insufficient in this problem. For simplicity we use the simple discrete distribution shown in Fig. 5.2.7.
The consequences of the decision are a function only of θ, the flow rate. The available actions, a1, a2, . . ., are various rates, f1, f2, . . ., of discharging the pollutant into the river. Assume that the utility function for any action-state pair is
![]()
in which 0.1θ is the “permitted” discharge rate. The consequences of mistakenly using a discharge rate in excess of this value include a flat “fine” of b units and other, exponentially rising losses.
Without an experiment the decision could only be based on the prior on θ, now a marginal to the joint prior given in Fig. 5.2.7:
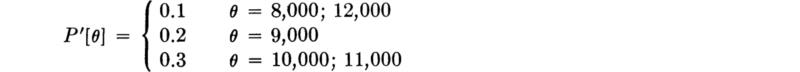
Given an observation on the reference depth Z, however, we can compute a posterior distribution on θ which reflects the uncertainty in the calibration “curve” and the dependence of that curve upon the uncertain velocity V.
The sample-likelihood function, now necessarily a function of θ and V, P[Z = z | θ,V], must be deduced † from the plot of observations of the careful surveys. In discrete form, for simplicity, this is given as a probability of 0.5 that Z will equal its “most likely” value, which, is linearly related to flow rate over reference velocity; specifically, it is 2 + 3 × 10–3 θ/V. The scatter about this empirical line is represented by discrete probabilities of 0.25 that Z will be 1.0 to 1.5 ft above or 1.0 to 1.5 ft below this most likely value.
Fig. 5.2.7 Joint prior on flow rate and reference velocity.
Suppose that the engineer measures the reference depth and observes a value of Z = 13 ft. Any pair of values of θ and V such that 2 + 3 × 10–3 θ/V is within 1.5 ft of 13 feet might have given rise to this observation. The nonzero sample liklihoods (that also match possible state pairs {θ,V} indicated in the prior) are thus
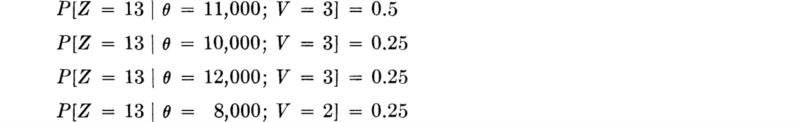
The latter three cases arise from possible errors of 1.0 to 1.5 ft in the empirical relationship. The last, for example, arises from an error of 1 ft, since 2 + (3 × 10–3) (8000/2) equals 14.
Based on an obvious extension of Bayes’ theorem [Eq. (5.2.2)] to a two-dimensional state of nature, the posterior (joint) probability mass function on θ and V is zero except at four points:
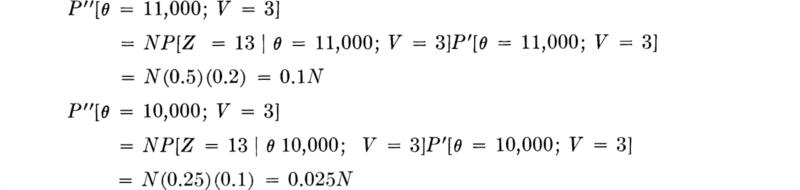
and, similarly,
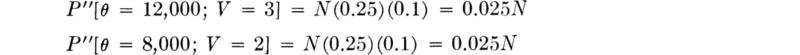
Therefore
![]()
The posterior joint distribution of θ and V is shown in Fig. 5.2.8. The
Fig. 5.2.8 Joint posterior on flow rate and reference velocity.
marginal distribution of θ is now
![]()
This distribution should be used to compute the expected utility associated with each action. For example, for aj with pollutant rate fj = 1000:
![]()
Reflection on this illustration will reveal the necessity of including the uncertainty in V in the analysis. It cannot, for example, be replaced by E[V] =2.4 ft/sec if a correct marginal posterior distribution on θ is to be obtained.
The role of the dispersion in an empirical formula is to introduce the probability of values away from the “calculated” or “most likely” values of θ (or here θ/V) being possible states given an observation of Z. The width of this dispersion controls the number and relative weights of these values of θ, through the sample-likelihood function.
Terminal analysis or decision analysis given new information follows the same pattern as prior analysis, Sec. 5.1, once posterior probabilities of state Pʺ[θ] have been calculated. These are based on Bayes’ theorem:
![]()
in which N is a normalizing constant, P'(θi) is the prior probability of state θi, and P[zk | θi] is the sample likelihood or conditional probability of observing the experimental outcome Z = zk, given that θi is the true state. Note that once zk has been observed, only the sample likelihoods of that result, P[zk | θi] for all θi, are needed for the decision analysis.
Posterior probabilities are influenced by the sample likelihoods and by the prior probabilities. If either set of probabilities is sharply concentrated at some particular θi’s, relative to the other set, the former set will have the dominant influence of the posterior probabilities. In short, information from a “reliable” experiment will dominate a vague prior distribution, and vice versa.
In the previous two sections we have dealt with decision making using given information and with processing of new information prior to the decision. In this section our concern is with deciding whether a price should be paid for new information and which source of information is the best choice.
Often the decision maker has the option of paying to observe the outcome of an experiment before making his choice of actions. If the cost of this experiment is sufficiently small compared to the information on θ that it promises, the engineer should select to experiment. If several types or levels of experimentation are possible, he should choose among them in a manner which achieves the best balance between experiment cost and reduced risk in the action choice.
Identifying the possible experiments as e1, e2, . . ., and denoting, for convenience, the choice of no further experimentation as e0, the complete, two-stage decision tree becomes that shown in Fig. 5.3.1. E is the set of available experiments, e0, e1, e2, . . . . Having chosen an experiment e, an outcome z in the sample space Z of the experiment will be observed. The decision maker must then choose an action a from the set of actions A, after which the state of nature θ will be found in the space θ. As a result of this sequence of consequences, value measured by a utility assignment, u(e,z,a,θ), will be received. Note in particular that these consequences include the cost of experimentation.
Fig. 5.3.1 Complete decision tree.
In practical situations the possible experiments are represented by a number of alternatives to collect more data on various quantities that might alter the present (prior) probabilities of the state of nature. Before deciding on the number of lanes in a highway, for example, the engineer might want to consider calling for an additional origin-destination survey to help predict the demand on the future road. The cost of this experiment may include delay of design and construction.
Before settling upon a foundation design, the engineer may want to consider drilling a series of test holes at the site, or if a preliminary survey is already available, he may consider a second set. Various kinds of experiments are possible, ranging from a single additional hole in a critical or questionable area, through a selective pattern over certain regions, to a fine-scale pattern over the entire building area. The costs and the potential information content vary from experiment to experiment.
By the analysis of such a decision tree we mean determining the best choice of experiment, and, in the process, determining the best choice of action given that a particular experiment has been chosen and a particular outcome of it has been observed. We shall outline the analysis procedure symbolically and then illustrate it.
The analysis of the tree proceeds from right to left in Fig. 5.3.1. We recognize that, given a particular experiment e and outcome z, the analysis of the remainder of a branch is precisely that which we studied in Sec. 5.2. It is a terminal or posterior analysis, that is, an analysis made after the experiment and outcome. Given the experiment and outcome, posterior probabilities can be computed and an optimal act can be selected on the basis of maximum expected utility. In the analysis of the complete tree, we must make all these posterior analyses for every possible experiment-outcome pair. The result of each pair is a corresponding optimal action and its associated expected utility, which we denote u*(e,z):
in which the (“posterior”) expected utilities are
The probabilities of state used in this equation are the posterior probabilities Pʺ[θi] or P[θi | e,z], except in the case of the no-experiment or e0 branch, when they remain the prior probabilities. Again for notational convenience we suppress the possible dependence of these probabilities of θ on the action a.
In order to chose from among the available experiments, we need only to calculate the expected value of each and select e to maximize expected value; that is, we must choose e to maximize:
To compute this expected value for each e we need, in addition to u*(e,z), only the probabilities of the various outcomes given that experiment e is taken. These are simply
The conditional probabilities of outcomes given the state, i.e., the sample likelihoods, are familiar to us. Here we only need multiply them by P'[θi] and sum to obtain the probability that a particular outcome will be observed.
Because a number of terminal or posterior analyses are made conditional upon, but actually before the experiment and the outcome, this entire analysis is called preposterior. The analysis procedure is illustrated numerically in the next example.
Illustration: Preposterior analysis A single, simple example will be given, for the computational aspects are similar to those already presented.
Reconsider the engineer who was faced with selecting a steel pile to be driven to a firm stratum at an uncertain depth below. We put him now in a more realistic setting than originally found in Secs. 5.1.1 or 5.2. The engineer now must place an order for a large number of piles to be used at the same site. The stratum is known to be at a constant but unknown depth below the entire site. The relative utilities are –400 if the short piles are ordered (a0) and the true depth is 50 ft (θ1), and –100 if the long piles are ordered (a1) and the depth is 40 ft (θ0). Otherwise, the losses are 0. The engineer’s prior probabilities are:

The losses are now associated with having to wait for more steel if insufficient lengths are obtained or having to scrap or return at a loss the excess steel if unnecessarily long piles are ordered.
The engineer has three options with regard to experimentation. He may choose to order on the basis of present information (e0), to use the imperfect sonic device discussed in Sec. 5.2 (e1), or to have a hole drilled to determine the true depth accurately (e2). In the latter two cases he will postpone ordering until the outcome has been determined. With the use of e1, the sonic tester, the experimental cost is small. It amounts to 20 units, which we assume can be subtracted from the relative utilities of 0, –100, and –400 associated with no experimentation to yield the utilities of the total consequences including experimentation, † The drilling operation is more reliable but more expensive, being represented by a cost of 50 units, subtractable, it is assumed, from other utilities. The elements of the decision tree, Fig. 5.3.2, are in their places, except for the probabilities.
For the e0 branch, no experiment is made, nothing is observed, and the probabilities of state are the prior probabilities. As indicated in Fig. 5.3.3, the expected value of action a0 is –120 and that of a1 is –70. The latter is preferred, so –70 becomes u*(e0,z); this figure is entered on the e0 branch.
Fig. 5.3.2 Pile-order illustration of preposterior analysis.
Fig. 5.3.3 Pile-order decision tree with probabilities and expected utilities.
Consider next the e2 or drilling-experiment branch. In this case, there is no possibility that an incorrect or ambiguous state indication will be made. Thus the posterior probabilities given the outcome z0 are:

and those given z1 are:

These intuitively obvious results can be verified through formal application of Bayes’ rule. The sample likelihoods needed for this formal analysis are:

Multiplying by prior probabilities and normalizing will yield the results deduced informally above.
Entering these probabilities, a posterior analysis is carried out on the {e,z0} branch and on the {e,z1} branch, as shown in Fig. 5.3.3. The results indicate, obviously, that a0 is optimal if z0 is observed and that a1 is optimal if z1 is observed. In both cases the maximum expected utilities are –50, the cost of obtaining this perfect information:
![]()
Because both these utilities equal –50, we conclude that the expected utility of e2 is –50 no matter what the probabilities of z0 and z1. This then is E[u(e2)]. This intuitive result is verified formally as follows. From Eq. (5.3.4)
and
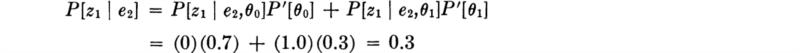
These are the probabilities that z0 or z1 will be found if experiment e2 is taken. The expected utility of this experiment is [Eq. (5.3.3)]:
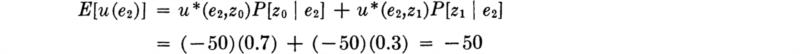
Finally, we consider again the sonic test e1. The sample likelihoods have been given in Sec. 5.2 as:
Sample likelihoods P[zk | θi,e1]
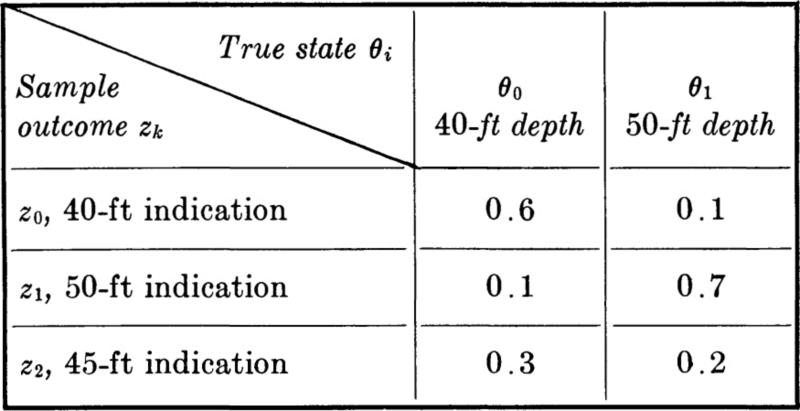
The posterior analysis given the ambiguous outcome z2 has been discussed in detail in Sec. 5.2. We found posterior probabilities † of state through Bayes’ rule as
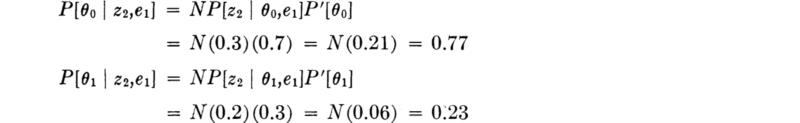
in which the normalizing constant N is 1/(0.21 + 0.06).
Multiplication of the posterior probabilities by corresponding utilities and summation leads to expected utilities. For example, for a0,
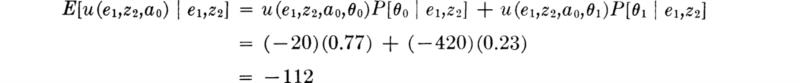
Similarly, the posterior expectation for a1 given experiment e1 and outcome z2 is (–120) (0.77) + (–20) (0.23) = –97. The better action in the event of outcome z2 to experiment e1 is a1; thus
![]()
The same steps must be repeated for experimental outcome z0 and outcome z1. The results are, for z0,
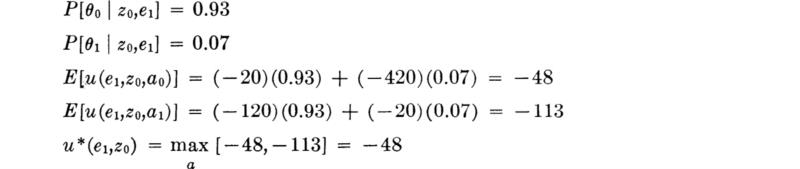
with a0 the better action. And, for z1,
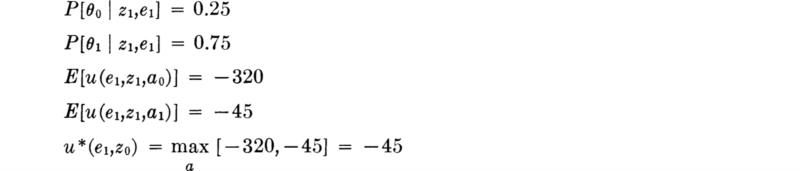
with a1 the better action. These values appear in Fig. 5.3.3.
The expected value associated with choosing experiment e1 is found by weighting the optimal utilities u*(e1,z) by the probabilities that z will be the outcome and summing. These probabilities are:
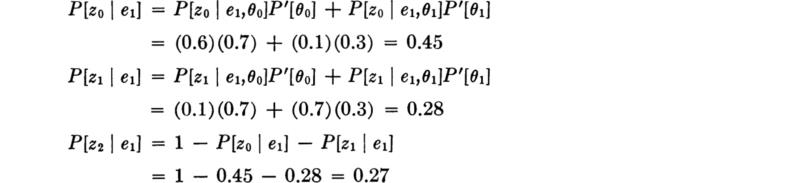
which are also shown in Fig. 5.3.3.
Thus the expected utility of e1 is:

Comparing the expected values of the three experiments, –70, –60, and – 50, shown in Fig. 5.3.3, it is apparent that the engineer should not make a decision before obtaining more information from one of the available experiments. Of the two experiments, the reliable but expensive one e2 is preferable (in this case) to the cheaper but less reliable sonic experiment e1. The engineer should absorb the initial cost of the drilling and then order accordingly, rather than run the risk of making an incorrect order. This risk results from his present uncertainty, which might be reduced but not eliminated by the less expensive sonic test e1.
Discussion on the value of information Because we have assumed additivity of utilities in this example, we can associate the costs of experimenting directly with the e branches, as shown in dashed boxes in Fig. 5.3.4. In this case, the cost of experimentation need not be considered until after the various terminal analyses. Therefore, all other utilities on this tree are simply increased in value (over those utilities entered in Fig. 5.3.3) by the costs of experimentation associated with their branches. Interpretation of the value of information is much simpler on this tree. Note, for instance, that the expected cost (– 70) of choosing e0 and making a decision with present information is entirely risk-related; there is no experimentation cost. In contrast, with the perfect experiment (e2), the cost (– 50) is entirely that required to “buy information.” Once the experiment is paid for, there is no risk (expected cost) involved. No matter what the outcome of the experiment, the decision appropriate to the true state of nature will be made with certainty. In this example, the perfect information is worth its price, 50 units. If this price were 75 units, or 50 percent higher, however, it would be more prudent for the engineer to run the risk on the basis of his present knowledge than to pay for this perfect information. † This is the decision which is consistent with his stated’ preference and uncertainty assignments. Recall that these preference statements may contain relatively subjective elements. If the engineer feels, for example, that there would be a serious loss of personal reputation if he makes an incorrect order on the basis of his present information (which may rest strongly upon his personal professional judgment), then this fact should be reflected in the utilities (now –400 and –100) assigned to these “bad outcomes” and experiment e0. His aversion to risk should be reflected in these utility or preference assignments, not in biased, “conservative” uncertainty assignments.
Fig. 5.3.4 Pile-order decision tree with separated experimental costs.
The e1, or imperfect, inexpensive experiment, offers a compromise between the two extreme level-of-experiment decisions e0 and e2. Note that if the outcome of the experiment favors either θ0 or θ1 (that is, if either z0 or z1 is observed), the risk is reduced from the no experiment or present expected utility of –70 to either –28 or –25. Because the method is not wholly reliable, however, the risk has not been eliminated entirely, as it is in e2. In particular, if the ambiguous result z2 is observed, the engineer has in fact increased the risk † that he faces from – 70 to –77. This ambiguous outcome is sufficiently unlikely, however, that the experiment choice e1 as a whole represents a risk of only –40. That this risk reduction can be purchased for 20 units makes it more attractive than not experimenting at all, but less attractive than paying 50 units for perfect information. Notice that only a 25 percent increase in the cost of the drilling would make e2 less attractive than e1.
Again, professional factors can be reflected in the decision analysis. Suppose that the engineer chooses e1; having observed outcome z1, he takes action a1, which is later revealed to be an incorrect decision (that is, θ0 was in fact the true state). He may not be held responsible for his choice if he can point to the fact that it was “based” on a sonic test result which happened to be misleading. If this is the case, under e1, the losses to the engineer given bad outcomes should be less than the no-experiment values of –100 and –400. In this case-utility is a function of e and z as well as θ and a.
Comment The authors look upon decision theory as an extremely accurate conceptual model of professional engineering decision making. It permits problems to be broken down, studied in detail (by different people, if appropriate), and then reassembled in a consistent manner. Quite apart from possible quantitative help, however, simple understanding of the concept of statistical decision theory may be a useful guide in a practical, professional decision situation. The model points out the need to balance cost and likelihood, to incorporate preference and judgment as well as data, and to consider the cost of obtaining more information in relation to its potential benefit in reducing uncertainty and risk. The theory deserves much wider understanding among civil engineers.
In the next chapter we shall consider some more advanced decision-theory topics. Conceptually we add nothing to the basic decision model; the emphasis will be on random variables and random processes rather than random events (or states) as in this chapter. Continuous sample spaces will be used more freely, with resulting enhancement of model accuracy and computational economy.
Preposterior analysis is designed to choose among available experiments or sources of information ei (including the “do-nothing” experiment e0). The analysis requires a terminal analysis of each experiment e and each possible outcome z of that experiment. For the various experiments, the resulting optimal-actions’ expected utilities u*(e,z) are weighted by the probabilities of each possible experimental outcome to obtain the expected utility of carrying out that experiment. (The probability of a particular experimental outcome z is obtained by weighting the sample likelihoods of that outcome by the prior probabilities of state θi.) The experiment with the highest expected utility is the best choice consistent with the engineer’s stated probabilities and preferences.
Preposterior analysis can reveal the value of information in the form of reductions in the risks (expected losses) associated with any particular experiment.
Bayesian decision theory is a prescriptive or normative † model for decision making under uncertainty. It demands that the decision maker state his (possibly subjective) prior probabilities of state P'(θ) and his preferences among different pairs of actions a and states of nature θ. If these preferences are properly assigned in the form of a utility function u(a,θ), then decisions should be based on a maximum-expected-utility criterion. Acceptance of the theory rests in principle on an acceptance of both subjective probabilities and utility functions, although these two factors may in practice be indistinguishable from “objective” relative frequencies and dollar values, respectively.
Decision analysis is simply the application of the fundamental probability theory of Chap. 2. It may include simple prior analysis, based on the prior probabilities of state P'[θ], or terminal analysis, based on the posterior probabilities of state Pʺ[θ], The latter are found through the application of Bayes’ theorem, given the outcome of an experiment Z = z. Required information includes, in addition to the prior probabilities, sample likelihoods P[z | θ]. These may be obtained directly or indirectly through theoretical analysis of the experimental scheme. In addition, decision analysis may include choosing from among several possible experiments prior to choosing the action. This preposterior analysis involves making a terminal analysis of each possible experiment-outcome {e,z} pair and combining this with prior probabilities of the possible outcomes to obtain the expected utility associated with each experiment.
Bayes, T. [1958]: Essay towards Solving a Problem in the Doctrine of Chances, Biometrika, vol. 45, pp. 293–315. (Reproduction of 1763 paper.)
Benjamin, J. R. [1968]: Probabilistic Models for Seismic Force Design, J. Structural Div. ASCE, vol. 94, no. ST7, p. 1175, July.
Benjamin, J. R. [1968]: Probabilistic Structural Analysis and Design, J. Structural Div. ASCE, vol. 94, no. ST5, p. 1665, May.
Fishburn, P. C. [1965]: “Decision and Value Theory,” John Wiley & Sons, Inc., New York.
Good, I. J. [1950]: “Probability and the Weighing of Evidence,” Charles Griffin & Company, Ltd., London.
Good, I. J. [1965]: “The Estimation of Probabilities,” Research monograph no. 30, Massachusetts Institute of Technology Press, Cambridge, Mass.
Grayson, C. J. Jr. [I960]: “Decisions Under Uncertainty, Drilling Decisions by Oil and Gas Operators,” Harvard University Press, Cambridge, Mass.
Hadley, G. [1967]: “Introduction to Probability and Statistical Decision Theory,” Holden-Day Inc., Publisher, San Francisco, Calif.
I.E.E.E. [1968]: “Special Issue on Decision Analysis,” IEEE Tran. vol. SSC-4, No. 3, September.
Jeffreys, H. [1961]: “Theory of Probability,” 3d ed., Clarendon Press, Oxford.
Jeffrey, R. C. [1965]: “The Logic of Decision,” McGraw-Hill Book Company, New York.
Kaufman, G. M. [1963]: “Statistical Decision and Related Techniques in Oil and Gas Exploration,” Prentice-Hall, Inc., Englewood Cliffs, N.J.
Lindley, D. V. [1965]: “Introduction to Probability and Statistics from a Bayesian Viewpoint,” parts 1 and 2, Cambridge University Press, Cambridge, England.
Luce, R. D. and H. Raiffa [1958]: “Games and Decisions,” John Wiley & Sons, Inc., New York.
Machol, R. and P. Gray [1962]: “Recent Developments in Information and Decision Processes,” The Macmillan Company, New York.
Pratt, J. W., H. Raiffa and R. Schlaifer [1965]: “Introduction to Statistical Decision Theory,” McGraw-Hill Book Company, New York.
Raiffa, H. [1968]: “Decision Analysis, Introductory Lectures on Choices under Uncertainty,” Addison-Wesley Press, Inc., Reading, Mass.
Raiffa, H. and R. Schlaifer [1961]: “Applied Statistical Decision Theory,” Harvard University Press, Cambridge, Mass.
Savage, L. J. [1954]: “The Foundations of Statistics,” John Wiley & Sons, Inc., New York.
Savage, L. J. [I960]: The Foundations of Statistics Reconsidered, 4th Berkeley Symp. Math. Statist. Probability, vol. 1, pp. 575–86.
Schlaifer, R. [1961]: “Introduction to Statistics for Business Decisions,” McGraw-Hill Book Company, New York.
Schlaifer, R. [1959]: “Probability and Statistics for Business Decisions,” McGraw-Hill Book Company, New York.
Schlaifer, R. [1969]: “Analysis of Decisions Under Uncertainty,” McGraw-Hill Book Company, New York.
Tribus, M. [1969]: “Rational Descriptions, Decisions, and Designs,” Pergamon Publishing Company, Elmsford, N.Y.
Turkstra, C. J. [1962]: A Formulation of Structural Design Decisions, Ph.D. dissertation, University of Waterloo, Waterloo, Ontario.
Von Neumann, J. and O. Morganstern [1953]: “Theory of Games and Economic Behavior,” Princeton University Press, Princeton, N.J.
Weiss, L. [1961]: “Statistical Decision Theory,” McGraw-Hill Book Company, New York.
Abraham, C. and J. Thedié [I960]: The Price of a Human Life in Economic Decisions, Revue Français de Recherche Opérationnelle, pp. 157–168.
Altouney, E. G. [1963]: The Role of Uncertainties in the Economic Evaluation of Water Resources Projects, Eng. Economic Planning Program Report EEP-7, Stanford Univ.
Howard, R. A. [1966]: Decision Analysis: Applied Decision Theory, Proc. 4th Inter. Conf. on Operational Research, Inter. Fed. Oper. Res. Soc, Boston.
Rascon, O. A. [1967]: Stochastic Model to Fatigue, J. Eng. Mech. Div., ASCE, vol. 93, no. EM3, pp. 147–156.
5.1. You are running a small (three-man) design office and suddenly the job you are working on is stopped pending the outcome of an election to occur 3 months from now. Office operation costs $3,000 per month.
(a) Set up the decision tree for the actions you can take now:
(i) Do nothing.
(ii) Close the office for one month. This reduces the losses to zero, but you cannot count on rehiring an adequate staff at that time. A small job may be received at the end of the month.
(iii) Same as (ii) except close office for 3 months.
(iv) Make the rounds of prospective clients and offer to work for a reduced fee. Note that it is very difficult to raise fee levels once they are dropped. You can expect to receive sufficient jobs to continue to operate your office. Be very careful in defining the possible states. Note that probability measures exist for each possible state—undesirable as well as desirable. It is a fact that many offices are totally unrealistic in such circumstances.
(b) What additional information do you need to make the outlined study in (a) useful. Note that the election may prove negative and the job may not resume.
5.2. Develop a utility function to represent the utility of your grade-point average. Assume a numerical grade scale from 0 to 4 with grades assigned numbers according to:
| Grade | grade points |
| Failure | 0 |
| D | 1 |
| C | 2 |
| B | 3 |
| A | 4 |
(a) First, assume that a grade-point average of 2.0 is required for graduation and your only concern is with obtaining a degree.
(b) Second, assume you are a graduate student and you need a grade-point average of 2.75 to receive your degree. Consider too the influence of grades on your social status.
(c) Third, assume that you require financial aid to continue your education. All other factors being equal, the level of aid you receive depends entirely on your grade-point average and no aid is likely for less than a 3.0 average.
(d) Comment on the difficulty in comparison of utilities for this problem and those for other situations involving economic decisions under uncertainty.
5.3. Construct your personal utility function for money in the range of –$1,000 to +$1,000. The decision situation is related to possible added income and/or expenses associated with traveling to Europe to interview for a possible job. How would this function change if you had no cash on hand? How would it change if you had $10,000 in personal savings?
How would the utility function change if you needed $500 to make the trip? Assume that a major loss is received if the trip is not made.
5.4. You are setting up your own consulting office with very limited financial backing. One of the first problems is to set a fee-per-hour level. If your fee is too large, you will lose clients, and if your fee is too small, you will not receive adequate payment for your services and, in addition, will find it difficult to increase your income from this set of clients. You are considering charging $20/hr or $25/hr. These are the actions.
If your fee level is $25/hr (a1) and the business response (θ1) is adequate, you assign the gain to be +100. If you charge the same rate and the response is unsatisfactory (θ2), the loss is 50. If you ask for $20/hr (a2) and the response is adequate (θ1), the gain is 50, while if the response is unsatisfactory (θ2), your loss is 100. Assume:
![]()
What is the optimum action under (a) and (b)?
5.5. Construct a decision tree and determine the optimum decision for an engineer in business for himself. The potential losses involved are small compared to his working capital.
The engineer either may accept the beam design his employee has selected and shown on the plans or he may ask for a revision in the design involving a drafting cost of $100. There is no gain or loss associated with a design which performs satisfactorily. If, however, the long-term creep deflection of the concrete beam is excessive, the engineer estimates a (discounted) future loss of $500 in potential fees and inconvenience to his client (as the client’s losses are reflected through professional responsibility in dollar loss to the engineer).
The sustained loads are quite well known for this structural type, but uncertainty exists in the long-term effective modulus of elasticity of a reinforced-concrete beam. The engineer is concerned because the likelihood of this modulus being greater than 4000 ksi, i.e., the value needed for satisfactory performance of the present design, is only 0.3. With redesign a value of the modulus of 3000 ksi would be satisfactory. This value will be exceeded, the engineer feels, with odds 3 in 4.
5.6. Reconsider the first example in Sec. 5.2. Based on the ambiguous depth indication and the utilities, the engineer used a long pile even though the shallow depth was more likely. Would this still be the correct action if the instrument had indicated a shallow depth? How large would the “error probability” P[z0 | θ1] have to be before the long pile would be the better decision no matter what depth the test indicated? Would the test be justified at any cost in this circumstance?
5.7. Opportunity loss or regret. Consider a simple decision problem with a general payoff table of utilities:
Payoff table of utilities
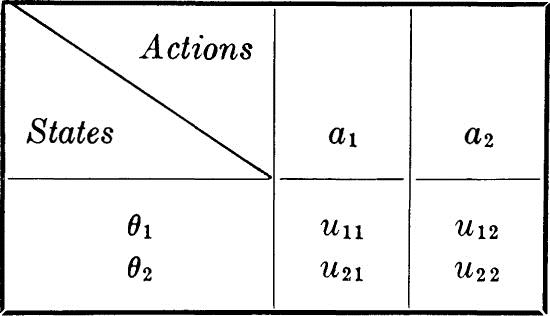
Assume that the actions are numbered such that u11 > u12 and u22 > u21. Note that if the engineer knew that θi was the true state he would choose action ai and obtain utility uii as the best he could do given that state.
If he had instead taken the other action, he would not receive this much utility but something less, namely, u12 or u21. We define the “lost” amount, u11 — u12 or u22 — u21, as the regret or opportunity loss associated with having not taken the best action given the state. We can construct, in general, an opportunity loss table for a decision problem by subtracting the utility values in any row from the largest utility value in that row. In this case:
Opportunity-loss table
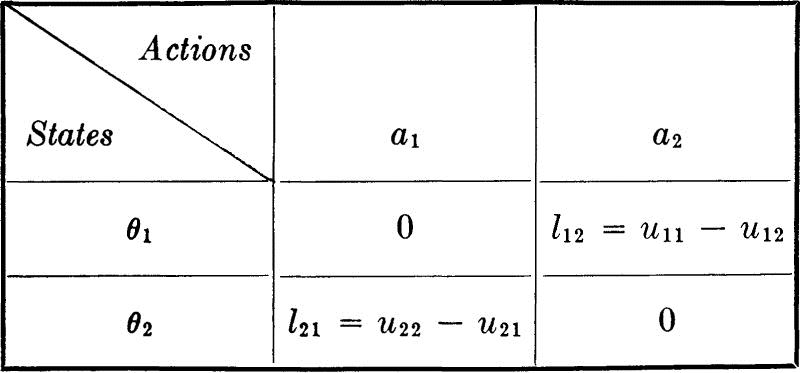
Show for this simple case that one will obtain the same choice of decisions if he maximizes expected utilities or minimizes expected opportunity losses. Hint: Compare the values of these expectations for the two actions for arbitrary p = P[θ1], showing that E[u(a1)] > E[u(a2)] if and only if E[l(a1)] < E[l(a2)].
This result holds in general for any number of states or actions. It is often easier to think about and evaluate the relative losses associated with several actions for SL fixed state θi than to deal with the absolute utilities. The negative of opportunity losses were in fact used in Table 5.1.1 and in Fig. 5.2.1 in the pile-selection illustration. Of course, to minimize expected opportunity losses is to maximize expected negative opportunity losses. The point remains that the engineer can concentrate on each state of nature separately and look at utilities or losses relative to the best action available, given that state.
5.8. Specifications for the shop welding of certain structural assemblies say that no welds with internal flaws greater than a critical volume can be permitted in order to guarantee adequate strength. An expensive x-ray inspection system is presently being used to inspect all welds. The test is considered to be absolutely accurate, and history shows that 15 percent of all welds are rejected and rewelded. The fabricator is considering introducing a new, less-expensive, but not perfectly reliable ultrasonic inspection device. By retesting known good and bad welds, the fabricator has found that the new device will, if a flaw is present, indicate this fact with probability 0.80 and erroneously pass the weld with probability 0.20. If no flaw is present, however, the device will pass the specimen with probability 0.90 and incorrectly indicate a critical flaw with probability 0.10.
(a) What is the probability of finding an indication of a bad weld using the sonic device? What are the probabilities of passing a poor weld and of a good weld being wrongly indicated as bad?
(b) If perfect inspection costs $1.00 per weld while the new method costs $0.50, and it costs $5.00 to redo a weld and $30.00 to have a defective weld leave the shop, should the new device be accepted?
5.9. Reconsider the flow-rate-measurement illustration in Sec. 5.2. Assume that the engineer incorrectly neglects the uncertainty in V and carries out a terminal analysis based on θ alone, using his point estimate of V = 2.5 ft/sec. Recompute the marginal posterior distribution of θ and compare it with that found in the illustration.
Discuss the influence of neglecting the possible uncertainty in variables such as V which are embedded within a problem (in the sense that utility does not depend on them nor are they observed in an experiment).
What is gained if the flow rate is estimated using a daily measurement of V as well as Z? How do these results differ for observations Z = 13 and V = 2?
5.10. Recompute the marginal posterior distribution of θ in the flow-rate illustration in Sec. 5.2, assuming now that there is negligible scatter about the relationship between Z and θ/V.
Consider two cases. An observation of:
![]()
Compute also the results for an observation of Z = 14 ft when equation uncertainty is retained. Then discuss such uncertainty in this type of problem.
5.11. Investigate the relative advantage of a “hedging” strategy in the pile-order- decision illustration in Sec. 5.3. This new strategy calls for a sonic measurement to be followed by a drill hole if and only if the sonic test is “ambiguous,” i.e., if z2 is observed. Keep the same experiment costs and assume additivity of utilities. Hint: Add a fourth alternative experiment to Fig. 5.3.5 with this form:
Fig. P5.11
Is the conclusion changed if it is recognized that the “double” experiment, sonic test and drilling, will lead to a delay in ordering with a loss of 50 units? Comment: This is a simple example of an n-stage sequential decision problem, where here n = 2. See Hadley [1967] for an elementary discussion of such problems.
5.12. † Discuss the construction of a decision tree for the engineer in the following situation. Which is the best action-state pair and how might utilities and probabilities be estimated? Make some reasonable guesses for numerical values.
A reinforced-concrete school building is under construction, and questions about concrete strength have arisen during construction. The contract cost of the entire structure is $2,161,713, and it is estimated that replacement of the concrete in question will cost $300,000 to $400,000. The superstructure of the two- and three-story building is specified to contain 4 percent of entrained air with a design strength of 3500 psi. Tests show up to 10 percent air, and tests made on concrete cylinders and 90 cores show a mean strength of 2100 psi when projected to a 28-day strength.
The situation is complicated by the results of load tests. In 16 tests using a superimposed load of 1.5 times the design live load plus half the dead load on the beams and slabs, the structure showed no signs of distress.
Replacement involves perhaps a year’s delay in the completion of the badly needed structure. Acceptance of the present structure involves assumption of liability in the event of poor future performance. The decision is complicated by the unknown relationships between beam capacity and concrete cylinder strength, particularly with underreinforced sections, and by the likelihood that the entire specified design strength is not needed in most of the structure.
Note that the decisive value is to be received at some unknown future time. Thus value to a well-established firm may differ from the value to an office that will cease operations in the near future.
5.13. A number of probabilistic, physical models of the process of fatigue damage have been proposed in the literature. Each leads to a different distribution of the number of load applications to failure. These include the Weibull distribution, the lognormal
distribution, and the gamma distribution. Other distributions exist (see, for example, Rascon [1967]), but several can be excluded on physical grounds, and others can be excluded because of their lack of ability to “fit” statistical observations. Remaining contending models have better or poorer physical arguments, and better or poorer “fits” to data. An expert in the field has summarized the situation at a particular point in time by saying, “Neither the Weibull nor gamma distributions can be excluded. If I had to give them relative weights now, I would say perhaps 60 to 40 Weibull over gamma.”
Two designs for a structural member are under consideration. If alternative a is analyzed assuming that the Weibull distribution holds, it has a reliability with respect to fatigue distress during its lifetime of 0.98, but the probability is 0.99 under the gamma model. On the other hand, the parameters are such that for the second design the reverse is true. The probability of failure is 0.01 under the Weibull hypothesis and 0.02 under the gamma hypothesis. (It is not known that these precise numbers could be constructed with these two particular distributions, but the situation is conceptually important even if there is only a change in the relative values of the probabilities.)
If the designs are of comparable initial cost and if the cost of failure is the same in both cases, which design should the designer use (to reflect best the information available to him)?
5.14. A large reinforced-concrete building is to be constructed on very poor foundation material. The building is 60 ft wide, 200 ft long, and 6 stories in height. Two basic foundation alternatives are friction piles or some type of raft foundation. A differential settlement on the order of 3 in. can be expected to involve legal problems with the client, since you have already indicated that the site is adequate for the proposed construction.
Routine tests and studies indicate that a pile foundation can be expected to show long-term differential settlements of up to 3 in. Odds cannot be quoted that the settlement will not be larger, but it is unlikely. The odds are approximately even that the differential settlement will be less than 1 in., approximately 4 to 1 that it will be less than 2 in., and perhaps approximately 1 in 100 that it will be approximately 3 in. The cost of a pile foundation is so large that it is “even money” that the client will abandon the job if this design is suggested. Use discrete states and note that the measures of likelihood must be normalized.
Studies for a raft foundation indicate that a relatively flexible slab coupled with rock surcharge around the building will be within the cost estimates. The odds are more or less even that the differential settlement will be less than 2 in. and approximately 10 to 1 that it will be less than 3 in.
If the settlement is too large, the client will take legal action against you; you expect the cost to you will be $1,000 or $10,000 with equal likelihood. Your profit on the job will probably be $3,000, providing that it goes to completion.
(a) Set up the decision tree for this decision and determine the optimum action.
(b) If the client now says he will not pay your usual fee, determine the offered fee level below which you would sue him for the original fee assuming that the cost of collection is $500. Assume that the client will be required to pay you $3,000 and normal engineering costs are not influenced by the legal problems. Note that this type of operation does not imply that you will not be offered future jobs. In fact, if you reduce your fee (under pressure), you can expect to receive future jobs (with attendant fee difficulties). Note that you could hedge against such problems by asking for more than you expect in the initial negotiations.
5.15. A large apartment complex for low-income renters is being considered. The choice must be made between conventional steel construction and using an innovative scheme of “pushup” construction that promises to cost less. There is uncertainty in the cost estimates in both of the proposals, but clearly it is greater in the case of the latter, untried, system of construction.
Assume that the best estimate of the conventional cost is x0, with uncertainty in the estimate being summarized by saying there is a 50–50 chance that the true cost will be within x0 ± 0.05x0. Assume that the best estimate of the pushup cost is 0.8x0, but that the “probable error” is 0.10x0; that is, there is a 50–50 chance that the true cost will be within 0.8x0 ± 0.1x0. Assume (for simplicity in your computations) that in both cases the engineer is prepared to state that his uncertainty in the costs can be described by symmetrical triangular distributions, centered on the “best estimates."
(a) As the technical representative of the nonprofit developer, decide which alternative to take if the project is being carried out with funding under government regulations which place a maximum rent on the units and which require that the rent be set so that no profit is made by the developer. The implication to the (charitable) developer is that he will make no money no matter what the construction cost, but he will lose money from his own “pocket” if the construction cost exceeds that value c which the maximum rents (minus interest, etc.) will just cover. This value can be accurately calculated to be c = 1.10x0. Sketch the function of utility to the developer versus the cost.
(b) As the technical representative of an association representing the steel industry, decide whether your industry should underwrite the pushup project by guaranteeing that it will pay any cost in excess of c. Your industry gains nothing if the pushup project is not undertaken, but gains information on a potentially profitable new development, no matter what its final cost. Assume that this benefit to the industry is judged to be worth 0.02x0, independently of the final cost, plus an amount which decreases linearly from 0.05x0 at 40 percent of conventional construction cost to zero at the cost of conventional construction x0. Sketch the utility to the industry versus true cost.
5.16. The Boston Port Authority (BPA) is trying to decide whether to begin immediate design and construction of a major airport in the Boston Harbor to supplement Logan Airport (a1) or to wait a number of years to make the decision (a2). The following information has been provided by their consultants, MADCO, Inc.:
(a) Passenger demand for conventional flights will do one of these things in the next decade:
θ1: Increase very rapidly (Logan overtaxed)
θ2: Increase moderately (Logan still satisfactory)
θ3: Remain about fixed owing to the introduction of new systems (highspeed ground transportation or vertical-takeoff aircraft)
(b) The losses to the BPA under the possible action-state pairs are
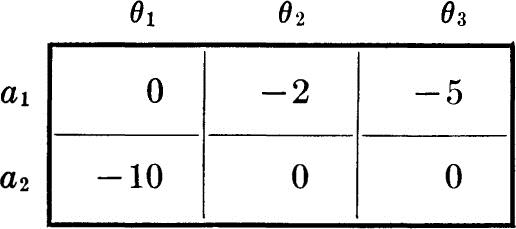
(c) Available information on demand and new system development projections can best be summarized by saying

(i) Based on the expected-cost criterion, determine the optimal choice of action for BPA.
(ii) Assume now that reliable information says there will be no new system (therefore P[θ1] = 0.4/(0.4 + 0.2) = ⅔ and P[θ2] = ⅓), but the demand remains uncertain. A major portion of the demand may be from New York-Boston commuters. Therefore, instead of choosing a1 or a2 at once, the BPA hired a second consultant, RIA, to conduct interviews with local businessmen. The “indication” of the survey was that demand would increase very rapidly. RIA pointed out, however, that such polls are not wholly reliable and that there is a 30 percent chance that this indication would be obtained even if the increase would be only moderate. On the other hand, if the true state is θ1, the polling procedure will “indicate” θ1 with 90 percent reliability. Reevaluate the BPA decision in the light of this new information.
5.17. Equivalent lotteries. The following decision-tree formulation and interpretation is often illuminating and useful. Return to the problem of assigning utilities to possible outcomes A, B, and C, which was discussed in Sec. 5.1.2. A and C were the most favorable and least favorable outcomes, respectively. Through interrogation, the decision analyst finds, as before, a probability p* of obtaining outcome A rather than C such that the decision maker is indifferent between obtaining outcome B and this “A versus C” lottery. Rather than calculating u(B) in terms of assigned values u(A) and u(C), we now replace outcome B by the “equivalent” lottery, namely, one with a probability p* of obtaining A and 1 — p* of obtaining C. Therefore, a decision tree which was of the form
Fig. P5.17a
is replaced by a tree of the form
Fig. P5.17b
Or, a more complicated tree (still with A and C as the extreme outcomes)
Fig. P5.17c
would become
Fig. P5.17d
(a) Demonstrate that the original criterion, “choose a to maximize the expected utility,” can now be replaced by the criterion “choose a to maximize the probability of obtaining the most favorable outcome A.” The reader can appreciate that this interpretation is more appealing to many users of decision theory.
(b) Apply this approach to the pavement-design illustration in Sec. 5.1.4.
5.18. A stream flows through a new residential area. An engineer must decide how much temporary flood protection should be provided during the 12-month period prior to completion of an upstream dam which will remove the threat. The channel has been reshaped and lined, and so the engineer has no historical data on stream heights at the site during floods. Based on limited data on flood flow rates and based on rough analysis of the channel’s hydraulic behavior, the engineer assigns to the coming year’s peak flood height an exponential distribution with mean 20 ft.
Find the expected utility of a design for the temporary protection which provides complete protection up to 24 ft. Assume that above 24 ft the damage
(a) Varies linearly:
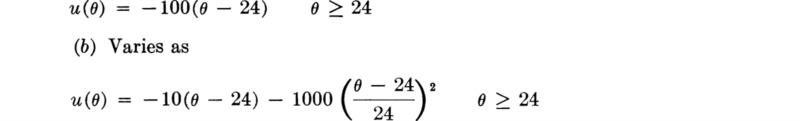
5.19. Consider the aggregate-borrow-pit illustration in Sec. 5.1. It is convenient to fit an analytical expression to the distribution on θ. The beta distribution with limits 3000 and 5250 yd3 is a reasonable choice.
Define and sketch a utility function over the same limits, a to b or 3000 to 5250 yd3, in a “beta form”:
![]()
Find the simple closed-form solution for the expected utility in terms of the state distribution parameters (a,b,r,t) and the utility parameters (ua,ub,<o<m). Fit a reasonable PDF to the CDF defined by Fig. 5.1.9. Evaluate u(θ) for ua = –10, ub = +1, m = 3.
5.20. The optimum design of a sewage-treatment plant involves minimizing the losses from possible over- and underdesign. Altouney [1963] has reviewed 71 public-works population projections after a 15-year period. The mean ratio of actual to predicted population was found to be 0.88 and the standard deviation of the ratio was found to be 0.12, with the normal distribution providing a satisfactory fit.
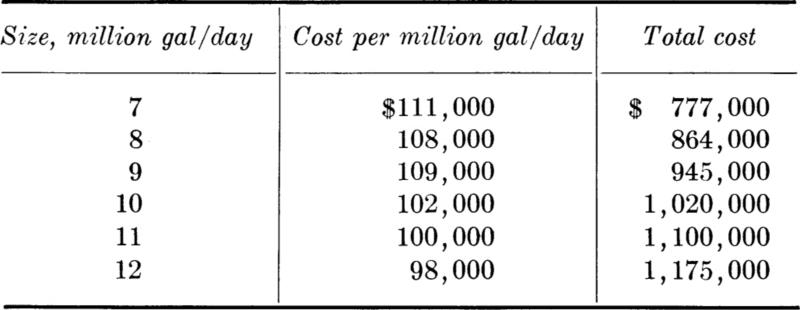
Use the accompanying cost figures.† Assume that the population is estimated to be 100,000 in 15 years and waste generation is 100 gal/(capita)(day). Design is to be based only on conditions 15 years from now. Study alternate actions of design for 7, 8, 9, 10, 11, 12 million gal/day. Assume that the cost of adding capacity is $150,000 per million gal/day needed.
5.21. An engineer has been called upon to judge the adequacy of an existing structure. Complete plans are available and preliminary computations show that the steel reinforcing is ample. Site inspection raises questions of quality of concrete and construction of a number of long-span slabs because of large deflections.
The engineer’s fee of $1,000 is guaranteed independent of his report conclusions. The owner has stated that he desires one of three reports based on strength according to code.
(i) Structure is unsafe.
(ii) Structure is safe for office loading, 50 psf.
(iii) Structure is safe for light storage load, 125 psf.
The engineer’s prior probabilities of capacity are
| State θ; live load capacity, psf | P′[θ] |
| 20 | 0.20 |
| 50 | 0.30 |
| 80 | 0.20 |
| 110 | 0.20 |
| 140 | 0.10 |
The owner believes very strongly that the structure is safe for light storage. If the engineer reports that the structure is unsafe, he faces loss of future jobs for the owner with a present worth of $5,000, whether he is correct or not. If he reports that the structure can be used for offices only, he has a probability of only 0.20 of receiving the desired jobs. If the engineer reports that the structure is safe for light storage, the future jobs are assured, provided that the performance is adequate. The total cost of reporting “adequate for office loading” and finding θ < 50 is $5,000; the cost of being wrong (θ > 125) with a report “adequate light storage” is $10,000.
Construct the decision tree for this situation. Is the fee of $1,000 important to the decision? Why?
5.22. As technical coordinator of a proposed harbor-bottom exploration device, you must report on the field of vision of a television camera which will be dropped without control to rest on the irregular floor of the harbor. One factor in your analysis is the slope of the floor at the point (a 1-ft circle) where the camera container comes to rest. In the Boston Harbor, which is to be explored, no appropriate data is avialable, but you must decide on certain dimensions of the device based in part on a probability distribution of the extent of the field of vision, and therefore you must obtain some probability distribution on the floor slope.
(a) Choose some engineering friend and assume (for all his probable ignorance of the subject) that he is the most knowledgeable consultant available on this topic. Find through a sequence of simple hypothetical lotteries the three slope values which have probabilities of 0.25, 0.50, and 0.75 of being exceeded. Sketch a CDF through these points.
(b) Repeat this with a second friend. Have the two compare their CDF’s. Can the differences be reconciled through discussion?
5.23. There is circumstantial evidence that a fraction of the cement was inadvertently left out of one batch of concrete now in place in a tall retaining wall. Core data has been obtained. If the cement has been left out, the mean core strength will now be 3000 psi; if not, it will be 3500 psi. In either case, the standard deviation of the (normally distributed) core strengths would be 450 psi.
(a) What are the relative values of the two sample likelihoods if the sample of four cores yielded values of 3000, 3300, 2800, and 3500?
(b) If the prior probabilities on the two mean strengths were 0.6 and 0.4 on 3000 psi and 3500 psi, respectively, what are the posterior probabilities?
(c) If only two actions are available—a0, “do nothing,” and a1, “order the concrete removed and replaced”—what decision should be made if the payoff table is
u(ai,θj)

(d) At what value of u(a1,θ0) would the engineer just be indifferent between a0 and a1?
5.24. Decide whether the engineer in Prob. 5.23 should test an additional four cores at a cost of eight (additive) units before making a decision? If cores cost two units each, plot the (preposterior) expected utility versus number of additional cores. How many should the engineer order? What is the value of perfect information?
† For example, an unpredictable flow is induced on a new highway if shorter travel times are provided by increasing the number of lanes.
† See Pratt, Raiffa, and Schlaifer [1965], and Hadley [1967], for example.
† See Prob. 5.17. An alternative approach is to replace outcomes by lotteries, and then to maximize the probability of a good outcome rather than expected utility.
† A study aimed at making highway design decisions assessed the value to the French society as a whole of an individual French life as about $30,000 in 1957 (Abraham and Thedié [1960].)
† See Engineering News-Record of January 7, 1965, and March 11, 1965, for further details.
† This is an experiment in the general sense of Sec. 2.1.1.
† As discussed in Prob. 5.7, these utilities are, in fact, the negative of opportunity losses, relative to the best action available for each state.
† The numbers z0 = 16 and z0 = 32 were chosen for illustrative purposes to give sample likelihood functions centered on a value of θ = 64. The numbers are kept small for ease of computation. For larger numbers, the binomial likelihood function could be replaced by an approximating normal distribution.
† Including V in the analysis avoids errors due to systematic seasonal changes in velocity. The choice of the form θ/V versus Z was based on its validity for a hypothetical, uniform flow in a rectangular river cross section.
† For example, by a regression analysis of Z on θ/V.
† The material in this section will not be used subsequently and might be excluded on a first reading.
† In general, the utility of the total consequence, u(e,z,a, θ), must be assessed. Recall from Sec. 5.1.2 that owing to possible nonlinearities in the cost-utility relationships, u($x + $y) does not necessarily equal u($x) + u($y).
† The state probabilities are independent of the action in this case and so the argument a is suppressed. By the same token, the argument z could have been suppressed in the utility function since the consequences do not depend on the outcome of the experiment.
† The value of perfect information is in general defined to be the difference between (1) the prior expectation ![]() u(θi)P'(θi), in which u(θi) is the utility associated with the best choice of action given that it is known with certainty that θi is the true state, and (2) the expected utility associated with no experiment e0. In this example, this is simply [(0)(0.7) + (0)(0.3)] – (–70) = 70. No experiment need even be considered if it costs more than the value of perfect information.
u(θi)P'(θi), in which u(θi) is the utility associated with the best choice of action given that it is known with certainty that θi is the true state, and (2) the expected utility associated with no experiment e0. In this example, this is simply [(0)(0.7) + (0)(0.3)] – (–70) = 70. No experiment need even be considered if it costs more than the value of perfect information.
† Some engineers might call for a drill hole in the event of this outcome to experiment e1. The relative advantage of this “hedging,” compound strategy can be investigated by considering it as a fourth type of experiment, e3. See Prob. 5.11.
† That is, it tells one how to make a decision; it does not describe how decisions are made, as a descriptive model would.
† Reference: Engineering News-Record, August, 29, 1963, pp. 20 and 72.
† C. J. Velz [1948], How Much Should Sewage Treatment Cost?, Engineering News-Record, October 14.