V. M. Panaretos, Y. ZemelAn Invitation to Statistics in Wasserstein SpaceSpringerBriefs in Probability and Mathematical Statisticshttps://doi.org/10.1007/978-3-030-38438-8_1

1. Optimal Transport

Victor M. Panaretos¹ and Yoav Zemel²

(1)

Institute of Mathematics, EPFL, Lausanne, Switzerland

(2)

Statistical Laboratory, University of Cambridge, Cambridge, UK

In this preliminary chapter, we introduce the problem of optimal transport, which is the main concept behind Wasserstein spaces. General references on this topic are the books by Rachev and Rüschendorf [107], Villani [124, 125], Ambrosio et al. [12], Ambrosio and Gigli [10], and Santambrogio [119]. This chapter includes only few proofs, when they are simple, informative, or are not easily found in one of the cited references.

1.1 The Monge and the Kantorovich Problems

In 1781, Monge [95] asked the following question: given a pile of sand and a pit of equal volume, how can one optimally transport the sand into the pit? In modern mathematical terms, the problem can be formulated as follows. There is a sand space $\mathcal X$ , a pit space $\mathcal Y$ , and a cost function $c:\mathcal X\times \mathcal Y\to \mathbb {R}$ that encapsulates how costly it is to move a unit of sand at $x\in \mathcal X$ to a location $y\in \mathcal Y$ in the pit. The sand distribution is represented by a measure μ on $\mathcal X$ , and the shape of the pit is described by a measure ν on $\mathcal Y$ . Our decision where to put each unit of sand can be thought of as a function $T:\mathcal X\to \mathcal Y$ , and it incurs a total transport cost of

$\displaystyle \begin{aligned} C(T)= {{\int_{\mathcal X} \! {c(x, T(x))} \, \mathrm{d}{\mu(x)}}} . \end{aligned}$

Moreover, one cannot put all the sand at a single point y in the pit; it is not allowed to shrink or expand the sand. The map T must be mass-preserving: for any subset $B\subseteq \mathcal Y$ representing a region of the pit of volume ν(B), exactly that same volume of sand must go into B. The amount of sand allocated to B is $\{x\in \mathcal X:T(x)\in B\}=T^{-1}(B)$ , so the mass preservation requirement is that μ(T ⁻¹(B)) = ν(B) for all $B\subseteq \mathcal Y$ . This condition will be denoted by T#μ = ν and in words: ν is the push-forward of μ under T, or T pushes μ forward to ν. To make the discussion mathematically rigorous, we must assume that c and T are measurable maps, and that μ(T ⁻¹(B)) = ν(B) for all measurable subsets of $\mathcal Y$ . When the underlying measures are understood from the context, we call T a transport map. Specifying $B=\mathcal Y$ , we see that no such T can exist unless $\mu (\mathcal X)=\nu (\mathcal Y)$ ; we shall assume that this quantity is finite, and by means of normalisation, that μ and ν are probability measures. In this setting, the Monge problem is to find the optimal transport map, that is, to solve

$\displaystyle \begin{aligned} \inf_{T:T\#\mu=\nu}C(T). \end{aligned}$

We assume throughout this book that $\mathcal X$ and $\mathcal Y$ are complete and separable metric spaces,¹ endowed with their Borel σ-algebra, which, we recall, is defined as the smallest σ-algebra containing the open sets. Measures defined on the Borel σ-algebra of $\mathcal X$ are called Borel measures. Thus, if μ is a Borel measure on $\mathcal X$ , then μ(A) is defined for any A that is open, or closed, or a countable union of closed sets, etc., and any continuous map on $\mathcal X$ is measurable. Similarly, we endow $\mathcal Y$ with its Borel σ-algebra. The product space $\mathcal X\times \mathcal Y$ is also complete and separable when endowed with its product topology; its Borel σ-algebra is generated by the product σ-algebra of those of $\mathcal X$ and $\mathcal Y$ ; thus, any continuous cost function $c:\mathcal X\times \mathcal Y\to \mathbb {R}$ is measurable. It will henceforth always be assumed, without explicit further notice, that μ and ν are Borel measures on $\mathcal X$ and $\mathcal Y$ , respectively, and that the cost function is continuous and nonnegative.

It is quite natural to assume that the cost is an increasing function of the distance between x and y, such as a power function. More precisely, that $\mathcal Y=\mathcal X$ is a complete and separable metric space with metric d, and

$\displaystyle \begin{aligned} c(x,y) =d^p(x,y), \qquad p\ge0, \quad x,y\in\mathcal X. \end{aligned}$

(1.1)

In particular, c is continuous, hence measurable, if p > 0. The limit case p = 0 yields the discontinuous function c(x, y) = 1{x = y}, which nevertheless remains measurable because the diagonal $\{(x,x):x\in \mathcal X\}$ is measurable in $\mathcal X\times \mathcal X$ . Particular focus will be put on the quadratic case p = 2 (Sect. 1.6) and the linear case p = 1 (Sect. 1.8.2).

The problem introduced by Monge [95] is very difficult, mainly because the set of transport maps {T : T#μ = ν} is intractable. And, it may very well be empty: this will be the case if μ is a Dirac measure at some $x_0\in \mathcal X$ (meaning that μ(A) = 1 if x ₀ ∈ A and 0 otherwise) but ν is not. Indeed, in that case the set B = {T(x ₀)} satisfies μ(T ⁻¹(B)) = 1 > ν(B), so no such T can exist. This also shows that the problem is asymmetric in μ and ν: in the Dirac example, there always exists a map T such that T#ν = μ—the constant map T(x) = x ₀ for all x is the unique such map. A less extreme situation occurs in the case of absolutely continuous measures. If μ and ν have densities f and g on $\mathbb {R}^d$ and T is continuously differentiable, then T#μ = ν if and only if for μ-almost all x

$\displaystyle \begin{aligned} f(x) =g(T(x))|\det \nabla T(x)|. \end{aligned}$

This is a highly non-linear equation in T, nowadays known as a particular case of a family of partial differential equations called Monge–Ampère equations. More than two centuries after the work of Monge, Caffarelli [32] cleverly used the theory of Monge–Ampère equations to show smoothness of transport maps (see Sect. 1.6.4).

As mentioned above, if μ = δ{x ₀} is a Dirac measure and ν is not, then no transport maps from μ to ν can exist, because the mass at x ₀ must be sent to a unique point x ₀. In 1942, Kantorovich [77] proposed a relaxation of Monge’s problem in which mass can be split. In other words, for each point $x\in \mathcal X$ one constructs a probability measure μ _x that describes how the mass at x is split among different destinations. If μ _x is a Dirac measure at some y, then all the mass at x is sent to y. The formal mathematical object to represent this idea is a probability measure π on the product space $\mathcal X\times \mathcal Y$ (which is $\mathcal X^2$ in our particular setting). Here π(A × B) is the amount of sand transported from the subset $A\subseteq \mathcal X$ into the part of the pit represented by $B\subseteq \mathcal Y$ . The total mass sent from A is $\pi (A\times \mathcal Y)$ , and the total mass sent into B is $\pi (\mathcal X\times B)$ . Thus, π is mass-preserving if and only if

$\displaystyle \begin{aligned} \begin{array}{rl} \pi(A\times \mathcal Y) &= \mu(A), \qquad A\subseteq\mathcal X\quad \mathrm{Borel};\\ \pi(\mathcal X\times B) &= \nu(B), \qquad B\subseteq\mathcal Y\quad \mathrm{Borel}. \end{array} \end{aligned}$

(1.2)

Probability measures satisfying (1.2) will be called transference plans, and the set of those will be denoted by Π(μ, ν). We also say that π is a coupling of μ and ν, and that μ and ν are the first and second marginal distributions, or simply marginals, of π. The total cost associated with π ∈ Π(μ, ν) is

$\displaystyle \begin{aligned} C(\pi) ={\int_{\mathcal X\times\mathcal Y} \! c(x,y) \, \mathrm{d}\pi(x,y)}. \end{aligned}$

In our setting of a complete separable metric space $\mathcal X$ , one can represent π as a collection of probability measures $\{\pi _x\}_{x\in \mathcal X}$ on $\mathcal Y$ , in the sense that for all measurable nonnegative g

$\displaystyle \begin{aligned} {\int_{\mathcal X\times\mathcal Y} \! g(x,y) \, \mathrm{d}\pi(x,y)} ={{\int_{\mathcal X} \! {\left[{{\int_{\mathcal Y} \! {g(x,y)} \, \mathrm{d}{\pi_x(y)}}} \right]} \, \mathrm{d}{\mu(x)}}}. \end{aligned}$

The collection {π _x} is that of the conditional distributions, and the iteration of integrals is called disintegration. For proofs of existence of conditional distributions, one can consult Dudley [47, Section 10.2] or Kallenberg [76, Chapter 5]. Conversely, the measure μ and the collection {π _x} determine π uniquely by choosing g to be indicator functions. An interpretation of these notions in terms of random variables will be given in Sect. 1.2.

The Kantorovich problem is to find the best transference plan, that is, to solve

$\displaystyle \begin{aligned} \inf_{\pi\in \varPi(\mu,\nu)}C(\pi). \end{aligned}$

The Kantorovich problem is a relaxation of the Monge problem, because to each transport map T one can associate a transference plan π = π _T of the same total cost. To see this, choose the conditional distribution π _x to be a Dirac at T(x). Disintegration then yields

$\displaystyle \begin{aligned} C(\pi) {=}{\int_{\mathcal X\times\mathcal Y} \! c(x,y) \, \mathrm{d}\pi(x,y)} {=}{{\int_{\mathcal X} \! {\left[{{\int_{\mathcal Y} \! {c(x,y)} \, \mathrm{d}{\pi_x(y)}}} \right]} \, \mathrm{d}{\mu(x)}}} {=}{{\int_{\mathcal X} \! {c(x,T(x))} \, \mathrm{d}{\mu(x)}}} {=}C(T). \end{aligned}$

This choice of π satisfies (1.2) because π(A × B) = μ(A ∩ T ⁻¹(B)) and ν(B) = μ(T ⁻¹(B)) for all Borel $A\subseteq \mathcal X$ and $B\subseteq \mathcal Y$ .

Compared to the Monge problem, the relaxed problem has considerable advantages. Firstly, the set of transference plans is never empty: it always contains the product measure μ ⊗ ν defined by [μ ⊗ ν](A) = μ(A)ν(B). Secondly, both the objective function C(π) and the constraints (1.2) are linear in π, so the problem can be seen as infinite-dimensional linear programming. To be precise, we need to endow the space of measures with a linear structure, and this is done in the standard way: define the space $M(\mathcal X)$ of all finite signed Borel measures on $\mathcal X$ . This is a vector space with (μ ₁ + αμ ₂)(A) = μ ₁(A) + αμ ₂(A) for $\alpha \in \mathbb {R}$ , $\mu _1,\mu _2\in M(\mathcal X)$ and $A\subseteq \mathcal X$ Borel. The set of probability measures on $\mathcal X$ is denoted by $P(\mathcal X)$ , and is a convex subset of $M(\mathcal X)$ . The set Π(μ, ν) is then a convex subset of $P(\mathcal X\times Y)$ , and as C(π) is linear in π, the set of minimisers is a convex subset of Π(μ, ν). Thirdly, there is a natural symmetry between Π(μ, ν) and Π(ν, μ). If π belongs to the former and we define $\tilde \pi (B\times A)=\pi (A\times B)$ , then $\tilde \pi \in \varPi (\nu ,\mu )$ . If we set $\tilde c(y,x)=c(x,y)$ , then

$\displaystyle \begin{aligned} C(\pi) ={\int_{\mathcal X\times\mathcal Y} \! c(x,y) \, \mathrm{d}\pi(x,y)} ={\int_{\mathcal Y\times\mathcal X} \! \tilde c(y,x) \, \mathrm{d}\tilde\pi(y,x)} =\tilde C(\tilde\pi). \end{aligned}$

In particular, when $\mathcal X=\mathcal Y$ and $c=\tilde c$ is symmetric (as in (1.1)),

$\displaystyle \begin{aligned} \inf_{\pi\in \varPi(\mu,\nu)}C(\pi) =\inf_{\tilde\pi\in \varPi(\nu,\mu)}\tilde C(\tilde\pi), \end{aligned}$

and π ∈ Π(μ, ν) is optimal if and only if its natural counterpart $\tilde \pi$ is optimal in Π(ν, μ). This symmetry will be fundamental in the definition of the Wasserstein distances in Chap. 2.

Perhaps most importantly, a minimiser for the Kantorovich problem exists under weak conditions. In order to show this, we first recall some definitions. Let $C_b(\mathcal X)$ be the space of real-valued, continuous bounded functions on $\mathcal X$ . A sequence of probability measures $\{\mu _n\}\in M(\mathcal X)$ is said to converge weakly ² to $\mu \in M(\mathcal X)$ if for all $f\in C_b(\mathcal X)$ , ${{\int \! f \, \mathrm {d}\mu _n}} \to {{\int \! f \, \mathrm {d}\mu }}$ . To avoid confusion with other types of convergence, we will usually write μ _n → μ weakly; in the rare cases where a symbol is needed we shall use the notation $\mu _n\stackrel {w}\to \mu$ . Of course, if μ _n → μ weakly and $\mu _n\in P(\mathcal X)$ , then μ must be in $P(\mathcal X)$ too (this is seen by taking f ≡ 1 and by observing that ${{\int \! f \, \mathrm {d}\mu }} \ge 0$ if f ≥ 0).

A collection of probability measures $\mathcal K$ is tight if for all 𝜖 > 0 there exists a compact set K such that $\inf _{\mu \in \mathcal K}\mu (K)>1-\epsilon$ . If $\mathcal K$ is represented by a sequence {μ _n}, then Prokhorov’s theorem (Billingsley [24, Theorem 5.1]) states that a subsequence of {μ _n} must converge weakly to some probability measure μ.

We are now ready to show that the Kantorovich problem admits a solution when c is continuous and nonnegative and $\mathcal X$ and $\mathcal Y$ are complete separable metric spaces. Let {π _n} be a minimising sequence for C. Then, according to [24, Theorem 1.3], μ and ν must be tight. If K ₁ and K ₂ are compact with μ(K ₁), ν(K ₂) > 1 − 𝜖, then K ₁ × K ₂ is compact and for all π ∈ Π(μ, ν), π(K ₁ × K ₂) > 1 − 2𝜖. It follows that the entire collection Π(μ, ν) is tight, and by Prokhorov’s theorem π _n has a weak limit π after extraction of a subsequence. For any integer K, $c_K(x,y)=\min (c(x,y),K)$ is a continuous bounded function, and

$\displaystyle \begin{aligned} C(\pi_n) ={\int \! c(x,y) \, \mathrm{d}\pi_n(x,y)} \ge{\int \! c_K(x,y) \, \mathrm{d}\pi_n(x,y)} \to{\int \! c_K(x,y) \, \mathrm{d}\pi(x,y)}, \qquad n\to\infty. \end{aligned}$

By the monotone convergence theorem

$\displaystyle \begin{aligned} \liminf_{n\to\infty} C(\pi_n) \ge \lim_{K\to\infty}{\int \! c_K(x,y) \, \mathrm{d}\pi(x,y)} =C(\pi) \qquad \mathrm{if} \pi_n\to\pi\mathrm{ weakly}. \end{aligned}$

(1.3)

Since {π _n} was chosen as a minimising sequence for C, π must be a minimiser, and existence is established.

As we have seen, the Kantorovich problem is a relaxation of the Monge problem, in the sense that

$\displaystyle \begin{aligned} \inf_{T:T\#\mu=\nu}C(T) =\inf_{\pi_T:T\#\mu=\nu}C(\pi) \ge\inf_{\pi\in\varPi(\mu,\nu)}C(\pi) =C(\pi^*), \end{aligned}$

for some optimal π ^∗. If π ^∗ = π _T for some transport map T, then we say that the solution is induced from a transport map. This will happen in two different and important cases that are discussed in Sects. 1.3 and 1.6.1.

A remark about terminology is in order. Many authors talk about the Monge–Kantorovich problem or the optimal transport(ation) problem. More often than not, they refer to what we call here the Kantorovich problem. When one of the scenarios presented in Sects. 1.3 and 1.6.1 is considered, this does not result in ambiguity.

1.2 Probabilistic Interpretation

The preceding section was an analytic presentation of the Monge and the Kantorovich problems. It is illuminating, however, to also recast things in probabilistic terms, and this is the topic of this section.

A random element on a complete separable metric space (or any topological space) $\mathcal X$ is simply a measurable function X from some (generic) probability space $(\varOmega ,\mathcal F,\mathbb {P})$ to $\mathcal X$ (with its Borel σ-algebra). The probability law (or probability distribution) is the probability measure $\mu _X=X\#\mathbb {P}$ defined on the space $\mathcal X$ ; this is the Borel measure satisfying $\mu _X(A)=\mathbb {P}(X\in A)$ for all Borel sets A.

Suppose that one is given two random elements X and Y taking values in $\mathcal X$ and $\mathcal Y$ , respectively, and a cost function $c:\mathcal X\times \mathcal Y\to \mathbb {R}$ . The Monge problem is to find a measurable function T such that T(X) has the same distribution as Y , and such that the expectation

$\displaystyle \begin{aligned} C(T) ={{\int_{\mathcal X} \! {c(x,T(x))} \, \mathrm{d}{\mu(x)}}} ={{\int_{\varOmega} \! {c[X(\omega),T(X(\omega))]} \, \mathrm{d}{\mathbb{P}(\omega)}}} =\mathbb{E} c(X,T(X))\end{aligned}$

is minimised.

The Kantorovich problem is to find a joint distribution for the pair (X, Y ) whose marginals are the original distributions of X and Y , respectively, and such that the probability law $\pi =(X,Y)\#\mathbb {P}$ minimises the expectation

$\displaystyle \begin{aligned} C(\pi) ={\int_{\mathcal X\times\mathcal Y} \! c(x,y) \, \mathrm{d}\pi(x,y)} ={{\int_{\varOmega} \! {c[X(\omega),Y(\omega))]} \, \mathrm{d}{\mathbb{P}(\omega)}}} =\mathbb{E}_\pi c(X,Y). \end{aligned}$

Any such joint distribution is called a coupling of X and Y . Of course, (X, T(X)) is a coupling when T(X) has the same distribution as Y . The measures π _x in the previous section are then interpreted as the conditional distribution of Y given X = x.

Consider now the important case where $\mathcal X=\mathcal Y=\mathbb {R}^d$ , c(x, y) = ∥x − y∥², and X and Y are square integrable random vectors ( $\mathbb {E}\|X\|{ }^2+\mathbb {E}\|Y\|{ }^2<\infty$ ). Let A and B be the covariance matrices of X and Y , respectively, and notice that the covariance matrix of a coupling π must have the form $C=\begin {pmatrix}A & V\\V^t & B\end {pmatrix}$ for a d × d matrix V . The covariance matrix of the difference X − Y is

$\displaystyle \begin{aligned} \begin{pmatrix} I_d & -I_d \end{pmatrix} \begin{pmatrix}A & V\\V^t & B\end{pmatrix} \begin{pmatrix} I_d \\ -I_d \end{pmatrix} = A + B - V^t - V \end{aligned}$

so that

$\displaystyle \begin{aligned} \mathbb{E}_\pi c(X,Y)= \mathbb{E}_\pi \|X-Y\|{}^2= \| \mathbb{E} X - \mathbb{E} Y\|{}^2 + {\mathrm{tr}}_\pi[A + B - V^t - V]. \end{aligned}$

Since only V depends on the coupling π, the problem is equivalent to that of maximising the trace of V , the cross-covariance matrix between X and Y . This must be done subject to the constraint that a coupling π with covariance matrix C exists; in particular, C has to be positive semidefinite.

1.3 The Discrete Uniform Case

There is a special case in which the Monge–Kantorovich problem reduces to a finite combinatorial problem. Although it may seem at first hand as an oversimplification of the original problem, it is of importance in practice because arbitrary measures can be approximated by discrete measures by means of the strong law of large numbers. Moreover, the discrete case is important in theory as well, as a motivating example for the Kantorovich duality (Sect. 1.4) and the property of cyclical monotonicity (Sect. 1.7).

Suppose that μ and ν are each uniform on n distinct points:

$\displaystyle \begin{aligned} \mu =\frac 1n\left(\delta\{x_1\}+\dots+\delta\{x_n\}\right) ,\qquad \nu =\frac 1n\left(\delta\{y_1\}+\dots+\delta\{y_n\}\right). \end{aligned}$

The only relevant costs are c _ij = c(x _i, y _j), the collection of which can be represented by an n × n matrix $\vec C$ . Transport maps T are associated with permutations in S _n, the set of all bijective functions from {1, …, n} to itself: given σ ∈ S _n, a transport map can be constructed by defining T(x _i) = y _σ(i). If σ is not a permutation, then T will not be a transport map from μ to ν. Transference plans π are equivalent to n × n matrices M with coordinates M _ij = π({(x _i, y _j)}) = M _ij; this is the amount of mass sent from x _i to y _j. In order for π to a be a transference plan, it must be that ∑_jM _ij = 1∕n for all i and ∑_iM _ij = 1∕n for all j, and in addition M must be nonnegative. In other words, the matrix M′ = nM belongs to B _n, the set of bistochastic matrices of order n, defined as n × n matrices M′ satisfying

$\displaystyle \begin{aligned} \sum_{j=1}^n M^{\prime}_{ij}=1,\quad i=1,\dots,n; \qquad \sum_{i=1}^n M^{\prime}_{ij}=1,\quad j=1,\dots,n; \qquad M^{\prime}_{ij}\ge0. \end{aligned}$

The Monge problem is the combinatorial optimisation problem over permutations

$\displaystyle \begin{aligned} \inf_{\sigma\in S_n}C(\sigma) =\frac 1n\inf_{\sigma\in S_n}\sum_{i=1}^n c_{i,\sigma(i)}, \end{aligned}$

and the Kantorovich problem is the linear program

$\displaystyle \begin{aligned} \inf_{nM\in B_n}\sum_{i,j=1}^n c_{ij}M_{ij} =\inf_{M\in B_n/n}\sum_{i,j=1}^n c_{ij}M_{ij} =\inf_{M\in B_n/n}C(M). \end{aligned}$

If σ is a permutation, then one can define M = M(σ) by M _ij = 1∕n if j = σ(i) and 0 otherwise. Then M ∈ B _n∕n and C(M) = C(σ). Such M (or, more precisely, nM) is called a permutation matrix.

The Kantorovich problem is a linear program with n ² variables and 2n constraints. It must have a solution because B _n (hence B _n∕n) is a compact (nonempty) set in $\mathbb {R}^{n^2}$ and the objective function is linear in the matrix elements, hence continuous. (This property is independent of the possibly infinite-dimensional spaces $\mathcal X$ and $\mathcal Y$ in which the points lie.) The Monge problem also admits a solution because S _n is a finite set. To see that the two problems are essentially the same, we need to introduce the following notion. If B is a convex set, then x ∈ B is an extremal point of B if it cannot be written as a convex combination tz + (1 − t)y for some distinct points y, z ∈ B. It is well known (Luenberger and Ye [89, Section 2.5]) that there exists an optimal solution that is extremal, so that it becomes relevant to identify the extremal points of B _n. It is fairly clear that each permutation matrix is extremal in B _n; the less obvious converse is known as Birkhoff’s theorem, a proof of which can be found, for instance, at the end of the introduction in Villani [124] or (in a different terminology) in Luenberger and Ye [89, Section 6.5]. Thus, we have:

Proposition 1.3.1 (Solution of Discrete Problem)

There exists σ ∈ S _n such that M(σ) minimises C(M) over B _n∕n. Furthermore, if {σ ₁, …, σ _k} is the set of optimal permutations, then the set of optimal matrices is the convex hull of {M(σ ₁), …, M(σ _k)}. In particular, if σ is the unique optimal permutation, then M(σ) is the unique optimal matrix.

Thus, in the discrete case, the Monge and the Kantorovich problems coincide. One can of course use the simplex method [89, Chapter 3] to solve the linear program, but there are n! vertices, and there is in principle no guarantee that the simplex method solves the problem efficiently. However, the constraints matrix has a very specific form (it contains only zeroes and ones, and is totally unimodular), so specialised algorithms for this problem exist. One of them is the Hungarian algorithm of Kuhn [85] or its variant of Munkres [96] that has a worst-case computational complexity of at most O(n ⁴). Another alternative is the class of net flow algorithms described in [89, Chapter 6]. In particular, the algorithm of Edmonds and Karp [50] has a complexity of at most $O(n^3\log n)$ . This monograph does not focus on computational aspects for optimal transport. This is a fascinating and very active area of contemporary research, and readers are directed to Peyré and Cuturi [103].

Remark 1.3.2

The special case described here could have been more precisely called “the discrete uniform case on the same number of points”, as “the discrete case” could refer to any two finitely supported measures μ and ν. In the Monge context, the setup discussed here is the most interesting case, see page 8 in the supplement for more details.

1.4 Kantorovich Duality

The discrete case of Sect. 1.3 is an example of a linear program and thus enjoys a rich duality theory (Luenberger and Ye [89, Chapter 4]). The general Kantorovich problem is an infinite-dimensional linear program, and under mild assumptions admits similar duality.

1.4.1 Duality in the Discrete Uniform Case

We can represent any matrix M as a vector in $\mathbb {R}^{n^2}$ , say $\vec M$ , by enumeration of the elements row by row. If nM is bistochastic, i.e., M ∈ B _n∕n, then the 2n constraints can be represented in a (2n) × n ² matrix A. For instance, if n = 3, then

$\displaystyle \begin{aligned} A=\begin{pmatrix} 1 & 1 & 1\\ &&& 1 & 1 & 1\\ &&& &&& 1 & 1 & 1\\ 1 &&& 1 &&& 1\\ & 1 &&& 1 &&& 1\\ && 1 &&& 1 &&& 1 \end{pmatrix} \in \mathbb{R}^{6\times 9}. \end{aligned}$

For general n, the constraints read $A\vec M=n^{-1}(1,\dots ,1)\in \mathbb {R}^{2n}$ and A takes the form

$\displaystyle \begin{aligned} A=\begin{pmatrix} {\mathbf{1}}_n & &\\ & {\mathbf{1}}_n & & \\ && \ddots & & \\ &&& {\mathbf{1}}_n\\ I_n & I_n & \dots & I_n \end{pmatrix} \in \mathbb{R}^{2n\times n^2}, \qquad {\mathbf{1}}_n =(1,\dots,1)\in \mathbb{R}^n, \end{aligned}$

with I _n the n × n identity matrix. Thus, the problem can be written

$\displaystyle \begin{aligned} \min_{\vec M} \vec C^t\vec M \qquad \mathrm{subject to} \qquad A\vec M=\frac 1n(1,\dots,1)\in\mathbb{R}^{2n};\quad \vec M\ge0. \end{aligned}$

The last constraint is to be interpreted coordinate-wise; all the elements of M must be nonnegative. The dual problem is constructed by introducing one variable for each row of A, transposing the constraint matrix and interchanging the roles of the objective vector $\vec C$ and the constraints vector b = n ⁻¹(1, …, 1). Call the new variables p ₁, …, p _n and q ₁, …, q _n, and notice that each column of A corresponds to exactly one p _i and one q _j, and that the n ² columns exhaust all possibilities. Hence, the dual problem is

$\displaystyle \begin{aligned} \max_{p,q\in\mathbb{R}^n} b^t\binom pq =\frac 1n \sum_{i=1}^n p_i + \frac 1n \sum_{j=1}^n q_j \qquad \mathrm{subject to} \quad p_i + q_j\le c_{ij} ,\quad i,j=1,\dots,n. \end{aligned}$

(1.4)

In the context of duality, one uses the terminology primal problem for the original optimisation problem. Weak duality states that if $\vec M$ and (p, q) satisfy the respective constraints, then

$\displaystyle \begin{aligned} b^t\binom pq = \sum_{i}p_i\frac 1n + \sum_jq_j\frac 1n = \sum_{i,j}(p_i+q_j)M_{ij} \le\sum_{i,j}C_{ij}M_{ij} =\vec C^t\vec M. \end{aligned}$

In particular, if equality holds, then $\vec M$ is primal optimal and (p, q) is dual optimal. Strong duality is the nontrivial assertion that there exist $\vec M^*$ and (p ^∗, q ^∗) satisfying $\vec C^t\vec M^*=b^t\binom {p^*}{q^*}$ .

1.4.2 Duality in the General Case

The vectors $\vec C$ and $\vec M$ were obtained from the cost function c and the transference plan π as C _ij = c(x _i, y _j) and M _ij = π({(x _i, y _j)}). Similarly, we can view the vectors p and q as restrictions of functions $\varphi :\mathcal X\to \mathbb {R}$ and $\psi :\mathcal Y\to \mathbb {R}$ of the form p _i = φ(x _i) and q _j = ψ(y _j). The constraint vector b = (1 _n, 1 _n) can be written as b _i = μ({x _i}) and b _n+j = ν({y _j}). In this formulation, the constraint p _i + q _j ≤ c _ij writes (φ, ψ) ∈ Φ _c with

$\displaystyle \begin{aligned} \varPhi_c =\big\{(\varphi,\psi)\in L_1(\mu)\times L_1(\nu):\varphi(x) + \psi(y)\le c(x,y)\mathrm{ for all} x,y\big\}, \end{aligned}$

and the dual problem (1.4) becomes

$\displaystyle \begin{aligned} \sup_{(\varphi,\psi)\in L_1(\mu)\times L_1(\nu)} \left[{{\int_{\mathcal X} \! {\varphi(x)} \, \mathrm{d}{\mu(x)}}} +{{\int_{\mathcal Y} \! {\psi(y)} \, \mathrm{d}{\nu(y)}}}\right] \qquad \mathrm{subject to} \quad (\varphi,\psi)\in \varPhi_c. \end{aligned}$

Simple measure theory shows that the set constraints (1.2) defining the transference plans set Π(μ, ν) are equivalent to functional constraints. For future reference, we state this formally as:

Lemma 1.4.1 (Functional Constraints)

Let μ and ν be probability measures. Then π ∈ Π(μ, ν) if and only if for all integrable functions φ ∈ L ₁(μ), ψ ∈ L ₁(ν),

$\displaystyle \begin{aligned} {\int_{\mathcal X\times\mathcal Y} \! [\varphi(x) + \psi(y)] \, \mathrm{d}\pi(x,y)} ={{\int_{\mathcal X} \! {\varphi(x)} \, \mathrm{d}{\mu(x)}}} +{{\int_{\mathcal Y} \! {\psi(y)} \, \mathrm{d}{\nu(y)}}}. \end{aligned}$

The proof follows from the fact that (1.2) yields the above equality when φ and ψ are indicator functions. One then uses linearity and approximations to deduce the result.

Weak duality follows immediately from Lemma 1.4.1. For if π ∈ Π(μ, ν) and (φ, ψ) ∈ Φ _c, then

$\displaystyle \begin{aligned} {{\int_{\mathcal X} \! {\varphi(x)} \, \mathrm{d}{\mu(x)}}} +{{\int_{\mathcal Y} \! {\psi(y)} \, \mathrm{d}{\nu(y)}}} ={\int_{\mathcal X\times\mathcal Y} \! [\varphi(x) + \psi(y)] \, \mathrm{d}\pi(x,y)} \le C(\pi). \end{aligned}$

Strong duality can be stated in the following form:

Theorem 1.4.2 (Kantorovich Duality)

Let μ and ν be probability measures on complete separable metric spaces $\mathcal X$ and $\mathcal Y$ , respectively, and let $c:\mathcal X\times \mathcal Y\to \mathbb {R}_+$ be a measurable function. Then

$\displaystyle \begin{aligned} \inf_{\pi\in\varPi(\mu,\nu)} {{\int_{\mathcal X\times\mathcal Y} \! c \, \mathrm{d}\pi}} =\sup_{(\varphi,\psi)\in \varPhi_c} \left[{{\int_{\mathcal X} \! {\varphi} \, \mathrm{d}\mu}} +{{\int_{\mathcal Y} \! \psi \, \mathrm{d}\nu}} \right]. \end{aligned}$

See the Bibliographical Notes for other versions of the duality.

When the cost function is continuous, or more generally, a countable supremum of continuous functions, the infimum is attained (see (1.3)). The existence of maximisers (φ, ψ) is more delicate and requires a finiteness condition, as formulated in Proposition 1.8.1 below.

The next sections are dedicated to more concrete examples that will be used through the rest of the book.

1.5 The One-Dimensional Case

When $\mathcal X=\mathcal Y=\mathbb {R}$ , the Monge–Kantorovich problem has a particularly simple structure, because the class of “nice” transport maps contains at most a single element. Identify $\mu ,\nu \in P(\mathbb {R})$ with their cumulative distribution functions F and G defined by

$\displaystyle \begin{aligned} F(t)=\mu((-\infty,t]), \qquad G(t) = \nu((-\infty,t]) ,\qquad t\in\mathbb{R}. \end{aligned}$

Let the cost function be (momentarily) quadratic: c(x, y) = |x − y|²∕2. Since for x ₁ ≤ x ₂, y ₁ ≤ y ₂

$\displaystyle \begin{aligned} c(y_2, x_1) + c(y_1, x_2) - c(y_1 , x_1) - c(y_2 , x_2) =(x_2 - x_1)(y_2 - y_1) \ge0, \end{aligned}$

it seems natural to expect the optimal transport map to be monotonically increasing. It turns out that, on the real line, there is at most one such transport map: if T is increasing and T#μ = ν, then for all $t\in \mathbb {R}$

$\displaystyle \begin{aligned} G(t) = \nu((-\infty,t]) =\mu((-\infty,T^{-1}(t)]) =F(T^{-1}(t)). \end{aligned}$

If t = T(x), then the above equation reduces to T(x) = G ⁻¹(F(x)). This formula determines T uniquely, and has an interesting probabilistic interpretation: it is well-known that if X is a random variable with continuous distribution function F, then F(X) follows a uniform distribution on (0, 1). Conversely, if U follows a uniform distribution, G is any distribution function, and

$\displaystyle \begin{aligned} G^{-1}(u) =\inf G^{-1}([u,1]) =\inf\{x\in\mathbb{R}:G(x)\ge u\}, \qquad 0<u<1, \end{aligned}$

is the quantile function of X, then the random variable G ⁻¹(U) has distribution function G. We say that G ⁻¹ is the left-continuous inverse of G. In terms of push-forward maps, we can write F#μ = Leb|_[0,1] and G ⁻¹#Leb|_[0,1] = ν, with Leb standing for Lebesgue measure, and it is restricted to the interval [0, 1]. Consequently, if F is continuous and G is arbitrary, then T#μ = ν; we can view T as pushing μ forward to ν in two steps: firstly, μ is pushed forward to Leb|_[0,1] and secondly, Leb|_[0,1] is pushed forward to ν.

Using the change of variables formula, we see that the total cost of T is

$\displaystyle \begin{aligned} C(T) ={{\int_{\mathbb{R}} \! {|G^{-1}(F(x)) - x|{}^2} \, \mathrm{d}{\mu(x)}}} ={{\int_{0}^{1} \! {|G^{-1}(u) - F^{-1}(u))|{}^2} \, \mathrm{d}{u}}} . \end{aligned}$

If F is discontinuous, then F#μ is not Lebesgue measure, and T is not necessarily defined. But there will exist an optimal transference plan π ∈ Π(μ, ν) that is monotone in the following sense: there exists a set $\varGamma \subset \mathbb {R}^2$ such that π(Γ) = 1 and whenever (x _i, y _i) ∈ Γ,

$\displaystyle \begin{aligned} |y_2 - x_1|{}^2 + |y_1 - x_2|{}^2 - |y_1 - x_1|{}^2 - |y_2 - x_2|{}^2 \ge0. \end{aligned}$

Thus, mass at x ₁ and x ₂ can be split if need be, but in a monotone way. For example, if μ puts mass 1∕2 at x ₁ = −1 and at x ₂ = 1 and ν is uniform on [−1, 1]. Then the transference plan spreads the mass of x ₁ uniformly on [−1, 0], and the mass of x ₂ uniformly on [0, 1]. This is a particular case of the cyclical monotonicity that will be discussed in Sect. 1.7.

Elementary calculations show that the inequality

$\displaystyle \begin{aligned} c(y_2, x_1) + c(y_1, x_2) - c(y_1 , x_1) - c(y_2 , x_2) \ge0,\qquad x_1\le x_2;\quad y_1\le y_2 \end{aligned}$

holds more generally than the quadratic cost c(x, y) = |x − y|². Specifically, it suffices that c(x, y) = h(|x − y|) with h convex on $\mathbb {R}_+$ .

Since any distribution can be approximated by continuous distributions, in view of the above discussion, the following result from Villani [124, Theorem 2.18] should not be too surprising.

Theorem 1.5.1 (Optimal Transport in $\mathbb {R}$ )

Let $\mu ,\nu \in P(\mathbb {R})$ with distribution functions F and G, respectively, and let the cost function be of the form c(x, y) = h(|x − y|) with h convex and nonnegative. Then

$\displaystyle \begin{aligned} \inf_{\pi\in\varPi(\mu,\nu)}C(\pi) ={{\int_{0}^{1} \! {h(G^{-1}(u) - F^{-1}(u))} \, \mathrm{d}{u}}} . \end{aligned}$

If the infimum is finite and h is strictly convex, then the optimal transference plan is unique. Furthermore, if F is continuous, then the infimum is attained by the transport map T = G ⁻¹ ∘ F.

The prototypical choice for h is h(z) = |z|^p with p > 1. This result allows in particular a direct evaluation of the Wasserstein distances for measures on the real line (see Chap. 2).

Note that no regularity is needed in order that the optimal transference plan be unique, unlike in higher dimensions (compare Theorem 1.8.2). The structure of solutions in the concave case (0 < p < 1) is more complicated, see McCann [94].

When p = 1, the cost function is convex but not strictly so, and solutions will not be unique. However, the total cost in Theorem 1.5.1 admits another representation that is often more convenient.

Proposition 1.5.2 (Quantiles and Distribution Functions)

If F and G are distribution functions, then

$\displaystyle \begin{aligned} {{\int_{0}^{1} \! {|G^{-1}(u) - F^{-1}(u)|} \, \mathrm{d}{u}}} ={{\int_{\mathbb{R}} \! {|G(x) - F(x)|} \, \mathrm{d}{x}}} . \end{aligned}$

The proof is a simple application of Fubini’s theorem; see page 13 in the supplement.

Corollary 1.5.3

If c(x, y) = |x − y|, then under the conditions of Theorem 1.5.1

$\displaystyle \begin{aligned} \inf_{\pi\in\varPi(\mu,\nu)}C(\pi) ={{\int_{\mathbb{R}} \! {|G(x) - F(x)|} \, \mathrm{d}{x}}} . \end{aligned}$

1.6 Quadratic Cost

This section is devoted to the specific cost function

$\displaystyle \begin{aligned} c(x,y) = \frac{\|x-y\|{}^2}2, \qquad x,y\in\mathcal X, \end{aligned}$

where $\mathcal X$ is a separable Hilbert space. This cost is popular in applications, and leads to a lucid and elegant theory. The factor of 1∕2 does not affect the minimising coupling π and leads to cleaner expressions. (It does affect the optimal dual pair, but in an obvious way.)

1.6.1 The Absolutely Continuous Case

We begin with the Euclidean case, where $\mathcal X=\mathcal Y=(\mathbb {R}^d,\|\cdot \|)$ is endowed with the Euclidean metric, and use the Kantorovich duality to obtain characterisations of optimal maps.

Since the dual objective function to be maximised

$\displaystyle \begin{aligned} {\int_{\mathbb{R}^d} \! \varphi \, \mathrm{d}\mu} +{\int_{\mathbb{R}^d} \! \psi \, \mathrm{d}\nu} \end{aligned}$

is increasing in φ and ψ, one should seek functions that take values as large as possible subject to the constraint φ(x) + ψ(y) ≤∥x − y∥²∕2. Suppose that an oracle tells us that some φ ∈ L ₁(μ) is a good candidate. Then the largest possible ψ satisfying (φ, ψ) ∈ Φ _c is

$\displaystyle \begin{aligned} \psi(y) =\inf_{x\in\mathbb{R}^d}\left[\frac{\|x-y\|{}^2}2 - \varphi(x)\right] =\frac{\|y\|{}^2}2 + \inf_{x\in\mathbb{R}^d}\left[\frac{\|x\|{}^2}2-\varphi(x)-{\left\langle {x},{y}\right\rangle} \right]. \end{aligned}$

In other words,

$\displaystyle \begin{aligned} \widetilde\psi(y) :=\frac{\|y\|{}^2}2 - \psi(y) =\sup_{x\in\mathbb{R}^d}\left[{\left\langle {x},{y}\right\rangle} - \widetilde\varphi(x)\right], \qquad \tilde\varphi(x) = \frac{\|x\|{}^2}2 - \varphi(x). \end{aligned}$

As a supremum over affine functions (in y), $\widetilde \psi$ enjoys some useful properties. We remind the reader that a function $f:\mathcal X\to \mathbb {R}\cup \{\infty \}$ is convex if f(tx + (1 − t)y) ≤ tf(x) + (1 − t)f(y) for all $x,y\in \mathcal X$ and t ∈ [0, 1]. It is lower semicontinuous if for all $x\in \mathcal X$ , f(x) ≤liminf_y→xf(y). Affine functions are convex and lower semicontinuous, and it straightforward from the definitions that both convexity and lower semicontinuity are preserved under the supremum operation. Thus, the function $\widetilde \psi$ is convex and lower semicontinuous. In particular, it is Borel measurable due to the following characterisation: f is lower semicontinuous if and only if {x : f(x) ≤ α} is a closed set for all $\alpha \in \mathbb {R}$ .

From the preceding subsection, we now know that optimal dual functions φ and ψ must take the form of the difference between ∥⋅∥²∕2 and a convex function. Given the vast wealth of knowledge on convex functions (Rockafellar [113]), it will be convenient to work with $\widetilde \varphi$ and $\widetilde \psi$ , and to assume that $\widetilde \psi =(\widetilde \varphi )^*$ , where

$\displaystyle \begin{aligned} f^*(y) =\sup_{x\in\mathbb{R}^d}[{\left\langle {x},{y}\right\rangle} - f(x)], \qquad y\in\mathbb{R}^d \end{aligned}$

is the Legendre transform of f ( [113, Chapter 26]; [124, Chapter 2]), and is of fundamental importance in convex analysis. Now by symmetry, one can also replace $\widetilde \varphi$ by $(\widetilde \psi )^*=(\widetilde \varphi )^{**}$ , so it is reasonable to expect that an optimal dual pair should take the form $(\|\cdot \|{ }^2/2 - \widetilde \varphi ,\|\cdot \|{ }^2/2-(\widetilde \varphi )^*)$ , with $\widetilde \varphi$ convex and lower semicontinuous.

The alternative representation of the dual objective value as

$\displaystyle \begin{aligned} {\int_{\mathbb{R}^d} \! \varphi \, \mathrm{d}\mu} +{\int_{\mathbb{R}^d} \! \psi \, \mathrm{d}\nu} =\frac 12{\int_{\mathbb{R}^d} \! \|x\|{}^2 \, \mathrm{d}\mu(x)} +\frac 12{\int_{\mathbb{R}^d} \! \|y\|{}^2 \, \mathrm{d}\nu(y)} -{\int_{\mathbb{R}^d} \! \widetilde\varphi \, \mathrm{d}\mu} -{\int_{\mathbb{R}^d} \! \widetilde\psi \, \mathrm{d}\nu} \end{aligned}$

is valid under the integrability condition

$\displaystyle \begin{aligned} {\int_{\mathbb{R}^d} \! \|x\|{}^2 \, \mathrm{d}\mu(x)} +{\int_{\mathbb{R}^d} \! \|y\|{}^2 \, \mathrm{d}\nu(y)} <\infty \end{aligned}$

that μ and ν have finite second moments. This condition also guarantees that an optimal φ exists, as the conditions of Proposition 1.8.1 are satisfied. An alternative direct proof for the quadratic case can be found in Villani [124, Theorem 2.9].

Suppose that an optimal φ is found. What can we say about optimal transference plans π? According to the duality, a necessary and sufficient condition is that

$\displaystyle \begin{aligned} {\int_{\mathbb{R}^d\times\mathbb{R}^d} \! \frac{\|x-y\|{}^2}2 \, \mathrm{d}\pi(x,y)} ={{\int_{{\mathbb{R}^d}} \! \varphi \, \mathrm{d}\mu}} +{{\int_{\mathbb{R}^d} \! \psi \, \mathrm{d}\nu}}, \end{aligned}$

where ψ = ∥⋅∥²∕2 − (∥⋅∥²∕2 − φ)^∗. Equivalently (using Lemma 1.4.1),

$\displaystyle \begin{aligned} {\int_{\mathbb{R}^d\times\mathbb{R}^d} \! [\widetilde\varphi(x) + (\widetilde\varphi)^*(y) - {\left\langle {x},{y}\right\rangle} ] \, \mathrm{d}\pi(x,y)} =0. \end{aligned}$

(1.5)

Since we have $\widetilde \varphi (x) + (\widetilde \varphi )^*(y)\ge {\left \langle {x},{y}\right \rangle }$ everywhere, the integrand is nonnegative. Hence, the integral vanishes if and only if π is concentrated on the set of (x, y) such that $\widetilde \varphi (x)+\widetilde \varphi ^*(y)={\left \langle {x},{y}\right \rangle }$ . By definition of the Legendre transform as a supremum, this happens if and only if the supremum defining $\widetilde \varphi ^*(y)$ is attained at x; equivalently

$\displaystyle \begin{aligned} \widetilde\varphi(z) - \widetilde\varphi(x) \ge {\left\langle {z-x},{y}\right\rangle} , \qquad z\in\mathcal X. \end{aligned}$

This condition is precisely the definition of y being a subgradient of $\widetilde \varphi$ at x [113, Chapter 23]. When $\widetilde \varphi$ is differentiable at x, its unique subgradient is the gradient $y=\nabla \widetilde \varphi (x)$ [113, Theorem 25.1]. If we are fortunate and $\widetilde \varphi$ is differentiable everywhere, or even μ-almost everywhere, then the optimal transference plan π is unique, and in fact induced from the transport map $\nabla \widetilde \varphi$ . The problem, of course, is that $\widetilde \varphi$ may fail to be differentiable μ-almost surely. This is remedied by assuming some regularity on the source measure μ in order to make sure that any convex function be differentiable μ-almost surely, and is done via the following regularity result, which, roughly speaking, states that convex functions are differentiable almost surely. A stronger version is given in Rockafellar [113, Theorem 2.25], with an alternative proof in Alberti and Ambrosio [6, Chapter 2]. One could also combine the local Lipschitz property of convex functions [113, Chapter 10] with Rademacher’s theorem (Villani [125, Theorem 10.8]).

Theorem 1.6.1 (Differentiability of Convex Functions)

Let $f:\mathbb {R}^d\to \mathbb {R}\cup \{\infty \}$ be a convex function with domain $\mathrm {dom} f=\{x\in \mathbb {R}^d:f(x)<\infty \}$ and let $\mathcal N$ be the set of points at which f is not differentiable. Then $\mathcal N\cap \overline {\mathrm {dom} f}$ has Lebesgue measure 0.

Theorem 1.6.1 is usually stated for the interior of domf, denoted int(domf), rather than the closure. But, since A = domf is convex, its boundary has Lebesgue measure zero. To see this assume first that A is bounded. If intA is empty, then A lies in a lower dimensional subspace [113, Theorem 2.4]. Otherwise, without loss of generality 0 ∈intA, and then by convexity of A, ∂A ⊆ (1 + 𝜖)A for all 𝜖 > 0. When A is unbounded, write it as ∪_nA ∩ [−n, n]^d.

Another issue that might arise is that optimal φ’s might not exist. This is easily dealt with using Proposition 1.8.1. If we assume that μ and ν have finite second moments:

$\displaystyle \begin{aligned} {\int_{\mathbb{R}^d} \! \|x\|{}^2 \, \mathrm{d}\mu(x)}<\infty \qquad \mathrm{ and} \qquad {\int_{\mathbb{R}^d} \! \|y\|{}^2 \, \mathrm{d}\nu(y)}<\infty, \end{aligned}$

then any transference plan π ∈ Π(μ, ν) has a finite cost, as is seen from integrating the elementary inequality ∥x − y∥² ≤ 2∥x∥² + 2∥y∥² and using Lemma 1.4.1:

$\displaystyle \begin{aligned} C(\pi) \le{\int_{\mathbb{R}^d\times\mathbb{R}^d} \! [\|x\|{}^2 + \|y\|{}^2] \, \mathrm{d}\pi(x,y)} ={\int_{\mathbb{R}^d} \! \|x\|{}^2 \, \mathrm{d}\mu(x)} +{\int_{\mathbb{R}^d} \! \|y\|{}^2 \, \mathrm{d}\nu(y)}<\infty. \end{aligned}$

With these tools, we can now prove a fundamental existence and uniqueness result for the Monge–Kantorovich problem. It has been proven independently by several authors, including Brenier [31], Cuesta-Albertos and Matrán [37], Knott and Smith [83], and Rachev and Rüschendorf [117].

Theorem 1.6.2 (Quadratic Cost in Euclidean Spaces)

Let μ and ν be probability measures on $\mathbb {R}^d$ with finite second moments, and suppose that μ is absolutely continuous with respect to Lebesgue measure. Then the solution to the Kantorovich problem is unique, and is induced from a transport map T that equals μ-almost surely the gradient of a convex function ϕ. Furthermore, the pair (∥x∥²∕2 − ϕ, ∥y∥²∕2 − ϕ ^∗) is optimal for the dual problem.

Proof

To alleviate the notation we write ϕ instead of $\widetilde \varphi$ . By Proposition 1.8.1, there exists an optimal dual pair (φ, ψ) such that ϕ(x) = ∥x∥²∕2 − φ(x) is convex and lower semicontinuous, and by the discussion in Sect. 1.1, there exists an optimal π. Since ϕ is μ-integrable, it must be finite almost everywhere, i.e., μ(domϕ) = 1. By Theorem 1.6.1, if we define $\mathcal N$ as the set of nondifferentiability points of ϕ, then $\mathrm {Leb}(\mathcal N\cap \mathrm {dom}\phi )=0$ ; as μ is absolutely continuous, the same holds for μ. (Here Leb denotes Lebesgue measure.)

We conclude that $\mu (\mathrm {int}(\mathrm {dom}\phi )\setminus \mathcal N)=1$ . In other words, ϕ is differentiable μ-almost everywhere, and so for μ-almost any x, there exists a unique y such that $\phi (x)+\phi ^*(y)={\left \langle {x},{y}\right \rangle }$ , and y = ∇ϕ(x). This shows that π is unique and induced from the transport map ∇ϕ(x). The gradient ∇ϕ is Borel measurable, since each of its coordinates can be written as $\limsup _{q\to 0,q\in \mathbb {Q}}q^{-1}(\phi (x+qv)-\phi (x))$ for some vector v (the canonical basis of $\mathbb {R}^d$ ), which is Borel measurable because the limit superior is taken on countably many functions (and ϕ is measurable because it is lower semicontinuous).

1.6.2 Separable Hilbert Spaces

The finite-dimensionality of $\mathbb {R}^d$ in the previous subsection was only used in order to apply Theorem 1.6.1, so one could hope to extend the results to infinite-dimensional separable Hilbert spaces.

Although there is no obvious parallel for Lebesgue measure (i.e., translation invariant) on infinite-dimensional Banach spaces, one can still define absolute continuity via Gaussian measures. Indeed, $\mu \in P(\mathbb {R}^d)$ is absolutely continuous with respect to Lebesgue measure if and only if the following holds: if $\mathcal N\subset \mathbb {R}^d$ is such that $\nu (\mathcal N)=0$ for any nondegenerate Gaussian measure ν, then $\mu (\mathcal N)=0$ . This definition can be extended to any separable Banach space $\mathcal X$ via projections, as follows. Let $\mathcal X^*$ be the (topological) dual of $\mathcal X$ , consisting of all real-valued, continuous linear functionals on $\mathcal X$ .

Definition 1.6.3 (Gaussian Measures)

A probability measure $\mu \in P(\mathcal X)$ is a nondegenerate Gaussian measure if for any $\ell \in \mathcal X^*\setminus \{0\}$ , $\ell \#\mu \in P(\mathbb {R})$ is a Gaussian measure with positive variance.

Definition 1.6.4 (Gaussian Null Sets and Absolutely Continuous Measures)

A subset $\mathcal N\subset \mathcal X$ is a Gaussian null set if whenever ν is a nondegenerate Gaussian measure, $\nu (\mathcal N)=0$ . A probability measure $\mu \in P(\mathcal X)$ is absolutely continuous if μ vanishes on all Gaussian null sets.

Clearly, if ν is a nondegenerate Gaussian measure, then it is absolutely continuous.

As explained in Ambrosio et al. [12, Section 6.2], a version of Rademacher’s theorem holds in separable Hilbert spaces: a locally Lipschitz function is Gâteaux differentiable except on a Gaussian null set of $\mathcal X$ . Theorem 1.6.2 (and more generally, Theorem 1.8.2) extend to infinite dimensions; see [12, Theorem 6.2.10].

1.6.3 The Gaussian Case

Apart from the one-dimensional case of Sect. 1.5, there is another special case in which there is a unique and explicit solution to the Monge–Kantorovich problem.

Suppose that μ and ν are Gaussian measures on $\mathbb {R}^d$ with zero means and nonsingular covariance matrices A and B. By Theorem 1.6.2, we know that there exists a unique optimal map T such that T#μ = ν. Since linear push-forwards of Gaussians are Gaussian, it seems natural to guess that T should be linear, and this is indeed the case.

Since T is a linear map that should be the gradient of a convex function ϕ, it must be that ϕ is quadratic, i.e., $\phi (x)-\phi (0)={\left \langle {x},{Qx}\right \rangle }$ for $x\in \mathbb {R}^d$ and some matrix Q. The gradient of ϕ at x is (Q + Q ^t)x and the Hessian matrix is Q + Q ^t. Thus, T = Q + Q ^t and since ϕ is convex, T must be positive semidefinite.

Viewing T as a matrix leads to the Riccati equation TAT = B (since T is symmetric). This is a quadratic equation in T, and so we wish to take square roots in a way that would isolate T. This is done by multiplying the equation from both sides with A ^1∕2:

$\displaystyle \begin{aligned}{}[A^{1/2}TA^{1/2}][A^{1/2}TA^{1/2}] =A^{1/2}TATA^{1/2} =A^{1/2}BA^{1/2} =[A^{1/2}B^{1/2}][B^{1/2}A^{1/2}]. \end{aligned}$

All matrices in brackets are positive semidefinite. By taking square roots and multiplying with A ^−1∕2, we finally find

$\displaystyle \begin{aligned} T=A^{-1/2}[A^{1/2}BA^{1/2}]^{1/2}A^{-1/2}. \end{aligned}$

A straightforward calculation shows that TAT = B indeed, and T is positive definite, hence optimal. To calculate the transport cost C(T), observe that (T − I)#μ is a centred Gaussian measure with covariance matrix

$\displaystyle \begin{aligned} TAT -TA -AT +A =A+B -A^{1/2}[A^{1/2}BA^{1/2}]^{1/2}A^{-1/2} -A^{-1/2}[A^{1/2}BA^{1/2}]^{1/2}A^{1/2}. \end{aligned}$

If $Y\sim \mathcal N(0,C)$ , then $\mathbb {E} \|Y\|{ }^2$ equals the trace of C, denoted trC. Hence, by properties of the trace,

$\displaystyle \begin{aligned} C(T) ={\mathrm{tr}}\left[A+B - 2(A^{1/2}BA^{1/2})^{1/2}\right]. \end{aligned}$

(1.6)

By continuity arguments, (1.6) is the total transport cost between any two Gaussian distributions with zero means, even if A is singular.

If AB = BA, the above formulae simplify to

$\displaystyle \begin{aligned} T=B^{1/2}A^{-1/2} ,\qquad C(T)={\mathrm{tr}}\left[A+B - 2A^{1/2}B^{1/2}\right] =\|A^{1/2} - B^{1/2}\|{}^2_F, \end{aligned}$

with F the Frobenius norm.

If the means of μ and ν are m and n, one simply needs to translate the measures. The optimal map and the total cost are then

$\displaystyle \begin{aligned} Tx=n +A^{-1/2}[A^{1/2}BA^{1/2}]^{1/2}A^{-1/2}(x-m); \end{aligned}$

$\displaystyle \begin{aligned} C(T) =\|n - m\|{}^2 +{\mathrm{tr}}[A+B - 2(A^{1/2}BA^{1/2})^{1/2}]. \end{aligned}$

From this, we can deduce a lower bound on the total cost between any two measures in $\mathbb {R}^d$ in terms of their second order structure. This is worth mentioning, because such lower bounds are not very common (the Monge–Kantorovich problem is defined by an infimum, and thus typically easier to bound from above).

Proposition 1.6.5 (Lower Bound for Quadratic Cost)

Let $\mu ,\nu \in P(\mathbb {R}^d)$ have means m and n and covariance matrices A and B and let π be the optimal map. Then

$\displaystyle \begin{aligned} C(\pi) \ge \|n - m\|{}^2 +{\mathrm{tr}}[A+B - 2(A^{1/2}BA^{1/2})^{1/2}]. \end{aligned}$

Proof

It will be convenient here to use the probabilistic terminology of Sect. 1.2. Let X and Y be random variables with distributions μ and ν. Any coupling of X and Y will have covariance matrix of the form $C=\begin {pmatrix}A & V\\V^t & B\end {pmatrix}\in \mathbb {R}^{2d\times 2d}$ for some matrix $V\in \mathbb {R}^{d\times d}$ , constrained so that C is positive semidefinite. This gives the lower bound

$\displaystyle \begin{aligned} \inf_{\pi\in\varPi(\mu,\nu)} \mathbb{E}_\pi\|X{-}Y\|{}^2 =\|m {-} n\|{}^2 + \inf_{\pi\in\varPi(\mu,\nu)} {\mathrm{tr}}_\pi [A+B{-}2V] \ge \|m - n\|{}^2 + \inf_{V:C\ge0}{\mathrm{tr}} [A+B{-}2V]. \end{aligned}$

As we know from the Gaussian case, the last infimum is given by (1.6).

1.6.4 Regularity of the Transport Maps

The optimal transport map T between Gaussian measures on $\mathbb {R}^d$ is linear, so it is of course very smooth (analytic). The densities of Gaussian measures are analytic too, so that T inherits the regularity of μ and ν. Using the formula for T, one can show that a similar phenomenon takes place in the one-dimensional case. Though we do not have a formula for T at our disposal when μ and ν are general absolutely continuous measures on $\mathbb {R}^d$ , d ≥ 2, it turns out that even in that case, T inherits the regularity of μ and ν if some convexity conditions are satisfied.

To guess what kind of results can be hoped for, let us first examine the case d = 1. Let F and G denote the distribution functions of μ and ν, respectively. Suppose that G is continuously differentiable and that G′ > 0 on some open interval (finite or not) I such that ν(I) = 1. Then the inverse function theorem says that G ⁻¹ is also continuously differentiable. Recall that the support of a (Borel) probability measure μ (denoted suppμ) is the smallest closed set K such that μ(K) = 1. A simple application of the chain rule (see page 19 in the supplement) gives:

Theorem 1.6.6 (Regularity in $\mathbb {R}$ )

Let $\mu ,\nu \in P(\mathbb {R})$ possess distribution functions F and G of class C ^k, k ≥ 1. Suppose further that suppν is an interval I (possibly unbounded) and that G′ > 0 on the interior of I. Then the optimal map is of class C ^k as well. If F, G ∈ C ⁰ are merely continuous, then so is the optimal map.

The assumption on the support of ν is important: if μ is Lebesgue measure on [0, 1] and the support of ν is disconnected, then T cannot even be continuous, no matter how smooth ν is.

The argument above cannot be easily extended to measures on $\mathbb {R}^d$ , d ≥ 2, because there is no explicit formula available for the optimal maps. As before, we cannot expect the optimal map to be continuous if the support of ν is disconnected. It turns out that the condition on the support of ν is not connectedness, but rather convexity. This was shown by Caffarelli, who was able to prove ( [32] and the references within) that the optimal maps have the same smoothness as the measures. To state the result, we recall the following notation for an open $\varOmega \subseteq \mathbb {R}^d$ , k ≥ 0 and α ∈ (0, 1]. We say that f ∈ C ^{k, α}(Ω) if all the partial derivatives of order k of f are locally α-Hölder on Ω. For example, if k = 1, this means that for any x ∈ Ω there exists a constant L and an open ball B containing x such that

$\displaystyle \begin{aligned} \|\nabla f(z) - \nabla f(y)\| \le L\|y-z\|{}^\alpha, \qquad y,z\in B. \end{aligned}$

Note that f ∈ C ^k+1⇒f ∈ C ^{k, β}⇒f ∈ C ^{k, α}⇒f ∈ C ^k, for 0 ≤ α ≤ β ≤ 1 so α gives a “fractional” degree of smoothness for f. Moreover, C ^{k, 0} = C ^k and C ^{k, 1} is quite close to C ^k+1, since Lipschitz functions are almost surely differentiable.

Theorem 1.6.7 (Regularity of Transport Maps)

Fix open sets $\varOmega _1,\varOmega _2\subseteq \mathbb {R}^d$ , with Ω ₂ convex, and absolutely continuous measures $\mu ,\nu \in P(\mathbb {R}^d)$ with finite second moments and bounded, strictly positive densities f, g, respectively, such that μ(Ω ₁) = 1 = ν(Ω ₂). Let ϕ be such that ∇ϕ#μ = ν.

1.
If Ω ₁ and Ω ₂ are bounded and f, g are bounded below, then ϕ is strictly convex and of class C ^{1, α}(Ω ₁) for some α > 0.
2.
If $\varOmega _1=\varOmega _2=\mathbb {R}^d$ and f, g ∈ C ^{0, α}, then ϕ ∈ C ^{2, α}(Ω ₁).

If in addition f, g ∈ C ^{k, α}, then ϕ ∈ C ^{k+2, α}(Ω ₁).

In other words, the optimal map T = ∇ϕ ∈ C ^{k+1, α}(Ω ₁) is one derivative smoother than the densities, so has the same smoothness as the measures μ, ν.

Theorem 1.6.7 will be used in two ways in this book. Firstly, it is used to derive criteria for a Karcher mean of a collection of measures to be the Fréchet mean of that collection (Theorem 3.1.15). Secondly, it allows one to obtain very smooth estimates for the transport maps. Indeed, any two measures μ and ν can be approximated by measures satisfying the second condition: one can approximate them by discrete measures using the law of large numbers and then employ a convolution with, e.g., a Gaussian measure (see, for instance, Theorem 2.2.7). It is not obvious that the transport maps between the approximations converge to the transport maps between the original measures, but we will see this to be true in the next section.

1.7 Stability of Solutions Under Weak Convergence

In this section, we discuss the behaviour of the solution to the Monge–Kantorovich problem when the measures μ and ν are replaced by approximations μ _n and ν _n. Since any measure can be approximated by discrete measures or by smooth measures, this allows us to benefit from both worlds. On the one hand, approximating μ and ν with discrete measures leads to the finite discrete problem of Sect. 1.3 that can be solved exactly. On the other hand, approximating μ and ν with Gaussian convolutions thereof leads to very smooth measures (at least on $\mathbb {R}^d$ ), and so the regularity results of the previous section imply that the respective optimal maps will also be smooth. Finally, in applications, one would almost always observe the measures of interest μ and ν with a certain amount of noise, and it is therefore of interest to control the error introduced by the noise. In image analysis, μ can represent an image that has undergone blurring, or some other perturbation (Amit et al. [13]). In other applications, the noise could be due to sampling variation, where instead of μ one observes a discrete measure μ _N obtained from realisations X ₁, …, X _N of random elements with distribution μ as $\mu _N=N^{-1}\sum _{i=1}^N\delta \{X_i\}$ (see Chap. 4).

In Sect. 1.7.1, we will see that the optimal transference plan π depends continuously on μ and ν. With this result under one’s belt, one can then deduce an analogous property for the optimal map T from μ to ν given some regularity of μ, as will be seen in Sect. 1.7.2.

We shall assume throughout this section that μ _n → μ and ν _n → ν weakly, which, we recall, means that ${{\int _{\mathcal X} \! {f} \, \mathrm {d}{\mu _n}}}\to {{\int _{\mathcal X} \! f \, \mathrm {d}\mu }}$ for all continuous bounded $f:\mathcal X\to \mathbb {R}$ . The following equivalent definitions for weak convergence will be used not only in this section, but elsewhere as well.

Lemma 1.7.1 (Portmanteau)

Let $\mathcal X$ be a complete separable metric space and let $\mu ,\mu _n\in P(\mathcal X)$ . Then the following are equivalent:

μ _n → μ weakly;
F _n(x) → F(x) for any continuity point x of F. Here $\mathcal X=\mathbb {R}^d$ , F _n is the distribution function of μ _n and F is that of μ;
for any open $G\subseteq \mathcal X$ , $\liminf \mu _n(G)\ge \mu (G)$ ;
for any closed $F\subseteq \mathcal X$ , $\limsup \mu _n(F)\le \mu (F)$ ;
${{\int \! h \, \mathrm {d}{\mu _n}}}\to {{\int \! h \, \mathrm {d}\mu }}$ for any bounded measurable h whose set of discontinuity points is a μ-null set.

For a proof, see, for instance, Billingsley [24, Theorem 2.1]. The equivalence with the last condition can be found in Pollard [104, Section III.2].

1.7.1 Stability of Transference Plans and Cyclical Monotonicity

In this subsection, we state and sketch the proof of the fact that if μ _n → μ and ν _n → ν weakly, then the optimal transference plans π _n ∈ Π(μ _n, ν _n) converge to an optimal π ∈ Π(μ, ν). The result, as stated in Villani [125, Theorem 5.20], is valid on complete separate metric spaces with general cost functions, and reads as follows.

Theorem 1.7.2 (Weak Convergence and Optimal Plans)

Let μ _n and ν _n converge weakly to μ and ν, respectively, in $P(\mathcal X)$ and let $c:\mathcal X^2\to \mathbb {R}_+$ be continuous. If π _n ∈ Π(μ _n, ν _n) are optimal transference plans and

$\displaystyle \begin{aligned} \limsup_{n\to\infty} {\int_{\mathcal X^2} \! c(x,y) \, \mathrm{d}\pi_n(x,y)} <\infty. \end{aligned}$

then (π _n) is a tight sequence and each of its weak limits π ∈ Π(μ, ν) is optimal.

One can even let c vary with n under some conditions.

Let c(x, y) = ∥x − y∥²∕2. We prefer to keep the notation c(⋅, ⋅) in order to stress the generality of the arguments. A key idea in the proof is the replacement of optimality by another property called cyclical monotonicity, which behaves nicely with respect to weak convergence. To motivate this property, we recall the discrete case of Sect. 1.3 where $\mu =N^{-1}\sum _{i=1}^N \delta \{x_i\}$ and $\nu =N^{-1}\sum _{i=1}^N\delta \{y_i\}$ . There exists an optimal transference plan π induced from a permutation σ ₀ ∈ S _N. Since the ordering of {x _i} and {y _i} is irrelevant in the representations of μ and ν, we may assume without loss of generality that σ ₀ is the identity permutation. Then, by definition of optimality,

$\displaystyle \begin{aligned} \sum_{i=1}^N c(x_i,y_i) \le \sum_{i=1}^N c(x_i,y_{\sigma(i)}) ,\qquad \sigma\in S_N. \end{aligned}$

(1.7)

If σ is the identity except for a subset i ₁, …, i _n, n ≤ N, then in particular

$\displaystyle \begin{aligned} \sum_{k=1}^n c(x_{i_k},y_{i_k}) \le \sum_{k=1}^n c(x_{i_k},y_{{\sigma(i_k)}}) ,\qquad \sigma\in S_n, \end{aligned}$

and if we choose σ(i _k) = i _k−1 with i ₀ = i _n, this writes

$\displaystyle \begin{aligned} \sum_{k=1}^n c(x_{i_k},y_{i_k}) \le \sum_{k=1}^n c(x_{i_k},y_{i_{k-1}}). \end{aligned}$

(1.8)

By decomposing a permutation σ ∈ S _N to disjoint cycles, one can verify that (1.8) implies (1.7). This will be useful since, as it turns out, a variant of (1.8) holds for arbitrary measures μ and ν for which there is no relevant finite N as in (1.7).

Definition 1.7.3 (Cyclically Monotone Sets and Measures)

A set $\varGamma \subseteq \mathcal X^2$ is cyclically monotone if for any n and any (x ₁, y ₁), …, (x _n, y _n) ∈ Γ,

$\displaystyle \begin{aligned} \sum_{i=1}^n c(x_i,y_i) \le \sum_{i=1}^n c(x_{i},y_{i-1}), \qquad (y_0=y_n). \end{aligned}$

(1.9)

A probability measure π on $\mathcal X^2$ is cyclically monotone if there exists a monotone Borel set Γ such that π(Γ) = 1.

The relevance of cyclical monotonicity becomes clear from the following observation. If μ and ν are discrete uniform measures on N points and σ is an optimal permutation for the Monge–Kantorovich problem, then the coupling $\pi =(1/N)\sum _{i=1}^N\delta \{(x_i,y_{\sigma (i)})\}$ is cyclically monotone. In fact, even if the optimal permutation is not unique, the set

$\displaystyle \begin{aligned} \varGamma =\{(x_i,y_{\sigma(i)}):i=1,\dots,N,\sigma\in S_N\mathrm{ optimal}\} \end{aligned}$

is cyclically monotone. Furthermore, π ∈ Π(μ, ν) is optimal if and only if it is cyclically monotone, if and only if π(Γ) = 1. It is heuristically easy to see that cyclical monotonicity is a necessary condition for optimality:

Proposition 1.7.4 (Optimal Plans Are Cyclically Monotone)

Let $\mu ,\nu \in P(\mathcal X)$ and suppose that the cost function c is nonnegative and continuous. Assume that the optimal π ∈ Π(μ, ν) has a finite total cost. Then suppπ is cyclically monotone. In particular, π is cyclically monotone.

The idea of the proof is that if for some (x ₁, y ₁), …, (x _n, y _n) in the support of π,

$\displaystyle \begin{aligned} \sum_{i=1}^n c(x_i,y_i) > \sum_{i=1}^n c(x_{i},y_{i-1}), \end{aligned}$

then by continuity of c, the same inequality holds on some balls of positive measure. One can then replace π by a measure having (x _i, y _i−1) rather than (x _i, y _i) in its support, and this measure will incur a lower cost than π. A rigorous proof can be found in Gangbo and McCann [59, Theorem 2.3].

Thus, optimal transference plans π solve infinitely many discrete Monge– Kantorovich problems emanating from their support. More precisely, for any finite collection (x _i, y _i) ∈suppπ, i = 1, …, N and any permutation σ ∈ S _N, (1.7) is satisfied. Therefore, the identity permutation is optimal between the measures $(1/N)\sum \delta \{x_i\}$ and $(1/N)\sum \delta \{y_j\}$ .

In the same spirit as Γ defined above for the discrete case, one can strengthen Proposition 1.7.4 and prove existence of a cyclically monotone set Γ that includes the support of any optimal transference plan π: take Γ = ∪supp(π) for π optimal.

The converse of Proposition 1.7.4 also holds.

Proposition 1.7.5 (Cyclically Monotone Plans Are Optimal)

Let $\mu ,\nu \in P(\mathcal X)$ , $c:\mathcal X^2\to \mathbb {R}_+$ continuous and π ∈ Π(μ, ν) a cyclically monotone measure with C(π) finite. Then π is optimal in Π(μ, ν).

Let us sketch the proof in the quadratic case c(x, y) = ∥x − y∥²∕2 and see how convexity comes into play. Straightforward algebra shows that (1.9) is equivalent, in the quadratic case, to

$\displaystyle \begin{aligned} \sum_{i=1}^n\left\langle {y_{i}},{x_{i+1}-x_{i}}\right\rangle \le0 ,\qquad (x_{n+1}=x_1). \end{aligned}$

(1.10)

Fix (x ₀, y ₀) ∈ Γ = suppπ and define $\phi :\mathcal X\to \mathbb {R}\cup \{\infty \}$ by

$\displaystyle \begin{aligned} \phi(x) &=\sup\left\{\left\langle {y_0},{x_1-x_0}\right\rangle+\dots+\left\langle {y_{m-1}},{x_m-x_{m-1}}\right\rangle\right.\\ {} &\quad \left.+\left\langle {y_m},{x-x_m}\right\rangle:m\in\mathbb{N},\quad (x_i,y_i)\in\varGamma\right\}. \end{aligned}$

This function is defined as a supremum of affine functions, and is therefore convex and lower semicontinuous. Cyclical monotonicity of Γ implies that ϕ(x ₀) = 0, so ϕ is not identically infinite (it would have been so if Γ were not cyclically monotone). Straightforward computations show that Γ is included in the subdifferential of ϕ: y is a subgradient of ϕ at x when (x, y) ∈ Γ. Optimality of π then follows by weak duality, since π assigns full measure to the set of (x, y) such that $\phi (x)+\phi ^*(y)={\left \langle {x},{y}\right \rangle }$ ; see (1.5) and the discussion around it.

The argument for more general costs follows similar lines and is sketched at the end of this subsection.

Given these intermediary results, it is now instructive to prove Theorem 1.7.2.

Proof (Proof of Theorem 1.7.2)

Since μ _n → μ weakly, it is a tight sequence, and similarly for ν _n. Consequently, the entire set of plans ∪_nΠ(μ _n, ν _n) is tight too (see the discussion before deriving (1.3)). Therefore, up to a subsequence, (π _n) has a weak limit π. We need to show that π is cyclically monotone and that C(π) is finite. The latter is easy, since $c_M(x,y)=\min (M,c(x,y))$ is continuous and bounded:

$\displaystyle \begin{aligned} C(\pi) =\lim_{M\to\infty}{{\int_{\mathcal X^2} \! {c_M} \, \mathrm{d}\pi}} =\lim_{M\to\infty}\lim_{n\to\infty}{\int_{\mathcal X^2} \! c_M \, \mathrm{d}\pi_n} \le \liminf_{n\to\infty}{\int_{\mathcal X^2} \! c \, \mathrm{d}\pi_n} <\infty. \end{aligned}$

To show that π is cyclically monotone, fix (x ₁, y ₁), …, (x _N, y _N) ∈suppπ. We show that there exist $(x^n_k,y^n_k)\in \mathrm {supp}\pi _n$ that converge to (x _k, y _k). Once this is established, we conclude from the cyclical monotonicity of suppπ _n and the continuity of c that

$\displaystyle \begin{aligned} \sum_{k=1}^N c(x_k,y_k) =\lim_{n\to\infty}\sum_{k=1}^N c(x_k^n,y_k^n) \le\lim_{n\to\infty}\sum_{k=1}^N c(x_k^n,y_{k-1}^n) =\sum_{k=1}^N c(x_k,y_{k-1}). \end{aligned}$

The existence proof for the sequence is standard. For 𝜖 > 0, let B = B _𝜖(x _k, y _k) be an open ball around (x _k, y _k). Then π(B) > 0 and by the portmanteau Lemma 1.7.1, π _n(B) > 0 for sufficiently large n. It follows that there exist $(x_k^n,y_k^n)\in B \cap \mathrm {supp}\pi _n$ . Let 𝜖 = 1∕m, say, then for all n ≥ N _m we can find $(x_k^n,y_k^n)\in \mathrm {supp}\mu _n$ of distance 2∕m from (x _k, y _k). We can choose N _m+1 > N _m without loss of generality in order to complete the proof.

A few remarks are in order. Firstly, quadratic cyclically monotone sets (with respect to ∥x − y∥²∕2) are included in the subdifferential of convex functions. The converse is also true, as can be easily deduced from summing up the subgradient inequalities

$\displaystyle \begin{aligned} \phi(x_{i+1}) \ge \phi(x_i) + \left\langle {y_i},{x_{i+1}-x_i}\right\rangle ,\qquad i=1,\dots,N, \end{aligned}$

where y _i is a subgradient of ϕ at x _i. For future reference, we state this characterisation as a theorem (which is valid in infinite dimensions too).

Theorem 1.7.6 (Rockafellar [112])

A nonempty $\varGamma \subseteq \mathcal X^{2}$ is quadratic cyclically monotone if and only if it is included in the graph of the subdifferential of a lower semicontinuous convex function that is not identically infinite.

Secondly, we have not used at all the Kantorovich duality, merely its weak form. The machinery of cyclical monotonicity can be used in order to prove the duality Theorem 1.4.2. This is indeed the strategy of Villani [125, Chapter 5], who explains its advantage with respect to Hahn–Banach-type duality proofs.

Lastly, the idea of the proof of Proposition 1.7.5 generalises to other costs in a natural way. Given a cyclically monotone (with respect to a cost function c) set Γ and a fixed pair (x ₀, y ₀) ∈ Γ, define (Rüschendorf [116])

$\displaystyle \begin{aligned} \varphi(x) {=}\inf\left\{c(x_1,y_0) {-} c(x_0,y_0) + c(x_m,y_{m-1}) {-} c(x_{m-1},y_{m-1}) + c(x,y_m) {-} c(x_m,y_m) \right\}. \end{aligned}$

Then under some conditions, (φ, ψ) is dual optimal for some ψ. As explained in Sect. 1.8, ψ can be chosen to be essentially φ ^c (as defined in that section).

1.7.2 Stability of Transport Maps

We now extend the weak convergence of π _n to π of the previous subsection to convergence of optimal maps. Because of the applications we have in mind, we shall work exclusively in the Euclidean space $\mathcal X=\mathbb {R}^d$ with the quadratic cost function; our results can most likely be extended to more general situations.

In this setting, we know that optimal plans are supported on graphs of subdifferentials of convex functions. Suppose that π _n is induced by T _n and π is induced by T. Then in some sense, the weak convergence of π _n to π yields convergence of the graphs of T _n to the graph of T. Our goal is to strengthen this to uniform convergence of T _n to T. Roughly speaking, we show the following: there exists a set A with μ(A) = 1 and such that T _n converge uniformly to T on every compact subset of A. For the reader’s convenience, we give a user-friendly version here; a more general statement is given in Proposition 1.7.11 below.

Theorem 1.7.7 (Uniform Convergence of Optimal Maps)

Let μ _n, μ be absolutely continuous measures with finite second moments on an open convex set $U\subseteq \mathbb {R}^d$ such that μ _n → μ weakly, and let ν _n → ν weakly with $\nu _n,\nu \in P(\mathbb {R}^d)$ with finite second moments. If T _n and T are continuous on U and C(T _n) is bounded uniformly in n, then

$\displaystyle \begin{aligned} \sup_{x\in\varOmega} \|T_n(x) - T(x)\| \to0 ,\qquad n\to\infty, \end{aligned}$

for any compact Ω ⊆ U.

Since T _n and T are only defined up to Lebesgue null sets, it will be more convenient to work directly with the subgradients. That is, we view T _n and T as set-valued functions that to each $x\in \mathbb {R}^d$ assign a (possibly empty) subset of $\mathbb {R}^d$ . In other words, T _n and T take values in the power set of $\mathbb {R}^d$ , denoted by $2^{\mathbb {R}^d}$ .

Let $\phi :\mathbb {R}^d\to \mathbb {R}\cup \{\infty \}$ be convex, y ₁ ∈ ∂ϕ(x ₁) and y ₂ ∈ ∂ϕ(x ₂). Putting n = 2 in the definition of cyclical monotonicity (1.10) gives

$\displaystyle \begin{aligned} \left\langle {y_2 - y_1},{x_2-x_1}\right\rangle \ge0. \end{aligned}$

This property (which is weaker than cyclical monotonicity) is important enough to have its own name. Following the notation of Alberti and Ambrosio [6], we call a set-valued function (or multifunction) $u:\mathbb {R}^d\to 2^{\mathbb {R}^d}$ monotone if whenever y _i ∈ u(x _i), i = 1, 2,

$\displaystyle \begin{aligned} \left\langle {y_2-y_1},{x_2-x_1}\right\rangle \ge0. \end{aligned}$

If d = 1, this simply means that u is a nondecreasing (set-valued) function. For example, one can define u(x) = {0} for x ∈ [0, 1), u(1) = [0, 1] and u(x) = ∅ if x∉[0, 1]. Next, u is said to be maximally monotone if no points can be added to its graph while preserving monotonicity:

$\displaystyle \begin{aligned} \left\{ \left\langle {y'-y},{x'-x}\right\rangle \ge0 \quad \mathrm{whenever} y\in u(x) \right\} \quad \Longrightarrow\quad y'\in u(x'). \end{aligned}$

It will be convenient to identify u with its graph; we will often write (x, y) ∈ u to mean y ∈ u(x). Note that u(x) can be empty, even when u is maximally monotone. The previous example for u is not maximally monotone, but it will be if we modify u(0) to be (−∞, 0] and u(1) to be [0, ∞).

Of course, if $\phi :\mathbb {R}^d\to \mathbb {R}\cup \{\infty \}$ is convex, then u = ∂ϕ is monotone. It follows from Theorem 1.7.6 that u is maximally cyclically monotone (no points can be added to its graph while preserving cyclical monotonicity). It can actually be shown that u is maximally monotone [6, Section 7]. In what follows, we will always work with subdifferentials of convex functions, so unless stated otherwise, u will always be assumed maximally monotone.

Maximally monotone functions enjoy the following very useful continuity property. It is proven in [6, Corollary 1.3] and will be used extensively below.

Proposition 1.7.8 (Continuity at Singletons)

Let $x\in \mathbb {R}^d$ such that u(x) = {y} is a singleton. Then u is nonempty on some neighbourhood of x and it is continuous at x: if x _n → x and y _n ∈ u(x _n), then y _n → y.

Notice that this result implies that if a convex function ϕ is differentiable on some open set $E\subseteq \mathbb {R}^d$ , then it is continuously differentiable there (Rockafellar [113, Corollary 25.5.1]).

If $f:\mathbb {R}^d\to \mathbb {R}\cup \{\infty \}$ is any function, one can define its subgradient at x locally as

$\displaystyle \begin{aligned} \partial f(x) &=\{y:f(z)\ge f(x) + {\left\langle {y},{z-x}\right\rangle} + o(\|z-x\|)\}\\ {} &=\left\{y: \liminf_{z\to x}\frac{f(z)- f(x) + {\left\langle {y},{z-x}\right\rangle} }{\|z-x\|} \ge0\right\}. \end{aligned}$

(See the discussion after Theorem 1.8.2.) When f is convex, one can remove the o(∥z − x∥) term and the inequality holds for all z, i.e., globally and not locally. Since monotonicity is related to convexity, it should not be surprising that monotonicity is in some sense a local property. Suppose that u(x ₀) = {y ₀} is a singleton and that for some $y^*\in \mathbb {R}^d$ ,

$\displaystyle \begin{aligned} \left\langle {y-y^*},{x-x_0}\right\rangle \ge0 \end{aligned}$

for all $x\in \mathbb {R}^d$ and y ∈ u(x). Then by maximality, y ^∗ must equal y ₀. By “local property”, we mean that the conclusion y ^∗ = y ₀ holds if the above inequality holds for x in a small neighbourhood of x ₀ (an open set that includes x ₀). We will need a more general version of this result, replacing neighbourhoods by a weaker condition that can be related to Lebesgue points. The strengthening is somewhat technical; the reader can skip directly to Lemma 1.7.10 and assume that G is open without losing much intuition.

Let B _r(x ₀) = {x : ∥x − x ₀∥ < r} for r ≥ 0 and $x_0\in \mathbb {R}^d$ . The interior of a set $G\subseteq \mathbb {R}^d$ is denoted by intG and the closure by $\overline G$ . If G is measurable, then LebG denotes the Lebesgue measure of G. Finally, convG denotes the convex hull of G.

A point x ₀ is a Lebesgue point (or of Lebesgue density) of a measurable set $G\subseteq \mathbb {R}^d$ if for any 𝜖 > 0 there exists t _𝜖 > 0 such that

$\displaystyle \begin{aligned} \frac{\mathrm{Leb}(B_t(x_0) \cap G)} {\mathrm{Leb}(B_t(x_0))} > 1 - \epsilon, \qquad 0<t<t_\epsilon. \end{aligned}$

An illuminating example is the set $\{y\le \sqrt {|x|}\}$ in $\mathbb {R}^2$ (see Fig. 1.1). Since the “slope” of the square root is infinite, x ₀ = (0, 0) is a Lebesgue point, but the fraction above is strictly smaller than one, for all t > 0.

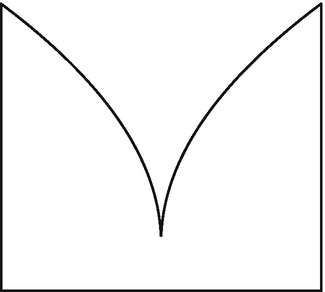
../images/456556_1_En_1_Chapter/456556_1_En_1_Fig1_HTML.png — Fig. 1.1
The set $G=\{(x, y):|x|\le 1,\ -0.2\le y\le \sqrt {|x|}\}$

$$G=\{(x, y):|x|\le 1,\ -0.2\le y\le \sqrt {|x|}\}$$ — Fig. 1.1
The set $G=\{(x, y):|x|\le 1,\ -0.2\le y\le \sqrt {|x|}\}$

We denote the set of points of Lebesgue density of G by G ^den. Here are some facts about G ^den: clearly, $\mathrm {int} G\subseteq G^{\mathrm{{den}}}\subseteq \overline G$ . Stein and Shakarchi [121, Chapter 3, Corollary 1.5] show that Leb(G ∖ G ^den) = 0 (and Leb(G ^den ∖ G) = 0, so G ^den is very close to G). By the Hahn–Banach theorem, G ^den ⊆int(conv(G)): indeed, if x is not in int(convG), then there is a separating hyperplane between x and convG ⊇ G, so the fraction above is at most 1∕2 for all t > 0.

The “denseness” of Lebesgue points is materialised in the following result. It is given as exercise in [121] when d = 1, and the proof can be found on page 27 in the supplement.

Lemma 1.7.9 (Density Points and Distance)

Let x ₀be a point of Lebesgue density of a measurable set $G\subseteq \mathbb {R}^d$ . Then

$\displaystyle \begin{aligned} \delta(z) =\delta_G(z) =\inf_{x\in G} \|z - x\| =o(\|z-x_0\|), \qquad \mathrm{as} z\to x_0. \end{aligned}$

Of course, this result holds for any $x_0\in \overline G$ if the little o is replaced by big O, since δ is Lipschitz. When x ₀ ∈intG, this is trivial because δ vanishes on intG.

The important part here is the following corollary: for almost all x ∈ G, δ(z) = o(∥z − x∥) as z → x. This can be seen in other ways: since δ is Lipschitz, it is differentiable almost everywhere. If $x\in \overline G$ and δ is differentiable at x, then ∇δ(x) must be 0 (because δ is minimised there), and then δ(z) = o(∥z − x∥). We just showed that δ is differentiable with vanishing derivative at all Lebesgue points of x. The converse is not true: $G=\{\pm 1/n\}_{n=1}^\infty$ has no Lebesgue points, but δ(y) ≤ 4y ² as y → 0.

The locality of monotone functions can now be stated as follows. It is proven on page 27 of the supplement.

Lemma 1.7.10 (Local Monotonicity)

Let $x_0\in \mathbb {R}^d$ such that u(x ₀) = {y ₀} and x ₀ is a Lebesgue point of a set G satisfying

$\displaystyle \begin{aligned} \langle y-y^*,x-x_0\rangle \ge0 \qquad \forall x\in G \ \forall y\in u(x). \end{aligned}$

Then y ^∗ = y ₀. In particular, the result is true if the inequality holds on $G=O\setminus \mathcal N$ with ∅≠O open and $\mathcal N$ Lebesgue negligible.

These continuity properties cannot be of much use unless u(x) is a singleton for reasonably many values of x. Fortunately, this is indeed the case: the set of points x such that u(x) contains more than one element has Lebesgue measure 0 (see Alberti and Ambrosio [6, Remark 2.3] for a stronger result). Another issue is that u may be empty, and convexity comes into play here again. Let domu = {x : u(x)≠∅}. Then there exists a convex closed set K such that

$\displaystyle \begin{aligned} \mathrm{int} K \subseteq \mathrm{dom} u \subseteq K. \end{aligned}$

[6, Corollary 1.3(2)]. Although domu itself may fail to be convex, it is almost convex in the above sense. By convexity, K ∖intK has Lebesgue measure 0 (see the discussion after Theorem 1.6.1) and so the set of points in K where u is not a singleton,

$\displaystyle \begin{aligned} \{x\in K:u(x)=\emptyset\} \cup\{x\in K:u(x)\mathrm{ contains more than one point}\}, \end{aligned}$

has Lebesgue measure 0, and u(x) is empty for all x∉K. (It is in fact not difficult to show that if x ∈ ∂K, then u(x) cannot be a singleton, by the Hahn–Banach theorem.)

With this background on monotone functions at our disposal, we are now ready to state the stability result for the optimal maps. We assume the following.

Assumptions 1

Let $\mu _n,\mu ,\nu _n,\nu \in P(\mathbb {R}^d)$ with optimal couplings (with respect to quadratic cost) π _n ∈ Π(μ _n, ν _n), π ∈ Π(μ, ν) and convex potentials ϕ _n and ϕ, respectively, such that

(convergence ) μ _n → μ and ν _n → ν weakly;
(finiteness ) the optimal couplings π _n ∈ Π(μ _n, ν _n) satisfy
$\displaystyle \begin{aligned} \limsup_{n\to\infty} {\int_{\mathcal X^2} \! \frac 12\|x - y\|{}^2 \, \mathrm{d}\pi_n(x,y)} <\infty; \end{aligned}$
(unique limit ) the optimal π ∈ Π(μ, ν) is unique.

We further denote the subgradients ∂ϕ _nand ∂ϕ by u _nand u, respectively.

These assumptions imply that π has a finite total cost. This can be shown by the $\liminf$ argument in the proof of Theorem 1.7.2 but also from the uniqueness of π. As a corollary of the uniqueness of π, it follows that π _n → π weakly; notice that this holds even if π _n is not unique for any n. We will now translate this weak convergence to convergence of the maximal monotone maps u _n to u, in the following form.

Proposition 1.7.11 (Uniform Convergence of Optimal Maps)

Let Assumptions 1 hold true and denote E = suppμ and E ^den the set of its Lebesgue points. Let Ω be a compact subset of E ^den on which u is univalued (i.e., u(x) is a singleton for all x ∈ Ω). Then u _n converges to u uniformly on Ω: u _n(x) is nonempty for all x ∈ Ω and all n > N _Ω, and

$\displaystyle \begin{aligned} \sup_{x\in \varOmega}\sup_{y\in u_n(x)} \|y - u(x)\| \to 0 ,\qquad n\to\infty. \end{aligned}$

In particular, if u is univalued throughout int(E) (so that ϕ ∈ C ¹ there), then uniform convergence holds for any compact Ω ⊂int(E).

The proof of Proposition 1.7.11, given on page 28 of the supplement, follows two separate steps:

if a sequence in the graph of u _n converges, then the limit is in the graph of u;
sequences in the graph of u _n are bounded if the domain is bounded.

Corollary 1.7.12 (Pointwise Convergence μ-Almost Surely)

If in addition μ is absolutely continuous, then u _n(x) → u(x) μ-almost surely.

Proof

We first claim that $E\subseteq \overline {\mathrm {dom} u}$ . Indeed, for any x ∈ E and any 𝜖 > 0, the ball B = B _𝜖(x) has positive measure. Consequently, u cannot be empty on the entire ball, because otherwise $\mu (B)=\pi (B\times \mathbb {R}^d)$ would be 0. Since domu is almost convex (see the discussion before Assumptions 1), this implies that actually int(convE) ⊆domu.

The rest is now easy: the set of points x ∈ E for which Ω = {x} fails to satisfy the conditions of Proposition 1.7.11 is included in

$\displaystyle \begin{aligned} (E\setminus E^{\mathrm{den}}) \cup \{x\in \mathrm{int}(\mathrm{conv}(E)):u(x)\mathrm{ contains more than one point}\}, \end{aligned}$

which is μ-negligible because μ is absolutely continuous and both sets have Lebesgue measure 0.

1.8 Complementary Slackness and More General Cost Functions

It is well-known (Luenberger and Ye [89, Section 4.4]) that the solutions to the primal and dual problems are related to each other via complementary slackness. In other words, solution of one problem provides a lot of information about the solution of the other problem. Here, we show that this idea remains true for the Kantorovich primal and dual problems, extending the discussion in Sect. 1.6.1 to more general cost functions.

Let $\mathcal X$ and $\mathcal Y$ be complete separable metric spaces, $\mu \in P(\mathcal X)$ , $\nu \in P(\mathcal Y)$ , and $c:\mathcal X\times \mathcal Y\to \mathbb {R}_+$ be a measurable cost function.

If one finds functions (φ, ψ) ∈ Φ _c and a transference plan π ∈ Π(μ, ν) having the same objective values, then by weak duality (φ, ψ) is optimal in Φ _c and π is optimal in Π(μ, ν). Having the same objective values is equivalent to

$\displaystyle \begin{aligned} {\int_{\mathcal X\times\mathcal Y} \! [c(x,y)-\varphi(x) - \psi(y)] \, \mathrm{d}\pi(x,y)} =0 \end{aligned}$

which is in turn equivalent to

$\displaystyle \begin{aligned} \varphi(x) + \psi(y) =c(x,y), \qquad \pi\mathrm{-almost surely}. \end{aligned}$

It has already been established that there exists an optimal transference plan π ^∗. Assuming that C(π ^∗) < ∞ (otherwise all transference plans are optimal), a pair (φ, ψ) ∈ Φ _c is optimal if and only if

$\displaystyle \begin{aligned} \varphi(x) + \psi(y) =c(x,y), \qquad \pi^*\mathrm{-almost surely}. \end{aligned}$

Conversely, if (φ ₀, ψ ₀) is an optimal pair, then π is optimal if and only if it is concentrated on the set

$\displaystyle \begin{aligned} \{(x,y):\varphi_0(x) + \psi_0(y) = c(x,y)\}. \end{aligned}$

In particular, if for a given x there exists a unique y such that φ ₀(x) + ψ ₀(y) = c(x, y), then the mass at x must be sent entirely to y and not be split; if this is the case for μ-almost all x, then this relation defines y as a function of x and the resulting optimal π is in fact induced from a transport map. This idea provides a criterion for solvability of the Monge problem (Villani [125, Theorem 5.30]).

1.8.1 Unconstrained Dual Kantorovich Problem

It turns out that the dual Kantorovich problem can be recast as an unconstrained optimisation problem of only one function φ. The new formulation is not only conceptually simpler than the original one, but also sheds light on the properties of the optimal dual variables. Since the dual objective function to be maximised,

$\displaystyle \begin{aligned} {{\int_{\mathcal X} \! {\varphi} \, \mathrm{d}{\mu}}} +{{\int_{\mathcal Y} \! {\psi} \, \mathrm{d}{\nu}}},\end{aligned}$

is increasing in φ and ψ, one should seek functions that take values as large as possible subject to the constraint φ(x) + ψ(y) ≤ c(x, y). Suppose that an oracle tells us that some φ ∈ L ₁(μ) is a good candidate. Then the largest possible ψ satisfying (φ, ψ) ∈ Φ _c is defined as

$\displaystyle \begin{aligned} \psi(y) =\inf_{x\in\mathcal X}[c(x,y) - \varphi(x)] :=\varphi^c(y).\end{aligned}$

A function taking this form is called c-concave [124, Chapter 2]; we say that ψ is the c-transform of φ. It is not necessarily true that φ ^c is integrable or even measurable, but if we neglect this difficulty, then it is obvious that

$\displaystyle \begin{aligned} \sup_{\psi\in L_1(\nu):(\varphi,\psi)\in\varPhi_c} \left[{{\int_{\mathcal X} \! {\varphi} \, \mathrm{d}{\mu}}} +{{\int_{\mathcal Y} \! {\psi} \, \mathrm{d}{\nu}}}\right] ={{\int_{\mathcal X} \! {\varphi} \, \mathrm{d}{\mu}}} +{{\int_{\mathcal Y} \! {\varphi^c} \, \mathrm{d}{\nu}}}.\end{aligned}$

The dual problem can thus be formulated as the unconstrained problem

$\displaystyle \begin{aligned} \sup_{\varphi\in L_1(\mu)} \left[{{\int_{\mathcal X} \! {\varphi} \, \mathrm{d}{\mu}}} +{{\int_{\mathcal Y} \! {\varphi^c} \, \mathrm{d}{\nu}}}\right].\end{aligned}$

One can apply this c-transform again and replace φ by

$\displaystyle \begin{aligned} \varphi^{cc}(x) =(\varphi^c)^c(x) =\inf_{y\in\mathcal Y}[c(x,y) - \varphi^c(y)] \ge \varphi(x), \end{aligned}$

so that φ ^cc has a better objective value yet still (φ ^cc, φ ^c) ∈ Φ _c (modulo measurability issues). An elementary calculation shows that in general φ ^ccc = φ ^c. Thus, for any function φ ₁, the pair of functions $(\varphi ,\psi )=(\varphi _1^{cc},\varphi _1^{c})$ has a better objective value than (φ ₁, ψ ₁), and satisfies (φ, ψ) ∈ Φ _c. Moreover, φ ^c = ψ and ψ ^c = φ; in words, φ and ψ are c-conjugate. An optimal dual pair (φ, ψ) can be expected to be c-conjugate; this is indeed true almost surely:

Proposition 1.8.1 (Existence of an Optimal Pair)

Let μ and ν be probability measures on $\mathcal X$ and $\mathcal Y$ such that the independent coupling with respect to the nonnegative and lower semicontinuous cost function is finite: $\int _{\mathcal X\times \mathcal Y} \! c(x,y) \, \mathrm {d}\mu (x)\mathrm {d}\nu (y)<\infty$ . Then there exists an optimal pair (φ, ψ) for the dual Kantorovich problem. Furthermore, the pair can be chosen in a way that μ-almost surely, φ = ψ ^c and ν-almost surely, ψ = φ ^c.

Proposition 1.8.1 is established (under weaker conditions) by Ambrosio and Pratelli [11, Theorem 3.2]. It is clear from the discussion above that once existence of an optimal pair (φ ₁, ψ ₁) is established, the pair $(\varphi ,\psi )=(\varphi _1^{cc},\varphi ^c_1)$ should be optimal. Combining Proposition 1.8.1 with the preceding subsection, we see that if φ is optimal (for the unconstrained dual problem), then any optimal transference plan π ^∗ must be concentrated on the set

$\displaystyle \begin{aligned} \{(x,y):\varphi(x) + \varphi^c(y) = c(x,y)\}. \end{aligned}$

If for μ-almost every x this equation defines y uniquely as a (measurable) function of x, then π ^∗ is induced by a transport map. Indeed, we have seen how this is the case, in the quadratic case c(x, y) = ∥x − y∥²∕2, when μ is absolutely continuous. An extension to p > 1 (instead of p = 2) is sketched in Sect. 1.8.3.

We remark that at the level of generality of Proposition 1.8.1, the function φ ^c may fail to be Borel measurable; Ambrosio and Pratelli show that this pair can be modified up to null sets in order to be Borel measurable. If c is continuous, however, then φ ^c is an infimum of a collection of continuous functions (in y). Hence − φ ^c is lower semicontinuous, which yields that φ ^c is measurable. When c is uniformly continuous, measurability of φ ^c is established in a more lucid way, as exemplified in the next subsection.

1.8.2 The Kantorovich–Rubinstein Theorem

Whether φ ^c(y) is tractable to evaluate depends on the structure of c. We have seen an example where c was the quadratic Euclidean distance. Here, we shall consider another useful case, where c is a metric. Assume that $\mathcal X=\mathcal Y$ , denote their metric by d, and let c(x, y) = d(x, y). If φ = ψ ^c is c-concave, then it is 1-Lipschitz. Indeed, by definition and the triangle inequality

$\displaystyle \begin{aligned} \varphi(z) =\inf_{y\in\mathcal Y} [d(z,y) - \psi(y)] \le \inf_{y\in\mathcal Y} [d(x,y) + d(x,z) - \psi(y)] =\varphi(x) + d(x,z). \end{aligned}$

Interchanging x and z yields |φ(x) − φ(z)|≤ d(x, z).³

Next, we claim that if φ is Lipschitz, then φ ^c(y) = −φ(y). Indeed, choosing x = y in the infimum shows that φ ^c(y) ≤ d(y, y) − φ(y) = −φ(y). But the Lipschitz condition on φ implies that for all x, d(x, y) − φ(x) ≥−φ(y). In view of that, we can take in the dual problem φ to be Lipschitz and ψ = −φ, and the duality formula (Theorem 1.4.2) takes the form

$\displaystyle \begin{aligned} \begin{array}{rcl} \inf_{\pi\in\varPi(\mu,\nu)} {\int_{\mathcal X^2} \! d(x,y) \, \mathrm{d}\pi(x,y)} &\displaystyle =&\displaystyle \sup_{\|\varphi\|{}_{\mathrm{Lip}}\le1} \left|{{\int_{\mathcal X} \! {\varphi} \, \mathrm{d}\mu}} -{{\int_{\mathcal X} \! {\varphi} \, \mathrm{d}\nu}}\right| , \\ \|\varphi\|{}_{\mathrm{Lip}}&\displaystyle =&\displaystyle \sup_{x\ne y}\frac{|\varphi(x) - \varphi(y)|}{d(x,y)}.{} \end{array} \end{aligned}$

(1.11)

This is known as the Kantorovich–Rubinstein theorem [124, Theorem 1.14]. (We have been a bit sloppy because φ may not be integrable. But if for some $x_0\in \mathcal X$ , x↦d(x, x ₀) is in L ₁(μ), then any Lipschitz function is μ-integrable. Otherwise one needs to restrict the supremum to, e.g., bounded Lipschitz φ.)

1.8.3 Strictly Convex Cost Functions on Euclidean Spaces

We now return to the Euclidean case $\mathcal X=\mathcal Y=\mathbb {R}^d$ and explore the structure of c-transforms. When c is different than ∥x − y∥²∕2, we can no longer “open up the square” and relate the Monge–Kantorovich problem to convexity. However, we can still apply the idea that φ(x) + φ ^c(y) = c(x, y) if and only if the infimum is attained at x. Indeed, recall that

$\displaystyle \begin{aligned} \varphi^c(y) =\inf_{x\in\mathcal X}[c(x, y) - \varphi(x)], \end{aligned}$

so that φ(x) + φ ^c(y) = c(x, y) if and only if

$\displaystyle \begin{aligned} \varphi(z) - \varphi(x) \le c(z,y) - c(x,y), \qquad z\in\mathcal X. \end{aligned}$

Notice the similarity to the subgradient inequality for convex functions, with the sign being reversed. In analogy, we call the collection of y’s satisfying the above in equality the c-superdifferential of φ at x, and we denote it by ∂ ^cφ(x). Of course, if c(x, y) = ∥x − y∥²∕2, then y ∈ ∂ ^c(x) if and only if y is a subgradient of (∥⋅∥²∕2 − φ) at x.

The following result generalises Theorem 1.6.2 to other powers p > 1 of the Euclidean norm. These cost functions define the Wasserstein distances of the next chapter.

Theorem 1.8.2 (Strictly Convex Costs on $\mathbb {R}^d$ )

Let c(x, y) = h(x − y) with h(v) = ∥v∥^p∕p for some p > 1 and let μ and ν be probability measures on $\mathbb {R}^d$ with finite p-th moments such that μ is absolutely continuous with respect to Lebesgue measure. Then the solution to the Kantorovich problem with cost function c is unique and induced from a transport map T. Furthermore, there exists an optimal pair (φ, φ ^c) of the dual problem, with φ c-concave. The solutions are related by

$\displaystyle \begin{aligned} T(x) = x - \nabla\varphi(x)\|\nabla\varphi(x)\|{}^{1/(p-1)-1} \qquad (\mu\mathrm{-almost surely}). \end{aligned}$

Proof (Assuming ν has Compact Support)

The existence of the optimal pair (φ, φ ^c) with the desired properties follows from Proposition 1.8.1 (they are Borel measurable because c is continuous). We shall now show that φ has a unique c-supergradient μ-almost surely.

Step 1: φ is c-superdifferentiable. Let π ^∗ be an optimal coupling. By duality arguments, π is concentrated on the set of (x, y) such that y ∈ ∂ ^cφ(x). Consequently, for μ-almost any x, the c-superdifferential of φ at x is nonempty.

Step 2: φ is differentiable. Here, we impose the additional condition that ν is compactly supported. Then φ can be taken as a c-transform on the compact support of ν. Since h is locally Lipschitz (it is C ¹ because p > 1) this implies that φ is locally Lipschitz. Hence, it is differentiable Lebesgue almost surely, and consequently μ-almost surely.

Step 3: Conclusion. For μ-almost every x there exists y ∈ ∂ ^cφ(x) and a gradient u = ∇φ(x). In particular, u is a subgradient of φ:

$\displaystyle \begin{aligned} \varphi(z) - \varphi(x)\ge {\left\langle {u},{z-x}\right\rangle} + o(\|z-x\|). \end{aligned}$

Here and more generally, o(∥z − x∥) denotes a function r(z) (defined in a neighbourhood of x) such that r(z)∕∥z − x∥→ 0 as z → x. (If φ were convex, then we could take r ≡ 0, so the definition for convex functions is equivalent, and then the inequality holds globally and not only locally.) But y ∈ ∂ ^cφ(x) means that as z → x,

$\displaystyle \begin{aligned} h(z-y) - h(x - y) =c(z,y) - c(x,y) \ge \varphi(z) - \varphi(x) \ge \left\langle {u},{z-x}\right\rangle + o(\|z-x\|) . \end{aligned}$

In other words, u is a subgradient of h at x − y. But h is differentiable with gradient ∇h(v) = v∥v∥^p−2 (zero if v = 0). We obtain ∇φ(x) = u = ∇h(x − y) and since the gradient of h is invertible, we conclude

$\displaystyle \begin{aligned} y = T(x) := x- (\nabla h)^{-1}[\nabla\varphi(x)], \end{aligned}$

which defines y as a (measurable) function of x.⁴ Hence, the optimal transference plan π is unique and induced from the transport map T.

The general result, without assuming compact support for ν, can be found in Gangbo and McCann [59]. It holds for a larger class of functions h, those that are strictly convex on $\mathbb {R}^d$ (this yields that ∇h is invertible), have superlinear growth (h(v)∕∥v∥→∞ as v →∞) and satisfying a technical geometric condition (which ∥v∥^p∕p does when p > 1). Furthermore, if h is sufficiently smooth, namely h ∈ C ^{1, 1} locally (it is if p ≥ 2, but not if p ∈ (1, 2)), then μ does not need to be absolutely continuous; it suffices that it not give positive measure to any set of Hausdorff dimension smaller or equal than d − 1. When d = 1 this means that Theorem 1.8.2 is still valid as long as μ has no atoms (μ({x}) = 0 for all $x\in \mathbb {R}$ ), which is a weaker condition than μ being absolutely continuous.

It is also noteworthy that for strictly concave cost functions (e.g., p ∈ (0, 1)), the situation is similar when the supports of μ and ν are disjoint. The reason is that h may fail to be differentiable at 0, but it only needs to be differentiated at x − y with x ∈suppμ and y ∈suppν. If the supports are not disjoint, then one needs to leave all common mass in place until the supports become disjoint (Villani [124, Chapter 2]) and then the result of [59] applies. As a simple example, let μ be uniform on [0, 1] and ν be uniform on [0, 2]. After leaving common mass in place, we are left with uniforms on [0, 1] and [1, 2] (with total mass 1∕2) with essentially disjoint supports, for which the optimal transport map is the decreasing map T(x) = 2 − x. Thus, the unique optimal π is not induced from a map, but rather from an equal weight mixture of T and the identity. Informally, each point x in the support of μ needs to be split; half stays and x and the other half transported to 2 − x. The optimal coupling from ν to μ is unique and induced from the map S(x) = x if x ≤ 1 and 2 − x if x ≥ 1, which is neither increasing nor decreasing.

1.9 Bibliographical Notes

Many authors, including Villani [124, Theorem 1.3]; [125, Theorem 5.10], give the duality Theorem 1.4.2 for lower semicontinuous cost functions. The version given here is a simplification of Beiglböck and Schachermayer [17, Theorem 1]. The duality holds for functions that take values in [−∞, ∞] provided that they are finite on a sufficiently large subset of $\mathcal X\times \mathcal Y$ , but there are simple counterexamples if c is infinite too often [17, Example 4.1]. For results outside the Polish space setup, see Kellerer [80] and Rachev and Rüschendorf [107, Chapter 4].

Theorem 1.5.1 for the one-dimensional case is taken from [124], where it is proven using the general duality theorem. For direct proofs and the history of this result, one may consult Rachev [106] or Rachev and Rüschendorf [107, Section 3.1]. The concave case is carefully treated by McCann [94].

The results in the Gaussian case were obtained independently by Olkin and Pukelsheim [98] and Givens and Shortt [65]. The proof given here is from Bhatia [20, Exercise 1.2.13]. An extension to separable Hilbert spaces can be found in Gelbrich [62] or Cuesta-Albertos et al. [39].

The regularity theory of Sect. 1.6.4 is very delicate. Caffarelli [32] showed the first part of Theorem 1.6.7; the proof can also be found in Figalli’s book [52, Theorem 4.23]. Villani [124, Theorem 4.14] states the result without proof and refers to Alesker et al. [7] for a sketch of the second part of Theorem 1.6.7. Other regularity results exist, Villani [125, Chapter 12]; Santambrogio [119, Section 1.7.6]; Figalli [52].

Cuesta-Albertos et al. [40, Theorem 3.2] prove Theorem 1.7.2 for the quadratic case; the form given here is from Schachermayer and Teichmann [120, Theorem 3].

The definition of cyclical monotonicity depends on the cost function. It is typically referred to as c-cyclical monotonicity, with “cyclical monotonicity” reserved to the special case of quadratic cost. Since we focus on the quadratic case and for readability, we slightly deviate from the standard jargon. That cyclical monotonicity implies optimality (Proposition 1.7.5) was shown independently by Pratelli [105] (finite lower semicontinuous cost) and Schachermayer and Teichmann [120] (possibly infinite continuous cost). A joint generalisation is given by Beiglböck et al. [18].

Section 1.7.2 is taken from Zemel and Panaretos [134, Section 7.5]; a slightly weaker version was shown independently by Chernozhukov et al. [35]. Heinich and Lootgieter [68] establish almost sure pointwise convergence. If μ _n = μ, then the optimal maps converge in μ-measure [125, Corollary 5.23] in a very general setup, but there are simple examples where this fails if μ _n≠μ [125, Remark 5.25]. In the quadratic case, further stability results of a weaker flavour (focussing on the convex potential ϕ, rather than its derivative, which is the optimal map) can be found in del Barrio and Loubes [42].

The idea of using the c-transform (Sect. 1.8) is from Rüschendorf [116].

Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.

The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.

References

6.
G. Alberti, L. Ambrosio, A geometrical approach to monotone functions in $\mathbb R^n$ . Math. Z. 230(2), 259–316 (1999)
7.
S. Alesker, S. Dar, V. Milman, A remarkable measure preserving diffeomorphism between two convex bodies in $\mathbb R^n$ . Geometriae Dedicata 74(2), 201–212 (1999)
10.
L. Ambrosio, N. Gigli, A user’s guide to optimal transport, in Modelling and Optimisation of Flows on Networks (Springer, Berlin, 2013), pp. 1–155
11.
L. Ambrosio, A. Pratelli, Existence and stability results in the L ¹-theory of optimal transportation, in Optimal Transportation and Applications (Springer, Berlin, 2003), pp. 123–160
12.
L. Ambrosio, N. Gigli, G. Savaré, Gradient Flows in Metric Spaces and in the Space of Probability Measures. Lectures in Mathematics. ETH Zürich, 2nd edn. (Springer, Berlin, 2008)
13.
Y. Amit, U. Grenander, M. Piccioni, Structural image restoration through deformable templates. J. Amer. Stat. Assoc. 86(414), 376–387 (1991)
17.
M. Beiglböck, W. Schachermayer, Duality for Borel measurable cost functions. Trans. Amer. Math. Soc. 363(8), 4203–4224 (2011)
18.
M. Beiglböck, M. Goldstern, G. Maresch, W. Schachermayer, Optimal and better transport plans. J. Func. Anal. 256(6), 1907–1927 (2009)
20.
R. Bhatia, Positive Definite Matrices (Princeton University Press, Princeton, 2009)
24.
P. Billingsley, Convergence of Probability Measures, 2nd edn. (Wiley, New York, 1999)
31.
Y. Brenier, Polar factorization and monotone rearrangement of vector-valued functions. Commun. Pure Appl. Math. 44(4), 375–417 (1991)
32.
L.A. Caffarelli, The regularity of mappings with a convex potential. J. Amer. Math. Soc. 5(1), 99–104 (1992)
35.
V. Chernozhukov, A. Galichon, M. Hallin, M. Henry, Monge–Kantorovich depth, quantiles, ranks and signs. Ann. Stat. 45(1), 223–256 (2017)
37.
J.A. Cuesta-Albertos, C. Matrán, Notes on the Wasserstein metric in Hilbert spaces. Ann. Probab. 17(3), 1264–1276 (1989)
39.
J.A. Cuesta-Albertos, C. Matrán-Bea, A. Tuero-Diaz, On lower bounds for the L ₂-Wasserstein metric in a Hilbert space. J. Theor. Probab. 9(2), 263–283 (1996)
40.
J.A. Cuesta-Albertos, C. Matrán, A. Tuero-Diaz, Optimal transportation plans and convergence in distribution. J. Multivar. Anal. 60(1), 72–83 (1997)
42.
E. del Barrio, J.-M. Loubes, Central limit theorems for empirical transportation cost in general dimension. Ann. Probab. 47(2), 926–951 (2019). https://projecteuclid.org/euclid.aop/1551171641
47.
R.M. Dudley, Real Analysis and Probability, vol. 74 (Cambridge University Press, Cambridge, 2002)
50.
J. Edmonds, R.M. Karp, Theoretical improvements in algorithmic efficiency for network flow problems. J. ACM 19(2), 248–264 (1972)
52.
A. Figalli, The Monge–Ampère Equation and Its Applications (European Mathematical Society, Zürich, 2017)
59.
W. Gangbo, R.J. McCann, The geometry of optimal transportation. Acta Math. 177(2), 113–161 (1996)
62.
M. Gelbrich, On a formula for the L ₂-Wasserstein metric between measures on Euclidean and Hilbert spaces. Math. Nachr. 147(1), 185–203 (1990)
65.
C.R. Givens, R.M. Shortt, A class of Wasserstein metrics for probability distributions. Mich. Math. J. 31(2), 231–240 (1984)
68.
H. Heinich, J.-C. Lootgieter, Convergence des fonctions monotones. C. R. Acad. Sci. ser. 1 Mathé 322(9), 869–874 (1996)
76.
O. Kallenberg, Foundations of Modern Probability (Springer, Berlin, 1997)
77.
L.V. Kantorovich, On the translocation of masses. (Dokl.) Acad. Sci. URSS 37(3), 199–201 (1942)
80.
H.G. Kellerer, Duality theorems for marginal problems. Zeitschrift für Wahrscheinlichkeitstheorie und verwandte Gebiete 67(4), 399–432 (1984)
83.
M. Knott, C.S. Smith, On the optimal mapping of distributions. J. Optim. Theory Appl. 43(1), 39–49 (1984)
85.
H.W. Kuhn, The Hungarian method for the assignment problem. Nav. Res. Log. Quart. 2, 83–97 (1955)
89.
D.G. Luenberger, Y. Ye, Linear and Nonlinear Programming (Springer, Berlin, 2008)
94.
R.J. McCann, Exact solutions to the transportation problem on the line. Proc. R. Soc. London, Ser. A: Math. Phys. Eng. Sci. 455(1984), 1341–1380 (1999)
95.
G. Monge, Mémoire sur la théorie des déblais et des remblais. Histoire de l’Académie R. des Sci. de Paris 177, 666–704 (1781)
96.
J. Munkers, Algorithms for the assignment and transportation problems. J. Soc. Indust. Appl. Math. 5, 32–38 (1957)
98.
I. Olkin, F. Pukelsheim, The distance between two random vectors with given dispersion matrices. Linear Algebra Appl. 48, 257–263 (1982)
103.
G. Peyré, M. Cuturi, Computational optimal transport. Found. Trends Mach. Learn. 11(5–6), 355–607 (2019). https://www.nowpublishers.com/article/Details/MAL-073
104.
D. Pollard. Convergence of Stochastic Processes (Springer, Berlin, 2012)
105.
A. Pratelli, On the sufficiency of c-cyclical monotonicity for optimality of transport plans. Mathe. Zeitschrift 258(3), 677–690 (2008)
106.
S.T. Rachev, The Monge–Kantorovich mass transference problem and its stochastic applications. Theory Probab. Appl. 29(4), 647–676 (1985)
107.
S.T. Rachev, L. Rüschendorf, Mass Transportation Problems: Volume I: Theory, Volume II: Applications (Springer, Berlin, 1998)
112.
R.T. Rockafellar, Characterization of the subdifferentials of convex functions. Pac. J. Math. 17(3), 497–510 (1966)
113.
R.T. Rockafellar, Convex Analysis (Princeton University Press, Princeton, 1970)
116.
L. Rüschendorf, On c-optimal random variables. Stat. Probab. Lett. 27(3), 267–270 (1996)
117.
L. Rüschendorf, S.T. Rachev, A characterization of random variables with minimum L ²-distance. J. Multivar. Anal. 32(1), 48–54 (1990)
119.
F. Santambrogio, Optimal Transport for Applied Mathematicians, vol. 87 (Springer, Berlin, 2015)
120.
W. Schachermayer, J. Teichmann, Characterization of optimal transport plans for the Monge–Kantorovich problem. Proc. Amer. Math. Soc. 137(2), 519–529 (2009)
121.
E.M. Stein, R. Shakarchi, Real Analysis: Measure Theory, Integration & Hilbert Spaces. (Princeton University Press, Princeton, 2005)
124.
C. Villani, Topics in Optimal Transportation (American Mathematical Society, Providence, 2003)
125.
C. Villani, Optimal Transport: Old and New (Springer, Berlin, 2008)
134.
Y. Zemel, V.M. Panaretos, Fréchet means and Procrustes analysis in Wasserstein space. Bernoulli 25(2), 932–976 (2019)