Why is it relevant to construct the Fréchet mean of a collection of measures with respect to the Wasserstein metric? A simple answer is that this kind of average will often express a more natural notion of “typical” realisation of a random probability distribution than an arithmetic average.1 Much more can be said, however, in that the Wasserstein–Fréchet mean and the closely related notion of an optimal multicoupling arise canonically as the appropriate framework for the formulation and solution to the problem of separation of amplitude and phase variation of a point process. It would almost seem that Wasserstein–Fréchet means were “made” for precisely this problem.
Amplitude variation. This is the “classical” variation that one would also encounter in multivariate analysis, and refers to the stochastic fluctuations around a mean level, usually encoded in the covariance kernel, at least up to second order.
In short, this is variation “in the y-axis” (ordinate).
Phase variation. This is a second layer of non-linear variation peculiar to continuous domain stochastic processes, and is rarely—if ever—encountered in multivariate analysis. It arises as the result of random changes (or deformations) in the time scale (or the spatial domain) of definition of the process. It can be conceptualised as a composition of the stochastic process with a random transformation (warp map) acting on its domain.
This is variation “in the x-axis” (abscissa).
Phase variation naturally arises in the study of random phenomena where there is no absolute notion of time or space, but every realisation of the phenomenon evolves according to a time scale that is intrinsic to the phenomenon itself, and (unfortunately) unobservable. Processes related to physiological measurements, such as growth curves and neuronal signals, are usual suspects. Growth curves can be modelled as continuous random functions (functional data), whereas neuronal signals are better modelled as discrete random measures (point processes). We first describe amplitude/phase variation in the former2 case, as that is easier to appreciate, before moving on to the latter case, which is the main subject of this chapter.
4.1 Amplitude and Phase Variation
4.1.1 The Functional Case
Let K denote the unit cube ![$$[0,1]^d\subset \mathbb {R}^d$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_IEq3.png) . A real random function Y = (Y (x) : x ∈ K) can, broadly speaking, have two types of variation. The first, amplitude variation, results from Y (x) being a random variable for every x and describes its fluctuations around the mean level
. A real random function Y = (Y (x) : x ∈ K) can, broadly speaking, have two types of variation. The first, amplitude variation, results from Y (x) being a random variable for every x and describes its fluctuations around the mean level  , usually encoded by the variance varY (x). For this reason, it can be referred to as “variation in the y-axis”. More generally, for any finite set x
1, …, x
n, the n × n covariance matrix with entries κ(x
i, x
j) = cov[Y (x
i), Y (x
j)] encapsulates (up to second order) the stochastic deviations of the random vector (Y (x
1), …, Y (x
n)) from its mean, in analogy with the multivariate case. Heuristically, one then views amplitude variation as the collection κ(x, y) for x, y ∈ K in a sense we discuss next.
, usually encoded by the variance varY (x). For this reason, it can be referred to as “variation in the y-axis”. More generally, for any finite set x
1, …, x
n, the n × n covariance matrix with entries κ(x
i, x
j) = cov[Y (x
i), Y (x
j)] encapsulates (up to second order) the stochastic deviations of the random vector (Y (x
1), …, Y (x
n)) from its mean, in analogy with the multivariate case. Heuristically, one then views amplitude variation as the collection κ(x, y) for x, y ∈ K in a sense we discuss next.
 and continuous sample paths, so that in particular Y (x) is a random variable for all x ∈ K. Then the mean function
and continuous sample paths, so that in particular Y (x) is a random variable for all x ∈ K. Then the mean function 
![$$\displaystyle \begin{aligned} \kappa(x,y)={\mathrm{cov}}[Y(x),Y(y)], \quad x,y\in K \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equb.png)
![$$\displaystyle \begin{aligned} \mathbb{E} [Y(y) - Y(x)]^2 \to0, \qquad y\to x. \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equc.png)
 , defined by
, defined by 
![$$\displaystyle \begin{aligned} \mathbb{E}{\left\langle {Y},{f}\right\rangle} {\left\langle {Y},{g}\right\rangle} =\mathbb{E}\left[{\int_{K^2} \! Y(x)f(x)Y(y)g(y) \, \mathrm{d}(x,y)}\right] ={{\int_{K} \! {g(y)(\mathcal Rf)(y)} \, \mathrm{d}y}} , \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Eque.png)
![$$\displaystyle \begin{aligned} {\mathrm{cov}}\left[{\left\langle {Y},{f}\right\rangle} , {\left\langle {Y},{g}\right\rangle} \right] ={{\int_{K} \! {g(y)(\mathcal Rf)(y)} \, \mathrm{d}y}} ={\left\langle {g},{\mathcal Rf}\right\rangle} . \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equf.png)
 such that
such that 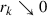 ,
,  and (ϕ
k) is an orthonormal basis of L
2(K). One then has the celebrated Karhunen–Loève expansion
and (ϕ
k) is an orthonormal basis of L
2(K). One then has the celebrated Karhunen–Loève expansion 
 is making ξ
k uncorrelated:
is making ξ
k uncorrelated: ![$$\displaystyle \begin{aligned} {\mathrm{cov}}(\xi_k,\xi_l) ={\mathrm{cov}}\left[{\left\langle {Y},{\phi_k}\right\rangle} , {\left\langle {Y},{\phi_l}\right\rangle} \right] =\left\langle {\phi_l},{\mathcal R\phi_k}\right\rangle \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equh.png)


 decay.
decay.

 and its eigendecomposition.
and its eigendecomposition.
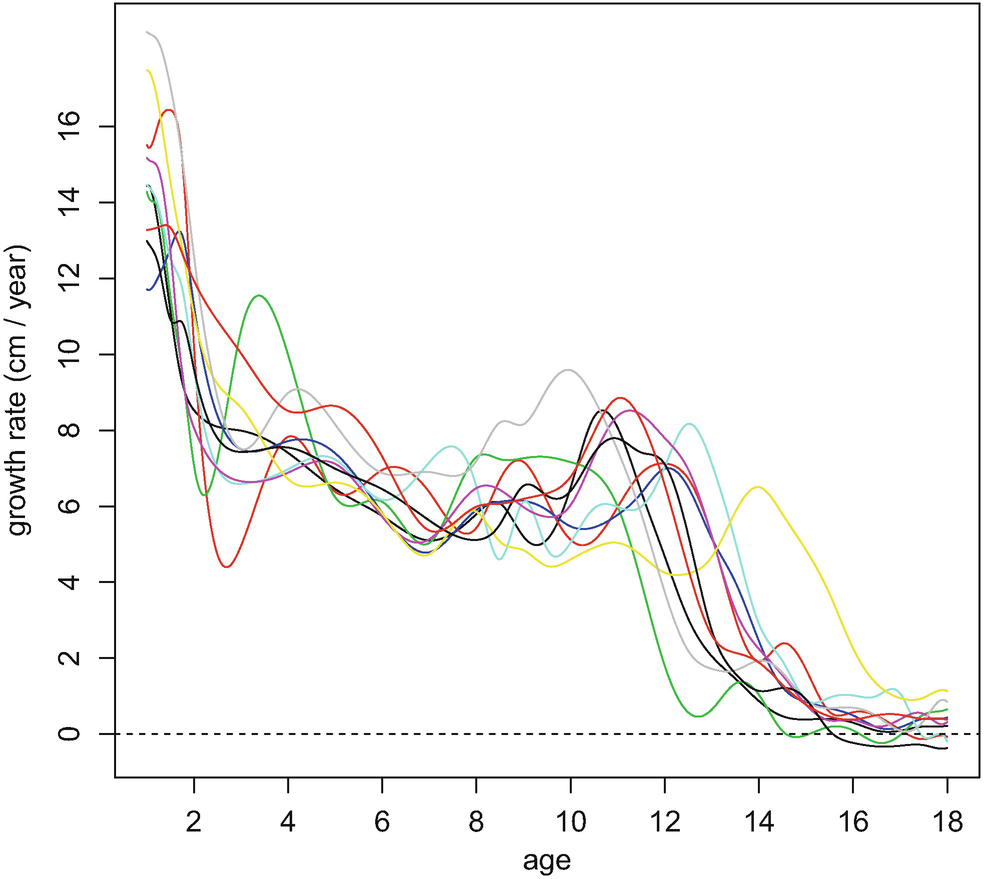
Derivatives of growth curves of ten girls from the Berkeley dataset. The data and the code for the figure are from the R package fda (Ramsay et al. [111])
![$$\displaystyle \begin{aligned} \tilde Y(x) =A\sin[8\pi(x + B)]. \end{aligned} $$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equ1.png)
 .) The random variable A generates the amplitude variation, while B represents the phase variation. In Fig. 4.2, we plot four realisations and the resulting empirical means for the two extreme scenarios where B = 0 (no phase variation) or A = 1 (no amplitude variation). In the left panel of the figure, we see that the sample mean (in thick blue) lies between the observations and has a similar form, so can be viewed as the curve representing the typical realisation of the random curve. This is in contrast to the right panel, where the mean is qualitatively different from all curves in the sample: though periodicity is still present, the peaks and troughs have been flattened, and the sample mean is much more diffuse than any of the observations.
.) The random variable A generates the amplitude variation, while B represents the phase variation. In Fig. 4.2, we plot four realisations and the resulting empirical means for the two extreme scenarios where B = 0 (no phase variation) or A = 1 (no amplitude variation). In the left panel of the figure, we see that the sample mean (in thick blue) lies between the observations and has a similar form, so can be viewed as the curve representing the typical realisation of the random curve. This is in contrast to the right panel, where the mean is qualitatively different from all curves in the sample: though periodicity is still present, the peaks and troughs have been flattened, and the sample mean is much more diffuse than any of the observations.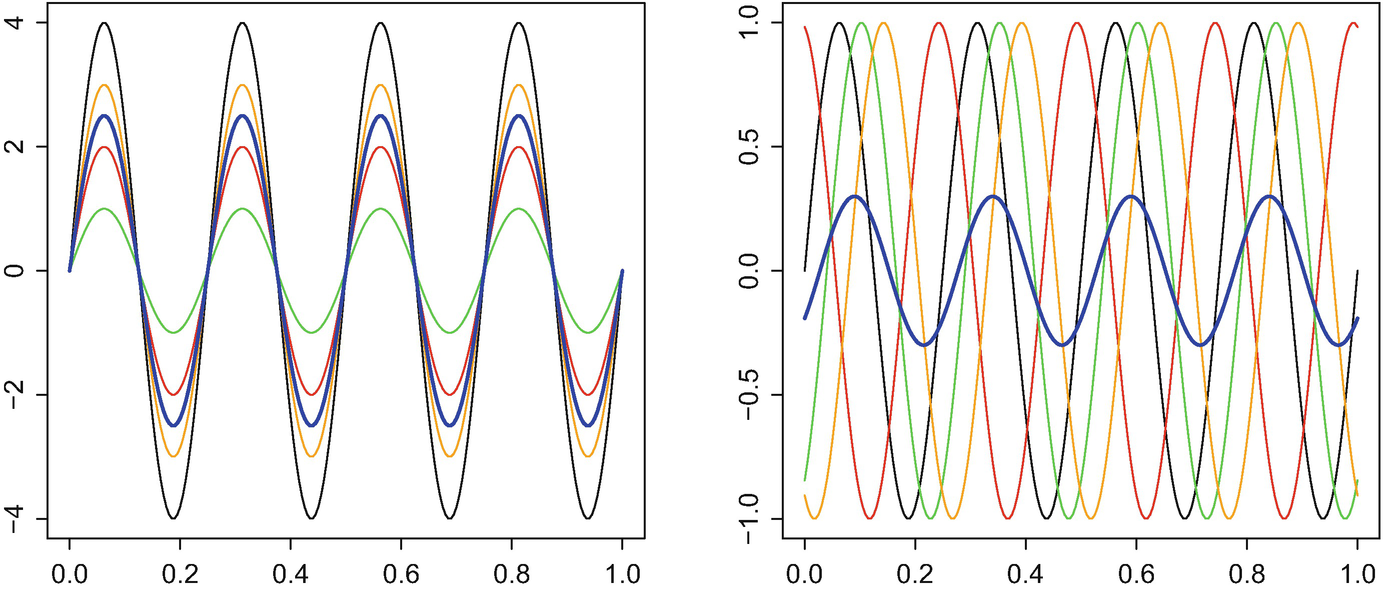
Four realisations of (4.1) with means in thick blue. Left: amplitude variation (B = 0); right: phase variation (A = 1)
![$$\displaystyle \begin{aligned} \mathbb{E} \tilde Y(x) =\sin (8\pi x) \mathbb{E} [\cos (8\pi B)] +\cos (8\pi x) \mathbb{E} [\sin (8\pi B)]. \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equn.png)
 is the original function
is the original function  multiplied by a constant of magnitude strictly less than one, resulting in peaks of smaller magnitude.
multiplied by a constant of magnitude strictly less than one, resulting in peaks of smaller magnitude. and Y and T are independent, we have
and Y and T are independent, we have ![$$\displaystyle \begin{aligned} \mathbb{E}\tilde Y(x) =\mathbb{E} [m(T^{-1}(x))] \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equo.png)
![$$\displaystyle \begin{aligned} {\mathrm{cov}}[\tilde Y(x),\tilde Y(y)] =\mathbb{E} [\kappa(T^{-1}(x),T^{-1}(y))] + {\mathrm{cov}}[m(T^{-1}(x),m(T^{-1}(y))]. \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equp.png)
 be the conditional mean function given T. Then the value of the mean function itself,
be the conditional mean function given T. Then the value of the mean function itself,  , at x
0 is determined not by a single point, say x, but rather by all the values of m at the possible outcomes of T
−1(x). In particular, if x
0 was a local maximum for m, then
, at x
0 is determined not by a single point, say x, but rather by all the values of m at the possible outcomes of T
−1(x). In particular, if x
0 was a local maximum for m, then ![$$\mathbb {E} [\tilde \mu (x_0)]$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_IEq19.png) will typically be strictly smaller than m(x
0); the phase variation results in smearing m.
will typically be strictly smaller than m(x
0); the phase variation results in smearing m. , then the standard empirical estimators will be consistent, since
, then the standard empirical estimators will be consistent, since  itself is a random function. But if it is rather m, the mean of Y , that is of interest, then the confounding of the amplitude and phase variation will lead to inconsistency. This can also be seen from the formula
itself is a random function. But if it is rather m, the mean of Y , that is of interest, then the confounding of the amplitude and phase variation will lead to inconsistency. This can also be seen from the formula 
 ; the simplest way to notice this is the observation that ϕ
k(T
−1(x)) includes both the functional component ϕ
k and the random component T
−1(x). The true Karhunen–Loève expansion of
; the simplest way to notice this is the observation that ϕ
k(T
−1(x)) includes both the functional component ϕ
k and the random component T
−1(x). The true Karhunen–Loève expansion of  will in general be qualitatively very different from that of Y , not only in terms of the mean function but also in terms of the covariance operator and, consequently, its eigenfunctions and eigenvalues. As illustrated in the trigonometric example, the typical situation is that the mean
will in general be qualitatively very different from that of Y , not only in terms of the mean function but also in terms of the covariance operator and, consequently, its eigenfunctions and eigenvalues. As illustrated in the trigonometric example, the typical situation is that the mean  is more diffuse than m, and the decay of the eigenvalues
is more diffuse than m, and the decay of the eigenvalues  of the covariance operator is slower than that of r
k; as a result, one needs to truncate the sum at high threshold in order to capture a substantial enough part of the variability. In the toy example (4.1), the Karhunen–Loève expansion has a single term besides the mean if B = 0, while having two terms if A = 1.
of the covariance operator is slower than that of r
k; as a result, one needs to truncate the sum at high threshold in order to capture a substantial enough part of the variability. In the toy example (4.1), the Karhunen–Loève expansion has a single term besides the mean if B = 0, while having two terms if A = 1. , i = 1, …, n, there is no point in taking pointwise means of
, i = 1, …, n, there is no point in taking pointwise means of  , because the curves are misaligned;
, because the curves are misaligned;  should not be compared with
should not be compared with  , but rather with
, but rather with  . To overcome this difficulty, one seeks estimators
. To overcome this difficulty, one seeks estimators  such that
such that 
 assuming only amplitude variation is now present: estimate the mean m by
assuming only amplitude variation is now present: estimate the mean m by 
There is an obvious identifiability problem in the model  . If S is any (deterministic) invertible function, then the model with (Y, T) is statistically indistinguishable from the model with (Y ∘ S, T ∘ S). It is therefore often assumed that
. If S is any (deterministic) invertible function, then the model with (Y, T) is statistically indistinguishable from the model with (Y ∘ S, T ∘ S). It is therefore often assumed that  is the identity and in addition, in nearly all application, that T is monotonically increasing (if d = 1).
is the identity and in addition, in nearly all application, that T is monotonically increasing (if d = 1).

 , consistent estimators of T
i and of the original, aligned functions Y
i.
, consistent estimators of T
i and of the original, aligned functions Y
i.In the bibliographic notes, we review some methods for carrying out this separation of amplitude and phase variation. It is fair to say that no single registration method arises as the canonical solution to the functional registration problem. Indeed, most need to make additional structural and/or smoothness assumptions on the warp maps, further to the basic identifiability conditions requiring that T be increasing and that  equal the identity. We will eventually see that, in contrast, the case of point processes (viewed as discretely observed random measures) admits a canonical framework, without needing additional assumptions.
equal the identity. We will eventually see that, in contrast, the case of point processes (viewed as discretely observed random measures) admits a canonical framework, without needing additional assumptions.
4.1.2 The Point Process Case
A point process is the mathematical object that represents the intuitive notion of a random collection of points in a space  . It is formally defined as a measurable map Π from a generic probability space into the space of (possibly infinite) Borel integer-valued measures of
. It is formally defined as a measurable map Π from a generic probability space into the space of (possibly infinite) Borel integer-valued measures of  in such a way that Π(B) is a measurable real-valued random variable for all Borel subsets B of
in such a way that Π(B) is a measurable real-valued random variable for all Borel subsets B of  . The quantity Π(B) represents the random number of points observed in the set B. Among the plethora of books on point processes, let us mention Daley and Vere-Jones [41] and Karr [79]. Kallenberg [75] treats more general objects, random measures, of which point processes are a peculiar special case. We will assume for convenience that Π is a measure on a compact subset
. The quantity Π(B) represents the random number of points observed in the set B. Among the plethora of books on point processes, let us mention Daley and Vere-Jones [41] and Karr [79]. Kallenberg [75] treats more general objects, random measures, of which point processes are a peculiar special case. We will assume for convenience that Π is a measure on a compact subset  .
.
![$$\displaystyle \begin{aligned} \lambda(A) =\mathbb{E} [\varPi(A)], \qquad A\subset K \mathrm{ Borel} \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equu.png)
![$$\mathbb {E} [\varPi (K)]^2<\infty $$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_IEq41.png) , the covariance measure
, the covariance measure ![$$\displaystyle \begin{aligned} \kappa(A,B) ={\mathrm{cov}} [\varPi(A),\varPi(B)] =\mathbb{E} [\varPi(A)\varPi(B)] - \lambda(A) \lambda(B), \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equv.png)

 . We refer to Π as the original point processes, and
. We refer to Π as the original point processes, and  as the warped point processes. An example of 30 warped and unwarped point processes is shown in Fig. 4.3. The point patterns in both panels present a qualitatively similar structure: there are two peaks of high concentration of points, while few points appear between these peaks. The difference between the two panels is in the position and concentration of those peaks. In the left panel, only amplitude variation is present, and the location/concentration of the peaks is the same across all observations. In contrast, phase variation results in shifting the peaks to different places for each of the observations, while also smearing or sharpening them. Clearly, estimation of the mean measure of a subset A by averaging the number of observed points in A would not be satisfactory as an estimator of λ when carried out with the warped data. As in the functional case, it will only be consistent for the measure
as the warped point processes. An example of 30 warped and unwarped point processes is shown in Fig. 4.3. The point patterns in both panels present a qualitatively similar structure: there are two peaks of high concentration of points, while few points appear between these peaks. The difference between the two panels is in the position and concentration of those peaks. In the left panel, only amplitude variation is present, and the location/concentration of the peaks is the same across all observations. In contrast, phase variation results in shifting the peaks to different places for each of the observations, while also smearing or sharpening them. Clearly, estimation of the mean measure of a subset A by averaging the number of observed points in A would not be satisfactory as an estimator of λ when carried out with the warped data. As in the functional case, it will only be consistent for the measure  defined by
defined by ![$$\displaystyle \begin{aligned} \tilde\lambda(A) =\mathbb{E} [\lambda(T^{-1}(A))] ,\qquad A\subseteq \mathcal X, \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equx.png)
![$$\tilde \lambda =\mathbb {E} [T\#\lambda ]$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_IEq45.png) misses most (or at least a significant part) of the bimodal structure of λ and is far more diffuse.
misses most (or at least a significant part) of the bimodal structure of λ and is far more diffuse.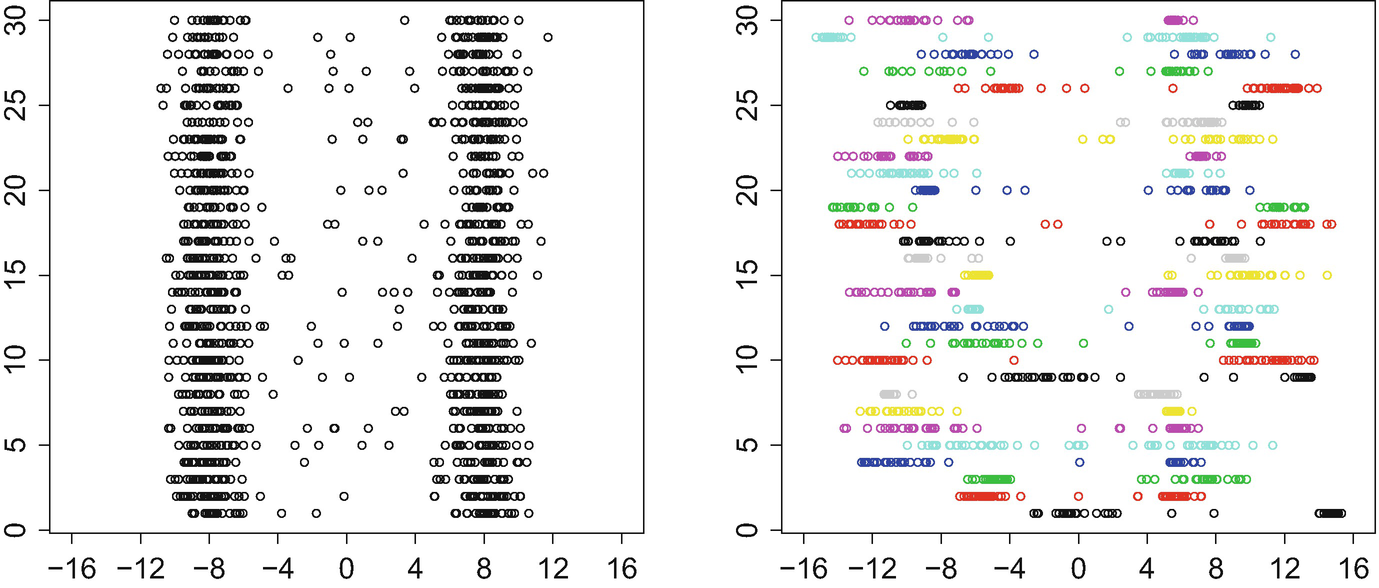
Unwarped (left) and warped Poisson point processes
 given T is
given T is ![$$\displaystyle \begin{aligned} \mathbb{E} [\widetilde\varPi(A)|T] =\mathbb{E} [\varPi(T^{-1}(A))|T] =\lambda(T^{-1}(A)) =[T\#\lambda](A). \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equy.png)
 , find estimators of (T
i) and (Π
i). Registering the point processes amounts to constructing estimators, registration maps
, find estimators of (T
i) and (Π
i). Registering the point processes amounts to constructing estimators, registration maps  , such that the aligned points
, such that the aligned points ![$$\displaystyle \begin{aligned} \widehat{\varPi_i} =\widehat{T_i^{-1}}\# \widetilde \varPi_i =[\widehat{T_i^{-1}}\circ T_i]\# \varPi_i \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equz.png)
![$$\displaystyle \begin{aligned} {\mathbb{P}}(\varPi(A)=k) =e^{-\lambda(A)}\frac{[\lambda(A)]^k}{k!}.\end{aligned} $$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equaa.png)
Conditional upon T, the random variables  , k = 1, …, n are independent as the sets (T
−1(A
k)) are disjoint, and
, k = 1, …, n are independent as the sets (T
−1(A
k)) are disjoint, and  follows a Poisson distribution with mean λ(T
−1(A)) = Λ(A). This is precisely the definition of a Cox process : conditional upon the driving measure Λ,
follows a Poisson distribution with mean λ(T
−1(A)) = Λ(A). This is precisely the definition of a Cox process : conditional upon the driving measure Λ,  is a Poisson process with mean measure λ. For this reason, it is also called a doubly stochastic process ; in our context, the phase variation is associated with the stochasticity of Λ while the amplitude one is associated with the Poisson variation conditional upon Λ.
is a Poisson process with mean measure λ. For this reason, it is also called a doubly stochastic process ; in our context, the phase variation is associated with the stochasticity of Λ while the amplitude one is associated with the Poisson variation conditional upon Λ.
As in the functional case there are problems with identifiability: the model (Π, T) cannot be distinguished from the model (S#Π, T ∘ S
−1) for any invertible S : K → K. It is thus natural to assume that  is the identity map4 (otherwise set
is the identity map4 (otherwise set  , i.e., replace Π by
, i.e., replace Π by ![$$[\mathbb {E} T]\#\varPi $$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_IEq54.png) and T by
and T by ![$$T\circ [\mathbb {E} T]^{-1}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_IEq55.png) ).
).
 to be identifiable. The reason is that given the two point sets
to be identifiable. The reason is that given the two point sets  and Π, there are many functions that push forward the latter to the former. This ambiguity can be dealt with by assuming some sort of regularity or parsimony for T. For example, when K = [a, b] is a subset of the real line, imposing T to be monotonically increasing guarantees its uniqueness. In multiple dimensions, there is no obvious analogue for increasing functions. One possible definition is the monotonicity described in Sect. 1.7.2:
and Π, there are many functions that push forward the latter to the former. This ambiguity can be dealt with by assuming some sort of regularity or parsimony for T. For example, when K = [a, b] is a subset of the real line, imposing T to be monotonically increasing guarantees its uniqueness. In multiple dimensions, there is no obvious analogue for increasing functions. One possible definition is the monotonicity described in Sect. 1.7.2: 
 and write y ≥ x if and only if y
i ≥ x
i for i = 1, 2. It is natural to expect the deformations to maintain the lexicographic order in
and write y ≥ x if and only if y
i ≥ x
i for i = 1, 2. It is natural to expect the deformations to maintain the lexicographic order in  :
: 

 , then ϕ must be convex and T is then cyclically monotone. Consequently, we will make the following assumptions:
, then ϕ must be convex and T is then cyclically monotone. Consequently, we will make the following assumptions: the expected value of T is the identity;
T is a gradient of a convex function.
4.2 Wasserstein Geometry and Phase Variation
4.2.1 Equivariance Properties of the Wasserstein Distance
 for deformations of the space
for deformations of the space  is that for all p ≥ 1 and all
is that for all p ≥ 1 and all  ,
, 
 . This is in contrast to metrics such as the bounded Lipschitz distance (that metrises weak convergence) or the total variation distance on
. This is in contrast to metrics such as the bounded Lipschitz distance (that metrises weak convergence) or the total variation distance on  . Recall that these are defined by
. Recall that these are defined by 

 . This is less so for the bounded Lipschitz distance that does take small distances into account but not large ones.
. This is less so for the bounded Lipschitz distance that does take small distances into account but not large ones. , a be a fixed point in
, a be a fixed point in  , X′ = X + a and Y ′ = Y + a. Joint couplings Z′ = (X′, Y ′) are precisely those that take the form (a, a) + Z for a joint coupling Z = (X, Y ). Thus
, X′ = X + a and Y ′ = Y + a. Joint couplings Z′ = (X′, Y ′) are precisely those that take the form (a, a) + Z for a joint coupling Z = (X, Y ). Thus 
This carries over to Fréchet means in an obvious way.
Let Λ be a random measure in  with finite Fréchet functional and
with finite Fréchet functional and  . Then γ is a Fréchet mean of Λ if and only if γ ∗ δ
a is a Fréchet mean of Λ ∗ δ
a.
. Then γ is a Fréchet mean of Λ if and only if γ ∗ δ
a is a Fréchet mean of Λ ∗ δ
a.
 by
by 
 is infinite-dimensional, this can be defined as the unique element
is infinite-dimensional, this can be defined as the unique element  satisfying
satisfying 
![$$\displaystyle \begin{aligned} W_2^2(\mu\ast\delta_a,\nu) =W_2^2(\mu,\nu) +(a - [m(\mu) - m(\nu)])^2 -[m(\mu) - m(\nu)]^2, \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equak.png)
 with finite Fréchet functional and Fréchet mean γ. Then
with finite Fréchet functional and Fréchet mean γ. Then
![$$\displaystyle \begin{aligned} {{\int_{\mathcal X} \! x \, \mathrm{d}{\gamma(x)}}} =\mathbb{E} \left[ {{\int_{\mathcal X} \! x \, \mathrm{d}{\varLambda(x)}}} \right]. \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equal.png)
4.2.2 Canonicity of Wasserstein Distance in Measuring Phase Variation
The purpose of this subsection is to show that the standard functional data analysis assumptions on the warp function T, having mean identity and being increasing, are equivalent to purely geometric conditions on T and the conditional mean measure Λ = T#λ. Put differently, if one is willing to assume that  and that T is increasing, then one is led unequivocally to the problem of estimation of Fréchet means in the Wasserstein space
and that T is increasing, then one is led unequivocally to the problem of estimation of Fréchet means in the Wasserstein space  . When
. When  , “increasing” is interpreted as being the gradient of a convex function, as explained at the end of Sect. 4.1.2.
, “increasing” is interpreted as being the gradient of a convex function, as explained at the end of Sect. 4.1.2.
The total mass  is invariant under the push-forward operation, and when it is finite, we may assume without loss of generality that it is equal to one, because all the relevant quantities scale with the total mass. Indeed, if λ = τμ with μ probability measure and τ > 0, then T#λ = τ × T#μ, and the Wasserstein distance (defined as the infimum-over-coupling integrated cost) between τμ and τν is τW
p(μ, ν) for μ, ν probabilities.
is invariant under the push-forward operation, and when it is finite, we may assume without loss of generality that it is equal to one, because all the relevant quantities scale with the total mass. Indeed, if λ = τμ with μ probability measure and τ > 0, then T#λ = τ × T#μ, and the Wasserstein distance (defined as the infimum-over-coupling integrated cost) between τμ and τν is τW
p(μ, ν) for μ, ν probabilities.
We begin with the one-dimensional case, where the explicit formulae allow for a more transparent argument, and for simplicity we will assume some regularity.
 is a nonempty compact convex set (an interval), and the continuous and injective random map
is a nonempty compact convex set (an interval), and the continuous and injective random map  (a random element in C
b(K)) satisfies the following two conditions:
(a random element in C
b(K)) satisfies the following two conditions: - (A1)
Unbiasedness:
![$$\mathbb {E}[T(x)]=x$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_IEq81.png) for all x ∈ K.
for all x ∈ K. - (A2)
Regularity: T is monotone increasing.
The relevance of the Wasserstein geometry to phase variation becomes clear in the following proposition that shows that Assumptions 2 are equivalent to geometric assumptions on the Wasserstein space  .
.
 )
) compact and convex and
compact and convex and
 continuous. Then Assumptions
2hold if and only if, for any
continuous. Then Assumptions
2hold if and only if, for any
 supported on K such that
supported on K such that
![$$\mathbb {E} [W_2^2(T\#\lambda ,\lambda )]<\infty $$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_IEq87.png) , the following two conditions are satisfied:
, the following two conditions are satisfied:
- (B1)Unbiasedness: for any

![$$\displaystyle \begin{aligned} \mathbb{E} [W_2^2(T\#\lambda,\lambda)] \le \mathbb{E} [W_2^2(T\#\lambda,\theta)]. \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equam.png)
- (B2)Regularity: if
 is such that T#λ = Q#λ, then with probability one
is such that T#λ = Q#λ, then with probability one 
These assumptions have a clear interpretation: (B1) stipulates that λ is a Fréchet mean of the random measure Λ = T#λ, while (B2) states that T must be the optimal map from λ to Λ, that is,  .
.
If T satisfies (B2) then, as an optimal map, it must be nondecreasing λ-almost surely. Since λ is arbitrary, T must be nondecreasing on the entire domain K. Conversely, if T is nondecreasing, then it is optimal for any λ. Hence (A2) and (B2) are equivalent.
 ,
, ![$$\displaystyle \begin{aligned} \mathbb{E} \|F_{T\#\lambda}^{-1} - F_\lambda^{-1} \|{}^2_{L_2(0,1)} =\mathbb{E} [W_2^2(T\#\lambda,\lambda)] \le \mathbb{E} [W_2^2(T\#\lambda,\theta)] =\mathbb{E} \|F_{T\#\lambda}^{-1} - F_\theta^{-1} \|{}^2_{L_2(0,1)}, \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equao.png)
![$$\mathbb {E} [F_{T\#\lambda }]^{-1}]=\mathbb {E} [F_\varLambda ^{-1}]=F_\lambda ^{-1}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_IEq92.png) (see Sect. 3.1.4). Condition (A2) and the assumptions on T imply that F
Λ(x) = F
λ(T
−1(x)). Suppose that F
λ is invertible (i.e., continuous and strictly increasing on K). Then
(see Sect. 3.1.4). Condition (A2) and the assumptions on T imply that F
Λ(x) = F
λ(T
−1(x)). Suppose that F
λ is invertible (i.e., continuous and strictly increasing on K). Then  . Thus (B1) is equivalent to
. Thus (B1) is equivalent to  for all x in the range of
for all x in the range of  , which is K. The assertion that (A1) implies (B1), even if F
λ is not invertible, is proven in the next theorem (Theorem 4.2.4) in a more general context.
, which is K. The assertion that (A1) implies (B1), even if F
λ is not invertible, is proven in the next theorem (Theorem 4.2.4) in a more general context.
 . The space
. The space  is defined similarly, with f taking values in
is defined similarly, with f taking values in  instead of
instead of  , and the norm will be denoted in the same way. These are nonseparable Banach spaces.
, and the norm will be denoted in the same way. These are nonseparable Banach spaces. and let
and let  be a (Bochner measurable) random optimal map with (Bochner) mean identity and such that
be a (Bochner measurable) random optimal map with (Bochner) mean identity and such that  . Then Λ = t#λ has Fréchet mean λ:
. Then Λ = t#λ has Fréchet mean λ: ![$$\displaystyle \begin{aligned} \mathbb{E} [W_2^2(\lambda,\varLambda)] \le \mathbb{E} [W_2^2(\theta,\varLambda)] \qquad \forall \theta\in \mathcal W_2(\mathcal X). \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equaq.png)
The generalisation with respect to the one-dimensional result is threefold. Firstly, since our main interest is the implication (A1–A2) ⇒ (B1–B2), we need not assume T to be injective. Secondly, the support of λ is not required to be compact. Lastly, the result holds in arbitrary dimension, including infinite-dimensional separable Hilbert spaces  . In particular, if t is a linear map, then
. In particular, if t is a linear map, then  coincides with the operator norm of t, so the assumption is that t be a bounded self-adjoint nonnegative operator with mean identity and finite expected operator norm.
coincides with the operator norm of t, so the assumption is that t be a bounded self-adjoint nonnegative operator with mean identity and finite expected operator norm.

 (since
(since  is the identity) yields
is the identity) yields ![$$\displaystyle \begin{aligned} \mathbb{E} [W_2^2(\theta,\varLambda)] \ge {{\int_{\mathcal X} \! {\left(\!\frac 12\|x\|{}^2 - \mathbb{E}\phi(x)\!\right)\!} \, \mathrm{d}{\theta(x)}}} +\mathbb{E} \left[{{\int_{\mathcal X} \! {\!\left(\!\frac 12\|y\|{}^2 - \phi^*(y)\!\right)\!} \, \mathrm{d}{\varLambda(y)}}} \right]\! =\mathbb{E} [W_2^2(\lambda,\varLambda)]\end{aligned} $$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equas.png)
as required. The rigorous mathematical justification for this is given on page 88 in the supplement.
The “natural” space fortwould be
 , but without the continuity assumption, the result may fail (Álvarez-Esteban et al. [
9, Example 3.1]). A simple argument shows that the growth condition imposed by the G
1assumption is minimal; see page 89 in the supplement or Galasso et al. [
58].
, but without the continuity assumption, the result may fail (Álvarez-Esteban et al. [
9, Example 3.1]). A simple argument shows that the growth condition imposed by the G
1assumption is minimal; see page 89 in the supplement or Galasso et al. [
58].
The same statement holds if
 is replaced by a (Borel) convex subset K thereof. The integrals will then be taken on K, showing that λ minimises the Fréchet functional among measures supported on K, and, by continuity, on
is replaced by a (Borel) convex subset K thereof. The integrals will then be taken on K, showing that λ minimises the Fréchet functional among measures supported on K, and, by continuity, on
 . By Proposition
3.2.4
, λ is a Fréchet mean.
. By Proposition
3.2.4
, λ is a Fréchet mean.
4.3 Estimation of Fréchet Means
4.3.1 Oracle Case
In view of the canonicity of the Wasserstein geometry in Sect. 4.2.2, separation of amplitude and phase variation of the point processes  essentially requires computing Fréchet means in the 2-Wasserstein space. It is both conceptually important and technically convenient to introduce the case where an oracle reveals the conditional mean measures Λ = T#λ entirely. Thus, assuming that
essentially requires computing Fréchet means in the 2-Wasserstein space. It is both conceptually important and technically convenient to introduce the case where an oracle reveals the conditional mean measures Λ = T#λ entirely. Thus, assuming that  is the unique Fréchet mean of a random measure Λ, the goal is to estimate the structural mean λ on the basis of independent and identically distributed realisations Λ
1, …, Λ
n of λ.
is the unique Fréchet mean of a random measure Λ, the goal is to estimate the structural mean λ on the basis of independent and identically distributed realisations Λ
1, …, Λ
n of λ.


 , λ
n can be seen to be an unbiased estimator of λ in a generalised sense of Lehmann [88] (see Sect. 4.3.5).
, λ
n can be seen to be an unbiased estimator of λ in a generalised sense of Lehmann [88] (see Sect. 4.3.5).The warp maps (and their inverses) can then be estimated as the optimal maps from λ n to each Λ i (see Sect. 4.3.4).
4.3.2 Discretely Observed Measures
 . The simplest situation is when
. The simplest situation is when  arises as an empirical measure of the form
arises as an empirical measure of the form  , where Y
j are independent with distribution Λ
i. More generally,
, where Y
j are independent with distribution Λ
i. More generally,  can be a normalised point process
can be a normalised point process  with mean measure τΛ
i, i.e.
with mean measure τΛ
i, i.e. ![$$\displaystyle \begin{aligned} \widetilde\varLambda_i =\frac 1 {\widetilde\varPi_i(\mathcal X)} \widetilde \varPi_i \quad \mathrm{with} \quad \mathbb{E} [\widetilde \varPi_i(A) | \varLambda_i] =\tau \varLambda_i(A), \qquad A\subseteq\mathcal X \mathrm{ Borel}. \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equav.png)
 is a binomial point process. The parameter τ is the expected number of observed points over the entire space
is a binomial point process. The parameter τ is the expected number of observed points over the entire space  ; the larger τ is, the more information
; the larger τ is, the more information  gives on Λ
i.
gives on Λ
i. is an empirical measure, there is one difficulty in the above setting that needs to be addressed. Unless
is an empirical measure, there is one difficulty in the above setting that needs to be addressed. Unless  is binomial, there is a positive probability that
is binomial, there is a positive probability that  and no points pertaining to Λ
i are observed. In the asymptotic setup below, conditions will be imposed to ensure that this probability becomes negligible as n →∞. For concreteness we define
and no points pertaining to Λ
i are observed. In the asymptotic setup below, conditions will be imposed to ensure that this probability becomes negligible as n →∞. For concreteness we define  for some fixed measure λ
(0) that will be of minor importance. This can be a Dirac measure at 0, a certain fixed Gaussian measure, or (normalised) Lebesgue measure on some bounded set in case
for some fixed measure λ
(0) that will be of minor importance. This can be a Dirac measure at 0, a certain fixed Gaussian measure, or (normalised) Lebesgue measure on some bounded set in case  . We can now replace the estimator λ
n by
. We can now replace the estimator λ
n by  , defined as any minimiser of
, defined as any minimiser of 
As a generalisation of the discrete case discussed in Sect. 1.3, the Fréchet mean of discrete measures can be computed exactly. Suppose that  is nonzero for all i. Then each
is nonzero for all i. Then each  is a discrete measure supported on N
i points. One can then recast the multimarginal formulation (see Sect. 3.1.2) as a finite linear program, solve it, and “average” the solution as in Proposition 3.1.2 in order to obtain
is a discrete measure supported on N
i points. One can then recast the multimarginal formulation (see Sect. 3.1.2) as a finite linear program, solve it, and “average” the solution as in Proposition 3.1.2 in order to obtain  (an alternative linear programming formulation for finding a Fréchet mean is given by Anderes et al. [14]). Thus,
(an alternative linear programming formulation for finding a Fréchet mean is given by Anderes et al. [14]). Thus,  can be computed in finite time, even when
can be computed in finite time, even when  is infinite-dimensional.
is infinite-dimensional.
Finally, a remark about measurability is in order. Point processes can be viewed as random elements in  endowed with the vague topology induced from convergence of integrals of continuous functions with compact support. If μ
n converge to μ vaguely, and a
n are numbers that converge to a, then a
nμ
n → aμ vaguely. Thus,
endowed with the vague topology induced from convergence of integrals of continuous functions with compact support. If μ
n converge to μ vaguely, and a
n are numbers that converge to a, then a
nμ
n → aμ vaguely. Thus,  is a continuous function of the pair
is a continuous function of the pair  and can be viewed as a random measure with respect to the vague topology. The restriction of the vague topology to probability measures is equivalent to the weak topology,5 and therefore vague, weak, and Wasserstein measurability are all equivalent.
and can be viewed as a random measure with respect to the vague topology. The restriction of the vague topology to probability measures is equivalent to the weak topology,5 and therefore vague, weak, and Wasserstein measurability are all equivalent.
4.3.3 Smoothing
Even when the computational complexity involved in calculating  is tractable, there is another reason not to use it as an estimator for λ. If one has a-priori knowledge that λ is smooth, it is often desirable to estimate it by a smooth measure. One way to achieve this would be to apply some smoothing technique to
is tractable, there is another reason not to use it as an estimator for λ. If one has a-priori knowledge that λ is smooth, it is often desirable to estimate it by a smooth measure. One way to achieve this would be to apply some smoothing technique to  using, e.g., kernel density estimation. However, unless the number of observed points from each measure is the same N
1 = ⋯ = N
n = N,
using, e.g., kernel density estimation. However, unless the number of observed points from each measure is the same N
1 = ⋯ = N
n = N,  will usually be concentrated on many points, essentially N
1 + ⋯ + N
n of them. In other words, the Fréchet mean is concentrated on many more points than each of the measures
will usually be concentrated on many points, essentially N
1 + ⋯ + N
n of them. In other words, the Fréchet mean is concentrated on many more points than each of the measures  , thus potentially hindering its usefulness as a mean because it will not be a representative of the sample.
, thus potentially hindering its usefulness as a mean because it will not be a representative of the sample.
 , in which case each
, in which case each  is a discrete uniform measure on points
is a discrete uniform measure on points  , where we assume for simplicity that the points are not repeated (this will happen with probability one if Λ
i is diffuse). If we now set G
i to be the distribution function of
, where we assume for simplicity that the points are not repeated (this will happen with probability one if Λ
i is diffuse). If we now set G
i to be the distribution function of  , then the quantile function
, then the quantile function  is piecewise constant on each interval (k, k + 1]∕N
i with jumps at
is piecewise constant on each interval (k, k + 1]∕N
i with jumps at 
 and will have jumps at every point of the form k∕N
i for k ≤ N
i and i = 1, …, n. In the worst-case scenario, when no pair from N
i has a common divisor, there will be
and will have jumps at every point of the form k∕N
i for k ≤ N
i and i = 1, …, n. In the worst-case scenario, when no pair from N
i has a common divisor, there will be 
 ’s have a jump at one which thus needs to be counted once rather than n times.)
’s have a jump at one which thus needs to be counted once rather than n times.)By counting the number of redundancies in the constraints matrix of the linear program, one can show that this is in general an upper bound on the number of support points of the Fréchet mean.
An alternative approach is to first smooth each observation  and then calculate the Fréchet mean. Since it is easy to bound the Wasserstein distances when dealing with convolutions, we will employ kernel density estimation, although other smoothing approaches could be used as well.
and then calculate the Fréchet mean. Since it is easy to bound the Wasserstein distances when dealing with convolutions, we will employ kernel density estimation, although other smoothing approaches could be used as well.
 , but a similar construction will work when the dimension of
, but a similar construction will work when the dimension of  is infinite. Let
is infinite. Let  be a continuous, bounded, strictly positive isotropic density function with unit variance: ψ(x) = ψ
1(∥x∥) with ψ
1 nonincreasing and
be a continuous, bounded, strictly positive isotropic density function with unit variance: ψ(x) = ψ
1(∥x∥) with ψ
1 nonincreasing and 
 even boundedness is not necessary.) A classical example for ψ is the standard Gaussian density in
even boundedness is not necessary.) A classical example for ψ is the standard Gaussian density in  . Define the rescaled version ψ
σ(x) = σ
−dψ(x∕σ) for all σ > 0. We can then replace
. Define the rescaled version ψ
σ(x) = σ
−dψ(x∕σ) for all σ > 0. We can then replace  by a smooth proxy
by a smooth proxy  . If
. If  is a sum of Dirac masses at
is a sum of Dirac masses at  , then
, then 
 , this convolution is an acceptable estimator, because as was seen in the proof of Theorem 2.2.7,
, this convolution is an acceptable estimator, because as was seen in the proof of Theorem 2.2.7, 
 has a strictly positive density throughout
has a strictly positive density throughout  . If we know that Λ is supported on a convex compact
. If we know that Λ is supported on a convex compact  , it is desirable to construct an estimator that has the same support K. The first idea that comes to mind is to project
, it is desirable to construct an estimator that has the same support K. The first idea that comes to mind is to project  to K (see Proposition 3.2.4), as this will further decrease the Wasserstein distance, but the resulting measure will then have positive mass on the boundary of K, and will not be absolutely continuous. We will therefore use a different strategy: eliminate all the mass outside K and redistribute it on K. The simplest way to do this is to restrict
to K (see Proposition 3.2.4), as this will further decrease the Wasserstein distance, but the resulting measure will then have positive mass on the boundary of K, and will not be absolutely continuous. We will therefore use a different strategy: eliminate all the mass outside K and redistribute it on K. The simplest way to do this is to restrict  to K and renormalise the restriction to be a probability measure. For technical reasons, it will be more convenient to bound the Wasserstein distance when the restriction and renormalisation is done separately on each point of
to K and renormalise the restriction to be a probability measure. For technical reasons, it will be more convenient to bound the Wasserstein distance when the restriction and renormalisation is done separately on each point of  . This yields the measure
. This yields the measure }\bigg|{}_K, \end{aligned} $$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equ2.png)
 for some finite constant C. It is apparent that
for some finite constant C. It is apparent that  is a continuous function of
is a continuous function of  and σ, so
and σ, so  is measurable; in any case this is not particularly important because σ will vanish, so
is measurable; in any case this is not particularly important because σ will vanish, so  asymptotically and the latter is measurable.
asymptotically and the latter is measurable. for λ is defined as the minimiser of
for λ is defined as the minimiser of 
 are absolutely continuous,
are absolutely continuous,  is unique. We refer to
is unique. We refer to  as the regularised Fréchet–Wasserstein estimator, where the regularisation comes from the smoothing and the possible restriction to K.
as the regularised Fréchet–Wasserstein estimator, where the regularisation comes from the smoothing and the possible restriction to K. ,
,  can be constructed via averaging of quantile functions. Let
can be constructed via averaging of quantile functions. Let  be the distribution function of
be the distribution function of  . Then
. Then  is the measure with quantile function
is the measure with quantile function 
![$$\displaystyle \begin{aligned} F_{\widehat\lambda_n}(x) =[F_{\widehat\lambda_n}^{-1}]^{-1}(x).\end{aligned} $$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Eqube.png)
 are continuous and strictly increasing, so the inverses are proper inverses and one does not to use the right-continuous inverse as in Sect. 3.1.4.
are continuous and strictly increasing, so the inverses are proper inverses and one does not to use the right-continuous inverse as in Sect. 3.1.4.If  and d ≥ 2, then there is no explicit expression for
and d ≥ 2, then there is no explicit expression for  , although it exists and is unique. In the next chapter, we present a steepest descent algorithm that approximately constructs
, although it exists and is unique. In the next chapter, we present a steepest descent algorithm that approximately constructs  by taking advantage of the differentiability properties of the Fréchet functional
by taking advantage of the differentiability properties of the Fréchet functional  in Sect. 3.1.6.
in Sect. 3.1.6.
4.3.4 Estimation of Warpings and Registration Maps
 , i = 1, …, n and
, i = 1, …, n and  are constructed, it is natural to estimate the map
are constructed, it is natural to estimate the map  and its inverse
and its inverse  (when Λ
i are absolutely continuous; see the discussion after Assumptions 3 below) by the plug-in estimators
(when Λ
i are absolutely continuous; see the discussion after Assumptions 3 below) by the plug-in estimators 
![$$\displaystyle \begin{aligned} \widehat{\varPi_i^{(n)}} =\widehat{T_i^{-1}} \# \widetilde\varPi_i^{(n)} =\left[ \widehat{T_i^{-1}} \circ T_i \right] \# \varPi_i^{(n)}. \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equbg.png)
 is a good estimator, then its composition with T
i should be close to the identity and
is a good estimator, then its composition with T
i should be close to the identity and  should be close to Π
i.
should be close to Π
i.4.3.5 Unbiased Estimation When 
 is a random element in H whose distribution μ
θ depends on a parameter θ ∈ H. Then
is a random element in H whose distribution μ
θ depends on a parameter θ ∈ H. Then  is unbiased for θ if for all θ ∈ H
is unbiased for θ if for all θ ∈ H 
 in the sequel.) This is equivalent to
in the sequel.) This is equivalent to 
 as measurable functions δ = δ(Λ
1, …, Λ
n) for which
as measurable functions δ = δ(Λ
1, …, Λ
n) for which 
Unbiased estimators allow us to avoid the problem of over-registering (the so-called pinching effect; Kneip and Ramsay [82, Section 2.4]; Marron et al. [90, p. 476]). An extreme example of over-registration is if one “aligns” all the observed patterns into a single fixed point x 0. The registration will then seem “successful” in the sense of having no residual phase variation, but the estimation is clearly biased because the points are not registered to the correct reference measure. Thus, requiring the estimator to be unbiased is an alternative to penalising the registration maps.
Due to the Hilbert space embedding of  , it is possible to characterise unbiased estimators in terms of a simple condition on their quantile functions. As a corollary, λ
n, the Fréchet mean of {Λ
1, …, Λ
n}, is unbiased. Our regularised Fréchet–Wasserstein estimator
, it is possible to characterise unbiased estimators in terms of a simple condition on their quantile functions. As a corollary, λ
n, the Fréchet mean of {Λ
1, …, Λ
n}, is unbiased. Our regularised Fréchet–Wasserstein estimator  can then be interpreted as approximately unbiased, since it approximates the unobservable λ
n.
can then be interpreted as approximately unbiased, since it approximates the unobservable λ
n.
 )
)Let Λ be a random measure in  with finite Fréchet functional and let λ be the unique Fréchet mean of Λ (Theorem 3.2.11
). An estimator δ constructed as a function of a sample (Λ
1, …, Λ
n) is unbiased for λ if and only if the left-continuous representatives (in L
2(0, 1)) satisfy
with finite Fréchet functional and let λ be the unique Fréchet mean of Λ (Theorem 3.2.11
). An estimator δ constructed as a function of a sample (Λ
1, …, Λ
n) is unbiased for λ if and only if the left-continuous representatives (in L
2(0, 1)) satisfy ![$$\mathbb {E} [F_\delta ^{-1}(x)]=F_\lambda ^{-1}(x)$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_IEq198.png) for all x ∈ (0, 1).
for all x ∈ (0, 1).

![$$\mathbb {E}_\lambda [F_\delta ^{-1}]=F_\lambda ^{-1}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_IEq199.png) . In other words, these two functions must equal almost everywhere on (0, 1), and their left-continuous representatives must equal everywhere (the fact that
. In other words, these two functions must equal almost everywhere on (0, 1), and their left-continuous representatives must equal everywhere (the fact that ![$$\mathbb {E}_\lambda [F_\delta ^{-1}]$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_IEq200.png) has such a representative was established in Sect. 3.1.4).
has such a representative was established in Sect. 3.1.4).![$$\displaystyle \begin{aligned} \mathbb{E} [F_\delta^{-1}] =\mathbb{E} \left[\frac 1n \sum_{i=1}^n F_{\varLambda_i}^{-1}\right] =\mathbb{E} [F_\varLambda^{-1}] =F_\lambda^{-1}, \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equbl.png)
4.4 Consistency
In functional data analysis, one often assumes that the number of curves n and the number of observed points per curve m both diverge to infinity. An analogous framework for point processes would similarly require the number of point processes n as well as the expected number of points τ per processes to diverge. A technical complication arises, however, because the mean measures do not suffice to characterise the distribution of the processes. Indeed, if one is given a point processes Π with mean measure λ (not necessarily a probability measure), and τ is an integer, there is no unique way to define a process Π (τ) with mean measure τλ. One can define Π (τ) = τΠ, so that every point in Π will be counted τ times. Such a construction, however, can never yield a consistent estimator of λ, even when τ →∞.

 such that
such that 

![$$\displaystyle \begin{aligned} L_\varPi(f) =\mathbb{E} \left[ e^{-\varPi f}\right] =\mathbb{E} \left[\exp \left(-{{\int_{\mathcal X} \! f \, \mathrm{d}\varPi}} \right)\right]\in[0,1], \qquad f:\mathcal X\to\mathbb{R}_+ \quad \mathrm{Borel}. \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equbp.png)
![$$\displaystyle \begin{aligned} L_1(f)=\mathbb{E}\left[e^{-\varPi^{(1)} f}\right] =\exp\left [{-}{\int_{M_+(\mathcal X)} \! (1{-}e^{-\mu f}) \, \mathrm{d}\boldsymbol\rho(\mu)}\right] \quad \mathrm{for some} \boldsymbol{\rho} \in M_+(M_+(\mathcal X)). \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equbq.png)
The Laplace functional of Π (τ) is L τ(f) = [L 1(f)]τ for any rational τ, which simply amounts to multiplying the measure ρ by the scalar τ. One can then do the same for an irrational τ, and the resulting Laplace functional determines the distribution of Π (τ) for all τ > 0.
4.4.1 Consistent Estimation of Fréchet Means
We are now ready to define our asymptotic setup. The following assumptions will be made. Notice that the Wasserstein geometry does not appear explicitly in these assumptions, but is rather derived from them in view of Theorem 4.2.4. The compactness requirement can be relaxed under further moment conditions on λ and the point process Π; we focus on the compact case for the simplicity and because in practice the point patterns will be observed on a bounded observation window.
 be a compact convex nonempty set, λ an absolutely continuous probability measure on K, and τ
n a sequence of positive numbers. Let Π be a point processes on K with mean measure λ. Finally, define U = intK.
be a compact convex nonempty set, λ an absolutely continuous probability measure on K, and τ
n a sequence of positive numbers. Let Π be a point processes on K with mean measure λ. Finally, define U = intK. For every n, let
 be independent point processes, each having the same distribution as a superposition of τ
n copies of Π.
be independent point processes, each having the same distribution as a superposition of τ
n copies of Π.Let T be a random injective function on K (viewed as a random element in C b(K, K) endowed with the supremum norm) such that T(x) ∈ U for x ∈ U (that is, T ∈ C b(U, U)) with nonsingular derivative
 for almost all x ∈ U, that is a gradient of a convex function. Let {T
1, …, T
n} be independent and identically distributed as T.
for almost all x ∈ U, that is a gradient of a convex function. Let {T
1, …, T
n} be independent and identically distributed as T.For every x ∈ U, assume that
![$$\mathbb {E} [T(x)]=x$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_IEq205.png) .
.Assume that the collections
 and
and  are independent.
are independent.Let
 be the warped point processes, having conditional mean measures
be the warped point processes, having conditional mean measures  .
.Define
 by the smoothing procedure (4.2), using bandwidth
by the smoothing procedure (4.2), using bandwidth ![$$\sigma _i^{(n)}\in [0,1]$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_IEq211.png) (possibly random).
(possibly random).
The dependence of the estimators on n will sometimes be tacit. But Λ idoes not depend on n.
By virtue of Theorem 4.2.4, λ is a Fréchet mean of the random measure Λ = T#λ. Uniqueness of this Fréchet mean will follow from Proposition 3.2.7 if we show that Λ is absolutely continuous with positive probability. This is indeed the case, since T is injective and has a nonsingular Jacobian matrix; see Ambrosio et al. [12, Lemma 5.5.3]. The Jacobian assumption can be removed when  , because Fréchet means are always unique by Theorem 3.2.11.
, because Fréchet means are always unique by Theorem 3.2.11.
Full independence: here the point processes are independent across rows, that is,
 and
and  are also independent.
are also independent.Nested observations: here
 includes the same points as
includes the same points as  and additional points, that is,
and additional points, that is,  is a superposition of
is a superposition of  and another point process distributed as (τ
n+1 − τ
n)Π.
and another point process distributed as (τ
n+1 − τ
n)Π.
We now state and prove the consistency result for the estimators of the conditional mean measures Λ i and the structural mean measure λ.
 almost surely and τ
n →∞ as n →∞, then:
almost surely and τ
n →∞ as n →∞, then: Convergence in 1. holds almost surely under the additional conditions that  and
and ![$$\mathbb {E}\left [\varPi (\mathbb {R}^d)\right ]^4<\infty $$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_IEq224.png) . If σ
n → 0 only in probability, then convergence in 2. still holds in probability.
. If σ
n → 0 only in probability, then convergence in 2. still holds in probability.
Theorem 4.4.1 still holds without smoothing (σ
n = 0). In that case,  is possibly not unique, and the theorem should be interpreted in a set-valued sense (as in Proposition 1.7.8): almost surely, any choice of minimisers
is possibly not unique, and the theorem should be interpreted in a set-valued sense (as in Proposition 1.7.8): almost surely, any choice of minimisers  converges to λ as n →∞.
converges to λ as n →∞.
The preceding paragraph notwithstanding, we will usually assume that some smoothing is present, in which case  is unique and absolutely continuous by Proposition 3.1.8. The uniform Lipschitz bounds for the objective function show that if we restrict the relevant measures to be absolutely continuous, then
is unique and absolutely continuous by Proposition 3.1.8. The uniform Lipschitz bounds for the objective function show that if we restrict the relevant measures to be absolutely continuous, then  is a continuous function of
is a continuous function of  and hence
and hence  is measurable; this is again a minor issue because many arguments in the proof hold for each ω ∈ Ω separately. Thus, even if
is measurable; this is again a minor issue because many arguments in the proof hold for each ω ∈ Ω separately. Thus, even if  is not measurable, the proof shows that the convergence holds outer almost surely or in outer probability.
is not measurable, the proof shows that the convergence holds outer almost surely or in outer probability.
The first step in proving consistency is to show that the Wasserstein distance between the unsmoothed and the smoothed estimators of Λ
i vanishes with the smoothing parameter. The exact rate of decay will be important to later establish the rate of convergence of  to λ, and is determined next.
to λ, and is determined next.

Since the smoothing parameter will anyway vanish, this restriction to small values of σ is not binding. The constant C
ψ,K is explicit. When  , a more refined construction allows to improve this constant in some situations, see Panaretos and Zemel [100, Lemma 1].
, a more refined construction allows to improve this constant in some situations, see Panaretos and Zemel [100, Lemma 1].
The idea is that (4.2) is a sum of measures with mass 1∕N i that can be all sent to the relevant point x j, and we refer to page 98 in the supplement for the precise details.
Proof(Proof of Theorem 4.4.1) The proof, detailed on page 97 of the supplement, follows the following steps: firstly, one shows the convergence in probability of  to Λ
i. This is basically a corollary of Karr [79, Proposition 4.8] and the smoothing bound from Lemma 4.4.2.
to Λ
i. This is basically a corollary of Karr [79, Proposition 4.8] and the smoothing bound from Lemma 4.4.2.
 :
: 
 , and
, and  . The first distance vanishes since the intensity τ →∞, and the second by the smoothing bound. Another compactness argument yields that
. The first distance vanishes since the intensity τ →∞, and the second by the smoothing bound. Another compactness argument yields that  uniformly on
uniformly on  , and so the minimisers converge.
, and so the minimisers converge. ,
, ![$$\displaystyle \begin{aligned} {\mathbb{P}}\left( \frac{\widetilde \varPi_i^{(n)}((-\infty,a])} {\tau_n} - \varLambda_i((-\infty,a]) \to 0 \right) = 1 \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equbu.png)
4.4.2 Consistency of Warp Functions and Inverses
We next discuss the consistency of the warp and registration function estimators. These are key elements in order to align the observed point patterns  . Recall that we have consistent estimators
. Recall that we have consistent estimators  for Λ
i and
for Λ
i and  for λ. Then
for λ. Then  is estimated by
is estimated by  and
and  is estimated by
is estimated by  . We will make the following extra assumptions that lead to more transparent statements (otherwise one needs to replace K with the set of Lebesgue points of the supports of λ and Λ
i).
. We will make the following extra assumptions that lead to more transparent statements (otherwise one needs to replace K with the set of Lebesgue points of the supports of λ and Λ
i).
- 1.
λ has a positive density on K (in particular, suppλ = K);
- 2.
T is almost surely surjective on U = intK (thus a homeomorphism of U).
As a consequence  almost surely.
almost surely.
 and any compact set S ⊆intK,
and any compact set S ⊆intK, 
Almost sure convergence can be obtained under the same provisions made at the end of the statement of Theorem 4.4.1.
A few technical remarks are in order. First and foremost, it is not clear that the two suprema are measurable. Even though T
i and  are random elements in
are random elements in  , their estimators are only defined in an L
2 sense. The proof of Theorem 4.4.3 is done ω-wise. That is, for any ω in the probability space such that Theorem 4.4.1 holds, the two suprema vanish as n →∞. In other words, the convergence holds in outer probability or outer almost surely.
, their estimators are only defined in an L
2 sense. The proof of Theorem 4.4.3 is done ω-wise. That is, for any ω in the probability space such that Theorem 4.4.1 holds, the two suprema vanish as n →∞. In other words, the convergence holds in outer probability or outer almost surely.
Secondly, assuming positive smoothing, the random measures  are smooth with densities bounded below on K, so
are smooth with densities bounded below on K, so  are defined on the whole of U (possibly as set-valued functions on a Λ
i-null set). But the only known regularity result for
are defined on the whole of U (possibly as set-valued functions on a Λ
i-null set). But the only known regularity result for  is an upper bound on its density (Proposition 3.1.8), so it is unclear what is its support and consequently what is the domain of definition of
is an upper bound on its density (Proposition 3.1.8), so it is unclear what is its support and consequently what is the domain of definition of  .
.
Lastly, when the smoothing parameter σ is zero,  and
and  are not defined. Nevertheless, Theorem 4.4.3 still holds in the set-valued formulation of Proposition 1.7.11, of which it is a rather simple corollary:
are not defined. Nevertheless, Theorem 4.4.3 still holds in the set-valued formulation of Proposition 1.7.11, of which it is a rather simple corollary:

 is uniquely defined on U = intK which is an open convex set, the restrictions on Ω in Proposition 1.7.11 are redundant. Uniform convergence of
is uniquely defined on U = intK which is an open convex set, the restrictions on Ω in Proposition 1.7.11 are redundant. Uniform convergence of  to T
i is proven in the same way.
to T
i is proven in the same way. ,
,

The division by the number of observed points ensures that the resulting measures are probability measures; the relevant information is contained in the point patterns themselves, and is invariant under this normalisation.
 , so in particular
, so in particular  is almost surely not zero when n is large. Since
is almost surely not zero when n is large. Since  , we have the upper bound
, we have the upper bound 


Possible extensions pertaining to the boundary of K are discussed on page 33 of the supplement.
4.5 Illustrative Examples
In this section, we illustrate the estimation framework put forth in this chapter by considering an example of a structural mean λ with a bimodal density on the real line. The unwarped point patterns Π originate from Poisson processes with mean measure λ and, consequently, the warped points  are Cox processes (see Sect. 4.1.2). Another scenario involving triangular densities can be found in Panaretos and Zemel [100].
are Cox processes (see Sect. 4.1.2). Another scenario involving triangular densities can be found in Panaretos and Zemel [100].
4.5.1 Explicit Classes of Warp Maps
As a first step, we introduce a class of random warp maps satisfying Assumptions 2, that is, increasing maps that have as mean the identity function. The construction is a mixture version of similar maps considered by Wang and Gasser [128, 129].

![$$\displaystyle \begin{aligned} \mathbb{E} \left[\zeta_k(x)\right] = x ,\qquad x\in[0,1]. \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equcb.png)

 for Y and X independent. When J = 10 is large, the function T deviates only mildly from the identity, since a law of large numbers begins to take effect. In contrast, J = 2 yields functions that are quite different from the identity. Thus, it can be said that the parameter J controls the variance of the random warp function T.
for Y and X independent. When J = 10 is large, the function T deviates only mildly from the identity, since a law of large numbers begins to take effect. In contrast, J = 2 yields functions that are quite different from the identity. Thus, it can be said that the parameter J controls the variance of the random warp function T.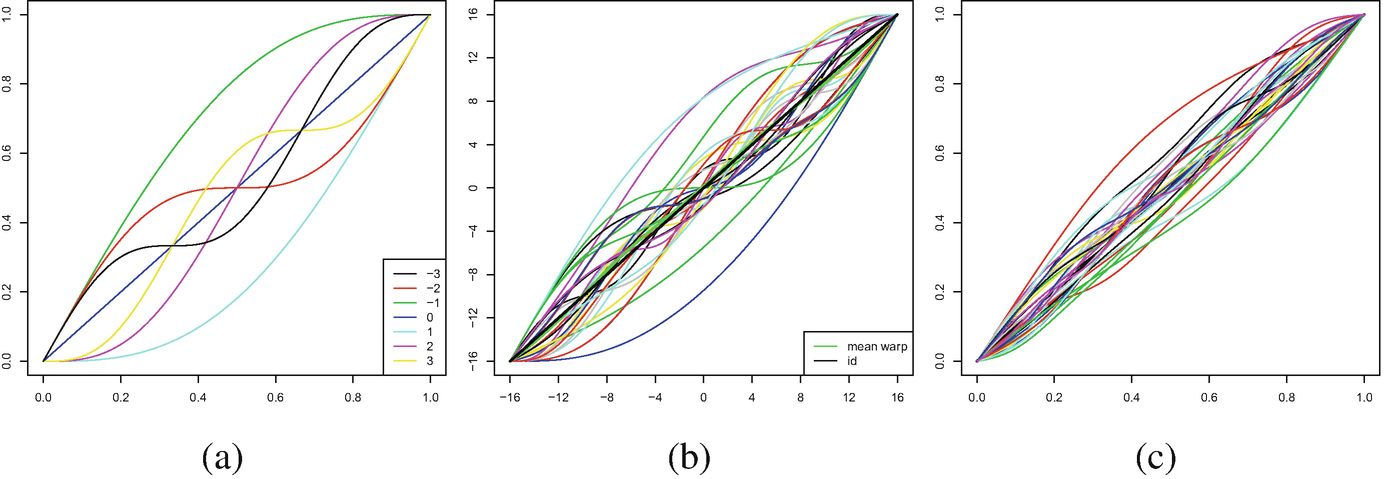
4.5.2 Bimodal Cox Processes
![$$\displaystyle \begin{aligned} f(x) =\frac{1-\epsilon}2[\varphi(x - 8) + \varphi(x + 8)] + \frac{\epsilon}{24} \beta_{1.5,1.5}\left(\frac{x+12}{24}\right) ,\qquad x\in[-16,16],\end{aligned} $$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equ6.png)
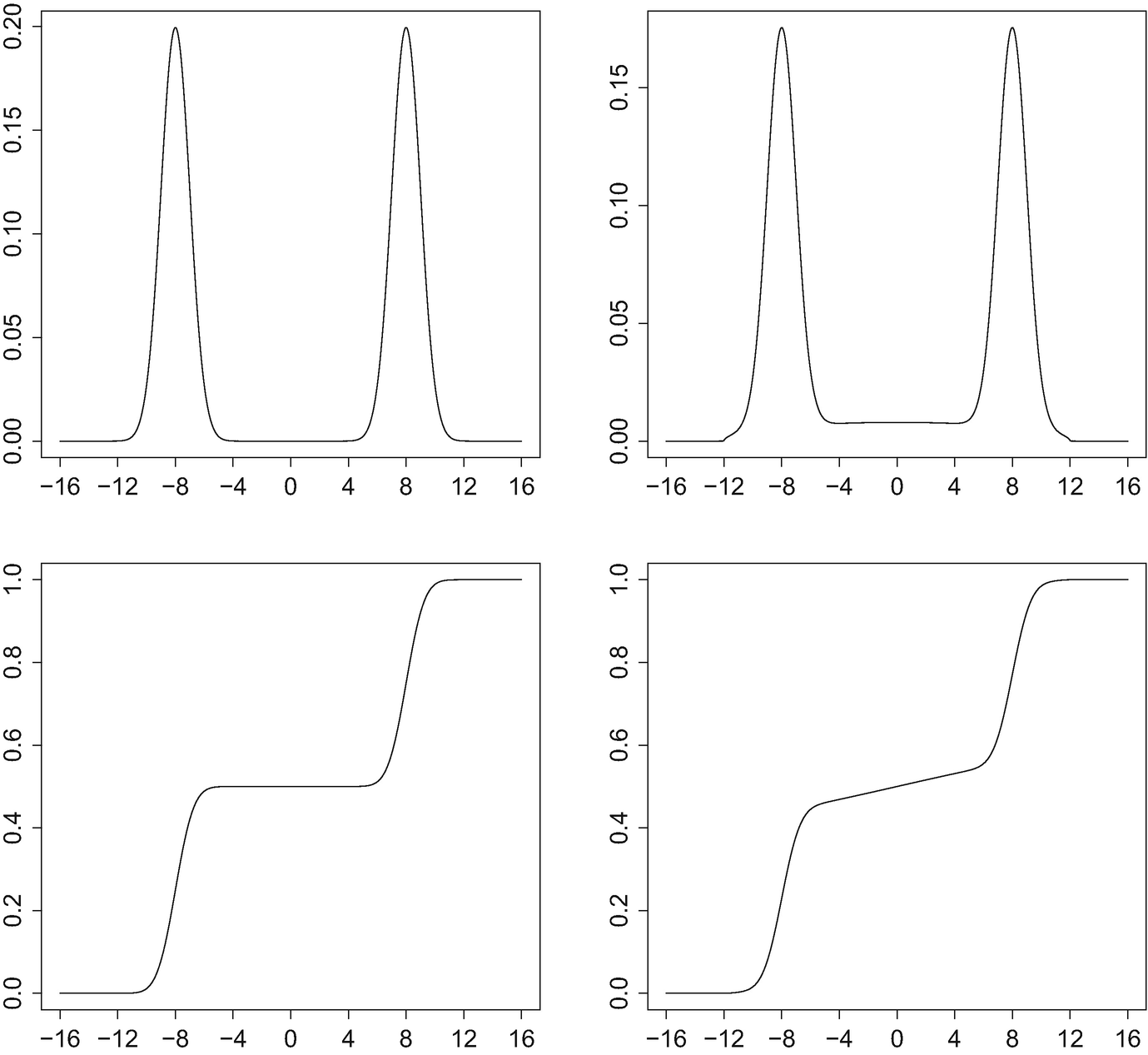
Density and distribution functions corresponding to (4.6) with 𝜖 = 0 and 𝜖 = 0.15
The main criterion for the quality of our regularised Fréchet–Wasserstein estimator will be its success in discerning the two modes at ± 8; these will be smeared by the phase variation arising from the warp functions.

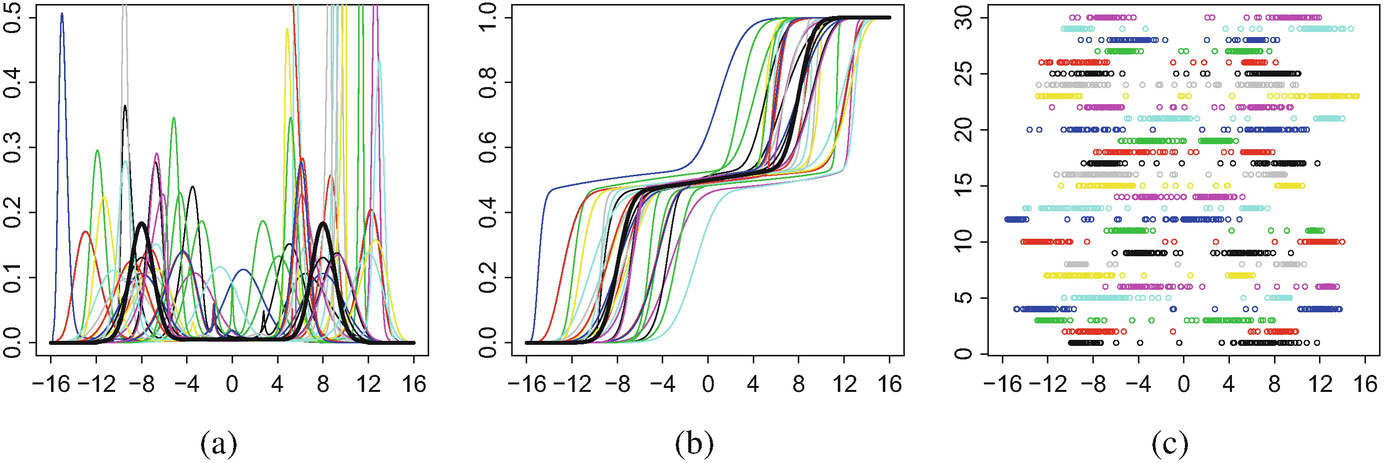
(a) 30 warped bimodal densities, with density of λ given by (4.6) in solid black; (b) their corresponding distribution functions, with that of λ in solid black; (c) 30 Cox processes, constructed as warped versions of Poisson processes with mean intensity 93f using as warp functions the rescaling to [−16.16] of (4.5)
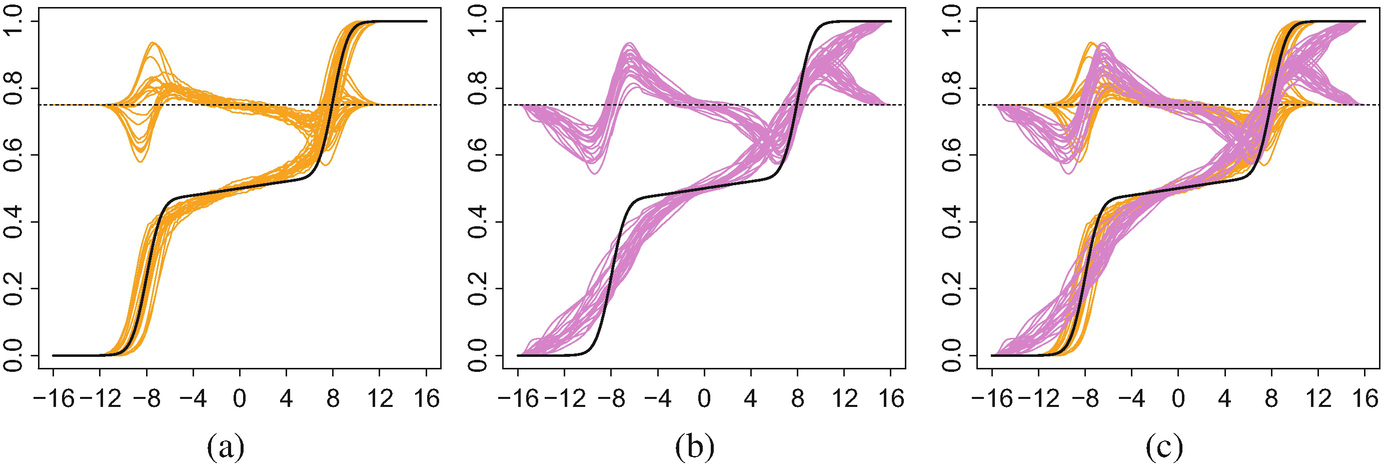
 was smoothed with a Gaussian kernel and bandwidth chosen by unbiased cross validation. We deviate slightly from the recipe presented in Sect. 4.3 by not restricting the resulting estimates to the interval [−16, 16], but this has no essential effect on the finite sample performance. The regularised Fréchet–Wasserstein estimator
was smoothed with a Gaussian kernel and bandwidth chosen by unbiased cross validation. We deviate slightly from the recipe presented in Sect. 4.3 by not restricting the resulting estimates to the interval [−16, 16], but this has no essential effect on the finite sample performance. The regularised Fréchet–Wasserstein estimator  serves as the estimator of the structural mean λ and is shown in Fig. 4.7a. It is contrasted with λ at the level of distribution functions, as well as with the empirical arithmetic mean; the latter, the naive estimator, is calculated by ignoring the warping and simply averaging linearly the (smoothed) empirical distribution functions across the observations. We notice that
serves as the estimator of the structural mean λ and is shown in Fig. 4.7a. It is contrasted with λ at the level of distribution functions, as well as with the empirical arithmetic mean; the latter, the naive estimator, is calculated by ignoring the warping and simply averaging linearly the (smoothed) empirical distribution functions across the observations. We notice that  is rather successful at locating the two modes of λ, in contrast with the naive estimator that is more diffuse. In fact, its distribution function increases approximately linearly, suggesting a nearly constant density instead of the correct bimodal one.
is rather successful at locating the two modes of λ, in contrast with the naive estimator that is more diffuse. In fact, its distribution function increases approximately linearly, suggesting a nearly constant density instead of the correct bimodal one.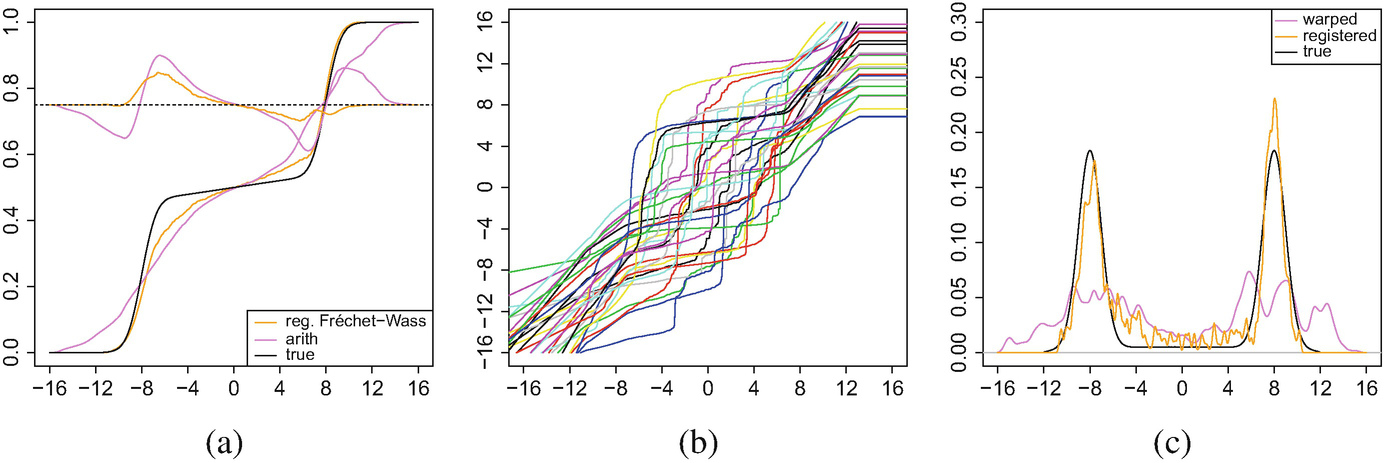
(a) Comparison between the regularised Fréchet–Wasserstein estimator, the empirical arithmetic mean, and the true distribution function, including residual curves centred at y = 3∕4; (b) The estimated warp functions; (c) Kernel estimates of the density function f of the structural mean, based on the warped and registered point patterns
 , depicted in Fig. 4.7b, and their inverses, are defined as the optimal maps between
, depicted in Fig. 4.7b, and their inverses, are defined as the optimal maps between  and the estimated conditional mean measures, as explained in Sect. 4.3.4. Then we register the point patterns by applying to them the inverse estimators
and the estimated conditional mean measures, as explained in Sect. 4.3.4. Then we register the point patterns by applying to them the inverse estimators  (Fig. 4.8). Figure 4.7c gives two kernel estimators of the density of λ constructed from a superposition of all the warped points and all the registered ones. Notice that the estimator that uses the registered points is much more successful than the one using the warped ones in discerning the two density peaks. This is not surprising after a brief look at Fig. 4.8, where the unwarped, warped, and registered points are displayed. Indeed, there is very high concentration of registered points around the true location of the peaks, ± 8. This is not the case for the warped points because of the phase variation that translates the centres of concentration for each individual observation. It is important to remark that the fluctuations in the density estimator in Fig. 4.7c are not related to the registration procedure, and could be reduced by a better choice of bandwidth. Indeed, our procedure does not attempt to estimate the density, but rather the distribution function.
(Fig. 4.8). Figure 4.7c gives two kernel estimators of the density of λ constructed from a superposition of all the warped points and all the registered ones. Notice that the estimator that uses the registered points is much more successful than the one using the warped ones in discerning the two density peaks. This is not surprising after a brief look at Fig. 4.8, where the unwarped, warped, and registered points are displayed. Indeed, there is very high concentration of registered points around the true location of the peaks, ± 8. This is not the case for the warped points because of the phase variation that translates the centres of concentration for each individual observation. It is important to remark that the fluctuations in the density estimator in Fig. 4.7c are not related to the registration procedure, and could be reduced by a better choice of bandwidth. Indeed, our procedure does not attempt to estimate the density, but rather the distribution function.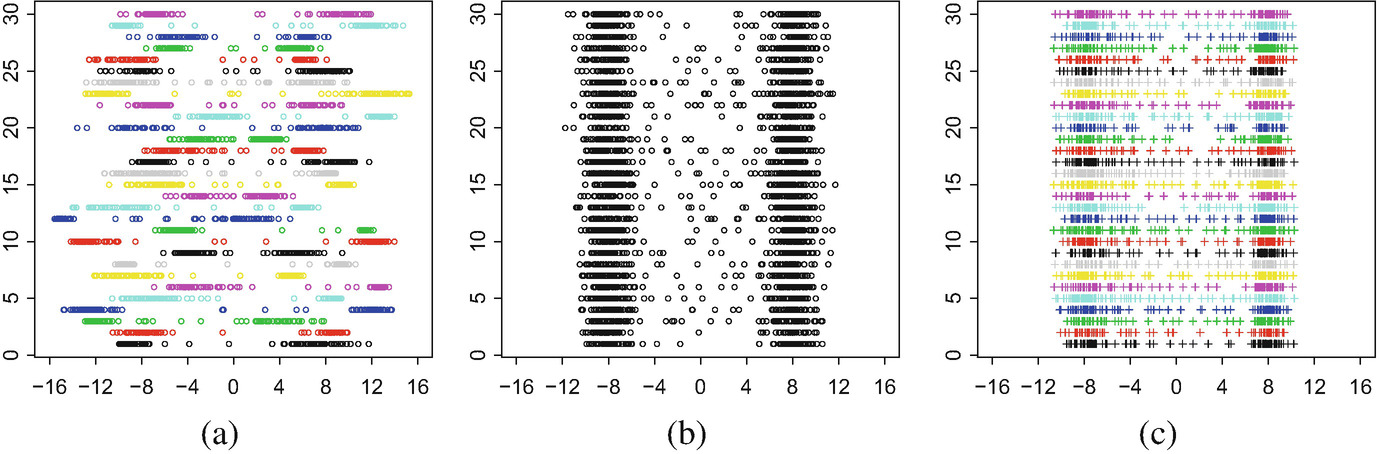
Bimodal Cox processes: (a) the observed warped point processes; (b) the unobserved original point processes; (c) the registered point processes
(a) Sampling variation of the regularised Fréchet–Wasserstein mean  and the true mean measure λ for 20 independent replications of the experiment; (b) sampling variation of the arithmetic mean, and the true mean measure λ for the same 20 replications; (c) superposition of (a) and (b). For ease of comparison, all three panels include residual curves centred at y = 3∕4
and the true mean measure λ for 20 independent replications of the experiment; (b) sampling variation of the arithmetic mean, and the true mean measure λ for the same 20 replications; (c) superposition of (a) and (b). For ease of comparison, all three panels include residual curves centred at y = 3∕4
 for λ as shown in Theorem 4.4.1, we let the number of processes n as well as the expected number of observed point per process τ to vary. Figures 4.10 and 4.11 show the sampling variation of
for λ as shown in Theorem 4.4.1, we let the number of processes n as well as the expected number of observed point per process τ to vary. Figures 4.10 and 4.11 show the sampling variation of  for different values of n and τ. We observe that as either of these increases, the realisations
for different values of n and τ. We observe that as either of these increases, the realisations  indeed approach λ. The figures suggest that, in this scenario, the amplitude variation plays a stronger role than the phase variation, as the effect of τ is more substantial.
indeed approach λ. The figures suggest that, in this scenario, the amplitude variation plays a stronger role than the phase variation, as the effect of τ is more substantial.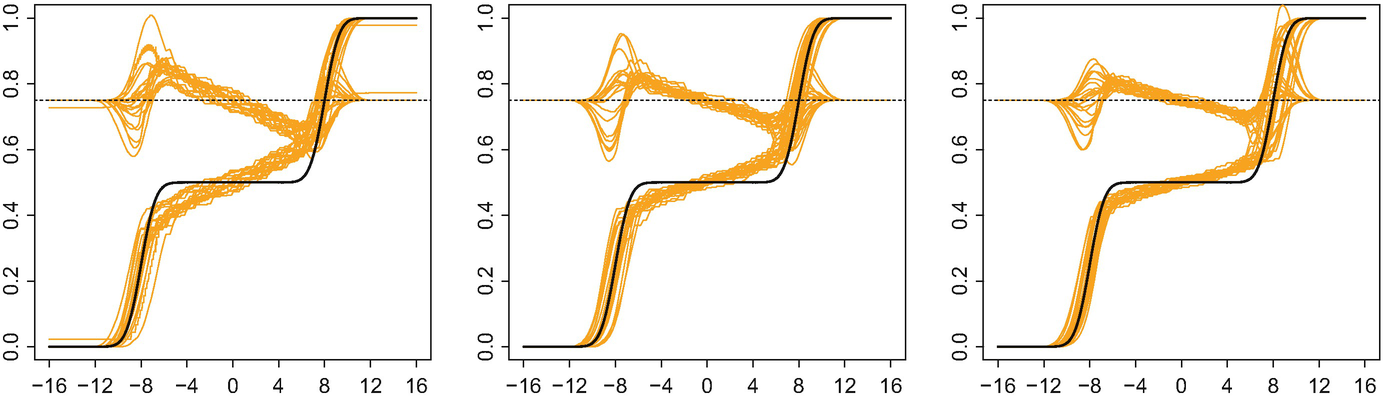
Sampling variation of the regularised Fréchet–Wasserstein mean  and the true mean measure λ for 20 independent replications of the experiment, with 𝜖 = 0 and n = 30. Left: τ = 43; middle: τ = 93; right: τ = 143. For ease of comparison, all three panels include residual curves centred at y = 3∕4
and the true mean measure λ for 20 independent replications of the experiment, with 𝜖 = 0 and n = 30. Left: τ = 43; middle: τ = 93; right: τ = 143. For ease of comparison, all three panels include residual curves centred at y = 3∕4
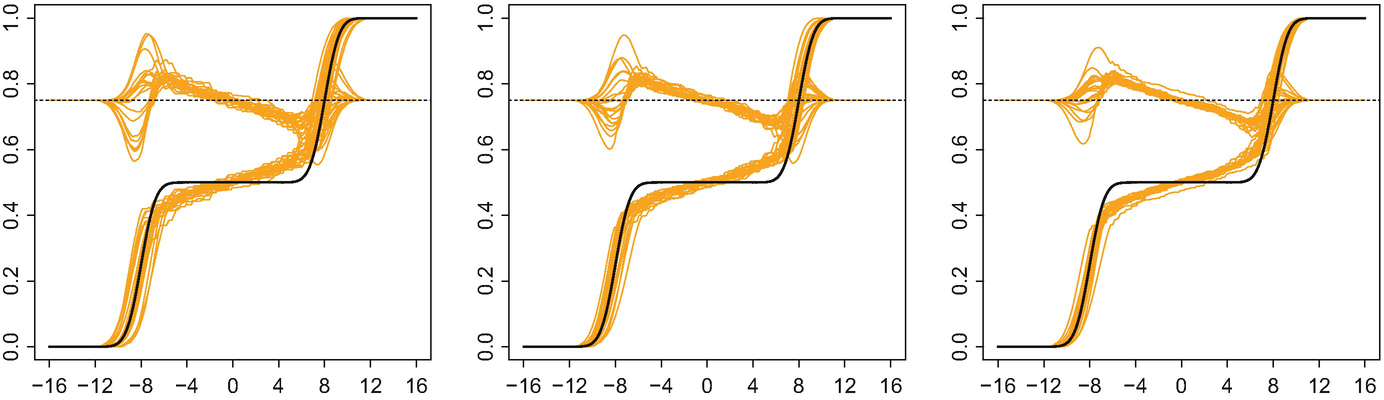
Sampling variation of the regularised Fréchet–Wasserstein mean  and the true mean measure λ for 20 independent replications of the experiment, with 𝜖 = 0 and τ = 93. Left: n = 30; middle: n = 50; right: n = 70. For ease of comparison, all three panels include residual curves centred at y = 3∕4.
and the true mean measure λ for 20 independent replications of the experiment, with 𝜖 = 0 and τ = 93. Left: n = 30; middle: n = 50; right: n = 70. For ease of comparison, all three panels include residual curves centred at y = 3∕4.
4.5.3 Effect of the Smoothing Parameter
 , provided that
, provided that  . In our simulations, we choose σ
i in a data-driven way by employing unbiased cross validation. To gauge for the effect of the smoothing, we carry out the same estimation procedure but with σ
i multiplied by a parameter s. Figure 4.12 presents the distribution function of
. In our simulations, we choose σ
i in a data-driven way by employing unbiased cross validation. To gauge for the effect of the smoothing, we carry out the same estimation procedure but with σ
i multiplied by a parameter s. Figure 4.12 presents the distribution function of  as a function of s. Interestingly, the curves are nearly identical as long as s ≤ 1, whereas when s > 1, the bias becomes more substantial.
as a function of s. Interestingly, the curves are nearly identical as long as s ≤ 1, whereas when s > 1, the bias becomes more substantial.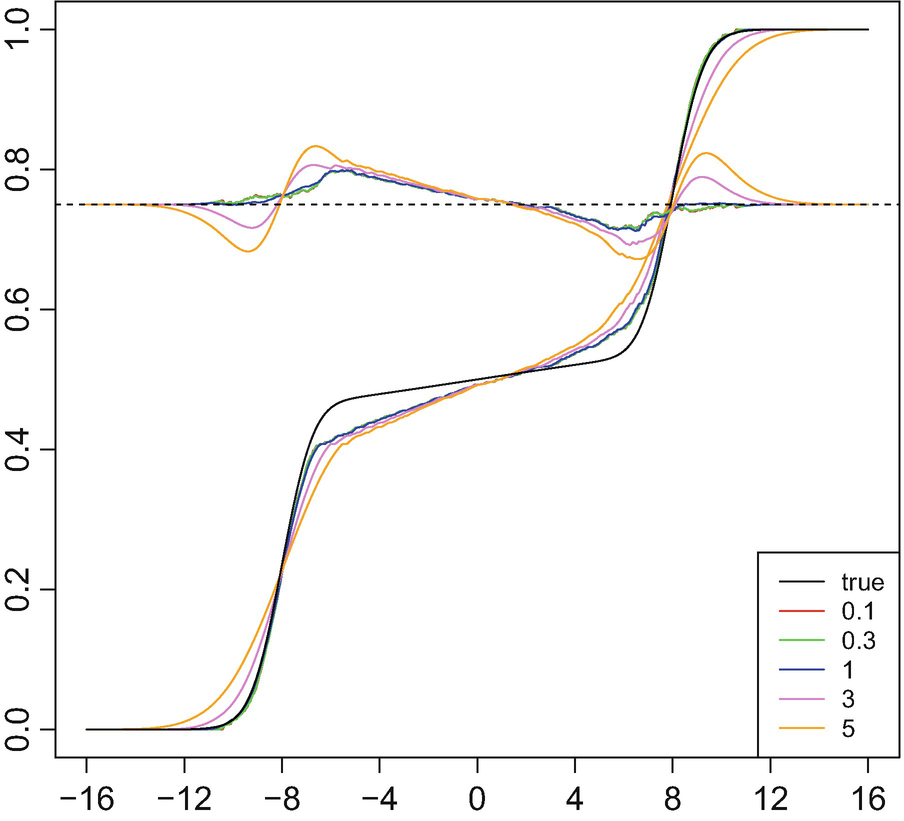
Regularised Fréchet–Wasserstein mean as a function of the smoothing parameter multiplier s, including residual curves. Here, n = 30 and τ = 143
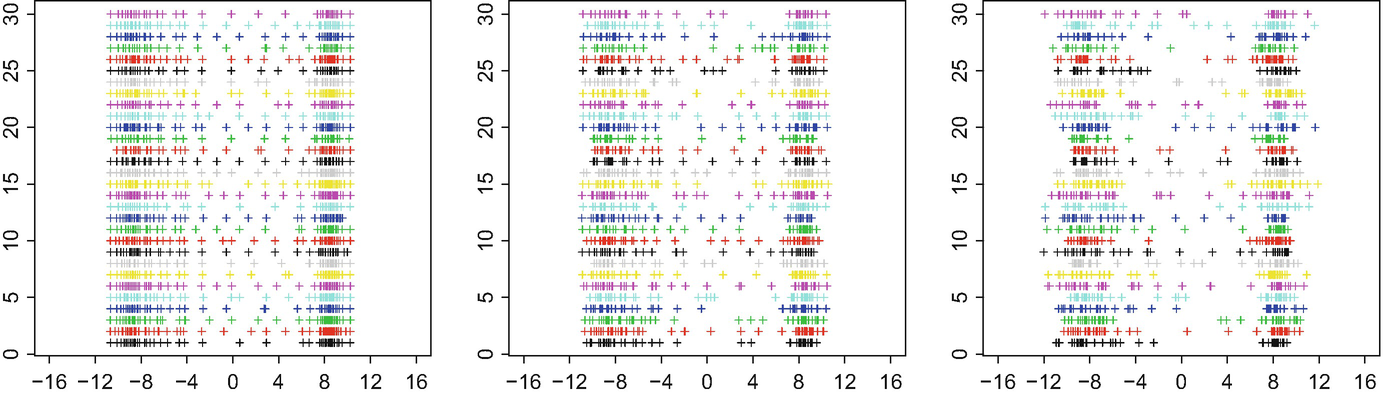
Registered point processes as a function of the smoothing parameter multiplier s. Left: s = 0.1; middle: s = 1; right: s = 3. Here, n = 30 and τ = 43
4.6 Convergence Rates and a Central Limit Theorem on the Real Line
Since the conditional mean measures Λ
i are discretely observed, the rate of convergence of our estimators will be affected by the rate at which the number of observed points per process  increases to infinity. The latter is controlled by the next lemma, which is valid for any complete separable metric space
increases to infinity. The latter is controlled by the next lemma, which is valid for any complete separable metric space  .
.
 denote the total number of observed points. If
denote the total number of observed points. If  , then there exists a constant C
Π > 0, depending only on the distribution of Π, such that almost surely
, then there exists a constant C
Π > 0, depending only on the distribution of Π, such that almost surely 

One can also show that the limit superior of the same quantity is bounded by a constant  . If
. If  is bounded below, then the same result holds but with worse constants. If only τ
n →∞, then the result holds for each i separately but in probability.
is bounded below, then the same result holds but with worse constants. If only τ
n →∞, then the result holds for each i separately but in probability.
The proof is a simple application of Chernoff bounds; see page 108 in the supplement.
 by the more transparent order τ
n. As in the consistency proof, the idea is to write
by the more transparent order τ
n. As in the consistency proof, the idea is to write 
 converges to λ is a sum of three separate terms. We recall the standard
converges to λ is a sum of three separate terms. We recall the standard  terminology: if X
n and Y
n are random variables, then
terminology: if X
n and Y
n are random variables, then  means that the sequence (X
n∕Y
n) is bounded in probability, which by definition is the condition
means that the sequence (X
n∕Y
n) is bounded in probability, which by definition is the condition 
 , we will sometimes write
, we will sometimes write  . The former notation emphasises the condition that X
n grows no faster than Y
n, while the latter stresses that Y
n grows at least as fast as X
n (which is of course the same assertion). Finally,
. The former notation emphasises the condition that X
n grows no faster than Y
n, while the latter stresses that Y
n grows at least as fast as X
n (which is of course the same assertion). Finally,  means that X
n∕Y
n → 0 in probability.
means that X
n∕Y
n → 0 in probability. )
) and that Π is either a Poisson process or a binomial process. Then
and that Π is either a Poisson process or a binomial process. Then ![$$\displaystyle \begin{aligned} W_2(\widehat\lambda_n,\lambda) \le O_{{\mathbb{P}}}\left(\frac 1{\sqrt{n}}\right) + O_{{\mathbb{P}}}\left(\frac 1{\sqrt[4]{\tau_n}}\right) + O_{{\mathbb{P}}}\left(\sigma_n\right), \qquad \sigma_n= \frac 1n\sum_{i=1}^n\sigma_i^{(n)}, \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equch.png)
where all the constants in the
 terms are explicit.
terms are explicit.
Unlike classical density estimation, no assumptions on the rate of decay of σ
n are required, because we only need to estimate the distribution function and not the derivative. If the smoothing parameter is chosen to be ![$$\sigma _i^{(n)}=[N_i^{(n)}]^{-\alpha }$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_IEq297.png) for some α > 0 and
for some α > 0 and  , then by Lemma 4.6.1
, then by Lemma 4.6.1  . For example, if Rosenblatt’s rule α = 1∕5 is employed, then the
. For example, if Rosenblatt’s rule α = 1∕5 is employed, then the  term can be replaced by
term can be replaced by ![$$O_{\mathbb {P}}(1/\sqrt [5]{\tau _n})$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_IEq301.png) .
.
One can think about the parameter τ as separating the sparse and dense regimes as in classical functional data analysis (see also Wu et al. [132]). If τ is bounded, then the setting is ultra sparse and consistency cannot be achieved. A sparse regime can be defined as the case where τ
n →∞ but slower than  . In that case, consistency is guaranteed, but some point patterns will be empty. The dense regime can be defined as τ
n ≫ n
2, in which case the amplitude variation is negligible asymptotically when compared with the phase variation.
. In that case, consistency is guaranteed, but some point patterns will be empty. The dense regime can be defined as τ
n ≫ n
2, in which case the amplitude variation is negligible asymptotically when compared with the phase variation.
The exponent − 1∕4 of τ
n can be shown to be optimal without further assumptions, but it can be improved to − 1∕2 if  for some 𝜖 > 0, where f
Λ is the density of Λ (see Sect. 4.7). In terms of T, the condition is that
for some 𝜖 > 0, where f
Λ is the density of Λ (see Sect. 4.7). In terms of T, the condition is that  for some 𝜖 and λ has a density bounded below. When this is the case, τ
n needs to compared with n rather than n
2 in the next paragraph and the next theorem.
for some 𝜖 and λ has a density bounded below. When this is the case, τ
n needs to compared with n rather than n
2 in the next paragraph and the next theorem.
Theorem 4.6.3 provides conditions for the optimal parametric rate  to be achieved: this happens if we set σ
n to be of the order
to be achieved: this happens if we set σ
n to be of the order  or less and if τ
n is of the order n
2 or more. But if the last two terms in Theorem 4.6.3 are negligible with respect to n
−1∕2, then a sort of central limit theorem holds for
or less and if τ
n is of the order n
2 or more. But if the last two terms in Theorem 4.6.3 are negligible with respect to n
−1∕2, then a sort of central limit theorem holds for  :
:
 and λ possesses an invertible distribution function F
λ on K. Then
and λ possesses an invertible distribution function F
λ on K. Then 

If the density f λ exists and is (piecewise) continuous and bounded below on K, then the weak convergence also holds in L 2(K).
In view of Sect. 2.3, Theorem 4.6.5 can be interpreted as asymptotic normality of  in the tangential sense:
in the tangential sense:  converges to a Gaussian random element in the tangent space Tanλ, which is a subset of L
2(λ). The additional smoothness conditions allow to switch to the space L
2(K), which is independent of the unknown template measure λ.
converges to a Gaussian random element in the tangent space Tanλ, which is a subset of L
2(λ). The additional smoothness conditions allow to switch to the space L
2(K), which is independent of the unknown template measure λ.
See pages 109 and 110 in the supplement for detailed proofs of these theorems. Below we sketch the main ideas only.
Proof(Proof of Theorem 4.6.3)
The quantile formula  from Sect. 1.5 and the average quantile formula for the Fréchet mean (Sect. 3.1.4) show that the oracle empirical mean
from Sect. 1.5 and the average quantile formula for the Fréchet mean (Sect. 3.1.4) show that the oracle empirical mean  follows a central limit theorem in L
2(0, 1). Since we work in the Hilbert space L
2(0, 1), Fréchet means are simple averages, so the errors in the Fréchet mean have the same rate as the errors in the Fréchet functionals. The smoothing term is easily controlled by Lemma 4.4.2.
follows a central limit theorem in L
2(0, 1). Since we work in the Hilbert space L
2(0, 1), Fréchet means are simple averages, so the errors in the Fréchet mean have the same rate as the errors in the Fréchet functionals. The smoothing term is easily controlled by Lemma 4.4.2.
Controlling the amplitude term is more difficult. Bounds can be given using the machinery sketched in Sect. 4.7, but we give a more elementary proof by reducing to the 1-Wasserstein case (using (2.2)), which can be more easily handled in terms of distributions functions (Corollary 1.5.3).
4.7 Convergence of the Empirical Measure and Optimality
One may find the term ![$$O_{\mathbb {P}}(1/\sqrt [4]{\tau _n})$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_IEq313.png) in Theorem 4.6.3 to be somewhat surprising, and expect that it ought to be
in Theorem 4.6.3 to be somewhat surprising, and expect that it ought to be  . The goal of this section is to show why the rate
. The goal of this section is to show why the rate ![$$1/\sqrt [4]{\tau _n}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_IEq315.png) is optimal without further assumptions and discuss conditions under which it can be improved to the optimal rate
is optimal without further assumptions and discuss conditions under which it can be improved to the optimal rate  . For simplicity, we concentrate on the case τ
n = n and assume that the point process Π is binomial; the Poisson case being easily obtained from the simplified one (using Lemma 4.6.1). We are thus led to study rates of convergence of empirical measures in the Wasserstein space. That is to say, for a fixed exponent p ≥ 1 and a fixed measure
. For simplicity, we concentrate on the case τ
n = n and assume that the point process Π is binomial; the Poisson case being easily obtained from the simplified one (using Lemma 4.6.1). We are thus led to study rates of convergence of empirical measures in the Wasserstein space. That is to say, for a fixed exponent p ≥ 1 and a fixed measure  , we consider independent random variables X
1, … with law μ and the empirical measure
, we consider independent random variables X
1, … with law μ and the empirical measure  . The first observation is that
. The first observation is that  :
:
 be any measure. Then
be any measure. Then


 is bounded by the sample average Z
n of a random variable
is bounded by the sample average Z
n of a random variable  that has a finite expectation. A version of the dominated converge theorem (given on page 111 in the supplement) implies that
that has a finite expectation. A version of the dominated converge theorem (given on page 111 in the supplement) implies that  . Now invoke Jensen’s inequality.
. Now invoke Jensen’s inequality.The sequence  is not monotone, as the simple example μ = (δ
0 + δ
1)∕2 shows (see page 111 in the supplement).
is not monotone, as the simple example μ = (δ
0 + δ
1)∕2 shows (see page 111 in the supplement).
The next question is how quickly  vanishes when
vanishes when  . We shall begin with two simple general lower bounds, then discuss upper bounds in the one-dimensional case, put them in the context of Theorem 4.6.3, and finally briefly touch the d-dimensional case.
. We shall begin with two simple general lower bounds, then discuss upper bounds in the one-dimensional case, put them in the context of Theorem 4.6.3, and finally briefly touch the d-dimensional case.
 Lower Bound)
Lower Bound) be nondegenerate. Then there exists a constant c(μ) > 0 such that for all p ≥ 1 and all n
be nondegenerate. Then there exists a constant c(μ) > 0 such that for all p ≥ 1 and all n 
 , a bounded 1-Lipschitz function such that f(a) = 0 < f(b). Then
, a bounded 1-Lipschitz function such that f(a) = 0 < f(b). Then 
by the central limit theorem and the Kantorovich–Rubinstein theorem (1.11).
For discrete measures, the rates scale badly with p. More generally:
 such that μ(A ∪ B) = 1,
such that μ(A ∪ B) = 1, 
Then for any p ≥ 1 there exists c
p(μ) > 0 such that  .
.
Any nondegenerate finitely discrete measure μ satisfies this condition, and so do “non-pathological” countably discrete ones. (An example of a “pathological” measure is one assigning positive mass to any rational number.)
Let k ∼ B(n, q = μ(A)) denote the number of points from the sample (X
1, …, X
n) that fall in A. Then a mass of |k∕n − q| must travel between A and B, a distance of at least  . Thus,
. Thus,  , and the result follows from the central limit theorem for k; see page 112 in the supplement for the full details.
, and the result follows from the central limit theorem for k; see page 112 in the supplement for the full details.


 . It turns out that this condition is necessary, and has a more subtle counterpart for any p ≥ 1. Let f denote the density of the absolutely continuous part of μ (so f ≡ 0 if μ is discrete).
. It turns out that this condition is necessary, and has a more subtle counterpart for any p ≥ 1. Let f denote the density of the absolutely continuous part of μ (so f ≡ 0 if μ is discrete). . The condition
. The condition ![$$\displaystyle \begin{aligned} J_p(\mu) ={{\int_{{\mathbb{R}}} \! {\frac{[F(t) (1 - F(t))]^{p/2}} {[f(t)]^{p-1}}} \, \mathrm{d}t}} <\infty ,\qquad (0^0=1) \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equcs.png)
is necessary and sufficient for  .
.
See Bobkov and Ledoux [25, Theorem 5.10] for a proof for the J p condition, and Theorems 5.1 and 5.3 for the values of the constants and a stronger result.
When p > 1, for J p(μ) to be finite, the support of μ must be connected; this is not needed when p = 1. Moreover, the J p condition is satisfied when f is bounded below (in which case the support of μ must be compact). However, smoothness alone does not suffice, even for measures with positive density on a compact support. More precisely, we have:

 . Indeed, by Jensen’s inequality and (2.2), for any μ ∈ P([0, 1]),
. Indeed, by Jensen’s inequality and (2.2), for any μ ∈ P([0, 1]), ![$$\displaystyle \begin{aligned} \mathbb{E} W_p(\mu_n,\mu) \le \left[\mathbb{E} W_p^p(\mu_n,\mu)\right]^{1/p} \le [\mathbb{E} W_1(\mu_n,\mu)]^{1/p} \le n^{-1/(2p)}. \end{aligned}$$](../images/456556_1_En_4_Chapter/456556_1_En_4_Chapter_TeX_Equcu.png)
 and each Λ
i are independent, we have
and each Λ
i are independent, we have 
 and then estimate its inverse square root as is done in the proof of Theorem 4.6.3.) Therefore, a sufficient condition for the rate
and then estimate its inverse square root as is done in the proof of Theorem 4.6.3.) Therefore, a sufficient condition for the rate  to hold is that
to hold is that  and a necessary condition is that
and a necessary condition is that  . These hold if there exists δ > 0 such that with probability one Λ has a density bounded below by δ. Since Λ = T#λ, this will happen provided that λ itself has a bounded below density and T has a bounded below derivative. Bigot et al. [23] show that the rate
. These hold if there exists δ > 0 such that with probability one Λ has a density bounded below by δ. Since Λ = T#λ, this will happen provided that λ itself has a bounded below density and T has a bounded below derivative. Bigot et al. [23] show that the rate  cannot be improved.
cannot be improved.We conclude by proving a lower bound for absolutely continuous measures and stating, without proof, an upper bound.
 have an absolutely continuous part with respect to Lebesgue measure, and let ν
n be any discrete measure supported on n points (or less). Then there exists a constant C(μ) > 0 such that
have an absolutely continuous part with respect to Lebesgue measure, and let ν
n be any discrete measure supported on n points (or less). Then there exists a constant C(μ) > 0 such that 




 , then N(μ, 𝜖, 0) ≤ K𝜖
−d.
, then N(μ, 𝜖, 0) ≤ K𝜖
−d.If for some d>2p, N(μ, 𝜖, 𝜖
dp∕(d−2p))≤K𝜖
−d, then  .
.
Comparing this with the lower bound in Lemma 4.7.4, we see that in the high-dimensional regime d > 2p, absolutely continuous measures have a worse rate than discrete ones. In the low-dimensional regime d < 2p, the situation is opposite. We also obtain that for d > 2 and a compactly supported absolutely continuous  ,
,  .
.
4.8 Bibliographical Notes
Our exposition in this chapter closely follows the papers Panaretos and Zemel [100] and Zemel and Panaretos [134].
Books on functional data analysis include Ramsay and Silverman [109, 110], Ferraty and Vieu [51], Horváth and Kokoszka [70], and Hsing and Eubank [71], and a recent review is also available (Wang et al. [127]). The specific topic of amplitude and phase variation is discussed in [110, Chapter 7] and [127, Section 5.2]. The next paragraph gives some selective references.
One of the first functional registration techniques employed dynamic programming (Wang and Gasser [128]) and dates back to Sakoe and Chiba [118]. Landmark registration consists of identifying salient features for each curve, called landmarks, and aligning them (Gasser and Kneip [61]; Gervini and Gasser [63]). In pairwise synchronisation (Tang and Müller [122]) one aligns each pair of curves and then derives an estimator of the warp functions by linear averaging of the pairwise registration maps. Another class of methods involves a template curve, to which each observation is registered, minimising a discrepancy criterion; the template is then iteratively updated (Wang and Gasser [129]; Ramsay and Li [108]). James [72] defines a “feature function” for each curve and uses the moments of the feature function to guarantee identifiability. Elastic registration employs the Fisher–Rao metric that is invariant to warpings and calculates averages in the resulting quotient space (Tucker et al. [123]). Other techniques include semiparametric modelling (Rønn [115]; Gervini and Gasser [64]) and principal components registration (Kneip and Ramsay [82]). More details can be found in the review article by Marron et al. [90]. Wrobel et al. [131] have recently developed a registration method for functional data with a discrete flavour. It is also noteworthy that a version of the Wasserstein metric can also be used in the functional case (Chakraborty and Panaretos [34]).
The literature on the point processes case is more scarce; see the review by Wu and Srivastava [133].
A parametric version of Theorem 4.2.4 was first established by Bigot and Klein [22, Theorem 5.1] in  , extended to a compact nonparametric formulation in Zemel and Panaretos [134]. There is an infinite-dimensional linear version in Masarotto et al. [91]. The current level of generality appears to be new.
, extended to a compact nonparametric formulation in Zemel and Panaretos [134]. There is an infinite-dimensional linear version in Masarotto et al. [91]. The current level of generality appears to be new.
Theorem 4.4.1 is a stronger version of Panaretos and Zemel [100, Theorem 1] where it was assumed that τ
n must diverge to infinity faster than  . An analogous construction under the Bayesian paradigm can be found in Galasso et al. [58]. Optimality of the rates of convergence in Theorem 4.6.3 is discussed in detail by Bigot et al. [23], where finiteness of the functional J
2 (see Sect. 4.7) is assumed and consequently
. An analogous construction under the Bayesian paradigm can be found in Galasso et al. [58]. Optimality of the rates of convergence in Theorem 4.6.3 is discussed in detail by Bigot et al. [23], where finiteness of the functional J
2 (see Sect. 4.7) is assumed and consequently  is improved to
is improved to  .
.
As far as we know, Theorem 4.6.5 (taken from [100]) is the first central limit theorem for Fréchet means in Wasserstein space. When the measures Λ
i are observed exactly (no amplitude variation: τ
n = ∞ and σ = 0) Kroshnin et al. [84] have recently proven a central limit theorem for random Gaussian measures in arbitrary dimension, extending a previous result of Agueh and Carlier [3]. It seems likely that in a fully nonparametric setting, the rates of convergence (compare Theorem 4.6.3) might be slower than  ; see Ahidar-Coutrix et al. [4].
; see Ahidar-Coutrix et al. [4].
The magnitude of the amplitude variation in Theorem 4.6.3 pertains to the rates of convergence of  to zero (Sect. 4.7). This is a topic of intense research, dating back to the seminal paper by Dudley [46], where a version of Theorem 4.7.8 with p = 1 is shown for the bounded Lipschitz metric. The lower bounds proven in this section were adapted from [46], Fournier and Guillin [54], and Weed and Bach [130].
to zero (Sect. 4.7). This is a topic of intense research, dating back to the seminal paper by Dudley [46], where a version of Theorem 4.7.8 with p = 1 is shown for the bounded Lipschitz metric. The lower bounds proven in this section were adapted from [46], Fournier and Guillin [54], and Weed and Bach [130].
The version of Theorem 4.7.8 given here can be found in [130] and extends Boissard and Le Gouic [27]. Both papers [27, 130] work in a general setting of complete separable metric spaces. An additional  term appears in the limiting case d = 2p, as already noted (for p = 1) by [46], and the classical work of Ajtai et al. [5] for μ uniform on [0, 1]2. More general results are available in [54]. A longer (but far from being complete) bibliography is given in the recent review by Panaretos and Zemel [101, Subsection 3.3.1], including works by Barthe, Dobrić, Talagrand, and coauthors on almost sure results and deviation bounds for the empirical Wasserstein distance.
term appears in the limiting case d = 2p, as already noted (for p = 1) by [46], and the classical work of Ajtai et al. [5] for μ uniform on [0, 1]2. More general results are available in [54]. A longer (but far from being complete) bibliography is given in the recent review by Panaretos and Zemel [101, Subsection 3.3.1], including works by Barthe, Dobrić, Talagrand, and coauthors on almost sure results and deviation bounds for the empirical Wasserstein distance.
The J
1 condition is due to del Barrio et al. [43], who showed it to be necessary and sufficient for the empirical process  to converge in distribution to
to converge in distribution to  , with
, with  Brownian bridge. The extension to 1 ≤ p ≤∞ (and a lot more) can be found in Bobkov and Ledoux [25], employing order statistics and beta distributions to reduce to the uniform case. Alternatively, one may consult Mason [92], who uses weighted approximations to Brownian bridges.
Brownian bridge. The extension to 1 ≤ p ≤∞ (and a lot more) can be found in Bobkov and Ledoux [25], employing order statistics and beta distributions to reduce to the uniform case. Alternatively, one may consult Mason [92], who uses weighted approximations to Brownian bridges.
An important aspect that was not covered here is that of statistical inference of the Wasserstein distance on the basis of the empirical measure. This is a challenging question and results by del Barrio, Munk, and coauthors are available for one-dimensional, elliptical, or discrete measures, as explained in [101, Section 3].

Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.





