© The Author(s) 2020
V. M. Panaretos, Y. ZemelAn Invitation to Statistics in Wasserstein SpaceSpringerBriefs in Probability and Mathematical Statisticshttps://doi.org/10.1007/978-3-030-38438-8_2

2. The Wasserstein Space

Victor M. Panaretos1  and Yoav Zemel2
(1)
Institute of Mathematics, EPFL, Lausanne, Switzerland
(2)
Statistical Laboratory, University of Cambridge, Cambridge, UK
 

The Kantorovich problem described in the previous chapter gives rise to a metric structure, the Wasserstein distance, in the space of probability measures $$P(\mathcal X)$$ on a space $$\mathcal X$$ . The resulting metric space, a subspace of $$P(\mathcal X)$$ , is commonly known as the Wasserstein space $$\mathcal W$$ (although, as Villani [125, pages 118–119] puts it, this terminology is “very questionable”; see also Bobkov and Ledoux [25, page 4]). In Chap. 4, we shall see that this metric is in a sense canonical when dealing with warpings, that is, deformations of the space $$\mathcal X$$ (for example, in Theorem 4.​2.​4). In this chapter, we give the fundamental properties of the Wasserstein space. After some basic definitions, we describe the topological properties of that space in Sect. 2.2. It is then explained in Sect. 2.3 how $$\mathcal W$$ can be endowed with a sort of infinite-dimensional Riemannian structure. Measurability issues are dealt with in the somewhat technical Sect. 2.4.

2.1 Definition, Notation, and Basic Properties

Let $$\mathcal X$$ be a separable Banach space. The p-Wasserstein space on $$\mathcal X$$ is defined as
$$\displaystyle \begin{aligned} \mathcal W_p(\mathcal X) =\left\{\mu\in P(\mathcal X): \int_{\mathcal{X}}{\|x\|{}^p} \! \mathrm{d} \, {\mu(x)} <\infty \right\} ,\qquad p\ge1. \end{aligned}$$
We will sometimes abbreviate and write simply $$\mathcal W_p$$ instead of $$\mathcal W_p(\mathcal X)$$ .
Recall that if $$\mu ,\nu \in P(\mathcal X)$$ , then Π(μ, ν) is defined to be the set of measures $$\pi \in P(\mathcal X^2)$$ having μ and ν as marginals in the sense of (1.​2). The p-Wasserstein distance between μ and ν is defined as the minimal total transportation cost between μ and ν in the Kantorovich problem with respect to the cost function c p(x, y) = ∥x − y∥p:
$$\displaystyle \begin{aligned} W_p(\mu,\nu) =\left(\inf_{\pi\in \varPi(\mu,\nu)}C_p(\pi)\right)^{1/p} =\left(\inf_{\pi\in \varPi(\mu,\nu)} {\int_{\mathcal X\times\mathcal X}^{} \! \|x_1 - x_2\|{}^p \, \mathrm{d}\pi(x_1,x_2)}\right)^{1/p}. \end{aligned}$$
The Wasserstein distance between μ and ν is finite when both measures are in $$\mathcal W_p(\mathcal X)$$ , because
$$\displaystyle \begin{aligned} \|x_1 - x_2\|{}^p \le 2^p\|x_1\|{}^p + 2^p\|x_2\|{}^p. \end{aligned}$$
Thus, W p is finite on $$[\mathcal W_p(\mathcal X)]^2=\mathcal W_p(\mathcal X)\times \mathcal W_p(\mathcal X)$$ ; it is nonnegative and symmetric and it is easy to see that W p(μ, ν) = 0 if and only if μ = ν. A proof that W p is a metric (satisfies the triangle inequality) on $$\mathcal W_p$$ can be found in Villani [124, Chapter 7].

The aforementioned setting is by no means the most general one can consider. Firstly, one can define W p and $$\mathcal W_p$$ for 0 < p < 1 by removing the power 1∕p from the infimum and the limit case p = 0 yields the total variation distance. Another limit case can be defined as W ∞(μ, ν) =limp→∞W p(μ, ν). Moreover, W p and $$\mathcal W_p$$ can be defined whenever $$\mathcal X$$ is a complete and separable metric space (or even only separable; see Clément and Desch [36]): one fixes some x 0 in $$\mathcal X$$ and replaces ∥x∥ by d(x, x 0). Although the topological properties below still hold at that level of generality (except when p = 0 or p = ∞), for the sake of simplifying the notation we restrict the discussion to Banach spaces. It will always be assumed without explicit mention that 1 ≤ p < ∞.

The space $$\mathcal W_p(\mathcal X)$$ is defined as the collection of measures μ such that W p(μ, δ 0) < ∞ with δ x being a Dirac measure at x. Of course, W p(μ, ν) can be finite even if $$\mu ,\nu \notin \mathcal W_p(\mathcal X)$$ . But if $$\mu \in \mathcal W_p(\mathcal X)$$ and $$\nu \notin \mathcal W_p(\mathcal X)$$ , then W p(μ, ν) is always infinite. This can be seen from the triangle inequality
$$\displaystyle \begin{aligned} \infty =W_p(\nu,\delta_0) \le W_p(\mu,\delta_0) + W_p(\mu,\nu). \end{aligned}$$
In the sequel, we shall almost exclusively deal with measures in $$\mathcal W_p(\mathcal X)$$ .
The Wasserstein spaces are ordered in the sense that if q ≥ p, then $$\mathcal W_q(\mathcal X)\subseteq \mathcal W_p(\mathcal X)$$ . This property extends to the distances in the form:
$$\displaystyle \begin{aligned} q\ge p\ge1 \quad \Longrightarrow \quad W_q(\mu,\nu) \ge W_p(\mu,\nu). \end{aligned} $$
(2.1)
To see this, let π ∈ Π(μ, ν) be optimal with respect to q. Jensen’s inequality for the convex function z↦z q∕p gives
$$\displaystyle \begin{aligned} W_q^q(\mu,\nu) ={\int_{\mathcal X^2}^{} \! \|x - y\|{}^q \, \mathrm{d}\pi(x,y)} \ge\left({\int_{\mathcal X^2}^{} \! \|x-y\|{}^p \, \mathrm{d}\pi(x,y)}\right)^{q/p} \ge W_p^q(\mu,\nu). \end{aligned}$$
The converse of (2.1) fails to hold in general, since it is possible that W p be finite while W q is infinite. A converse can be established, however, if μ and ν are bounded:
$$\displaystyle \begin{aligned} q{\kern-1pt}\ge{\kern-1pt} p{\kern-1pt}\ge {\kern-1pt} 1, \quad \mu(K){\kern-1pt}={\kern-1pt}\nu(K){\kern-1pt}={\kern-1pt}1 \quad \!\! \Longrightarrow \!\!\quad W_q(\mu,\nu) {\kern-1pt}\le{\kern-1pt} W_p^{p/q}(\mu,\nu) \left(\sup_{x,y\in K}\|x{\kern-1pt}-{\kern-1pt}y\|\right)^{1-p/q}. \end{aligned} $$
(2.2)
Indeed, if we denote the supremum by d K and let π be now optimal with respect to p, then π(K × K) = 1 and
$$\displaystyle \begin{aligned} W_q^q(\mu,\nu) \le{\int_{K^2}^{} \! \|x - y\|{}^q \, \mathrm{d}\pi(x,y)} \le d_K^{q-p}{\int_{K^2}^{} \! \|x-y\|{}^p \, \mathrm{d}\pi(x,y)} =d_K^{q-p} W_p^p(\mu,\nu). \end{aligned} $$
Another useful property of the Wasserstein distance is the upper bound
$$\displaystyle \begin{aligned} \mathcal W_p(\mathbf{t}\#\mu,\mathbf{s}\#\mu) \le \left({\int_{\mathcal{X}} {\|\mathbf{t}(x) - \mathbf{s}(x)\|{}^p} \! \mathrm{d}\, {\mu(x)}} \right)^{1/p} =\|\ \|\mathbf{t} - \mathbf{s}\|{}_{\mathcal{X}}\ \|{}_{L_p(\mu)} \end{aligned} $$
(2.3)
for any pair of measurable functions $$\mathbf {t},\mathbf {s}:\mathcal X\to \mathcal X$$ . Situations where this inequality holds as equality and t and s are optimal maps are related to compatibility of the measures μ, ν = t#μ and ρ = s#μ (see Sect. 2.3.2) and will be of conceptual importance in the context of Fréchet means (see Sect. 3.​1).

We also recall the notation B R(x 0) = {x : ∥x − x 0∥ < R} and $$\overline B_R(x_0)=\{x:\|x-x_0\|\le R\}$$ for open and closed balls in $$\mathcal X$$ .

2.2 Topological Properties

2.2.1 Convergence, Compact Subsets

The topology of a space is determined by the collection of its closed sets. Since $$\mathcal W_p(\mathcal X)$$ is a metric space, whether a set is closed or not depends on which sequences in $$\mathcal W_p(\mathcal X)$$ converge. The following characterisation from Villani [124, Theorem 7.12] will be very useful.

Theorem 2.2.1 (Convergence in Wasserstein Space)
Let $$\mu ,\mu _n\in \mathcal W_p(\mathcal X)$$ . Then the following are equivalent:
  1. 1.

    W p(μ n, μ) → 0 as n →∞;

     
  2. 2.

    μ n → μ weakly and $${\int _{\mathcal {X}}{\|x\|{ }^p} \mathrm {d}{\mu _n(x)}} \to \int _{\mathcal {X}}{\|x\|{ }^p}\mathrm {d}{\mu (x)}$$ ;

     
  3. 3.
    μ n → μ weakly and
    $$\displaystyle \begin{aligned} \sup_n{\int_{\{x:\|x\|&gt;R\}}^{} \! \|x\|{}^p \, \mathrm{d}\mu_n(x)} \to 0, \qquad R\to\infty; \end{aligned} $$
    (2.4)
     
  4. 4.
    for any C > 0 and any continuous $$f:\mathcal X\to \mathbb {R}$$ such that |f(x)|≤ C(1 + ∥x∥p) for all x,
    $$\displaystyle \begin{aligned} {\int_{\mathcal{X}}{f(x)}\mathrm{d}{\mu_n(x)}} \to{\int_{\mathcal{X}}{f(x)}\mathrm{d}{\mu(x)}}. \end{aligned}$$
     
  5. 5.

    (Le Gouic and Loubes [ 87, Lemma 14]) μ n → μ weakly and there exists $$\nu \in \mathcal W_p(\mathcal X)$$ such that W p(μ n, ν) → W p(μ, ν).

     

Consequently, the Wasserstein topology is finer than the weak topology induced on $$\mathcal W_p(\mathcal X)$$ from $$P(\mathcal X)$$ . Indeed, let $$\mathcal A\subseteq \mathcal W_p(\mathcal X)$$ be weakly closed. If $$\mu _n\in \mathcal A$$ converge to μ in $$\mathcal W_p(\mathcal X)$$ , then μ n → μ weakly, so $$\mu \in \mathcal A$$ . In other words, the Wasserstein topology has more closed sets than the induced weak topology. Moreover, each $$\mathcal W_p(\mathcal X)$$ is a weakly closed subset of $$P(\mathcal X)$$ by the same arguments that lead to (1.​3). In view of Theorem 2.2.1, a common strategy to establish Wasserstein convergence is to first show tightness and obtain weak convergence, hence a candidate limit, and then show that the stronger Wasserstein convergence actually holds. In some situations, the last part is automatic:

Corollary 2.2.2

Let $$K\subset \mathcal X$$ be a bounded set and suppose that μ n(K) = 1 for all n ≥ 1. Then W p(μ n, μ) → 0 if and only if μ n → μ weakly.

Proof

This is immediate from (2.4).

The fact that convergence in $$\mathcal W_p$$ is stronger than weak convergence is exemplified in the following result. If μ n → μ and ν n → ν in $$\mathcal W_p(\mathcal X)$$ , then it is obvious that W p(μ n, ν n) → W p(μ, ν). But if the convergence is only weak, then the Wasserstein distance is still lower semicontinuous:
$$\displaystyle \begin{aligned} \liminf_{n\to\infty} W_p(\mu_n,\nu_n) \ge W_p(\mu,\nu). \end{aligned} $$
(2.5)
This follows from Theorem 1.​7.​2 and (1.​3).

Before giving some examples, it will be convenient to formulate Theorem 2.2.1 in probabilistic terms. Let X, X n be random elements on $$\mathcal X$$ with laws $$\mu ,\mu _n\in \mathcal W_p(\mathcal X)$$ . Assume without loss of generality that X, X n are defined on the same probability space $$(\varOmega ,\mathcal F,\mathbb {P})$$ and write W p(X n, X) to denote W p(μ n, μ). Then W p(X n, X) → 0 if and only if X n → X weakly and $$\mathbb {E} \|X_n\|{ }^p\to \mathbb {E} \|X\|{ }^p$$ .

An early example of the use of Wasserstein metric in statistics is due to Bickel and Freedman [21]. Let X n be independent and identically distributed random variables with mean zero and variance 1 and let Z be a standard normal random variable. Then $$Z_n=\sum _{i=1}^nX_i/\sqrt {n}$$ converge weakly to Z by the central limit theorem. But $$\mathbb {E} Z_n^2=1=\mathbb {E} Z^2$$ , so W 2(Z n, Z) → 0. Let $$Z_n^*$$ be a bootstrapped version of Z n constructed by resampling the X n’s. If $$W_2(Z_n^*,Z_n)\to 0$$ , then $$W_2(Z_n^*,Z)\to 0$$ and in particular $$Z_n^*$$ has the same asymptotic distribution as Z n.

Another consequence of Theorem 2.2.1 is that (in the presence of weak convergence) convergence of moments automatically yields convergence of smaller moments (there are, however, more elementary ways to see this). In the previous example, for instance, one can also conclude that $$\mathbb {E} |Z_n|{ }^p\to \mathbb {E}|Z|{ }^p$$ for any p ≤ 2 by the last condition of the theorem. If in addition $$\mathbb {E} X_1^4&lt;\infty $$ , then
$$\displaystyle \begin{aligned} \mathbb{E} Z_n^4 =3 - \frac 3n + \frac{\mathbb{E} X_1^4}n \to 3 =\mathbb{E} Z^4 \end{aligned}$$
(see Durrett [49, Theorem 2.3.5]) so W 4(Z n, Z) → 0 and all moments up to order 4 converge.

Condition (2.4) is called uniform integrability of the function x↦∥x∥p with respect to the collection (μ n). Of course, it holds for a single measure $$\mu \in \mathcal W_p(\mathcal X)$$ by the dominated convergence theorem. This condition allows us to characterise compact sets in the Wasserstein space. One should beware that when $$\mathcal X$$ is infinite-dimensional, (2.4) alone is not sufficient in order to conclude that μ n has a convergent subsequence: take μ n to be Dirac measures at e n with (e n) an orthonormal basis of a Hilbert space $$\mathcal X$$ (or any sequence with ∥e n∥ = 1 that has no convergent subsequence, if $$\mathcal X$$ is a Banach space). The uniform integrability (2.4) must be accompanied with tightness, which is a consequence of (2.4) only when $$\mathcal X=\mathbb {R}^d$$ .

Proposition 2.2.3 (Compact Sets in $$\mathcal W_p$$ )
A weakly tight set $$\mathcal K{\,\subseteq \,} \mathcal W_p$$ is Wasserstein-tight (has a compact closure in $$\mathcal W_p$$ ) if and only if
$$\displaystyle \begin{aligned} \sup_{\mu\in\mathcal K}{\int_{\{x:\|x\|&gt;R\}}^{} \! \|x\|{}^p \, \mathrm{d}\mu(x)} \to 0, \qquad R\to\infty. \end{aligned} $$
(2.6)
Moreover, (2.6) is equivalent to the existence of a monotonically divergent function $$g:\mathbb R_+\to \mathbb R_+$$ such that
$$\displaystyle \begin{aligned} \sup_{\mu\in\mathcal K} {\int_{\mathcal X}^{} \! \|x\|{}^pg(\|x\|) \, \mathrm{d}\mu(x)} &lt;\infty. \end{aligned}$$

The proof is on page 41 of the supplement.

Remark 2.2.4

For any sequence (μ n) in $$\mathcal W_p$$ (tight or not) there exists a monotonically divergent g with $${\int _{\mathcal X} \|x\|{ }^p g(\|x\|) \, \mathrm {d}\mu _n(x)}&lt;\infty $$ for all n.

Corollary 2.2.5 (Measures with Common Support)
Let $$K\subseteq \mathcal X$$ be a compact set. Then
$$\displaystyle \begin{aligned} \mathcal K=\mathcal W_p(K) =\{\mu\in P(\mathcal X):\mu(K)=1\} \subseteq\mathcal W_p(\mathcal X) \end{aligned}$$

is compact.

Proof

This is immediate, since $$\mathcal K$$ is weakly tight and the supremum in (2.6) vanishes when R is larger than the finite quantity supx ∈ K∥x∥. Finally, K is closed, so $$\mathcal K$$ is weakly closed, hence Wasserstein closed, by the portmanteau Lemma 1.​7.​1.

For future reference, we give another consequence of uniform integrability, called uniform absolute continuity
$$\displaystyle \begin{aligned} \forall\epsilon\ \exists\delta\ \forall n\ \forall A\subseteq \mathcal X\mathrm{ Borel}: \qquad \mu_n(A)\le\delta \quad \Longrightarrow\quad {\int_{A}{\|x\|{}^p}\mathrm{d}{\mu_n(x)}} &lt;\epsilon. \end{aligned} $$
(2.7)
To show that (2.4) implies (2.7), let 𝜖 > 0, choose R = R 𝜖 > 0 such that the supremum in (2.4) is smaller than 𝜖∕2, and set δ = 𝜖∕(2R p). If μ n(A) ≤ δ, then
$$\displaystyle \begin{aligned} {\int_{A}{\|x\|{}^p}\mathrm{d}{\mu_n(x)}} \le {\int_{A\cap \overline B_R(0)}^{} \! \|x\|{}^p \, \mathrm{d}\mu_n(x)} +{\int_{A\setminus \overline B_R(0)}^{} \! \|x\|{}^p \, \mathrm{d}\mu_n(x)} &lt; \delta R^p + \epsilon/2 \le\epsilon. \end{aligned}$$

2.2.2 Dense Subsets and Completeness

If we identify a measure $$\mu \in \mathcal W_p(\mathcal X)$$ with a random variable X (having distribution μ), then X has a finite p-th moment in the sense that the real-valued random variable ∥X∥ is in L p. In view of that, it should not come as a surprise that $$\mathcal W_p(\mathcal X)$$ enjoys topological properties similar to L p spaces. In this subsection, we give some examples of useful dense subsets of $$\mathcal W_p(\mathcal X)$$ and then “show” that like $$\mathcal X$$ itself, it is a complete separable metric space. In the next subsection, we describe some of the negative properties that $$\mathcal W_p(\mathcal X)$$ has, again in similarity with L p spaces.

We first show that $$\mathcal W_p(\mathcal X)$$ is separable. The core idea of the proof is the feasibility of approximating any measure with discrete measures as follows.

Let μ be a probability measure on $$\mathcal X$$ , and let X 1, X 2, … be a sequence of independent random elements in $$\mathcal X$$ with probability distribution μ. Then the empirical measure μ n is defined as the random measure $$(1/n)\sum _{i=1}^n\delta \{X_i\}$$ . The law of large numbers shows that for any (measurable) bounded or nonnegative $$f:\mathcal X\to \mathbb {R}$$ , almost surely
$$\displaystyle \begin{aligned} \int_{\mathcal{X}}f(x) \mathrm{d}\mu_n(x) =\frac 1n\sum_{i=1}^n f(X_i) \to \mathbb{E} f(X_1) =\int_{\mathcal{ X}}f(x)\mathrm{d}{\mu(x)}. \end{aligned}$$
In particular when f(x) = ∥x∥p, we obtain convergence of moments of order p. Hence by Theorem 2.2.1, if $$\mu \in \mathcal W_p(\mathcal X)$$ , then μ n → μ in $$\mathcal W_p(\mathcal X)$$ if and only if μ n → μ weakly. We know that integrals of bounded functions converge with probability one, but the null set where convergence fails may depend on the chosen function and there are uncountably many such functions. When $$\mathcal X=\mathbb {R}^d$$ , by the portmanteau Lemma 1.​7.​1 we can replace the collection $$C_b(\mathcal X)$$ by indicator functions of rectangles of the form (−∞, a 1] ×⋯ × (−∞, a d] for $$a=(a_1,\dots ,a_d)\in \mathbb {R}^d$$ . It turns out that the countable collection provided by rational vectors a suffices (see the proof of Theorem 4.​4.​1 where this is done in a more complicated setting). For more general spaces $$\mathcal X$$ , we need to find another countable collection {f j} such that convergence of the integrals of f j for all j suffices for weak convergence. Such a collection exists, by using bounded Lipschitz functions (Dudley [47, Theorem 11.4.1]); an alternative construction can be found in Ambrosio et al. [12, Section 5.1]. Thus:
Proposition 2.2.6 (Empirical Measures in $$\mathcal W_p$$ )

For any $$\mu \in P(\mathcal X)$$ and the corresponding sequence of empirical measures μ n, W p(μ n, μ) → 0 almost surely if and only if $$\mu \in \mathcal W_p(\mathcal X)$$ .

Indeed, if $$\mu \notin \mathcal W_p(\mathcal X)$$ , then W p(μ n, μ) is infinite for all n, since μ n is compactly supported, hence in $$\mathcal W_p(\mathcal X)$$ .

Proposition 2.2.6 is the basis for constructing dense subsets of the Wasserstein space.

Theorem 2.2.7 (Dense Subsets of $$\mathcal W_p$$ )
The following collections of measures are dense in $$\mathcal W_p(\mathcal X)$$ :
  1. 1.

    finitely supported measures with rational weights;

     
  2. 2.

    compactly supported measures;

     
  3. 3.

    finitely supported measures with rational weights on a dense subset $$A\subseteq \mathcal X$$ ;

     
  4. 4.

    if $$\mathcal X=\mathbb {R}^d$$ , the collection of absolutely continuous and compactly supported measures;

     
  5. 5.

    if $$\mathcal X=\mathbb {R}^d$$ , the collection of absolutely continuous measures with strictly positive and bounded analytic densities.

     

In particular, $$\mathcal W_p$$ is separable (the third set is countable as $$\mathcal X$$ is separable).

This is a simple consequence of Proposition 2.2.6 and approximations, and the details are given on page 43 in the supplement.

Proposition 2.2.8 (Completeness)

The Wasserstein space $$\mathcal W_p(\mathcal X)$$ is complete.

One may find two different proofs in Villani [125, Theorem 6.18] and Ambrosio et al. [12, Proposition 7.1.5]. On page 43 of the supplement, we sketch an alternative argument based on completeness of the weak topology.

2.2.3 Negative Topological Properties

In the previous subsection, we have shown that $$\mathcal W_p(\mathcal X)$$ is separable and complete like L p spaces. Just like them, however, the Wasserstein space is neither locally compact nor σ-compact. For this reason, existence proofs of Fréchet means in $$\mathcal W_p(\mathcal X)$$ require tools that are more specific to this space, and do not rely upon local compactness (see Sect. 3.​1).

Proposition 2.2.9 ( $$\mathcal W_p$$ is Not Locally Compact)
Let $$\mu \in \mathcal W_p(\mathcal X)$$ and let 𝜖 > 0. Then the Wasserstein ball
$$\displaystyle \begin{aligned} \overline B_\epsilon(\mu) =\{\nu\in\mathcal W_p(\mathcal X):W_p(\mu,\nu)\le\epsilon\} \end{aligned}$$

is not compact.

Ambrosio et al. [12, Remark 7.1.9] show this when μ is a Dirac measure, and we extend their argument on page 43 of the supplement.

From this, we deduce:

Corollary 2.2.10

The Wasserstein space $$\mathcal W_p(\mathcal X)$$ is not σ-compact.

Proof

If $$\mathcal K$$ is a compact set in $$\mathcal W_p(\mathcal X)$$ , then its interior is empty by Proposition 2.2.9. A countable union of compact sets has an empty interior (hence cannot equal the entire space $$\mathcal W_p(\mathcal X)$$ ) by the Baire property, which holds on the complete metric space $$\mathcal W_p(\mathcal X)$$ by the Baire category theorem (Dudley [47, Theorem 2.5.2]).

2.2.4 Covering Numbers

Let $$\mathcal K\subset \mathcal W_p(\mathcal X)$$ be compact and assume that $$\mathcal X=\mathbb {R}^d$$ . Then for any 𝜖 > 0 the covering number
$$\displaystyle \begin{aligned} N(\epsilon;\mathcal K) {\kern-1pt}={\kern-1pt}\min \left\{n{\kern-1pt}:{\kern-1pt}\exists \mu_1,\dots,\mu_n\in \mathcal W_p(\mathcal X) \mathrm{ such that }\mathcal K\subseteq \bigcup_{i=1}^n\{\mu:W_p(\mu,\mu_i){\kern-1pt}&lt;{\kern-1pt}\epsilon\}\right\} \end{aligned}$$
is finite. These numbers appear in statistics in various ways, particularly in empirical processes (see, for instance, Wainwright [126, Chapter 5]) and the goal of this subsection is to give an upper bound for $$N(\epsilon ;\mathcal K)$$ . Invoking Proposition 2.2.3, introduce a continuous monotone divergent f : [0, ∞) → [0, ∞] such that
$$\displaystyle \begin{aligned} \sup_{\mu\in\mathcal K} {\int_{\mathbb{R}^d}^{} \! \|x\|{}^pf(\|x\|) \, \mathrm{d}\mu(x)} \le 1. \end{aligned}$$
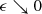The function f provides a certain measure of how compact $$\mathcal K$$ is. If $$\mathcal K=\mathcal W_p(K)$$ is the set of measures supported on a compact $$K\subseteq \mathbb {R}^d$$ , then f(L) can be taken infinite for L large, and L can be treated as a constant in the theorem. Otherwise L increases as ../images/456556_1_En_2_Chapter/456556_1_En_2_IEq122_HTML.gif, at a speed that depends on f: the faster f diverges, the slower L grows with decreasing 𝜖 and the better the bound becomes.
Theorem 2.2.11
Let 𝜖 > 0 and L = f −1(1∕𝜖 p). If d𝜖 ≤ L, then
$$\displaystyle \begin{aligned} \log N(\epsilon) \le C_1(d)\left(\frac L\epsilon\right)^d\left[(p+d)\log \frac L\epsilon + C_2(d,p)\right], \end{aligned}$$

with C 1(d) = 3deθ d, $$C_2(d,p)=(p+d)\log 3+ (p+2)\log 2 + \log \theta _d$$ and $$\theta _d=d[5+\log d+\log \log d]$$ .

Since 𝜖 > 0 is small and L is increasing in 𝜖, the restriction that d𝜖 ≤ L is typically not binding. We provide some examples before giving the proof.

Example 1: if all the measures are supported on the d-dimensional unit ball, then L can be taken equal to one, independently of 𝜖. We obtain
$$\displaystyle \begin{aligned} \widetilde N(\epsilon) :=\frac{\log N(\epsilon)}{\log1/\epsilon} \le (d+p)C_1(d)\epsilon^{-d}+\mathrm{ smaller order terms}. \end{aligned}$$
Example 2: if all the measures in $$\mathcal K$$ have uniform exponential moments, then f(L) = e L and $$\widetilde N(\epsilon )$$ is a constant times 𝜖 −d[log 1∕𝜖]d. The exponent p appears only in the constant.
Example 3: suppose that $$\mathcal K$$ is a Wasserstein ball of order p + δ, that is, f(L) = L δ. Then L ∼ 𝜖 −p∕δ and
$$\displaystyle \begin{aligned} \widetilde N(\epsilon) \le C_1(d)(p+d)(1+p/\delta)\epsilon^{-d[1+p/\delta]} \end{aligned}$$
up to smaller order terms. Here (when 0 < δ < ∞) the behaviour of $$\widetilde N(\epsilon )$$ depends more strongly upon p: if p′ < p, then we can replace δ by δ′ = δ + p − p′ > δ, leading to a smaller magnitude of $$\widetilde N(\epsilon )$$ .

Example 4: if f(L) is only $$\log L$$ , then $$\widetilde N$$ behaves like $$\epsilon ^{-(d+p)}\exp (\epsilon ^{-pd})$$ , so p has a very dominant effect.

Proof

The proof is divided into four steps.

Step 1: Compact support. Let $$P_L:\mathbb {R}^d\to \mathbb {R}^d$$ be the projection onto $$\overline B_L(0)=\{x\in \mathbb {R}^d:\|x\|\le L\}$$ and let $$\mu \in \mathcal K$$ . Then
$$\displaystyle \begin{aligned} W_p^p(\mu,P_L\#\mu) \le {\int_{\mathbb{R}^d}^{} \! \|x-P_L(x)\|{}^{p} \, \mathrm{d}\mu(x)} ={\int_{\|x\|&gt;L}^{} \! \|x - P_L(x)\|{}^{p} \, \mathrm{d}\mu(x)}\\ \le{\int_{\|x\|&gt;L}^{} \! \|x\|{}^{p} \, \mathrm{d}\mu(x)} \le \frac 1{f(L)}{\int_{\|x\|&gt;L}^{} \! \|x\|{}^{p}f(\|x\|) \, \mathrm{d}\mu(x)} \le \frac 1{f(L)}, \end{aligned} $$
and this vanishes as L →∞.
Step 2: n-Point measures. Let n = N(𝜖;B L(0)) be the covering number of the Euclidean ball in $$\mathbb {R}^d$$ . There exists a set $$x_1,\dots ,x_n\in \mathbb {R}^d$$ such that B L(0) ⊆∪B 𝜖(x i). If $$\mu \in \mathcal W_p(B_L(0))$$ , there exists a measure μ n supported on the x i’s and such that
$$\displaystyle \begin{aligned} W_p(\mu,\mu_n)\le \epsilon. \end{aligned}$$
Indeed let C 1 = B 𝜖(x 1), C i = B 𝜖(x i) ∖∪j<iB 𝜖(x j) and define μ n({x i}) = μ(C i). The transport map defined by t(x) = x i for x ∈ C i pushes μ forward to μ n and
$$\displaystyle \begin{aligned} W_p^p(\mu_n,\mu) \le \sum_{i=1}^n {\int_{C_i}^{} \! \|x-x_i\|{}^p \, \mathrm{d}\mu(x)} \le \sum_{i=1}^n \epsilon^p\mu(C_i) =\epsilon^p. \end{aligned}$$
According to Rogers [114], we have the bound
$$\displaystyle \begin{aligned} n\le e\theta_d[L/\epsilon]^d, \qquad \theta_d=d[5+\log d+\log\log d], \end{aligned}$$
whenever 𝜖 ≤ L∕d.
Step 3: Common weights. If $$\mu =\sum a_k\delta _{x_k}$$ and $$\nu =\sum b_k\delta _{x_k}$$ , then $$W_p^p(\mu ,\nu )\le \sum _k |a_k - b_k|\sup _{i,j}\|x_i - x_j\|{ }^p$$ . Let
$$\displaystyle \begin{aligned} \mu_{n,\epsilon,\delta} =\left\{ \sum_{k=1}^n a_k\delta_{x_k}: a_k\in \{0,\delta,2\delta,\dots,\lceil{1/\delta}\rceil\delta\} ;\sum a_k=1\right\}. \end{aligned}$$
This set contains fewer than (2 + 1∕δ)n−1 elements, and any measure supported on {x 1, …, x n} can be approximated by a measure in μ n,𝜖,δ with error 2L(nδ)1∕p.
Step 4: Conclusion. Let L = f −1(1∕𝜖 p), n = N(𝜖;B L(0)) and δ = [𝜖∕(2L)]p∕n. Combining the previous three steps, we obtain in the case L ≥ 𝜖d that
$$\displaystyle \begin{aligned} N(3\epsilon) \le(2+1/\delta)^{n-1} \le\!\! \left[2{\kern-1pt}+\!\left(\!\frac L\epsilon\!\right)^{p+d}2^pe\theta_d\right]^{e\theta_d[L/\epsilon]^d} \le\!\! \left[\!\left(\!\frac L\epsilon\!\right)^{p+d}2^{p+2}\theta_d\right]^{e\theta_d[L/\epsilon]^d}, \end{aligned}$$
because L∕𝜖 ≥ 1 and θ d ≥ 5. Conclude that
$$\displaystyle \begin{aligned} N(\epsilon) \le \left[3^{p+d}\left(\frac L\epsilon\right)^{p+d}2^{p+2}\theta_d\right]^{3^de\theta_d[L/\epsilon]^d}. \end{aligned}$$

2.3 The Tangent Bundle

Although the Wasserstein space $$\mathcal W_p(\mathcal X)$$ is non-linear in terms of measures, it is linear in terms of maps. Indeed, if $$\mu \in \mathcal W_p(\mathcal X)$$ and $$T_i:\mathcal X\to \mathcal X$$ are such that ∥T i∥∈ L p(μ), then $$(\alpha T_1 + \beta T_2)\#\mu \in \mathcal W_p(\mathcal X)$$ for all $$\alpha ,\beta \in \mathbb {R}$$ . Later, in Sect. 2.4, we shall see that $$\mathcal W_p(\mathcal X)$$ is in fact homeomorphic to a subset of the space of such functions. The goal of this section is to exploit the linearity of the latter in order to define the tangent bundle of $$\mathcal W_p$$ . This in particular will be used for deriving differentiability properties of the Wasserstein distance in Sect. 3.​1.​6. However, the latter can be understood at a purely analytic level, and readers uncomfortable with differential geometry can access most of the rest of the monograph without reference to this section.

We assume here that $$\mathcal X$$ is a Hilbert space and that p = 2; the results extend to any p > 1. Absolutely continuous measures are assumed to be so with respect to Lebesgue measure if $$\mathcal X=\mathbb {R}^d$$ and otherwise refer to Definition 1.​6.​4.

2.3.1 Geodesics, the Log Map and the Exponential Map in $$\mathcal W_2(\mathcal X)$$

Let $$\gamma \in \mathcal W_2(\mathcal X)$$ be absolutely continuous and $$\mu \in \mathcal W_2(\mathcal X)$$ arbitrary. From Sect. 1.​6.​1, we know that there exists a unique solution to the Monge–Kantorovich problem, and that solution is given by a transport map that we denote by $${{\mathbf {t}}_{\gamma }^{\mu }}$$ . Recalling that $$\mathbf i:\mathcal X\to \mathcal X$$ is the identity map, we can define a curve
$$\displaystyle \begin{aligned} \gamma_t=\left[\mathbf i +t({\mathbf{t}}_{\gamma}^{\mu} - \mathbf i)\right] \#\gamma,\qquad t\in[0,1]. \end{aligned}$$
This curve is known as McCann’s [93] interpolant. As hinted in the introduction to this section, it is constructed via classical linear interpolation of the transport maps $${{\mathbf {t}}_{\gamma }^{\mu }}$$ and the identity. Clearly γ 0 = γ, γ 1 = μ and from (2.3),
$$\displaystyle \begin{aligned} \begin{array}{rcl} W_2(\gamma_t,\gamma) &amp;\displaystyle &amp;\displaystyle \le \sqrt{\int_{\mathcal{X}}{\left[t(\mathbf{ t}_{\gamma}^{\mu} - \mathbf{ i})\right]^2}\mathrm{d}\gamma} =tW_2(\gamma,\mu);\\ W_2(\gamma_t,\mu) &amp;\displaystyle &amp;\displaystyle \le \sqrt{\int_{\mathcal{X}}{\left[(1-t)(\mathbf{ t}_{\gamma}^{\mu} - \mathbf{ i})\right]^2}\mathrm{d}\gamma} =(1-t)W_2(\gamma,\mu). \end{array} \end{aligned} $$
It follows from the triangle inequality in $$\mathcal W_2$$ that these inequalities must hold as equalities. Taking this one step further, we see that
$$\displaystyle \begin{aligned} W_2(\gamma_t,\gamma_s) =(t-s)W_2(\gamma,\mu), \qquad 0\le s\le t\le 1. \end{aligned}$$
In other words, McCann’s interpolant is a constant-speed geodesic in $$\mathcal W_2(\mathcal X)$$ .
In view of this, it seems reasonable to define the tangent space of $$\mathcal W_2(\mathcal X)$$ at μ as (Ambrosio et al. [12, Definition 8.5.1])
$$\displaystyle \begin{aligned} \mathrm{Tan}_\mu =\overline{\{t(\mathbf{t}-\mathbf i):\mathbf{t}={{\mathbf{t}}_{\mu}^{\nu}}\mathrm{ for some} \nu\in\mathcal W_2(\mathcal X); t&gt;0\}}^{L_2(\mu)}. \end{aligned}$$
It follows from the definition that Tanμ ⊆ L 2(μ). (Strictly speaking, Tanμ is a subset of the space of functions $$f:\mathcal X\to \mathcal X$$ such that ∥f∥∈ L 2(μ) rather than L 2(μ) itself, as in Definition 2.4.3, but we will write L 2 for simplicity.)
Although not obvious from the definition, this is a linear space. The reason is that, in $$\mathbb {R}^d$$ , Lipschitz functions are dense in L 2(μ), and for t Lipschitz the negative of a tangent element
$$\displaystyle \begin{aligned} -t(\mathbf{t} - \mathbf i) =s(\mathbf{s} - \mathbf i) ,\qquad s&gt;t\|\mathbf{t}\|{}_{\mathrm{Lip}}, \qquad \mathbf{s} = \mathbf i + \frac ts(\mathbf i - \mathbf{t}) \end{aligned}$$
lies in the tangent space, since s can be seen to belong to the subgradient of a convex function by definition of s. This also shows that Tanμ can be seen to be the L 2(μ)-closure of all gradients of $$C_c^\infty $$ functions. We refer to [12, Definition 8.4.1 and Theorem 8.5.1] for the proof and extensions to other values of p > 1 and to infinite dimensions, using cylindrical functions that depend on finitely many coordinates [12, Definition 5.1.11]. The alternative definition highlights that it is essentially the inner product in Tanμ, but not the elements themselves, that depends on μ.
The tangent space definition is valid for arbitrary measures in $$\mathcal W_2(\mathcal X)$$ . The exponential map at $$\gamma \in \mathcal W_2(\mathcal X)$$ is the restriction to Tanγ of the mapping that sends r ∈ L 2(γ) to $$[\mathbf r+\mathbf i]\#\gamma \in \mathcal W_2(\mathcal X)$$ . More explicitly, $${\exp }_\gamma :\mathrm {Tan}_\gamma \to \mathcal W_2 $$ takes the form
$$\displaystyle \begin{aligned} {\exp}_{\gamma}(t(\mathbf{t} - \mathbf i)) ={\exp}_{\gamma}([t\mathbf{t} + (1-t)\mathbf i] - \mathbf i) = [t\mathbf{t} + (1-t)\mathbf i]\#\gamma \quad (t\in\mathbb{R}). \end{aligned}$$
Thus, when γ is absolutely continuous, expγ is surjective, as can be seen from its right inverse, the log map
$$\displaystyle \begin{aligned} {\log}_\gamma:\mathcal W_2 \to \mathrm{Tan}_\gamma \qquad \log_{\gamma}(\mu) ={\mathbf{t}}_{\gamma}^{\mu} - \mathbf i, \end{aligned}$$
defined throughout $$\mathcal W_2$$ (by virtue of Theorem 1.​6.​2). In symbols,
$$\displaystyle \begin{aligned} \exp_\gamma(\log_\gamma(\mu))=\mu ,\quad \mu\in \mathcal W_2, \quad \ \mathrm{and}\quad \ \log_\gamma(\exp_\gamma(t(\mathbf{t} - \mathbf i))) = t(\mathbf{t} - \mathbf i) \quad (t\in[0,1]), \end{aligned}$$
because convex combinations of optimal maps are optimal maps as well. In particular, McCann’s interpolant $$\left [\mathbf i+t({\mathbf {t}}_{\gamma }^{\mu } - \mathbf i)\right ]\#\gamma $$ is mapped bijectively to the line segment $$t({\mathbf { t}_{\gamma }^{\mu }} - \mathbf { i})\in \mathrm {Tan}_{\gamma }$$ through the log map.
It is also worth mentioning that McCann’s interpolant can also be defined as
$$\displaystyle \begin{aligned}{}[tp_2+(1-t)p_1]\#\pi, \qquad p_1(x,y)=x, \quad p_2(x,y)=y, \end{aligned}$$
where $$p_1,p_2:\mathcal X^2\to \mathcal X$$ are projections and π is any optimal transport plan between γ and μ. This is defined for arbitrary measures $$\gamma ,\mu \in \mathcal W_2$$ , and reduces to the previous definition if γ is absolutely continuous. It is shown in Ambrosio et al. [12, Chapter 7] or Santambrogio [119, Proposition 5.32] that these are the only constant-speed geodesics in $$\mathcal W_2$$ .

2.3.2 Curvature and Compatibility of Measures

Let $$\gamma ,\mu ,\nu \in \mathcal W_2(\mathcal X)$$ be absolutely continuous measures. Then by (2.3)
$$\displaystyle \begin{aligned} W_2^2(\mu,\nu) \le\int_{\mathcal{X}}{\|{\mathbf{t}}_{\gamma}^{\mu}(x) - {\mathbf{t}}_{\gamma}^{\nu}(x)\|{}^2}\mathrm{d}{\gamma(x)} =\|\log_{\gamma}(\mu) - \log_\gamma(\nu)\|{}^2. \end{aligned}$$
In other words, the distance between μ and ν is smaller in $$\mathcal W_2(\mathcal X)$$ than the distance between the corresponding vectors logγ(μ) and logγ(ν) in the tangent space Tanγ. In the terminology of differential geometry, this means that the Wasserstein space has nonnegative sectional curvature at any absolutely continuous γ.
It is instructive to see when equality holds. As $${\mathbf { t}_{\nu }^{\gamma }}=(\mathbf { t}_{\gamma }^{\nu })^{-1}$$ , a change of variables gives
$$\displaystyle \begin{aligned} W_2^2(\mu,\nu) \le \int_{\mathcal{X}}{\|{\mathbf{t}}_{\gamma}^{\mu}({\mathbf{t}}_{\nu}^{\gamma}(x)) - x\|{}^2}\mathrm{d}{\nu(x)}. \end{aligned}$$
Since the map $$\mathbf { t}_{\gamma }^{\mu }\circ {\mathbf {t}}_{\nu }^{\gamma }$$ pushes forward ν to μ, equality holds if and only if $${\mathbf {t}}_{\gamma }^{\mu }\circ {\mathbf {t}}_{\nu }^{\gamma }={\mathbf {t}}_{\nu }^{\mu }$$ . This motivates the following definition.
Definition 2.3.1 (Compatible Measures)

A collection of absolutely continuous measures $$\mathcal C\subseteq \mathcal W_2(\mathcal X)$$ is compatible if for all $$\gamma ,\mu ,\nu \in \mathcal C$$ , we have $${\mathbf {t}}_{\gamma }^{\mu }\circ {\mathbf {t}}_{\nu }^{\gamma }={\mathbf {t}}_{\nu }^{\mu }$$ (in L 2(ν)).

Remark 2.3.2

The absolute continuity is not necessary and was introduced for notational simplicity. A more general definition that applies to general measures is the following: every finite subcollection of $$\mathcal C$$ admits an optimal multicoupling whose relevant projections are simultaneously pairwise optimal; see the paragraph preceding Theorem 3.1.9.

A collection of two (absolutely continuous) measures is always compatible. More interestingly, if $$\mathcal X=\mathbb {R}$$ , then the entire collection of absolutely continuous (or even just continuous) measures is compatible. This is because of the simple geometry of convex functions in $$\mathbb {R}$$ : gradients of convex functions are nondecreasing, and this property is stable under composition. In a more probabilistic way of thinking, one can always push-forward μ to ν via the uniform distribution Leb|[0,1] (see Sect. 1.​5). Letting $$F_\mu ^{-1}$$ and $$F_\nu ^{-1}$$ denote the quantile functions, we have seen that
$$\displaystyle \begin{aligned} W_2(\mu,\nu) =\| F_\mu^{-1} - F_\nu^{-1} \|{}_{L_2(0,1)}. \end{aligned}$$
(As a matter of fact, in this specific case, the equality holds for all p ≥ 1 and not only for p = 2.) In other words, $$\mu \mapsto F_\mu ^{-1}$$ is an isometry from $$\mathcal W_2(\mathbb {R})$$ to the subset of L 2(0, 1) formed by (equivalence classes of) left-continuous nondecreasing functions on (0, 1). Since this is a convex subset of a Hilbert space, this property provides a very simple way to evaluate Fréchet means in $$\mathcal W_2(\mathbb {R})$$ (see Sect. 3.​1). If γ = Leb|[0,1], then $$F_\mu ^{-1}={\mathbf {t}}_{\gamma }^{\mu }$$ for all μ, so we can write the above equality as
$$\displaystyle \begin{aligned} W_2^2(\mu,\nu) =\| F_\mu^{-1} - F_\nu^{-1} \|{}_{L_2(0,1)} =\|\log_\gamma(\mu) - \log_\gamma(\nu)\|{}^2, \end{aligned}$$
so that if $$\mathcal X=\mathbb {R}$$ , the Wasserstein space is essentially flat (has zero sectional curvature).
The importance of compatibility can be seen as mimicking the simple one-dimensional case in terms of a Hilbert space embedding. Let $$\mathcal C\subseteq \mathcal W_2(\mathcal X)$$ be compatible and fix $$\gamma \in \mathcal C$$ . Then for all $$\mu ,\nu \in \mathcal C$$
$$\displaystyle \begin{aligned} W_2^2(\mu,\nu) =\int_{\mathcal{X}}{\|{\mathbf{t}}_{\gamma}^{\mu}(x) - {\mathbf{t}}_{\gamma}^{\nu}(x)\|{}^2}\mathrm{d}{\gamma(x)} =\|\log_\gamma(\mu) - \log_\gamma(\nu)\|{}^2_{L_2(\gamma)}. \end{aligned}$$
Consequently, once again, $$\mu \mapsto {\mathbf {t}}_{\gamma }^{\mu }$$ is an isometric embedding of $$\mathcal C$$ into L 2(γ). Generalising the one-dimensional case, we shall see that this allows for easy calculations of Fréchet means by means of averaging transport maps (Theorem 3.​1.​9).
Example: Gaussian compatible measures. The Gaussian case presented in Sect. 1.​6.​3 is helpful in shedding light on the structure imposed by the compatibility condition. Let $$\gamma \in \mathcal W_2(\mathbb {R}^d)$$ be a standard Gaussian distribution with identity covariance matrix. Let Σ μ denote the covariance matrix of a measure $$\mu \in \mathcal W_2(\mathbb {R}^d)$$ . When μ and ν are centred nondegenerate Gaussian measures,
$$\displaystyle \begin{aligned} {\mathbf{t}}_{\gamma}^{\mu} =\varSigma_\mu^{1/2}; \qquad {\mathbf{t}}_{\gamma}^{\nu} =\varSigma_\nu^{1/2}; \qquad {\mathbf{t}}_{\mu}^{\nu} =\varSigma_\mu^{-1/2}[\varSigma_\mu^{1/2}\varSigma_\nu\varSigma_\mu^{1/2}]^{1/2}\varSigma_\mu^{-1/2}, \end{aligned}$$
so that γ, μ, and ν are compatible if and only if
$$\displaystyle \begin{aligned} {\mathbf{t}}_{\mu}^{\nu} ={\mathbf{t}}_{\gamma}^{\nu}\circ {\mathbf{t}}_{\mu}^{\gamma} =\varSigma_\nu^{1/2}\varSigma_\mu^{-1/2}. \end{aligned}$$
Since the matrix on the left-hand side must be symmetric, it must necessarily be that $$\varSigma _\nu ^{1/2}$$ and $$\varSigma _\mu ^{-1/2}$$ commute (if A and B are symmetric, then AB is symmetric if and only if AB = BA), or equivalently, if and only if Σ ν and Σ μ commute. We see that a collection $$\mathcal C$$ of Gaussian measures on $$\mathbb {R}^d$$ that includes the standard Gaussian distribution is compatible if and only if all the covariance matrices of the measures in $$\mathcal C$$ are simultaneously diagonalisable. In other words, there exists an orthogonal matrix U such that D μ = UΣ μU t is diagonal for all $$\mu \in \mathcal C$$ . In that case, formula (1.​6)
$$\displaystyle \begin{aligned} \mathcal W_2^2(\mu,\nu) ={\mathrm{tr}}[\varSigma_\mu+\varSigma_\nu - 2(\varSigma_\mu^{1/2}\varSigma_\nu \varSigma_\mu^{1/2})^{1/2}] ={\mathrm{tr}}[\varSigma_\mu+\varSigma_\nu - 2\varSigma_\mu^{1/2}\varSigma_\nu^{1/2}] \end{aligned}$$
simplifies to
$$\displaystyle \begin{aligned} \mathcal W^2_2(\mu,\nu) ={\mathrm{tr}}[D_\mu+D_\nu - 2D_\mu^{1/2}D_\nu^{1/2}] =\sum_{i=1}^d (\sqrt{\alpha_i} - \sqrt{\beta_i})^2, \ \ \alpha_i= [D_\mu]_{ii}; \ \ \beta_i= [D_\nu]_{ii}, \end{aligned}$$
and identifying the (nonnegative) number $$a\in \mathbb {R}$$ with the map x↦ax on $$\mathbb {R}$$ , the optimal maps take the “orthogonal separable” form
$$\displaystyle \begin{aligned} {\mathbf{t}}_{\mu}^{\nu} =\varSigma_\nu^{1/2}\varSigma_\mu^{-1/2} =UD_\nu^{1/2}D_\mu^{-1/2}U^t =U\circ\ \left(\sqrt{\beta_{1}/\alpha_1},\dots,\sqrt{\beta_d/\alpha_d}\right)\ \circ U^t. \end{aligned}$$
In other words, up to an orthogonal change of coordinates, the optimal maps take the form of d nondecreasing real-valued functions. This is yet another crystallisation of the one-dimensional-like structure of compatible measures.
With the intuition of the Gaussian case at our disposal, we can discuss a more general case. Suppose that the optimal maps are continuously differentiable. Then differentiating the equation $${\mathbf {t}}_{\mu }^{\nu } ={\mathbf {t}}_{\gamma }^{\nu }\circ {\mathbf {t}}_{\mu }^{\gamma } $$ gives
$$\displaystyle \begin{aligned} \nabla{\mathbf{t}}_{\mu}^{\nu}(x) =\nabla{\mathbf{t}}_{\gamma}^{\nu} ({\mathbf{t}}_{\mu}^{\gamma}(x)) \nabla{\mathbf{t}}_{\mu}^{\gamma}(x). \end{aligned}$$
Since optimal maps are gradients of convex functions, their derivatives must be symmetric and positive semidefinite matrices. A product of such matrices stays symmetric if and only if they commute, so in this differentiable setting, compatibility is equivalent to commutativity of the matrices $$\nabla {\mathbf {t}}_{\gamma }^{\nu } ({\mathbf {t}}_{\mu }^{\gamma }(x))$$ and $$\nabla {\mathbf {t}}_{\mu }^{\gamma }(x)$$ for μ-almost all x. In the Gaussian case, the optimal maps are linear functions, so x does not appear in the matrices.

Here are some examples of compatible measures. It will be convenient to describe them using the optimal maps from a reference measure $$\gamma \in \mathcal W_2(\mathbb {R}^d)$$ . Define $$\mathcal C=\mathbf {t}\#\gamma $$ with t belonging to one of the following families. The first imposes the one-dimensional structure by varying only the behaviour of the norm of x, while the second allows for separation of variables that splits the d-dimensional problem into d one-dimensional ones.

Radial transformations. Consider the collection of functions $$\mathbf {t}:\mathbb {R}^d\to \mathbb {R}^d$$ of the form t(x) = xG(∥x∥) with $$G:\mathbb {R}_+\to \mathbb {R}$$ differentiable. Then a straightforward calculation shows that
$$\displaystyle \begin{aligned} \nabla\mathbf{t}(x) =G(\|x\|)I +[G'(\|x\|)/\|x\|] \ xx^t. \end{aligned}$$
Since both I and xx t are positive semidefinite, the above matrix is so if both G and G′ are nonnegative. If s(x) = xH(∥x∥) is a function of the same form, then s(t(x)) = xG(∥x∥)H(∥x∥G(∥x∥)) which belongs to that family of functions (since G is nonnegative). Clearly
$$\displaystyle \begin{aligned} \nabla \mathbf{s}(\mathbf{t}(x)) =H\big[\|x\|G(\|x\|)\big]I + \Big[G(\|x\|) H'(\|x\|G(\|x\|))/\|x\|\Big] \ xx^t \end{aligned}$$
commutes with ∇t(x), since both matrices are of the form aI + bxx t with a, b scalars (that depend on x). In order to be able to change the base measure γ, we need to check that the inverses belong to the family. But if y = t(x), then x = ay for some scalar a that solves the equation
$$\displaystyle \begin{aligned} aG(a\|y\|) =1. \end{aligned}$$
Such a is guaranteed to be unique if a↦aG(a) is strictly increasing and it will exist (for y in the range of t) if it is continuous. As a matter of fact, since the eigenvalues of ∇t(x) are G(a) and
$$\displaystyle \begin{aligned} G(a) +G'(a)a =(aG(a))', \qquad a=\|x\|, \end{aligned}$$
the condition that a↦aG(a) is strictly increasing is sufficient (this is weaker than G itself increasing). Finally, differentiability of G is not required, so it is enough if G is continuous and aG(a) is strictly increasing.
Separable variables. Consider the collection of functions $$\mathbf {t}:\mathbb {R}^d\to \mathbb {R}^d$$ of the form
$$\displaystyle \begin{aligned} \mathbf{t}(x_1,\dots,x_d) =(T_1(x_1),\dots,T_d(x_d)), \qquad T_i:\mathbb{R}\to\mathbb{R}, \end{aligned} $$
(2.8)
with T i continuous and strictly increasing. This is a generalisation of the compatible Gaussian case discussed above in which all the T i’s were linear. Here, it is obvious that elements in this family are optimal maps and that the family is closed under inverses and composition, so that compatibility follows immediately.
This family is characterised by measures having a common dependence structure. More precisely, we say that C : [0, 1]d → [0, 1] is a copula if C is (the restriction of) a distribution function of a random vector having uniform margins. In other words, if there is a random vector V = (V 1, …, V d) with $$\mathbb {P}(V_i\le a)=a$$ for all a ∈ [0, 1] and all j = 1, …, d, and
$$\displaystyle \begin{aligned} \mathbb{P}(V_1\le v_1,\dots,V_d\le v_d) =C(v_1,\dots,v_d), \qquad u_i\in[0,1]. \end{aligned}$$
Nelsen [97] provides an overview on copulae. To any d-dimensional probability measure μ, one can assign a copula C = C μ in terms of the distribution function G of μ and its marginals G j as
$$\displaystyle \begin{aligned} G(a_1,\dots,a_d) =\mu((-\infty,a_1]\times\dots\times (-\infty,a_d]) =C(G_1(a_1),\dots,G_d(a_d)). \end{aligned}$$
If each G j is surjective on (0, 1), which is equivalent to it being continuous, then this equation defines C uniquely on (0, 1)d, and consequently on [0, 1]d. If some marginal G j is not continuous, then uniqueness is lost, but C still exists [97, Chapter 2]. The connection of copulae to compatibility becomes clear in the following lemma, proven on page 51 in the supplement.
Lemma 2.3.3 (Compatibility and Copulae)

The copulae associated with absolutely continuous measures $$\mu ,\nu \in \mathcal W_2(\mathbb {R}^d)$$ are equal if and only if $${\mathbf {t}}_{\mu }^{\nu }$$ takes the separable form (2.8).

Composition with linear functions. If $$\phi :\mathbb {R}^d\to \mathbb {R}$$ is convex with gradient t and A is a d × d matrix, then the gradient of the convex function x↦ϕ(Ax) at x is t A = A tt(Ax). Suppose ψ is another convex function with gradient s and that compatibility holds, i.e., ∇s(t(x)) commutes with ∇t(x) for all x. Then in order for
$$\displaystyle \begin{aligned} \nabla{\mathbf{s}}_A({\mathbf{t}}_A(x)) =A^t\nabla\mathbf{s}(AA^t\mathbf{t}(Ax)) A \qquad \mathrm{and}\qquad \nabla{\mathbf{t}}_A(x) =A^t\nabla\mathbf{t}(Ax) A \end{aligned}$$
to commute, it suffices that AA t = I, i.e., that A be orthogonal. Consequently, if {t#μ}t ∈T are compatible, then so are {t U#μ}t ∈T for any orthogonal matrix U.

2.4 Random Measures in Wasserstein Space

Let μ be a fixed absolutely continuous probability measure in $$\mathcal W_2(\mathcal X)$$ . If $$\varLambda \in \mathcal W_2(\mathcal X)$$ is another probability measure, then the transport map $${\mathbf {t}}_{\mu }^{\varLambda }$$ and the convex potential are functions of Λ. If Λ is now random, then we would like to be able to make probability statements about them. To this end, it needs to be shown that $${\mathbf {t}}_{\mu }^{\varLambda }$$ and the convex potential are measurable functions of Λ. The goal of this section is to develop a rigorous mathematical framework that justifies such probability statements. We show that all the relevant quantities are indeed measurable, and in particular establish a Fubini-type result in Proposition 2.4.9. This technical section may be skipped at first reading.

Here is an example of a measurability result (Villani [125, Corollary 5.22]). Recall that $$P(\mathcal X)$$ is the space of Borel probability measures on $$\mathcal X$$ , endowed with the topology of weak convergence that makes it a metric space. Let $$\mathcal X$$ be a complete separable metric space and $$c:\mathcal X^2\to \mathbb {R}_+$$ a continuous cost function. Let $$(\varOmega ,\mathcal F,\mathbb {P})$$ be a probability space and $$\varLambda ,\kappa :\varOmega \to P(\mathcal X)$$ be measurable maps. Then there exists a measurable selection of optimal transference plans. That is, a measurable $$\pi :\varOmega \to P(\mathcal X^2)$$ such that π(ω) ∈ Π(Λ(ω), κ(ω)) is optimal for all ω ∈ Ω.

Although this result is very general, it only provides information about π. If π is induced from a map T, it is not obvious how to construct T from π in a measurable way; we will therefore follow a different path. In order to (almost) have a self-contained exposition, we work in a somewhat simplified setting that nevertheless suffices for the sequel. At least in the Euclidean case $$\mathcal X=\mathbb {R}^d$$ , more general measurability results in the flavour of this section can be found in Fontbona et al. [53]. On the other hand, we will not need to appeal to abstract measurable selection theorems as in [53, 125].

2.4.1 Measurability of Measures and of Optimal Maps

Let $$\mathcal X$$ be a separable Banach space. (Most of the results below hold for any complete separable metric space but we will avoid this generality for brevity and simpler notation). The Wasserstein space $$\mathcal W_p(\mathcal X)$$ is a metric space for any p ≥ 1. We can thus define:

Definition 2.4.1 (Random Measure)

A random measure Λ is any measurable map from a probability space $$(\varOmega ,\mathcal F,\mathbb {P})$$ to $$\mathcal W_p(\mathcal X)$$ , endowed with its Borel σ-algebra.

In what follows, whenever we call something random, we mean that it is measurable as a map from some generic unspecified probability space.

Lemma 2.4.2

A random measure Λ is measurable if and only if it is measurable with respect to the induced weak topology.

Since both topologies are Polish, this follows from abstract measure-theoretic results (Fremlin [57, Paragraph 423F]). We give an elementary proof on page 53 of the supplement.

Optimal maps are functions from $$\mathcal X$$ to itself. In order to define random optimal maps, we need to define a topology and a σ-algebra on the space of such functions.

Definition 2.4.3 (The Space $$\mathcal L_p(\mu )$$ )
Let $$\mathcal X$$ be a Banach space and μ a Borel measure on $$\mathcal X$$ . Then the space $$\mathcal L_p(\mu )$$ is the space of measurable functions $$f:\mathcal X\to \mathcal X$$ such that
$$\displaystyle \begin{aligned} \|f\|{}_{\mathcal L_p(\mu)} =\left( \int_{\mathcal{X}}{\|f(x)\|{}^p_{\mathcal{ X}}}\mathrm{d}{\mu(x)} \right)^{1/p} &lt;\infty.\end{aligned} $$

When $$\mathcal X$$ is separable, $$\mathcal L_p(\mu )$$ is an example of a Bochner space, though we will not use this terminology.

It follows from the definition that $$\|f\|{ }_{\mathcal L_p(\mu )}$$ is the L p norm of the map $$x\mapsto \|f(x)\|{ }_{\mathcal X}$$ from $$\mathcal X$$ to $$\mathbb {R}$$ :
$$\displaystyle \begin{aligned} \|f\|{}_{\mathcal L_p(\mu)} =\|\ \ \|f\|{}_{\mathcal X}\ \ \|{}_{L_p(\mu)}.\end{aligned} $$
As usual we identify functions that coincide almost everywhere. Clearly, $$\mathcal L_p(\mu )$$ is a normed vector space. It enjoys another property shared by L p spaces—completeness:
Theorem 2.4.4 (Riesz–Fischer)

The space $$\mathcal L_p(\mu )$$ is a Banach space.

The proof, a simple variant of the classical one, is given on page 53 of the supplement.

Random maps lead naturally to random measures:

Lemma 2.4.5 (Push-Forward with Random Maps)

Let $$\mu \in \mathcal W_p(\mathcal X)$$ and let t be a random map in $$\mathcal L_p(\mu )$$ . Then Λ = t#μ is a continuous mapping from $$\mathcal L_p(\mu )$$ to $$\mathcal W_p(\mathcal X)$$ , hence a random measure.

Proof
That Λ takes values in $$\mathcal W_p$$ follows from a change of variables
$$\displaystyle \begin{aligned} \int_{\mathcal{X}}{\|x\|{}^p}\mathrm{d}{\varLambda(x)} =\int_{\mathcal{X}}{\|\mathbf{ t}(x)\|{}^p}\mathrm{d}{\mu(x)} =\|\mathbf{ t}\|{}_{\mathcal{ L}_p(\mu)} &lt;\infty.\end{aligned} $$
Since $$W_p(\mathbf {t}\#\mu ,\mathbf {s}\#\mu )\le \|\ \|\mathbf {t} - \mathbf {s}\|{ }_{\mathcal X}\ \|{ }_{L_p(\mu )}=\|\mathbf {t} - \mathbf {s}\|{ }_{\mathcal L_p(\mu )}$$ (see (2.3)), Λ is a continuous (in fact, 1-Lipschitz) function of t.

Conversely, t is a continuous function of Λ:

Lemma 2.4.6 (Measurability of Transport Maps)

Let Λ be a random measure in $$\mathcal W_p(\mathcal X)$$ and let $$\mu \in \mathcal W_p(\mathcal X)$$ such that $$(\mathbf i, {\mathbf {t}}_{\mu }^{\varLambda })\#\mu $$ is the unique optimal coupling of μ and Λ. Then $$\varLambda \mapsto {\mathbf {t}}_{\mu }^{\varLambda }$$ is a continuous mapping from $$\mathcal W_p(\mathcal X)$$ to $$\mathcal L_p(\mu )$$ , so $${\mathbf {t}}_{\mu }^{\varLambda }$$ is a random element in $$\mathcal L_p(\mu )$$ . In particular, the result holds if $$\mathcal X$$ is a separable Hilbert space, p > 1, and μ is absolutely continuous.

Proof

This result is more subtle than Lemma 2.4.5, since $$\varLambda \mapsto {\mathbf {t}}_{\mu }^{\varLambda }$$ is not necessarily Lipschitz. We give here a self-contained proof for the Euclidean case with quadratic cost and μ absolutely continuous. The general case builds on Villani [125, Corollary 5.23] and is given on page 54 of the supplement.

Suppose that Λ n → Λ in $$\mathcal W_2(\mathbb {R}^d)$$ and fix 𝜖 > 0. For any $$S\subseteq \mathbb {R}^d$$ ,
$$\displaystyle \begin{aligned} \|{\mathbf{t}}_{\mu}^{\varLambda_n} - {\mathbf{t}}_{\mu}^{\varLambda}\|{}^2_{\mathcal L_2(\mu)} =\int_{S}{\|{\mathbf{t}}_{\mu}^{\varLambda_n} - {\mathbf{t}}_{\mu}^{\varLambda}\|{}^2}\mathrm{d}{\mu} +{\int_{\mathbb{R}^d\setminus S}^{} \! \|{\mathbf{t}}_{\mu}^{\varLambda_n} - {\mathbf{t}}_{\mu}^{\varLambda}\|{}^2 \, \mathrm{d}\mu}. \end{aligned}$$
Since ∥a − b∥p ≤ 2p∥a∥p + 2p∥b∥p, the last integral is no larger than
$$\displaystyle \begin{aligned} 4{\int_{\mathbb{R}^d\setminus S}^{} \! \|{\mathbf{t}}_{\mu}^{\varLambda_n}\|{}^2 \, \mathrm{d}\mu} +4{\int_{\mathbb{R}^d\setminus S}^{} \! \|{\mathbf{t}}_{\mu}^{\varLambda}\|{}^2 \, \mathrm{d}\mu} =4{\int_{({\mathbf{t}}_{ \mu}^{\varLambda_n})^{-1}(\mathbb{R}^d\setminus S)}^{} \! \|x\|{}^2 \, \mathrm{d}\varLambda_n(x)} +4{\int_{({\mathbf{t}}_{ \mu}^{\varLambda})^{-1}(\mathbb{R}^d\setminus S)}^{} \! \|x\|{}^2 \, \mathrm{d}\varLambda(x)}. \end{aligned}$$
Since (Λ n) and Λ are tight in the Wasserstein space, they must satisfy the absolute uniform continuity (2.7). Let δ = δ 𝜖 as in (2.7), and notice that by the measure preserving property of the optimal maps, the last two integrals are taken on sets of measures 1 − μ(S). Since μ is absolutely continuous, we can find a compact set S of μ-measure at least 1 − δ and on which Proposition 1.​7.​11 applies (see Corollary 1.​7.​12), yielding
$$\displaystyle \begin{aligned} \int_{S}{\|{\mathbf{t}}_{\mu}^{\varLambda_n} - {\mathbf{t}}_{\mu}^{\varLambda}\|{}^2}\mathrm{d}{\mu} \le \|{\mathbf{t}}_{\mu}^{\varLambda_n} - {\mathbf{t}}_{\mu}^{\varLambda}\|{}_\infty^2 \to0, \qquad n\to\infty, \end{aligned}$$
so that
$$\displaystyle \begin{aligned} \limsup_{n\to\infty} \|{\mathbf{t}}_{\mu}^{\varLambda_n} - {\mathbf{t}}_{\mu}^{\varLambda}\|{}_{\mathcal L_2(\mu)} \le 8\epsilon, \end{aligned}$$
and this completes the proof upon letting 𝜖 → 0.

In Proposition 5.​3.​7, we show under some conditions that $$\|{\mathbf {t}}_{\mu }^{\varLambda }\|{ }_{\mathcal L_2(\mu )}$$ is a continuous function of μ.

2.4.2 Random Optimal Maps and Fubini’s Theorem

From now on, we assume that $$\mathcal X$$ is a separable Hilbert space and that p = 2. The results can most likely be generalised to all p > 1 (see Ambrosio et al. [12, Section 10.2]), but we restrict to the quadratic case for simplicity.

Theorem 3.​2.​13 below requires the application of Fubini’s theorem in the form
$$\displaystyle \begin{aligned} \mathbb{E}\int_{\mathcal{ X}}{\left\langle {{\mathbf{t}}_{\theta_0}^{\varLambda} - \mathbf{ i}},{{\mathbf{t}}_{\theta_0}^{\theta} - \mathbf{ i}}\right\rangle}\mathrm{d}{\theta_0} =\int_{\mathcal{ X}}{\mathbb{E}\left\langle {{\mathbf{t}}_{\theta_0}^{\varLambda} - \mathbf{ i}},{{\mathbf{t}}_{\theta_0}^{\theta} - \mathbf{ i}}\right\rangle}\mathrm{d}{\theta_0} =\int_{\mathcal{ X}}{\left\langle {\mathbb{E}{\mathbf{t}}_{\theta_0}^{\varLambda} - \mathbf{ i}},{{\mathbf{t}}_{\theta_0}^{\theta} - \mathbf{ i}}\right\rangle}\mathrm{d}{\theta_0}. \end{aligned}$$
In order for this to even make sense, we need to have a meaning for “expectation” in the spaces $$\mathcal L_2(\theta _0)$$ and L 2(θ 0), both of which are Banach spaces. There are several (nonequivalent) definitions for integrals in such spaces (Hildebrant [69]); the one which will be the most convenient for our needs is the Bochner integral.
Definition 2.4.7 (Bochner Integral)
Let B be a Banach space and let $$f:(\varOmega ,\mathcal F, \mathbb {P})\to B$$ be a simple random element taking values in B:
$$\displaystyle \begin{aligned} f(\omega) =\sum_{j=1}^n f_j \mathbf1\{\omega\in \varOmega_j\}, \qquad \varOmega_j\in \mathcal F, \qquad f_j\in B. \end{aligned}$$
Then the Bochner integral (or expectation) of f is defined by
$$\displaystyle \begin{aligned} \mathbb{E} f =\sum_{j=1}^n \mathbb{P}(\varOmega_j)f_j \in B. \end{aligned}$$
If f is measurable and there exists a sequence f n of simple random elements such that ∥f n − f∥→ 0 almost surely and $$\mathbb {E}\|f_n - f\|\to 0$$ , then the Bochner integral of f is defined as the limit
$$\displaystyle \begin{aligned} \mathbb{E} f =\lim_{n\to\infty}\mathbb{E} f_n. \end{aligned}$$

The space of functions for which the Bochner integral is defined is the Bochner space L 1(Ω;B), but we will use neither this terminology nor the notation. It is not difficult to see that Bochner integrals are well-defined: the expectations do not depend on the representation of the simple functions nor on the approximating sequence, and the limit exists in B (because it is complete). More on Bochner integrals can be found in Hsing and Eubank [71, Section 2.6] or Dunford et al. [48, Chapter III.6]. A major difference from the real case is that there is no clear notion of “infinity” here: the Bochner integral is always an element of B, whereas expectations of real-valued random variables can be defined in $$\mathbb {R}\cup \{\pm \infty \}$$ . It turns out that separability is quite important in this setting:

Lemma 2.4.8 (Approximation of Separable Functions)

Let f : Ω → B be measurable. Then there exists a sequence of simple functions f n such that ∥f n(ω) − f(ω)∥→ 0 for almost all ω if and only if $$f(\varOmega \setminus \mathcal N)$$ is separable for some $$\mathcal N\subseteq \varOmega $$ of probability zero. In that case, f n can be chosen so that ∥f n(ω)∥≤ 2∥f(ω)∥ for all ω ∈ Ω.

A proof can be found in [48, Lemma III.6.9], or on page 55 of the supplement. Functions satisfying this approximation condition are sometimes called strongly measurable or Bochner measurable. In view of the lemma, we will call them separately valued, since this is the condition that will need to be checked in order to define their integrals.

Two remarks are in order. Firstly, if B itself is separable, then f(Ω) will obviously be separable. Secondly, the set $$\mathcal N'\subset \varOmega \setminus \mathcal N$$ on which $$(g_{n_k})$$ does not converge to f may fail to be measurable, but must have outer probability zero (it is included in a measurable set of measure zero) [48, Lemma III.6.9]. This can be remedied by assuming that the probability space $$(\varOmega ,\mathcal F,\mathbb {P})$$ is complete. It will not, however, be necessary to do so, since this measurability issue will not alter the Bochner expectation of f.

Proposition 2.4.9 (Fubini for Optimal Maps)
Let Λ be a random measure in $$\mathcal W_2(\mathcal X)$$ such that $$\mathbb {E} W_2(\delta _0,\varLambda )&lt;\infty $$ and let $$\theta _0,\theta \in \mathcal W_2(\mathcal X)$$ such that $${\mathbf {t}}_{\theta _0}^{\varLambda }$$ and $${\mathbf {t}}_{\theta _0}^{\theta }$$ exist (and are unique) with probability one. (For example, if θ 0is absolutely continuous.) Then
$$\displaystyle \begin{aligned} \mathbb{E}\int_{\mathcal{X}}{\left\langle {{\mathbf{t}}_{\theta_0}^{\varLambda} - \mathbf{ i}},{{\mathbf{t}}_{\theta_0}^{\theta} - \mathbf{ i}}\right\rangle}\mathrm{d}{\theta_0} =\!\int_{\mathcal{X}}{\mathbb{E}\left\langle {{\mathbf{t}}_{\theta_0}^{\varLambda} - \mathbf{ i}},{{\mathbf{t}}_{\theta_0}^{\theta} - \mathbf{ i}}\right\rangle}\mathrm{d}{\theta_0} =\int_{\mathcal{ X}}{\left\langle {\mathbb{E}{\mathbf{t}}_{\theta_0}^{\varLambda} - \mathbf i},{{\mathbf{t}}_{\theta_0}^{\theta} - \mathbf{ i}}\right\rangle}\mathrm{d}{\theta_0}. \end{aligned} $$
(2.9)

This holds by linearity when Λ is a simple random measure. The general case follows by approximation: the Wasserstein space is separable and so is the space of optimal maps, by Lemma 2.4.6, so we may apply Lemma 2.4.8 and approximate $${\mathbf {t}}_{\theta _0}^{\varLambda }$$ by simple maps for which the equality holds by linearity. On page 56 of the supplement, we show that these simple maps can be assumed optimal, and give the full details.

2.5 Bibliographical Notes

Our proof of Theorem 2.2.11 borrows heavily from Bolley et al. [29]. A similar result was obtained by Kloeckner [81], who also provides a lower bound of a similar order.

The origins of Sect. 2.3 can be traced back to the seminal work of Jordan et al. [74], who interpret the Fokker–Planck equation as a gradient flow (where functionals defined on $$\mathcal W_2$$ can be differentiated) with respect to the 2-Wasserstein metric. The Riemannian interpretation was (formally) introduced by Otto [99], and rigorously established by Ambrosio et al. [12] and others; see Villani [125, Chapter 15] for further bibliography and more details.

Compatible measures (Definition 2.3.1) were implicitly introduced by Boissard et al. [28] in the context of admissible optimal maps where one defines families of gradients of convex functions (T i) such that $$T_j^{-1}\circ T_i$$ is a gradient of a convex function for any i and j. For (any) fixed measure $$\gamma \in \mathcal C$$ , compatibility of $$\mathcal C$$ is then equivalent to admissibility of the collection of maps $$\{{\mathbf {t}}_{\gamma }^{\mu }\}_{\mu \in \mathcal { C}}$$ . The examples we gave are also taken from [28].

Lemma 2.3.3 is from Cuesta-Albertos et al. [38, Theorem 2.9] (see also Zemel and Panaretos [135]).

Creative Commons

Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.

The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.