10
Quantum Mechanics is Incomplete
Because….Okay, I Give Up
The View from Charybdis: Everett, Many Worlds, and the Multiverse
You will gather from the title I’ve chosen for this final chapter that I’m not particularly enamoured of the interpretations we will consider here. Whilst this is certainly true, my ambition is nevertheless to make the case both in favour and against these interpretations, as best I can, so that you can judge for yourself. I’ll explain my problems with them as we go.
Irrespective of what I think, it has never ceased to amaze me that one of the simplest solutions to the problem of the collapse of the wavefunction leads to one of the most bizarre conclusions in all of quantum mechanics, if not all of physics. This solution involves first recognizing that we have absolutely no evidence for the collapse. It was introduced by von Neumann as a postulate. We have seen quantum systems in various stages of coherence, and we can create superpositions of objects that are intermediate between quantum and classical, but we have to date never seen a system undergo collapse, nor have we seen superpositions of large, cat-sized objects. In any realistic interpretation of the wavefunction, the notion of collapse has always been nothing more than a rather ad hoc device to get us from a system we are obliged to describe as a superposition of possible measurement outcomes to a system with a single outcome.
There’s another reason to question the need for the collapse, as I already mentioned in passing in Chapter 6. This is related to the relationship between quantum theory and the spacetime described by Einstein’s general theory of relativity.
Einstein presented the general theory in a series of lectures delivered to the Prussian Academy of Sciences in Berlin, culminating in a final, triumphant lecture on 25 November 1915. Yet within a few short months he was back, advising the Academy that his new theory of gravitation might need to be modified: ‘the quantum theory should, it seems, modify not only Maxwell’s electrodynamics but also the new theory of gravitation’.1
Attempts to construct a quantum theory of gravity were begun in 1930 by Bohr’s protégé, Leon Rosenfeld. As I explained in Chapter 5, there are three ‘roads’ that can be taken, one of which involves the quantization of spacetime in general relativity and leads to structures such as loop quantum gravity. The result is a quantum theory of the gravitational field, a quantum theory of spacetime itself.
The difficulties are not to be underestimated. Quantum mechanics is formulated against an assumed background spacetime, conceived not much differently from the absolute space and time of Newton’s classical mechanics. Quantum mechanics is ‘background-dependent’. In contrast, the spacetime of general relativity is dynamic. The geometry of spacetime is variable: it emerges as a consequence of physical interactions involving mass–energy. General relativity is ‘background-independent’.
In any realistic interpretation of the wavefunction, these different ways of conceiving of space and time give us a real headache. In quantum mechanics, we routinely treat a quantum system as though it is sitting in a box, isolated from an outside world that, for the sake of simplicity, we prefer not to consider. Inside this box, we apply the Schrödinger equation and the wavefunction of the system evolves smoothly and continuously as it moves in time in a distributed, non-local fashion from place to place. This is Axiom #5, or von Neumann’s process 2. Satisfied, we now turn our attention to the classical measuring device, which is located in the world outside the box. When this interacts with the quantum system we suppose that the wavefunction collapses according to process 1.
Just how are we meant to apply this logic to a quantum spacetime? Aside from some ‘spooky’ non-local effects, we can regard a quantum system formed from a material particle or ensemble of particles as being broadly ‘here’, in this place in the Universe, and therefore inside this box. The box is clearly defined by boundaries imagined in spacetime. But if we consider the entirety of spacetime itself, no such boundaries can be imagined. A quantum theory of spacetime is, kind of by definition, a quantum theory of the entire Universe, or a quantum cosmology.
In any realistic interpretation of the wavefunction, the need to invoke a separate process for ‘measurement’ really makes quite a mess of things, as this necessarily assumes a perspective that is outside of the system being measured and, so far as we know, there can be nothing outside the Universe. This dilemma caught the attention of Hugh Everett III, a chemical engineering graduate who had migrated first to mathematics (including military game theory) at Princeton University, and then in 1955 to studies for a PhD in physics under the supervision of John Wheeler. In a 1957 paper based on his dissertation, he wrote:2
No way is it evident to apply the conventional formulation of quantum mechanics to a system that is not subject to external observation. The whole interpretative scheme of that formalism rests upon the notion of external observation.
Given the problems that the collapse creates and the lack of any direct evidence for it, why not simply get rid of it? I’ve already explained that scientists down the centuries have made a useful habit of eliminating from their theories all the unnecessary baggage and frills, typically introduced to satisfy certain metaphysical preconceptions but ultimately unsupported by the empirical facts. This is what Everett chose to do. In his dissertation, he followed von Neumann’s logic in assuming that the quantum mechanics of process 2 applies equally to large-scale, classical objects, and offered the following alternative interpretation:3
To assume the universal validity of the quantum description, by the complete abandonment of Process 1. The general validity of pure wave mechanics, without any statistical assertions, is assumed for all physical systems, including observers and measuring apparata. Observation processes are to be described completely by the [wave]function of the composite system which includes the observer and his object-system, and which at all times obeys the [Schrödinger] wave equation (Process 2).
At first sight, this suggestion seems somewhat counterproductive. If it is indeed our experience that pointers point in only one direction at a time and cats are either alive or dead, then giving up the collapse would seem to be taking us in the wrong direction. Surely, we are confronted by Schrödinger’s infinite regress, with an endless complexity of superpositions of measuring devices, cats, and ultimately human observers?
But, of course, we never experience superpositions of large-scale, classical objects. Everett argued that the only way out of this contradiction is to suppose that all possible measurement outcomes are realized.
How can this be? Once again, it’s easier to follow Everett’s logic using an example so, for the last time, let’s return to our quantum particle A prepared in a superposition of ↑ and ↓ spin states. The total wavefunction encounters a measuring device, and the larger system evolves smoothly into a superposition of the outcomes A↑ and A↓. These trigger a response from a gauge attached to the measuring device, entangling the outcomes with the ‘pointer states’ of the gauge, as before, resulting in a superposition of the product states A↑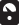
and A↓
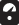. But this is no longer the kind of superposition we’ve been considering thus far. In his dissertation, Everett wrote:4
Whereas before the observation we had a single observer state afterwards there were a number of different states for the observer, all occurring in a superposition. Each of these separate states is a state for an observer, so that we can speak of the different observers described by the different states. On the other hand, the same physical system is involved, and from this viewpoint it is the same observer, which is in different states for different elements of the superposition (i.e. has had different experiences in the separate elements of the superposition).
Everett was not proposing that the observer enters some kind of conscious superposition, in which both outcomes are experienced simultaneously, but rather that the observer ‘splits’ between different states. In our example, one of these observer states corresponds to the experience of A↑ and another corresponds to the experience of A↓:
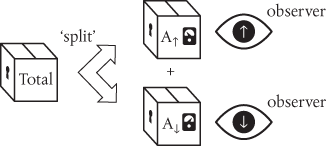
Everett was not clear on the nature or cause of the ‘split’, but there is evidence in his writings that he interpreted it quite literally as a physical phenomenon acting on (or promoted by) a real wavefunction. Wheeler was much more cautious, annotating one of Everett’s manuscripts with the comment ‘Split? Better words needed’, and recommending that Everett rephrase his arguments to avoid ‘mystical misinterpretations by too many unskilled readers’.5
This is Everett’s ‘relative state’ interpretation, the use of the word ‘relative’ deriving from the correlations established between the components of the superposition in the total wavefunction and the different experiences of the observer following the split. One observer state corresponds to A↑ and the other to A↓ relative to the first. Everett argued that quantum probability is then nothing more than a subjective probability imposed by an observer who, in a succession of observations on identically prepared A particles, notes that the outcomes are random, with a 50:50 probability of observing ↑ or ↓. Everett wrote: ‘We are then led to the novel situation in which the formal theory is objectively continuous and causal, while subjectively discontinuous and probabilistic.’6
Despite his concern about some of Everett’s phraseology, Wheeler sent his dissertation to Bohr and later visited Bohr in Copenhagen in an effort to drum up support for what he judged to be a promising approach. These efforts culminated in a visit by Everett himself in March 1959. But all was in vain. Bohr, ever mindful of the use and misuse of language in physical descriptions, had no wish even to discuss ‘any new (strange) upstart theory’.7 Everett’s approach challenged too many elements of the Copenhagen orthodoxy, such as the complementarity of waves and particles and the interpretation of quantum probability. The Copenhagen school rejected outright any suggestion that quantum mechanics could be applied to classical objects.
Everett was dismayed. By this time he had already been working for two and a half years with the Pentagon’s Weapons Systems Evaluation Group, and he rebuffed Wheeler’s attempts to lure him back to academia. He was invited to present his relative state interpretation at a conference in 1962, but his ideas were largely ignored by the physics community at the time.
With one notable exception.
Bryce DeWitt had been intrigued by Everett’s analysis and had written to him in 1957 with a lengthy critique. If the observer state splits every time an observation is made then why, DeWitt wondered, is the observer not aware of this? Everett responded with an analogy. We have no reason to question the conclusions of astronomy and classical physics which tell us that the Earth spins on its axis as it orbits the Sun. And yet because of our own inertia, we don’t directly experience this motion. Likewise, an observer maintains a sense of a single identity and a single history that can be reconstructed from memories, unaware that there exist multiple versions of him or herself, all with different recollections of the sequence of events. Everett slipped this argument into the proofs of his 1957 paper as a footnote.
DeWitt was convinced. Struggling to come to terms with a quantum cosmology seemingly at odds with a formalism that appeared to place far too much emphasis on external ‘measurement’, DeWitt sought to raise the profile of Everett’s interpretation in a paper published by Physics Today in September 1970. Bohr had died in 1962, and there might have been signs that the Copenhagen interpretation was starting to lose its stranglehold. DeWitt may have judged that the time for pussyfooting around with politically correct language was over, and he chose to describe the interpretation using words that the old guard (including Wheeler) would never have approved.
He wrote: ‘I shall focus on one [interpretation] that pictures the universe as continuously splitting into a multiplicity of mutually unobservable but equally real worlds, in each one of which a measurement does give a definite result.’8 Thus Everett’s relative state formulation became the many-worlds interpretation of quantum mechanics. Almost overnight, Everett’s interpretation transformed from being one of the most obscure to one of the most controversial.
Everett appears to have been pleased with DeWitt’s choice of words.* Wheeler once advised him that, whilst he ‘mostly’ believed in the interpretation, he reserved Tuesdays once a month to disbelieve it. But his reservations were stronger than this anecdote would imply, and in time he withdrew his support, such as it had been, later accepting that the interpretation ‘carried too much metaphysical baggage along with it’, and made ‘science into a kind of mysticism’.9 But even as he distanced himself he acknowledged Everett’s contribution as one of the most original and important in decades.10
DeWitt secured a copy of Everett’s original dissertation from his wife Nancy. With Everett’s blessing and the help of his student Neill Graham, DeWitt published this in 1973, together with Everett’s 1957 paper, an ‘assessment’ of this paper published back to back in the same journal by Wheeler, DeWitt’s Physics Today article, and a couple of further supportive articles by DeWitt, Graham, and Leon Cooper and Deborah van Vechten. The book is titled The Many Worlds Interpretation of Quantum Mechanics.
Schrödinger’s cat is no longer simultaneously alive and dead in one and the same world, it is alive in one world and dead in another. With repeated measurements, the number of worlds splitting off from each other multiplies rapidly. The act of measurement has no special place in the many-worlds interpretation, so there is no reason to define measurement to be distinct from any process involving a quantum superposition. We can suppose that a great many such processes have occurred since the Big Bang origin of the Universe, some 13.8 billion years ago. Each will have split the world into as many branches as there have been components in the various superpositions that have formed since.
In his Physics Today article, DeWitt estimated that by now there must be more than 10100+ different branches, or distinct worlds. Each of these worlds contain ‘slightly imperfect copies of oneself all splitting into further copies, which ultimately become unrecognizable…. Here is schizophrenia with a vengeance.’11
Because it assumes only the continuous mechanics described by the Schrödinger equation, and nothing more, the many-worlds interpretation is often advertised as satisfying the demand that quantum mechanics be regarded as a complete theory. If that’s the case, then the title I’ve chosen for this chapter is incorrect. Needless to say, I don’t agree. Whilst the theory might be mathematically complete (and there are more arguments to come on this score), I think completing the theory by invoking an enormous multiplicity of mutually unobservable real worlds is rather costly, and certainly not ‘nothing’. It has been observed that the many-worlds interpretation is ‘cheap on assumptions, but expensive on universes’.12
Caught in a strong trade wind, the Ship of Science is hurtling relentlessly towards Charybdis, that dangerous whirlpool of metaphysical nonsense about the nature of reality.
There have been many efforts at rehabilitation in the years that have followed. It’s not clear what splitting the world implies for the interference terms in the superposition, and one of Dieter Zeh’s motivations for developing ideas about decoherence was to replace the notion of ‘many worlds’ with that of ‘multiconsciousness’, or what is now known as the ‘many minds’ interpretation.13 The splitting or branching of worlds or universes is replaced by the splitting or branching of the observer’s consciousness. The observer is never consciously aware of the superposition, since environmental decoherence destroys (or, more correctly, suppresses) the interference terms. The observer is only ever consciously aware of one outcome, but the other outcomes nevertheless exist in the observer’s mind, although these alternative states of consciousness are inaccessible. In short, the observer does not possess a single mind but rather a multiplicity (or even a continuous infinity) of minds, each weighted according to the amplitude of the wavefunction such that one is dominant.
Space precludes a more detailed discussion of the many minds interpretation, a term coined by philosophers David Albert and Barry Loewer in 1988. The relationship between the mind–body problem and quantum mechanics was independently explored by philosopher Michael Lockwood, in his 1989 book Mind, Brain & the Quantum: The Compound ‘I’.14 The many minds interpretation is presented in Albert’s popular book Quantum Mechanics and Experience, first published in 1992.15
John Bell saw close similarities between many worlds and de Broglie–Bohm theory, arguing that Everett’s original interpretation could be rationalized as the pilot wave theory but without particle paths. In this sense, the splitting or ‘branching’ implied by many worlds is no more or less extravagant than the ‘empty waves’ of de Broglie–Bohm theory. Like Wheeler, Bell regarded the endless multiplication of worlds to be rather over the top, arguing that it serves no real purpose and so can be safely eliminated. The novel element that Everett had introduced was ‘a repudiation of the concept of the “past” ’.16 Instead of a branching system of worlds sprouting like the limbs of a tree, Bell suggested instead that the various particle ‘histories’ run in parallel, sometimes coalescing to produce interference effects. The outcomes are then determined by summing over these histories, with no association discernible between any particular present and any particular past.
But this ‘neo-Everettian’ line of reasoning really just locks us into an endless debate about trading off different metaphysical preconceptions. If you personally prefer to stick with the simplicity of a real universal wavefunction whose motion is fully described by process 2, then you must decide whether you’re ready to accept a multiplicity of worlds, defined either as physically real or simply ‘effective’, for all practical purposes. You can avoid this by resorting to de Broglie–Bohm theory, but then as we’ve seen you then need to reconcile yourself to non-local spooky action at a distance.
Zeh introduced decoherence into the mix as a way of sharpening the relationship between quantum and classical systems. Bell talked about replacing many worlds with many particle ‘histories’. It’s therefore a relatively short step from this back to the decoherent histories interpretation which I presented in Chapter 6. In his popular book The Quark and the Jaguar, published in 1994, Murray Gell-Mann explained it like this:17
We believe Everett’s work to be useful and important, but we believe that there is much more to be done. In some cases too, his choice of vocabulary and that of subsequent commentators on his work have created confusion. For example, his interpretation is often described in terms of ‘many worlds’, whereas we believe that ‘many alternative histories of the universe’ is what is really meant. Furthermore, the many worlds are described as being ‘all equally real’, whereas we believe it is less confusing to speak of ‘many histories, all treated alike by the theory except for their different probabilities’.
This is fine, as far as it goes. But note that this change of perspective isn’t only about reinterpreting the words we use. The many-worlds interpretation is fundamentally realist—it assumes the existence of a real universal wavefunction and possibly a multiplicity of real worlds—whereas, as we saw in Chapter 6, decoherent histories is broadly anti-realist: ‘all equally real’ is diluted to ‘all treated alike by the theory’. You begin to get the sense that there’s no easy way out.
And herein lies the rub. Many theoretical physicists and philosophers who advocate the many-worlds interpretation, or who claim to be ‘Everettians’ or ‘neo-Everettians’, don’t necessarily buy into a single interpretation or a single set of metaphysical preconceptions.* ‘After 50 years, there is no well-defined, generally agreed set of assumptions and postulates that together constitute “the Everett interpretation of quantum theory”,’ wrote Adrian Kent in 2010.18 The chances are that advocates of many worlds buy into their own, possibly individually unique, understanding of what this actually means for them. This is important for what follows, as my criticism is confined to those theorists and philosophers who have not only embraced their inner metaphysician, but who have decided to go all-in with the metaphysics.
In May 1977, DeWitt and Wheeler invited Everett to participate in a conference organized at the University of Texas in Austin. The subjects of the conference were human consciousness and computer-generated artificial intelligence, likely reflecting Wheeler’s growing interest in the role of consciousness in helping define the laws of physics in a ‘participatory universe’. Everett gave a seminar not on many worlds, but on machine self-learning.
During a lunchtime break at a beer-garden restaurant, DeWitt arranged for Everett to sit alongside one of Wheeler’s young graduate students. Over lunch the student probed Everett about his interpretation, and about how he himself preferred to think about it. Although Everett’s career had by now taken him far from academia and he was no longer immersed in questions about the interpretation of quantum mechanics, the student was very impressed. Everett was still very much in tune with the debate.
The student’s name was David Deutsch.
Deutsch would go on to develop his own singular version of the many-worlds interpretation. He argued that the notion of a universe ‘branching’ with each and every transition involving a quantum superposition couldn’t be right. The simple fact that interference is possible with a single particle tells us that reality consists of an infinity of parallel universes, which form what is now generally known as the multiverse.
To follow Deutsch’s arguments let’s return to the description of two-slit interference involving electrons in Chapter 1, and especially Figure 4. Look again at Figure 4a, in which we see just a few scattered points of brightness each indicating that ‘an electron struck here’. In Chapter 1, I explained that interference effects with single electrons arguably demonstrate that each individual electron behaves as a wave—conceived of as a real wave or a ‘wave of information’ (whatever that means)—passing through both slits at once. But what if electrons really do maintain their integrity as real, localized particles, capable of passing through only one slit or the other? Deutsch argues that the only way to recover interference from this is to propose that each electron is accompanied by a host of ‘shadow’ or ‘ghost’ electrons, which pass through both slits and interfere with the path of the visible electron.
Whilst these ‘shadow’ electrons clearly influence the path of the visible electron, they are themselves not detectable—they make no other tangible impression. One explanation for this is that the ‘shadow’ electrons do not exist in ‘our’ universe. Instead they inhabit ‘a huge number of parallel universes, each similar in composition to the tangible one, and each obeying the same laws of physics, but differing in that the particles are in different positions in different universes’.19 When we observe single-particle interference, what we see is not a quantum wave–particle interfering with itself, but rather a host of particles in parallel universes interfering with a particle in our own, tangible universe.
In this interpretation, the ‘tangible’ universe is simply the one which you experience and with which you are familiar. It is not privileged or unique: there is no ‘master universe’. In fact, there is a multiplicity of ‘you’ in a multiplicity of universes, and each regards their universe as the tangible one. Because of the quantum nature of the reality on which these different universes are founded, some of these ‘you’s have had different experiences and have different histories or recollections of events. As Deutsch explained: ‘Many of those Davids are at this moment writing these very words. Some are putting it better. Others have gone for a cup of tea.’20
This is quite a lot to swallow, particularly when we consider that we have absolutely no empirical evidence of the existence of all these parallel universes. But Deutsch argues that the multiverse interpretation is the only way we can explain the extraordinary potential for quantum computing.
This is worth a short diversion.
The processors that sit in every desktop computer, laptop, tablet, smartphone, smartwatch, and item of wearable technology perform their computations on strings of binary information called ‘bits’, consisting of ‘0’s and ‘1’s. Now, classical bits have the values 0 or 1. Their values are one or the other. They can’t be added together in mysterious ways to make superpositions of 0 and 1. However, if we make bits out of quantum particles such as photons or electrons, then curious superpositions of 0 and 1 become perfectly possible. For example, we could assign the value ‘0’ to the spin state ↑ and the value ‘1’ to the spin state ↓. Such ‘quantum bits’ are referred to as ‘qubits’. Because we can form superpositions of qubits, the processing of quantum information works very differently compared with the processing of classical information.
A system of classical bits can form only one ‘bit string’ at a time, such as 01001101. But in a system consisting of qubits we can form superpositions of all the different possible combinations. The physical state of the superposition is determined by the amplitudes of the wavefunctions of each qubit combination, subject to the restriction that the squares of these amplitudes sum to 1 (measurement can give one, and only one, bit string).
And here’s where it gets very interesting. If we apply a computational process to a classical bit, then the value of that bit may change from one possibility to another. For example, a string with eight bits may change from 01001101 to 01001001. But applying a computational process to a qubit superposition changes all the components of the superposition simultaneously. An input superposition yields an output superposition.
A computation performed on an input in a classical computer is achieved by a few transistors which turn on or off. A linear input gives us a linear output, and if we want to perform more computations within a certain time we need to pack more transistors into the processor. We’ve been fortunate to witness an extraordinary growth in computer power in the past 30 years.* The Intel 4004, introduced in 1971, held 2,300 transistors in a processor measuring 12 square millimetres. The Apple 12 Bionic, used in the iPhone XS, XS Max, and XR, which were launched in September 2018, packs about 7 billion transistors into a processor measuring 83 square millimetres. The record is currently on the order of 20 to 30 billion transistors, depending on the type of chip.
But this is nothing compared with a quantum computer that promises an exponential amount of computation in the same amount of time.
The cryptographic systems used for most Internet-based communications and financial transactions are based on the simple fact that finding the prime factors of very large integer numbers requires a vast amount of computing power.† For example, it has been estimated that a network of a million conventional computers would require over a million years to find the prime factors of a 250-digit number. Yet this feat could, in principle, be performed in a matter of minutes using a single quantum computer.‡
Deutsch claims that this kind of enhancement in computing power is only possible by leveraging the existence of the multiverse. When using a quantum computer to factor a number requires 10500 or so times the computational resources that we see to be physically present, where then is the number factorized?21 Given that there are only about 1080 atoms in the visible Universe, Deutsch argues that to complete a quantum computation we need to call on the resources available in a multitude of other parallel universes.
Needless to say, a quantum computer with this kind of capability is not yet available. As I’ve already mentioned, systems prepared in a quantum superposition are extremely sensitive to environmental decoherence and, in a quantum computer, the superposition must be manipulated without destroying it. It is allowed to decohere only when the computation is complete. To date, quantum computing has been successfully demonstrated using only a relatively small number of qubits.* We may still be 20–30 years away from the kind of quantum computer that could threaten the encryption systems used today.
Practical considerations notwithstanding, we need to address Deutsch’s principal assertion—that the existence of the multiverse is the only explanation for the enhancement of processing speed in a quantum computer.
It should come as no real surprise to learn that there are more than a few problems with the many-worlds interpretation that carry through to Deutsch’s multiverse. First, there is a problem with the way that many worlds handles quantum probability, and for many years arguments have bounced back and forth over whether it is possible to derive the Born rule using this interpretation. Everett claimed to have solved this problem already in his dissertation, but not everybody is satisfied. There seems nothing to prevent an observer in one particular universe observing a sequence of measurement outcomes that do not conform to Born-rule expectations.
A colourful example was provided by many-worlds enthusiast Max Tegmark (another former student of Wheeler’s). He proposed an experiment to test the many-worlds interpretation that is not for the faint of heart. Indeed, experimentalists of weak disposition should look away now.
Instead of connecting our measuring device to a gauge, imagine that we connect it to a machine gun. This is set up so that when particle A is detected to be in a ↓ state, a bullet is loaded into the chamber of the machine gun and the gun fires. If particle A is detected to be in an ↑ state, no bullet is loaded and the gun instead just gives an audible ‘click’. We stand well back, and turn on our preparation device. This produces a steady stream of A particles in a superposition of ↑ and ↓ states. We satisfy ourselves that the apparatus fires bullets and gives audible clicks with equal frequency in an apparently random sequence.
Now for the grisly bit.
You stand with your head in front of the machine gun. (I’m afraid I’m not so convinced by arguments for the many-worlds interpretation that I’m prepared to risk my life in this way, and somebody has to do this experiment.) Of course, as an advocate of many worlds, you presume that all you will hear is long series of audible clicks. You are aware that there are worlds in which your brains have been liberally distributed on the laboratory walls, but you are not particularly worried by this because there are other worlds where you are spared.
By definition, if you are not dead, then your history is one in which you have heard only a long series of audible clicks. You can check that the apparatus is still working properly by moving your head to one side, at which point you will start to hear gunfire again. If, on the other hand, the many-worlds interpretation is wrong and the wavefunction simply represents coded information, or the collapse is a physically real phenomenon, then you might be lucky with the first few measurements but, make no mistake, you will soon be killed. Your continued existence (indeed, you appear to be miraculously invulnerable to an apparatus that really should kill you) would appear to be convincing evidence that the many-worlds interpretation is right.
Apart from the obvious risk to your life, the problem with this experiment becomes apparent as soon as you try to publish a paper describing your findings to a sceptical physics community. There may be worlds in which all you recorded was a long series of audible clicks. There are, however, many other worlds where I was left with a very unpleasant mess and a lot of explaining to do. The possibility of entering one of these worlds when you repeat the experiment does not disappear, and you will find that you have a hard time convincing your peers that you are anything other than quite mad. Tegmark wrote:22
Perhaps the greatest irony of quantum mechanics is that…. if once you feel ready to die, you repeatedly attempt quantum suicide: you will experimentally convince yourself that the [many-worlds interpretation] is correct, but you can never convince anyone else!
I’d like to make a further point. A history in which all you’ve heard is a long series of audible clicks suggests a world in which the superposition only ever produces an A↑ result. This is much like tossing a fair coin but only ever getting ‘heads’, or rolling a dice and only getting six. Yet the Born rule insists that there should be a 50:50 probability of observing A↑ and A↓. How can the Born rule be recovered from this?
Philosopher David Wallace devotes three long chapters to probability and statistical inference in his book The Emergent Multiverse: Quantum Theory According to the Everett Interpretation, published in 2012. This is perhaps the most comprehensive summary of the Everett interpretation available, though readers should note that this is not a popular account, nor is it likely to be accessible to graduate students without some training in both physics and philosophy. Wallace seeks to avoid the connotations of ‘many worlds’ (the reader can almost hear Wheeler, whispering over his shoulder: ‘better words needed!’) but, like Everett, Wallace resorts to subjective, Bayesian decision theory, arguing that the components of the wavefunction are translated to different ‘weights’ for different branches. The observer then subjectively assigns ‘probabilities to the outcomes of future events in accordance with the Born Rule’.23
But in Tegmark’s quantum suicide experiment, you only ever experience a long series of audible clicks, and this would surely lead you to conclude that in future events you’re only ever going to get the result A↑. Getting around this challenge requires some interesting mental gymnastics. If this is about the expectation of different subjective experiences, then we might be inclined to accept that death is not an experience. The experiment is flawed precisely because of the way it is set up. Wallace writes: ‘experiments which provide the evidential basis for quantum mechanics do not generally involve the death of the experimenter, far less of third parties such as the writer!’24
I confess I’m not entirely convinced. And I’m not alone. Lev Vaidman—another many-worlds enthusiast—isn’t completely convinced, either.25
Look back briefly at the discussion in Chapter 5. Suppose we prepare an ensemble of A particles in a superposition of spin states ↑ and ↓, but we measure the outcomes in the basis + and −. With any one of a potentially large number of ways of expressing the superposition in terms of different basis states we can freely choose from, how are the branches supposed to ‘know’ which basis corresponds to the outcomes that are to be observed? This is the problem of the ‘preferred basis’.
As we’ve seen, the localization of the different measurement outcomes through decoherence arguably helps to get rid of (or, at least, minimize) the interference terms, but the wavefunction must still be presumed to be somehow steered towards the preferred basis in the process. In Wallace’s version of the Everett interpretation, the real wavefunction interacts with the classical measuring device and the environment, evolving naturally into a superposition of the measurement outcomes. The interference terms are dampened, and the eventual outcomes are realized in different branches. Wallace writes: ‘Decoherence is a dynamical process by which two components of a complex entity (the quantum state) come to evolve independently of one another, and it occurs owing to rather high-level, emergent consequences of the particular dynamics and the initial state of our universe.’26 So, decoherence naturally and smoothly connects the initial wavefunction with the preferred basis, determined by how the experiment is set up.
This might sound quite plausible, but now let’s—at last—return to quantum computing. It turns out that there is more than one way to process qubits in a quantum computer. Instead of processing them in sequence, a ‘one-way’ quantum computer based on a highly entangled ‘cluster state’ proceeds by feeding forward the outcomes of irreversible measurements performed on single qubits. The (random) outcome from one step determines the basis to be applied for the next step, and the nature of the measurements and the order in which they are executed can be configured so that they compute a specific algorithm.* Such a computer was proposed in 2001 by Robert Raussendorf and Hans Briegel,27 and a practical demonstration of computations using a four-qubit cluster state was reported in 2005.28
So, in a cluster state computer, the basis for each measurement changes randomly from one step in the calculation to the next, and will differ from one qubit to the next. Note that whilst ‘measurement’ here is irreversible, it does not involve an act of amplification, in which we might invoke decoherence. Quite the contrary. The superpositions required for quantum computing must remain coherent—the maximum length of a computation is determined by the length of time that coherence can be maintained. In such a system, decoherence is unwanted ‘noise’.
Even if it were possible for a preferred basis somehow to emerge during one step of the computation, this is not necessarily the basis needed for the next step in the sequence. Decoherence can’t help us here. Philosopher Michael Cuffaro writes: ‘Thus there is no way in which to characterise the cluster state computer as performing its computations in many worlds, for there is no way, in the context of the cluster state computer, to even define these worlds for the purposes of describing the computation as a whole.’29
In this case, it’s doubtful that many worlds or the multiverse serve any useful purpose as a way of thinking about quantum computation. Cuffaro believes that those advocates who take the physical reality of the different worlds or branches rather less seriously should be broadly in agreement with his arguments.30 In other words, if the many different worlds simply represent a useful way of thinking about the problem, but are not assumed to be physically real, then this is no big deal.
Wallace acknowledges that whilst what he calls ‘massive parallelism’ (i.e. the multiverse) might have been helpful historically as a way of thinking about quantum computation, it ‘has not been especially productive subsequently’. He continues: ‘Nor would the Everett interpretation particularly lead one to think otherwise: the massively parallel-classical-goings-on way to understand a quantum state is something that occurs only emergently, in the right circumstances, and there’s no reason it has to be available for inherently microscopic (i.e. not decoherent) systems.’31 But, in circumstances where decoherence is possible, as far as Wallace is concerned the many emergent worlds are real ‘in the same sense that Earth and Mars are real’.32
Wallace is a philosopher, and his musings on the reality of the multiverse are largely confined to philosophy journals and books. But Deutsch is a scientist. Yet he too insists that we accept that these worlds really do exist: ‘It’s my opinion that the state of the arguments, and evidence, about other universes closely parallels that about dinosaurs. Namely: they’re real—get over it.’33
I believe we’ve now crossed a threshold. I’ve claimed that it is impossible to do science of any kind without metaphysics. But when the metaphysics is completely overwhelming and the hope of any contact with Empirical Reality is abandoned—when the metaphysics is all there is—I would argue that such speculations are no longer scientific. Now perched on the very edge of Charybdis, the Ship of Science is caught in its powerful grip. We watch, dismayed, as it starts to slip into the maelstrom.
In recent years, other varieties of multiverse theory have entered the public consciousness, derived from the cosmological theory of ‘eternal inflation’ and the so-called ‘cosmic landscape’ of superstring theory. These variants are very different: they were conceived for different reasons and purport to ‘explain’ different aspects of foundational physics and cosmology. But these variants provoke much the same line of argument. Thus, Martin Rees, Britain’s Astronomer Royal, declares that the cosmological multiverse is not metaphysics but exciting science, which ‘may be true’, and on which he’d bet his dog’s life.34
Despite their different origin and explanatory purpose, some theorists have sought to conflate these different multiverse theories into a single structure. In his recent book Our Mathematical Universe, Tegmark organizes these different approaches into a nested hierarchy of four ‘levels’.35 The Level I multiverse comprises universes with different sets of initial Big Bang conditions and histories but the same fundamental laws of physics. This is the multiverse of eternal inflation. Level II is a multiverse in which universes have the same fundamental laws of physics but different effective laws (different physical constants, for example). We happen to live in a universe for which the laws and constants enable intelligent life to exist (this is the ‘fine-tuning’ problem). Level III is the multiverse of the many-worlds interpretation of quantum mechanics. Level IV is the multiverse of all possible mathematical structures corresponding to different fundamental laws of physics.
I’ll leave you to decide what to make of this.
The many-worlds interpretation and the different varieties of multiverse theory have attracted some high-profile advocates, such as Sean Carroll, Neil deGrasse Tyson, David Deutsch, Brian Greene, Alan Guth, Lawrence Krauss, Andre Linde, Martin Rees, Leonard Susskind, Max Tegmark, Lev Vaidman, and David Wallace. Note once again that this list includes ‘neo-Everettians’ who do not necessarily interpret the multiverse realistically, but prefer to think about it as a useful conceptual device. Curiously, these tend to be philosophers: it is frequently the scientists who want to be so much more literal. Those raising their voices against this kind of approach—for all kinds of different reasons—include Paul Davies, George Ellis, David Gross, Sabine Hossenfelder, Roger Penrose, Carlo Rovelli, Joe Silk, Paul Steinhardt, Neil Turok, and Peter Woit. I’m inclined to agree with them.36
Of course, academic scientists are free to choose what they want to believe and within reason they can publish and say what they like. But in their public pronouncements and publications, the highly speculative and controversial nature of multiverse theories are often overlooked, or simply ignored. The multiverse is cool. Put multiverse in the title or in the headlines of an article and it is more likely to capture attention, get reported in the mainstream media, and invite that all-important click, or purchase.
Many worlds can also be positioned as a rather fashionable rejection of the Copenhagen interpretation, with its advocates (especially Everett and DeWitt) romanticized and portrayed as heroes, ‘sticking it to the man’, the ‘man’ in question being Bohr and Heisenberg, and their villainous orthodoxy.37 This is the picture that Adam Becker paints in his recent popular book What is Real? Becker argues that theories ‘need to give explanations, unify previously disparate concepts, and bear some relationship with the world around us’.38 But when all contact with Empirical Reality is lost and all we are left with is the metaphysics, who decides what constitutes ‘some relationship’?
In his recent book on quantum mechanics, Lee Smolin calls this tendency ‘magical realism’,39 and I personally believe this is very dangerous territory. The temptation to fight dogma with yet more dogma can be hard to resist. When taken together with other speculative theories of foundational physics, the multiverse tempts us away from what many regard as rather old-fashioned notions of the scientific method; they want to wean us off our obsession with empirical evidence and instead just embrace the ‘parsimony’ that comes with purely metaphysical explanations.
At a time when the authority of science is increasingly questioned by those promoting a firmly anti-scientific agenda, this kind of thing can’t be good. As noted Danish historian Helge Kragh concluded:40
But, so it has been argued, intelligent design is hardly less testable than many multiverse theories. To dismiss intelligent design on the ground that it is untestable, and yet to accept the multiverse as an interesting scientific hypothesis, may come suspiciously close to applying double standards. As seen from the perspective of some creationists, and also by some non-creationists, their cause has received unintended methodological support from multiverse physics.
Don’t get me wrong. I fully understand why those theorists and philosophers who prefer to adopt a realist perspective feel they have no choice but to accept the many-worlds interpretation. But, in the absence of evidence, personal preferences don’t translate into really existing physical things. For my part I’ll happily accept that many worlds were of enormous value as a way of thinking about quantum computation. But thinking about them doesn’t make them real. And, whilst alternative anti-realist interpretations may be less philosophically acceptable to some, it must be admitted that they just don’t drag quite so much metaphysical baggage around with them. The formalism itself remains passively neutral and inscrutable. It doesn’t care what we think it means.
One last point. Unlike even the more outrageously speculative realist interpretations we’ve considered thus far, interpretations based on many worlds or the multiverse offer no real clues as to how we might gain any further empirical evidence one way or the other. This is, for me at least, where the multiverse theories really break down. Whatever we think they might be ‘explaining’ about the nature of quantum reality, we have to admit that there’s little or nothing practical to be gained from such explanations. They provide no basis for taking any kind of action according to Proposition #4. Even when predictions are claimed, they’re little different from the vague soothsayers’ tricks cited by Popper. Unsurprising, really, as this is surely what Einstein was warning us about in 1950, when he explained that the ‘passion for understanding’ leads to the ‘illusion that man is able to comprehend the objective world rationally by pure thought without any empirical foundations—in short, by metaphysics’.41
As I explained in Chapter 3, the philosopher James Ladyman suggests that we look to the institutions of science to demarcate between science and non-science, and so defend the integrity of science by excluding claims to objective knowledge based on pure metaphysics. But these institutions haven’t so far prevented the publication, in scientific journals, of research papers empty of empirical content, filled with speculative theorizing that offers little or no promise of ever making any kind of contact with Empirical Reality. Despite efforts by cosmologist George Ellis and astrophysicist Joe Silk to raise a red flag in 2014 and call on some of these institutions to ‘defend the integrity of physics’,42 little has changed. Ladyman seems resigned to this fate: ‘Widespread error about fundamentals among experts can and does happen,’ he tells me.43 He believes a correction will come in the long run, when a real scientific breakthrough is made.
Until that happens, we have no choice but to watch in horror as the Ship of Science disappears into the maelstrom. All hands are lost.