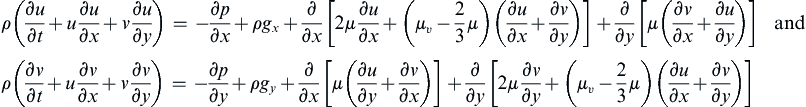4.6. Navier-Stokes Momentum Equation
The momentum conservation equation for a Newtonian fluid is obtained by substituting (4.36) into Cauchy’s equation (4.24) to obtain:
 (4.38)
(4.38)
where we have used (∂p/∂xi)δij = ∂p/∂xj, (3.5) with F = uj, and (3.12). This is the Navier-Stokes momentum equation. The viscosities, μ and μυ, in this equation can depend on the thermodynamic state and indeed μ, for most fluids displays a rather strong dependence on temperature, decreasing with T for liquids and increasing with T for gases. Together, (4.7) and (4.38) provide 1 + 3 = 4 scalar equations, and they contain ρ, p, and uj for 1 + 1 + 3 = 5 dependent variables. Therefore, when combined with suitable boundary conditions, (4.7) and (4.38) provide a complete description of fluid dynamics when ρ is a known constant or when a single known relationship exists between p and ρ. In the later case, the fluid or the flow is said to be barotropic. When the relationship between p and ρ also includes the temperature T, the internal (or thermal) energy e of the fluid must also be considered. These additions allow a caloric equation of state to be added to the equation listing, but introduces two more dependent variables, T and e. Thus, in general, a third field equation representing conservation of energy is needed to fully describe fluid dynamics.
When temperature differences are small within the flow, μ and μυ can be taken outside the spatial derivative operating on the contents of the [,]-brackets in (4.38), which then reduces to
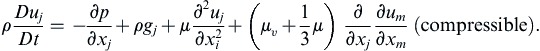 (4.39a)
(4.39a)
 (4.39b)
(4.39b)
Interestingly, the net viscous force per unit volume in incompressible flow, the last term on the right in this equation = μ ( ∂ 2 u j / ∂ x i 2 ) 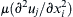 , can be obtained from the divergence of the strain rate tensor or from the curl of the vorticity (see Exercise 4.46):
, can be obtained from the divergence of the strain rate tensor or from the curl of the vorticity (see Exercise 4.46):
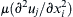 , can be obtained from the divergence of the strain rate tensor or from the curl of the vorticity (see Exercise 4.46):
, can be obtained from the divergence of the strain rate tensor or from the curl of the vorticity (see Exercise 4.46):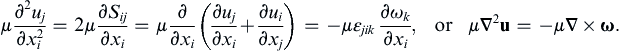 (4.40)
(4.40)
This result would seem to pose a paradox since it shows that the net viscous force depends on the vorticity even though rotation of fluid elements was explicitly excluded from entering (4.36), the precursor of (4.40). This paradox is resolved by realizing that the net viscous force is given by either a spatial derivative of the vorticity or a spatial derivative of the deformation rate. The net viscous force vanishes when ω is uniform in space (as in solid-body rotation), in which case the incompressibility condition requires that the deformation rate is zero everywhere as well.
If viscous effects are negligible, which is commonly true in exterior flows away from solid boundaries, (4.39a) further simplifies to the Euler equation:
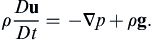 (4.41)
(4.41)