13.14. Barotropic Instability
In Section 11.9, the inviscid stability of a shear flow U(y) in a non-rotating frame of reference was analyzed and it was found that a necessary condition for instability is that d2U/dy2 must change sign somewhere in the flow. This condition is called Rayleigh's inflection point criterion. In terms of mean flow vorticity, ζ ¯ = − d U / d y 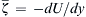 , the criterion states that
, the criterion states that d ζ ¯ / d y 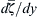 must change sign somewhere in the flow. That analysis is extended here to a rotating earth to find that the criterion requires that
must change sign somewhere in the flow. That analysis is extended here to a rotating earth to find that the criterion requires that d ( ζ ¯ + f ) / d y 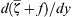 must change sign somewhere within the flow.
must change sign somewhere within the flow.
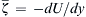 , the criterion states that
, the criterion states that 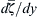 must change sign somewhere in the flow. That analysis is extended here to a rotating earth to find that the criterion requires that
must change sign somewhere in the flow. That analysis is extended here to a rotating earth to find that the criterion requires that 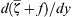 must change sign somewhere within the flow.
must change sign somewhere within the flow.Consider a horizontal wind profile or current U(y) in a medium of uniform density. In the absence of horizontal density gradients only the barotropic mode is allowed, and U(y) does not vary with depth. The vorticity equation is:
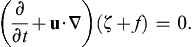 (13.121)
(13.121)
which is (13.94), D/Dt[(ζ + f)/h] = 0, with the added simplification that the layer depth h is constant because w = 0. Let the total flow be decomposed into a background flow plus a disturbance:
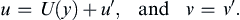
The total vorticity is then:
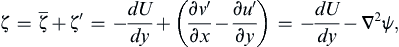 (13.122)
(13.122)
where ψ is the stream function for the disturbance, u′ = ∂ψ/∂y and v′ = –∂ψ/∂x, defined to be consistent with (7.3). Substituting these relationships into (13.121) and linearizing, leads to the perturbation vorticity equation:
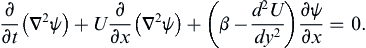 (13.123)
(13.123)
Because the coefficients of (13.123) are independent of x and t, it's solutions can be of the form ψ = ψ ˆ ( y ) exp { i k ( x − c t ) } 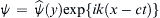 . Here, the phase speed, c = cr + ici, may be complex and solutions are unstable when ci > 0. The perturbation vorticity equation (13.123) then becomes:
. Here, the phase speed, c = cr + ici, may be complex and solutions are unstable when ci > 0. The perturbation vorticity equation (13.123) then becomes:
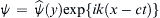 . Here, the phase speed, c = cr + ici, may be complex and solutions are unstable when ci > 0. The perturbation vorticity equation (13.123) then becomes:
. Here, the phase speed, c = cr + ici, may be complex and solutions are unstable when ci > 0. The perturbation vorticity equation (13.123) then becomes: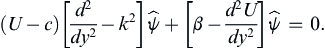
Comparing this with (11.81) derived without the Coriolis acceleration, the effect of planetary rotation is the replacement of −d2U/dy2 by (β − d2U/dy2). The analysis of the Section 11.9 therefore carries over to the present case, resulting in the following criterion: A necessary condition for the inviscid instability of a barotropic current U(y) is that the gradient of the absolute vorticity:
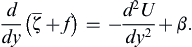 (13.124)
(13.124)
must change sign somewhere in the flow, a result first derived by Kuo (1949).
Barotropic instability quite possibly plays an important role in the instability of currents in the atmosphere and in the ocean. The instability has no preference for any latitude, because the criterion involves β and not f. However, the mechanism presumably dominates in the tropics because mid-latitude disturbances prefer the baroclinic instability mechanism discussed in the following section. An unstable distribution of westward tropical wind is shown in Figure 13.30.
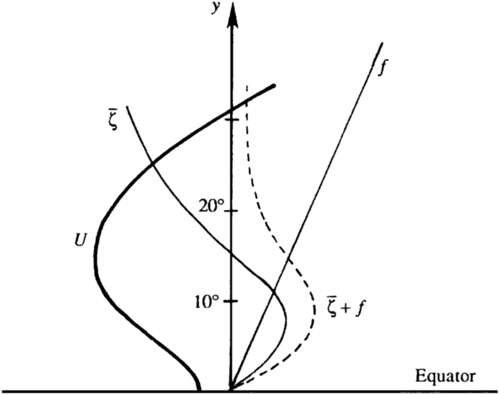
Figure 13.30 Profiles of velocity U(y), vorticity ζ ¯ 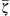 , and Coriolis parameter f in a westward tropical wind as a function of latitude. The velocity distribution is barotropically unstable as
, and Coriolis parameter f in a westward tropical wind as a function of latitude. The velocity distribution is barotropically unstable as d ( ζ ¯ + f ) / d y 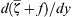 changes sign within the flow near 8°. J. T. Houghton, The Physics of the Atmosphere, 1986; reprinted with the permission of Cambridge University Press.
changes sign within the flow near 8°. J. T. Houghton, The Physics of the Atmosphere, 1986; reprinted with the permission of Cambridge University Press.
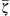 , and Coriolis parameter f in a westward tropical wind as a function of latitude. The velocity distribution is barotropically unstable as
, and Coriolis parameter f in a westward tropical wind as a function of latitude. The velocity distribution is barotropically unstable as 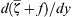 changes sign within the flow near 8°. J. T. Houghton, The Physics of the Atmosphere, 1986; reprinted with the permission of Cambridge University Press.
changes sign within the flow near 8°. J. T. Houghton, The Physics of the Atmosphere, 1986; reprinted with the permission of Cambridge University Press.