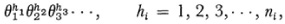
Perhaps I may without immodesty lay claim to the appellation of Mathematical Adam, as I believe that I have given more names (passed into general circulation) of the creatures of the mathematical reason than all the other mathematicians of the age combined.
J. J. SYLVESTER
In abstract algebra, as in the case of most twentieth-century developments, the basic concepts and goals were fixed in the nineteenth century. The fact that algebra can deal with collections of objects that are not necessarily real or complex numbers was demonstrated in a dozen nineteenth-century creations. Vectors, quaternions, matrices, forms such as ax2 + bxy + cy2, hyper-numbers of various sorts, transformations, and substitutions or permutations are examples of objects that were combined under operations and laws of operation peculiar to the respective collections. Even the work on algebraic numbers, though it dealt with classes of complex numbers, brought to the fore the variety of algebras because it demonstrated that only some properties are applicable to these classes as opposed to the entire complex number system.
These various classes of objects were distinguished in accordance with the properties that the operations on them possessed; and we have seen that such notions as group, ring, ideal, and field, and subordinate notions such as subgroup, invariant subgroup, and extension field were introduced to identify the sets of properties. However, nearly all of the nineteenth-century work on these various types of algebras dealt with the concrete systems mentioned above. It was only in the last decades of the nineteenth century that the mathematicians appreciated that they could move up to a new level of efficiency by integrating many separate algebras through abstraction of their common content. Thus permutation groups, the groups of classes of forms treated by Gauss, hypernumbers under addition, and transformation groups could all be treated in one swoop by speaking of a set of elements or things subject to an operation whose nature is specified only by certain abstract properties, the foremost of these being that the operation applied to two elements of the set produces a third element of the set. The same advantages could be achieved for the various collections that formed rings and fields. Though the idea of working with abstract collections preceded the axiomatics of Pasch, Peano, and Hilbert, the latter development undoubtedly accelerated the acceptance of the abstract approach to algebras.
Thus arose abstract algebra as the conscious study of entire classes of algebras, which individually were not only concrete but which served purposes in specific areas as substitution groups did in the theory of equations. The advantage of obtaining results that might be useful in many specific areas by considering abstract versions was soon lost sight of, and the study of abstract structures and the derivation of their properties became an end in itself.
Abstract algebra has been one of the favored fields of the twentieth century and is now a vast area. We shall present only the beginnings of the subject and indicate the almost unlimited opportunities for continued research. The great difficulty in discussing what has been done in this field is terminology. Aside from the usual difficulties, that different authors use different terms and that terms change meaning from one period to another, abstract algebra is marked and marred by the introduction of hundreds of new terms. Every minor variation in concept is distinguished by a new and often imposing sounding term. A complete dictionary of the terms used would fill a large book.
The first abstract structure to be introduced and treated was the group. A great many of the basic ideas of abstract group theory can be found implicitly and explicitly at least as far back as 1800. It is a favorite activity of historians, now that the abstract theory is in existence, to trace how many of the abstract ideas were foreshadowed by the concrete work of Gauss, Abel, Galois, Cauchy, and dozens of other men. We shall not devote space to this reexamination of the past. The only significant point that bears mentioning is that, once the abstract notion was acquired, it was relatively easy for the founders of abstract group theory to obtain ideas and theorems by rephrasing this past work.
Before examining the development of the abstract group concept, it may be well to know where the men were heading. The abstract definition of a group usually used today calls for a collection of elements, finite or infinite in number, and an operation which, when applied to any two elements in the collection, results in an element of the collection (the closure property). The operation is associative; there is an element, e, say, such that for any element a of the group, ae = ea = a; and to each element a there exists an inverse element a′ such that aa′ = a′a — e. When the operation is commutative the group is called commutative or Abelian and the operation is called addition and denoted by +. The element e is then denoted by 0 and called the zero element. If the operation is not commutative it is called multiplication and the element e is denoted by 1 and called the identity.
The abstract group concept and the properties that should be attached to it were slow in coming to light. We may recall (Chap. 31, sec. 6) that Cayley had proposed the abstract group in 1849, but the merit of the notion was not recognized at the time. In 1858 Dedekind,1. far in advance of his time, gave an abstract definition of finite groups which he derived from permutation groups. Again in 18772. he observed that his modules of algebraic numbers, which call for a+ β and α — β belonging when α and β do, can be generalized so that the elements are no longer algebraic numbers and the operation can be general but must have an inverse and be commutative. Thus he suggested an abstract finite commutative group. Dedekind’s understanding of the value of abstraction is noteworthy. He saw clearly in his work on algebraic number theory the value of structures such as ideals and fields. He is the effective founder of abstract algebra.
Kronecker,3. taking off from work on Kummer’s ideal numbers, also gave what amounts to the abstract definition of a finite Abelian group similar to Cayley’s 1849 concept. He specifies abstract elements, an abstract operation, the closure property, the associative and commutative properties, and the existence of a unique inverse element of each element. He then proves some theorems. Among the various powers of any element θ, there is one which equals the unit element, 1. If v is the smallest exponent for which θv equals the unit element, then to each divisor μ of v there is an element φ for which φ” = 1. If θp and φσ both equal 1 and p and σ are the smallest numbers for which this holds and are relatively prime, then (θφ)pσ = 1. Kronecker also gave the first proof of what is now called a basis theorem. There exists a fundamental finite system of elements θ1, θ2, θ3,… such that the products
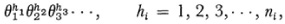
represent all elements of the group just once. The lowest possible values n1, n2 n3… that correspond to θ1, θ2, θ3,… (that is, for which are such that each is divisible by the following one and the product n1, n2, n3… equals the number n of elements in the group. Moreover all the prime factors of n are in n1.
In 1878 Cayley wrote four more papers on finite abstract groups.4. In these, as in his 1849 and 1854 papers, he stressed that a group can be considered as a general concept and need not be limited to substitution groups, though, he points out, every (finite) group can be represented as a substitution group. These papers of Cayley had more influence than his earlier ones because the time was ripe for an abstraction that embraced more than substitution groups.
In a joint paper, Frobenius and Ludwig Stickelberger (1850-1936)5.made the advance of recognizing that the abstract group concept embraces congruences and Gauss’s composition of forms as well as the substitution groups of Galois. They mention groups of infinite order.
Though Eugen Netto, in his book Substitutionentheorie und ihre Anwendung auf die Algebra(1882), confined his treatment to substitution groups, his wording of his concepts and theorems recognized the abstractness of the concepts. Beyond putting together results established by his predecessors, Netto treated the concepts of isomorphism and homomorphism. The former means a one-to-one correspondence between two groups such that a·b = c, where a, b, and c are elements of the first group, then a′ b′ = c′, where a′, b′, and c′ are the corresponding elements of the second group. A homomorphism is a many-to-one correspondence in which again a·b = c implies a′·b′ = c′
By 1880 new ideas on groups came into the picture. Klein, influenced by Jordan’s work on permutation groups, had shown in his Erlanger Programm (Chap. 38, sec. 5) that infinite transformation groups, that is, groups with infinitely many elements, could be used to classify geometries. These groups, moreover, are continuous in the sense that arbitrarily small transformations are included in any group or, alternatively stated, the parameters in the transformations can take on all real values. Thus in the transformations that express rotation of axes the angle θ can take on all real values. Klein and Poincaré in their work on automorphic functions had utilized another kind of infinite group, the discrete or noncontinuous group (Chap. 29, sec. 6).
Sophus Lie, who had worked with Klein around 1870, took up the notion of continuous transformation groups, but for other purposes than the classification of geometries. He had observed that most of the ordinary differential equations that had been integrated by older methods were invariant under classes of continuous transformation groups, and he thought he could throw light on the solution of differential equations and classify them.
In 1874 Lie introduced his general theory of transformation groups.6.Such a group is represented by
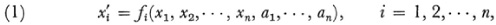
where the fi are analytic in the xi and ai. The ai, are parameters as opposed to the Xj, which are variables, and (x1, x2, x3…) stands for a point in rc-dimen-sional space. Both the parameters and the variables may take on real or complex values. Thus in one dimension the class of transformations
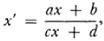
where a, b, c, and d take on all real values, is a continuous group. The groups represented by (1) arc called finite, the word finite referring to the number of parameters. The number of transformations is, of course, infinite. The one-dimensional case is a three-parameter group because only the ratios of a, b, and d to d matter. In the general case the product of two transformations
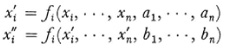
is
where the ct are functions of the ai and bi. In the case of one variable Lie spoke of the group as a simply extended manifold; for n variables he spoke of an arbitrarily extended manifold.
In a paper of 1883 on continuous groups, published in an obscure Norwegian journal,7. Lie also introduced infinite continuous transformation groups. These are not defined by equations such as (1) but by means of differential equations. The resulting transformations do not depend upon a finite number of continuous parameters but on arbitrary functions. There is no abstract group concept corresponding to these infinite continuous groups, and though much work has been done on them, we shall not pursue it here.
It is perhaps of interest that Klein and Lie at the beginning of their work defined a group of transformations as one possessing only the closure property. The other properties, such as the existence of an inverse to each transformation, were established by using the properties of the transformations, or, as in the case of the associative law, were used as obvious properties of transformations. Lie recognized during the course of his work that one should postulate as part of the definition of a group the existence of an inverse to each element.
By 1880 four main types of groups were known. These are the discontinuous groups of finite order, exemplified by substitution groups; the infinite discontinuous (or discrete) groups, such as occur in the theory of auto-morphic functions; the finite continuous groups of Lie exemplified by the transformation groups of Klein and the more general analytic transformations of Lie; and the infinite continuous groups of Lie defined by differential equations.
With the work of Walther von Dyck (1856-1934), the three main roots of group theory—the theory of equations, number theory, and infinite transformation groups—were all subsumed under the abstract group concept. Dyck was influenced by Cayley and was a student of Felix Klein. In 1882 and 18838. he published papers on abstract groups that included discrete and continuous groups. His definition of a group calls for a set of elements and an operation that satisfy the closure property, the associative but not the commutative property, and the existence of an inverse element of each element.
Dyck worked more explicitly with the notion of the generators of a group, which is implicit in Kronecker’s basis theorem and explicit in Netto’s work on substitution groups. The generators are a fixed subset of independent elements of a group such that every member of the group can be expressed as the product of powers of the generators and their inverses. When there are no restrictions on the generators the group is called a free group. If A1 A2,… are the generators, then an expression of the form
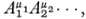
where the μi are positive or negative integers, is called a word. There may be relations among the generators, and these would be of the form
Fi (Ai) = 1;
that is, a word or combination of words equals the identity element of the group. Dyck then shows that the presence of relations implies an invariant subgroup and a factor group G of the free group G. In his 1883 paper he applied the abstract group theory to permutation groups, finite rotation groups (symmetries of polyhedra), number-theoretic groups, and transformation groups.
Sets of independent postulates for an abstract group were given by Huntington,9. E. H. Moore,10. and Leonard E. Dickson (1874-1954).11.These as well as other postulate systems are minor variations of each other.
Having arrived at the abstract notion of a group, the mathematicians turned to proving theorems about abstract groups that were suggested by known results for concrete cases. Thus Frobenius12. proved Sylow’s theorem (Chap. 31, sec. 6) for finite abstract groups. Every finite group whose order, that is, the number of elements, is divisible by the vth power of a prime p always contains a subgroup of order pv.
Beyond searching concrete groups for properties that may hold for abstract groups, many men introduced concepts directly for abstract groups.
Dedekind13. and George A. Miller (1863-1951)14. treated non-Abelian groups in which every subgroup is a normal (invariant) subgroup. Dedekind in his 1897 paper and Miller15. introduced the notions of commutator and commutator subgroup. If s and t are any two elements of a group G, the element s–1.t–1st is called the commutator of s and t. Both Dedekind and Miller used this notion to prove theorems. For example, the set of all commutators of all (ordered) pairs of elements of a group G generates an invariant subgroup of G. The automorphisms of a group, that is, the one-to-one transformations of the members of a group into themselves under which if a·b = c then a′ -b′ = ′, were studied on an abstract basis by Holder16. and E. H. Moore.17.
The further development of abstract group theory has pursued many directions. One of these taken over from substitution groups by Holder in the 1893 paper is to find all the groups of a given order, a problem Cayley had also mentioned in his 1878 papers.18. The general problem has defied solution. Hence particular orders have been investigated, such as p2.q2 where p and q are prime. A related problem has been the enumeration of intransitive and primitive and imprimitive groups of various degrees (the number of letters in a substitution group).
Another direction of research has been the determination of composite or solvable groups and simple groups, that is, those which have no invariant subgroups (other than the identity). This problem of course derives from Galois theory. Holder, after introducing the abstract notion of a factor group,19. treated simple groups20. and composite groups.21. Among results are the fact that a cyclic group of prime order is simple and so is the alternating group of all even permutations on 11 letters for n ≥ 5. Many other finite simple groups have been found.
As for solvable groups, Frobenius devoted several papers to the problem. He found, for example,22. that all groups whose order is not divisible by the square of a prime are solvable.23. The problem of investigating which groups are solvable is part of the broader problem of determining the structure of a given group.
Dyck in his papers of 1882 and 1883 had introduced the abstract idea of a group defined by generators and relations among the generators. Given a group defined in terms of a finite number of generators and relations, the identity or word problem, as formulated by Max Dehn,24. is the task of determining whether any “word” or product of elements is equal to the unit element. Any set of relations may be given because at worst the trivial group consisting only of the identity satisfies them. To decide whether a group given by generators and relations is trivial is not trivial. In fact there is no effective procedure. For one defining relation Wilhelm Magnus ( 1907—) showed25. that the word problem is solvable. But the general problem is not.26.
Another famous unsolved problem of ordinary group theory is Burn-side’s problem. Any finite group has the properties that it is finitely generated and every element has finite order. In 190227. William Burnside (1852-1927) asked whether the converse was true; that is, if a group G is finitely generated and if every element has finite order, is G finite? This problem has attracted a great deal of attention and only specializations of it have received solutions. Still another problem, the isomorphism problem, is to determine when two groups, each defined by generators and relations, are isomorphic.
One of the surprising turns in group theory is that shortly after the abstract theory had been launched, the mathematicians turned to representations by more concrete algebras in order to obtain results for the abstract groups. Cayley had pointed out in his 1854 paper that any finite abstract group can be represented by a group of permutations. We have also noted (Chap. 31, sec. 6) that Jordan in 1878 introduced the representation of substitution groups by linear transformations. These transformations or their matrices have proved to be the most effective representation of abstract groups and are called linear representations.
A matrix representation of a group G is a homomorphic correspondence of the elements g of G to a set of non-singular square matrices A (g) of fixed order and with complex elements. The homomorphism implies that
A(gigi) = A(gi)A(gi)
for all gti and gi of G. There are many matrix representations of a group G because the order (number of rows or columns) can be altered, and even for a given order the correspondence can be altered. Also one can add two
representations. If for each element g of G, Ag is the corresponding matrix of one representation of order m and Bg is the corresponding matrix of order n, then
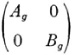
is another representation, which is called the sum of the separate representations. Likewise if
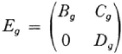
is another representation, when Bg. and Dg, are non-singular matrices of orders m and n respectively, the Bg. and Dg. are also representations, and of lower order than is called a graduated representation; it and any representation equivalent to it is (Fg–1EgFg an equivalent representation if F is nonsingular and of the order of E.g) is called reducible. A representation not equivalent to a graduated one is called irreducible. The basic idea of an irreducible representation consisting of a set of linear transformations in n variables is that it is a homomorphic or isomorphic representation in which it is impossible to choose m < n linear functions of the variables which are transformed among themselves by every operation of the group they represent. A representation that is equivalent to the sum of irreducible representations is called completely reducible.
Every finite group has a particular representation called regular. Suppose the elements are labeled g1, g2,…gn. Let a be any one of the g’ s. We consider an n by n matrix. Suppose agi = gi. Then we place a 1 in the (i, j) place of the matrix. This is done for all gt and the fixed a. All the other elements of the matrix are taken to be 0. The matrix so obtained corresponds to a. There is such a matrix for each g of the group and this set of matrices is a left regular representation. Likewise by forming the products gia we get a right regular representation. By reordering the g’s of the group we can get other regular representations. The notion of a regular representation was introduced by Charles S. Peirce in 1879.28..
The representation of substitution groups by linear transformations of the form
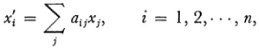
initiated by Jordan was broadened to the study of representations of all finite abstract groups by Frobenius, Burnside, Theodor Molien (1861-1941), and Issai Schur (1875-1941) in the latter part of the nineteenth century and
the first part of the twentieth. Frobenius29. introduced for finite groups the notions of reducible and completely reducible representations and showed that a regular representation contains all the irreducible representations. In other papers published from 1897 to 1910, some in conjunction with Schur, he proved many other results, including the fact that there are only a few irreducible representations, out of which all the others are composed.
Burnside30. gave another major result, a necessary and sufficient condition on the coefficients of a group of linear transformations in n variables in order that the group be reducible. The fact that any finite group of linear transformations is completely reducible was first proved by Heinrich Maschke (1853-1908).31. Representation theory for finite groups has led to important theorems for abstract groups. In the second quarter of this century, representation theory was extended to continuous groups, but this development will not be pursued here.
Aiding in the study of group representations is the notion of group character. This notion, which can be traced back to the work of Gauss, Dirichlet, and Heinrich Weber (see note 35), was formulated abstractly by Dedekind for Abelian groups in the third edition of Dirichlet’s Vorlesungen über Zahlentheorie(1879). A character of a group is a function x(s) defined on all the elements s such that it is not zero for any s and x(ss′) = x(s)x(s′). Two characters are distinct if x(s) ≠ x′(s) for at least one s of the group.
This notion was generalized to all finite groups by Frobenius. After having formulated a rather complex definition,32. he gave a simpler definition,33. which is now standard. The character function is the trace (sum of the main diagonal elements) of the matrices of an irreducible representation of the group. The same concept was applied later by Frobenius and others to infinite groups.
Group characters furnish in particular a determination of the minimum number of variables in terms of which a given finite group can be represented as a linear transformation group. For commutative groups they permit a determination of all subgroups.
Displaying the usual exuberance for the current vogue, many mathematicians of the late nineteenth and early twentieth centuries thought that all mathematics worth remembering would ultimately be comprised in the theory of groups. Klein in particular, though he did not like the formalism of abstract group theory, favored the group concept because he thought it would unify mathematics. Poincaré was equally enthusiastic. He said,34. “… the
theory of groups is, so to say, the whole of mathematics divested of its matter and reduced to pure form.”
The concept of a field R generated by n quantities a1 a2,…, an, that is, the set of all quantities formed by adding, subtracting, multiplying, and dividing these quantities (except division by 0) and the concept of an extension field formed by adjoining a new element λ not in R, are in Galois’s work. His fields were the domains of rationality of the coefficients of an equation and extensions were made by adjunction of a root. The concept also has a quite different origin in Dedekind’s and Kronecker’s work on algebraic numbers (Chap. 34, sec. 3), and in fact the word “field” (Körper) is due to Dedekind.
The abstract theory of fields was initiated by Heinrich Weber, who had already espoused the abstract viewpoint for groups. In 189335. he gave an abstract formulation of Galois theory wherein he introduced (commutative) fields as extensions of groups. A field, as Weber specifies, is a collection of elements subject to two operations, called addition and multiplication, which satisfy the closure condition, the associative and commutative laws, and the distributive law. Moreover each element must have a unique inverse under each operation, except for division by 0. Weber stressed group and field as the two major concepts of algebra. Somewhat later, Dickson36. and Huntington37. gave independent postulates for a field.
To the fields that were known in the nineteenth century, the rational, real and complex numbers, algebraic number fields, and fields of rational functions in one or several variables, Kurt Hensel added another type, p-adic fields, which initiated new work in algebraic numbers (Theorie der algebraischen Zahlen, 1908). Hensel observed, first of all, that any ordinary integer D can be expressed in one and only one way as a sum of powers of a prime p. That is,
D = d0 + dip + … + dkp pk,
in which di is some integer from 0 to p— 1. For example,
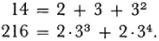
Similarly any rational number r (not 0) can be written in the form
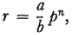
where a and b are integers not divisible by p and n is 0 or a positive or negative integer. Hensel generalized on these observations and introduced p-adic numbers. These are expressions of the form
where p is a prime and the coefficients, the cit’s, are ordinary rational numbers reduced to their lowest form whose denominator is not divisible by p. Such expressions need not in general have values as ordinary numbers. However, by definition they are mathematical entities.
Hensel denned the four basic operations with these numbers and showed that they are a field. A subset of the p-adic, numbers can be put into one-toone correspondence with the ordinary rational numbers, and in fact this subset is isomorphic to the rational numbers in the full sense of an isomorphism between two fields. In the field of p-adic numbers, Hensel defined units, integral p-adic numbers, and other notions analogous to those of the ordinary rational numbers.
By introducing polynomials whose coefficients are p-adic numbers, Hensel was able to speak of p-adic roots of polynomial equations and extend to these roots all of the concepts of algebraic number fields. Thus there are p-adic integral algebraic numbers and more general p-adic algebraic numbers, and one can form fields of p-adic algebraic numbers that are extensions of the “rational” p-adic numbers defined by (2). In fact, all of the ordinary theory of algebraic numbers is carried over to p-adic numbers. Surprisingly perhaps, the theory of p-adic algebraic numbers leads to results on ordinary algebraic numbers. It has also been useful in treating quadratic forms and has led to the notion of valuation fields.
The growing variety of fields motivated Ernst Steinitz (1871–1928), who was very much influenced by Weber’s work, to undertake a comprehensive study of abstract fields; this he did in his fundamental paper, Algebraischen Theorie der Xorper.38. All fields, according to Steinitz, can be divided into two principal types. Let K be a field and consider all subfields of K (for example, the rational numbers are a subfield of the real numbers). The elements common to all the subfields are also a subfield, called the prime field P of K. Two types of prime fields are possible. The unit element e is contained in P and, therefore, so are
e, 2e,…, ne,….
These elements are either all different or there exists an ordinary integer p such that pe = 0. In the first case P must contain all fractions ne/me, and
since these elements form a field, P must be isomorphic to the field of rational numbers and K is said to have characteristic 0.
If, on the other hand, pe = 0, it is readily shown that the smallest such p must be a prime and the field must be isomorphic to the field of integral residues modulo p, that is, 0, 1,…, p – 1. Then K is said to be a field of characteristic p. Any subfield of K has the same characteristic. Then pa = pea = 0; that is, all expressions in K can be reduced modulo p.
From the prime field P in either of the types just described, the original field K can be obtained by the process of adjunction. The method is to take an element a in K but not in P and to form all rational functions R(a) of a with coefficients in P and then, if necessary, to take b not in R(a) and do the same with b, and to continue the process as long as necessary.
If one starts with an arbitrary field K one can make various types of adjunctions. A simple adjunction is obtained by adjoining a single element x. The enlarged field must contain all expressions of the form
where the a, are elements of K. If these expressions are all different, then the extended field is the field K (x) of all rational functions of x with coefficients in K. Such an adjunction is called a transcendental adjunction and K(x) is called a transcendental extension. If some of the expressions (3) are equal, one can show that there must exist a relation (using α for x)
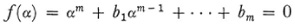
with the bi in K and with f(x) irreducible in K. Then the expressions
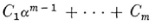
with the Ci in K constitute a field K(a) formed by the adjunction of α to K. This field is called a simple algebraic extension ofK. In K(α), f(x) has a root, and conversely, if an arbitrary irreducible f(x) in K is chosen, then one can construct a K (α) in which f(x) has a root.
A fundamental result due to Steinitz is that every field can be obtained from its prime field by first making a series of (possibly infinite) transcendental adjunctions and then a series of algebraic adjunctions to the transcendental field. A field K′ is said to be an algebraic extension of K if it can be obtained by successive simple algebraic adjunctions. If the number of adjunctions is finite, K′ is said to be of finite rank.
Not every field can be enlarged by algebraic adjunctions. For example, the complex numbers cannot be because every f(x) is reducible in this field. Such a field is algebraically complete. Steinitz also proved that for every field A′ there is a unique algebraically complete field K′ which is algebraic over K in the sense that all other algebraically complete fields over A′ (containing K) contain a subfield equivalent to K′.
Steinitz considered also the problem of determining the fields in which the Galois theory of equations holds. To say that Galois theory holds in a field means the following: A Galois field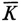 
over a given field K is an algebraic field in which every irreducible f(x) in K either remains irreducible or decomposes into a product of linear factors. To every Galois field 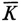there exists a set of automorphisms, each of which transforms the elements of 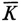into other elements of 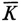and such that α±γ and αγ correspond to α′ ± γ′ and αβ′ while all elements of 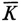remain invariant (correspond to themselves). The set of automorphisms forms a group G, the Galois group of 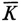with respect to K. The main theorem of Galois theory asserts that there is a unique correspondence between the subgroups G′ of G and the subfields of G′ such that to any subgroup G’ of G there corresponds a subfield K’ consisting of all elements left invariant by G’ and conversely. Galois theory is said to hold for those fields in which this theorem holds. Steinitz’s result is essentially that Galois theory holds in those fields of finite rank that can be obtained from a given field by a series of adjunctions of roots of irreducible f(x) which have no equal roots. Fields in which all irreducible f (x) have no equal roots are called separable. (Steinitz said vollkommen or complete.)
The theory of fields also includes, as Steinitz’s classification indicates, finite fields of characteristic p. A simple example of the latter is the set of all residues (remainders) modulo a prime p. The concept of a finite field is due to Galois. In 1830 he published a definitive paper, “Sur la théorie des nombres."39. Galois wished to solve congruences
F(x) ≡ 0 mod p,
where p is a prime and F(x) is a polynomial of degree n. He took F(x) to be irreducible (modulo p), so that the congruence did not have integral or irrational roots. This obliged him to consider other solutions, which were suggested by the imaginary numbers. Galois denoted one of the roots of F (x) by i(which is not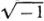 
). He then considered the expression
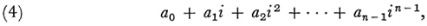
where the ai are whole numbers. When these coefficients assume separately all the least positive residues, modulo p, this expression can take on only pv values. Let α be one of these non-zero values, of which there are pv— 1. The powers of α also have the form (4). Hence these powers cannot be all different. There must then be at least one power am = 1, where m is the smallest of such values. Then there will be m different values
If we multiply these m quantities by an expression β of the same form, we obtain a new group of quantities different from (5) and from each other.
Multiplying the set (5) by γ will produce more such quantities, until we obtain all of the form (4). Hence m must divide pv — 1 or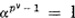 
so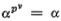 
The pv values of the form (4) constitute a finite field. Galois had shown in this concrete situation that the number of elements in a Galois field of characteristic p is a power of p.
E. H. Moore40. showed that any finite abstract field is isomorphic to a Galois field of order pn, p a prime. There is such a field for every primed and positive integer n. The characteristic of each field is p. Joseph H. M. Wedder-burn (1882-1948), a professor at Princeton University,41. and Dickson proved simultaneously that any finite field is necessarily commutative (in the multiplication operation). A great deal of work has been done to determine the structure of the additive groups contained in Galois fields and the structure of the fields themselves.
Though the structures rings and ideals were well known and utilized in Dedekind’s and Kronecker’s work on algebraic numbers, the abstract theory is entirely a product of the twentieth century. The word ideal had already been adopted (Chap. 34, sec. 4). Kronecker used the word “order” for ring; the latter term was introduced by Hilbert.
Before discussing the history, it may be well to be clear about the modern meanings of the concepts. An abstract ring is a collection of elements that form a commutative group with respect to one operation and are subject to a second operation applicable to any two elements. The second operation is closed and associative but may or may not be commutative. There may or may not be a unit element. Moreover the distributive law a(b + c) = ab + ac and (b + c)a = ba + ca holds.
An ideal in a ring R is a sub-ring M such that if a belongs to M and r is any element of R, then ar and ra belong to M. If only ar belongs to M, then Mis called a right ideal. If only ra belongs to M, then M is a left ideal. If an ideal is both right and left, it is called a two-sided ideal. The unit ideal is the entire ring. The ideal (a) generated by one element a consists of all elements of the form
ra + na,
where r belongs to R and n is any whole number. If R has a unit element, then ra + na = ra + nea = (r + ne)a = r′a, where r′ is now any element of R. The ideal generated by one element is called a principal ideal. Any ideal other than 0 and A is a proper ideal. Similarly if a1 a2,…, am are m given elements of a ring R with unit element the set of all sums r1 a1 +…+ rmam
with coefficients r in R is an ideal of R denoted by (a1( a2,…, am). It is the smallest ideal containing a1, a2, a1, a2, am, commutative ring R is called Noetherian if every ideal has this form.
An ideal M in a ring, since it is a subgroup of the additive group of the ring, divides the ring into residue classes. Two elements of R, a and b, are congruent relative to M if a — b belongs to M or a ≡ b(mod M). Under a homomorphism T from a ring R to a ring R′, which calls for T (ab) = (Ta)·(Tb), T (a + b) = Ta + Tb and T1 = 1′, the elements of R which correspond to the zero element of R′ constitute an ideal called the kernel of R, and R′ is isomorphic to the ring of residue classes of R modulo the kernel. Conversely, given an ideal L in R one may form a ring R modulo L and a homomorphism of R into R modulo L which has L as its kernel. R modulo L or R/L is called a quotient ring.
The definition of a ring does not call for the existence of an inverse to each element under multiplication. If an inverse (except for 0) and the unit element both exist, the ring is called a division ring (division algebra) and it is in effect a non-commutative (or skew) field. Wedderburn’s result already noted (1905) showed that a finite division ring is a commutative field. Up to 1905 the only division algebras known were commutative fields and quaternions. Then Dickson created a number of new ones, commutative and non-commutative. In 1914 he42. and Wedderburn43. gave the first examples of non-commutative fields with centers (the set of all elements which commute with each other) of rank n2..44.
In the late nineteenth century a great variety of concrete linear associative algebras were created (Chap. 32, sec. 6). These algebras, abstractly considered, are rings, and when the theory of abstract rings was formulated it absorbed and generalized the work on these concrete algebras. This theory of linear associative algebras and the whole subject of abstract algebra received a new impulse when Wedderburn, in his paper “ On Hypercomplex Numbers,”45. took up results of Elie Cartan (1869-1951)46. and generalized them. The hypercomplex numbers are, we may recall, numbers of the form
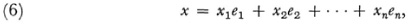
where the ei are qualitative units and the xi are real or complex numbers. Wedderburn replaced the x¿ by members of an arbitrary field F. He called
these generalized linear associative algebras simply algebras. To treat these generalized algebras he had to abandon the methods of his predecessors because an arbitrary field F is not algebraically closed. He also adopted and perfected Benjamin Peirce’s technique of idempotents.
In Wedderburn’s work, then, an algebra consists of all linear combinations of the form (6) with coefficients now in a field F. The number of et,, called basal units, is finite and is the order of the algebra. The sum of two such elements is given by
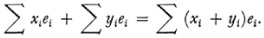
The scalar product of an element x of the algebra and an element a of the field F is defined as
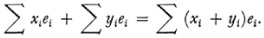
and the product of two elements of the algebra is defined by
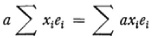
which is completed by a table expressing all products eiej as some linear combination of the ei with coefficients in F. The product is required to satisfy the associative law. One can always add a unit element (modulus) 1 such that x·1 = 1· x= x for every x and then the elements of the algebra include the field F of the coefficients.
Given an algebra A, a subset B of elements which itself forms an algebra is called a sub-algebra. If x belongs to A and y to B and yx and xy both belong to B, then B is called an invariant sub-algebra. If an algebra A is the sum of two invariant sub-algebras with no common element, then A is called reducible. It is also said to be the direct sum of the sub-algebras.
A simple algebra is one having no invariant sub-algebra. Wedderburn also used and modified Cartan’s notion of a semi-simple algebra. To define this notion, Wedderburn made use of the notion of nilpotent elements. An element x is nilpotent if xn = 0 for some integer n. An element x is said to be properly nilpotent if xy and also yx are nilpotent for every y in an algebra A. It can be shown that the set of properly nilpotent elements of an algebra A form an invariant sub-algebra. Then a semi-simple algebra A is one having no nilpotent invariant sub-algebra.
Wedderburn proved that every semi-simple algebra can be expressed as a direct sum of irreducible algebras and each irreducible algebra is equivalent to the direct product of a matrix algebra and a division algebra (primitive algebra in Wedderburn’s terminology). This means that each element of the irreducible algebra can be taken to be a matrix whose elements are members of the division algebra. Since semi-simple algebras can be reduced to the direct sum of several simple algebras, this theorem amounts to the determination of all semi-simple algebras. Still another result uses the notion of a total matrix algebra, which is just the algebra of all n by n matrices. An algebra for which the coefficient field F is the complex numbers and which contains no properly nilpotent elements is equivalent to a direct sum of total matrix algebras. This sample of results obtained by Wedderburn may give some indication of the work done on the generalized linear associative algebras.
The theory of rings and ideals was put on a more systematic and axiomatic basis by Emmy Noether, one of the few great women mathematicians, who in 1922 became a lecturer at Göttingen. Many results on rings and ideals were already known when she began her work, but by properly formulating the abstract notions she was able to subsume these results under the abstract theory. Thus she reexpressed Hubert’s basis theorem (Chap. 39, sec. 2) as follows: A ring of polynomials in any number of variables over a ring of coefficients that has an identity element and a finite basis, itself has a finite basis. In this reformulation she made the theory of invariants a part of abstract algebra.
A theory of ideals for polynomial domains had been developed by Emanuel Lasker (1868-1941)47. in which he sought to give a method of deciding whether a given polynomial belongs to an ideal generated by r polynomials. In 192148. Emmy Noether showed that this ideal theory for polynomials can be deduced from Hubert’s basis theorem. Thereby a common foundation was created for the ideal theory of integral algebraic numbers and integral algebraic functions (polynomials). Noether and others penetrated much farther into the abstract theory of rings and ideals and applied it to rings of differential operators and other algebras. However, an account of this work would take us too far into special developments.
Modern ring theory, or, more properly, an extension of ring theory, also includes non-associative algebras. The product operation is non-associative and non-commutative. The other properties of linear associative algebras are applicable. There are today several important non-associative algebras. Historically the most important is the type called a Lie algebra. It is customary in such algebras to denote the product of two elements a and b by [a, b]. In place of the associative law the product operation satisfies two conditions,
[a, b] = —[b, a] and [a, [b, c]] + [b, [c, a]] + [c, [a, b]] = 0.
The second property is called the Jacobi identity. Incidentally, the vector product of two vectors satisfies the two conditions.
An ideal in a Lie algebra L is a sub-algebra L1 such that the product of any element of L and any element of L1 is in L1·A A simple Lie algebra is one that has no nontrivial ideals. It is semi-simple if it has no Abelian ideals.
Lie algebras arose out of Lie’s efforts to study the structure of his continuous transformation groups. To do this Lie introduced the notion of infinitesimal transformations.49. Roughly speaking, an infinitesimal transformation is one that moves points an infinitesimal distance. Symbolically it is represented by Lie as
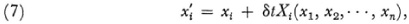
where δt is an infinitesimally small quantity, or
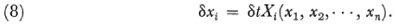
The δt is a consequence of a small change in the parameters of the group. Thus suppose a group of transformations is given by
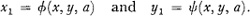
Let a0 be the value of the parameter for which φ and ψ are the identity transformation so that
If a0 is changed to ao + δa, then by Taylor’s theorem
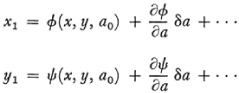
so that neglecting higher powers of δa gives
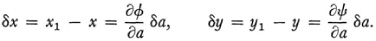
For the fixed a0, ∂ψ/∂a and ∂ψ/∂a are functions of x and y so that
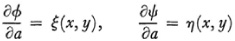
and
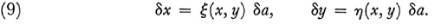
If δa is δt we get the form (7) or (8). The equations (9) represent an infinitesimal transformation of the group.
lîf(x, y) is an analytic function of x and y, the effect of an infinitesimal transformation on it is to replace f(x, y) by f(x + ξa, y + θ ξa), and by applying Taylor’s theorem one finds that to first order
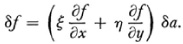
The operator
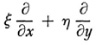
is another way of representing the infinitesimal transformation (9) because knowledge of one gives the other. Such operators can be added and multiplied in the usual sense of differential operators.
The number of independent infinitesimal transformations or the number of corresponding independent operators is the number of parameters in the original group of transformations. The infinitesimal transformations or the corresponding operators, now denoted by X1 X2,…, Xn,, do determine the Lie group of transformations. But, equally important, they are themselves generators of a group. Though the product Xi Xj is not a linear operator, the expression called the alternant of Xi and Xj,
XiXj – XiXj
is a linear operator and is denoted by [Xi Xj] With this product operation, the group of operators becomes a Lie algebra.
Lie had begun the work on finding the structure of his simple finite (continuous) groups with r parameters. He found four main classes of algebras. Wilhelm K. J. Killing (184 7-192 3)50. found that these classes are correct for all simple algebras but that in addition there are five exceptional cases of 14, 52, 78, 133, and 248 parameters. Killing’s work contained gaps and Elie Cartan undertook to fill them.
In his thesis, Sur la structure des groupes de transformations finis et continus,51. Cartan gave the complete classification of all simple Lie algebras over the field of complex values for the variables and parameters. Like Killing, Cartan found that they fall into four general classes and the five exceptional algebras. Cartan constructed the exceptional algebras explicitly. In 191452.Cartan determined all the simple algebras with real values for the parameters and variables. These results are still basic.
The use of representations to study Lie algebras has been pursued much as in the case of abstract groups. Cartan, in his thesis and in a paper of 1913,53.
found irreducible representations of the simple Lie algebras. A key result was obtained by Hermann Weyl.54. Any representation of a semi-simple Lie algebra (over an algebraically closed field of characteristic 0) is completely reducible.
Our few indications of the accomplishments in the field of abstract algebra certainly do not give the full picture of what was created even in the first quarter of this century. It may, however, be helpful to indicate the vast area that was opened up by the conscious turn to abstraction.
Up to about 1900 the various algebraic subjects that had been studied, whether matrices, the algebras of forms in two, three, or n variables, hyper-numbers, congruences, or the theory of solution of polynomial equations, had been based on the real and complex number systems. However, the abstract algebraic movement introduced abstract groups, rings, ideals, division algebras, and fields. Beyond investigating the properties of such abstract structures and relationships as isomorphism and homomorphism, mathematicians now found it possible to take almost any algebraic subject and raise questions about it by replacing the real and complex numbers with any one of the abstract structures. Thus in place of matrices with complex elements, one can study matrices with elements that belong to a ring or field. Similarly one can take problems of the theory of numbers and, replacing the positive and negative integers and 0 by a ring, reconsider every question that has previously been investigated for the integers. One can even consider functions and power series with coefficients in an arbitrary field.
Such generalizations have indeed been made. We have noted that Wedderburn in his 1907 work generalized previous work on linear associative algebras (hypernumbers) by replacing the real or complex coefficients by any field. One can replace the field by a ring and investigate the theorems that hold under this change. Even the theory of equations with coefficients in arbitrary or finite fields has been studied.
As another example of the modern tendency to generalize, consider quadratic forms. These were important with integer coefficients in the study of the representation of integers as sums of squares and with real coefficients as the representation of conic and quadric surfaces. In the twentieth century quadratic forms are studied with any and every field as coefficients. As more abstract structures are introduced, these can be used as the base or coefficient field of older algebraic theories, and the process of generalization goes on indefinitely. This use of abstract concepts calls for the use of abstract algebraic techniques; thus many formerly distinct subjects were absorbed in
abstract algebra. This is the case with large parts of number theory, including algebraic numbers.
However, abstract algebra has subverted its own role in mathematics. Its concepts were formulated to unify various seemingly diverse and dissimilar mathematical domains as, for example, group theory did. Having formulated the abstract theories, mathematicians turned away from the original concrete fields and concentrated on the abstract structures. Through the introduction of hundreds of subordinate concepts, the subject has mushroomed into a welter of smaller developments that have little relation to each other or to the original concrete fields. Unification has been succeeded by diversification and specialization. Indeed, most workers in the domain of abstract algebra are no longer aware of the origins of the abstract structures, nor are they concerned with the application of their results to the concrete fields.
Artin, Emil: “The Influence of J. H. M. Wedderburn on the Development of Modern Algebra,” Amer. Math. Soc. Bull., 56, 1950, 65-72.
Bell, Eric T.: “Fifty Years of Algebra in America, 1888-1938,” Amer. Math. Soc. Semicentennial Publications, II, 1938, 1-34.
Bourbaki, N.: Eléments d’histoire des mathématiques, Hermann, 1960, pp. 110-28.
Cartan, Elie: “Notice sur les travaux scientifiques,” Œuvres complètes, Gauthier-Villars, 1952-55, Part I, Vol. 1, pp. 1-98.
Dicke, Auguste: Emmy Noether, 1882-1935, Birkhäuser Verlag, 1970.
Dickson, L. E.: “An Elementary Exposition of Frobenius’s Theory of Group-Characters and Group-Determinants,” Annals of Math., 4, 1902, 25-49.
_______: Linear Algebras, Cambridge University Press, 1914.
________: Algebras and Their Arithmetics(1923), G. E. Stechert (reprint), 1938.
Frobenius, F. G.: Gesammelte Abhandlungen, 3 vols., Springer-Verlag, 1968.
Hawkins, Thomas: “The Origins of the Theory of Group Characters,” Archive for History of Exact Sciences, 7, 1971, 142-70.
MacLane, Saunders: “Some Recent Advances in Algebra,” Amer. Math. Monthly, 46, 1939, 3-19. Also in Albert, A. A., ed.: Studies in Modern Algebra, The Math. Assn. of Amer., 1963, pp. 9-34.
_____________: “Some Additional Advances in Algebra,” in Albert, A. A., ed.: Studies in Modern Algebra, The Math. Assn. of Amer., 1963, pp. 35-58.
Ore, Oystein: “Some Recent Developments in Abstract Algebra,” Amer. Math. Soc. Bull., 37, 1931, 537-48.
___________: “Abstract Ideal Theory,” Amer. Math. Soc. Bull., 39, 1933, 728-45.
Steinitz, Ernst: Algebraische Theorie der Körper, W. de Gruyter, 1910; 2nd rev. ed., 1930; Chelsea (reprint), 1950. The first edition is the same as the article in Jour, für Math., 137, 1910, 167-309.
Wiman, A.: “Endliche Gruppen linearer Substitutionen,” Encyk. der Math. Wiss., B. G. Teubner, 1898-1904, I, Part 1, 522-54.
Wussing, H. L.: Die Genesis des abstrakten Gruppenbegriffes, VEB Deutscher Verlag der Wissenschaften, 1969.