The purpose of this chapter is to summarize a number of methodological issues, including certain research design and analysis paradigms, familiarity with which I deem to be essential for the reader to understand the design of the studies reported in this volume and to interpret their findings correctly. I begin with a brief exposition of the relationship between cross-sectional and longitudinal data within the context of what I have called the general developmental model (Schaie, 1965, 1967, 1977, 2007a; Schaie & Willis, 2002). I then present the rationale for a variety of simple and sequential schemes for data acquisition and analysis. Next, I deal with the problems of internal validity of developmental studies and sketch designs for the measurement and control of the most obvious internal validity problems that plague developmental studies. Finally, I deal with the relationship between observed measures and latent (unobserved) variables and describe how confirmatory (restricted) factor analysis can be applied to assess construct equivalence across cohorts, age, and time in the study of developmental problems.
One of the major contributions of the Seattle Longitudinal Study (SLS) has been the didactic interplay between data acquisition and the formulation and testing of analytic models of interest to developmental scientists. Once the original cross-sectional study had been converted (in the first follow-up) to a mixed cross-sectional and longitudinal design, it became necessary for me to try to understand the relationship of the two forms of data acquisition to interpret the differing cross-sectional and longitudinal findings occurring in a particular data set. This need led me to explore what I termed a general developmental model (Schaie, 1965, 1967, 1977, 2007a), which would help organize and clarify the relationships among these data. Interestingly, the model parallels the age-period-cohort model introduced into sociology by Ryder (1965; also cf. Alwin, 2009).
The general developmental model characterizes the developmental status of a given behavior B as a function of three components, such that B = f (A, C, T). In this context, age (A) refers to the number of years from birth to the chronological point at which the organism is observed or measured. Cohort (C) denotes a group of individuals who enter the environment at the same point in time (usually, but not necessarily, at birth), and time of measurement or period (T) indicates the temporal occasion (calendar date) on which a given individual or group of individuals is observed or measured.1 The three components are confounded in the sense that once any two are specified, then the third is known—similar to the confounding of temperature, pressure, and volume in the physical sciences. Nevertheless, each of the three components may be of primary interest for certain scientific questions in the developmental sciences, and it is therefore often useful to be able to estimate the specific contribution attributable to each component.
The general developmental model allows us to specify how the above-described components are confounded in the research designs traditionally used by developmental scientists. In addition, novel designs can be derived from the model that allow estimation of the components confounded in different combinations, even though their unconfounded estimation remains elusive, except under specific circumstances, and with certain collateral assumptions (Schaie, 1986, 1994b). In turn, these designs can lead to new departures in theory building (Schaie, 1988c, 1992, 2002, 2006a, 2006b; Schaie, Willis, & Pennak, 2005).
Most empirical studies in the developmental sciences involve age comparisons either at one point in time or at successive time intervals (see also Nesselroade & Labouvie, 1985). The cross-sectional, longitudinal, and time lag designs represent the traditional strategies used for this purpose.
The hypothesis to be investigated simply asks whether there are differences in a given characteristic for samples drawn from different cohorts but measured at the same point in time. This is an important question for the study of interindividual differences. Age differences in behavior at a particular point in historical time may require different societal responses regardless of the antecedent conditions that may be responsible for the age differences. It must be recognized, however, that age differences detected in a cross-sectional data set are inextricably confounded with cohort differences. Because cross-sectional subsamples are measured only once, no information is available on intraindividual change. Unless there is independent evidence to suggest that older cohorts performed at the same level as younger cohorts at equivalent ages, it would be most parsimonious to assume, at least in comparisons of adult samples, that cross-sectional age differences represent estimates of cohort differences that may be either inflated or reduced by maturational changes occurring over a specified age range.
For longitudinal strategy, the hypothesis to be investigated is whether there are age-related changes within the same population cohort measured on two or more occasions. This is the question that must be asked whenever there is interest in predicting age differentiation in behavior occurring over time (cf. Schaie, 2005b). However, longitudinal data do not provide unambiguous estimates of intraindividual change. Unless the behavior to be studied is impervious to environmental influences, it must be concluded that a single-cohort longitudinal study will confound age-related (maturational) change with time-of-measurement (period) effects that are specific to the particular historical period over which the behavior is monitored (Schaie, 1972). The time-of-measurement effects could either mask or grossly inflate maturational changes. In addition, longitudinal studies are subject to additional threats to their internal validity that would be controlled for in cross-sectional designs (see discussion of internal validity).
In the time lag design, two samples of individuals drawn from successive cohorts are compared at successive points in time at the same chronological age. The hypothesis to be tested is whether there are differences in a given behavior for samples of equal age that are drawn at different points in time. This strategy is of particular interest to social and educational psychologists. It is particularly appropriate when one wishes to study performance of individuals of similar age in successive cohorts (e.g., comparing baby boomers with the preceding generation). The simple time lag design, however, also confounds the cohort effect with time-of-measurement effects and therefore may provide cohort estimates that are inflated or reduced depending on whether the temporal interval between the cohorts represents a period of favorable or adverse environmental influences.
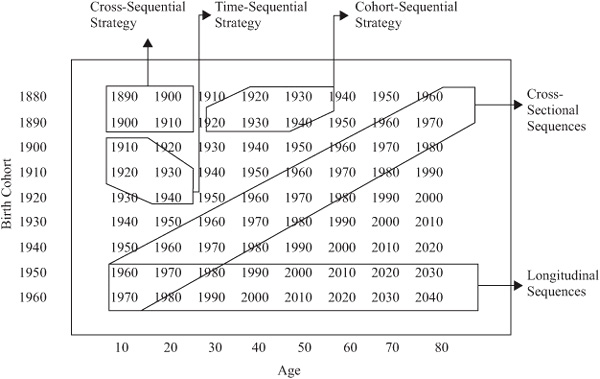
To reduce the limitations inherent in the simple data collection schemes, several alternative sequential strategies have been suggested (see Baltes, 1968; Schaie, 1965, 1973b, 1977, 1986, 2007a, 2009; Schaie & Caskie, 2005; Schaie & Willis, 2002). The term sequential implies that the required sampling strategy includes acquisition of a sequence of samples taken across several measurement occasions. To understand the application of sequential strategies, we must first distinguish between their roles as sampling designs and as data analysis strategies (see Schaie, 1983b; Schaie & Baltes, 1975). Sampling design refers to the particular cells of a Cohort × Age (time) matrix that are to be sampled in a developmental study. Analysis strategies refer to the manner in which the cells that have been sampled can be organized to disaggregate the effects of A, C, and T. Figure 2.1 presents a typical Cohort × Age matrix identifying the several possible sequential designs. This figure also illustrates the confounding of the three developmental parameters of interest. A and C appear as the rows and columns of the matrix; T is the parameter listed inside the matrix cells. There has been an extended debate on how these effects might be unconfounded. Those interested in this debate are referred to the work of Adam (1978); Buss (1979–1980); George, Siegler, and Okun (1981); Glenn (1976, 1981); Horn and McArdle (1980); Mason, Mason, Winsborough, and Poole (1973); Schaie (1965, 1967, 1973b, 1977, 1984a, 1986, 1994b, 2011); Schaie and Hertzog (1982); Schaie and Willis (1986a).

FIGURE 2.1. Example of a cohort/age matrix identifying the several possible sequential designs.
It is possible to distinguish two types of sequential sampling designs: those using the same panel of individuals repeatedly to fill the cells of the matrix and those using independent random samples of individuals (each observed only once) from the same cohorts. The matrix shown in figure 2.1 could be filled by either approach. Using Baltes’ (1968) terminology, the two approaches can be called longitudinal and cross-sectional sequences, respectively. A cross-sectional sequence will usually involve the replication of a cross-sectional study so that the same age range of interest is assessed for at least two time periods, obtaining the estimate for each age level across multiple cohorts, with each sample measured only once. By contrast, the longitudinal sequence represents the measurement of at least two cohorts over the same age range. Here also, estimates from each cohort are obtained at two or more points in time. The critical difference between the two approaches is that the longitudinal sequence permits the evaluation of intraindividual age change and interindividual differences in rate of change, information about which cannot be obtained from cross-sectional sequences. Figure 2.1 has equal intervals for the age ranges and cohort ranges investigated. However, intervals do not have to be equal, although unequal intervals introduce special problems in analysis and should be avoided if possible (see Botwinick & Arenberg, 1976).
Data matrices of the type shown in figure 2.1 permit a variety of alternative analytic strategies (see Schaie, 1965, 1977, 1992, 2006a, 2008a, 2011; Schaie & Caskie, 2005. Specifically, each row of the matrix can be treated as a single-cohort longitudinal study, each diagonal as a cross-sectional study, and each column as a time lag study. The sequential designs (except under the special circumstance when one of the components is reconceptualized [see Schaie, 1986]) do not permit complete disentanglement of all components of the B = f (A, C, T) function owing to the obvious linear dependency of the three factors. Despite this problem, I have suggested that, given the model, there exist three distinct analytic designs, created by considering the distinct effects of any two of the components while assuming the constancy or irrelevance of the third component on theoretical or empirical grounds.
The minimum designs indicated in figure 2.1 provide examples of three analytic approaches. The first, which I have called the cohort-sequential strategy, permits separation of age changes from cohort differences under the assumption of trivial time-of-measurement (period) effects. The second or time-sequential strategy further permits the separation of age differences from period differences, assuming only trivial cohort effects. Finally, the cross-sequential strategy permits the separation of cohort differences from period differences.
When data are collected in the form of longitudinal sequences, as in the SLS, to examine intraindividual age changes it is possible to apply both the cohort-sequential and the cross-sequential strategies for data analysis. Developmental psychologists often find the cohort-sequential design of greatest interest because it explicitly differentiates intraindividual age changes within cohorts from interindividual differences between cohorts (see Baltes & Nesselroade, 1979; Schaie & Baltes, 1975; but see Schaie, 1986).
This design also permits a check of the consistency of age functions over successive cohorts, thereby offering greater external validity than would be provided by a single-cohort longitudinal design.
As noted, a critical assumption for the application of the cohort-sequential analysis strategy is the absence of time-of-measurement effects in the data under consideration. This assumption may be parsimonious for many psychological variables, but others may still be affected by “true” period effects or other internal validity threats, such as differences in instrumentation or experimenter behavior across test occasions (see section on internal and external validity). The question arises, then, how violations of the assumption of no T effects would be reflected in the results of the cohort-sequential analysis. Logical analysis suggests that all estimated effects would be perturbed, although the most direct evidence of the violation would be shown by a significant C × A interaction (see Schaie, 1973b). However, lack of such an interaction does not necessarily guarantee the absence of T effects; in extensive studies such as ours, they might well be localized in a small subset of test occasions, thus biasing all estimates.
The essential consequence of the interpretational determinacy in sequential analysis is that, if design assumptions are violated, then all effect estimates will be biased to some degree. The problem of interpretation may be lessened, however, by estimating the relative likelihood of confounded T effects given a strong theory about the nature and direction of estimated and confounded effects. We have found that the practical application of a strong theory to sequential designs may require the specification of confounds in an “invalid” design to obtain direct estimates of the confounded effects (see Schaie, 1994b).
An example of the planned violation of design assumptions is use of the cross-sequential strategy under the assumption of the absence of A effects, an assumption that most developmental psychologists might find hard to swallow. Such an approach may be quite reasonable, however, when longitudinal data are available for only a limited number of measurement occasions but extend over a wide range of cohort groupings. The cross-sequential design can then be implemented after only two measurement occasions, whereas a cohort-sequential design would require at least three such occasions. Moreover, the number of measurement occasions required to estimate cohort-sequential designs that span a wide age and/or cohort range would be prohibitive if we insist that no data analyses be performed until the data for the entire cohort-sequential design appropriate for the research question of interest have been acquired. Given a strong developmental theory about the nature of the confounded A effects, a misspecified cross-sequential design can provide useful information about the significance of the A effects represented in both the C and T components. As will be seen, the early work in the SLS (analysis of the data from the first two cycles) began with such misspecification in a cross-sequential design to permit preliminary inferences regarding the relative importance of C and A effects prior to the availability of data that permitted direct simultaneous assessment of these effects (see Schaie & Labouvie-Vief, 1974; Schaie & Strother, 1968b).
Although it is always preferable to estimate parameter effects from the most appropriate design—one that incorporates the correct limiting assumptions— one must often settle for something less than the optimal, whether this is a temporary expedient or one dictated by the phenomenon studied.
Although the longitudinal approach has advantages over studies based on onetime observations, it is also beset with many methodological problems, some of which have necessitated a variety of design refinements, which may be noted in following the account of the SLS from its earlier to its later phases. In this section, I wish to alert the reader to some of these issues by discussing threats to the internal and external validity of our study, and I suggest approaches to possible solutions of the remaining problems, which will again be encountered as they are applied to various analyses described in this volume.
Longitudinal studies cannot meet all of the rules for designing true experiments because age is a fixed personal attribute that cannot be experimentally assigned. Consequently, longitudinal studies are subject to all the problems inherent in the type of study that Campbell and Stanley (1963) have denoted as a “quasi experiment.” These problems may result in threats to the internal validity of the study. That is, factors analyzed in a given design that are thought to assess the hypothesized construct may in fact be confounded by other factors not explicitly included in the design. Alternatively, design problems may threaten the external validity of a study, that is, the extent to which valid generalizations from the sample can be applied to other populations.
Because longitudinal studies represent quasi experiments, Campbell and Stanley (1963) describe eight threats to the internal validity of such studies: maturation, effects of history, testing, instrumentation, statistical regression, mortality, selection, and the selection–maturation interaction. The first two, history and maturation, have special meaning for the developmental psychologist beyond their threat to the internal validity of any pretest–posttest type of study design. They may be topics of investigation in their own right. Maturation, quite obviously, is not a threat to the validity of developmental studies but, rather, is the specific effect of primary interest to the developmentally oriented investigator. Nevertheless, the measurement of maturation is not always unambiguous because, given a specific developmental model, it may be necessary to go beyond a test of the null hypothesis negating maturational effects to test instead some quite explicit alternative hypotheses that specify direction and magnitude of the expected maturational effect.
By contrast, historical effects are indeed the primary internal validity problem for the developmental scientist. History is directly involved in both cohort and time-of-measurement (period) effects. However, cohort effects represent the impact of historical effects on a group of individuals who share similar environmental circumstances at equivalent points in their maturation sequence (cf. Schaie, 2011). On the other hand, time-of-measurement effects represent those events that have an impact on all members of the population experiencing a common historical exposure, regardless of cohort membership. The specific threat to longitudinal studies is that historical effects may threaten the internal validity of designs that attempt to measure the effect of maturation (aging effects).
The traditional single-cohort longitudinal design is a special case of the pretest–posttest design in that it repeatedly measures the same individuals over time. Hence, such studies are affected also by the other six threats to internal validity described by Campbell and Stanley (1963). There are actually two different aspects of testing: reactivity and practice. Reactivity involves the possible effect on subsequently observed behavior of exposure to certain procedures that are part of the experimental protocol. Longitudinal study participants might respond to a second test in a very different manner than would be the case if they had not been tested previously, a behavior change that could be confused with the effects of maturation. Practice effects, on the other hand, may simply mean that, on subsequent tests, study participants will spend less time in figuring out items previously solved and thus can improve their overall performance by attempting a greater range of problems in the time allowed.
The internal validity threat of instrumentation refers to differences in measurement techniques that covary with measurement occasions. In long-term longitudinal studies, such differences may occur when study personnel changes occur or when records regarding the study protocol on previous occasions have been lost and slight variations in protocol are introduced inadvertently. Such effects, again, may either lead to the erroneous inference of having demonstrated maturational trends or may obscure reliable, but small, developmental changes that are actually occurring.
Statistical regression involves the tendency of variables containing measurement error to regress toward the population mean from one occasion to the next. This problem is of particular importance in two-occasion longitudinal studies (see Baltes, Nesselroade, Schaie, & Labouvie, 1972, and Schaie & Willis, 1986b, for examples of applications of the time-reversal method, which tests for the effect of regression in such studies). It has been shown, however, that regression effects do not necessarily cumulate over extended longitudinal series (Nesselroade, Stigler, & Baltes, 1980).
Members of longitudinal panels obviously cannot be forced to continue their participation. Consequently, another serious threat to the internal validity of longitudinal studies is experimental mortality. This term describes the attrition of participants from a sample between measurement occasions, whether such attrition is because of biological mortality, morbidity, or simply experimenter ineptness in maintaining good relations with panel members. Most empirical studies of experimental mortality suggest that attrition is nonrandom at least between the first and second measurement occasions (Cooney, Schaie, & Willis, 1988; Gribbin & Schaie, 1979; Riegel & Riegel, 1972; Schaie, 1988d, 1996b; Schaie, Labouvie, & Barrett, 1973; also see chapter 8).
Selection refers to the process of obtaining a sample from the population such that the observed effect is because of the specific sample characteristics rather than the maturational effect we wish to estimate. For example, a change over time may occur in a subset of the population regardless of age. The selection–maturation interaction refers, of course, to the case where maturational effects may be found in some samples of one age, but not in samples of other ages.
It is not possible to control or measure the effects of any of the above internal validity threats in single-cohort longitudinal studies. When multiple data sets such as ours are available, however, the magnitude of some of these effects can be estimated and appropriate corrections applied to obtain less-biased estimates in the substantive studies. Specific designs for the appropriate analyses have been provided (Schaie, 1977, 1988d) and are applied to some of the data sets presented in chapter 8.
As quasi experiments, longitudinal-sequential studies also share certain limitations with respect to the generalizability of their findings (see Cook & Campbell, 1979; Schaie, 1978). Four major issues can be identified. The first concerns experimental units, that is, the extent to which longitudinal data collected on one sample can be generalized to other populations (see Gribbin et al., 1976; chapter 8). The second involves experimental settings, or the extent to which findings have cross-situational validity (see Scheidt & Schaie, 1978; Willis & Schaie, 1986a). The third is concerned with treatment variables, that is, the limitations imposed by specific settings or measurement-implicit reinforcement schedules (see Birkhill & Schaie, 1975; Schaie & Goulet, 1977). Finally, external validity may be threatened by certain aspects intrinsic to the measurement variables to the extent to which task characteristics remain appropriate at different developmental stages as a longitudinal study progresses (see Schaie, 1977–1978; Schaie, Maitland, Willis, & Intrieri, 1998; Schaie, Willis, Jay, & Chipuer, 1989; Sinnott, 1989).
Given the considerations above, I have collected data in the SLS using an approach that allows some useful analyses early on in the course of a longitudinal study, but that over time generates data that can be used eventually to address most of the methodological questions I have raised here. I include a description of this design here (see also Schaie & Willis, 2002, pp. 116–120) to provide some guidance to those who would start a longitudinal study de novo as well as to describe the design rationale of the SLS.
As should be obvious from the preceding discussion, the “most efficient design” is a combination of cross-sectional and longitudinal sequences created in a systematic way. In brief, the researchers begin with a cross-sectional study that includes multiple age groups. Then, after a period of years, all of those participants who can be retrieved are retested, providing longitudinal data on several cohorts (a longitudinal sequence). At the same time, a new group of participants over the same age range as the original sample is tested. The new sample together with the first cross-sectional study forms a cross-sectional sequence. This whole process can be repeated over and over (ideally, with age groups and time intervals identical), retesting the previously tested participants (adding to the longitudinal data) and initially testing new participants (adding to the cross-sectional data).
In the SLS, we first tested seven groups of people ranging in age from 22 to 70 years in 1956 (see chapter 3). This was a straightforward cross-sectional study. In 1963, those participants who could be found were retested. Hence, we were able to examine, for each of seven cohorts, what happened to average ability scores as the participants aged 7 years. At the same time, we recruited new participants in the same age groups as the original participants (plus an additional group at the age now attained by the oldest original group) and tested them for the first time. The second cross-sectional study represents a replication of the first study. A discrepancy between the two replications suggests the presence of either cohort or time-of-measurement effects. In 1970, we retested the original sample for the third time, adding more data to the longitudinal sequence. Participants who were added at T2 in 1963 were also retested, adding a new longitudinal sequence. Again, new participants were recruited to form a third replication of the cross-sectional study. A similar approach was taken on subsequent test occasions, which in our case occurred in 1970, 1977, 1984, 1991, and 1998.
Data from the most efficient design or comparable designs can be analyzed in several ways. The approach of greatest interest to developmental psychologists is to contrast age changes and cohort effects (Schaie & Baltes, 1975), termed a cohort-sequential analysis. Such a comparison permits a strong test of an irreversible age decrement model (Schaie, 1973b). At least two cohorts are required, and each cohort must be observed at least at two different ages. In a traditional longitudinal study, data would be available only for a single cohort, and it would not be known, therefore, whether the observed change holds true beyond the specific cohort studied. For example, one cohort may show an increase and the other a decrease, or one cohort may increase at a slower rate than the other. One cohort may have a higher average IQ than the other at both 60 and 70 years of age, although the increase or decrease may be similar for the two cohorts.
In cross-sequential analyses, cohort effects are contrasted with time of measurement. At least two cohorts are compared at two or more times of measurement. This strategy may be particularly appropriate for data sets that cover age ranges for which, on average, stability is likely to obtain (such as in mid-life). No age changes are expected, and the primary interest turns to identifying the presence and magnitude of cohort and time-of-measurement effects. The cross-sequential analysis is helpful when the researcher is interested in, say, the effects of some event or sociocultural change that occurs between the two times of measurement and suspects that different cohorts might react differently to such change. In addition, if there is reason to suppose that time-of-measurement effects are slight or nonexistent, then cross-sequential analysis can be used to estimate age changes because participants are obviously older at the second time of measurement.
If the cohort-sequential analysis contrasts cohort and age and the cross-sequential analysis contrasts cohort and time of measurement, there is one logical possibility left: the time-sequential strategy, which contrasts age and time of measurement. We might find that the difference between age groups narrows over a given period, or perhaps both age groups change in the same manner, but the gap between them remains sizable. The time-sequential approach would be appropriate also for a test of a decrement-with-compensation model. When a new compensatory method is introduced (say, a computerized memory prosthesis or a drug affecting declining memory), the time-sequential method could show that age differences over the same age range would be smaller at Time 1 than at Time 2.
In a typical longitudinal study, repeated measures are taken of the same participants at different times. Another possibility is to use the same research design but with independent samples at each point on the longitudinal timescale. A longitudinal study usually begins by testing participants at an initial time point, with plans to retest the same individuals at intervals. The alternative strategy would be to draw a new (independent) sample from the same cohort at each test occasion. The independent sampling approach works well when large samples are drawn from a large population. If small samples are used, it is of course necessary to make sure that successive samples are matched on factors such as gender, income, and education to avoid possible differences because of selection biases.
The independent samples procedure, used conjointly with the repeated-measurement procedure, permits estimation of the effects of experimental mortality and of instrumentation (practice) effects. The independent samples are initially drawn at each occasion; hence, they reflect the likely composition of the single sample the repeated-measurement study would have had if no participants had been lost between testing—and of course if the participants would not have had any practice on the test instruments.
Time 1. The first occasion of any multiple-cohort longitudinal study will simply represent an n-group cross-sectional comparison.
Time 2. The second occasion provides a replication of the original cross-sectional study. There are as many two-point longitudinal studies as there are different age groups in the T1 design. Both time-sequential and cross-sequential analysis schemes can be applied. A simple cross-sectional experimental mortality by age/cohort analysis can be done by contrasting T1 scores for those participants who return and those who do not. Simple cross-sectional practice analyses can be conducted by contrasting T1 means for Sample 1 participants with the T2 scores of Sample 2 participants at equivalent ages.
Time 3. A third cross-sectional replication is now available, as well as a second replication of the two-point longitudinal study. Three-point longitudinal studies are now available from the initial sample. It is now possible to conduct 2 × 2 cohort sequential analyses. Time-sequential and cross-sequential analyses can be extended to n × 3 designs, allowing estimation of quadratic trends. Alternatively, it is also possible to estimate either experimental mortality or practice effects in the time- or cross-sequential analyses.
Time 4. The data collection at Time 4 adds a fourth cross-sectional replication, a third two-point longitudinal replication, a second replication of the three-point longitudinal study, and an initial four-point longitudinal study. It is now possible to conduct n × 3 cohort sequential analyses, allowing quadratic estimates, as well as n × 4 time-sequential and cross-sequential analyses that allow estimation of cubic trends. It is also possible to estimate the joint effects of experimental mortality and practice effects in the time- or cross-sequential analyses and to estimate either of these effects in the cohort-sequential analysis.
Time 5. In addition to adding one further layer to all of the above analyses, these additional data will allow estimation of joint effects of experimental mortality and practice in the cohort-sequential schema.
Except for a limited number of demographic attributes and gross anthropometric indices, there are very few observable characteristics that directly contribute to our understanding of human behavior. Behavioral scientists who investigate phenomena in areas such as intellectual abilities, motivation, and personality are rarely interested in their participants’ response to specific items or even the summary scores obtained on a particular measurement scale. Instead, such responses are treated as one of many possible indicators of the respondents’ location on an unobservable construct that has either been theoretically defined or has been abstracted from empirically observed data. By the same token, scientists studying psychopathology are rarely interested in the occurrence of specific clinically observed symptoms, other than the fact that such symptoms serve as indicators of diagnostic syndromes associated with broader import and consequences (cf. Schaie, 2000d).
Although we can directly measure only the observable phenotype or surface trait, it is usually the unobserved (latent) genotype or source trait that is the object of inquiry for the definition of developmental change. In fact, directly observable variables in the developmental sciences are typically used to define independent variables. Most dependent variables, by contrast, usually represent latent constructs that must be measured indirectly by means of multiple observations or indicators. This is perhaps fortunate because the equivalence of single measures of a particular construct over wide age ranges and time periods is often questionable.
Horn, McArdle, and Mason (1983) drew attention to an important distinction between two levels of invariance in factor loadings, a distinction first introduced by L. L. Thurstone (1947, pp. 360–369), that may have different implications for age change and age difference research: configural invariance and metric invariance. Meredith (1993) spelled out in greater detail what he considered necessary conditions to satisfy this factorial invariance at different levels of stringency.
To demonstrate factorial invariance, it is necessary to show at least that factor patterns across groups or time would display configural invariance. In this case, all measures marking the factors (latent constructs) have their primary nonzero loading on the same ability construct across test occasions or groups. They must also have zero loadings on the same measures for all factor dimensions.
A second (more desirable) level of factorial invariance (termed weak factorial invariance by Meredith) requires that the unstandardized factor pattern weights (factor loadings) can be constrained equal across groups or time. The technical and substantive considerations for this level of factorial invariance have found extensive discussion in the literature (cf. Horn, 1991; Horn & McArdle, 1992; Jöreskog, 1979; Meredith, 1993; Schaie & Hertzog, 1985; Sörbom, 1975; L. L. Thurstone, 1947). If this level of invariance can be accepted, then it becomes possible to test hypotheses about the equivalence of factor means. One can then also test further hypotheses about the latent factor variances and covariances.
However, it should be stressed that it is probably questionable whether even the assumptions of weak factorial invariance can be met in complex empirical data sets such as those found in many aging studies. In fact, Horn et al. (1983) early on argued that configural invariance is likely the best solution that can be obtained. Nevertheless, it should be possible to demonstrate more stringent levels of invariance for subsystems across some ages and cohorts. Byrne, Shavelson, and Muthén (1989) have proposed, therefore, that one should test for partial measurement invariance. This proposition has been received with much controversy in the factor-analytic literature. Because of the undue sensitivity of most standard error of measurement (SEM) estimates to local disturbances of model fit, it seems that testing for partial invariance is quite reasonable as seen from the point of view of the substantively oriented scientist.
In any event, it is evident that, for both cross-sectional and longitudinal studies, configural invariance remains a minimal requirement; demonstration of some form of metric invariance is essential before valid comparisons of factor scores can be created. A detailed description of an optimal plan of analysis is provided in Schaie (2000d). The required tests of factorial invariance would proceed as follows:
1. Test the least restricted acceptable model, configural invariance:
a. Constrain all nonsalient factor loadings to zero.
b. Estimate all other loadings for each group/time.
c. Estimate factor variances/covariances for each group/time.
2. Test the weak invariance model:
a. Constrain all factor loading to be equal across groups/time.
b. Estimate factor variances/covariances for each group/time.
3. If necessary, test partial invariance model:
a. Examine modification indices and/or SEMs for factor loadings to determine the partial invariance model.
b. Constrain all factor loading to be equal across groups/time, except those determined to be freed up in Step a.
c. Estimate all other loadings for each group/time.
d. Estimate factor variances/covariances for each group/time.
Improvement of fit would generally be examined in terms of delta chi-square, but other fit indices can obviously be used as well, although their distributional characteristics are not as well established for the purpose of model comparison (cf. Browne & Cudeck, 1993).
Equivalence of groups must be considered whenever (a) cross-sectional data have been collected and age differences in score level are to be interpreted under the assumption that factor structure is equivalent across the different age groups; (b) when we wish to demonstrate equivalence of factor structure across multiple cohort groups; (c) when the same population is followed by means of drawing successive random samples across time; and (d) when subpopulations are to be compared on multiple dependent variables of interest.
Contradictory findings in the literature on age group differences in factor structure can often be attributed to problems associated with conducting separate exploratory factor analyses of correlations specific to a particular group (see Cunningham, 1978, 1991; Jöreskog, 1971; Reinert, 1970). However, as has been shown by Meredith (1964, 1993), when level of performance differs across groups, it is only the unstandardized factor loadings that can remain invariant across groups. These difficulties can readily be overcome by the joint SEM analysis of multiple covariance matrices in which equality constraints are imposed across groups. Likelihood ratio tests are then available that can test the hypothesis that the unstandardized regression coefficients mapping variables on their latent constructs are indeed equivalent across groups (see also Alwin & Jackson, 1981).
Alternatively, if large enough population samples are available, a population factor structure can be determined, and then how well a subpopulation structure can be fitted by the factor structure obtained for the total population can be tested (e.g., Schaie et al., 1989, 1998; chapter 8).
The demonstration of factorial invariance is also important in showing that the relations between observations and latent constructs remain stable across time or that the introduction of an intervention might affect such relationships. When multiple measures of a set of latent constructs are available for two or more occasions across time, the highest covariances among observed variables will often be the covariances of the variables with themselves across measurement occasions. Exploratory factor analyses of such matrices would result in test-specific factors that would be less than optimal in representing change processes over time.
The longitudinal factor analysis procedures developed by Jöreskog and Sörbom (1977; also see Meredith, 1993) represent a particularly appropriate method for the study of factorial equivalence across time. First, they allow testing of the hypothesis that the regressions of variables on latent constructs can be constrained to be equal across the successive longitudinal testing occasions. Second, they permit assessment of interindividual differences in intraindividual change by testing longitudinal changes in factor variance (change in factor variance over time could occur only if there were individual differences in magnitude of change over time). Third, they allow estimation of the stability of intraindividual differences (high factor covariances across time represent stability of individuals about their own factor means). Finally, they allow the simultaneous test of stability of means on the latent factor scores. Extensions of these models suitable for the cohort-sequential designs used in the SLS have been discussed by Jöreskog and Sörbom (1980) and Hertzog (1985) and in the SLS have been applied to longitudinal data (Hertzog & Schaie, 1986, 1988; Maitland, Intrieri, Schaie, & Willis, 2000; Schaie et al., 1998) and to the evaluation of intervention effects on factorial invariance (Schaie, Willis, Herzog, & Schulenberg, 1987; see also chapter 8).
For completeness, it should be noted that all the design recommendations provided for the comparison of repeated or independent estimates of performance level can also be applied to the analyses of structural invariance described in this section.
One of the major controversies in the literature on adult development concerns the question as to whether evidence is available from longitudinal studies of adults that would offer support for the concept of dedifferentiation in cognitive abilities structures from young adulthood to old age.
The conceptual basis for this controversy comes from the theorizing of Kurt Lewin (1935; also see Schaie, 1962) and particularly Heinz Werner (1948), who argued that the cognitive structures of young children were amorphous and undifferentiated, but that the process of development would lead to a greater differentiation of distinct mental processes. The reason for the original lack of differentiation was attributed to the fact that, during early development, all psychological processes are heavily dependent on their physiological infrastructures and hence would need to develop in an undifferentiated tandem with the physiological development. As adulthood is reached, however, environmental and experiential phenomena tend to dominate the psychological processes, with far less dependence on their physiological bases.
Once late midlife is reached, however, the declines of sensory, motor, and central nervous system functions tend to lead to a renewed dependence of individual differences on physiological infrastructures. Hence, a reversal of the earlier differentiation is to be expected as psychological processes increasingly depend on the physiological infrastructure (cf. Baltes & Lindenberger, 1997). This dedifferentiation can be expressed in more modern terms as the progressive increase of individual differences variance and the corresponding decrease of individual differences covariance.
Evidence for the dedifferentiation phenomenon has been reported for individual variables since the 1940s (e.g., Balinsky, 1941; Cornelius, Willis, Nesselroade, & Baltes, 1983; Garrett, 1946; Reinert, 1970). More recent work has also demonstrated increases in correlations between cognitive sensory functions (e.g., Lindenberger & Baltes, 1994; Salthouse, Hancock, Meinz, & Hambrick, 1996). Much of this work, however, either has been at the level of individual marker variables or has relied heavily on cross-sectional data (e.g., Schaie et al., 1989). However, there is now work, particularly in the SLS (Maitland et al., 2000; Schaie et al., 1998) as well as the Victoria Longitudinal Study (Hultsch, Hertzog, Dixon, & Small, 1998), which suggests that dedifferentiation can also be demonstrated at the latent construct level. These studies also permit direct comparison of longitudinal and cross-sectional dedifferentiation patterns by contrasting covariation of change trajectories across different abilities to dedifferentiation in age/cohort differences. Our own findings with respect to this controversy are reported in chapter 8, but here I provide the methodological requirements for testing relevant paradigms.
If factorial invariance within cohorts can be demonstrated, it is then possible to conduct a substantive test of the proposition that factor variances decrease and factor covariance increases with age during adulthood. This is essentially an operationalization of the differentiation-dedifferentiation hypothesis. These tests proceed essentially as indicated above for the tests of factorial invariance except that they involve placing additional constraints on the factor variance–covariance matrix across groups or time (also see Schaie, 2000d, 2005b, 2008b; Schaie, Maitland, & Willis, 2000).
One of the common limitations ascribed to longitudinal studies is the problem that, as new questions arise and new measurement instruments are added at advanced stages of the study, such information is difficult to relate back to other information obtained at earlier points in time. One possible solution of this problem is to study the concurrent relationship between the new instruments and measures of related variables for which earlier (longitudinal) data are available. Such studies can attempt to project the new measures into the latent variable space for the variables in the longitudinal data set. The analytic procedure used for this purpose is the method of extension analysis, originally proposed by Dwyer (1937). If sufficiently strong projections of the new measures on the longitudinal measures are found, it is then possible to “postdict” estimated scores for the new measures for earlier data points.
An important application of confirmatory factor analysis is to use this procedure to implement the Dwyer (1937) extension method. As Tucker (1971) demonstrated, it is not appropriate to use factor scores on a latent variable to estimate their regression on an observed variable. However, confirmatory factor analysis permits the estimation of the location of some new observed variable or variables of interest within a previously known factor (latent construct) space. This is a situation that frequently arises in aging studies as samples are followed over long time periods.
To conduct an optimal extension analysis, it is necessary to have a sample for which data are concurrently available both on a set of measures with dimensionality (i.e., latent constructs) that has been well established and the other measures with a relation to these constructs that is to be studied. We have thus far used this approach in two studies designed to postdict longitudinal data for measures for which only concurrent observations are available. The first of these studies postdicted NEO scores from our measure of 13 personality factors (PF13; Schaie, Willis, & Caskie, 2004), and the second postdicted scores for our neuropsycho-logical test battery from the longitudinal psychometric factors (Schaie, Caskie, et al., 2005).
In the extension analyses, factor loadings were constrained to the unstandardized values from the confirmatory factor analysis solution for the respective personality or cognitive variables for the concurrent sample. Factor loadings for the new measures were then freely estimated, providing information on the projection of these measures into the previously established factor space. The factor loadings were then orthonormalized to provide weights for the estimation of the postdicted factor scores. Descriptions of the results of these analyses can be found in chapters 13 and 20, respectively.
This chapter discusses the methodological issues that have arisen from the SLS data collections and in a dialectic process have led to subsequent empirical study components. I summarize the general developmental model and specify the relationship between cross-sectional and longitudinal data in the context of that model. A rationale is presented for the simple and sequential schemes of data acquisition and analysis employed in the study. Consideration is then given to the problems of internal and external validity of developmental studies, and designs are presented that are used in the SLS to control for internal validity problems. I include a description of what has been called Schaie’s most efficient design for multiple-cohort longitudinal studies and describe the analysis modes available at each of the first five test occasions in a longitudinal study thus designed.
The data presented in the following chapters concern both observed variables and latent constructs inferred from them. Therefore, I also discuss the relationship between observed measures and latent variables and describe the applicability of confirmatory (restricted) factor analysis to the assessment of construct equivalence across cohorts, age, and time in the study of developmental problems. Also explained is the differentiation-dedifferentiation hypothesis, one of the major theoretical propositions in adult development, and I indicate how this hypothesis can be tested by means of SEM modeling. Finally, I preview the application of extension analysis to the postdiction of nonobserved data for more recently added measurement variables.