Chapter 12. The Hard Way

For our last chapter, we want to take a bit of a step down into the murky world of implementation specifics. Most of this book has used neural networks to do some pretty impressive stuff, but in Chapter 10 and Chapter 11 we discussed the principles underlying machine learning, we haven’t looked at how you make one of these things. How does CoreML actually create a neural network? How would you go about building one yourself from scratch? In this chapter, we peek behind the curtain and build a complete neural network using the same tools and frameworks that Apple uses.

Behind CoreML’s Magic

At the very high level, CoreML works by loading in a pretrained model file, created in a tool such as CreateML or TensorFlow, and then running the model and returning predictions based upon the input you give it.

In “A Look Inside CoreML”, we spoke a bit about how the programmatic internals of CoreML work, but we glossed over the structure of the model format because it isn’t important to understanding how CoreML works.

To understand what CoreML is doing, we do need at least a basic look into the format. The CoreML model format itself is based on the protobuf serialized data format with a custom schema that allows you to define, among other things, the type of machine-learning model, the features of the model, labels, inputs and output, attributes, metadata, and anything else you need to fully describe your model.

At its core the data format precisely describes the model in such a way that another program could read, understand, and then rebuild the exact model.

Note

For more details on the CoreML model format, check back to “The MLModel format”, earlier in the book.

This means that CoreML must read the model file and turn it into a neural network, generalized linear model, tree classifier, or whatever model type it happens to be, and then run that. The model that CoreML receives from us (an .mlmodel) is essentially a generic description of a model.

CoreML builds a device-specific version of the model that is optimized for the hardware it is running on. This device-specific version is built up using similar approaches to what we are going to be doing in this chapter, and doesn’t change the workings of the model; it’s just optimized for the device.

This new form, after it’s created, is then compiled and saved as an .mlmodelc format and is what CoreML is actually using for running.

CoreML doesn’t so much run the MLmodels, but converts them into a new form that it then runs.

Despite this being the main approach for the bulk of the book, and also the general approach you should be taking, it isn’t the best for seeing how CoreML works. So for this chapter, we are going to take a step back and build up a neural network ourselves using the Basic Neural Network Subroutines (BNNS) library, which is part of Apple’s Accelerate framework (we mentioned this framework back in “Apple’s Other Frameworks”).

This covers only the case of neural networks, and CoreML (and machine learning in general) supports far more than just neural networks, but they are currently the most popular form of machine learning and the most interesting to build from scratch.

Tip

The Accelerate framework contains more than just BNNS; it has a variety of different libraries for fast CPU acceleration.

Alongside BNNS, Accelerate also has code for vector and quaternion operations, signal processing, and sparse-matrix linear algebra solvers, among others.

Although you could write any of these yourself, Apple has already written highly optimized and hardware-accelerated versions of these that are well worth checking out.

BNNS is one of the underlying libraries that CoreML makes use of and is designed to run on the CPU. You won’t often find yourself writing code that uses BNNS directly, but there is a good chance that any models you run through CoreML will be making use of it. You can use BNNS to build neural networks of any size or complexity supporting three different layer types:

  • Convolution layers

  • Pooling layers

  • Dense layers

Note

BNNS is often jokingly called bananas. Get it?

If your neural network design can be made up using those layer types (and many can be) you can create it using BNNS. BNNS is written in C, and Swift is calling the library through a bridge that lets you communicate with it as if it were native Swift code. It isn’t, however, so there are a few quirks to be wary of—we point these out when we get to them.

Note

BNNS is just one of many different technologies that Apple uses as part of CoreML.

Another technology used by CoreML that works in a very similar fashion with a similar designed, albeit slightly different-looking, API is Metal Performance Shaders (or rather, the parts of Metal Performance Shaders designed for building neural networks).

The main difference between BNNS and Metal Performance Shaders is that BNNS is CPU exclusive, whereas Metal Performance Shader are GPU exclusive. We are using BNNS over performance shaders for a simple reason: BNNS works on both macOS and iOS, and Metal Performance Shaders are primarily iOS-focused.

Although some macOS devices support Metal Performance Shaders, every modern Apple device supports BNNS. So this means that we can run our code in a Playground on macOS and also build it over onto iOS.

Task: Building XOR

For this task, we create a neural net that can approximate the logical XOR function. This means that it will be taking in two values, x and y, and returning one value that is the result of XORing the two values.

Essentially, what we want to create is a neural network that can match Table 12-1.

Table 12-1. Our training and testing data
x y Output

0

0

0

0

1

1

1

0

1

1

1

0
Warning

Please, please, please never use this neural network instead of the existing XOR function in Swift (or any other programming language). Not only is let output = x ^ y many orders of magnitude faster to run, it is already written and tested, has a lower energy consumption, and is easier to read (it is also 100% correct).

Our neural network can do only an approximation of XOR, and although it will be a very good approximation, neural networks are terrible choices for basic functions such as this. This is a learning exercise. Learn from it, don’t use it.

We are going to be building an XOR neural network for a few different reasons. First, XOR has a bit of history in the neural net world. When neural networks were new (called perceptrons), it was discovered that as they were initially presented they couldn’t perform the XOR function.

The clever AI boffins later solved this problem (through the use of hidden layers), but it is often considered one of the reasons why neural network research slowed down for a while, so it’s interesting to build a solution to an old problem.

Second, XOR is a very easy function to understand. The training and testing data is very easy to come by (in fact, the testing and training data are the same, and must be) and it can’t be overfitted no matter how hard or crudely you train the model.

Finally, XOR can be created using a very simple neural network, and as we are going to be making the network ourselves layer by layer, we don’t want it to be too complex.

Basically, XOR is an easy, forgiving, and simple enough function with which to build a working neural net from scratch. We also hope that it’s kind of fun!

The Shape of Our Network

We’ll be making a multilayer perceptron with two input neurons (x and y), two hidden neurons (hidden0 and hidden1), and one output neuron (output), with each layer being fully connected to the previous layer.

We have six weights (four for the neurons connecting from the input to the hidden layer, two for the hidden layer feeding into the output), and three biases (two for the hidden neurons and one for the output neuron). Figure 12-1 shows the structure of the neural network.

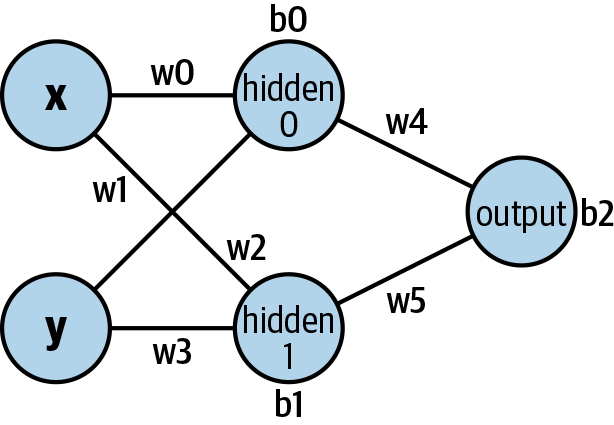
pais 1201
Figure 12-1. Our neural network

All of our inputs, outputs, weights, and biases are going to be floats, or more specifically, they will be arrays of floats. BNNS expects and often defaults to using this format.

Most of the time you should think of neural networks as operating over arrays of values instead of individuals. In our case, our neural network is simple enough that it might make sense to do it with scalar values passed in, but BNNS (and all ML software) is designed to support much larger networks and, as such, are set up to handle that.

As the goal of this chapter is to take a peek at how CoreML works, if we made the example too different from the approach underlying CoreML, it wouldn’t really serve much of a purpose.

The Code

We’re going to do all of our coding for this in a Playground. We could create a new application or service project and write our code in there, but for this example, a Playground is more than enough:

  1. Create a new macOS-flavor Playground in Xcode.

  2. Import the Accelerate framework. This will give us access to the BNNS library:

    import Accelerate

  1. Declare two optional BNNSFilter variables:

    var inputFilter: BNNSFilter?
var outputFilter: BNNSFilter?

    These will be the individual layers of our neural net. inputFilter will be the layer connecting the input to the hidden layer, and outputFilter will be the layer connecting from the hidden neurons to the output.

In almost every other neural network tool out there, these would be called layers, but in BNNS they are called filters. You can think of the filters as being the individual neuron layers that represent the connection between the layers themselves.

It doesn’t really change anything, however; the basic structure remains identical, but BNNS tends to word its API to focus more on the connections between layers rather than the layers themselves. Our variables are optional because we haven’t built up our layers yet, and after we are finished using the network we will want to free up the memory.

Neural networks can be quite heavy on the system, so we don’t want to keep them around when we aren’t using them. As such they can be nil, so we need to make them optional.

  1. Create function stubs:

    func buildNetwork(inputWeights: [Float],
                  inputBiases: [Float],
                  outputWeights: [Float],
                  outputBiases: [Float]) {

}

func runNetwork(_ x: Float, _ y: Float) -> Float
{

}

func destroyNetwork()
{
}

Here, we have three different functions for us to fill in later: buildNetwork, runNetwork, and destroyNetwork. The first one is responsible for creating the network itself, using the values passed in for weights and biases. The second will run our network with the provided values for x and y. Finally, destroyNetwork destroys our neural network and removes it from memory.

Building It Up

With our code set up, it is time to start filling out some of our function stubs; we begin by writing the code to create our neural network. The purpose of this function is to create a neural network that matches the image in Figure 12-1.

It has four parameters that give it its weight and biases, and stores the generated network into the two filter variables we set up earlier:

  1. Add the following code to the buildNetwork function:

    let activation = BNNSActivation(function: .sigmoid, alpha: 0, beta: 0)

let inputToHiddenWeightsData = BNNSLayerData(
    data: inputWeights,
    data_type: .float,
    data_scale: 0,
    data_bias: 0,
    data_table: nil)

let inputToHiddenBiasData = BNNSLayerData(
    data: inputBiases,
    data_type: .float,
    data_scale: 0,
    data_bias: 0,
    data_table: nil)

var inputToHiddenParameters = BNNSFullyConnectedLayerParameters(
    in_size: 2,
    out_size: 2,
    weights: inputToHiddenWeightsData,
    bias: inputToHiddenBiasData,
    activation: activation)

// these describe the shape of the data being passed around
var inputDescriptor = BNNSVectorDescriptor(
    size: 2,
    data_type: .float,
    data_scale: 0,
    data_bias: 0)

var hiddenDescriptor = BNNSVectorDescriptor(
    size: 2,
    data_type: .float,
    data_scale: 0,
    data_bias: 0)

inputFilter = BNNSFilterCreateFullyConnectedLayer(
    &inputDescriptor,
    &hiddenDescriptor,
    &inputToHiddenParameters,
    nil)

guard inputFilter != nil else
{
    return
}

There is a fair amount going on in here so let’s try to break it down. The first line of code is creating an activation. This will be used as the activation function for the layer. We are going to be reusing the same activation function for both of our layers, although this is unlikely to be the case for larger neural networks.

We’ve chosen the sigmoid function as our activation function because it is a good choice for this sort of task. There are heaps of other activation functions out there, many of which might do as good or better job than sigmoid, but for this case, we know sigmoid will work, so we’ll stick with it.

Note

Although we’re not using them, there are two other parameters as part of initializing the sigmoid: alpha and beta. Our example is simple enough that we don’t need to worry about tweaking those, but the alpha can be considered the scaling of the sigmoid, and beta is basically the offset.

Next, we start making layer data. The first, inputToHiddenWeightsData, is the data holding the weights of the input layer to the hidden layer (weights w0, w1, w2, w3 in Figure 12-1). The specific values for these come from the inputWeights parameter.

The most interesting part about this method is the data_type parameter, which lets you set what type of data is held within. Because we are planning on doing everything with floats, our data type is BNNSDataType.float, but there are many different options.

If we were to use data other than floats we would need to set some of the other parameters to values other than 0 because they essentially instruct the initializer how to take nonfloat data and convert it into a float. Because we’ve stuck with floats, we are all good without this tweaking.

Next, we do the same with inputToHiddenBiasData but this time this is for the biases for the hidden layer (b0 and b1), again coming from the function parameters.

Note

You might notice that there is both a .float and .float16 data type in BNNS. .float16 represents a 16-bit floating-point number (also called half-precision floating-point number) whereas .float is the full-precision form.

This means that if you don’t need the full-precision floating points (and quite often you don’t), you can use a half-precision float, instead, which essentially means you use less memory creating and running your network.

For our example, using half-precision floats would work fine, and if this were intended to be more than an exercise, we really should use them to reduce our memory footprint.

The next call, BNNSFullyConnectedLayerParameters, is where we start to hook up our input layer to our hidden layer. This struct holds all the parameters necessary for BNNS to know how to hook up the different layers, but it doesn’t perform the connection itself.

In this case, we are creating a dense (fully connected) parameter list; it has an input and output of two neurons per layer (input_size and output_size), uses the weights and biases we just created, and activates using the sigmoid function we defined earlier.

After that is done, we create two BNNSVectorDescriptor structs. These, as their name implies, describe a vector (sometimes called a shape) that basically defines the number of elements and type of data.

In a language like Swift, this feels unnecessary because collections can normally automatically determine this information themselves. But BNNS is written in C, so we need to let it know.

Finally, we actually create our input and hidden layers and their connections. This is done using the function BNNSFilterCreateFullyConnectedLayer, which takes in all our previously configured weights, biases, parameters, and descriptors and creates a dense connection between our input and hidden layer. This all gets stored in our variable inputFilter for later use when we want to run the network. After that is done, we also perform a quick check using a guard statement to make sure that the creation worked before continuing.

With that done we can move onto the next step, creating our output layer and connecting it to the hidden layer:

  1. Add the following code to the buildNetwork function, just below the code you previously added:

    let hiddenToOutputWeightsData = BNNSLayerData(
    data:outputWeights,
    data_type: .float,
    data_scale: 0,
    data_bias: 0,
    data_table: nil)

let hiddenToOutputBiasData = BNNSLayerData(
    data: outputBiases,
    data_type: .float,
    data_scale: 0,
    data_bias: 0,
    data_table: nil)

var hiddenToOutputParams = BNNSFullyConnectedLayerParameters(
    in_size: 2,
    out_size: 1,
    weights: hiddenToOutputWeightsData,
    bias: hiddenToOutputBiasData,
    activation: activation)

var outputDescriptor = BNNSVectorDescriptor(
    size: 1,
    data_type: .float,
    data_scale: 0,
    data_bias: 0)

outputFilter = BNNSFilterCreateFullyConnectedLayer(
    &hiddenDescriptor,
    &outputDescriptor,
    &hiddenToOutputParams,
    nil)

guard outputFilter != nil else
{
    print("error getting output")
    return
}

This works in the exact same fashion as the preceding code, but it creates the layer and connections from the hidden layer to the output layer.

Now, when we call this function, we’ll have a fully configured neural network built and ready to go.

Making It Work

Having a configured neural network isn’t really that useful without some way of making it run, so now we’re going to write the code that will actually use our neural net:

  1. Add the following to the runNetwork function:

    var hidden: [Float] = [0, 0]
var output: [Float] = [0]

    This code just creates two arrays of floats, which you can think of as representing the individual neurons for the hidden and output layer (so two neurons in the hidden layer, and one in the output layer). Both are initially given zeros, because we are about to use them in conjunction with the filters we built up before and we need to them have some value.

    When we write some more code, our final value for the neural network will be stored back into the output variable.

  1. Add code to connect our input values to the hidden layer:

    guard BNNSFilterApply(inputFilter, [x,y], &hidden) == 0 else
{
    print("Hidden Layer failed.")
    return -1
}

    The call to BNNSFilterApply takes our input (which we’ve wrapped up into an array), connects them to the hidden neurons using the configuration we saved in our inputFilter, and stores the results back into the hidden array.

    Basically, it runs part of the neural network shown in Figure 12-2.

    The function returns an Int which tells us if it was able to run, with 0 meaning it worked and -1 meaning a failure. Because of this we can wrap it up inside a guard statement to check that it all works, as there is no point in going ahead if we can’t get the input → hidden layer working.

    One nice side effect of our code is that we have this clean step before we get an output, meaning we could output the values of our hidden neurons if we wanted to for testing purposes. With that done we now need to move from the hidden layer to the output.

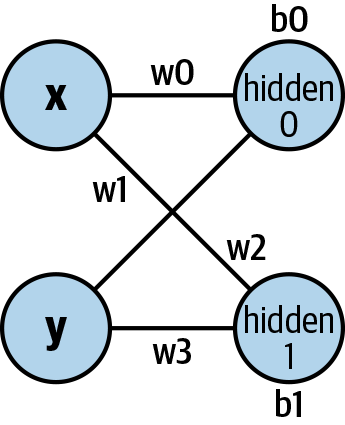
pais 1202
Figure 12-2. First half of the net

  1. Add code to connect the value of our hidden neurons to the output layer:

    guard BNNSFilterApply(outputFilter, hidden, &output) == 0 else
{
    print("Output Layer failed.")
    return -1
}

    This code works identically to the previous code; the only difference is now we are using the hidden layer as input into the output and saving the result into the output layer.

    From this point, whenever this code is run, the result will be stored in our output neuron, so the final step is to return it:

    return output[0]

Tearing It Down

The last function we need to fill in is to clean up our neural network. A neural network requires a great deal of resources, so as soon as you are finished with one you should remove it so that it isn’t sitting around taking up space.

Unlike most of your Swift code, we need to explicitly inform BNNS that it is safe to destroy the network.

Add the following code to the destroyNetwork function:

BNNSFilterDestroy(inputFilter)
BNNSFilterDestroy(outputFilter)

This function is very straightforward. It instructs BNNS to destroy the two filters that made up our neural network. After calling this method it would be impossible to run the neural network without first rebuilding it.

Approximations of XOR

At this point you might be a bit confused as to what is going on. 10 normally doesn’t equal 0.966, and 01 and 10 should be exactly the same, so what is going on? Neural nets are universally a terrible choice for such basic functions, and that’s because of how they work—it is going to be almost impossible to train one that can perfectly hit 0 and 1.

We haven’t created a neural network that can perform XOR, but we’ve created one that makes a pretty decent guess as to what XOR is (within 96% correct of the actual answer). So what can we do about it?

Not much, really. We could try some different weights and biases, but we’ll never get a perfect result. We can round and truncate the result using something similar to the following:

Int(runNetwork(1, 0).rounded())

This at least will make it look a lot closer to what we’d expect, but this is just covering up the weirdnes that is a side effect of how the neural network operates; we will never have a perfect one. But if we look at this from another angle, we have created something very interesting.

Neural networks don’t “think,” so it would never occur to the neural network that although something like 0.3 \^ 0.9 is gibberish to us, it will happily crunch that down and give you an answer. This means that we could add the following code just before we destroy our neural network and see what it thinks the result is of XORing all different values for 0 to 1 going up by 0.1 increments is:

for a: Float in stride(from: 0, through: 1, by: 0.1)
{
    for b: Float in stride(from: 0, through: 1, by: 0.1)
    {
        runNetwork(a, b)
    }
}

Training

Earlier when we built our neural network, we needed to give it some weights and biases for the various layers. Where did these come from?

These came out of training our neural network. BNNS (and CoreML, for that matter) are read-only—they are designed to run through the model as presented and have no capability to train or modify a model. In machine-learning lingo, they are for inference.

Note

This also means that, currently, any training you want to do must be done seperately from CoreML. We wouldn’t be surprised if this changes over time, because modern iPhones and iPads are incredibly powerful devices and doing updates to models on device (especially when plugged in) just makes sense. For now, however, you need to do this step in isolation from your apps using CoreML.

But in our case, we don’t have a pretrained model to get weights and biases from, and we can’t use BNNS to do the training. Normally, when working with CoreML you can use tools like Turi Create or CreateML to create your own models, but we’re even one step below that; we can’t use them, so we need to try something else.

In our case, we did our training in and got those numbers from using TensorFlow. TensorFlow is an open source project by Google that is designed for various different types of scientific numerical applications, but has become particularly big for its machine learning capabilities.

TensorFlow supports the creation, training, and running of neural networks and in some respects is a direct competitor to CoreML (as much as two free tools can be in competition). We chose TensorFlow because it is a good tool for training neural networks, and through coremltools you can convert between TensorFlow trained models and .mlmodel files.

This isn’t a chapter about TensorFlow, however, so we won’t be going into too much detail as to how we trained our model. You can trust us, it works.

Tip

Chapter 9 covers one of the versions of TensorFlow: Swift for TensorFlow. Here we are using TensorFlow for Python.

Although Swift for TensorFlow is good, it is also in flux. So when creating very low-level networks like this one, it is a bit clunkier than we’d like; hence, Python to the rescue. In the future we expect the low level elements of Swift TensorFlow to settle down in which case building an XOR in it would be as straightforward as it is in Python.

To perform the training, we created the exact same structure of our XOR neural network in Python TensorFlow, gave it a cost function and gradient descent optimizer to train it, and let it run more than 10,000 iterations.

After that was complete, we simply asked it what the weights and biases were, and copied those over into our BNNS code. The Python code for this looks like the following:

import tensorflow as tf
import numpy as np

inputStream = tf.placeholder(tf.float32, shape=[4,2])
inputWeights = tf.Variable(tf.random_uniform([2,2], -1, 1))
inputBiases = tf.Variable(tf.zeros([2]))

outputStream = tf.placeholder(tf.float32, shape=[4,1])
outputWeights = tf.Variable(tf.random_uniform([2,1], -1, 1))
outputBiases = tf.Variable(tf.zeros([1]))

inputTrainingData = [[0,0],[0,1],[1,0],[1,1]]
outputTrainingData = [0,1,1,0]
# only reshaping the data because our training input is one-dimensional
outputTrainingData = np.reshape(outputTrainingData, [4,1])

# making two activations for ouy layers
hiddenNeuronsFormula = tf.sigmoid(
    tf.matmul(inputStream, inputWeights) + inputBiases
)

outputNeuronFormula = tf.sigmoid(
    tf.matmul(hiddenNeuronsFormula, outputWeights) + outputBiases
)

# the cost function for training, this is the number the training wants to
# minimise
cost = tf.reduce_mean(
    (
        (
            outputStream * tf.log(outputNeuronFormula)
        ) + (
            (1 - outputStream) * tf.log(1.0 - outputNeuronFormula)
        )
    ) * -1)

train_step = tf.train.GradientDescentOptimizer(0.1).minimize(cost)
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

# actually training the model
for i in range(10000):
    tmp_cost, _ = sess.run([cost,train_step], feed_dict={
        inputStream: inputTrainingData,
        outputStream: outputTrainingData
    })
    if i % 500 == 0:
        print("training iteration " + str(i))
        print('loss= ' + "{:.5f}".format(tmp_cost))

# reshaping the weights/biases into something easily printable
inputWeights = np.reshape(sess.run(inputWeights), [4,])
inputBiases = np.reshape(sess.run(inputBiases), [2,])
outputWeights = np.reshape(sess.run(outputWeights),[2,])
outputBiases = np.reshape(sess.run(outputBiases), [1,])

print('Input weights: ', inputWeights)
print('Input biases: ', inputBiases)
print('Output weights: ', outputWeights)
print('Output biases: ', outputBiases)

To start the training and get results, all you need do is install TensorFlow and run the script through Python.

Note

Check back to “Python” if you need a refresher on how to set up a Python environment.

Next Steps

So we made bad XOR? In the end, what did we actually achieve here?

We have a slightly unusual XOR, that gives us a very close answer to actual XOR with the added benefit (or is that a detriment?) that it doesn’t care whether the numbers being XORed make sense. But, importantly, we got to see a simplified example of steps that CoreML follows whenever it runs a model, and we also got to make a neural net from scratch.

Hopefully, you’ve also seen why this is a lot of work and why letting CoreML handle it is generally the best option. If you really want to take it further, take a look at Apple’s Metal Performance Shaders. The Metal Performance Shaders framework contains a whole bunch of stuff that makes it easier to make neural networks. Particularly, there are tools for hand-building convolutional neural network kernels, and recurrent neural networks.

Tip

We recommend starting with Apple’s article on training a neural network with metal performance shaders, as well as the session from Apple’s WWDC 2019 conference, “Metal for Machine Learning”. This goes way outside practical, and Swift (the code in the sample is in Objective-C++).

Keep our website bookmarked, since we post pointers for further resources there, too!

Tip

If you’re a bit lost for what to read next, and have already bookmarked our website, we recommend the book Practical Deep Learning for Cloud and Mobile. It’s a great next-step, taking a different approach to the idea of practical, and it complements our book perfectly.