2 Monetary Aggregation Theory
Economic measurement is a formidable subfield within the field of economics and has been evolving with increasing sophistication over more than a century. Economic measurement includes “aggregation theory” and “index-number theory.” Perhaps the most widely known applications of that subfield are the consumer price index (CPI) and the national income accounts. Economic measurement is not simply accounting. Flow of funds accounting is taken as given in economic measurement, which goes far beyond accounting and makes extensive use of economic theory. Aggregation theory can become very mathematical, but the basic ideas can be understood without the mathematics. This chapter makes the basic principles accessible.
2.1 Adding Apples and Oranges
Economic theory deals primarily with flows of services, including the demand and supply for those services. To apply economic theory, measurement of the quantity and price of the service flows is necessary. With perishable goods, the service flow is the same as the stock, and the price of the service flow is the same as the price of the stock. If you purchase an apple, all of its services must be consumed in the current time period before it spoils, so purchasing one apple provides the total services of one apple during the current period of time. The same is true for an orange. Durables providing services for multiple periods are a more complicated matter. When you buy a house, you are purchasing the service flow over the lifetime of the house, not just its services during the current period. As a result, renting the services for only one period is less expensive than buying the house.
This section considers initially only the case of perishable goods, so that the stock and the service flow are the same. Suppose that you want to measure the service flow from fruit, consisting of apples and oranges. Perhaps you have five apples and four oranges. Clearly, the service flow from the apples can be measured as five apples, while the service flow of the oranges can be measured as four oranges. But would you wish to measure the service flow of the basket of fruit to be nine units of aggregate fruit, regardless of the prices of oranges and apples and your preferences over them? Suppose that it was five grapes and four watermelons? Is that nine “fruit” units, the same as for nine grapes or nine watermelons? A sophisticated area of economic theory deals with that problem. The theory is called “aggregation theory,” along with the closely related area of “index-number theory.” The specialized professional literatures on aggregation theory and index-number theory comprise the foundations for “economic measurement.” Major advances have been made in those areas of research over the past century, and the relevancy and validity of that literature are accepted by all economists. While the literature is highly mathematical and sophisticated, the basic insight is easily understood by everyone and is consistent with a common admonition: “you can add apples and apples but not apples and oranges.” That’s it!
That idiom is in fact widely known; it exists in similar forms in most languages throughout the world, as explained in the Wikipedia. In Quebec French, it takes the form comparer des pommes avec des oranges, while in European French the analogous saying is comparer des pommes et des poires. In Latin American Spanish, it takes the form comparar papas y boniatos or comparar peras con manzanas, while in Spain it becomes sumar peras con manzanas. In Romanian the popular idiom takes various forms: a aduna merele cu perele; baba ¸i mitraliera; baba s¸i mitraliera, vaca sizmenele; or tiganul ¸i carioca, while in Hungarian the expression ízlések és pofonok has similar meaning. In Serbian it becomes 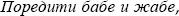 while in Welsh it takes the form mor wahanol â mêl a menyn. An equivalent Danish idiom is Hvad er højest, Rundetårn eller et tordenskrald? In Russian, the phrase
while in Welsh it takes the form mor wahanol â mêl a menyn. An equivalent Danish idiom is Hvad er højest, Rundetårn eller et tordenskrald? In Russian, the phrase 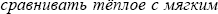 is used. In Argentina, a common question has that purpose: En qué se parecen el amor y el ojo del hacha? In Colombia, a similar version is well known: confundir la mierda con la pomada. In Polish, the expression co ma piernik do wiatraka? is used. In British English, the phrase chalk and cheese is used for that purpose instead of apples and oranges and perhaps makes the point more clearly.
is used. In Argentina, a common question has that purpose: En qué se parecen el amor y el ojo del hacha? In Colombia, a similar version is well known: confundir la mierda con la pomada. In Polish, the expression co ma piernik do wiatraka? is used. In British English, the phrase chalk and cheese is used for that purpose instead of apples and oranges and perhaps makes the point more clearly.
It is not necessary to understand the mathematics in this book’s appendixes to recognize the basic principle on which economic measurement is based. You need only speak any of the world’s major languages to recognize the principle as a truism known to everyone. To make the point more clearly, let’s change from apples and oranges (or chalk and cheese in the British English version) to subway trains and roller skates. Suppose that the city includes 10 subway trains and 10,000 pairs of roller skates. To measure the city’s transportation services, would you be willing to say it is 10,010? Of course, not! A subway train provides far more transportation services than a pair of roller skates. The two are not perfect substitutes in the production of transportation services. Translating the common idiom into technical economics terminology, economists would say: you can aggregate over the quantities of goods by addition, only if all of them are indistinguishable perfect substitutes. If they are not perfect substitutes, quantity aggregation by addition is wrong.1 It is tempting to think perhaps the solution is to multiply the quantities by prices and then to add up the cost of buying the 10 subway trains and 10,000 roller skates. But that can’t be right either, since the result would be in units of dollars. Expenditures are in units of dollars, but not service flow quantities.2 The services from consuming a good need not change, if its price changes. We are seeking to measure the quantity of services produced by the goods, not the dollar expenditure on them. The latter is a subject of accounting flow-of-funds measurement. The former is a subject of economic measurement.
Clearly, some sort of weighting is needed. We need to weight each subway train far more heavily than each pair of roller skates in aggregating over roller skates and subway trains to measure the city’s flow of transportation services. How to produce that weighting is the subject of economic aggregation and index-number theory, and many economists are specialists in that field. The appendixes to this book provide the derivation of the theory needed to aggregate over financial services. Provided here is only the relevant intuition.
Simply applying weights to the quantities of subway trains and roller skates and computing the weighted average is not an adequate solution. Suppose, for example, that we apply a weight of a million to each subway train and a weight of one to each pair of roller skates and then compute the weighted average. The conclusion would be the city’s transportation services can be measured as 10,000,000 + 10,000 = 10,010,000. That would certainly seem to be more reasonable than the previous conclusion of 10,010, and would recognize the fact that a subway train provides far more services than a pair of roller skates. But there remains a problem. We would implicitly be assuming the services of one subway train are always perfect substitutes for exactly one million pairs of roller skates, regardless of the number of subway trains and roller skates existing in the city. But the nature of the services of a subway train is different from the nature of the services of a pair of roller skates, and the services of another subway train or another pair of roller skates is not independent of the number that already exists in the city. If the city already has a large number of subway trains crowding the tracks, acquiring another one might be far from desirable. So a simple linear weighted average cannot reflect the imperfect substitutability of subway trains for roller skates. The magnitude of the error from such linear aggregation can be large, and the magnitude of the error from the more restrictive simple-sum aggregation is extremely large. For a formal derivation of that error range in appendix A, see equations (A.132) and (A.133) and the illustration in appendix A’s figure A.3.
In the jargon of mathematics, the theoretically correct way to aggregate over imperfect substitutes is nonlinear. Linear aggregation, with or without weighting, implies perfect substitutability. The weights only change the units of measurement of the individual component goods. The correct formula, called the “aggregator function” in aggregation theory, must be nonlinear, often involving multiplication and division, not just addition. Readers familiar with elementary economics will recognize that “utility functions” and “production functions” are nonlinear functions, permitting imperfect substitutability. Such functions potentially can serve as valid aggregator functions.
The field of economic “aggregation theory” determines the valid aggregator functions. But there remains the need to measure the aggregate. Statistically estimating the theoretical, nonlinear aggregator function is a challenging application of “econometrics” and is the subject of many published articles in professional economics journals. But governmental agencies need a way to measure the growth rate of the aggregate, without using the economics professions’ advanced statistical methodology. The field of “index-number theory” deals specifically with that need. Index-number theory determines formulas that can be used to measure the growth rate of the theoretical aggregate without the need for econometrics.
Elementary economics courses usually explain the “cost of living index,” the “true cost of living index,” the Paasche index, and the Laspeyres index. The “true cost of living index” is produced by aggregation theory, while the Paasche and Laspeyres indexes are produced from index-number theory to approximate the true cost-of-living index. For example, the Department of Labor’s widely used CPI is a Laspeyres price index, and the Commerce Department’s corresponding price index (the “implicit price deflator”) has, until recently, been a Paasche index.
2.2 Dual Price Aggregation
The previous section emphasized quantity aggregation over imperfect substitutes. But that section did briefly mention the cost-of-living index, which is a price aggregate, and also mentioned the total expenditure in dollars, which is an accounting flow-of-funds concept. The three are rigorously interconnected through an area of mathematics called “duality theory,” which can be found in the appendixes (e.g., equation A.46 of appendix A). But there is an easy way to see the connection without getting into that deep theory. Suppose that you have three numbers: a measure of the aggregate quantity of automobiles, Q, the aggregate price of automobiles, P, and total expenditure on automobiles, E. Clearly you would want Q multiplied by P to equal E. Satisfaction of that elementary accounting identity is a fundamental axiom in aggregation theory.3 As a result the aggregate price of automobiles, P, must equal the total expenditure on automobiles, E, divided by the aggregate quantity of automobiles, Q.
As explained in the previous section, a highly regarded literature exists on identifying the quantity aggregator function and measuring it, when the goods are imperfect substitutes. The corresponding “dual” price aggregate then can be computed by dividing the measured accounting expenditure on the goods by their quantity aggregate. In short, the correct quantity aggregate implies the correct price aggregate, and vice versa. The two are not independent concepts. They are linked together by the accounting identity requiring consistency with actual dollar expenditure.
Consider aggregating over automobile-tire prices and buggy-whip prices for use in the cost-of-living index. Would you compute the unweighted average of the two prices? That would give buggy-whip prices an equal role in determine the cost of living with automobile tire prices. Surely you would not do that. But in fact a century ago British newspapers did compute the inflation rate from unweighted averages of prices of goods. The need for nonlinear weighting from index-number theory has now been known and used by governmental agencies throughout the world for nearly a century.
But there is a complication. We have so far abstracted from the problem of durability. We now must take that into consideration. Consider a house or an automobile. You can buy either and then consume its services during its lifetime, or you can rent either and use its services for only one time period (perhaps a week, month, or year). The prices are not the same. To buy a house or car will cost a lot more than renting it for one period. The perfect-market price of the single-period services of a durable good is called the “user-cost price,” and the mathematical procedure for determining that price is known to the economics profession. The rental rate is the valuation placed by the rental market on the theoretical user-cost price. If the rental market were a perfect market, the user-cost price and the rental price would be identical, and both would be much less than the price to buy and hold the stock of the good, in order to consume all of its services during the good’s lifetime.
Recall that economic theory is primarily about the demand and supply for service flows per unit of time. For internal consistency with that objective, the correct price of a durable in a cost-of-living or other price index is the user-cost or rental price, not the purchase price of the stock. This fact is well understood in computation of the cost-of-living index and other price indexes in the national accounts.
2.3 Financial Aggregation
The discussion above is about consumer goods. But the same theory is relevant to financial assets, so long as they are treated as durables, providing financial services for more than one period. Clearly, financial assets are not perishables, immediately destroyed by consumption of their services. In particular, let us now consider monetary aggregation.
As is widely known, the Federal Reserve and most central banks compute and publish monetary aggregates. The Fed for many decades published four monetary aggregates: M1, M2, M3, and L. The aggregate M1 is the narrowest aggregate, defined to include only transactions balances used as a medium of exchange, such as currency and demand deposits (checking accounts).4 The aggregate M2 is broader, including some close substitutes for money, such as bank saving accounts. The aggregates M3 and L are even broader, with L being the broadest aggregate, intended to measure total financial “liquidity” of the economy, hence the symbol L. The Fed has discontinued computation and publication of L. More recently, in 2006, the Fed discontinued supplying M3, leaving only M1 and M2.
Discontinuing M3 was particularly unfortunate, since assets in M3 but not in M2 include financial assets contributing a significant amount of liquidity to the economy. Studies have repeatedly shown that M3 or L, when properly constructed as an index number, is the most informative available monetary aggregate.5 But the official simple-sum M3 and L were so badly distorted by improper component weighting as to be virtually useless. I fully agree with the Federal Reserve’s discontinuing publication of the simple-sum M3 and L monetary aggregates. In fact the world’s central banks should do what all other governmental agencies have done, since the publication of Fisher’s (1922) book, and discontinue publishing all of their simple-sum and arithmetic-average aggregates. But when the Fed discontinued publishing simple-sum M3 and L, the Fed also discontinued supplying much of their consolidated, seasonally adjusted, monthly component data. As a result construction of reputable index numbers, using that component data, has become needlessly difficult. The cost of supplying the component data was negligible to the Fed. Then why did they discontinue it? I would not presume to answer that question for the Fed, but here might be an unpleasant “clue.” M3 picked up repurchase agreements (repos), which were huge elements of the shadow banking system’s creation of money.6
Perhaps even more puzzling is the fact that the Federal Reserve has terminated publication of all interest rates paid by banks on deposits, such as average interest rates on checking accounts, small certificates of deposit, and savings accounts. Nearly every other central bank in the world provides interest rates paid on the country’s various categories of bank deposits, averaged across banks. Unlike most of the world’s central banks, the Federal Reserve no longer acquires those interest rates directly from banks, but instead purchases that information for internal use from Bank Rate Monitor. Bank Rate Monitor will not provide the historical data to the public, since the contract between Bank Rate Monitor and the Federal Reserve permits publication of the back data only by the Fed, which is not doing so. If that data were not useful for policy research by Fed staffers, the Fed would not subscribe to the expensive Bank Rate Monitor Survey. By failing to make the data public, the Fed hampers research on monetary policy by academic economists and investors.
Yes, the Federal Reserve should retain, solely for internal use, the interest rate data on individual banks. But it is not in the public interest to withhold interest rate data averaged over the country’s banks. Here are a few of the central banks that do provide that data to the public: the central banks of Turkey, Saudi Arabia, Iran, Pakistan, and China, each of which has more understandable reasons to be hesitant about making that data available than the Federal Reserve does. I can indeed think of another central bank that does not provide that data—the central bank of North Korea.
Now let us consider only M2, which is still being computed and supplied by the Fed. Among the assets included in M2 are currency, demand deposits, and savings deposits. Would you consider savings deposits to be perfect substitutes for cash? Cash pays no interest, and savings deposits are not legal means of payment. To pay a bill with noncheckable savings deposits, you must withdraw cash from those deposits or transfer funds from the savings account to your checking account. Savings deposits are a “joint product,” providing both monetary services (liquidity) and investment yield (interest income). Currency is pure money providing only liquidity.
Monetary assets are durable goods, and hence the user-cost prices of their services need to be determined. That formula is derived in Barnett (1978, 1980a).7 The proof is repeated in the part II of this book, and the resulting formula is provided as equation (A.5) of appendix A. Without going into the details of the proofs or of the formula, the basic intuition is the following: the user-cost price of consuming the services of a monetary asset is its opportunity cost, measured by the interest forgone by employing the services of the asset. If the asset is currency, which yields no interest at all, then the foregone interest is the interest rate that could have been earned on the best available pure investment, called the “benchmark interest rate.” Alternatively, suppose that the asset is a savings deposit. Then the forgone interest is the benchmark interest rate minus the interest rate paid on the savings deposit. The user-cost price of a monetary asset is not its own rate of interest, which is not a price paid for using the liquidity services of the asset, but just the opposite. The return received on the asset’s nonmonetary investment services needs to be subtracted out of the benchmark rate to compute the user-cost price of its liquidity services.
For future reference, we now provide a formal definition of the user cost of money.
Definition 1 The “user cost price of a monetary asset” is the forgone interest from holding the asset, when the interest yielded by the asset is less than the interest rate that could have been earned on an alternative investment.
In the most elementary case, the forgone interest is the difference between the two interest rates mentioned in the definition, although the formula in the appendixes incorporates some refinements.8 The complete formula, provided in this book’s appendix A as equation (A.5), is more formally derived in appendix B as equation (B.4). Even if you do not choose to read the proof, it is important to understand that the formula is not just a matter of opinion based on plausible reasoning. What is provided in the appendix is a mathematical proof, deriving the formula directly from the microeconomic theory of rational decision-making by consumers and firms.
In accordance with the principles explained in the prior sections of this chapter, currency and savings deposits should not be aggregated by addition, since they contribute differently to the economy’s monetary service flow and have different user-cost prices. Index-number theory needs to be used to measure the service flow properly. In this regard a short quote from the Federal Reserve Act, Section 2a, may be instructive:
The Board of Governors of the Federal Reserve System and the Federal Open Market Committee shall maintain long-run growth of the monetary and credit aggregates commensurate with the economy's long-run potential to increase production, so as to promote effectively the goals of maximum employment, stable prices, and moderate long-term interest rates.
[12 USC 225a. As added by act of November 16, 1977 (91 Stat. 1387) and amended by acts of October 27, 1978 (92 Stat. 1897); Aug. 23, 1988 (102 Stat. 1375); and Dec. 27, 2000 (114 Stat. 3028).]
Central banks produce a product. It is the liquidity of the economy. Without money, there would be only barter and extreme illiquidity. In particular, Fed open market operations (purchases and sales of Treasury securities in New York) change the balance sheet of the Federal Reserve and thereby change what, in economics jargon, is called “high-powered money,” the “monetary base,” or “outside money” (currency plus bank reserves). Changes in high-powered money, the primary product, are transmitted through the banking system to produce the economy’s monetary services and thereby the liquidity of the economy. That liquidity is heavily dependent on the “inside money” produced by private firms as intermediate products, conditionally upon the Federal Reserve’s production of outside money.9 Properly computed monetary aggregates are designed to measure that service flow in the economy. The Fed does not “produce” interest rates. The economy itself produces interest rates, although the Federal Reserve intervenes to influence some of them. Focusing solely on interest rates, while ignoring monetary aggregates, ignores the product produced by the central bank. The relevancy of that product to public understanding of monetary policy is independent of whether or not the central bank itself targets or otherwise uses measurements of that product in conducting its monetary policy.10
Yet in recent years the Fed has not produced and supplied monetary aggregates consistent with modern index-number theory. The Fed discontinued providing M3 and L and supplies simple-sum M1 and M2 aggregates inconsistent with index-number theory. As you will learn from this book, these data defects are far from trivial. They have done much damage to policy, to the profession’s research, to the expectations of the private sector—and to the world’s economies. Is it reasonable to expect Wall Street firms, commercial banks, mortgage lenders, mortgage borrowers, the press, and the economics profession to have assessed systemic risk correctly when the Fed was minimizing its own information-reporting responsibilities under the Federal Reserve Act? How much confidence should we have in the Fed’s own monetary policy, formulated without access to highly relevant data?
This observation is not unknown within the Federal Reserve System. The president of the St. Louis Federal Reserve Bank, James Bullard (2009), has written recently:
I have described three funerals. . . . The ongoing financial market turmoil may have caused the death of many cherished ideals about how the macroeconomy operates. One funeral was for the idea of the Great Moderation. . . . A second funeral was for our financial system as we have known it. . . . A third funeral was for monetary policy defined as nominal interest rate targeting . . . . The focus of monetary policy may turn to quantity measures.
Indeed this assessment is long overdue. But again, availability of reputable monetary quantity measures to the public is important, regardless of what the Federal Reserve chooses to target in its policy.
More recently Greg Robb (2009) has reported:
The Federal Reserve should return to the practice of setting monetary policy by targeting the growth of monetary aggregates, St. Louis Fed president James Bullard said Tuesday. Bullard said the Fed should set a target for expanding the monetary base because it needs a credible weapon to fight the risk of deflation. Although the Fed has already expanded its balance sheet by about $1 trillion, much of the increase to date has come from temporary programs that could quickly be reversed and so do not count as an expansion of money, he said. The Fed needs to communicate that it is expanding the money supply, which has historically created inflation, he said. This will end market expectations that a general decline in prices might take hold in the US as it has in Japan.11
I wish to emphasize that I am not personally an advocate of any simplifying “ism,” whether it be monetarism, new-monetarism, Keynesianism, New-Keynesianism, Post-Keynesianism, Austrianism, or Marxism. I am an advocate of professional scientific standards for economic measurement. The economy responds strongly to the information available to private economic agents, governmental policy makers, and academic researchers. Inadequate, distorted, and fraudulent information is damaging to the economy as a whole, not just to those who have used that information personally.
When I was an engineer at Rocketdyne, we would never have been able to develop the rocket engines for Apollo, if we had not heavily instrumented the rocket engines we tested nearly every day on test stands in the Santa Susana Mountains north of Los Angeles and at Edwards Air Force Base. When something went wrong during a rocket engine test, we poured over voluminous data to determine the cause. Theory alone or talk alone was never acceptable as an answer. The cost of those tests was enormous but necessary for success. Economic measurement is even more challenging, since the measurement methodology needs to be related to aggregation theory. All economic data from the economy is aggregated over goods and over economic agents.
2.4 The Commerce Department and the Department of Labor
The first modern monetary aggregate, based on averages of daily data, was constructed by William Abbott and Marie Wahlig of the Federal Reserve Bank of St. Louis and published in Abbott (1960).12 By their definition, “money,” labeled M1, consisted only of currency plus noninterest-bearing demand deposits (bank checking accounts). Interest-bearing NOW checking accounts and interest-bearing, checkable, money-market deposit accounts (MMDAs) did not exist. Savings deposits were not viewed as producing any monetary services at all without the current ease of transfer among accounts by online banking. As a result saving accounts were not included in that monetary aggregate. In those days, over half a century ago, the components of the monetary aggregate, M1, could reasonably be viewed as perfect substitutes. Both currency and demand deposits were means of payment, and both produced no investment return.13 Currency and demand deposits had the same user-cost price, with the entire benchmark rate being forgone to consume the services of either cash or demand deposits. Hence both were considered to be “pure” money. Adding them up made sense and was consistent with aggregation and index-number theory, since aggregation by summation is correct over perfect substitutes having identical prices. But that is “ancient history.” Most assets in monetary aggregates now yield interest. Monetary aggregation by addition has been inconsistent with economic theory and best-practice measurement for over a half century.
In contrast, the other data-producing agencies in Washington, DC have been using index-number theory to compute and publish their data for many decades. The two primary data-producing agencies, the Commerce Department and the Department of Labor, have separate data-producing bureaus with authority to produce best-practice data, and those autonomous organizations employ experts in aggregation and index-number theory. The Department of Labor has the Bureau of Labor Statistics (BLS), which is respected in academe for its expertise in economic measurement. The BLS produces the well-known CPI along with many other valuable data series. The BLS has never used simple-sum aggregation or unweighted arithmetic-average aggregation. The BLS has always recognized that it is aggregating over imperfect substitutes and needs to use the procedures available from index-number theory. Similarly the Department of Commerce has the Bureau of Economic Analysis (BEA), which employs experts in economic index-number theory. The BEA produces the national accounts of the United States. The BEA has never used simple-sum or unweighted arithmetic-average aggregation and has always based its data on economic index-number theory.
The Federal Reserve has no autonomous data-production bureau, such as the BEA or BLS. The Fed certainly could produce a similar autonomous data bureau within the Federal Reserve System. Data published by the BEA and BLS are far from flawless. But the contrast between the BEA and the BLS, on the one hand, and the Fed, on the other hand, is clear—there is no “Bureau of Financial Statistics” anywhere within the Federal Reserve System. Expertise in index-number theory is marginalized and spread very thinly throughout the Federal Reserve. Setting up such a bureau might be viewed as inconsistent with the self-interests of the Federal Reserve. If so, perhaps the Treasury, which tracks some international financial statistics, could institute such an independent bureau for US financial statistics; or Congress could create a new independent bureau for that purpose. In effect such a potential office now exists within Washington, DC, the Office of Financial Research (OFR), set up under the recently passed Dodd–Frank Act. In section 2.7.6 below, I consider whether the OFR might be able to provide a satisfactory solution to this serious problem.
Exceptions within the Federal Reserve are few and far between, such as the Fed’s industrial production index, which admirably does use reputable index-number theory with input from the BLS and industrial trade organizations. This fact raises another interesting question. Why does the Federal Reserve Board recognize the measurement issue and use the best available methodology in measurement of industrial production, over which Fed policy has limited influence, but is unwilling to devote comparable resources to state-of-the-art measurement of the most fundamental variable over which a central bank does have influence—money? Why is the Board’s staff unique in Washington, DC, in selectively resisting the fundamental principles of aggregation and index-number theory, accepted by the profession for over a half a century? Perhaps by the time you have finished reading this book, you may have an opinion on this question.
We examine the question in a later section, but it is worthwhile at this point to observe that the Federal Reserve Board staff is unique in another way. Most bureaucracies in Washington, DC, have little influence, through their own policies, on the variables they measure. The policy decisions of the Department of Labor have little, if any, effect on the country’s inflation rate, measured by the CPI. The policy decisions of the Commerce Department have little effect on the country’s gross domestic product or other variables in the national accounts measured by the BEA. The industrial production index, which the Federal Reserve Board’s staff supplies in a manner consistent with best-practice standards of the profession, does not contain financial or monetary data heavily influenced by Fed policy. In contrast, the financial and monetary data produced by the Federal Reserve measure economic variables heavily influenced by the Fed’s own policy decisions. The Federal Reserve is accountable to Congress and to the public for its actions, but the Fed itself measures and produces the financial and monetary data relevant to monitoring the product that the Fed produces: the liquidity of the economy. Is there a conflict of interests? We will return to that question in a later section.
2.5 The Major Academic Players
The first wave of research, on which this book’s research is based, appeared in Paris (François Divisia) and Princeton (Irving Fisher) early in the twentieth century. Controversies regarding the lives and work of Divisia and Fisher extended far outside the field of economics. The second wave appeared in the 1960s and early 1970s and came primarily from the University of California at Berkeley (Dale Jorgenson and W. Erwin Diewert) and the University of Chicago (Milton Friedman and Henri Theil). Intellectual activity at Berkeley and Chicago was far from dull and calm in those days. During the 1960s and early 1970s at Berkeley, there were two explosions. One was the student rebellion against the university’s administration and the war in Vietnam. That rebellion became known internationally as the “Free Speech Movement.” The other explosion at Berkeley took place inside the economics department’s building, where many of the tools used in this book were evolving with remarkable speed through the research of the faculty and students. At the University of Chicago, research emphasized the application of the same approach, called “neoclassical,” based on the use of calculus. But the Department of Economics at the University of Chicago was at the other end of the political spectrum from the student explosion at Berkeley, with conservatism being central to the Chicago department’s philosophy. A Chicago professor, Arnold Zellner, once said to me: “As we say at Chicago, if you don’t know which way to go, turn right.” This section tells the stories of the major players and how their work is needed to understand the contributions of this book.
2.5.1 Irving Fisher
As in all areas of important research, there are “major players,” whose contributions to the field were pathbreaking and whose names are forever attached to the subject. While index-number theory and associated areas of economic measurement have been evolving for over a century, the first enormous contribution was the classic book, Fisher (1922), by the famous American economist, Irving Fisher (1867–1947). To clarify the discussion that follows, I’ll now provide a relevant definition. This definition applies equally to a price or quantity index number, so the definition is provided in a form that can be used for either.
Definition 2 A quantity (or price) “statistical index number” measures the change in the aggregated quantity (or price) of a group of goods between two time periods. The index number must be a formula depending on both the quantities and prices of the goods in that group during the two time periods. The index number cannot depend on any other data or on any unknown parameters.
As can be seen from that definition, there is an enormous number of such formulas that can be viewed as contenders, so long as they depend only on prices and quantities of the component goods in the two periods and contain no unknown parameters. Indeed by the time that Fisher’s book appeared in 1922, a large number of such formulas had been proposed. What Fisher did, in a very thick book, was to define many good and bad properties of possible index numbers. He then classified all of the existing formulas in terms of how many good and how many bad properties each had. Among the indexes he concluded did best in those classifications, the one that later became known as the “Fisher ideal index” was the one he liked best. But there were others that remained serious contenders. In contrast, only two met his criteria for “worst”: the simple-summation index and the arithmetic-average index.
On p. 29 of that book he wrote:
The simple arithmetic average is put first merely because it naturally comes first to the reader’s mind, being the most common form of average. In fields other than index numbers, it is often the best form of average to use. But we shall see that the simple arithmetic average produces one of the very worst of index numbers, and if this book has no other effect than to lead to the total abandonment of the simple arithmetic type of index number, it will have served a useful purpose.
On p. 361 Fisher wrote:
The simple arithmetic should not be used under any circumstances, being always biased and usually freakish as well. Nor should the simple aggregative ever be used; in fact this is even less reliable.
At the time Fisher’s book appeared, government agencies were not the source of British price-index data. British newspapers computed the inflation rate from unweighted averages of prices of goods. Following the appearance of Fisher’s book, the British newspapers stopped their use of unweighted averages of price changes and instead adopted index numbers that performed well in Fisher’s book.
Fisher was a giant in the field of economics, and within the economics profession his name is equated with his famous research in economic science. In the minds of most American economists, Fisher ranks among the top five economists in American history. Milton Friedman (1994, p. 37) called Fisher “the greatest economist the United States ever produced.” But while he was alive, Fisher’s visibility to the public spanned many other areas. He did not shy away from controversy. Among his most controversial views were his advocacy of prohibition, his views on health, and his advocacy of eugenics. Even his views in applied economics created controversy in his time, since he published favorable views of the stock market shortly before the 1929 crash. After the crash he continued to publish reassurances that recovery was just around the corner. As a public spokesman on economics and the stock market, his reputation was destroyed for the rest of his life.
On the subject of prohibition, he published three books favoring total abolition of alcoholic beverages. His views on health were even stranger. He argued that avoidance of exercise is a health benefit. He was an outspoken advocate of the “focal sepsis” theory of physician Henry Cotton, who believed mental illness was caused by infections in various locations in the body and advocated surgical removal of the infected materials. When Fisher’s daughter was diagnosed with schizophrenia, he had surgical removals done at Dr. Cotton’s hospital, resulting in his daughter’s death. In eugenics, his publications, along with that entire field, were discredited during and after the Second World War, because of the association of eugenics with the racist views of the Nazis.
Greatness in science is not always associated with greatness in other areas. This book is associated with Fisher’s research only in index-number theory. His book on that subject is acknowledged by all economists to be historic. In many other areas of economic science, he was similarly among history’s greatest researchers. In other fields—well—you can judge for yourself.
2.5.2 François Divisia
The next major contribution, which changed the field forever, was produced by a brilliant French engineer and mathematician, François Divisia. He was born in Tizi-Ouzou, Algeria, in 1889 and died in Paris in 1964. Divisia contributed extensively to the field of economics, as evidenced by his books, Divisia (1926b, 1928, 1950, 1962). Some economists believe Divisia’s macroeconomic theory was more advanced than the well-known theory of John Maynard Keynes, and perhaps Divisia’s views may have been closer to a more modern theory, now called New Keynesian economics.14 Divisia (1963) rejected the research published by Keynes as not based on microeconomics, but of course the microfoundations of New Keynesian economics did not exist at the time. Divisia’s macroeconomic theory is less widely known than that of Keynes, but Divisia published in French, which might have constrained his visibility. Also, by not accepting Keynesian economics, his influence within the growing Keynesian movement was marginalized. In France, Divisia’s most celebrated book is his book on mathematical economics, Divisia (1928), rather than his criticisms of Keynesian economics.
Although less well known than Keynes in macroeconomics, Divisia was among the French intellectual elite and a leader of the French school of mathematical economics. After studying at the École Polytechnique and the École Nationale des Ponts et Chaussées, two of the greatest French Grandes Écoles, he worked as an engineer for ten years. As an engineering graduate student, he had previously been mobilized as an engineer at the beginning of World War 1 in 1913 as “an officer of genius.” Rapidly promoted to captain and wounded, he was named chevalier of the Légion d’Honneur. Following his ten years as an engineer after the war, he worked for the rest of his career as an economist, although his education was as an engineer and mathematician. He was a professor at the École Polytechnique and the Conservatoire Nationale des Arts et Métiers from 1929 to 1959. He also was a professor at the École Nationale des Ponts et Chaussées from 1932 to 1950 and was one of the founding members of the Econometric Society and its president in 1935. During the latter years of his life, he was out of touch with his family and friends. It is not clear why.15
Divisia’s famous articles and book on index-number theory, Divisia (1925, 1926a, b), are historic and justly famous. Even by current standards, that book is astonishingly brilliant. Prior to the publication of that book, all economists publishing in index-number theory proposed approximate formulas. At best, those index numbers were shown to have some good statistical properties, as systematically classified by Fisher (1922). But such classifications by properties could not conclude that an index was the exactly right one to measure aggregate quantity or aggregate price. In an astonishing tour de force, Divisia proved that one formula would exactly track the unknown aggregator functions of economic theory, so long as the aggregator functions were consistent with rational economic behavior.16
Recall that the aggregator functions are derived directly from economic theory and are uniquely correct for aggregation over quantities and prices. This book’s appendixes derive those functions for consumers, firms, and financial intermediaries. The aggregator functions of economic theory depend on unknown functional forms and unknown parameters, which, at best, can be estimated by statistical inference methods. But index numbers, which do not depend on unknown functional forms or unknown parameters, are easily computed formulas. As a result, index numbers are much preferred by data-producing governmental agencies to aggregator functions. François Divisia’s proof of the existence of such an index number, which can track any theoretical aggregator function perfectly, stunned the profession. His index-number formula measures without error, regardless of the degree of substitutability among the goods over which the index aggregates. There was a reason that he was able to derive that proof, while no economist had previously been able to do so. He used an area of advanced mathematics, the “line integral,” known to engineers and mathematicians, but not known by many, if any, economists at that time.
The precise mathematical formula for the Divisia index is provided in appendix A as equation (A.79), or in its approximate discrete time form as equation (A.80). Less formally, here is his remarkably simple formula, which is exactly correct in aggregating over quantities or over prices:
Definition 3 The growth rate of the “Divisia quantity (or price) index” is the weighted average of the quantities (or prices) of the component goods over which the index aggregates, where the weight of each good is that good’s expenditure share in the total expenditure on all of the goods over which the index aggregates.17
While this formula is deceptively simple in its appearance, computation, and use, the mathematics in Divisia’s paper, proving its exact tracking ability, are not at all simple.18 Divisia was so far ahead of his time that economists continued suspecting his index was flawed (“path dependent”), until the Divisia index was proved to be free from that mathematical flaw, a half century later by the American economist Hulten (1973) in the journal, Econometrica.19
2.5.3 Henri Theil
Although controversy remained about Divisia’s proof until Hulten’s paper appeared in 1973, a Dutch econometrician, Henri Theil (1924– 2000), in a citation classic book, Theil (1967), made extensive use of the Divisia index. Theil demonstrated its value in applications and its connection with well-known economic models. The book appeared one year after he moved from the Netherlands to accept an endowed chair at the University of Chicago. In addition, Theil demonstrated that the Divisia index can be derived from the field of “information theory,” associated with an engineer, Shannon (1951), working at Bell Laboratories on measuring information transmitted over telephone lines.
I have mentioned the role of the First World War in the life of François Divisia. Theil’s life was heavily influenced by the Second World War. Theil was an exceptionally determined man, who did not easily compromise and was dedicated to his work. He published 15 important books, of which three are citation classics, and over 250 articles. Much of his research established the central role of the Divisia index in applied economic modeling and in economic measurement. His decisiveness was more than evident to me, during a two-day stay in his Michigan weekend home. The source of his single-minded determination and dedication has been the subject of speculation by many economists, including his own colleagues at the University of Chicago.
Here is a possibly relevant source, as explained to me by Theil after he had retired from the University of Chicago. During the Second World War, he was a student at a university in Amsterdam. The Wehrmacht (German Army) required all students to sign a loyalty oath to Germany. Theil was a patriotic Dutchman who refused to sign the oath. The penalty was deportation to Germany into forced labor in a factory. He hid in the crawl space below his parents’ home with nothing but a radio to use to listen to the BBC. Eventually he was caught and deported to a factory in Germany. His parents were well off and well regarded in the Netherlands, so were able to bribe the German officials to get him released. When he was back in Amsterdam, the Wehrmacht soldiers came looking for him again with the loyalty oath in hand. He refused to sign, and went back into hiding. This happened three times. The last time he was in forced labor in Germany, he was near death, when the war ended. How many people are so patriotic and determined as to be willing to die to avoid signing a meaningless piece of paper? Yes, he was a person whose dedication was beyond admirable, and his contributions to index-number theory, aggregation theory, and econometrics are of historic proportions.
His influence on a generation of econometricians is, to this day, not fully recognized. Divisia and Theil were extraordinary people, whose roles in this literature are historic. To my knowledge, they never met, although Theil recognized the practical applications of Divisia’s contribution long before most of the rest of the economics profession did and developed it in ways that still are not fully absorbed into mainstream economics.
2.5.4 Dale Jorgenson
In this professional drama, five more major players need to be introduced, before our discussion can be considered up to date. In economic theory, prices are opportunity costs: the costs in forgone resources to buy one more unit of the services of the good being priced. As we have seen, no ambiguity arises, when the goods are perishable. But with a durable good, the price of services per unit of time is not the same as the price to purchase the services of the good for its lifetime. The mathematical implications of that distinction did not become clear until Dale Jorgenson (1963) derived the user-cost price of consuming the services of a durable capital good.20 He published that famous paper, while a professor at the University of California at Berkeley. He moved to Harvard six years later, where he is an endowed full professor to this day.
Prior to Jorgenson’s paper, capital theory had been troubled by paradoxes created by using the purchase price of the capital stock, when the rental price should have been used. Such misunderstandings were central to much of the confusion in Marxist theory, which purported to dispute mainstream capital theory. Financial assets are durable goods, subject to the same potential problems. In fact similar confusion evolved over many decades on the “price of money.” Is it the inflation rate, an interest rate, or what? As we have seen in definition 1, the correct answer is the user-cost price of the monetary asset, as first derived mathematically by Barnett (1978) and provided as equation (A.5) of this book’s appendix A.
In the 1960s, while Jorgenson was a professor at the University of California, three Berkeley PhD students had become well known: W. Erwin Diewert, Lawrence Lau, and Laurits Christensen. In a subsection below, Diewert’s important role in this literature will be discussed. Regarding Christensen and Lau, they coauthored important work with their former professor in their papers, Christensen, Jorgenson, and Lau (1971, 1973, 1975), originating a modeling approach called “translog.”21 The translog also was important in the work of Erwin Diewert, since the translog “aggregator function” connected the Divisia index to aggregation theory.
At the height of the political and intellectual turmoil at Berkeley, there was another graduate student there. But he was not an economist, yet. He was on leave from his work as an aerospace engineer in Los Angeles. He did not know Jorgenson, Christensen, Lau, or Diewert at that time. His name was William A. Barnett. We’ll get to that guy later.
2.5.5 Milton Friedman
The scene is now set for the arrival of the great monetary economist and Nobel laureate, Milton Friedman (1912–2006), at the University of Chicago. The Economist magazine described him as “the most influential economist of the second half of the 20th century (Keynes died in 1946), possibly of all of it [the century].”22 He became such a well-known economist to the public that nearly everyone has heard of him. But what is less well known is there were two Milton Friedmans. (1) There was the mathematical statistician, who produced the important Friedman rank test before the Second World War and worked as a statistician for the federal government during the war. The Friedman rank test is a classical statistical test in the highly technical field of nonparametric statistical inference. That test is known to all serious mathematical statisticians. (2) There also was the economist Milton Friedman, known to all economists as well as to almost everyone else. What is not so widely known is that the two Milton Friedmans were—the same person.23
As an economist, Friedman was the world’s best-known “monetarist.” He was a strong advocate of controlling the rate of growth of the money supply, which he viewed as causal for inflation in the long run and for the business cycle in the short run. Although he based most of his advocacy on the official simple-sum M2 monetary aggregate, he was well aware of the serious and growing problems with the official monetary aggregates. Distant substitutes for money were evolving and growing, while providing less monetary services per dollar of asset than the more liquid means-of-payment monetary assets, currency, and demand deposits. Friedman with his coauthor Anna Schwartz (1970, pp. 151–52) published, in their landmark book on United States monetary history, the following statement:
This [simple summation] procedure is a very special case of the more general approach. In brief, the general approach consists of regarding each asset as a joint product having different degrees of “moneyness,” and defining the quantity of money as the weighted sum of the aggregated value of all assets, the weights for individual assets varying from zero to unity with a weight of unity assigned to that asset or assets regarded as having the largest quantity of “moneyness” per dollar of aggregate value. The procedure we have followed implies that all weights are either zero or unity.
The more general approach has been suggested frequently but experimented with only occasionally. We conjecture that this approach deserves and will get much more attention than it has so far received.
In a long footnote to that statement, Friedman and Schwartz listed the PhD dissertations of many of Friedman’s students at the University of Chicago. Those dissertations attempted to produce weighted sums of monetary assets, but without use of index-number theory or aggregation theory. Such ad hoc weighted averages were “experimented with” by Friedman’s students in his famous monetary economics workshop at the University of Chicago, but were never accepted by the profession. Those students did not yet have available the derivation of the user-cost price of monetary assets in Barnett (1978) or the unification of index-number theory with aggregation theory in Diewert (1976). The literature on rigorous monetary-aggregation theory and the resulting monetary index numbers began with Barnett (1980a), who at that time had available the necessary tools for the derivation.24
When Barnett (1980a) first appeared, Friedman had retired from the University of Chicago and was at the Hoover Institution at Stanford University. Arnold Zellner, who was on the faculty at the University of Chicago, was a friend of Milton Friedman. Zellner had lunch with Friedman at the Hoover Institution, and Friedman raised the subject of my 1980 paper. He requested Zellner to ask me to cite his above statement in the Friedman and Schwartz book, as evidence that he had recognized the problem ten years before I solved it, although he and his students did not yet have the tools needed to solve the problem themselves. I was happy to cite Friedman and Schwartz’s valid statement and have done so in many publications since then.
Friedman was well aware of the seriousness of the problems produced by the Fed’s simple-sum monetary aggregation. By equally weighting components, simple-sum aggregation can badly distort an aggregate and obscure the effects of policy. As an example, suppose that the money supply is measured by the Fed’s former, broadest simple-sum monetary aggregate, L, which included much of the national debt of short and intermediate maturity. That debt could be monetized (bought and paid for with freshly printed currency) without increasing either taxes or L, since the public would simply have exchanged component securities in L for currency, which also is in L. The inflationary printing of money to pay the government’s debt would be successfully hidden from public view.25
However, if the Divisia aggregate over the components of L were reported by the Fed, that valid aggregate would not treat this transfer as an exchange of “pure money” for “pure money.” Divisia L would instead rise at about the same rate as the resulting inflation in prices, since Divisia L would weight the growth of currency more heavily than the decline in government debt. The inflationary consequence of the policy would be revealed to the public and to the Congress.
The traditionally constructed high-level aggregates (e.g., M2 or the now discontinued M3 and L) implicitly view distant substitutes for money as perfect substitutes for currency. Rather than capturing only part of the economy’s monetary services, as M1 does, the broad simple-sum aggregates swamp the included monetary services with excessively weighted, nonmonetary services. The need remains for an official aggregate capturing the monetary-services contributions of all monetary assets in accordance with best-practice economic measurement, as by Divisia or Fisher-ideal aggregation.
Milton Friedman’s successor at the University of Chicago is Robert E. Lucas. In an article in the journal, Econometrica, Lucas (2000, p. 270) wrote:
I share the widely held opinion that M1 is too narrow an aggregate for this period [the 1990s], and I think that the Divisia approach offers much the best prospects for resolving this difficulty.
Amen.
2.5.6 W. Erwin Diewert
Index numbers, as defined above, depend on both prices and quantities. As a result, a valid index-number-theoretic money aggregate must contain both prices and quantities. Dale Jorgenson’s concept of the user cost of a durable good was needed to be able to derive the user-cost price of the services of a monetary asset. My derivation of that formula for “the price of money” removed one source of arbitrariness from construction of a monetary quantity index number.
But there remained another source of non-uniqueness. While François Divisia’s famous formula provided an immediate good choice, Fisher had shown that many index-number formulas move very closely together and have excellent properties, including his own preferred Fisher-ideal index. This fact had produced a wedge between economic theorists, who advocated estimating the exact aggregator functions of economic theory, and index-number theorists, who advocated easily computed statistical index numbers. In particular, how should we choose among the index-number formulas shown to have good properties by Fisher? While Theil clearly advocated and used the Divisia index, other index-number theorists advocated other formulas having good properties. What was needed was a link between the best index numbers and the underlying theoretical aggregator functions of pure economic theory.
Precisely that result was provided in a transformative paper by W. Erwin Diewert (1976) at the University of British Columbia in Canada. He proved that all of the index numbers in a particular class of index-number formulas track the exact aggregator function equally well in discrete time. He called those index numbers “superlative” index numbers.26 He had thereby unified aggregation theory with index-number theory, since all index numbers in the superlative class have equally good ability to track the exact, aggregator function. His superlative index-number class included both the Fisher-ideal index and the (discrete time) Divisia index. Barnett (1980a) advocated either the Divisia index or Fisher ideal index with user-cost prices to measure the economy’s monetary-service flow. The two formulas move so closely together that there usually is little reason to prefer one over the other. The differences in growth rates among index numbers in the superlative class are usually less than the round off error in the component data used in the index.
It is interesting to observe that Diewert got his PhD from the University of California at Berkeley at the time that Jorgenson was a Berkeley professor, producing his famous user cost of capital paper. In addition Diewert’s first faculty position was as an assistant professor at the University of Chicago, at the time that Theil was producing his famous research on the Divisia index. I got my MBA degree from the University of California at Berkeley at the time that Jorgenson and Diewert were there. No, I never met Divisia, but few, if any, American economists ever did. The famous engineer and economist, François Divisia, died in 1964, long before I had become an economist, but while I myself was working as an engineer at Rocketdyne.
With definitions 1 and 3 providing the Divisia index and user-cost price of money, and with Erwin Diewert’s definition of “superlative index numbers,” the scene is now set to provide a formal definition of the Divisia monetary aggregates, in accordance with Barnett (1980a).
Definition 4 The “Divisia monetary aggregates” are produced by substituting into the Divisia quantity index formula, definition 3, the quantities of individual monetary assets and their corresponding user-cost prices, in accordance with definition 1.
The resulting index is a “statistical index number,” in accordance with definition 2, and hence the entire literature on index number and aggregation theory is relevant, including Diewert’s and Theil’s work, as well as Divisia’s famous proof.27 Several authors have studied the empirical properties of the Divisia monetary-quantity index compared with the simple-sum index.28 The theory developed at this stage of the literature’s evolution is summarized in this book’s appendix A and is fundamental to modern monetary aggregation.
I mentioned previously that I was at Berkeley as a graduate student at the peak of the Berkeley intellectual and political explosion in the 1960s, while on leave from my Rocketdyne employment. What about the subsequent intellectual explosion at the University of Chicago in the early 1970s? I knew about that too, and yes, I was there on another leave from Rocketdyne. Friedman, Diewert, and Theil were on the faculty. I took their courses. In those days of cost-plus-fixed-fee contracts and the race to the moon, Rocketdyne provided one year of educational leave for each year of engineering work completed. I took full advantage of those opportunities.29
2.5.7 James Poterba and Julio Rotemberg
When I derived the theory summarized in appendix A and began to apply it empirically, I thought that was the end of the story. The theory unified aggregation theory, index-number theory, and monetary economics in a manner uniquely internally consistent. In addition the theory was proving to be very successfully applied in empirical research, including research at many central banks throughout the world. But I was stunned when Julio Rotemberg, then a professor at the Massachusetts Institute of Technology’s (MIT) Department of Economics, presented a startling paper at a conference I organized at the University of Texas at Austin.30 Rotemberg’s paper was coauthored with James Poterba, also at MIT. Their paper challenged the state of the art of index-number theory and thereby brought into question whether using that theory in monetary aggregation was really the “end of the story.” Poterba now is not only the Mitsui Professor of Economics at MIT, but also is the president of the National Bureau of Economic Research. Rotemberg now is the William Ziegler Professor of Business at the Harvard University Business School.
Poterba and Rotemberg (1987) emphasized the fact that user-cost prices of monetary services for monetary-assets are not known with perfect certainty, since interest rates are not paid in advance. So, for example, if you deposit money into a passbook savings account at a bank, you cannot be certain how much interest you will be paid that month. In contrast, prices of most consumer goods are known at the instant of purchase of those goods.31 For that reason, the classical literature on index-number theory, including the work of Fisher, Theil, and Diewert, assumed prices are known at the instant of purchase. The issue is not knowledge of future prices or interest rates. Risk and uncertainty about future prices and interest rates have been shown not to be a problem for index-number theory.32 But risk about current-period purchase prices is ignored in classical index-number theory, although is potentially relevant to monetary aggregation, if current-period interest rate risk is not negligible. This distinction had not previously occurred to me.
Julio Rotemberg’s presentation at the conference at the University of Texas excited the audience with the challenge it presented to us. Leonard Rapping, who was one of my former professors, when I was a student at Carnegie Mellon University, was in the audience. He walked over to me after Rotemberg’s presentation and said to me with great enthusiasm that I should take the challenge seriously and seek to advance the field in a manner dealing with the fundamental issues raised by Poterba and Rotemberg. Sadly Rapping did not live to see that happen. He had serious problems with his heart. But I have fond memories of his excitement at what he saw and recognized at that conference.
In their paper, Poterba and Rotemberg proved that some of the fundamental tools of classical index-number theory are undermined, if current prices are not known with certainty. In the case of monetary aggregation, Poterba and Rotemberg advocated instead the direct econometric estimation of monetary aggregator functions by advanced statistical methodology permitting risk. I accepted that idea and used it with two coauthors in Barnett, Hinich, and Yue (1991, 2000). While that approach is elegant and suitable for publication in professional journals, it would not be appropriate as a data production procedure for a governmental agency. Such organizations produce their data using index-number theory, specifically designed for that purpose. Index-number theory does not require econometric modeling or estimation.
In thinking about this problem, it occurred to me that there should be a way to extend index-number theory to incorporate risk by using techniques developed in the field of finance. After leaving the University of Texas for Washington University in St. Louis, I suggested the approach I had in mind to two of my PhD students at Washington University. We succeeded in producing that extension and published it in Barnett, Liu, and Jensen (1997). The resulting extension of the literature on index-number theory to include risky prices is presented in sections D.1 through D.6 of this book’s appendix D.33
But a further challenge remained in this direction of research. The common finance approach to adjustment for risk is known to produce an inadequately small adjustment for risk. This under-adjustment has become known as the “equity premium puzzle.” I delayed addressing this problem for a few years, while the controversy played itself out in the finance literature. After leaving Washington University for my current position at the University of Kansas, I worked with my colleague, Shu Wu, on application of the newest approach from the finance literature.34 The result was Barnett and Wu (2005), summarized in sections D.8 through D.10 of this book’s appendix D. That research, in many ways, represents the state of the art of monetary aggregation and currently is motivating research by many economists throughout the world. The risk-adjusted Divisia monetary aggregates are especially relevant to countries in which substantial foreign-denominated money-market assets and accounts are held. In such cases interest rates can be subject to substantial exchange rate risk.
Well, that was not all from Poterba and Rotemberg. With one of their students at MIT, they subsequently published Rotemberg, Driscoll, and Poterba (1995), applying a new monetary-aggregation formula, called the currency equivalent (CE) index. That index was first proposed by Rotemberg (1991). I was able to prove that the CE index, as the flow index they advocated, was a special case of my Divisia monetary index, and hence seemed to provide no gain over the monetary aggregates I was advocating. But I had learned never to take Poterba and Rotemberg lightly. Looking at their index more carefully, I found that I could derive it in a different manner as a measure of the economic capital stock of money. The capital stock evaluates the discounted present value of the future flow, rather than only the current flow of monetary services. I published that alternative derivation in Barnett (1991). Here was now a new challenge. Measuring the economic capital stock, depending on future service flows, requires the ability to forecast future flows. Improvements to the CE index’s measure of future flows have motivated much of my current research with students and colleagues.35 You can find an introduction to that research in this book’s appendix B. Poterba and Rotemberg have certainly been keeping me busy with their deep and challenging insights.
From the early path-breaking work of Fisher and Divisia through the recent developments motivated by the prodding of Poterba and Rotemberg, there has been a long progression of insights and developments. That progression and those developments have led to the most recent, state-of-the-art Divisia monetary aggregates. Are there any shortcomings in measurement to prevent a central bank from using Divisia monetary aggregates? Is there any reason at all to prefer the disreputable simple-sum monetary aggregates to the state-of-the-art Divisia monetary aggregates? The answer to both questions is one simple unequivocal word—no! In measurement, central banks should do the best they can, not the worst they can. It doesn’t get any worse than simple-sum aggregation.
2.6 Banks throughout the World
Divisia monetary aggregates exist for over 37 countries throughout the world and are available within many central banks.36 But let’s look at the differences among some of the most relevant central banks in this regard.
2.6.1 The Federal Reserve Board
As the originator of the Divisia monetary aggregates and, nearly equivalently, the Fisher-ideal monetary aggregates, I was the first to compute them, while on the staff of the Special Studies Section of the Federal Reserve Board (FRB) in Washington, DC. Later sections of this book provide information about what transpired in those and subsequent years at the Fed. But this section will mention only the start. When I first produced the Divisia monetary aggregates for the United States, I was asked to produce a monthly memorandum reporting on those aggregates and their implications for the economy. The monthly memorandum was to be delivered to Stephen Axilrod, the staff director of monetary policy, which was the highest policy position on the FRB’s staff.37 He was the most powerful person on the Board’s staff and was occasionally more influential on policy than some of the governors. In fact, while the weakest of the chairmen, William Miller, was there, Axilrod was widely believed to be running the show.
I do not know whether Axilrod ever passed my memoranda on to the governors, who were being provided with the severely defective, official simple-sum monetary aggregates. But during a Board meeting, I was asked to provide information about the Divisia monetary aggregates directly to the governors. To my surprise, three of the governors turned to me and asked me to send them a memorandum answering questions they asked. Of course, I immediately agreed and was pleased by the display of interest. But when I returned to my office, two high-level staff members came to my office looking alarmed. One was the director of research, whom I had never before met, since our offices were in different buildings. The two of them instructed me to write the memorandum and send it to them. They told me they might let me reply to the governors’ request at a later date, once they approved of my reply. So I wrote the memorandum and sent it to them. One of them sent me comments for revision. The primary comment was about what to call the Commerce Department’s inflation index. I changed the terminology to the one he requested and sent the revised memorandum back to both of them. The other officer then sent me comments. His primary comment was to change the terminology back to the one I originally had used. The memorandum bounced back and forth between the two staff officers in that circular manner for many months. Eventually they both said the memorandum was OK and would be delivered to the three governors. I was not permitted to deliver it myself, so I have no way of knowing whether the governors ever received it. But if they did, they probably had forgotten about the questions they had asked.
As mentioned earlier, I left the Fed in 1981 for the University of Texas. My first PhD student at Texas was a very dedicated man, with a prior background in engineering. He had the technical background to work with me on research using my Divisia monetary aggregates. To be able to explore policy problems in the past, I needed back data. The student produced those data extending back to 1959. For long-run research in this area, his PhD dissertation data remain the authoritative source of the early data to this day. He was a determined and unusual person. But I could not have anticipated he would one day end up in the position he now holds. His dissertation is Fayyad (1986). Yes, he is Salam Fayyad, the current prime minister of the Palestinian Authority.
The contrast in economic measurement expertise between the Fed and the BEA or BLS is evident from the following example. When I first originated the Divisia monetary aggregates, while on the staff of the FRB, a number of reporters wanted to interview me about it. Articles appeared in Business Week, The Boston Globe, and The Wall Street Journal. The Business Week article appeared in the September 22, 1980 issue (p. 25) shortly after my paper, Barnett (1980a), had appeared in the Journal of Econometrics. The Business Week reporter had attended my presentation at the annual meetings of the American Economic Association and interviewed me in the lobby of the Hilton Hotel later that day. He asked me many good questions, seemed genuinely interested, and appeared to understand what I was saying, including my explanation of the role of user-cost prices in computing the weights in quantity index numbers. When his article appeared, he devoted a half page to reporting in a very positive manner on my presentation at the conference. I was pleased to see such a supportive article in that magazine, but he made a mistake in describing the weighting formula. He wrote that I was using “turnover rates” as the prices in the quantity index. Of course, this was wrong. The user-cost price measures opportunity cost, which for a monetary asset is forgone interest. I cut out the article and posted it on a bulletin board at the Board in Washington, DC. I underlined the statement about turnover rates, assuming the economists would realize that I had done so as a joke. Turnover rates make no sense as user-cost prices in quantity indexes.
A few months after I left the Board for the University of Texas, I learned, to my astonishment, that one of my former colleagues had actually begun producing monetary aggregate “index numbers” using turnover rates as prices. Perhaps my joke had been taken seriously. The resulting new index was called MQ and was supplied to the profession for a couple of years.38 No one at the BLS or BEA would have taken my joke seriously. They are sophisticated people in economic measurement and understand the connection with economic aggregation theory.
2.6.2 The Bank of Japan
Four years after I had originated the Divisia monetary aggregates, I was invited to speak on my research at a conference in Tokyo on the topic of “Information and Data Management.” At that time, I was on the faculty of the University of Texas at Austin. The invitation was very appealing. It included air fare for both my wife and me, a room at one of Tokyo’s best hotels, all meals and transportation, along with other special arrangements. This was in 1984, when Tokyo was in a dramatic boom, and the cost of living in Tokyo was very high. When invited to conferences, I am accustomed to being told the amount of time I have for my presentation, the topic of the session, and the time available for open discussion. Although I was a friend of the conference’s primary organizer, Ryuzo Sato, I could not get an answer to such questions from any of the organizers. All I was told was that the financial arrangements and accommodations would be first rate, and indeed they were. The organizers did not ask me to prepare a paper or to provide the subject or title of a talk.
I began to recognize the nature of the situation, while on my JAL flight to Tokyo. The airline’s magazine, at every seat in the airplane, contained an article about the experiences of scientists invited to speak at conferences in Tokyo. What I was experiencing and what happened subsequently in Tokyo fit what I read. The article explained that the procedure was designed to acquire information by putting scientists in a high-pressure situation. The article also said that Carnegie Mellon University, from which I had received my PhD, prohibited its faculty from participating in any of those conferences. The University of Texas was subject to no such prohibitions. I did want my work to be used, so if the Bank of Japan might act faster than the Fed, that was fine with me.
The conference was held in a very large auditorium with hundreds of people in the audience. I was on the stage as a panel member for an entire day, with only two coffee breaks and a break for lunch. I was not permitted to present a prepared paper. The other people on the stage were speaking many languages, including Japanese, German, French, and English, among other languages. We all were wearing headphones providing simultaneous translation of what was being said, and the simultaneous translation was into many languages. I had my headphones set for translation into English. Simultaneous translation of technical discussion is far from flawless, so it was hard to know precisely what was being said. One of the speakers on that panel was Marvin Minsky at MIT. He was America’s leading authority on artificial intelligence and cofounder of MIT’s Artificial Intelligence Laboratory. Isaac Asimov (1980, p. 217 and 301) described Minsky as one of only two people he would admit were more intelligent than he was, the other being Carl Sagan.
Being on the stage so long with confusing simultaneous translation from other languages was stressful, especially with no ability to present a prepared paper. The moderator sat at the head of the table. He was my old friend, Ryuzo Sato, who spoke fluent English and Japanese. If you were not regularly participating in the conversation, he would turn to you and ask you a question. No one wanted that, since he asked unexpected, difficult questions. In short, we all were under pressure to continue participating in the discussion all day long. About the only way to do that was to reveal whatever you knew about the subject of the conference. Indeed Minsky revealed much about his research on artificial intelligence, and I revealed much about my research on monetary aggregation theory. It was becoming clear how Japanese industry was acquiring so much information about American research, and then adopting it faster than American industry was.
At lunch, I sat at a table in a group including a Japanese economist, who had been educated in the United States. I mentioned to him that Carnegie Mellon University, which is a leader in artificial intelligence research, did not permit its faculty to participate in conferences in Japan. His reply was, “they are smart.” I also asked him about the unusual conference procedure, which I had never experienced anywhere else in the world. He explained the intent was to induce speakers to reveal what they knew. But he also said that it was designed to attract a large Japanese audience. In Japan, arguing in public is frowned upon as a “loss of face,” so such public arguments are not often seen. By setting up a procedure inducing foreign speakers to be argumentative, the conference provided a form of unusual entertainment for the audience.
My Divisia monetary aggregates were unavailable to the American public at the time. In section 2.7.3 below, I explain the secretive way in which they were being used at the FRB by the model manager, after I moved to Texas. But to my astonishment, a few months after I returned to Texas from Tokyo, I saw an article by Ishida (1984) in the Bank of Japan’s official publication. He published a collection of empirical comparisons demonstrating that Divisia monetary aggregates for Japan work better than the official monetary aggregates. I had no doubt that Ishida’s research had been motivated by what I had said in the Tokyo conference. Because I was pleased by the results in Ishida’s paper, I wrote to him. He did not reply. I wrote again. He did not reply. Serious scientists throughout the world correspond freely. I had never before encountered an author who used and properly cited my work, but failed to reply to my correspondences. I then asked my friend, Ryuzo Sato, whether he could explain that odd behavior. Sato told me this is a common problem among Japanese government employees, since their written English is often not very good, and they do not want to make that evident by replying to a letter. I found that odd, but I assumed it was true. Two years later I met Ishida at a conference in the United States. He got his PhD from the London School of Economics, and his English is perfect.
2.6.3 The St. Louis Federal Reserve Bank
I remained on the faculty of the University of Texas for eight years, until I was offered a professorship at Washington University in St. Louis with a reduced teaching load. I welcomed the proximity to the St. Louis Federal Reserve Bank, at which I have friends and colleagues. In fact two of my PhD students at the University of Texas got their first positions at that Reserve Bank, including Salam Fayyad. At the time, a senior officer of that bank, Michael Belongia, had a full understanding of the Board’s defective measurement procedures and was publishing valid criticisms of them himself (e.g., see Belongia and Chalfant 1989 and Belongia 1995, 1996).
The St. Louis Fed decided to take over production and distribution of my Divisia monetary aggregates and to make the data available to the public. The database was constructed and announced to the public in the publication, Thornton and Yue (1991). Dan Thornton is a well-known, highly published, vice president at the bank and Piyu Yue was a former PhD student of mine at the University of Texas. Although the new Divisia data were produced and used in research there, no mechanism was set up for regular monthly updates to be made available to the public. Subsequently Mike Belongia left for a university position, when the director of research at that bank retired. The two were close friends.
Subsequently the St. Louis Fed hired a new director of research, William Dewald. He was a well-known academic economist, who had been a professor at Ohio State University for many years, and had been the long-time editor of a respected journal, The Journal of Money, Credit and Banking. Fortunately, Dewald’s commitment to continuation and improvement of the Divisia data was clear. I’ve heard he regularly said to his staff that “data live forever and data collection and dissemination are a fundamental purpose of a central bank.” Dewald’s professionalism played a key role in continuing the availability of those data.
Dewald’s commitment resulted not only in a substantial upgrade in the quality of the data, but also in the creation of an internal procedure for regular monthly distribution of the data on the bank’s website. The importance of this commitment cannot be overestimated. Setting up that database for regular public release was not a trivial matter. The economist Dewald put in charge was Richard Anderson, a vice president at the St. Louis Fed. He was previously on the staff of the Money and Reserves Projection Section at the Federal Reserve Board in Washington, DC, where he had been in charge of producing the Fed’s monetary aggregates for its official release (called the H.6). His PhD in economics is from MIT. He is a senior Fed insider with expertise in monetary data construction and policy. He employed two of my PhD students at Washington University to help with improving the database. One was Barry Jones, now a professor at the State University of New York at Binghamton. The other was Travis Nesmith, now a senior economist on the Federal Reserve Board’s staff in Washington, DC. In addition I was myself included on the Advisory Board for the St. Louis Fed’s Divisia database.
There was good reason to set up the database at the St. Louis Fed, which has long been a major source of Federal Reserve data. As I’ve mentioned above, the only person who had regular access to the Divisia monetary aggregates, while I was on the Board’s staff, was the staff director of monetary policy, a position that no longer exists at the FRB. There was no official channel allocated to making the data available to the public. As discussed in section 2.7.3 below, the internal use of the Divisia monetary aggregates after I left became more secretive, unknown even to the Board’s governors. They were making policy decisions based on model simulations, without knowing that their own model contained Divisia M2, not the Board’s official simple-sum M2.
Anderson, Jones, and Nesmith (1997) set up the revised database, making it available to the public online on the Bank’s website, and provided the details of the construction process in an issue of the St. Louis Fed’s Monthly Review publication. Instead of calling the aggregates the Divisia monetary aggregates, as I do, they called them the monetary services index (MSI). Two reasons exist to use the MSI terminology. One is the emphasis on the index’s measure of service flow. The other is to emphasize that any index number formulas can be used from Die wert’s superlative index-number class, such as the Fisher ideal or Divisia, so long as the prices in the formulas are measured using the user-cost price formula. I nevertheless continue using the terminology, Divisia monetary aggregates, to emphasize the roots of modern index-number theory in the brilliant work of François Divisia in Paris. In addition the Divisia index formula is more easily explained without mathematics (see definitions 3 and 4 above) than the Fisher-ideal index and provides access to the dispersion measures defined in appendix C, section C.7.
However, there was a rather disturbing note to the St. Louis Fed’s admirable work in making its Divisia index available to the public. The database was “temporarily” frozen in February 2006 for “revisions.” Those minor revisions, requiring no extensions to the theory, should not have taken five years to complete. At the time of the freeze, the economists responsible for the revisions posted online that the freeze would last for a few months, not years. Throughout the five years of the data freeze, the target date for revisions’ completion changed repeatedly from months to years. I am aware of no credible reason for denial of public access to the Divisia data for so many years. But it is worthwhile to consider the time period, during which we all were denied access to those data. Keep in mind that the housing downturn, which started in 2006, is a primary cause of the recession that followed. Is it a coincidence that the MSI (Divisia) data were frozen at precisely the time that the economic malaise began and remained frozen during the financial crisis and the recession? Is it a coincidence that a month later, in March 2006, the M3 data were closed down permanently?39 The most charitable explanation would be that there is something wrong with the Fed’s priorities. But if I were a comedian, I’d conclude that the devil made them do it. That is about as good an explanation as any I heard during the five-year freeze.
Sometimes a system is more than the sum of its individuals and has a life of its own. The economics profession has been hearing that for nearly a century from economists who call themselves “institutionalists” specializing in “institutionalism.”40 During the five years of the MSI data freeze, there were substantial changes in the high-level officer staff at the St. Louis Fed, including the director of research and the president of the bank. When the freeze began, most of those having authority over funding decisions for the Divisia project were no longer at the bank. In addition the St. Louis Fed, along with the other regional reserve banks, is not fully autonomous of the Federal Reserve Board in Washington, DC. Hence the multidimensional, institutional complexities of decisions at the St. Louis Fed cannot be understood independently of pressures from the Board in Washington, DC. See Toma and Toma (1985), regarding penalties that the Board has imposed on “maverick” regional reserve banks.
Here is the good news. The revisions of the Divisia MSI database are now complete, and MSI went back online in April 2011, with monthly updates expected, at http://research.stlouisfed.org/msi/index.html. But the interest rate (user cost) aggregates and component data are still being withheld from the public. The documentation on the revisions is in Anderson and Jones (2011). Particularly positive is the fact that the new vintage of the MSI Divisia data is expected eventually to be included within the St. Louis Fed’s excellent, interactive, relational database, called FRED (Federal Reserve Economic Data).
The long-delayed, updated data were available within the St. Louis Fed from mid-2010. The St. Louis Fed withheld the data from the public until April 2011, shortly after the manuscript for this book was completed and delivered to MIT Press. I am nevertheless displaying two figures supplied by one of my coauthors, Marcelle Chauvet, using the new vintage Divisia data. She had authorized access to those data, prior to their going online. Those results are in this book as figures 4.11 and 4.12 in section 4.3.3 of chapter 4. The St. Louis Fed graciously provided me with the new vintage Divisia data, when the data first became available for internal use. But I was not willing to use the data in my own research prior to the data’s availability to the public. Since February 2006, there has been a dark cloud over the entire world from the financial crisis and the subsequent Great Recession. During that same time period, there has been a gray cloud over the highly relevant Divisia database. The gray cloud seems to be lifting, and what now is appearing may be better than what was previously there. Let’s hope the same for the economy.
Regarding transparency of policy, the reappearance of the Divisia database is some of the best news that has come out of the Federal Reserve System in years, but is only a first step in the right direction. In fact even the encouraging reappearance of the Divisia database should give us pause. I have been confronted frequently with the following questions at conferences: (1) What should we do the next time the Fed decides to deny public access to Divisia monetary aggregates data, as it did throughout the entire financial crisis and Great Recession? (2) The economist who maintains the Divisia database is admirably motivated by his own research and publications using those data. What will happen if he retires or leaves the St. Louis Fed?41 You think someone else at the St. Louis Fed would pick up the ball? Without FRB advocacy in Washington, don’t bet on it. (3) Since no autonomous Bureau of Financial Statistics exists within the Federal Reserve, what would happen if the person who maintains MSI is subjected to Fed policy-advocacy pressures from the Board or is confronted with data problems about which inadequate expertise exists within the Federal Reserve? As can be seen from part II of this book, economic measurement is a formidable area of expertise. (4) Since the Fed stopped publishing its broad aggregates, M3 and L, the Federal Reserve no longer supplies consolidated, seasonally adjusted, monthly data on much of the highly liquid money market. Why not acquire whatever data exist from available sources, regarding those highly relevant assets, and produce a properly weighted, broad Divisia monetary aggregate?
Since I originated the Divisia monetary aggregates in 1980, I have never wanted to spend time personally maintaining that database, despite growing “popular demand” for me to do precisely that. But because of the questions I have just enumerated and the frustration of many experts with the five-year MSI freeze, I have reluctantly agreed personally to supervise an independent Divisia monetary aggregates data site, hosted by a major international research center, the Center for Financial Stability (CFS). The CFS is a nonpartisan, nonprofit, independent, global think tank, focused on financial markets. I am indebted to Steve Hanke at Johns Hopkins University for suggesting this option. The CFS Divisia database should be online by the time this book is in print and can be found at www.CenterforFinancialStability.org. The Divisia data are planned to be in a CFS section called Advances in Monetary and Financial Measurement (AMFM), under my direction. Additional information can be found at the “Data” tab of my personal website, hosted by Carnegie Mellon University and linked to the following URL at the Massachusetts Institute of Technology: http://alum.mit.edu/www/barnett.
Initially the information in AMFM will be similar to the Divisia database maintained by the St. Louis Fed, but with minor refinements, full disclosure, broader aggregation, and my analysis. Among the objectives will be to serve as a hedge against the possible MSI problems enumerated above. In addition the initial data are expected to include broader monetary aggregates, incorporating data from non-Fed sources, and more adequate accounting for shadow banking system activities. The primary new monetary aggregate will be called Divisia M4. But in the future the AMFM data will introduce more advanced extensions, such as the adjustment for risk in appendix D’s section D.7, the discounted monetary capital-stock measurement in appendix B’s section B.5, and the closely related Fisher-ideal and distribution-effect measures of appendix C’s section C.7.
AMFM should be particularly useful to researchers interested in recent advances in economic measurement; properly weighted, broad measures of the economy’s financial liquidity; and rapid adjustment to structural changes in financial markets. The scope of AMFM will be wider than Divisia monetary aggregation and will encompass state-of-the-art advances in monetary and financial measurement. I also expect to provide relevant international data, such as the admirable, official, Divisia monetary aggregates supplied by the Bank of England and the National Bank of Poland, along with the newly available Divisia monetary aggregates provided by the Bank of Israel. If the European Central Bank and the Bank of Japan should decide to make their Divisia monetary aggregates public, AMFM will provide them. International multilateral aggregation, in accordance with this book’s appendix C, will likely also be incorporated eventually within AMFM, as economic globalization progresses. Periodic commentaries also are contemplated within AMFM. But as director of AMFM, my initial priorities are focused on the measurement science.
The Fed should put much higher priority on the competent use of economic index-number theory and reputable economic measurement and should create an autonomous Bureau of Financial Statistics. The Divisia monetary aggregates are only the tip of the iceberg. The public has the right to know. The public has the need to know.
2.6.4 The Bank of England
It is interesting to compare the way the Federal Reserve Board (FRB) has dealt with the Divisia monetary aggregates with the way the Bank of England (BOE) has. Although the origins of the Divisia monetary aggregates were at the FRB, when I was on the Board’s staff, the FRB has never made those data available in its official data releases to the Congress and the public. The Board’s official data releases do not include data produced and supplied by the St. Louis Fed. However, the Board’s staff has continued to supply to the public its official monetary aggregates, based on the simple-sum index, disreputable among professionals in economic measurement for nearly a century. Many other examples exist of FRB poor-practice economic measurement, such as reporting of negative values of nonborrowed reserves (an oxymoron) and distortion of demand-deposit data by about 50 percent through failure to report “pre-sweep” data, as explained in detail in section 4.2 of this book’s chapter 4.
In contrast, the BOE has gone about this in precisely the right way. That central bank provides to the public a Divisia money data series—officially. When that central bank decided to start producing Divisia data many years ago, the bank’s economists corresponded extensively by fax with experts in the field, including me. Once the data were constructed, the BOE continued providing them monthly to the present day. The data never were frozen for any reason. What the BOE did was professional and admirable, and is what every central bank in the world should have done long ago. In getting it right officially and publicly, the BOE is not alone. The National Bank of Poland also produces Divisia monetary aggregates officially and provides them to the public on its web site. The Bank of Israel similarly plans to be providing Divisia monetary aggregates to the public by the time this book is in print.
2.6.5 The European Central Bank
When the European Central Bank (ECB) in Frankfurt took over producing the euro currency for countries in the European Monetary Union (EMU), a challenging problem arose in application of index-number theory to monetary aggregation. The ECB needed the ability to aggregate over monetary assets within countries and then over countries. This two-stage nested procedure is called “multilateral” aggregation. No one had ever previously worked out the theory of multilateral Divisia monetary aggregation, since separate monetary aggregation within the individual states of the United States has never been of interest. But within the EMU, good reason exists to monitor the distribution effects of ECB monetary policy across countries.42 Changing the total supply of euro-denominated monetary assets does not necessarily affect all countries within the monetary unions in the same way or to the same degree.
The ECB employed me as a consultant to derive the relevant theory for multilateral Divisia monetary aggregation. I met with the relevant economists at the ECB in Frankfurt a few times and derived the theory they sought. I wrote a working paper available from the ECB in its working paper series. Since the result was a contribution to economic theory, a version of the paper was published in the Journal of Econometrics (Barnett 2007). My theoretical results, which are applicable to any multicountry economic union, are provided in appendix C to this book. The theory provides the internally consistent aggregation procedure applicable to three stages of economic progress toward convergence of an economic union, along with the formulas needed to monitor that progress. Those formulas, based on Divisia variances across countries, are provided in section C.7 of appendix C.
While I was in Frankfurt, one of the ECB economists provided me with graphs of the behavior of some of their Divisia monetary aggregates, produced using my theory. I have displayed what they provided in section 4.1 of this book’s chapter 4. But oddly they have not made those data available to the public. I do not know why. Until very recently I did not even know whether the ECB was using the data internally. In May 2010, when I visited the Bank of Greece in Athens, a high-level official informed me that the ECB is providing Divisia monetary aggregates to the ECB Governing Council, along with policy analyses of the implications of those data. If the data are useful to the highest level officials of the EMU, why would the data not be useful to the public? Is this “transparency” of central bank policy?
Based on what is being made available to the ECB Governing Council, I’d say that the ECB is dealing with these matters in a better way than the FRB and its staff in Washington. But in this area, neither the ECB nor the Fed meet the standards of openness and genuine transparency of the Bank of England, which is the model of a central bank that fully recognizes and respects its obligations to the public. The National Bank of Poland also provides its Divisia monetary aggregates to the public. The Bank of Israel and the Bank of Japan are similar to the ECB in keeping its Divisia monetary aggregates internal to the central bank, although the Bank of Israel has plans to begin making its data available to the public, perhaps through the Center for Financial Stability in New York City.
2.6.6 The International Monetary Fund
The International Monetary Fund (IMF) is an unusual organization, having the luxury of being above the fray of local politics within individual countries. The IMF is an institution within the United Nations system. The Bank’s formal relationship with the United Nations is defined by a 1947 agreement, which recognizes the Bank as an independent, specialized UN agency. Although the IMF is located in Washington, DC, its staff is international and very highly qualified, including many very sophisticated economists. In addition, employees of the IMF are not subject to US income tax. The IMF’s high after-tax salaries make it possible for them to employ and retain exceptional economists. When I first moved to Washington, DC, my real estate agent told me about the neighborhoods to avoid, since only IMF and World Bank economists could afford the housing in those neighborhoods.
With its exceptional expertise and independence of national political pressures, the IMF’s views on this subject are interesting. The IMF produces an official document, called Monetary and Financial Statistics: Compilation Guide.43 The most recent edition is dated 2008. Its sections 6.60 through 6.63 are on the subject of “Divisia Money.” Without comment, I provide the following direct quotations from pages 183 and 184 of those sections.44 The quotations speak for themselves:
In constructing broad-money aggregates, it is necessary to evaluate the degree of moneyness of a wide array of financial assets, focusing on the extent to which each type of financial asset provides liquidity and a store of value.
Divisia money is a measure of the money supply that weights the money components—currency, transferable deposits, time deposits, etc.—according to the usefulness of each component for transactions purposes.
A monetary aggregate that is an unweighted sum of components has the advantage of simplicity, but a monetary aggregate with weighted components may be expected to exhibit a stronger link to aggregate spending in an economy.
In a Divisia money formulation, the money components are weighted unequally in accordance with their relative usefulness for making transactions.
By weighting the monetary components, a Divisia money formulation takes account of the trade-off between the medium-of-exchange and store-of-value functions of holding of money components.
It is assumed that relatively illiquid deposits are less likely to be used for transactions purposes than highly liquid financial assets in the money supply and that higher interest rates are paid on the less liquid money components.
The largest weights tend to be attached to components that are directly usable as media of exchange (national currency and noninterest-bearing transferable deposits), but that are least useful as stores of value.
Divisia money formulations originated in the United States, but have become most prominent at the Bank of England (BOE), which has published Divisia money series since 1993.
The BOE publishes a Divisia money series for a broad money aggregate, as well as Divisia series for the money-holdings of separate money-holding series—that is, for the household sector, private nonfinancial corporations sector, and OFCs sector.
On the development of the Divisia index for monetary aggregates, see Barnett (1980a); Barnett, Offenbacher, and Spindt (1984); and Barnett, Fisher, and Serletis (1992).
2.7 Mechanism Design: Why Is the Fed Getting It Wrong?
2.7.1 The Theory
I frequently present research on this subject at conferences, often as keynote speaker. At the end of my presentation, there is one question someone almost invariably asks me. It goes something like this: “We know that the Federal Reserve Board’s official monetary aggregates are nearly useless. You make a very good case for adoption of your Divisia monetary aggregates, which in fact are computed and made available by the St. Louis Federal Reserve Bank and are official data at the Bank of England and the National Bank of Poland. Why does the Federal Reserve Board’s staff in Washington, DC, not adopt them as official data for the United States and provide them to the public, the profession, and the Congress through Board release channels?”
I hate being asked that question. My usual initial reply is: “I am not responsible for the FRB’s bad data. Ask them. It’s their problem, not mine.” Recently I also have added that I am very happy the FRB is “getting it wrong,” since that is in my own personal best interests. I doubt I would have received such an attractive contract from MIT Press for this book, if it had been titled, Getting It Right. This usually gets a laugh and some knowing smiles, but rarely stops the questioning. As is often then observed, I was on the Board’s staff in Washington, DC, for eight years, so I should know why the Divisia monetary data have still not been made official in Washington, DC.
This is a serious question, but the answer is much more complicated than might seem to be the case. Accusing the Board’s staff of incompetence in this area is a shallow oversimplification. The FRB’s staff is highly sophisticated in many areas and far from “stupid.” But there is a highly mathematical area of economic research, called “mechanism design,” originated by and developed by Nobel laureates Leonid Hurwicz and Eric Maskin. The field seeks mathematically to design economic systems and organizations in such a manner as to meet certain desirable objectives. The literature makes extensive use of mathematical game theory.45 A key property of a successful mechanism design is “incentive compatibility,” as defined by the brilliant mathematician Leonid Hurwicz. Formally, a process is defined to be incentive compatible if all of the participants fare best when they truthfully reveal any private information asked for by the mechanism. Incentive compatibility assures that satisfaction of the optimal outcome of the mechanism is consistent with decentralized pursuit of personal best interests by all participants. In that deeply mathematical literature, nothing is more important than the mechanism’s design for acquisition, allocation, and distribution of information in an incentive compatible manner. There is the key!
With this in mind, consider the different ways in which the Bank of Japan, the BOE, the National Bank of Poland, the ECB, the FRB, the St. Louis Fed, the Bank of Israel, and the IMF have dealt with these data and information matters. How would you explain, for example, the difference in behavior between the Bank of England and the Federal Reserve Board staff in Washington, DC? Clearly all of the central banks I’ve listed above are structurally designed differently—very differently. So there is the answer. It is a “mechanism design” problem.
Consider an analogy between the chairman of the Federal Reserve Board and the chairman of the board of directors of a corporation, such as Enron. It is widely believed that the CEO of Enron was fully informed and involved in the major decisions of the corporation, while the stockholders were not. Clearly, there was an incentive compatibility problem. In the literature on mechanism design, such problems are called “principal-agent” problems. In political science and economics, the principal-agent problem arises under conditions of incomplete or asymmetric information, when a “principal” hires an “agent” and needs to find an incentive system that will align the interests of the agent in solidarity with those of the principal. The problem arises in most employer–employee relationships and in the delegation of legislative authority to bureaucratic agencies. Because of the design of the Federal Reserve System, there is reason to be concerned about such matters. But mechanism design is an extremely complicated area of economic theory. Attempts at reform can have very negative consequences, if motivated more by politics than by a full understanding of the prob-lem’s complexities. In fact misguided “Fed bashing” is dangerous.
I am not an authority on economic mechanism design. Also I am not a political scientist. It would be unprofessional of me to presume to know how best to modify the design of the Federal Reserve System or how to isolate and identify the system’s design defects. An extensive comparison of the BOE with the Fed could be productive in that regard, but such research is far outside my areas of expertise.
2.7.2 NASA’s Space Program
While I do not presume to explore the design of the Federal Reserve System, I can provide an observation that may be analogous. This possible analogy is based on my early experience as a rocket-engine systems engineer on the space program long ago. While the work of engineers on the Apollo project was very different from the work of economists at central banks, there is something in common: existence of governmental oversight. The contractors that produced Apollo were subject to oversight by NASA (National Aeronautic and Space Administration), while the Federal Reserve is accountable to the Congress, which created the Fed.
I worked for Rocketdyne Division of North American Aviation (now part of the Boeing Corp). Rocketdyne produced the rocket engines for all three stages of the Saturn vehicle for the Apollo Project. Many years earlier another aerospace contractor, Lockheed Corporation, was exceptionally successful with a military contract to produce the Polaris submarine for the Navy. Lockheed completed the design, development, and delivery of Polaris ahead of schedule and at below the estimated cost. With the “cost-plus” military contracts of the time, such ahead-of-schedule under-contract-cost completion was virtually unheard of. Lockheed credited its dramatic success with a project-planning tool the corporation used for the first time on that project. The innovation was called a PERT chart, standing for Program Evaluation and Review Technique.
The fact that the PERT chart’s success became widely known was itself rather surprising at the time. Of the large aerospace contractors, the most secretive was Lockheed. For example, Lockheed had a super-secret division in Burbank, California, known to the locals as “the Skunk Works,” which had developing the U-2 spy plane. When I was at Rocketdyne, also in the San Fernando Valley of Los Angeles, most of the engineers had Confidential Security Clearances. For a couple of years I needed and had a higher level, Secret Security Clearance. But I never heard of any Rocketdyne engineers having the even higher level, Top Secret Security Clearance, despite the fact that some of the Rocket-dyne engineers worked on military rocket engines for ICBM missiles. In contrast, everyone at the Skunk Works was reputed to have a Top Secret Security Clearance. The security level was so high that employees were not even permitted to reveal their employer to their families. As a result, if PERT had been originated by Lockheed, we might never have learned about it. But PERT was developed for Lockheed by Bill Pocock, Booz Allen Hamilton, and Gordon Pehrson of the US Navy Special Projects Office, as an innovative application of the “scientific management” literature of the time.
The PERT chart is a tree-diagram flowchart with each node representing tasks during the development process. At the far right of the chart is only one node: project completion. At the far left of the flowchart are many nodes, identifying many development tasks needed to start up the engineering design and development. The tree eventually converges from its many branches at the start of the project to the final completion node. At each node, various numerical values had to be entered, identifying progress completed and remaining to be completed at that node. All of the node information was entered into a computer periodically to determine the critical path delaying completion. Resources then were reallocated to the critical path.
NASA found out from the Navy about the success of PERT. Rocket-dyne had a PERT chart for the F-1 rocket engine program, on which I worked. NASA, knowing about the technique and its success at Lock-heed, insisted that Rocketdyne supply the PERT chart to NASA on a regular basis. I observed that two groups of planners worked on the PERT chart. One group regularly came around asking for information on each group’s progress and plans. The other group never did. I asked an engineering executive in the project office why we never seemed to see anyone from the other PERT group. What was the reply? That group produced a different chart supplied to NASA. I assume you “get the picture.”46
I have been out of that industry for decades, but at that time the attitude of Rocketdyne engineers regarding NASA was that oversight by NASA was often an obstacle and a nuisance. The unspoken “message” in the minds of many Rocketdyne engineers toward NASA administrators was: “Leave us alone. We know what we need to do better than you do. You are just in our way.”47 Rightly or wrongly, the attitude of the FRB’s staff toward the Congress is similar, as is well known to any congressional economics staffer or to any employee of the FRB’s Congressional Liaison Office, which serves as an information filter.
As mentioned, when I was on the staff of the Federal Reserve Board, I was told to send my Divisia monetary aggregates only to the staff director of monetary policy, to delay replying to requests from the governors, and to stay far away from the Congressional Liaison Office. These requirements all had a very familiar ring to me, going back to the years I was an engineer at Rocketdyne. Unlike the other economists on the staff of the FRB, I also was not surprised when Chairman Arthur Burns brought in the FBI to investigate his entire staff, including hundreds of economists, to track down the economist who had provided bank interest rate data to Consumer Reports. That magazine published a series of articles revealing which banks in the United States were paying the highest interest rates on various categories of saving accounts and certificates of deposit. Of course, anyone can call any bank and ask for the interest rates offered on its accounts. But Burns immediately recognized that the only computer file having information on interest rates paid by every bank in the country was at the Federal Reserve Board, so the source must have been an FRB staff member. The FBI found the person who did it, and Burns fired him.48
I have no doubt that the fired employee never dreamed he would be hunted down by the FBI, since no bank hides the information on its interest rates offered. But he would not have been surprised, and would not have provided the requested information, if he had previously worked for an aerospace contractor or had been an expert in economic mechanism design. He would have understood the rational constraints on information availability by organizations subject to oversight.
Are you still wondering why the FRB does not provide Divisia monetary aggregates through its official releases? If so, perhaps it will be clearer by the time you finish reading this book.
2.7.3 The Locked Office
The Board has an econometric model used in policy decisions. Years of problems have existed with such models. In section 3.1 of this book’s chapter 3, I provide graphs demonstrating those problems resulted from the use of the Board’s simple-sum monetary aggregates and could have been avoided by adoption of index-number-theoretic data. The model manager at the time was a very fine economist by the name of Jerry Enzler. He had seen my research, which had independently been confirmed by two other economists at the FRB, but Jerry never discussed the subject with me.
After I had left the Board for the University of Texas, I received a surprising telephone call from a senior economist at the Federal Reserve. He told me that Jerry sadly had been in a serious automobile accident, suffered brain injury, and had to go on permanent disability. Unlike the other economists in the Special Studies Section and its sister section, Econometrics and Computer Applications, Jerry had a lock on his door. No one had access to the work in his office, unless he provided it. The primary reason he had a lock on his office was his access to some classified CIA data.49 When he went on disability, one of his colleagues was given the key to Jerry’s office. His colleague, an economist in the same section, discovered Jerry had changed the M2 monetary aggregate used in the model from the Board’s official, simple-sum aggregate, to my Divisia M2 aggregate. As a result, for a few years, the model simulations, sent to the governors for use in policy decisions, were based on my Divisia M2 data, not the official M2 data.
The model manager is fully authorized to use whatever data and whatever equations he finds to be useful in producing policy simulations for the Board and the FOMC. In addition, the monetary aggregates were neither a final target of policy nor a policy instrument at that time. As a result his policy simulations transmitted to the Board did not likely mention the role of the monetary aggregates, which were internal to the model’s transmission mechanism of policy, along with hundreds of other variables. No breach of fiduciary responsibility was involved in his use of Divisia M2 within the equations of the model.
Unfortunately, Jerry’s colleague revealed what Jerry had done and switched back to the official simple-sum M2 data. Jerry, as the model manager, had never revealed his use of Divisia M2 to anyone, including me. Even the governors did not know. Unfortunately, not many economists like Jerry Enzler have positions in governments anywhere in the world. I wish there were more.
2.7.4 The Relationship between the Board’s Staff, the Governors, the FOMC, and the Regional Banks
The relationships among the Board’s staff in Washington, DC, the governors, the FOMC, and the regional banks are often misunderstood. The chairman of the Board of Governors is sometimes viewed as analogous to the CEO of a large corporation. A closer, but not entirely accurate, analogy might be with the chairman of the board of directors of a corporation.
The Board’s staff, although not formally part of the civil service, consists of career bureaucrats; and the Board’s staff operates in a manner similar to the civil service. For example, Board staff salaries are on a table of levels and steps, similar to that for the civil service. The governors are not career civil servants. A field of economics, called “public choice,” studies and models the ways in which bureaucracies function. Public choice is closely connected with political science formal theory, as well as with mechanism design. Serious consideration is given to problems of incentive compatibility. In contrast, the governors, not being part of the staff’s bureaucracy, tend to be dedicated solely to the pursuit of the public interest. Many studies have sought to find conflicts of interests among the governors. None of those studies has ever found convincing evidence of conflicts of interests. In fact many of the governors are paid significantly less as governors than they were paid in their prior employment. About the only significant material benefit that they receive from their positions as Federal Reserve Governors is an exceptionally dramatic office in the Board Building.
Conspiracy theorists are fond of viewing the Fed as being nongovernmental and under the control of mysterious private interests. In fact the FRB staff and the Board of Governors are 100 percent federal government employees, but with some differences in motivation and self-interests. The regional banks are semi-governmental and semi-private. The decentralization designed into the system by creation of the regional banks is noteworthy in many ways, providing closer contact with the commercial banks and the university professors in their regions and a channel for policy dissent.
Much of the role of the Fed in monetary policy is executed through the actions of the FOMC, which meets in Washington, DC, but provides its instructions to the Open Market Desk located at the New York Federal Reserve Bank in New York City. The Open Market Desk buys and sells securities as a means of influencing interest rates and the money supply. The FOMC includes representation from the regional banks, as well as heavy influence from the FRB in Washington, DC. Dissent by presidents of the regional banks takes place at FOMC meetings and often in a more visible manner in public speeches and interviews. The complexity and sophistication of the system is evident at the FOMC, along with the balance between centralization in Washington, DC, and decentralization to regions throughout the country.
But the independence of the regional banks from the Board should not be overestimated. Prior to the three years of the “monetarist experiment” in the United States (1979–1982), the research staff of the Philadelphia Federal Reserve Bank produced a large document containing research supporting a change in policy direction—the same change in direction that subsequently was adopted by Paul Volcker during the years of the “monetarist experiment.” The purpose was to deal with the accelerating inflation of the 1970s. But that research at the Philadelphia Fed was prior to the arrival of Paul Volcker as chairman of the FRB. Since the Board was not yet favoring Volcker’s subsequent change in direction, the Board staff at the time was instructed to crush the research at the Philadelphia Fed and discredit its staff.50 The Board staff succeeded to the degree that almost the entire research staff of the Philadelphia Fed resigned. Prior to their resignation, I was invited to the Philadelphia Fed as a possible new hire, who might be able to help hold the staff together. I had said nothing about this invitation at the Board. But on the morning I returned from Philadelphia to the Board staff in Washington, DC, I was called into the office of the director of personnel and given an immediate raise along with instructions not to help “those bad people” in Philadelphia.
The Philadelphia Fed at that time had an eminent group of vice presidents, who supported their research economists’ critique of Board policy. But there was an exception. One vice president backed the Board against his bank’s own staff. Yes, you guessed it. He was promoted to president of the bank. Most of the research staff left. While I witnessed this evolve firsthand, what happened was far from unique. Toma and Toma (1985) provided evidence that some regional reserve banks received systematic and significantly lowered budget increases than the other regional reserve banks for their “maverick” views on monetary policy.
Not long after the purge of the research staff in Philadelphia, as inflation was becoming intolerable to the Carter administration, Paul Volcker was moved from the New York Fed to become Board chairman in Washington, DC. He then instituted the policies previously advocated by the former staff at the Philadelphia Fed. Chairman Volcker, knowing that his staff in Washington had been geared up to oppose precisely that approach, did not confer with or inform his large staff before his announced policy change. Reputedly only three staff members at the top were informed of the impending change. The rest of us learned from the newspaper the next morning. That morning, I had breakfast at the Board’s cafeteria and observed the stunned looks on the faces of the staff and the bewildered conversations among us over our eggs and coffee. In contrast, Professor Carl Christ was visiting from Johns Hopkins University that day and joined us at that breakfast. He was clearly amused and pleased by what had just happened.
2.7.5 The Right and the Wrong Kinds of Reform
Not being an expert in mechanism design, political science, or public choice economics, I would not presume to recommend fundamental change to the structure of the system. But my experience does tell me that some congressional proposals for reform of the Fed reflect lack of appreciation of the merits of the system. In the following section, I discuss some of those proposals and their history, and offer a suggestion for an overlooked minor reform, which would have only positive effects, as opposed to the more sweeping, and potentially damaging, reforms periodically proposed in the Congress. First, let us look at the context relevant to the recently passed reforms and others still circulating among congressional staffers.
Fed Chairman Ben Bernanke spoke out against congressional bills to audit the Federal Reserve. Why? Proponents argue that the purpose of the audits would be to increase the transparency of policy and improve the quality of Fed data. Aren’t these purposes both in the public interest? Growing evidence exists that defective Fed data played a role in producing the misperceptions of decreased systemic risk, leading up to the current recession.
Discussion of the debates about auditing the Fed can be found in my New York Times article, Barnett (2009), and my journal article, Barnett (2010). A Rasmussen reports survey found that 75 percent of Americans favored auditing the Fed and making the results available to the public, while only 9 percent opposed it, with 15 percent being unsure. After all, as a previous New York Fed president remarked, the Fed is independent within the federal government, but not of the federal government.51 Since the Federal Reserve was created by the Congress, the Fed is inherently accountable to the Congress. Isn’t therefore an audit in the interests of good governance? Despite the public support, the bills failed to pass.52 Let’s consider the ramifications of this outcome.
The debate needs to be set against the background of long-running tensions among the central bank and the legislative and executive branches of government. When in 1978 the Congress passed a bill mandating audits by the Government Accountability Office (GAO) for most government agencies, the bill excluded from audit a vast sweep of the Federal Reserve System’s activities. Operations of some Fed activities, including monetary policy, were also addressed in the same year in the Humphrey–Hawkins Act. The following year Chairman Paul Volcker made major policy changes to lower the inflation rate. Bernanke has stated that the 1978 audit exclusions were necessary to allow Chairman Volcker’s ability to act decisively. Personally, I doubt this. I was on the staff of the Board in Washington at that time. Paul Volcker was a determined chairman, whose actions were based on his own strong convictions. Since the GAO has no policy-making authority, the GAO could not have prevented him from implementing his chosen policy.
Certainly the Fed has reasons to oppose an increased role in monetary economics by the GAO. From the standpoint of the Federal Reserve, the biggest danger would be that increased audit authority by the Congress would allow politicians to second-guess unpopular policy actions, which might have been chosen for good reasons by the Federal Reserve. Indeed the Fed should avoid short-term politics and focus on policies that are good for markets and the economy over the long run. The recent Dodd–Frank Act provided for an audit of the Fed—once. However, audit authority is hardly necessary for the Congress to take an interest in the Fed’s business, as has been demonstrated time and again by the actions of past congress members, senators, and presidents. From its point of view, the Congress created the Fed and thereby has responsibility for its oversight.
There are well-known examples of such pressures. When I had lunch with Arthur Burns, following his term as Federal Reserve chairman (1970–1978), I asked him whether any of his decisions had ever been influenced by congressional pressure. He emphatically said no—not ever. On the other hand, Milton Friedman reported Nixon himself believed he had influenced Burns.53 Similarly Fed Chairman William M. Martin (1951–1970) discussed pressures from President Lyndon Johnson.54 Chairman Martin emphasized that, in his views, the Congress and the president set the nation’s economic priorities, including spending, taxes, and borrowing. The role of the Federal Reserve, in Martin’s view, was to assist in fulfilling those policies, including facilitating Treasury borrowing at reasonable interest rates. In 1966, when he led a sharp contraction of monetary policy to offset aggregate demand pressures from President Johnson’s policies, Martin was sharply reprimanded by President Johnson. In 1969 the FOMC did respond unwisely to administration pressures to ease policy. Occasionally presidents have been supportive. President Reagan’s support was important to the success of Chairman Volcker’s anti-inflation policy.
Perhaps the closest antecedent to recent congressional audit proposals was the upswell of monetarist sentiment in the Congress in 1975 to 1978, following puzzling phenomena in 1974 money markets. Later analysis revealed flaws in the published monetary aggregates during that period. Those flaws contaminated economic research for years afterward and remain a source of misunderstanding to the present day.55 Two congressional measures—House Concurrent Resolution 133 in 1975 and the Humphrey–Hawkins Act of 1978—subsequently required the Fed chairman to appear twice each year before the Congress to report the FOMC’s target ranges for money growth.56 The Federal Reserve bristled under such supervision. Never before in the Fed’s history had the Congress imposed a reporting requirement on Fed policy makers—and a requirement far less invasive than a GAO audit. The Humphrey–Hawkins Act reporting requirement came up for renewal in 2003 but quietly was allowed to expire. Semiannual reports to the Congress continue but without the force of law.
There are several instances when faulty monetary data led policy makers astray. My research, summarized in section 3.3 of this book’s chapter 3, shows that Volcker’s disinflationary policy was overdone and contributed to an unnecessarily severe recession. Poor monetary aggregates data led Volcker inadvertently to decrease monetary growth to a rate that, appropriately measured, was half what he thought it was.57 Volcker wrote to me years later that he “still is suffering from an allergic reaction” to my findings about the actual monetary growth rate during that period. Suppose that a GAO audit had investigated whether data being published were best practice among experts in economic measurement, and concluded that they were not. With better data, would Volcker have selected a more gradual disinflationary policy?
Focus, for a moment, on the Federal Reserve’s published monetary data. Is its quality the best possible? Are the reported items constructed appropriately to the task of operating and understanding the path of monetary policy? Unfortunately, no. Consider, for example, the important and widely monitored data on banks’ “nonborrowed reserves.” Every analyst understands that banks hold reserves at the Fed to satisfy legal requirements and to settle interbank payments, such as wire transfers and check clearing. The total of such reserves may be partitioned into two parts: the portion borrowed from the Federal Reserve and the portion that is not. Clearly, the borrowed portion of reserves cannot exceed total reserves, so nonborrowed reserves cannot be negative. Yet recently Fed reported values of nonborrowed reserves were minus 50 billion dollars, as shown in section 4.2 of this book’s chapter 4. How can this happen?58 Such confusing accounting practices would not likely survive scrutiny by an outside audit, assuming it was competently performed. Ah, but that is the problem. Is GAO audit the best solution? I have my doubts.
Other serious defects exist in the data currently published. According to Section 2a of the Federal Reserve Act, the Fed is mandated to “maintain long run growth of the monetary and credit aggregates commensurate with the economy’s long run potential. . . .” Neglecting these instructions, Fed policy makers have stated that monetary aggregates currently are unimportant to their decisions. Whatever the merits of this attitude might be, external analysts and researchers continue to depend on monetary aggregates to obtain an accurate picture of the stance of policy, and many other central banks throughout the world continue to report data on multiple monetary aggregates. During the 30 years since the Congress excluded monetary policy from GAO audits and mandated reporting of money growth in the Humphrey–Hawkins Act, two of the then four published monetary aggregates have been discontinued: M1 and M2 remain, but M3 and L do not. In quiet times, perhaps this is of little importance, but these broad monetary aggregates and the underlying data detail were greatly missed during the 2008 financial crisis.
Furthermore the M1 aggregate is severely biased downward. Since 1994, banks have been permitted by the Fed to reclassify, for purposes of calculating legal reserve requirements, certain checking account balances as if they were MMDA saving deposits. The reclassified deposits are euphemistically called “sweeps.” Banks supply to the Federal Reserve only the post-sweeps checking account data. The resulting published data on checking deposits understate, by approximately half, the amount of such deposits held by the public at banks. Why doesn’t the Federal Reserve require banks to report the pre-sweeps data? Does such published monetary data satisfy the requirement of the Federal Reserve Act? Again, it seems unlikely that such an omission would survive an unconstrained examination by persons qualified in economic index-number theory. But who should those persons be?
Now we come to the bills recently debated in the Senate and the House to expand upon GAO audit authority. The House bill was introduced by Texas Republican Congressman Ron Paul and had 317 cosponsors, including over 100 Democrats. The Senate bill was introduced by Vermont Independent Senator Bernie Sanders; bipartisan cosponsors included Kansas Republican Senator Sam Brownback and Wisconsin Democratic Senator Russell Feingold. In Washington, DC, I met with a senator and his staff, who supported the Senate bill, and with a Federal Reserve Board division director, who opposed part of it. Since my conversations in Washington were about the Senate bill, I comment on only that failed bill.
Current law contains four audit exclusions for the Fed. That Senate bill would have removed all four of the current audit exclusions. The four exclusions are:
1. transactions for or with a foreign central bank, government of a foreign country, or nonprivate international financing organization;
2. deliberations, decisions, or actions on monetary policy matters, including discount window operations, reserves of member banks, securities credit, interest on deposits, and open market operations;
3. transactions made under the direction of the Federal Open Market Committee; or
4. a part of a discussion or communication among or between members of the Board of Governors and officers and employees of the Federal Reserve System related to clauses 1, 2, and 3 of this subsection.
Exclusions 1 and 3 are arguably not in the public interest and could have been removed. I would not support unconditional removal of the other two exclusions, because they appear to overlap roles outside the GAO’s primary areas of expertise.
Many economists signed a “Petition for Fed Independence,” often interpreted as opposing audit of the Federal Reserve. However, the petition makes no mention of auditing the Federal Reserve. The petition opposes possible infringements on Fed policy independence, and I support that view. Audits ask whether a firm or organization is following best practice and existing regulations in its business dealings. Audits do not tell management how to run a business or conduct policy. But again, the question remains: Who has the relevant expertise to provide such oversight for the Federal Reserve?
With respect to the collection and publication of accurate data, creation of an independent data institute for monetary and financial data would be preferable to expanded audit, since such institutes possess specialized expertise in economic measurement, including the latest advances in index-number and aggregation theory. An obvious potential for a conflict of interests exists in having data reported by the same agency that influences data through its own policy actions. Perhaps an economy of scale exists in such collection, but the risks outweigh any benefits, unless those responsible for producing the data have a relevant degree of autonomy and authority, as through the creation of a data bureau within the Federal Reserve. I return to this subject in section 2.7.6 below.
Such autonomous bureaus exist elsewhere in the government. The Bureau of the Census, the BEA, and the BLS, collect data later used for policy purposes by the administration and the Congress. An “independent” federal data institute need not be outside the Federal Reserve System. Varying degrees of independence exist within the admirably decentralized Federal Reserve System, with, for example, regional bank presidents free to vote against the Federal Reserve Board’s positions at FOMC meetings. The deeply respected BLS is within the Department of Labor, but has sole responsibility for production of Department of Labor data and employs a staff of formidable experts in economic aggregation and index-number theory. Expertise in those areas within the Federal Reserve System is minimal and is not centralized into any autonomous single group anywhere within the system.
Regarding Federal Reserve independence, concern should be focused on the recently renewed “coordination” of Fed monetary policy with Treasury fiscal policy. That coordination is in conflict with the 1951 Treasury–Fed Accord that established independence of the Fed from the Treasury. Unwise Federal Reserve actions in support of Treasury bond prices during periods of heavy Treasury borrowing have ignited inflation twice before: once following World War II (a trend that ended with the 1951 Accord) and once following Chairman Martin’s capitulation to President Johnson’s Great Society pressures, as already mentioned. During World War II, good reason existed for the Fed to be expected to assist the Treasury in its financing of the war through bond issues. After the war, the Treasury tried to retain that obligation of the Federal Reserve to assist the Treasury; but the Fed, recognizing the inflationary implications of printing money to finance federal debt, resisted. Following a long struggle, the Accord was reached, by which the Federal Reserve was freed from further obligations to assist in Treasury financing. The violations of the Accord that took place during the recent financial crisis and Great Recession could have long-run consequences.
Federal Reserve spokesmen are right to warn of the risks and dangers that expanded audit would entail. The best solution would be to set up an independent institute for monetary and financial data. The Fed could create such an institute on its own within the Federal Reserve System, without the need for congressional intervention. I admire and respect the role that the St. Louis Fed plays in producing high-quality data. But the only Fed data having widespread visibility to the public and the press are the official data produced and distributed by the FRB staff in Washington, DC. The cause of the existing inadequacies is the failure of the original design of the system to recognize the conflict of interests inherent in having a system, with policy authority, report the data that the Fed itself influences. However, expanded audit would be an inferior solution to the creation of an independent data institute. While it has expertise in accounting, the GAO is not known for its expertise in economic aggregation and index-number theory. Those areas of expertise are of greatest importance to any federal economic data institute, such as the BLS.
But sad to say, within the Federal Reserve System, which employs thousands of highly educated professionals, I currently can think of only three economists who have demonstrated published knowledge in the field of economic measurement (i.e., economic index-number and aggregation theory): Richard Anderson, vice president at the St. Louis Fed; my former student, Travis Nesmith, senior economist at the FRB; and my former student, Mark Jensen, financial economist and associate policy adviser at the Atlanta Fed. No two of them are in the same group, or even the same city. This is in stark contrast with other major data and information generating federal agencies in Washington, DC.
While the subject of audit of the Fed has been an issue in Washington recently, and may return in the future, more troubling proposals exist for fundamental structural change to the Federal Reserve. While the most worrisome of them have not passed in the Congress, the fact that they appeared in a major bill is disturbing. These proposals for major structural change have made the mistake of blaming the regional banks for the financial crisis and recession. Shooting from the hip, when you’re target is bank regulation reform, overlooks the complexity of mechanism design, public choice, and political science. Some examples, which could have done more harm than good, appeared in Senator Christopher Dodd’s original bill and Representative Gary Peters’ original proposal.
The Federal Reserve is built on a decentralized structure encouraging businesses, banks, and the public to participate and cooperate in getting things done. For any single group—including the Congress—to dominate decision making, is nearly impossible. Parts of Dodd’s original bill threatened that structure under the guise of removing conflicts of interest. Those parts would only have reduced the professionalism of the Federal Reserve and increased the political role of the Congress in monetary policy.
The choice of Federal Reserve Bank presidents is at the core of the Fed’s populism—and success. The selection process balances the interests of business, the public, and banks, while also giving voice to the small, medium, and large entities within each group. No Federal Reserve Bank ever “appoints” a president—a candidate becomes a president only after having been nominated by the regional Federal Reserve Bank’s directors and approved by the Fed’s Board of Governors. This veto power in Washington assures only well-qualified persons are nominated and, eventually, accepted.
Dodd’s original bill proposed Senate confirmation power over appointment of Federal Reserve regional bank presidents. This reform would have been misdirected and fortunately did not pass. Even worse would have been Representative Gary Peters’s proposal to take away the vote of Federal Reserve regional bank presidents on the FOMC.
Dodd’s original bill would have changed the current approach into a Washington-centric one laced with opportunities for political meddling. His bill would have increased the power of the Federal Reserve Board at the expense of the system’s regional banks. The bill also would have created a new centralized regulatory agency, vulnerable to regulatory capture by the powerful, as happened to the now defunct Interstate Commerce Commission.
Poorly conceived attempts to fix the Fed’s problems risk losing its best features. One great asset is the Fed’s intellectual capital. Many of the Fed’s economists are thought-leaders in their fields, both publishing in, and serving as associate editors of, professional journals. For example, Jim Bullard, president of the St. Louis Fed, is a well regarded economic researcher, who has published in some of the profession’s best journals, including the one I edit.
Since I left the Federal Reserve Board staff 28 years ago, the economics profession’s respect for the research staffs and presidents at those regional banks has steadily grown. The vast majority of the 12 presidents are PhD economists. The only other central bank in the world having comparable research competence is the ECB in Frankfurt.
Yet there are some regulatory changes that need to be made. The 1980 Monetary Control Act granted all banks, along with other depository financial institutions, the right to offer checkable deposits, settle payments at the Federal Reserve, and borrow from the Fed’s discount window—but it did not require them to become members of the Federal Reserve System. It is time that all banks were required to be Fed members. That would eliminate “regulatory shopping,” by which banks seek the most permissive regulator among state regulators, the FDIC, the comptroller’s office, and the Fed. Such behavior produces an incentive for regulators to adopt lax regulatory policies.
I am also concerned about the 1956 Bank Holding Company Act and its Gramm–Leach–Bliley revision. Under this act the Federal Reserve regulates all large financial holding companies, including most large commercial banks and the surviving investment banks. The problems of troubled Citicorp do not speak well of the existing approach. But that regulatory authority is centralized to the FRB staff’s Supervision and Regulation Division in Washington, so Citicorp’s problems cannot be blamed on the regional banks. In fact, involving the decentralized Federal Reserve Banks in that supervision might be a positive change, by reducing opportunities for political meddling.
Many Fed reform proposals reflect inside-the-beltway politics, seeking increased centralization of Fed policy. GAO audit, instead of bringing in autonomous expertise in economic measurement, as exists in the BLS and the BEA, would introduce oversight from another Washington bureaucracy, having no established expertise in index-number theory or aggregation theory. In the published professional literature on economic measurement, I have seen many important articles published by economists at the BEA and BLS over the years. I have known many of those economists, and those agencies frequently hire PhD economists with expertise in those areas. While I can think of only three such economists within the Federal Reserve System, which has no such autonomous data production bureau, I can think of none at all at the GAO; and I do not recall having ever read any serious contributions to the relevant professional literature from employees of the GAO.
While there may be some merit to increased accounting audit of the Federal Reserve data in some areas, the net effect of a significantly increased role for the GAO in central bank policy would be increased centralization to a federal agency having little claim on relevant expertise in the area. Similarly the congressional bills designed to decrease the policy role of the regional banks would have increased the role of the Federal Reserve Board and its staff at the expense of the decentralized regional banks—again, increasing centralization to inside-the-beltway Washington, DC. While the media have made much of the questionable actions of the regional banks in bank regulation prior to the financial crisis, the media seem to have overlooked the fact that the FRB in Washington contains three divisions, one of which is the Division of Supervision and Regulation. Why have the media failed to take into consideration the failures of that large Division inside the beltway?
Transparency and information-availability from the Fed are critical to the successful role of decentralized free enterprise. As this book documents, the quality of data coming from the Federal Reserve Board staff has been declining for years, as the need for data has grown in the face of increasing complexity of financial markets and instruments. In contrast, data coming from the St. Louis Fed have been improving, but are less visible than the official data provided by the FRB. With decreasing data quality coming from the Board in Washington, DC, and growing need for those data by the public, an increasing need for regulation is unavoidable to constrain poorly informed decisions by the private sector. The preference in Washington appears to be for increased regulation to be centralized there, as a means of dealing with the effects of the problem, rather than the cause.
Finally, little in Dodd’s original bill would have addressed the problems of inadequate policy transparency, the sometimes shockingly low Federal Reserve data quality, and the anticompetitive concept of “too big to fail.” But there is a very positive exception, which is the subject of the next section. Regarding Federal Reserve policy, the Congress has been asleep for 25 years. Now that it is waking up, I am worried that sooner or later the sleeping giant may stomp in the wrong places.
2.7.6 The Office of Financial Research
The existence of a system design problem at the Federal Reserve was recognized within Title 1 of the Dodd–Frank Act, by creation of the new Office of Financial Research (OFR), currently housed within the Treasury building. The broad charge of the office is in Section 151 of Subtitle B of Title 1 of the Dodd–Frank Act. That charge is to acquire and report to the Congress data relevant to monitoring and regulating systemic risk. The director of OFR does not report to the Secretary of the Treasury, and the OFR’s budget does not come from the Congress. The director of OFR is appointed by the president and confirmed by the Congress. The Secretary of Treasury has no authority to require the OFR’s director to submit in advance any documents, speeches, or testimony. The OFR’s budget comes from the Federal Reserve initially, but that arrangement is only temporary. Once fully established within two years, the OFR will acquire its budget from banks via levy. As a result Dodd–Frank has made the OFR an independent federal agency.
The creation of the OFR by the Congress is a rebuke to the Fed’s stewardship of the financial system. The prior view of political scientists was that the Congress does not and cannot know all future regulatory and monetary policy risks. That view resulted in the theory of “delegated monitoring,” by which the Federal Reserve is charged with bringing to the attention of the Congress any and all innovations presenting risks to the financial system. The creation of the OFR reflected the congressional view that the Fed did not adequately monitor the economy for systemic risk and failed to bring to the Congress needed reforms. According to that point of view, the Fed assumed markets would self-regulate, investors would not buy instruments they did not understand, and owners of financial firms would not allow managers to undertake undue risk, which would harm the brand name of the firms.
Aren’t aggregated financial data relevant to systemic risk? Of course, they are. The systemic risk at the root of the financial crisis and the Great Recession was the risk of recession. That risk was underestimated by those who imprudently increased their personal risk exposure. The financial data relevant to inflation and the business cycle are aggregated financial data, such as the monetary aggregates, dealt with by the FRB in an irresponsible manner. But at present the OFR is concentrating on disaggregated micro data about individual firms.
The OFR’s current focus on micro data is down to the individual loan and security level, with particular emphasis on derivatives and securitization and on whether the outstanding set of securities is consistent with market stability. The emphasis is on assessing, as a regulator, whether entities/markets are pricing risk correctly. Ongoing debate within the OFR is focused on the extent of analysis and information to be returned to the market. In particular, concern exists about whether the results of analysis should be held confidential and used for regulation, or whether aggregated results should be made public to assist the public in making correct decisions. Anyone reading this book should have no difficulty in guessing my views on that debate.
The charge of the OFR under the Dodd–Frank Act easily could encompass aggregated financial macro data. How could it not? The micro sources of risk that evolved, and now rightfully will be monitored by the OFR, were consequences of the misperceptions of macro systemic risk. This book distinguishes between cause and effect. No mistake is involved in governmental policy makers concentrating on availability and quality of aggregated macro data.
Need exists for the creation of a new Bureau of Financial Statistics (BFS) to provide competently aggregated macro financial data to the Congress and to the public. As this book documents, the Federal Reserve Board has been failing in that area, and therein lies much of the misperception of systemic risk, which led to the financial crisis and the Great Recession. To be consistent with the basic principles of mechanism design and incentive compatibility, data production must be logically prior to data use. Those who produce economic data should be experts in index-number and aggregation theory and should have no role in the use of those data in policy. The BFS could be created as an autonomous group within the Federal Reserve, in a manner analogous to the role of the BLS within the Department of Labor.
But considering the poor record of the Fed in production and distribution of aggregated financial data, I would not be at all surprised, if the Fed were to believe that providing adequate, professionally produced financial data would be inconsistent with the Fed’s best interests. Such data are relevant to Fed policy oversight by the Congress, the profession, and the public. No rational bureaucracy voluntarily seeks to facilitate or increase oversight. As a result the OFR may very well recognize the need for a BFS and decide to create the BFS within the OFR. Since the OFR has the authority to recommend policy to the Congress, the employees of the BFS, if within the OFR, should be separated from that policy authority. The sole responsibility of the employees of the BFS should be best-practice economic measurement of financial aggregates, which this book documents are being poorly produced and inadequately supplied by the Fed.
It should be emphasized that nothing I have written in this section or anywhere else in this book recommends decreasing the Federal Reserve’s autonomy, independence, or authority in making monetary policy. In fact separation of the reporting role from the policy-making role would increase the independence of the Fed’s policy makers, by removing an overlap creating a conflict of interests within the system—a fundamental violation of elementary principles of mechanism design.
2.7.7 A Quiz: Answer True or False
In a sense, a large gap exists between part I of this book and the first four appendices in part II. Part I assumes little, if any, prior knowledge of economic theory. In contrast, part II assumes extensive prior knowledge of the relevant literature on index-number theory and aggregation theory and is provided for the benefit of professionals in those areas of specialization. Appendix E addresses the middle ground: people having some knowledge of microeconomic theory, but without prior expertise in aggregation and index-number theory. That group includes a large percentage of potential users of the Divisia monetary aggregates. If you read this section, you will find out whether you are in the middle-ground group, who would benefit from reading appendix 5. If you already know the answer to that question, just skip this section and move on to chapter 3.
In teaching the relevant economic theory to my students, I sometimes give examinations containing true or false questions, to see if my students have misunderstood the economic implications of definitions 1, 2, and 3. If I give such an exam soon after the students have seen that material for the first time, some students often will answer “true” to the following intentionally misleading questions.
Question 1: If the interest rate on a monetary asset increases, its user cost price will decline. Hence the weight given to that asset in the Divisia monetary aggregate will necessarily decline. True or false?
Question 2: If the interest rate on a monetary asset is high, its user cost will be low. Hence monetary assets with high interest rates necessarily contribute less to the Divisia monetary service flow than monetary assets with low interest rates. True or false?
Question 3: Quantity aggregator functions contain only quantities, but quantity index numbers contain both prices and quantities. As a result something must be wrong with the entire field of index-number theory. Index numbers cannot accurately measure the correct quantity aggregate, which does not include prices (or interest rates, in the case of monetary aggregation). True or false.
The correct answer in all these cases is “false.” Once the students have completed reading appendixes A through D, no students get those questions wrong. But since some readers of this book may not read those appendixes, written for professional economists, I have provided another appendix (appendix E), which explains why the correct answer to all of those questions is “false.” Appendix E, while not assuming knowledge of appendixes A through D, does assume knowledge of technical jargon not explained in part I.
Anyone who teaches economics would recognize question 2 immediately, since it is a variation on a famous trick question, appearing in almost every elementary economics textbook as the “diamonds versus water paradox.” The lower price of water does not imply that the total stock of the world’s water, which is needed for survival, has less value than the total stock of the world’s diamonds. If you have taken an elementary course in economics, you will surely have seen this before and will recognize the following technical statement: low “marginal utility” does not imply low “total utility.”
Questions 1 and 2 both reflect an inaccurate reading of definition 3. Recall that the “weights” in the Divisia index are not prices. The weights are expenditure shares. But even students who recognize that fact often are tricked into answering “true” to question 2. It is tempting to think that increasing the price of a good will increase the share of income spent on that good and thereby its weight in the Divisia quantity index. But increasing the price of a good will change the quantity of that good purchased, as well as the quantities of other goods purchased. Whether the share of expenditure spent on that good will increase, decrease, or stay the same is not predictable.59
Question 3 contains an implicit misrepresentation of the objectives of index-number theory. Index-number theory does not seek to reveal the complete aggregator function along with all of its properties and everything it can do. Index-number theory seeks only to track the value of the aggregate actually attained by the economy. In continuous time, the Divisia index tracks that value exactly correctly without any error at all. The Divisia index cannot reveal values of the aggregate that may be possible but are not attained by the economy. You may recognize the analogy with Paul Samuelson’s famous theory of “revealed preference,” and you may have seen an explanation of how the CPI, provided by the BLS, tracks the “true cost-of-living index.” The true cost-of-living index contains only prices and no quantities, but the CPI contains both prices and quantities.60 The CPI accurately measures that actual cost-of-living in the economy but cannot answer “what if” questions about what the cost-of-living might be under different circumstances. Only the “true cost of living index” can do that. The reason is the same.
Hopefully you have not gotten questions 1, 2, or 3 wrong and have no need for further explanation of those “trick” questions. If you got any of those questions wrong and feel the need for further explanation, you can find the full explanations in appendix E, but with some prior knowledge of microeconomic theory assumed.
2.8 Conclusion
In this chapter you have met some of the star players on the team: Fisher, Divisia, Theil, Jorgenson, Diewert, Poterba, and Rotemberg. They are among the best of the best. Are you still wondering why the FRB is “getting it wrong”? I have a better question for you to consider. Why are the BOE, the National Bank of Poland, the Bank of Israel, the ECB, the IMF, the St. Louis Fed, and every other federal data-producing agency in Washington—“getting it right”?
By creating the new OFR within the Treasury, the United States Congress has clearly recognized the existence of a Federal Reserve system-design problem. Through the OFR, the Dodd–Frank Act has taken away from the Fed part of its role in monitoring systemic risk. As this book documents, good reason does exist to be concerned about the role of the Federal Reserve in providing the needed information relevant to assessment of systemic risk. But the OFR has been concentrating primarily on disaggregated financial micro data about individual firms, rather than aggregated financial macro data about the economy as a whole. The financial crisis and the Great Recession were produced by excess risk-taking in response to underestimation of the systemic risk of the macroeconomy. The data relevant to inflation, unemployment, and recession are aggregated financial macro data.
By creating the OFR, the Dodd–Frank Act was critical of the Fed’s performance in reporting systemic-risk information to the Congress. But that reporting problem is not limited to financial micro data. The problem is even greater regarding financial macro data. A new BFS needs to exist to provide competently aggregated financial statistics. The BFS could be either within the Federal Reserve or within the OFR, but would need to be dedicated to economic measurement and should employ experts in index-number and aggregation theory. The BFS should have no authority over policy, since economic measurement is logically prior to use. The role of the BFS would be analogous to that of the BLS within the Department of Labor. Overlap between measurement and policy-use authority produces conflict of interest—a fundamental mechanism design defect violating incentive compatibility.
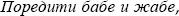 while in Welsh it takes the form mor wahanol â mêl a menyn. An equivalent Danish idiom is Hvad er højest, Rundetårn eller et tordenskrald? In Russian, the phrase
while in Welsh it takes the form mor wahanol â mêl a menyn. An equivalent Danish idiom is Hvad er højest, Rundetårn eller et tordenskrald? In Russian, the phrase 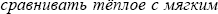 is used. In Argentina, a common question has that purpose: En qué se parecen el amor y el ojo del hacha? In Colombia, a similar version is well known: confundir la mierda con la pomada. In Polish, the expression co ma piernik do wiatraka? is used. In British English, the phrase chalk and cheese is used for that purpose instead of apples and oranges and perhaps makes the point more clearly.
is used. In Argentina, a common question has that purpose: En qué se parecen el amor y el ojo del hacha? In Colombia, a similar version is well known: confundir la mierda con la pomada. In Polish, the expression co ma piernik do wiatraka? is used. In British English, the phrase chalk and cheese is used for that purpose instead of apples and oranges and perhaps makes the point more clearly.