CHAPTER 14
	USING RADIOACTIVE ISOTOPES

OVERVIEW

In the geochemist’s arsenal of techniques for unraveling geological problems, the study of radioactive isotopes and their decay products has become very prominent. This chapter begins with a discussion of nuclide stability and decay mechanisms. After equations that describe radioactive decay are derived, we examine the utility of certain naturally occurring radionuclide systems (K-Ar, Rb-Sr, Sm-Nd, and U-Th-Pb) in geochronology. The concept of extinct radionuclides that were present in the early solar system is also discussed. The principles behind both mass spectrometry and fission track techniques are introduced. We discuss how induced radioactivity can be used to solve geochemical problems. Examples include neutron activation analysis, ⁴⁰Ar-³⁹Ar dating, and the use of cosmogenic nuclides (¹⁴C and ¹⁰Be) for dating geological and archeological materials and for detecting the subduction of sediments. We explore how radionuclides can be used as geochemical tracers in such global problems as determining when the Earth accreted and differentiated, quantifying mantle heterogeneity, assessing the cycling of material between crust and mantle, revealing global oceanic mixing patterns, and understanding degassing of the Earth’s interior to produce the atmosphere.

PRINCIPLES OF RADIOACTIVITY

Nuclide Stability

In chapter 13, we learned how stable isotopes can be used to solve geochemical problems. The study of unstable (that is, radioactive) nuclides, considered in this chapter, is also an extremely powerful technique. In chapter 2, we saw that only ∼260 of the 1700 known nuclides are stable, so we can infer that nuclide stability is the exception rather than the rule. Most of the known radioactive isotopes do not occur in nature. Although some of these may have occurred naturally in the distant past, their decay rates were so rapid that they have long since been transformed into other nuclides. In most cases, radioactive isotopes that are of interest to geochemists require very long times for decay or are produced continually by naturally occurring nuclear reactions.

In chapter 13, we explored how variations in stable isotopes are caused by mass fractionation during the course of chemical reactions or physical processes. With the exception of radioactive ¹⁴C and a few other nuclides, the atomic masses of most of the unstable isotopes of geochemical interest are very large, so that mass differences with other nuclides of the same element are minuscule. Consequently, these isotopic systems can be considered to be immune to mass fractionation processes. Thus, all of the measured variations in these nuclides are normally ascribed to radioactive decay.

Decay Mechanisms

Radioactivity is the spontaneous transformation of an unstable nuclide (the parent) into another nuclide (the daughter). The transformation process, called radioactive decay, results in changes in N (the number of neutrons) and Z (the number of protons) of the parent atom, so that another element is produced. Such processes occur by emission or capture of a variety of nuclear particles. Isotopes produced by the decay of other isotopes are said to be radiogenic. The radiogenic daughter may be stable or unstable; if it is unstable, the decay process continues until a stable nuclide is produced.

Beta decay involves the emission of negatively charged beta particles (electrons emitted by the nucleus), commonly accompanied by radiation in the form of gamma rays. This is equivalent to the transformation of a neutron into a proton and an electron. As illustrated in figure 14.1, Z increases by one and N decreases by one for each beta particle emitted.

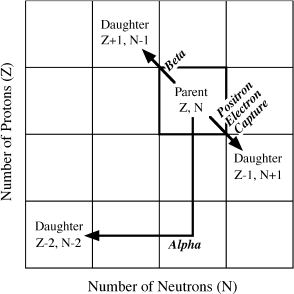
FIG. 14.1. A portion of the nuclide chart illustrating the N-Z relationships for daughter nuclides formed from a hypothetical parent by emission of beta particles, positrons, alpha particles, or by electron capture.

Another type of radioactivity occurs as a result of positron decay. A positron is a positively charged electron expelled from the nucleus. This process can be regarded as the conversion of a proton into a neutron, a positron, and a neutrino (a particle with appreciable kinetic energy, but without mass). Positron decay produces a nuclide with N increased by one and Z decreased by one, as illustrated in figure 14.1.

Inspection of figure 14.1 allows us to predict which nuclides tend to transform by beta decay or positron decay. Unstable atoms that lie below the band of stability (as seen in fig. 2.3), and therefore have excess neutrons, are likely to decay by emission of beta particles, so that their N values are reduced. Similarly, nuclides that lie above the band of stability, having excess protons, may experience positron decay. In each case, these processes occur in such a way that the resulting daughter nuclides fall within the band of nuclear stability.

An alternate type of decay mechanism is electron capture. In this process, the nuclide increases its N and decreases its Z by addition of an electron from outside the nucleus. A neutrino is also liberated during this process. The daughter nuclide produced during electron capture occupies exactly the same position relative to its parent in figure 14.1 as that produced during positron decay.

Alpha decay proceeds by the emission of heavy alpha particles from the nucleus. An alpha particle is composed of two neutrons and two protons. Therefore, the N and Z values for the daughter nuclide both decrease by two, as shown in figure 14.1.

To be complete, we should also add to this list of radioactive decay processes spontaneous fission, which is an alternate mode of decay for some heavy atomic nuclei. These atoms may break apart, because electrostatic repulsion between the Z positively charged protons overcomes the strong nuclear binding force. Fission products generally have excess neutrons and tend to decay further by beta emission. For most geochemical applications, fission can be considered a relatively minor side effect.

The decay of natural radionuclides may be much more complex than suggested by the simple decay mechanisms just introduced. A particular transformation may employ several of these decay mechanisms simultaneously, so that the parent atoms form more than one kind of daughter. Such a process is called branched decay. As an example, consider the decay of ⁴⁰K. Most atoms of the parent nuclide decay by positron emission and electron capture into ⁴⁰Ar, but ⁴⁰Ca is produced from the remainder by beta decay. Branched decay decreases the yield of daughter atoms of a particular nuclide, requiring more sensitivity in measurement.

Worked Problem 14.1

How many atoms of ⁴⁰Ar would be produced by the complete decay of ⁴⁰K in a 1 cm³ crystal of orthoclase? To answer this question, we must first calculate the number of atoms of parent ⁴⁰K in the sample. We can convert the volume of orthoclase to weight by multiplying by its density, and weight to moles by dividing by the gram formula weight of orthoclase:

1 cm³(2.59 g cm⁻³)/ 278.34 g mol⁻¹ = 9.30 × 10⁻³ mol.

Each mole of orthoclase contains one mole of potassium, so there are 9.30 × 10⁻³ moles of K in this sample. Multiplication of this result by Avogadro’s number gives the number of atoms of potassium:

9.30 × 10⁻³ mol (6.023 × 10²³ atoms mol⁻¹) = 5.60 × 10¹⁹ atoms.

The natural abundance of ⁴⁰K in potassium (before decay) is 0.01167%. Therefore, this orthoclase sample contains:

5.60 × 10¹⁹ atoms (1.167 × 10⁻⁴) = 6.535 × 10¹⁵ atoms ⁴⁰K.

We have already mentioned that ⁴⁰K undergoes branched decay, and we are concerned here with only one of the daughter nuclides. A total of 11.16% of the ⁴⁰K atoms decay into ⁴⁰Ar by electron capture and positron decay, the remainder transforming to ⁴⁰Ca. Consequently, the number of atoms of ⁴⁰Ar produced by complete decay is:

6.535 × 10¹⁵ (0.1116) = 7.293 × 10¹⁴ atoms ⁴⁰Ar.

Rate of Radioactive Decay

In each of the decay mechanisms just discussed, the rate of disintegration of a parent nuclide is proportional to the number of atoms present. In more quantitative terms, the number of atoms (because of convention, we use the symbol N, not to be confused with the symbol for the number of neutrons used in earlier paragraphs) remaining at any time t is:

−dN/dt = λN,

(14.1)

where λ is the constant of proportionality, usually called the decay constant. The value of the decay constant is characteristic for a particular radionuclide and is expressed in units of reciprocal time. Rearranging the terms of equation 14.1 and integrating gives:

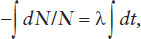
or

−ln N = λt + C,

(14.2)

where C is the constant of integration. If N = N₀ at time t = 0, then:

C = −ln N₀.

By substituting this value into equation 14.2, we obtain:

−ln N = λt − ln N₀,

or

ln N/N₀ = −λt.

This is more commonly expressed as:

N/N₀ = e^−λt.

(14.3)

Equation 14.3 is the basic relationship that describes all radioactive decay processes. With it, we can calculate the number of parent atoms (N) that remain at any time t from an original number of atoms (N₀) present at time t = 0.

We can also express this relationship in terms of atoms of the daughter nuclide rather than the parent. If no daughter atoms are present at time t = 0 and none are added to or lost from the system during decay, then the number of radiogenic daughter atoms produced by decay D* (not to be confused with the same symbol used for tracer diffusion coefficients in chapter 11) at any time t is:

D* = N₀ − N.

(14.4)

By rearranging equation 14.3 and substituting it into 14.4, we see that:

D* = Ne^λt − N,

or

D* = N(e^λt − 1).

(14.5)

Equation 14.5 gives the number of daughter atoms produced by decay at any time t as a function of parent atoms remaining. If some atoms of the daughter nuclide were present initially (D₀), then the total number of daughter atoms (D) is:

D = D₀ + D*.

Combining this equation with 14.5 produces the useful result:

D = D₀ + N(e^λt − 1).

(14.6)

This important equation is the basis for geochronology. Both D and N are measurable quantities, and D₀ is a constant whose value can be determined.

It is common practice to express radioactive decay rates in terms of half-lives. The half-life (t_1/2) is defined as the time required for one-half of a given number of atoms of a nuclide to decay. Therefore, when t = t_1/2, it follows that 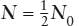. Substitution of these values into equation 14.3 gives:

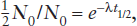
or

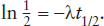
This is equivalent to:

ln 2 = λt_1/2.

Solving for t_1/2 gives:

t_1/2 = ln 2/λ = 0.693/λ.

(14.7)

Equation 14.7 expresses the relationship between the half-life of a nuclide and its decay constant.

The equations above show that the disintegration of a parent radioactive isotope and the generation of daughter nuclides are both exponential functions of time. This is illustrated in the following worked problem.

Worked Problem 14.2

Follow the decay of radioactive parent ⁸⁷Rb and the growth of daughter ⁸⁷Sr in a granite sample over the course of six half-lives. Assume that the granite sample initially contains 1.2 × 10²⁰ atoms of ⁸⁷Rb and 0.3 × 10²⁰ atoms of ⁸⁷Sr.

The half-life of ⁸⁷Rb is 48.8 × 10⁹ years. The decay constant for this radionuclide can be calculated by using equation 14.7:

λ = 0.693/(48.8 × 10⁹ yr) = 1.42 × 10⁻¹¹ yr⁻¹.

Using equation 14.3, we can determine the number of atoms (N) of parent ⁸⁷Rb remaining after one half-life:

N/(1.2 × 10²⁰) = e^{−(1.42 × 10−11)(48.8 × 109)},

or

N = 6.00 × 10¹⁹ atoms after one half-life.

To calculate the number of atoms of the parent nuclide remaining after two half-lives, we substitute for N₀ in the same equation the value of N just calculated:

N/6.00 × 10¹⁹ = e^{−(1.42 × 10−11)(48.8 × 109)},

or

N = 3.00 × 10¹⁹ atoms after two half-lives,

and so forth.

To calculate the number of atoms (D) of daughter ⁸⁷Sr after one half-life, we use equation 14.6:

D = 0.3 × 10²⁰ + 6.00 × 10¹⁹[e^{(1.42 × 10−11)(48.8 × 109)} − 1]

or

D = 9.00 × 10¹⁹ atoms after one half-life.

We follow a similar procedure for calculating daughter atoms after each successive half-life.

The easiest way to summarize these calculations is by means of a graph, plotting the number of atoms of parent (N) or daughter (D) versus time in units of half-life. This diagram is shown in figure 14.2. The exponential character of the radioactive decay is obvious. After six half-lives, N approaches zero asymptotically and, for most practical purposes, the production of daughter atoms ceases.

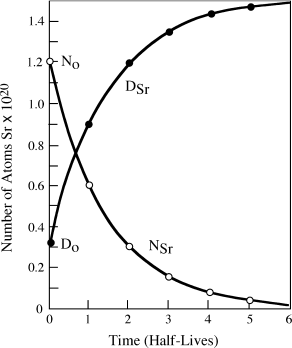
FIG. 14.2. The decay of radioactive ⁸⁷Sr (N) into its stable radiogenic daughter, ⁸⁷Rb (D), as a function of time measured in half-lives. N₀ and D₀ represent the initial number of atoms of parent and daughter, respectively.

Decay Series and Secular Equilibrium

The calculations above presume that a radioactive parent decays directly into a stable daughter. However, many radionuclides decay to a stable nuclide by way of transitory, unstable daughters; that is, a parent N₁ may decay to a radioactive daughter N₂, which in turn decays to a stable daughter N₃. Naturally occurring decay series arising from radioactive isotopes of uranium and thorium behave in this manner. For example, ²³⁸U produces 13 separate radioactive daughters before finally arriving at stable ²⁰⁶Pb, as illustrated in figure 14.3. Equations giving the number of atoms of any member of a decay series at any time t are presented in a text by Gunter Faure (1986), and will not be reproduced here. It is interesting, however, to examine the special case in which the half-life of the parent nuclide is very much longer than those of the radioactive daughters. In this situation, it can be shown that after some initial time interval has passed,

λ₁N₁ = λ₂N₂ = λ₃N₃ = λ_nN_n,

where λ_{1, 2, . . ., n} are the decay constants for each nuclide (N) in the series. This condition, in which the rate of decay of the daughters equals that of the parent, is known as secular equilibrium. It allows an important simplification of decay series calculations, because the system can be treated as if the original parent decayed directly to the stable daughter without intermediate steps. Secular equilibrium is assumed in uranium prospecting methods that utilize radiation measurements to calculate uranium abundances.

FIG. 14.3. Representation of the radioactive decay of ²³⁸U to ²⁰⁶Pb through a series of daughter isotopes. Alpha and beta particles produced at each step are labeled.

GEOCHRONOLOGY

One of the prime uses of radiogenic isotopes is, of course, to determine the ages of rocks. All radiometric dating systems assume that certain conditions are satisfied:

1. The system, which may be defined as the rock or as an individual mineral, must have remained closed so that neither parent nor daughter atoms were lost or gained except as a result of radioactive decay.
2. If atoms of the daughter nuclide were present before system closure, it must be possible to assign a value to this initial amount of material.
3. The value of the decay constant must be known accurately. (This is particularly critical for nuclides with long half-lives, because a small error in the decay constant will translate into a large uncertainty in the age.)
4. The isotopic compositions of analyzed samples must be representative and must be measured accurately.

PROSPECTING AND WELL-LOGGING TECHNIQUES THAT USE RADIOACTIVITY

Uranium prospecting tools rely principally on detection of gamma radiation, because alpha and beta particles cannot penetrate an overburden cover of even a few cm thickness. The Geiger counter is commonly used for field surveys, although it is a rather inefficient detector. The instrument consists of a sealed glass tube containing a cathode and anode with a voltage applied. The tube is filled with a gas that is normally nonconducting, but when gamma radiation passes through the gas, it is ionized and the ions accelerate toward the electrodes. The resulting current pulses are recorded on a meter or heard as “clicks.”

The scintillation counter is a more efficient tool for gamma ray detection. Certain kinds of crystals scintillate; that is, they emit tiny flashes of visible light when they absorb gamma radiation. These scintillations are detected by photomultiplier tubes and converted to electrical pulses that can be counted. This instrument can be used in either ground or airborne surveys.

A commonly used well-logging tool employs natural radioactivity to identify sedimentary lithologic boundaries in drill holes. The gamma ray log depends on scintillation detection of gamma rays produced by decay of ⁴⁰K and radioactive daughter products in the uranium and thorium decay series. These large ions are incompatible in most crystal structures, but are accommodated in clay minerals. Therefore, increases in gamma radiation are ascribed to clay concentrations (that is, shale formations) and, conversely, decreased radiation to cleaner sandstone or limestone units. An example of a portion of a gamma ray well log is shown in figure 14.4. Gamma rays from decay of any one nuclide have a particular energy, and the energy spectrum of this radiation is resolved in some gamma ray logs. This permits estimates to be made of the concentrations of potassium, uranium, and thorium (assuming secular equilibrium), and the K/U or K/Th ratios may serve as geochemical signatures for certain shale horizons, which may be useful in stratigraphic correlation.

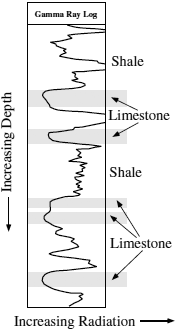
FIG. 14.4. An example of a gamma ray well log used in identifying sedimentary lithologic variations. The horizontal scale is radioactivity (increasing to the right) and the vertical scale is depth in the bore hole. Limestone horizons have low radioactivity relative to shale units because of lower contents of potassium, uranium, and thorium.

A number of naturally occurring radionuclides are in current use for geochronology; some of the most common are listed in table 14.1 and discussed below. Each of these is employed for its special properties, such as rate of decay, response to heating and cooling, or concentration range in certain rocks.

Potassium-Argon System

In worked problem 14.1, we have seen that radioactive ⁴⁰K undergoes branching decay to produce two different daughter products. Its decay into ⁴⁰Ca is not a useful chronometer, because ⁴⁰Ca is also the most abundant stable isotope of calcium. As a result, the addition of radiogenic ⁴⁰Ca increases its abundance only slightly. Even though ⁴⁰Ar is the most abundant isotope of atmospheric argon, potassium-bearing minerals do not commonly contain argon. The radioactive decay of ⁴⁰K can therefore be monitored through time by measuring ⁴⁰Ar.

TABLE 14.1. Radionuclides Commonly Used in Geochronology

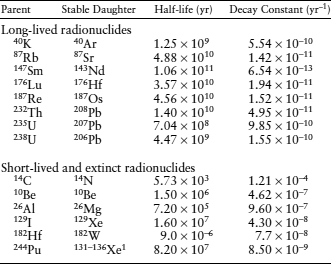
¹Many other fission products are also produced.

Each branch of the decay scheme has its own separate decay constant. The total decay constant λ is therefore the sum of these:

λ = λ_Ca + λ_Ar.

The commonly adopted value for the total decay constant and the corresponding half-life are given in table 14.1. The proportion of ⁴⁰K atoms that decay to ⁴⁰Ar is given by the ratio of decay constants, λ_Ar/(λ_Ar + λ_Ca), which has a value of 0.105.

We can use equation 14.6 to specify the increase in ⁴⁰Ar through time:

⁴⁰Ar = ⁴⁰Ar₀ + 0.105 ⁴⁰K(e^λt − 1).

Notice that N, the number of atoms of ⁴⁰K, has been multiplied by λ_Ar/(λ_Ar + λ_Ca) to correct for the fact that most of these atoms will decay to another daughter nuclide. Because most minerals initially contain virtually no argon, ⁴⁰Ar₀ = 0 and the equation reduces to:

⁴⁰Ar = 0.105 ⁴⁰K(e^λt − 1).

(14.8)

Application of equation 14.8 then requires only the measurement of ⁴⁰Ar and potassium in the sample; ⁴⁰K is calculated from total potassium using its relative isotopic abundance of 0.01167%.

The K-Ar system is useful for dating igneous and, in a few cases, sedimentary rocks. Sediments containing glauconite and certain clay minerals that formed during diagenesis may be suitable for K-Ar chronology. However, because the daughter isotope is a gas, it may diffuse out of many minerals, especially if they have been buried deeply or have protracted thermal histories. Metamorphism appears to reset the system in most cases, and K-Ar dates may record the time of peak metamorphism in cases for which cooling was relatively rapid. During slow cooling, argon diffusion continues until the system reaches some critical temperature (the blocking temperature), at which it becomes closed to further diffusion. Different minerals in the same rock may have different blocking temperatures and thus yield slightly different ages.

Rubidium-Strontium System

⁸⁷Rb produces ⁸⁷Sr by beta decay, at a rate given in table 14.1. Unlike the K-Ar system, the radiogenic daughter is added to a system that already contains some ⁸⁷Sr. Thus, the difficulty in applying this geochronometer lies in determining how much of the ⁸⁷Sr measured in the sample was produced by decay of the parent isotope.

For the Rb-Sr system, equation 14.6 takes the form:

⁸⁷Sr = ⁸⁷Sr₀ + ⁸⁷Rb(e^λt − 1).

Another isotope of strontium, ⁸⁶Sr, is stable and is not produced by decay of any naturally occurring isotope. If both sides of the equation are divided by the number of atoms of ⁸⁶Sr in the sample (a constant), we will not affect the equality:

⁸⁷Sr/⁸⁶Sr = ⁸⁷Sr₀/⁸⁶Sr + ⁸⁷Rb/⁸⁶Sr(e^λt − 1).

(14.9)

Let’s see how the initial ratio of ⁸⁷Sr₀/⁸⁶Sr in this equation, as well as the age, can be derived from graphical analysis of a suite of rock samples. Equation 14.9 is the expression for a straight line (of the form y = b + mx). We will construct a plot of ⁸⁷Sr/⁸⁶Sr versus ⁸⁷Rb/⁸⁶Sr; that is, y versus x, as shown in figure 14.5. Both of these ratios are readily measurable in rocks. We can assume that, at the time of crystallization (t = 0), all minerals in a given rock will have the same ⁸⁷Sr/⁸⁶Sr value, because they cannot discriminate between these relatively heavy isotopes. The various minerals will have different contents of rubidium and strontium, however, and thus different values of ⁸⁷Rb/⁸⁶Sr.

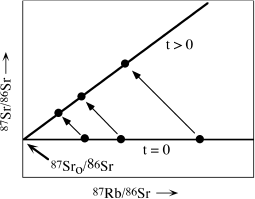
FIG. 14.5. Schematic Rb-Sr isochron diagram, illustrating the isotopic evolution of three samples with time. All samples have the same initial ⁸⁷Sr/⁸⁶Sr ratio but different ⁸⁷Rb/⁸⁶Sr ratios at time t = 0. The isotopic composition of each sample moves along a line of slope −1 as ⁸⁷Rb decays to ⁸⁷Sr. After some time has elapsed, the samples define a new isochron, the slope of which is (e^λt − 1). Extrapolation of this isochron to the abcissa gives the initial Sr isotopic composition.

This situation is illustrated schematically by the line labeled t = 0 in figure 14.5. After some time has elapsed, a fraction of the ⁸⁷Rb atoms in each mineral have decayed to ⁸⁷Sr. Obviously, the mineral that had the greatest initial concentration of ⁸⁷Rb now has the greatest concentration of radiogenic ⁸⁷Sr. The position of each mineral in the rock shifts along a line with a slope of −1, as shown by arrows in figure 14.5. The slope of the resulting straight line is (e^λt − 1), and its intercept on the y axis is the initial strontium isotopic ratio, ⁸⁷Sr₀/⁸⁶Sr. The diagonal line is called an isochron, and its slope increases with time. The fit of data points to a straight line is never perfect, and a linear regression is required. Analytical errors that lead to dispersion of data about the line give rise to corresponding uncertainties in ages.

Isochron diagrams such as figure 14.5 can be constructed by using data from coexisting minerals in the same rock (producing a mineral isochron) or from fractionated comagmatic rock samples that have concentrated different minerals to varying degrees (producing a whole-rock isochron). Metamorphism may rehomogenize rubidium and strontium isotopes, so that the timing of peak metamorphism may be recorded by this geochronometer. A mineral isochron is more likely than a whole-rock isochron to be reset by metamorphism, because it is easier to re-equilibrate adjacent minerals than different portions of a rock body. Diagenetic minerals in some sedimentary rocks may also have high enough rubidium contents that the age of burial and diagenesis can be determined using this system. The half-life of ⁸⁷Rb is long, so that this geochronometer complements the K-Ar system in terms of the accessible time range to which it can be applied.

Worked Problem 14.3

Larry Nyquist and his coworkers (1979) measured the following isotopic data for a whole-rock (WR) sample and for plagioclase (Plg), pyroxene (Px), and ilmenite (Ilm) mineral separates in an Apollo 12 lunar basalt (sample 12014).

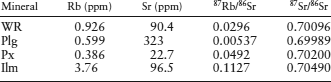
What is the age of this rock?

We can determine the age and the initial Sr isotopic ratio, ⁸⁷Sr₀/⁸⁶Sr, by plotting these data on an isochron diagram (fig. 14.6). A least-squares regression through the data can then be calculated, as illustrated by the diagonal line in the figure. The y intercept of this regression line corresponds to an initial isotopic ratio of 0.69964.

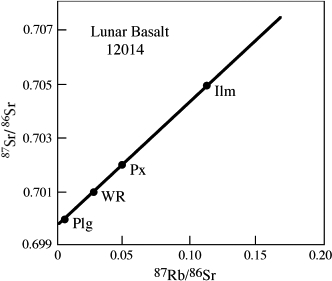
FIG. 14.6. Rb-Sr isochron for lunar basalt 12014. Isotopic data for the whole-rock (WR), pyroxene (Px), plagioclase (Plg), and ilmenite (Ilm) were obtained by Nyquist et al. (1979). The slope of this isochron corresponds to an age of 3.09 b.y.

Equation 14.9 can be solved for t:

t = 1/λ ln([(⁸⁷Sr/⁸⁶Sr − ⁸⁷Sr₀/⁸⁶Sr)]/(⁸⁷Rb/⁸⁶Sr) + 1).

(14.10)

If we now insert the initial Sr isotopic ratio and the measured isotopic data for one sample (we use WR) into this expression, we find:

t	= 1/(1.42 × 10−11) ln([(0.70096
	− 0.69964)/(0.0296)] + 1),

or

t = 3.09 b.y.

This age corresponds to the time that the minerals in the basaltic magma crystallized. It differs slightly from the age published by Nyquist and coworkers, because they used a different decay constant for ⁸⁷Rb than that given in table 14.1. The estimated uncertainty in age based on fitting the regression line is +0.11 billion years.

Samarium-Neodymium System

The rare earth elements samarium and neodymium form the basis for another geochronometer. ¹⁴⁷Sm decays to ¹⁴³Nd at a rate indicated in table 14.1. The complication in this system is the same as that in the Rb-Sr system; that is, some ¹⁴³Nd is already present in rocks before radiogenic ¹⁴³Nd is added, so we must find a way to specify its initial abundance. This can be done by graphical methods after normalizing parent and daughter to a stable, nonradiogenic isotope of neodymium (¹⁴⁴Nd), in the same way we normalized to ⁸⁶Sr in the Rb-Sr system. An expression for the Sm-Nd system analogous to equation 14.9 can then be written:

143Nd/144Nd	= 143Nd0/144Nd
	+ 147Sm/144Nd(eλt − 1),

where the subscript 0 indicates the initial isotopic composition of neodymium at the time of system closure. On an isochron plot of ¹⁴³Nd/¹⁴⁴Nd versus ¹⁴⁷Sm/¹⁴⁴Nd, the y intercept is the initial isotopic ratio ¹⁴³Nd₀/¹⁴⁴Nd and the slope of the line becomes steeper with time.

The Sm-Nd radiometric clock is analogous in its mathematical form to that of the Rb-Sr system, but the two systems are applicable to different kinds of rocks. Basalts and gabbros usually cannot be dated precisely using the Rb-Sr system, because their contents of rubidium and strontium are so low. The Sm-Nd system is ideal for determination of the crystallization ages of mafic igneous rocks. This system may also be useful, in some cases, to “see through” a metamorphic event to the earlier igneous crystallization. Because both parent and daughter are relatively immobile elements, they are less likely to be disturbed by later thermal overprints.

Uranium-Thorium-Lead System

The U-Th-Pb system is actually a set of independent geochronometers that depend on the establishment of secular equilibrium. ²³⁸U decays to ²⁰⁶Pb, ²³⁵U to ²⁰⁷Pb, and ²³²Th to ²⁰⁸Pb, all through independent series of transient daughter isotopes. The half-lives of all three parent isotopes are much longer than those of their respective daughters, however, so that the prerequisite condition for secular equilibrium is present and the production rates of the stable daughters can be considered to be equal to the rates of decay of the parents at the beginning of the series. The half-lives and decay constants for the three parent isotopes are given in table 14.1. We refer to the decay constant for ²³⁸U as λ₁, that for ²³⁵U as λ₂, and that for ²³²Th as λ₃.

In addition to these three radiogenic isotopes, lead also has a nonradiogenic isotope (²⁰⁴Pb) that can be used for reference. (²⁰⁴Pb is actually weakly radioactive, but it decays so slowly that it can be treated as a stable reference isotope.) We can express the isotopic composition of lead in minerals containing uranium and thorium by the following equations, analogous to equations 14.9 and 14.11:

206Pb/204Pb	= 206Pb0/204Pb
	+ 238U/204Pb (eλ1t − 1), (14.12a)

207Pb/204Pb	= 207Pb0/204Pb
	+ 235U/204Pb (eλ2t − 1), (14.12b)

208Pb/204Pb	= 208Pb0/204Pb
	+ 232Th/204Pb (eλ3t − 1). (14.12c)

The subscript 0 in each case denotes an initial lead isotopic composition at the time the clock was set.

Each of these isotopic systems gives an independent age. In an ideal situation, the dates should all be the same. In many instances, though, these dates are not concordant, because the minerals do not remain completely closed to the diffusion of uranium, thorium, lead, or some of the intermediate daughter nuclides. To simplify this complicated situation, let’s consider a system without thorium, so that we have to deal with only two radiogenic lead isotopes. From equation 14.5, we know that the amount of radiogenic ²⁰⁶Pb at any time must be:

²⁰⁶Pb* = ²³⁸U(e^λ₁t − 1),

or

²⁰⁶Pb*/²³⁸U = e^λ₁t − 1,

(14.13a)

where the superscript * denotes radiogenic lead; that is, ²⁰⁶Pb − ²⁰⁶Pb₀. Similarly, the amount of radiogenic ²⁰⁷Pb at any time can be expressed as:

²⁰⁷Pb*/²³⁵U = e^λ₂t − 1.

(14.13b)

If a uranium-bearing mineral behaves as a closed system, we know that equations 14.13a and 14.13b should yield concordant ages (that is, the same value of t). Logically, then, we can reverse the procedure and calculate compatible values for ²⁰⁶Pb*/²³⁸U and ²⁰⁷Pb*/²³⁵U at any given time t. Figure 14.7 shows the results of such a calculation. The curve labeled concordia in this figure represents the locus of all concordant U-Pb systems.

At the time of system closure (t₀), no decay has occurred yet, so there is no radiogenic lead present. The system’s isotopic composition, therefore, plots at the origin of figure 14.7. At any time thereafter, the system is represented by some point along the concordia curve; numbers along the curve indicate the elapsed time in billions of years since formation of the system. If, instead, the system experiences loss of lead at time t₁, the system’s composition shifts along a chord connecting t₁ to the origin. A complete loss of radiogenic lead would displace the isotopic composition all the way back to the origin, but this rarely happens. If some fraction of lead is lost, as is the more common situation, the system composition is represented by a point (such as x) along the chord. A series of related samples with discordant ages that have experienced varying degrees of lead loss will define the chord, called a discordia curve, more precisely. After the disturbing event, each point x on the discordia evolves along a path similar in form but not coincident with the concordia curve.

The result is that the discordia curve retains its linear form but changes slope, intersecting the concordia curve at a new set of points. The time of lead loss is translated along the concordia curve to t₃, and t₀ is similarly translated to t₂, the overall effect being a rotation of discordia about point x. This is illustrated by the dashed discordia curve in figure 14.7.

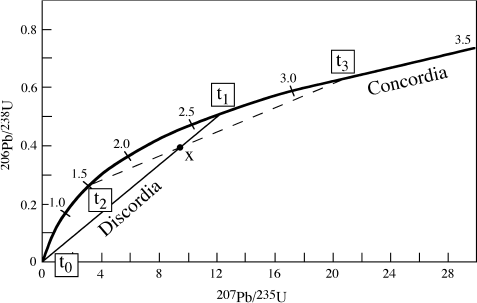
FIG. 14.7. Concordia diagram comparing isotopic data for two U-Pb systems. An undisturbed system formed at time t₀ will move along the concordia curve; the age at any time after formation is indicated by numbers (in billions of years) along the curve. If episodic lead loss occurs at time t₁, the position of the system will be displaced toward the origin by some amount, as illustrated by point x. Other samples that lose different amounts of lead are displaced along the same chord and give discordant dates. With further elapsed time, the discordia line will subsequently be rotated (dashed line) as t₀ moves to t₂ and t₁ moves to t₃.

If the discordia chord can be adequately defined, then this diagram may yield two geologically useful dates: the time of formation of the rock unit (t₂), and the time of a subsequent disturbance (possibly metamorphism or weathering) that caused lead loss (t₃). This interpretation assumes that loss of lead was instantaneous; if lead was lost by continuous diffusion over a long period of time, then t₃ is a fictitious date without geologic significance. Unfortunately, it is not possible to distinguish between these alternatives without other geological information.

It is possible to compensate for the effect of lead loss on U-Pb ages by calculating ages based on the ²⁰⁷Pb/²⁰⁶Pb ratio. This ratio is, of course, insensitive to lead mobilization, because it is practically impossible to fractionate isotopes of the same heavy element. By combining equations 14.12a and 14.12b, we obtain:

(²⁰⁷Pb/²⁰⁴Pb − ²⁰⁷Pb₀/²⁰⁴Pb)/(²⁰⁶Pb/²⁰⁴Pb − ²⁰⁶Pb₀/²⁰⁴Pb) = (²³⁵U[e^λ₂t − 1])/(²³⁸U[e^λ₁t − 1]).

(14.14a)

The left side of this equation is equivalent to the ratio of radiogenic ²⁰⁷Pb to radiogenic ²⁰⁶Pb; that is, to (²⁰⁷Pb/²⁰⁶Pb)*. This is determined by subtracting initial ²⁰⁷Pb/²⁰⁴Pb and ²⁰⁶Pb/²⁰⁴Pb values from the measured values for these ratios. Consequently, ages can be determined solely on the basis of the isotopic ratios in the sample, without having to determine lead concentrations. Moreover, because the ratio ²³⁵U/²³⁸U is constant (1/137.8) for all natural materials at the present time, ages can be calculated without measuring uranium concentrations. Equation 14.14a can therefore be expressed as:

(²⁰⁷Pb/²⁰⁶Pb)* = 1/137.8([e^λ₂t − 1]/[e^λ₁t − 1]).

(14.14b)

This is the expression for the ²⁰⁷Pb/²⁰⁶Pb age, also called the lead-lead age. The only difficulty in applying this method is that equation 14.14b cannot be solved for t by algebraic methods. However, the equation can be iteratively solved by a computer method of successive approximations until a solution is obtained within an acceptable level of precision.

The U-Th-Pb dating system is applicable to rocks containing such minerals as zircon, apatite, monazite, and sphene. These phases provide large structural sites for uranium and thorium. Igneous or metamorphic rocks of granitic composition are most suitable for dating by this method. Several generations of zircons, recognizable by distinct morphologies, have been found to give distinct ages in some rocks, and measurements of U-Th-Pb ages in zoned zircons using ion microprobes have shown overgrowths with younger ages. The possibility of minerals inherited from earlier events or affected by later events further complicates the interpretation of U-Th-Pb ages.

Worked Problem 14.4

John Aleinikoff and coworkers (1985) measured the following lead isotopic data for a zircon from a granitic pluton in Maine (units are atom %): ²⁰⁴Pb = 0.010, ²⁰⁶Pb = 90.6, ²⁰⁷Pb = 4.91, ²⁰⁸Pb = 4.43. The measured U concentration was 1396 ppm, and that for Pb was 62.2 ppm. What are the ²⁰⁶Pb/²³⁸U, ²⁰⁷Pb/²³⁵U, and ²⁰⁷Pb/²⁰⁶Pb ages for this rock, and are they concordant?

We begin by determining the proportions of ²³⁵U and ²³⁸U in this sample. All natural uranium has ²³⁵U/²³⁸U = 1/137.8, corresponding to 99.27% ²³⁸U. Aleinikoff and coworkers assumed that the nonradiogenic lead in this sample had isotopic ratios of 204:206:207:208 = 1:18.2:15.6:38, corresponding to an average atomic weight of 207.23. From these proportions, we can calculate the following ratios:

238U/204Pb	= (1396/62.2)(207.23/238.03)(99.27/0.010)
	= 193,970,
235U/204Pb	= 193,970/137.8 = 1407.6,
206Pb/204Pb	= (90.6/0.010) − 18.2 = 9041.8,
207Pb/204Pb	= (4.91/0.010) − 15.6 = 475.4,
206Pb0/204Pb	= 18.2,
207Pb0/204Pb	= 15.6.

We can now insert values into equation 14.12 and solve for t. The expression for the ²⁰⁶Pb/²³⁸U age, corresponding to equation 14.12a, is:

t206 =	1/λ1 ln([(206Pb/204Pb)
	− (206Pb0/204Pb)]/[238U/204Pb] + 1).

Substitution of the ratios above into this equation gives:

t206 =	1/(1.55 × 10−10) ln([9041.8 − 18.2]/[193,970]
	+ 1) = 293 m.y.

The ²⁰⁷Pb/²³⁵U age, calculated from the analogous expression derived from equation 14.12b, is:

t207 =	1/(9.85 × 10−10) ln([475.4 − 15.6]/[1407.6] + 1)
	= 287 m.y.

Subtracting the initial ratios for the isotopic composition of nonradiogenic lead gives:

²⁰⁷Pb/²⁰⁴Pb = 491 − 15.6 = 475.4,

and

²⁰⁶Pb/²⁰⁴Pb = 9060 − 18.2 = 9041.8.

Dividing these results gives:

(²⁰⁷Pb/²⁰⁶Pb)* = 475.4/9041.8 = 0.0526.

We substitute this ratio into equation 14.14b and solve for t to find that the ²⁰⁷Pb/²⁰⁶Pb age is 308 m.y.

These ages are similar and date the approximate time of crystallization of the pluton. This sample would plot on the concordia curve, because ages determined by both U-Pb systems are nearly identical.

Extinct Radionuclides

All of the naturally occurring radionuclides that we have considered so far have very long half-lives, so that most of the parent isotopes still occur naturally on the Earth. However, some terrestrial rock samples and meteorites contain evidence of the former presence of now extinct radionuclides that had short half-lives. The stable daughter products and rates of decay for ²⁶Al, ¹²⁹I, ¹⁸²Hf, and ²⁴⁴Pu are given in table 14.1. That these isotopes occurred at all as “live” radionuclides demands that the samples that contain them formed very soon after the nuclides were created. In worked problem 14.5, we see how decay of now extinct ¹⁸²Hf can be used as a geochronological tool. Because of rapid decay rates, a few extinct radionuclides such as ²⁶Al may have been important sources of heat during the early stages of planet formation. The implications of the former presence of ²⁶Al and ¹⁸²Hf in meteorites will be considered in chapter 15.

Worked Problem 14.5

How can the now extinct radionuclide ¹⁸²Hf be used to constrain the time of core formation in the Earth? ¹⁸²Hf decays to ¹⁸²W with a half-life of only 9 million years, so any ¹⁸²Hf present in the early Earth has long since decayed. Hafnium is partitioned into silicates (that is, it is lithophile), and tungsten is concentrated in metal (it is siderophile). Consequently, tungsten was partitioned into the Earth’s core when it separated from the mantle. If core separation happened after ¹⁸²Hf had decayed, then all of the daughter ¹⁸²W would have been sequestered in the core. If the core formed while ¹⁸²Hf was still alive, however, this nuclide would have remained in the silicate mantle, and its subsequent decay would have produced an excess of radiogenic ¹⁸²W relative to nonradiogenic ¹⁸⁴W in the mantle. An anomalous ¹⁸²W/¹⁸⁴W ratio in the mantle would then be passed on to basaltic magmas derived from it.

Geochemists Alex Halliday and Der-Chuen Lee (1999) compared the tungsten isotopic composition in terrestrial silicate rocks with those measured in meteorites (fig. 14.8). In figure 14.8, tungsten isotopes are expressed as ε_w, defined as the deviation between ¹⁸²W/¹⁸⁴W in a sample relative to that ratio in a chondrite of identical age. The ¹⁸²W/¹⁸⁴W ratio in the Earth is indistinguishable from that of chondritic meteorites that have never experienced metal fractionation. However, iron meteorites, which are samples of the cores of differentiated asteroids, exhibit ¹⁸²W deficits. The absence of excess ¹⁸²W in the silicate portion of the Earth suggests that the Earth’s core formation must have happened many ¹⁸²W half-lives after core formation in asteroids. Based on the elapsed time that would be necessary to resolve a ¹⁸²W/¹⁸⁴W ratio higher than in chondrites, Halliday and Lee estimated that core formation in the Earth occurred >50 m.y after the formation of iron meteorites. A recent revision in the initial ratio of ¹⁸²Hf to stable ¹⁸⁰Hf (Yin et al. 2002) indicates a value half that assumed by Halliday and Chuen, which lowers the time of formation of the Earth’s core to 29 m.y.

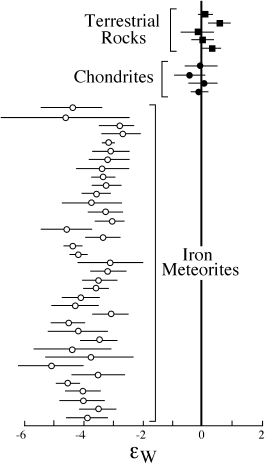
FIG. 14.8. The isotopic composition of tungsten (¹⁸²W/¹⁸⁴W), expressed as ε_w values, of terrestrial samples compared with those of meteorites. Terrestrial values are indistinguishable from those of carbonaceous chondrites, which have never experienced metal fractionation, but are distinct from iron meteorites, which formed as differentiated cores in asteroids. These data suggest that core formation in the Earth occurred after ¹⁸²Hf had decayed to ¹⁸²W, so that no excess radiogenic tungsten was produced in the mantle. (After Halliday and Lee 1999.)

Fission Tracks

If you have examined micas or cordierite under the petrographic microscope, you may have noticed zones of discoloration around tiny inclusions of zircon and other uranium-bearing minerals. These pleochroic haloes are manifestations of radiation damage produced by alpha particles. The crystal lattices of minerals that contain dispersed uranium atoms also record the disruptive passage of alpha particles in the form of fission fragments. The fragments are very small, but they nevertheless produce fission tracks as they pass through the host mineral. Although the tracks are only ∼10 microns long, they can be enlarged and made optically visible by etching with suitable solutions, because the damaged regions are more soluble than the unaffected regions. A microscopic view of fission tracks can be seen in figure 14.9. The density of fission tracks in a given area of sample can be determined by counting the tracks under a microscope.

These tracks, except in rare instances, are produced solely by spontaneous fission of ²³⁸U. The observed track density is proportional to the concentration of ²³⁸U in the sample and to the amount of time over which tracks have been accumulating; that is, the age of the host mineral. If a means can be found to measure the uranium concentration in the sample, fission tracks can then be used for geochronology. The uranium abundance can be determined by measuring the density of tracks induced by irradiating the sample in a reactor, where bombardment with neutrons causes more rapid decay (induced radioactivity is explained more fully in the next section). P. B. Price and Robert Walker (1963) formulated a solution for the fission track age equation (presented here without derivation):

t = ln(1 + [ρ_s/ρ_I][λ₂ϕσU/λ_F])1/λ₂.

Explaining the terms in this equation illustrates how a fission track age is determined. λ₂ and λ_F are the decay constants for ²³⁸U and spontaneous fission (8.42 × 10⁻¹⁷ yr⁻¹), respectively. The area density of fission tracks in the sample, ρ_s, is a function of age and uranium content. We noted earlier that the age can be determined uniquely if the uranium content can be measured. Uranium concentration is measured by placing the sample (after ρ_s has been visually counted) into a nuclear reactor, which induces rapid ²³⁸U decay and increases the number of fission tracks in the sample. The remaining terms in the equation above are related to this irradiation process: ρ_i is the area density of induced tracks, ϕ is the flux of neutrons passed through the sample, σ is the target cross section for the induced fission reaction, and U is the (constant) atomic ratio ²³⁵U/²³⁸U.

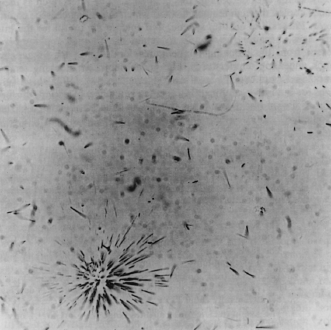
FIG. 14.9. Photomicrograph of fission tracks in mica. Radiating tracks emanate from point sources, such as small zircon inclusions; isolated tracks probably formed from single U or Th atoms. (Courtesy of G. Crozaz.)

Annealing of the sample at elevated temperatures causes fission tracks to fade, as the damage done to the crystal structure is healed. The annealing temperatures for most minerals used in fission track work are quite modest (several hundred degrees Centigrade or less), so the ages derived by this method must be interpreted as times the host rocks cooled through temperatures at which annealing ceased, commonly called cooling ages. Such phases as apatite, sphene, and epidote are useful for the interpretation of cooling histories, and they begin to retain fission tracks at temperatures that are different from the blocking temperatures for argon isotopes. Fission track annealing temperatures, like radiogenic isotope blocking temperatures, can be extrapolated from experimental data. The determination of cooling history using a combination of fission tracks and other isotopic methods is illustrated in the following worked problem.

Worked Problem 14.6

How can we determine cooling history from isotope blocking temperatures and fission track retention ages? The elucidation of cooling history usually requires integration of several different kinds of data, tempered with thoughtful geologic reasoning. D. L. Nielson and coworkers (1986) characterized the temperature history of a Cenozoic pluton in Utah in the this way. Critical observations for their interpretation of the cooling history are:

1. The K-Ar age of a hornblende sample from the pluton is 11.8 million years. The argon blocking temperature for hornblende is ∼525° C.
2. The K-Ar age of a biotite sample from the pluton is 10.8 million years. The argon blocking temperature for biotite is ∼275° C.
3. The fission track ages for zircons in these rocks range from 8.3 to 8.9 million years. The temperature at which zircon begins to retain tracks depends on the cooling rate, but is generally ∼175° C.
4. The fission track ages for apatites range from 8.1 to 9.1 million years. Apatite begins to retain tracks at ∼125° C.

Using these data, we can construct a temperature versus time plot that describes the cooling history of this pluton (fig. 14.10). We can also speculate about geologic controls on the cooling path. The temperature-time curve in figure 14.10 implies that this body cooled from >500° C through ∼100° C within a span of only 4 million years. This rapid cooling could not have taken place very deep in the crust and must indicate uplift and erosion. Nielson and coworkers calculated that uplift proceeded at a rate between 0.6 and 1.1 mm yr⁻¹ for this interval, based on an assumed geothermal gradient of 30° km⁻¹.

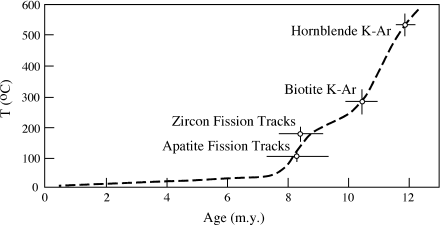
FIG. 14.10. The cooling history of an igneous pluton, inferred from argon blocking temperatures for hornblende and biotite and fission track ages for zircon and apatite. (Data reported by Nielson et al. 1986.)

GEOCHEMICAL APPLICATIONS OF INDUCED RADIOACTIVITY

In medieval times, alchemists toiled endlessly to turn various metals into gold. They were unsuccessful, but only because they did not know about nuclear irradiation. It is now possible to make gold, but it is still not economical, because the starting material must be platinum.

Nuclei that are bombarded with neutrons, protons, or other charged particles are transformed into different nuclides. In many cases, the nuclides produced by such irradiation are radioactive. Monitoring their decay provides useful analytical information. Nuclear irradiation can occur naturally or can be induced artificially. Here we consider some geochemical applications of both situations.

Neutron Activation Analysis

Nuclear reactions caused by neutron bombardment are commonly used to perform quantitative analyses of trace elements in geological samples. Fission of ²³⁵U in a nuclear reactor produces large quantities of neutrons, which can be used to induce nuclear changes in mineral or rock samples. Slow neutrons are readily absorbed by the nuclei of most stable isotopes, transforming them into heavier elements. Because many of the irradiation products are radioactive, this procedure is called neutron activation.

In earlier sections, we described radioactivity in terms of N, the number of atoms remaining. In neutron activation analysis, radioactivity is monitored using activity (A), defined as:

A = cλN,

(14.15)

where c is the detection coefficient (determined by calibrating the detector) and λN is the rate of decay. The easiest way to determine the concentration of an element by neutron activation is by irradiating a standard containing a known amount of that element at the same time as the unknown. After irradiation, the activities of both standard and unknown are measured at intervals using a scintillation counter to detect emitted gamma rays. (This step may be complicated for geological samples because they contain so many elements. It is necessary to screen out radiation at energies other than that corresponding to the decay of interest. This can normally be done by adjusting the detector to filter unwanted gamma radiation but, in some cases, chemical separations may be required to eliminate interfering radioactivities.) The activities are then plotted, as shown in figure 14.11; the exponential decay curves are transformed into straight lines by plotting ln A. Extrapolation of these lines back to zero time gives values of A₀, the activities when the samples were first removed from the reactor. The amount of element X in the unknown can then be determined from the following relationship:

A_{0 unkn}/A_{0 stnd} = amount of X_unkn/ amount of X_stnd.

The concentration of element X in the unknown can be calculated by dividing its amount by the measured weight of sample.

It is also possible to calculate A₀ theoretically by using the following relationship:

A₀ = cN₀ϕσ(l − e^−λt_i),

(14.16)

where c is the detection coefficient, N₀ is the number of target nuclei, ϕ is the neutron flux in the reactor, σ is the neutron capture crosssection of target nuclei, and t_i is the time of irradiation. This computation, normally done by computer, makes it easier to handle many elements simultaneously in complex samples.

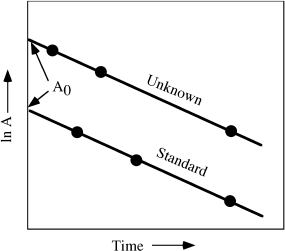
FIG. 14.11. Plot of the measured activity A of an unknown and a standard after neutron irradiation, as a function of time. Extrapolation of these straight lines gives A₀, the activity at the end of irradiation. These data are then used to determine the concentration of the irradiated element in the unknown.

⁴⁰Argon-³⁹Argon Geochronology

One of the disadvantages of the K-Ar geochronometer is that gaseous argon tends to diffuse out of many minerals, even at modest temperatures. Loss of the radiogenic daughter can thus lead to an erroneously young radiometric age. ⁴⁰Ar-³⁹Ar measurements provide a way to get around the problem of argon loss. Let’s examine how this technique works.

We might expect that the rims of crystals would lose argon more readily than the crystal interiors because of shorter diffusion distances. In this case, the ratio of radiogenic ⁴⁰Ar to ³⁹K, a stable isotope of potassium, will be highest in crystal centers and lower in crystal rims. Irradiating the sample with neutrons in a reactor causes some ³⁹K to be converted to ³⁹Ar. Consequently, the ratio ⁴⁰Ar/³⁹K becomes ⁴⁰Ar/³⁹Ar, which is readily analyzed using mass spectrometry.

The number of ³⁹Ar atoms produced during the irradiation is given by:

(14.17)

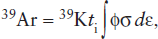
where t_i is the irradiation time, ϕ is the neutron flux in the reactor, σ is the neutron capture cross section, and the integration is carried out over the neutron energy spectrum dε. The number of radiogenic ⁴⁰Ar atoms produced by decay of ⁴⁰K is given by equation 14.8. Dividing equation 14.8 by 14.17 gives the ⁴⁰Ar/³⁹Ar ratio in the sample after irradiation:

(14.18)

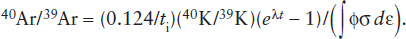
Because equation 14.18 can be solved for t, measurement of the ⁴⁰Ar/³⁹Ar ratio of a sample defines its age.

In practice, the sample is heated incrementally, and the isotopic composition of argon released at each temperature step is measured. Figure 14.12 illustrates a series of ⁴⁰Ar/³⁹Ar ages, calculated using equation 14.18, for samples of mica and amphibole in a blueschist sample from Alaska, as a function of total ³⁹Ar released. Each step represents a temperature increment of 50°, starting at 550° C. If this sample had remained closed to argon loss since its formation, all of the ages would have been the same. The spectrum of ages that we see in figure 14.12 results from ⁴⁰Ar leakage over time. Argon from the cores of crystals is released at the higher temperature steps, and the plateau of ages at ∼185 million years seen at high temperatures represents the time of metamorphism for this sample, because the mica blocking temperature is approximately equal to the peak metamorphic temperature.

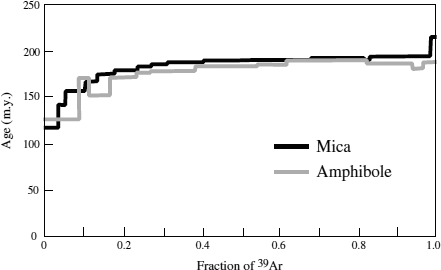
FIG. 14.12. ⁴⁰Ar-³⁹Ar age versus cumulative ³⁹Ar released for mica and amphibole samples from blueschist. The argon was released at successive temperature steps; each step in this figure corresponds to a 50° increment, starting at 550°C. The plateau of ages at 185 million years corresponds to radiogenic argon from the interiors of crystals. (After Sisson and Onstott 1986.)

Cosmic-Ray Exposure

In both of the examples we have just considered, the samples were irradiated intentionally by humans. Natural irradiation can also have useful geochemical applications. Cosmic rays, consisting mostly of high energy protons but also of neutrons and other charged particles generated in the Sun and outside the Solar System offer a natural irradiation source. Isotopes produced by interaction of matter with cosmic rays are called cosmogenic nuclides.

Radioactive ¹⁴C is produced continuously in the atmosphere by the interaction of ¹⁴N and cosmic rays. This isotope is then incorporated into carbon dioxide molecules, which in turn enter plant tissue through photosynthesis. The concentration of cosmogenic ¹⁴C in living plants (and in the animals that eat them) is maintained at a constant level by atmospheric interaction and isotope decay. When the plant or animal dies, addition of ¹⁴C from the atmosphere stops, so its concentration decreases due to decay. Measurement of the activity of ¹⁴C in plant or animal remains thus provides a way to determine the time elapsed since death.

The activity A of carbon from a plant or animal that died t years ago is given by:

A = A₀e^−λt.

(14.19)

where A₀ is the ¹⁴C activity during life = 13.56 dpm g⁻¹(expressed as disintegrations per minute per gram of sample), and the decay constant λ is given in table 14.1. (Compare equations 14.19 and 14.15. Both express activity in terms of λN times a constant, c or A₀.) Radiocarbon ages have only a limited geologic range because of the short half-life of ¹⁴C, but they are very useful for archaeological dating and for some environmental geochemistry applications.

Cosmic rays sometimes fragment other nuclides, a process called spallation. ¹⁰Be and ²⁶Al are spallation products formed from oxygen and nitrogen in the atmosphere. Both are rapidly transferred to the oceans or to Earth’s surface in rain or snow, where they can be incorporated into sediments on the ocean floor or into continental ice sheets. After deposition, these cosmogenic nuclides decay at rates given in table 14.1, so they can be used to date sediment or ice cores.

Rocks and soils at the Earth’s surface are also exposed to cosmic rays, so the accumulation of cosmogenic nuclides in them can be used to measure the durations of sample exposure. These time intervals, called cosmic ray exposure ages, assess how long materials were situated on the Earth’s surface, because a meter or more of overburden effectively shields out cosmic rays. Measured concentrations of cosmogenic nuclides are converted to exposure ages by knowing nuclide production rates, which can be determined experimentally. Quartz is an especially favorable target for measurement of cosmogenic ¹⁰Be and ²⁶Al because of its simple chemistry, resistance to weathering, and common occurrence in many kinds of rocks. By measuring exposure ages, it is possible to quantify the rates of uplift and erosion. In a later section, we see how cosmogenic ¹⁰Be can be employed as a tracer for the subduction of surface materials into the mantle and as a way of constraining subduction rates.

RADIONUCLIDES AS TRACERS OF GEOCHEMICAL PROCESSES

In biological research, certain organic molecules may be “tagged” with a radioactive isotope so that their participation in reactions or progress through an organism can be followed. Radionuclide tracers can be used in an analogous way to understand geochemical processes that have already taken place within the Earth. This usually requires a knowledge of the geochemical behavior of parent and daughter elements. In this section, we consider several examples of the use of these tracers.

Heterogeneity of the Earth’s Mantle

We have already noted that most radioactive nuclides and their decay products cannot be fractionated by mass. However, radioactive isotopes generally have very different solid-liquid distribution coefficients from their stable daughter isotopes, so that partial melting can fractionate radioactive elements from their radiogenic daughters. As melts have been progressively extracted from the mantle to form the crust, the abundances of radioactive isotopes in these reservoirs have changed, and these differences have been magnified by subsequent decay of the fractionated radioactive isotopes. The resulting isotopic heterogeneity within the mantle can be monitored by analyzing magmas that are derived from different mantle depths.

Samarium and neodymium are partitioned differently between the continental crust and mantle. Although both elements are incompatible and thus are fractionated into the crust, neodymium is more incompatible and so is ∼25 times more abundant in the crust than in the mantle, whereas samarium is only ∼16 times more abundant. This means that the Sm/Nd ratio is higher in the mantle than in the crust. ¹⁴⁷Sm decays to ¹⁴³Nd over time, so the ratio of radiogenic ¹⁴³Nd to nonradiogenic ¹⁴⁴Nd changes in both crust and mantle. It is thought that the mantle originally contained samarium and neodymium in the same relative proportion as in chondritic meteorites. The deviation between ¹⁴³Nd/¹⁴⁴Nd measured in a mantle-derived rock and the same ratio in a chondrite of identical age is called ε_Nd (analogous to ε_W, defined in worked problem 14.5) and can be used to estimate the degree to which the mantle may have evolved from its original pristine state.

Similar arguments can be used to trace the evolution of the ⁸⁷Sr/⁸⁶Sr ratio, which is related to the Rb/Sr ratio through the decay of ⁸⁷Rb to ⁸⁷Sr. In this case, rubidium is more incompatible than strontium, so the Rb/Sr ratio is higher in the crust and the crust becomes more radiogenic over time—the opposite of the Sm-Nd system. The isotopic composition of strontium can also be expressed as ε_Sr.

If basalts are derived from melting of mantle material, their initial neodymium and strontium isotopic ratios should be the same as those of their mantle sources at the time of melting. Measured ε_Nd and ε_Sr values for young basalts from various tectonic settings are summarized in figure 14.13. Midocean ridge basalts (MORB) have positive ε_Nd and negative ε_Sr values; that is, they have high ¹⁴³Nd/¹⁴⁴Nd ratios and low ⁸⁷Sr/⁸⁶Sr ratios that are complementary to those of continental crust. From this, we infer that the upper mantle source regions for MORB have been depleted of materials used to form the continents. Ocean island basalts plot along an extension of the MORB trend in figure 14.13, defining what is commonly called the mantle array. The position of ocean island basalts in the diagram indicates that their source is less depleted than that of MORB. These basalts also show a wider range in isotopic composition. Ocean island basalts may be derived from the relatively undepleted lower mantle and are carried through the upper mantle in plumes, where they mix to varying degrees with depleted materials. Magmas in subduction zones (not shown in fig. 14.13) often plot off the mantle array, reflecting the effects of mixing of seawater expelled from the subducted slab and crustal materials during ascent.

NATURAL NUCLEAR REACTORS

Certain heavy nuclides (²³⁵U being the only naturally occurring example) are fissile; that is, on absorbing a neutron, they split into two nuclear fragments of unequal mass. Because fission is exothermic, it is the energy source for nuclear power reactors and for the atomic bomb. When ²³⁵U fissions, it releases additional neutrons that collide with other ²³⁵U nuclei, prompting further fission reactions. The nuclides produced by fission have higher ratios of N to Z than stable nuclides and are thus radioactive. This process is used to advantage in the design of breeder reactors, which produce plutonium and other transuranic elements. It also accounts for the radioactivity of nuclear wastes.

In 1972, workers at a nuclear-fuel processing plant in France found that some of the uranium ore shipped from the Oklo mine in the Republic of Gabon, Africa, was deficient in ²³⁵U relative to ²³⁸U. By exquisite analytical detective work, scientists at the French Atomic Energy Commission eventually traced this uranium isotopic anomaly to 17 individual pockets within the Oklo deposit and the surrounding area. They had discovered the intact remains of Precambrian natural nuclear reactors. Besides the depletion in ²³⁵U in the spent nuclear fuel, these pockets contain fission-produced nuclides of Nd, Sm, Zr, Mo, Ru, Pd, Ag, Cd, Sn, Cs, Ba, and Te. These isotopes are also part of the radioactive waste from modern man-made nuclear reactors.

The Oklo reactors are small (usually 10–50 cm thick) seams of sandstone-hosted uraninite ore mantled by clay. Today, that ore would be unable to initiate self-sustaining neutron chain reactions, because the proportion of ²³⁵U in natural uranium is too low. However, 1.9 billion years ago when these reactors were active, the proportion of ²³⁵U was nearly five times greater. The high uranium concentration in quantities exceeding the critical mass was a necessary condition for the Oklo reactors. These ores contained few “pile poisons,” which absorb neutrons and prevent a chain reaction. In modern reactors, neutrons are slowed (moderated) by water, which allows them to be absorbed by other nuclei. Geological observations show that water was also present as a moderator in the Oklo natural reactors. Moreover, the deposits also contain fission products of plutonium and other transuranic elements, which indicates that they functioned as fast breeder reactors. Breeding fissile material would have allowed the reactors to operate continuously for longer periods of time. You can read more about the Oklo reactors in a paper published by F. Gauthier-Lafaye and coworkers (1989).

Besides providing information on the physics of a fascinating natural phenomenon, these reactors are important for understanding radioactive waste containment. Oklo is the only occurrence in the world where actinides and fission products have been in a near-surface geological environment for an extremely long period of time. The fission products at these sites allow characterization of the geochemical mobility of various isotopes and thereby permit assessment of the effectiveness of radionuclide waste repositories.

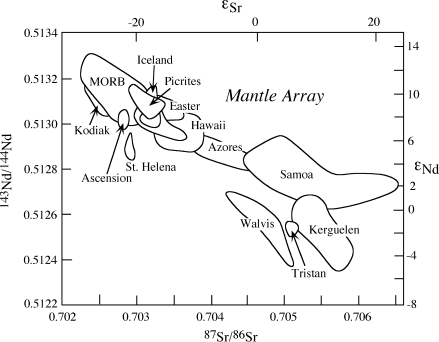
FIG. 14.13. Neodymium and strontium isotopic compositions of basalts. MORBs and ocean island basalts define a diagonal mantle array. MORBs are derived from a homogenized, depleted upper mantle, whereas ocean island basalts represent mixing of magmas derived from a less depleted lower mantle with upper mantle materials. (After Anderson 1994.)

In terms of its radiogenic isotopes, the mantle can be visualized as consisting of two layers: the lower portion undifferentiated and the upper mantle highly fractionated. The lower mantle has presumably remained relatively undepleted since its formation, sampled only infrequently at hot spots to produce flood basalts and oceanic islands. However, periodic sinking of crustal plates into the lower mantle provides a mechanism for enriching it in incompatible elements. The upper mantle has been continuously cycled by the formation and subduction of oceanic crust, as well as the production of continental crust made in magmatic arcs at subduction zones. Its isotopic composition has become homogenized but remains relatively depleted in incompatible elements. This two-layer model of the mantle was previously presented in chapter 12, based on trace element abundances.

The estimated +12ε_Nd value of the upper mantle is counterbalanced by the −15ε_Nd value for continental crust. Knowing these values and the mass of the continental crust, it is possible to perform a mass balance calculation to determine the proportion of the depleted upper mantle. The mass of the continental crust is ∼2 × 10²⁵ g and its neodymium abundance is ∼50 times greater than the upper mantle. The mass of the upper mantle is thus 100 × 10²⁵ g, which corresponds to a thickness on the order of 600–700 km. This depth range coincides with a prominent seismic discontinuity separating the upper and lower mantles.

If this view of a layered mantle is correct, other isotopic systems should be correlated with neodymium and strontium isotopic data. As an example, ε_Pb, the deviation in ²⁰⁶pb/²⁰⁴pb from chondritic evolution, varies systematically, so we should actually consider a Nd-Sr-Pb mantle array. Stan Hart and coworkers (1986) suggested that inclusion of additional isotopic systems may require that compositional models for the mantle be expanded to as many as five components.

Magmatic Assimilation

In some cases, ascending magmas are contaminated by assimilation of crustal materials, with the result that their compositions are altered. Radiogenic isotopes provide the least ambiguous way of recognizing this process. In uncontaminated basalts, the initial ⁸⁷Sr/⁸⁶Sr ratio is the same as that of the mantle source region. This ratio always has a relatively low value (ranging from ∼0.699 to 0.704, depending on the age of the rock—the mantle slowly accumulates radiogenic ⁸⁷Sr over time), because the amount of parent rubidium relative to strontium in mantle rocks is low. Rb/Sr ratios in rocks of the continental crust are much higher; therefore, over time, crustal rocks evolve to contain more radiogenic ⁸⁷Sr. We can infer then that magmas derived from mantle sources should have low initial ⁸⁷Sr/⁸⁶Sr ratios. Conversely, those derived from, or contaminated with, continental crust should have high initial ⁸⁷Sr/⁸⁶Sr ratios. A corollary is that rocks related only through fractional crystallization of the same parental magma should have identical ⁸⁷Sr₀/⁸⁶Sr ratios.

Other isotopic systems can also be used to test for assimilation of crustal materials. Contaminated basalts should have lower ¹⁴³Nd/¹⁴⁴Nd ratios than uncontaminated rocks. It is not possible to predict the exact isotopic composition of crustal lead, but if Pb isotopes can be analyzed in plausible contaminating materials, its mixing effects can be assessed.

Assimilation is actually a rather complicated process, because it requires a great deal of heat. In chapter 12, we learned that melting requires enough heat to raise the temperature of the wall rocks to their melting points plus the heat necessary to fuse them. Most magmas are already below their liquidus temperatures, so the only plausible source of heat is exothermic crystallization of the magmas themselves. Consequently, we might expect assimilation and fractional crystallization to occur concurrently. An equation to model the change in isotopic composition of a magma experiencing both assimilation and fractionation is given below. Here we assume that a magma body of mass M^o is affected by two rate processes: the rate at which the magma assimilates a mass of rock, M_a; and the rate at which crystals separate during fractionation of the magma, M_c. At any time during the combined processes, the mass of magma remaining is M, and the parameter F = M/M^o describes the mass of magma relative to the mass of the original magma. Any isotopic ratio in the magma I_m resulting from the combined effects of assimilation and fractional crystallization is given by:

(14.20)

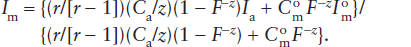
In this equation, r is defined as M_a/M_c, C_a is the concentration of the element of interest in the assimilated rock, 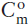is its initial concentration in the original magma, and 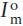and I_a are the initial isotopic ratios of the magma and assimilated rocks, respectively. The term z is defined as:

z = (r + D − 1)/(r − 1),

where D is the bulk distribution coefficient between the fractionating crystals and the magma. Equation 14.20 predicts the isotopic composition of a magma (I_m) resulting from combined assimilation and fractionation. I_m could be any isotope ratio, for example, ⁸⁷Sr/⁸⁶Sr, or any normalized parameter describing such a ratio, such as ε_Sr.

Worked Problem 14.6

By considering the combined effects of assimilation and fractional crystallization, geochemist Don DePaolo (1981) showed that elevated ⁸⁷Sr/⁸⁶Sr ratios in modern andesitic lavas in the Andes resulted from crustal contamination. The inferred isotopic compositions of the initial magma and a plausible crustal contaminant (wallrock) are illustrated in figure 14.14. Measured data for most Andean volcanic rocks (open circles in fig. 14.14) do not lie on a straight mixing line connecting these compositions, which might suggest that mixing was not important in determining the isotopic compositions of these rocks. However, the combined effects of assimilation and fractional crystallization give a different result.

Models for the combined processes can be constructed using equation 14.20. To illustrate, we calculate the magma isotopic composition (I_m) using the following parameters: the original magma contained 400 ppm Sr and 10 ppm Rb and had an initial strontium isotopic ratio ⁸⁷Sr/⁸⁶Sr = 0.7030. The contaminant had 500 ppm Sr and 40 ppm Rb, with an initial ratio ⁸⁷Sr/⁸⁶Sr = 0.71025. We assume that r = 0.8, D_Sr = 0.5, and F = 2. The corresponding value for z is then:

z = (0.8 + 0.5 − 1)/(0.8 − 1) = −1.5.

Substitution of the above parameters into equation 14.20 gives:

Im	= {(0.8/−0.2)(500/−1.5)(1 − 21.5)(0.71025)
	+ (400)(21.5)(0.7030)}/
	{(0.8/−0.2)(500/−1.5)(1 − 21.5) + (400)(21.5)}
	= 0.7078.

This calculated value is only one point on a curve like those in figure 14.14, which illustrates how the strontium isotopic ratio changes during the combined processes. The curves actually shown in figure 14.14 are the values for Andean volcanics calculated by DePaolo. He assumed that D_Sr had a range of values as shown in figure 14.14 (we might expect that D_Sr would vary during fractional crystallization and assimilation as different phases crystallized and the liquid composition changed). The measured strontium isotopic compositions and Rb/Sr ratios in the lavas fall within the calculated curves, thus supporting the model of assimilation and concurrent fractional crystallization.

FIG. 14.14. Strontium isotopic data for volcanic rocks of the Peruvian Andes. The data points do not lie on a simple mixing line connecting the isotopic compositions of initial magma and wallrock contaminant, but do lie near calculated mixing lines for an assimilation-fractional crystallization model with various values of D_Sr. It is expected that D_Sr increases in the latter stages of magma evolution. This model appears to explain the observed isotopic data fairly well. (After DePaolo 1981.)

Subduction of Sediments

Sediments deposited near oceanic trenches and subsequently subducted into the mantle could conceivably be melted and incorporated into arc volcanics. However, some geological and geophysical studies have stressed the mechanical difficulty of subducting low density sediments into the mantle. Radiogenic isotopes that are concentrated in such sediments may serve as tracers to follow their fate. These sediments characteristically have high ²⁰⁸Pb/²⁰⁴Pb and ²⁰⁷Pb/²⁰⁴Pb ratios. We have already seen that uranium and thorium are incompatible elements that are concentrated in the crust, and the high radiogenic lead contents of these sediments are the result of their derivation from old U- and Th-enriched rocks on continents. The isotopic compositions of lead in some arc volcanics and in abyssal sediments are very similar, but are so distinct from those of oceanic basalts that recycling of crustal materials must occur. Mass balance calculations suggest that 1–2% sediment in the source could account for the observed lead isotope data.

This conclusion is supported by hafnium isotopic data on arc volcanics. We have not discussed the Lu-Hf system, but it is similar in most respects to the Sm-Nd system, with specifics given in table 14.1. Hafnium is partitioned strongly into the mineral zircon, which is commonly concentrated in continent-derived sands. Thus, there should be a major difference in Lu/Hf ratios between these sands and deep-sea muds. This behavior is distinct from Sm/Nd, which shows no fractionation during sedimentation. Therefore, the isotopic variations in hafnium and neodymium expected from mixing mantle with various types of sediment can be predicted and compared with data from arc volcanics. Jonathan Patchett and his collaborators (1984) estimated that <2% of nearly equal proportions of continental sand and oceanic mud could account for the measured Hf-Nd isotopic array.

The cosmogenic isotope ¹⁰Be can also be used to shed light on this problem. The short half-life of this isotope, only 1.5 million years (table 14.1), is comparable to the time scale for subduction and magma generation. Young pelagic sediments contain appreciable amounts of ¹⁰Be, so it is possible that this isotope might make the round trip from the Earth’s surface into the mantle and back again if subduction and melting are fast enough. Analyses indicate that lavas that should not have incorporated crustal materials (MORB, ocean island basalts) do not contain significant amounts of ¹⁰Be, but this isotope is enriched by factors of 10–100 in some arc volcanic rocks (e.g., Aleutians, Andes, Kurile arcs). ¹⁰Be is absent in the lavas of some arcs, but its absence does not necessarily prove the absence of sediments, because the ¹⁰Be signal depends on the rate of subduction and melting. Julie Morris (1991) provided a comprehensive review of the subject.

It might be argued that ¹⁰Be in lavas reflects cosmic ray exposure on the surface after eruption, rather than incorporation of subducted sediments. However, analyses of modern lavas show a constant ratio of ¹⁰Be to non-cosmogenic ⁹Be in all minerals of the rocks, indicating that ¹⁰Be must have been incorporated prior to igneous crystallization. Estimates of the amount of sediments incorporated into arc lavas are generally <3%. The time scales for subduction to mantle depths, transfer of material from the slab, and subsequent melting, ascent, and eruption are still debated. Constraints from decay of ¹⁰Be can be coupled with U-Th disequilibrium systematics to give times ranging from a few hundred thousand years to as little as 10,000 years.

Isotopic Composition of the Oceans

The isotopic composition of ocean water depends on inputs from various sources. These are primarily (1) submarine weathering of and magmatic interaction with young basaltic rocks of the ocean floor, (2) recycling of marine carbonate rocks that now reside on continents, and (3) weathering of crystalline continental crust, which consists mostly of granitic igneous and metamorphic rocks. We briefly consider the behavior of strontium and neodymium isotopes in the oceanic system.

At the present time, all oceans have a ⁸⁷Sr/⁸⁶Sr ratio of 0.7090. In contrast, the measured ¹⁴³Nd/¹⁴⁴Nd ratios of ocean water indicate that each ocean has a distinct and characteristic compositional range, as summarized in figure 14.15 in terms of ε_Nd. What causes this difference in isotopic behavior?

It is thought that much of the strontium in seawater is derived from weathering of marine carbonates on continents. The ⁸⁷Sr/⁸⁶Sr ratio in these carbonates has varied during Phanerozoic time, decreasing to a minimum of 0.7067 during the Jurassic and increasing again to the current high value of 0.7090. The isotopic composition of marine carbonates mimics that of the ocean in which they formed, so the oceans have varied in strontium isotopic composition over time. In fact, changes in the oceanic ⁸⁷Sr/⁸⁶Sr ratio have now been documented with sufficient precision that this isotope ratio can be used to date some fossil shells and carbonate sediments (the technique is most precise for intervals when the ⁸⁷Sr/⁸⁶Sr ratio is rapidly changing due to climatic or tectonic events). Different oceans drain continents with different carbonate sources, so the fact that oceans have the same strontium isotopic composition everywhere must relate to a long residence time (∼4 million years) for this element in seawater. Interoceanic circulation patterns are rapid compared with strontium residence, so that a worldwide isotopic composition results at any given time.

Continental crystalline rocks probably supply most of the neodymium to the oceans. Differences in the ages of continental rocks whose weathering products are drained into the oceans produce distinct radiogenic isotopic signatures in river waters. We might expect that, as with strontium isotopes, these differences would be erased by global circulation, but they are not. The Atlantic is supplied by very old continental regions, with high ¹⁴³Nd/¹⁴⁴Nd, whereas the Pacific is ringed by younger regions with correspondingly lower values of neodymium isotope ratios. Waters in the two oceans retain these isotopic signatures. This can be explained only by assuming that the residence time for neodymium in seawater is short; that is, that neodymium entering the oceans is lost to the seafloor before interoceanic circulation patterns can homogenize the isotopic composition between oceans.

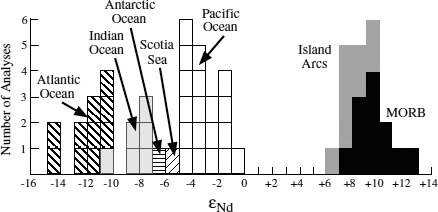
FIG. 14.15. The neodymium isotopic compositions of seawater and ferromagnesian nodules from different oceans, expressed as ε_Nd. Boxes represent individual analyses. These compositions are distinct from each other and from oceanic volcanic rocks. (After Piepgras et al. 1979.)

Radiogenic isotopic studies of seawater thus offer the possibility of shedding light on the rates at which oceans mix, provided that residence times can be fixed. Neodymium isotope measurements may even be able to identify the location of currents responsible for such mixing. Strontium isotopes also provide information on the kinds of rocks exposed to weathering on continents over geologic time.

Worked Problem 14.7

What are reasonable values for input into the modern oceans from various geochemical reservoirs? Gunter Faure (1986) presented a mass balance model based on the premise that the strontium isotopic composition of the oceans could be explained by input from oceanic volcanics, marine carbonates, and crystalline continental crust. The ⁸⁷Sr/⁸⁶Sr ratio of seawater (sw) is given by:

(87Sr/86Sr)sw =	(87Sr/86Sr)VV + (87Sr/86Sr)mM
	+ (87Sr/86Sr)cC,

where (⁸⁷Sr/⁸⁶Sr)_v,m,c are strontium isotopic ratios contributed by volcanic, marine carbonate, and continental crustal rocks, respectively, and the coefficients V, M, and C are the fractions of the total input contributed by these sources. By substituting present-day estimates for the strontium isotopic compositions of each of these sources, we obtain:

(⁸⁷Sr/⁸⁶Sr)_sw = 0.704V + 0.708M + 0.720C.

(14.21)

FIG. 14.16. A model to explain the strontium isotopic composition of seawater. Mixtures of various proportions of volcanic rocks (V), marine carbonates (M), and continental crustal rocks (C) can account for the ⁸⁷Sr/⁸⁶Sr ratio of modern ocean water (dashed horizontal line at 0.709). (After Faure 1986.)

If we then plot (⁸⁷Sr/⁸⁶Sr)_sw versus V, as illustrated in figure 14.16, we can contour values of M and C from equation 14.21. Plausible solutions are limited by the restriction that no source can supply a negative amount of material; that is, V, M, and C must be ≥ 0. The isotopic composition of modern seawater is illustrated in figure 14.16 by a horizontal dashed line at ⁸⁷Sr/⁸⁶Sr = 0.7090. From this figure, we can see that V cannot be >0.68. However, V cannot be very close to this upper bound, because marine carbonates must make a substantial contribution. The high strontium contents and susceptibility to chemical weathering demand an important role for the volcanic rocks in this system. This model does not provide a unique solution to the problem unless the input from any one of the sources can be fixed unambiguously. However, it does allow us to assess the relative contributions from these sources if a reasonable value for one of them can be guessed. For example, if we assume that M has the value 0.7, then the contributions from other sources are V = 0.16 and C = 0.14.

Degassing of the Earth’s Interior to Form the Atmosphere

The atmosphere is thought to have formed primarily by degassing of the interior of the Earth, and isotopic variations in gases dissolved in basalts provide information on this process. Noble gases are potentially very useful in understanding atmospheric evolution, because they are chemically inert and thus are not fractionated by chemical reactions, and because all except helium are too heavy to escape from the atmosphere to space. Helium and neon cannot be subducted but are continuously released at midocean ridges, demonstrating that the Earth’s interior has not been completely degassed.

Radioactive decay results in the production of many noble gas isotopes. This is easily monitored by considering ratios of radiogenic and stable nuclides. For example, variations observed at the present time in ³He/⁴He ratios reflect the balance between primordial (stable) ³He and radiogenic ⁴He formed by decay of ²³²Th, ²³⁵U, and ²³⁸U. (Why the radiogenic isotope is not the numerator in this ratio, as is conventional for other radiogenic isotope ratios, is a mystery.) Neon has one radiogenic isotope (²¹Ne) and two nonradiogenic isotopes (²⁰Ne and ²²Ne), as does argon. The ⁴⁰Ar/³⁶Ar ratio is controlled by the progressive decay of ⁴⁰K to ⁴⁰Ar. The isotopic composition of xenon reflects several processes. Radiogenic ¹²⁹Xe was produced by decay of now extinct ¹²⁹I. Fission of ²³⁸U also generates ¹³⁴Xe, ¹³⁶Xe, and several other xenon isotopes, creating variations in the ratios of these isotopes to nonradiogenic ¹³⁰Xe.

Two different geological processes also affect these isotopic ratios. Degassing occurs by volcanic and hydrothermal activity. Decreases in gas concentrations in the mantle reservoir affect both radiogenic and stable nuclides, but not the nongaseous parent nuclides. For example, degassing decreases the amount of ³⁶Ar (the isotope to which radiogenic ⁴⁰Ar is normalized) but does not affect ⁴⁰K (which generates ⁴⁰Ar). Fractionation of incompatible elements also affects these ratios. We have already learned that K, U, and Th can be fractionated into the crust by magmatic processes. Because some isotopes of these elements are parent nuclides for noble gas isotopes, this process leads to depletion of radiogenic gas isotopes in mantle source regions.

Degassing and crustal formation have occurred on different time scales, and the parent nuclides that produce the isotopic variations in noble gases have very different half-lives. Consequently, these isotopic systems may permit us to trace these geologic processes and determine their time dependence.

Claude Allegre and his coworkers (1986) modeled degassing of the mantle using mass balance calculations that employed argon and xenon isotopic ratios. Their model employs four noble gas reservoirs: the atmosphere, continental crust, upper mantle, and lower mantle. Their calculations indicate that approximately half the Earth’s mantle is 99% degassed. Based on other isotopic evidence, such as neodymium isotopes discussed earlier, this is a larger mantle proportion than that corresponding to the depleted upper mantle. The disagreement might be rationalized by assuming that some of the primitive lower mantle has also lost a portion of its noble gases.

Helium was not used in the mass balance calculations because it has limited residence time in the atmosphere. However, this becomes an advantage if we want to calculate the gas flux from the mantle. Assuming a steady state condition in which the mantle releases as much He as is lost from the atmosphere to space, Allegre and coworkers calculated He fluxes in the mantle-atmosphere system. Fluxes of Ar and Xe can also be estimated based on correlations of their isotopic ratios with ³He/⁴He. The model of Allegre and his collaborators is summarized in figure 14.17. From this diagram, we can see that the only recycling occurs at subduction zones, and that this recycling is temporary because gases in the subducted slabs are eventually returned to the atmosphere by arc volcanism.

FIG. 14.17. Schematic representation of noble gas reservoirs and fluxes in the mantle-crust-atmosphere system. Degassing of the upper mantle occurs through volcanism at spreading centers, and degassing of a portion of the lower mantle results from hot spot volcanic activity. In this model, helium diffuses between mantle reservoirs, but they behave as closed systems to other noble gases. Subducted oceanic crust contains atmospheric gases, but these are only temporarily recycled, because arc volcanism returns them to the atmosphere. Continental crust is a significant reservoir for radiogenic gases, because their parent isotopes are fractionated into the crust and remain there for long periods of time. Helium is the only noble gas that escapes from the atmosphere to space. (Modified from Allegre et al. 1986.)

However, the ratio ²⁰Ne/²²Ne in the mantle differs considerably from that in the atmosphere, and this difference cannot be attributed to nuclear processes (both are nonradiogenic isotopes). This implies that mantle degassing to form the atmosphere has not been a closed system process. Either some dynamic process caused loss of some early atmosphere (escape processes can result in significant fractionations), or some of the atmosphere has a different origin (perhaps carried in impacting comets). Although the neon isotopic data appear to require a more complex evolution of the Earth’s atmosphere, simple degassing of the mantle as advocated by Allegre and coworkers is probably sufficient to explain the argon isotopes, because the mantle is such a huge reservoir of potassium. Noble gas isotopes in the Earth’s mantle were reviewed by Ken Farley and Elizabeth Neroda (1998).

SUMMARY

In this chapter, we have seen that isotope stability is the exception rather than the rule. Radionuclides may decay by emission of beta particles, alpha particles, positrons, capture of electrons, or spontaneous fission. Branched decay involving several of these decay mechanisms occurs in some cases. The rate of radioactive decay is exponential and is most easily expressed in terms of half-life. We have derived equations that allow determination of the isotopic evolution of a system as a function of time. These equations permit the age dating of rocks, based on the decay of certain naturally occurring radionuclides, such as ⁴⁰K, ¹⁴⁷Sm, ⁸⁷Rb, ²³²Th, ²³⁵U, and ²³⁸U. In such systems, it is possible to determine the age of rocks even though the daughter isotope may have been present in the system initially. Uranium and thorium isotopes decay through a series of intermediate radioactive daughters, but the half-lives of transitory daughters are short enough that each system can usually be treated as the decay of parent directly to the stable daughter. Independent U-Th-Pb geochronometers can give the same or different results, but useful information can be gained even in cases of discordancy. The interpretation of geochronological data can be complicated by the failure of rock systems to remain closed, as well as other factors. The earlier presence of now extinct radionuclides can, in some cases, be determined, and their existence places constraints on early processes such as planetary differentiation.

The abundances of radiogenic isotopes can be determined directly from mass spectrometry or indirectly from fission track techniques. The production of radioactive isotopes can also be induced artificially in a nuclear reactor, which forms the basis for elemental quantitative analysis by neutron activation. The ⁴⁰Ar-³⁹Ar geochronometer also depends on induced radioactivity. Cosmogenic nuclides are produced naturally by cosmic ray exposure, which forms ¹⁴C for dating recent events and other radionuclides useful in quantifying surface processes such as erosion.

Radionuclides also provide powerful tracers for geochemical processes. Uses we have explored here include understanding mantle heterogeneity, cycling of materials between crust and mantle reservoirs, global oceanic mixing, and degassing of the Earth’s interior to form the atmosphere. The importance of radiogenic isotopes is considered further in the following chapter on the early solar system and processes at planetary scales.

SUGGESTED READINGS

There are an increasing number of textbooks that treat isotope geochemistry. The books by Faure and Dickin are required reading for anyone seriously interested in this subject, and the other references provide further elaboration on certain aspects of radiogenic isotopes.

 

Bowen, R. 1988. Isotopes in the Earth Sciences. London: Elsevier Applied Science. (Chapter 2 provides a thorough discussion of mass spectrometry, and later chapters deal primarily with radiometric dating techniques.)

Dickin, A. P. 1995. Radiogenic Isotope Geology. Cambridge: Cambridge University Press. (An up-to-date treatment of this field; everything you want to know about geochronology.)

Durrance, E. M. 1986. Radioactivity in Geology: Principles and Applications. New York: Wiley. (This unconventional book deals with many applications of radioactivity not treated here; examples include its use in prospecting for radioactive ores and petroleum, environmental applications, and the heat generated by radioactive decay.)

Farley, K. A., and E. Neroda. 1998. Noble gases in the Earth’s mantle. Annual Reviews of Earth and Planetary Sciences 26: 189–218. (A lucid review of a particularly complex subject; noble gas geochemistry is complex and often understood only by its practitioners, but this paper really helps.)

Faure, G. 1986. Principles of Isotope Geology, 2nd ed. New York: Wiley. (One of the best available texts on isotope geochemistry. This is an excellent source for detailed information of radiogenic isotopes; geochronology is covered more exhaustively than other aspects of this subject.)

Jager, E., and J. C. Hunziker, eds. 1979. Lectures in Isotope Geology. Berlin: Springer-Verlag. (A series of lectures given in Switzerland by respected isotope geochemists; the first half of the book deals with geochronology.)

McLennan, S. M., S. Hemming, D. K. McDaniel, and G. N. Hanson. 1993. Geochemical approaches to sedimentation, provenance, and tectonics. Geological Society of America Special Paper 284:21–40. (This review paper is a primer on the use of radiogenic isotopes in deciphering the tectonic setting of clastic sediments.)

Philpotts, A. R. 1990. Principles of Igneous and Metamorphic Petrology. Englewood Cliffs: Prentice-Hall. (Chapter 21 gives a particularly good overview of isotope geochemistry, and especially of the use of radiogenic isotopes in understanding magma sources.)

Vertes, A., S. Nagy, and K. Suvegh. 1998. Nuclear Methods in Mineralogy and Geology. New York: Plenum. (This is an excellence source for learning about neutron activation analysis, and other subjects not covered here, such as dating groundwater.)

Walker, F. W., D. G. Miller, and F. Feiner. 1983. Chart of the Nuclides. San Jose: General Electric Company. (A real bargain that contains physical constants, conversion factors, and periodic table; order from General Electric Nuclear Energy Operations, 175 Curtner Ave., M/C 684, San Jose, California 95125.)

The following references were cited in this chapter. These provide more thorough treatments of the applications of radionuclides in solving geochemical problems.

 

Aleinikoff, J. N., R. H. Moench, and J. B. Lyons. 1985. Carboniferous U-Pb age of the Sebago batholith, southwestern Maine: Metamorphic and tectonic implications. Geological Society of America Bulletin 96:990–996.

Allegre, C. J., T. Staudacher, and P. Sarda. 1986. Rare gas systematics: Formation of the atmosphere, evolution and structure of the Earth’s mantle. Earth and Planetary Science Letters 81:127–150.

Anderson, D. L. 1994. Komatiites and picrites: Evidence that the “plume” source is depleted. Earth and Planetary Science Letters 128:303–311.

DePaolo, D. J. 1981. Trace element and isotopic effects of combined wallrock assimilation and fractional crystallization. Earth and Planetary Science Letters 53:189–202.

Gauthier-Lafaye, F., F. Weber, and H. Ohomoto. 1989. Natural fission reactors of Oklo. Economic Geology 84:2286–2295.

Halliday, A. N., and D.-C. Lee. 1999. Tungsten isotopes and the early development of the Earth and Moon. Geochimica et Cosmochimica Acta 63:4157–4179.

Hart, S. R., D. C. Gerlach, and W. M. White. 1986. A possible Sr-Nd-Pb mantle array and consequences for mantle mixing. Geochimica et Cosmochimica Acta 50:1551–1557.

Morris, J. D. 1991. Applications of cosmogenic ¹⁰Be to problems in the earth sciences. Annual Reviews of Earth and Planetary Sciences 19:313–350.

Nielson, D. L., S. H. Evans, and B. S. Sibbett. 1986. Magmatic, structural, and hydrothermal evolution of the Mineral Mountains intrusive complex, Utah. Geological Society of America Bulletin 97:765–777.

Nyquist, L. E., C. –Y. Shih, J. L. Wooden, B. M. Bansal, and H. Wiesmann. 1979. The Sr and Nd isotopic record of Apollo 12 basalts: Implications for lunar geochemical evolution. Proceedings of the Lunar and Planetary Science Conference 10:77–114.

Patchett, P. J., W. M. White, H. Feldman, S. Kielinszuk, and A. W. Hoffman. 1984. Hafnium rare-earth element fractionation in the sedimentary system and crustal recycling into the earth’s mantle. Earth and Planetary Science Letters 69:365–378.

Piepgras, D. J., G. J. Wasserburg, and E. J. Dasch. 1979. The isotopic composition of Nd in different ocean masses. Earth and Planetary Science Letters 45:223–236.

Price, P. B., and R. M. Walker. 1963. Fossil tracks of charged particles in mica and the age of minerals. Journal of Geophysical Research 68:4847–4862.

Sisson, V. B., and T. C. Onstott. 1986. Dating blueschist metamorphism: A combined ⁴⁰Ar/³⁹Ar and electron microprobe approach. Geochimica et Cosmochimica Acta 50:2111–2117.

Yin, Q., S. B. Jacobsen, K. Yamashita, J. Blichert-Toft, P. Talouk, and F. Albarede. 2002. A short timescale for terrestrial planet formation from Hf-W chronometry of meteorites. Nature 418:949–952.

PROBLEMS

(14.1) Given the following Rb-Sr isotopic data for whole-rock samples of a granitic pluton, determine the initial strontium isotopic ratio and age of the pluton.

(14.2) (a) Solve equation 14.8 for t. (b) Use the equation you just derived to determine the age of a biotite sample, for which the following data have been obtained: K = 7.10 wt. %, ⁴⁰Ar = 1.5 × 10¹² atoms g⁻¹.

(14.3) A zircon grain initially contained 1000 ppm ²³⁵U and 100 ppm ²⁰⁷Pb. How many atoms of ²⁰⁷Pb will this zircon contain after 1 billion years?

(14.4) Using the data below and figure 14.7, construct a concordia diagram. Are these samples concordant? Interpret your results, explaining any assumptions that you make.

(14.5) You obtain the following geochronological data for a portion of the Appalachians. A gneiss unit gives whole-rock Rb-Sr and zircon U-Pb ages of 315 million years. Mineral geothermometers in this unit give a peak metamorphic temperature of 530° C. ⁴⁰Ar-³⁹Ar gas retention ages are 295 million years for hornblende and 283 million years for biotite. Fission track ages for apatites range from 130 to 150 million years. Using these data, construct a time-temperature path illustrating the late Paleozoic thermal history of this part of the Appalachian orogen.

(14.6) The measured activity of a sample of charcoal found at an archaeological site is 5.30 dpm g⁻¹. What is the age of the sample?

(14.7) How much heat energy would be generated in 100,000 years by a one cubic meter sample of rock containing live ²⁶Al? The half-life of ²⁶Al is given in table 14.1. Assume that the sample initially contains 100 g of aluminum with a ²⁶Al/²⁷Al atomic ratio of 0.1. Also assume that the energy of decay for ²⁶Al is 10⁻¹⁴ cal atom⁻¹.

(14.8) A magma containing 200 ppm strontium is contaminated by crustal rocks containing 1000 ppm Sr. The magma simultaneously undergoes fractional crystallization of phases with a bulk distribution coefficient D_Sr = 0.75. The initial Sr isotopic ratios of the magma and crustal rocks are 0.704 and 0.713, respectively. Assume that r = 0.5. Use equation 14.20 to calculate the isotopic composition of the resulting hybrid magma as a function of mass of magma relative to original mass (F), and illustrate the result with a graph.