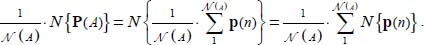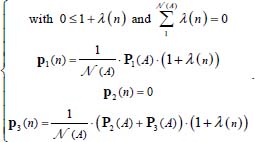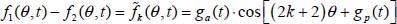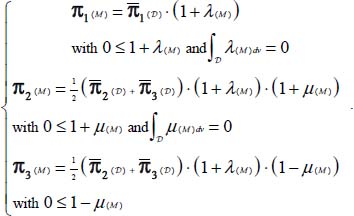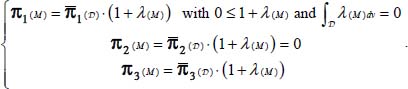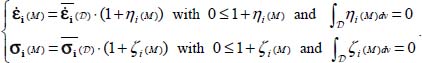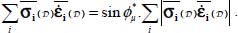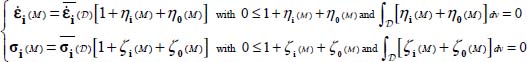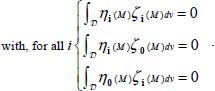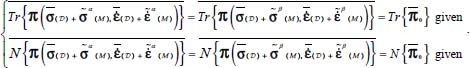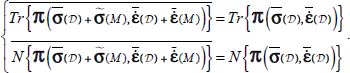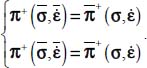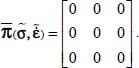2
Natural Compatibility With Mechanical Heterogeneity

As granular materials in motion are inherently heterogeneous and fluctuating at a small scale, this chapter develops key macroscopic consequences of the previously exposed tensor structures, regarding the validity of corresponding dissipation equations, when expressed with average values of measurable macroscopic quantities (average stress, average strain rates, and so on). This analysis will make grounds for the developments of Chapter 3 about localization and shear banding. However, it first requires us to answer three basic questions:

• – Under which conditions is the inherent heterogeneity allowable in the framework of dissipation equations?
• – Which physical reasons justify such compatibility conditions?
• – Under the limitations of these compatibility conditions, is allowable heterogeneity still representative of experimental reality?

For this purpose, we represent this heterogeneity by decomposition of any relevant local quantity G (with scalar values, or vector, or tensors) over the considered material domain 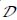, resulting from the sum of an average component and a component of local fluctuations (with a null average over the considered domain)

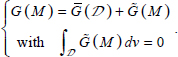
Then, the question of compatibility with heterogeneity becomes essentially the question of required conditions on these local fluctuations.

First, it is shown in this chapter that the vicinity of a minimum in energy dissipation results in a general compatibility with the inherent heterogeneity of internal actions at mesoscopic and macroscopic scales: the dissipation equation, operating locally on the internal actions, still holds globally on their average values, despite the presence of strong heterogeneities and fluctuations in the spatial distribution of the internal actions. This very peculiar characteristic is shown to result from the piecewise linearity of the dissipation equation. As an illustration, this section ends with the analysis of specific characteristics of statistical distributions of internal contact actions within the discontinuous granular mass in motion. It is shown that these statistical distributions are solutions of a certain set of equations, forming a convex set of solutions, only determined within a set of fluctuations. An admissible set of these fluctuations is also derived.

Second, it is shown that the vicinity of a minimum in energy dissipation results in a general compatibility with a wide field of inherent heterogeneity of internal forces and internal motions at the macroscopic scale: the dissipation equation, operating locally on the internal forces and internal motions, still holds globally on their average values, despite the presence of strong heterogeneities and fluctuations in their spatial distribution. The corresponding conditions – in terms of thermodynamic consistency – constitute a kind of extension to discontinuous granular materials of the Hill–Mandel macro-homogenization condition. Finally, it is shown that these admissible heterogeneities in stress and strain rates do correspond, in practice, with the simultaneous presence of shear bands and linear concentrations of stress (force-chains).

2.1. Compatibility with the heterogeneity of internal actions

2.1.1. Discontinuous granular mass in motion near minimal dissipation

In a discontinuous granular mass A, in motion close to the conditions of minimal dissipation, the tensor of internal actions P(A) complies with the minimal dissipation relation, and its equivalent relation on input power and output power is as follows:

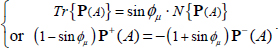
This property is also verified over any sub-domain of A, provided that the motion is sufficiently close to the minimal dissipation conditions, as a result of the internal similarity attached to the corresponding minimal dissipation solutions (section 1.2.5), and this property remains valid until the ultimate partitions of discontinuous granular mass individualize each elementary contact. In short, near the conditions of minimal dissipation, the tensors of local elementary contact actions, and the global tensor of internal actions over the whole granular mass A, satisfy using the same energy dissipation relation and have at least one eigendirection in common with the same signature, whereas these properties result from the particularities of the minimal dissipation modes.

These particularities result from a key property of minimal dissipation modes:

• – For these modes, the global tensor of internal actions of the granular mass P(A) resulting from the sum of elementary contact actions tensors p(n), extended to all 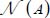contacts included within the granular mass, satisfies the following condition:
  
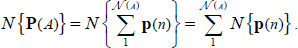
• – In other words, by averaging the above-mentioned equation over the 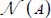contacts, under minimal dissipation conditions, the norm of average internal actions over the whole granular mass is equal to the average of the norms of all the local contacts’ internal actions included in the granular mass

[2.1]

Note that this property establishes a link between the distribution of local contact actions, and the global internal actions, taking also into account the other properties of minimal dissipation modes:

• – In Mode I, global and local internal actions tensors have in common the eigendirection no. 1 bearing their unique positive eigenvalue, thus the features of local tensor distribution may be represented by a scalar distribution λ(n) binding the eigenvalues of the local contact action tensor p(n), which is always a plane tensor, to those of the internal action global tensor P(A)
  [2.2]
• – In Mode II, the configuration obtained is symmetrical, by permutation of eigendirections no. 1 and no. 3.
• – In plane strain border mode (P₂(A) = p₂(n) = 0), all three eigendirections are in common, but the above-mentioned relations remain valid.

The above-mentioned conditions [2.2] are binding the distribution of local contact tensors to the average of the global tensor over the granular mass, through a discrete distribution λ(n), whose resultant is null, which represents the local deviation from the average value. Therefore, it is a representation of admissible local heterogeneity in the discontinuum.

The above-mentioned conditions are thus the sought conditions of compatibility regarding the heterogeneity of internal actions in the granular mass. Note that:

• – these conditions do not bring additional information on the physical conditions on internal actions attached to the minimal dissipation (mode signature, at least one eigendirection in common), and are just the translation of such physical conditions over the local heterogeneity, without creating any new constraint; “the internal actions of discontinuous granular mass in motion near minimal dissipation are thus naturally compatible with local heterogeneity under the above-mentioned conditions”;
• – the condition of mode signature restrains any change of sign of eigenvalues, but does not limit the amplitude of local deviations in absolute value;
• – there is no limitation in eventual concentration of internal actions in a subset A₁ of the considered granular mass, with λ(n) = −1 anywhere outside A₁, i.e. a dissipation (and then a “deformation”) localized in A₁ and the rest of the granular mass remaining as “frozen in the motion”;
• – there is no limitation in the eventual geometrical structure of such material subsets concentrating localized dissipation;
• – for a given global tensor of internal actions P(A), the set of admissible heterogeneous distributions of local contact actions defined by the above-mentioned conditions is a convex set, and the homogeneous distribution (λ(n) = 0 anywhere) is a part of this convex set.

2.1.2. Relationship on statistical distributions of contact action orientation

Section 2.1.1 suggests to extend the analysis to wider neighborhoods of minimal dissipation (with R(A) ≠ 0) and deeper into the statistical distributions of local contact actions tensors. Coming back to the energy dissipation equation [1.16] with “internal feedback” interactions, ruling the global tensor of internal actions P(A), the following questions arise:

• – which conditions may be satisfied by a statistical distribution of local contact actions tensors, so that its result is P(A)?
• – can these conditions bring information on the specific properties of such a statistical distribution, and its compatibility with heterogeneity?

To obtain answers in the following and limit tedious discussions, the analysis is focused on situations with R(A) < 1 corresponding to the kind of motions of interest here. The first focus is on two-dimensional (2D) granular materials (often used in numerical simulations) corresponding to strict plane strain motion, where all local contact actions tensors have in common the eigendirection bearing their null eigenvalue. The case of three-dimensional (3D) granular materials is treated later.

2.1.2.1. Case of 2D granular materials

In the considered 2D configuration, the local contact action tensors remain as plane tensors (similar with each other, up to a simple rotation), and on the natural basis of global tensor P(A), their orientation depends on a single angular parameter (the measure of rotation of their positive eigendirection, by an angle θ; see Figure 2.1). Using the simplified notation S for the material constant sin ϕ_μ, a simple expression of local contact actions tensor within the global natural basis is derived

After deriving f(θ)dθ, the participation to the global dissipation of all the local tensors of contact actions between θ and θ+dθ and their contribution to the global resultant tensor P are as follows:

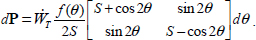
where 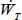is the total rate of energy dissipated within the granular mass and f(θ) is the density of dissipation by local contact actions, as a function of their orientation, and varies with time during motion.

As the global tensor P of our granular mass in motion under plane strain remains the solution of dissipation equation [1.16], its expression in its natural basis is as follows:

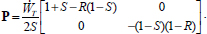
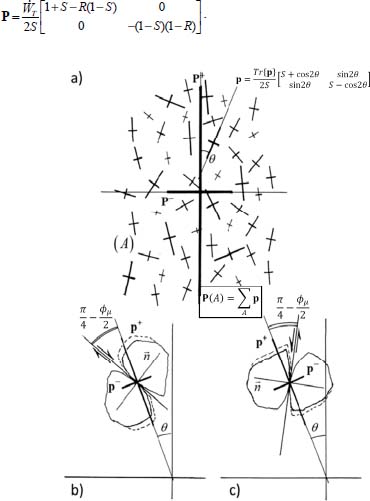
Figure 2.1. Distributions of elementary contact actions (2D medium)

Then, by simple integration over θ (between −π/2 and +π/2), we obtain the following tensor identity in the natural basis of the global tensor P:

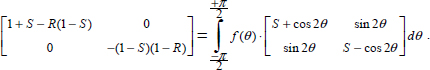
Therefore, in the natural basis of the global tensor of internal actions in the granular mass P (or the natural basis of average tensor), the distribution f(θ), considering density of dissipation by local contact actions as a function of their orientation, satisfies, at any time of the motion, the following system of four conditions:

[2.3]

These four conditions strongly constrain the distribution f(θ) when R takes small values: it may be easily shown that, for R = 0, the only distribution satisfying these four conditions is a Dirac distribution δ(0), which provides a complete polarization of all local tensors of contact actions. Again, we find a more general result already proven by algebraic means (Chapter 1, section 1.2.5). When R takes larger values closer to 1, there is a relaxation in the constraints of the four conditions [2.3] on distribution f(θ), and a wider set of particular solutions may be found.

Finally, note that for a given value of R, the set of solutions f(θ) satisfying the four conditions [2.3] is a convex set.

Otherwise, the orientation of normal vectors to sliding contacts is linked to the orientation of tensors of local contact actions, up to a symmetry, even if the sliding is dextral or sinistral [Figure 2.1(b) and (c)]. This indetermination can be objectively resolved in situations such as motions under regular boundary conditions with rigid boundaries kinematics: the configurations provided in this figure can be considered as equiprobable because, in such situation, the rigid boundaries forbid the full development of a unique shear band, which would break the symmetry of elementary shear movement distribution. Here, the explicit link appears between:

• – the distribution of orientations of sliding contacts and the distribution of local tensors of contact actions;
• – the distribution f(θ) and the distribution of sliding contacts orientations weighted by their participation to the total dissipation.

The four conditions [2.3] allow us to build a sampling of these distributions f(θ) using R as a parameter. Figure 2.2 details the solutions consisting of elementary triangular distributions, for R = 0 (Dirac distribution), R = 0.1, 0.3, 0.45, 0.6, and 0.9:

• – as a direct representation of f(θ), Figure 2.2(a);
• – as a polar representation of normal to contacts (Figure 2.2(b)), which is equivalent to put down on the normal, the participation to global dissipation (drawn in the equiprobable repartition over the minimum dissipation directions).

Figure 2.2, built with a typical value of S = 0.5 (i.e. 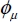= 30°), shows that, provided R is approximately less than 0.5, the corresponding distributions are clearly polarized on the directions of minimal dissipation (found for R = 0). This shows that for such range of R values:

• – the global distribution of all contact orientations may not display a clear polarization, which is generally the case in numerical simulations;
• – nevertheless, one should expect that the distribution restricted to the active contacts only (those which slide and dissipate energy), weighted by their participation to the total dissipation, appears as clearly polarized.

Note that the system of four conditions [2.3] also provides information on the variation over the time of the distribution f(θ,t), according to the evolution of the internal feedback rate R(A,t) during motion, and on the fluctuations of these distributions f(θ,t). If f₁(θ,t) and f₂(θ,t) are two particular solutions of system [2.3], then their difference satisfies the homogeneous linear system of conditions, consisting of the three last conditions of system [2.3] with zero on their left-hand side. A remarkable set of solutions is obtained as follows:

[2.4]

where k is a positive integer and g_a(t),g_p(t) are the functions of time. These particular solutions may be interpreted as fluctuations in time of distribution f(θ,t), allowed by the system of conditions [2.3], whose amplitude is g_a(t) and g_p(t), respectively. Therefore, if we define a particular reference solution f₀ of the system of conditions [2.3] with a given feedback R(A,t), any other solution f will be of the form: 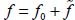(Figure 2.3).

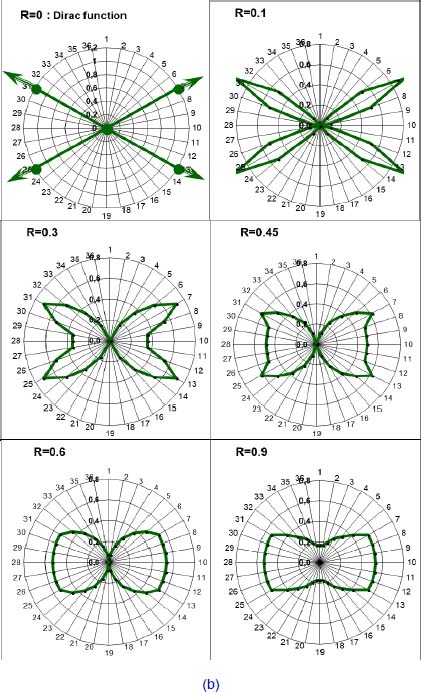
Figure 2.2. Sample of solutions f(θ), as triangular distributions function of parameter R. (a) Direct representation. (b) Polar representation on normal to contacts. For a color version of the figure, please see www.iste.co.uk/frossard/geomaterials.zip

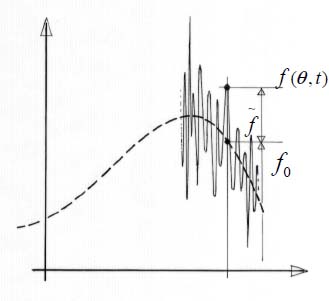
Figure 2.3. Distribution f(θ) and its fluctuating component

Hence, these terms of fluctuation have two meanings:

• – Under given feedback conditions R(A,t), the corresponding distribution of local contact actions f(θ,t) is only determined up to a set of fluctuations (i.e. a term .
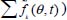• – If an experimental mean is found for determining the distribution f(θ,t), it is expected that the more precise the measurements, the more details will be found in fluctuations.

The following statements conclude this analysis of the fluctuations in 2D granular materials:

• – note that the homogeneous linear system that rules these fluctuations does not bring any additional condition relative to system [2.3]. Again, we find here through a direct analysis of statistical distributions of local contact actions the natural compatibility of internal actions with heterogeneity, already outlined, but here with more general conditions (R ≠ 0);
• – note also that this compatibility results from the convexity of the set of solutions of system [2.3];
• – if experimental data may be obtained on distributions f(θ,t), conditions [2.3] may be reversed, for instance, to assess the function R(A,t), as it implies that
  

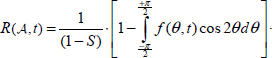
2.1.2.2. General case of 3D granular materials

The above-mentioned developments may generally be extended to 3D motions, indexing the local tensors of contact actions by the Euler angles of their natural referential within the global referential of their resultant P (see Appendix A.2.1). The system of conditions includes two more diagonalization conditions to be satisfied by the distribution f, which depends on three angular quantities instead of one; the system of conditions also includes a partition condition, setting the participation of eigenvalue no. 2 in the global tensor P.

The set of solutions is still a convex set as in 2D, and also allows for fluctuations, solutions of the homogeneous linear kernel of the system. However, the system of conditions is far more complex in three dimensions (seven conditions to be satisfied with three angular quantities, instead of four conditions with one angular quantity in two dimensions), leaving room for a wider set of allowed fluctuations. Given this complexity, the detailed analysis, in a similar way as performed earlier in 2D, is yet to be performed.

2.1.3. Equivalent pseudo-continuum in motion near minimal dissipation

In the material domain by which we represent the discontinuous granular mass A in motion near minimal dissipation, the average tensor of internal actions 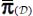is bound to the tensor of the discontinuous granular mass P(A) by relation [1.25]. Therefore, it complies with the equation of minimal dissipation, its equivalent form on input power and output power, and other properties verified by P(A), as in section 2.1.1. These properties are also verified in any sub-domain of , as a result of the property of internal similarity attached to the minimal dissipation. Thus, in any sub-domain , the input power of and the input power of 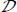are borne by the same set of eigendirections (and similarly for the output powers), as for the tensor of discontinuous granular mass.

In brief, when the domain is in motion near minimal dissipation:

• – The local tensors of internal actions, and the average tensor over , satisfy the same equation of minimal dissipation, have at least one eigendirection in common, and include the same signature.
• – Furthermore, the internal actions tensor complies with the “equivalent pseudo-continuum” form of equality [2.1], i.e. the norm of the average tensor 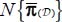equals the average norm of local tensors .
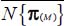• – However, the local tensor π(M) (in fact, average in the REV) is no longer a plane tensor, unlike in the discontinuous mass, and the correspondence is restricted to the similarity between π⁺(M) and 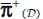, and symmetrically for the output power π⁻(M) and .

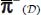This quite general situation results in the following representation of allowable heterogeneity:

• – Under Mode I, the local and average tensors have in common the eigendirection 1, bearing the unique positive eigenvalue, and the local heterogeneity can be represented by two scalar functions λ_(M) and μ_(M), which link the eigenvalues of local and average tensors
  [2.5a]
• – Under Mode II, a symmetrical characteristic results with a permutation of roles between eigendirections 1 and 3.
• – Under the border mode in plane strain (π₂ = 0), the three eigendirections are in common, and the local heterogeneity reduces to only one scalar function λ_(M), linking the eigenvalues of local and average tensors

[2.5b]

Therefore, the above-mentioned conditions [2.5b] constitute the compatibility conditions regarding the heterogeneity of internal actions in the equivalent pseudo-continuum. Their validity covers the general situations of minimal dissipation motions, as well, with or without the coaxiality between stress and strain rate tensors. Finally, for the discontinuous mass, these conditions are merely the direct expression of minimal dissipation properties inside the local heterogeneities of internal actions, without causing any new restriction.

2.1.4. Conclusions on the compatibility with the heterogeneity of internal actions

2.1.4.1. In close neighborhood of minimal dissipation

Sections 2.1.1 and 2.1.3 show that the granular mass and its representation by an equivalent pseudo-continuum satisfy a set of properties constituting their natural compatibility with heterogeneity under motions near minimal dissipation, which may be summarized as follows:

• – for a given global tensor P(A) or its equivalent 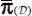satisfying the minimal dissipation equation;
• – any discontinuous distribution of contact actions p(n) present in the same neighborhood of minimal dissipation as P(A), such that 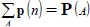, is an allowable heterogeneous solution, which also complies with the minimal dissipation conditions;
• – similarly, any continuous heterogeneous distribution π(M) present in the same neighborhood of minimal dissipation as 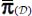, such that 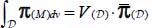, is an allowable heterogeneous solution, which also complies with the minimal dissipation conditions;
• – conversely, giving heterogeneous distributions near minimal dissipation (i.e. p(n) or π(M)), then their average on the material domain in motion (i.e. 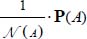or 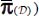is an allowable homogeneous solution, belonging to the same neighborhood of minimal dissipation, and also satisfying the minimal dissipation equation;
• – in other words, under motions near minimal dissipation, the minimal dissipation equation is verified either by local internal actions, or on average internal actions, in spite of heterogeneity.

From these results, it can also be shown [FRO 04] that in a neighborhood of a given mode of minimal dissipation, the set of allowable solutions for internal actions is a convex set. Two noticeable consequences, given the average conditions (either global tensor P(A) or its equivalent 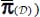, are:

• – the average on a given material point of all the set of allowable heterogeneous solutions (local average) is equal to the average over the whole material domain of one of these allowable heterogeneous solutions (global average), and this average is 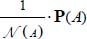or ;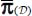
• – the set of allowable heterogeneous solutions also includes the homogeneous solution 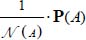or .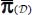

Finally, note that for the minimal dissipation equation, and its diverse mechanical consequences (volume changes associated to shear development, failure criterion, etc.), the above-mentioned properties allow the internal actions to be summarized by their average values without introducing any distortion due to heterogeneity.

2.1.4.2. Situations with internal feedback

Under a given level of disorder fixed by the value of R, section 2.1.2 shows that the heterogeneous distribution of local participation to global dissipation, directly linked to the distribution of orientations, is still a convex set.

Therefore, we will assume that, where R is sufficiently small and not null, the set of allowable heterogeneous solutions for internal actions is a convex set regarding heterogeneity and the distribution of their orientation.

2.2. Compatibility with the heterogeneity of internal forces and internal movement distributions (stress and strain rates)

In the equivalent pseudo-continuum, the internal actions are the result of the symmetric product of stress and strain rate tensors. The precedent sections show that, close to minimal dissipation, the products of local tensors σ(M) and 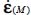, and the average over of these products, satisfy the same dissipation equation.

However:

• – the measurements usually available in mechanical experiments performed in laboratories on such materials are not made on local tensors σ(M) and , but are made on average tensors 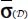and 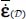over the material domain of the experiment;
• – these experimental results show that, over a wide range of experimental conditions including axisymmetric stresses with monotonic or cyclic motion, plane strain with or without rotation of eigendirections, and large amplitude 3D cyclic solicitations including cyclic torsional shear, the dissipation equation with internal feedback appears to be verified by the product of average tensors (Chapter 6) and these experimental verifications appear on various expressions of direct consequences of dissipation equation such as stress–dilatancy relations, existence of a “characteristic domain,” and existence of a failure criterion;
• – the use of a dissipation equation to indirectly assess an apparent inter-granular friction coefficient provides results that are consistent with other methods for mono-mineral media [FRO 78].

However, there is no a priori reason that the product of these average tensors satisfies, in a general manner, the same constitutive relationship as satisfied by the average of the products of local tensors. In most of the above-mentioned experiments, it may be shown (see Appendix A.2.2) that the boundary conditions impose that the products of averages and averages of the products appear identical with regard to the dissipation equation at least at the first order. However, there are other experiments that satisfy this property, but with boundary conditions that do not a priori impose this identity product of averages/average of the products (plane strain with axis rotation, such as “simple shear apparatus”, cyclic torsional shear, and so on).

The above analysis raises two main questions:

• – Why do the products of the average tensors satisfy the same constitutive relation (the dissipation equation) as the average of the products of the local tensors?
• – Which conditions on local fluctuations of stress and strain rates ensure that it can be so?

These questions are more complex than those analyzed before, as they involve the relationship between the six tensors including the local tensors σ(M) and 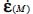, their averages 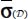and 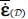, besides the two previous ones (the local tensor π(M) and its average 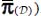). We will approach these questions in progressive steps, starting from the simplest situation, when the six tensors have the same natural referential (coaxiality with fixed axis), before entering into more general situations.

2.2.1. Case of coaxiality – compatibility with heterogeneity of stresses and strain rate distributions

In a simple coaxiality situation, local tensors σ(M) and 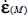have the same eigendirections that are also the eigendirections for π(M) and constitute the local natural referential. From one point to another in a domain near the minimal dissipation, these local natural referential values have at least one common eigendirection, signed, and differ by simple rotation around their common eigendirection. 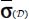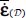For the average tensors, the natural referential of and differ from the natural referential of 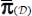by simple rotations around this common eigendirection.

Under a situation of fixed axis coaxiality, this parameter of rotation disappears, the natural referential values of local and average tensors are identical, so, on the one hand, averages 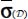and 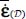have the same natural referential as local σ(M) and 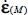and, on the other hand, this natural referential is also common to average 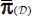and local π(M).

In this fixed natural referential, we can represent the heterogeneity of local tensors directly on their eigenvalues by simple local fluctuation functions:

• – for local stresses heterogeneity by 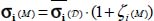with , the no-tension condition imposes that normal stress values, including principal stress, remain in compression (no-tension condition), locally and on average, thus the heterogeneity functions verify ;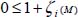
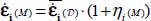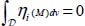• – for local strain rates by with ; otherwise, the condition of mode signature discussed in section 1.2.5 allows the eigenvalues of internal actions 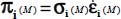to maintain the same signature over the domain; as the principal stress values remain positive (no-tension condition), the condition of mode signature is transferred to local strain rates heterogeneity fluctuation functions that verify 0 ≤ 1 + η_i (M).

In summary, within a domain in motion near minimal dissipation, the conditions of no-tension and mode signature allow, under coaxiality with the fixed axis, local heterogeneities of strain and stress rates to satisfy, on every eigendirection, the following:

[2.6]

Note that, although for completely different physical reasons, the relative fluctuations of stress and strain rates are bound on the side of negative values in a totally symmetrical way, while they have no limitations on the side of positive fluctuations. This situation has strong physical concrete significance:

• – the local eigenvalues retain the same signature over the domain, which means that local values cannot be against the average trend (with regard to the eigenvalues);
• – the local strain rates cannot go against the average trend;
• – this corresponds to practical experience under regular boundary conditions (allowing to reach the minimal dissipation neighborhood): during such experiments, a significant part of the material domain is never seen to deform in a way counter to the average trend.

This last property can be seen as a specificity of the mechanical heterogeneity structure generated by contact friction dissipation. Indeed, other types of energy dissipation-related mechanical heterogeneities, such as hydrodynamic turbulence related to viscous dissipation, allow local strain rates to progress against the average trend over a significant part of the observed domain (e.g. countercurrents near river banks).

Otherwise, the above-defined heterogeneity implies another particularity:

• – the conditions of null resultant and limitation of negative values over the domain impose that strong fluctuations can be separated by “quiet zones.” This property also applies to large heterogeneities emerging at the macroscopic scale; for a given average value, the stronger the fluctuations, the wider these “quiet zones” will be;
• – for a given average value, zones that concentrate energy dissipation, such as deformation localization in shear bands, will be separated by inactive zones whose width and inactivity will be more pronounced as the localization intensifies.

Similar considerations may be developed for stress concentrations such as chains of forces.

2.2.1.1. Compatibility with concentrations of deformations (localization)

Here, we focus only on the heterogeneities on strain rates, which leads us to temporarily neglect the heterogeneities on stresses, which will be considered as homogeneous (here, 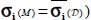). The situation considered is close to classical patterns of localization (Figure 2.4).

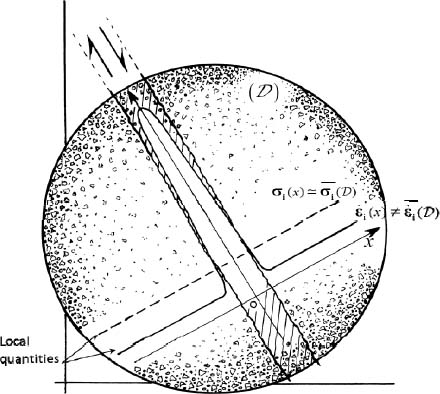
Figure 2.4. Strain localization under homogeneous stress

By integration of the local dissipation equation, we can write the following, in the fixed natural referential:

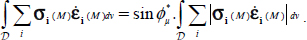
Principal stress, being considered homogeneous (equal to the average) and all in compression (>0), can be factored outside the integration, and outside the absolute values. As there is no change on each of the 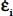over 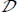(mode signature condition), despite fluctuations, we have .

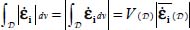Therefore, by integration of the above-mentioned local dissipation equation, we derive the following equation:

[2.7]

This is the same dissipation equation but written on average values over 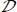of principal stress and strain rates.

Note that this result is totally independent of the eventual specific orientation of concentration of deformation (shear band orientation), as it comes from the algebraic structure of the dissipation equation.

2.2.1.2. Compatibility with concentrations of stresses (chains of forces)

As the dissipation equation and conditions [2.6] are totally symmetric between stress and strain rates, the concentration of stress in a homogeneous field of strain rates may be treated in an asymmetric manner, leading us to the obtain the same result.

2.2.1.3. Compatibility with simultaneous presence of strain localization and concentrations of stresses

By considering quite a general mixed heterogeneity of the above-considered type, including:

• – an anisotropic tensor heterogeneity component on stress ζ_i(M) (i = 1,2,3), and another on strain rates η_i(M), without spatial correlation between both on the same eigendirection;
• – a scalar heterogeneity component, ζ₀(M), η₀ (M), with possibly a spatial correlation between both;
• – the above two components are not correlated.

The corresponding analytical form, taking the mode signature and no-tension conditions into account, is

[2.8a]

[2.8b]

Note that for the anisotropic tensor components there is no restriction on possibly organized spatial structures of strain concentrations (spatial correlations between the η_i(M)) like shear bands systems, and symmetrically for possible organized systems of stress concentrations or chains of forces. Note also that for the scalar component, in case of simultaneous presence of shear band and stress concentration on a same “point”, there is no restriction on intensity or orientations of gradients of local heterogeneities ζ₀(M), η₀(M).

By integration over the material domain 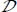of the local dissipation equation with these mixed local heterogeneities, it is shown in Appendix A.2.3 that the same dissipation equation [2.7] is written with average stresses and average strain rates.

2.2.1.4. Conclusions on coaxiality situation with fixed natural referential

From the above results, in the situation of coaxiality with fixed eigendirections over the material domain 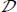, for motions near minimal dissipation, the dissipation equation is widely compatible with the presence, separately or simultaneously, of deformation localized in shear bands (or possibly other kind of strain concentration) and stress concentrations in chains of forces (or possibly other kind of stress concentration) (Figure 2.5).

Note that this situation of fixed coaxiality is particularly restrictive relative to more general situations (e.g. with just one eigendirection fixed as in minimal dissipation modes) which would open room for wider sets of allowable heterogeneities.

Here, in the situation with mixed heterogeneity, we have shown that this compatibility is secured for a selected wide range of heterogeneities, as defined by relation [2.8]. However, this range includes some additional limitations as compared with basic requirements [2.6], these additional limitations constitute sufficient conditions for the compatibility.

This leads to the question of the conditions necessary and sufficient to be complied with the heterogeneities, to secure this compatibility near minimal dissipation, in general situations.

Figure 2.5. Compatible mixed heterogeneity with shear bands and stress concentrations

2.2.2. General situations near minimal dissipation

To enter in more general situations, without assumptions on coaxiality, it requires us to follow internal actions that are considered as functions of stress and strain rates. Using the properties attached to the neighborhood of a thermodynamical minimum (the minimal dissipation), associated with the specific properties of internal actions near the minimal dissipation analyzed previously (section 2.1), we will establish the compatibility conditions for heterogeneity.

By using the components of internal actions (relation [1.22]), making a distinction between average values and local fluctuations of stress and strain rates, and then integrating over the material domain for averaging, the following expression is derived:

[2.9]

This leads to looking out for compatibility conditions with heterogeneity attached to dissipation equation through conditions on tensor .

2.2.2.1. Global conditions on heterogeneity

During motion, internal efforts and internal movements have local fluctuations that vary quickly in time. This very specific characteristic of granular materials, due to the (weak) part of dynamic effects still present even in “pseudo-static” movements, is widely confirmed by detailed numerical simulations of granular materials with discrete virtual particles [CAM 09]. For a given average of relevant quantities (stresses, strain rates, etc.), the corresponding local quantities can be considered as constituting a set, in which the observed real quantities fluctuate.

Consider a material domain in slow motion near minimal dissipation, under boundary conditions, consisting of imposed stress over a part of boundaries and regular displacements over the other part of the boundaries. In this situation, we can consider as given quantities the main energy fluxes (input power and output power, then the Trace and the Norm) attached to average internal actions . Together with its attached homogeneous average stress and strain rates 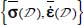, the allowed local heterogeneities 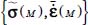, that verify 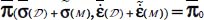constitute a set of solutions in which the real configuration is fluctuating rapidly centered around their barycenter {0,0}.

The minimum dissipation rule implies that the total dissipation 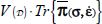remains in a neighborhood of a minimum, so the allowed heterogeneities that satisfy this minimum value are indifferent with regard to dissipation, in addition to satisfying the dissipation equation. Thus, two of these allowed heterogeneity configurations α and β, associated with the same average quantities 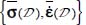, satisfy the following:

[2.10]

As the set of heterogeneous solutions for a given internal action tensor constitutes a regular convex set (section 2.1.4), which includes the homogeneous average solution, any of the allowed heterogeneous solutions will satisfy

[2.11]

The first of these conditions [2.11] is the classical “Macro-homogeneity condition of Hill–Mandel” [GER 86], which states that the expression of the average work rate of internal efforts is derived with the average stress and strain rates¹ under regular conditions. The second condition is specific to the present dissipative structure induced by contact friction in granular materials and states that the expression of the dissipation function is derived with average stress and average strain rates under regular conditions.

These two conditions also imply that, under the regular conditions considered here, local heterogeneities have no incidence on input power and output power (half sum and half difference of Trace and Norm), which also verifies the following identity:

[2.12]

Otherwise, these input and output powers, which are objective physical quantities, correspond to energy fluxes borne by sets of eigendirections of corresponding tensors. The physical consistency of identity [2.12] requires the directions (or set of directions) bearing these fluxes to be identical.

2.2.2.2. Necessary and sufficient conditions on local heterogeneity

The detailed analysis of the consequences of the condition [2.11] on 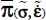is displayed in Appendix A.2.4 in the vicinity of the three modes of minimal dissipation:

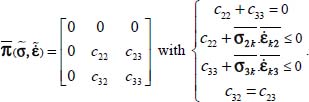
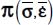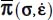• – Under Mode I, with signature (+,−,−), the natural basis of and correspond to each other by a rotation around their common eigendirection bearing the unique positive eigenvalue π+; in the natural basis of 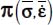, the average product of fluctuations will satisfy
  [2.13a]
• – Symmetrically under Mode II, with signature (+,+,−), the natural basis of 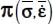and 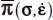correspond to each other by a rotation around their common eigendirection bearing the unique negative eigenvalue π⁻; in the natural basis of 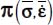, the average product of fluctuations will satisfy
  [2.13b]
• – Under the border mode in plane strain, in the natural basis of 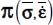, the symmetric product of local fluctuations is simultaneous for both kinds found for Modes I and II, thus the following condition is valid in any referential:

[2.13c]

These sufficient and necessary conditions on local fluctuations of stress and strain rates constitute the compatibility conditions looked for, as a kind of tensor extension of the macro-homogeneity condition of Hill–Mandel.

2.2.2.3. Physical meaning

Under 3D strain (Mode I or Mode II), the above conditions define an anisotropic structure inside the local fluctuations due to heterogeneity: the conditions depend on the eigendirection. It is only under the border mode in plane strain that these conditions become isotropic. Contrary to the compatibility conditions for the internal actions only (section 2.1), these conditions [2.13] bring additional restrictions restraining the covariances between local fluctuations in stress and strain rates.

Coming back to the analysis in the case of coaxiality (section 2.2.1), we note that the macro-homogeneity condition of Hill–Mandel, which complies with the macroscopic scale, sets, beyond a certain scale, the internal correlation between isotropic fluctuations, although bearable by the dissipation equation, to nevertheless disappear in the heterogeneity characteristics. This suggests that heterogeneity could include various scales, coming back to the terms of section 2.2.1:

• – from the “small” scale, anisotropic heterogeneity terms shall remain decorrelated;
• – up to a certain intermediary scale, isotropic heterogeneity terms can remain correlated;
• – beyond this intermediary scale, the correlation between these isotropic terms disappear.

A likely physical reason for this situation has been found through the analysis of the internal structure of shear bands and stress concentrations [FRO 04]. Indeed, there are no restrictions to the possibility of shear bands development at the macroscopic; whereas there are two strong macroscopic physical limitations to the development of stress concentrations which add to the no-tension condition:

• – the condition of static equilibrium (slow motion quasi-static assumption) restrains the development of isotropic heterogeneity in stresses because of its consequences on the divergence of the stress tensor;
• – the condition of macroscopic Failure Criterion restrains the emergence of stress concentrations at the macroscopic scale, confining these heterogeneities to smaller scales;
• – moreover, the no-tension condition (no tensile normal stress allowed) restrains the negative stress fluctuations relative to the average.

Therefore, this scale separation effect implies that by selecting a large enough REV:

• – the only significant heterogeneities which subsist at the macroscopic scale are the sole deformations (shear bands);
• – the local stress fluctuations, which could subsist at this macroscopic scale, are weak structures compared to those related to deformations;
• – as a result, the remaining macroscopic covariance terms are weak as compared to the products of average values, therefore .

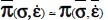2.2.3. Conclusions on heterogeneity of stresses and strain rates

The conditions of compatibility that are detailed above display a behavior depending on the kind of motion near minimal dissipation, i.e. of the mode ruling the movement in the considered material domain (reminding that these modes are exclusive: near minimal dissipation, only one mode may be found in the domain), i.e. depending on the signature of tensor π. This can be also linked to the concept of “tensor zone,” developed long ago and implemented on the phenomenological basis in “incremental constitutive models” of mechanical behavior [DAR 85] with formulations depending on the signature of strain rates.

Note also that these conditions, in true 3D motion (Modes I and II), are anisotropic, leaving room for the development of anisotropy induced by motion fed by the anisotropic heterogeneity fluctuations allowed.

In the following chapters, we will consider that the motions considered in the equivalent pseudo-continuum and their boundary conditions are sufficiently regular so that the necessary and sufficient conditions [2.13] are satisfied.

In this framework, the dissipation equation [1.30] applies either to average macroscopic quantities or to their corresponding local values, with regard to stress and strain rates, including the possible presence of shear bands and stress concentrations (chains of forces).

1 This condition was originally stated in the development of plasticity theory for metals, and the classical proof (refer, for instance, to [MAN 82]) relies on the assumption of material continuity, allowing the use of the divergence theorem. Granular materials being intrinsically discontinuous, another approach has been preferred here.