Before I was a scientist I was an artist. Okay, maybe that’s going a little far, but as a child I loved to draw. I always had a pencil in my hand, drawing racing motorcycles, horses, and everything else that was on the move (hint: The constructal law started then). Seeing something in these designs, my parents sent me to art classes after school. In my office at Duke, I still have a drawing of two Dutch ships I made in the fourth grade—and a portrait of my younger daughter, Teresa, I drew in a restaurant in Rome in 1990.
In retrospect, I realize that I had the feeling that I “saw” how things moved and how they fit together. Drawings provide the first clue about operation; they begin to tell us what something is by suggesting what it does. As Michelangelo reportedly observed five centuries ago, “Design (drawing)…is the root of all sciences.” I am always offering my amateur sketches to my students at Duke so they can see what we’re talking about, to remind them that the physical world is not made up of ivory-tower abstractions but images with shape and structure that move across the landscape and conform to physical laws.
Where a drawing provides the outline of an object, science allows us to burrow in and see how it functions—drawings show us the parts; science shows us how they move. Science is effective because it is concise. It converts physical phenomena into statements, formulas, and mathematical equations that have great explanatory power. In the process, it also tends to sever objects from their natural state. The mighty Danube ferrying water from central Europe or an elegant antelope jumping across the savanna loses its essential character when translated into data.
Speaking practically, this wouldn’t matter if design were simply an aesthetic concern. Science goes with what works, pleasantries be damned! The rendering of nature as charts, tables of numbers, graphs, and equations has opened up vast areas of knowledge and understanding. It underpins much of my work. However, it has also blinded us to deeper truths. Like the muck-raker in John Bunyan’s classic novel The Pilgrim’s Progress, it has focused the researcher’s gaze downward on his own small patch of ground.
When we raise our eyes and look around, we encounter a wondrous world of living drawings: birds and airplanes painted against an azure sky, pine trees and skyscrapers reaching for the heavens, rivers and roads snaking across the Earth’s surface. If we take a closer and wider look at the same time, we also see how much these images have in common: similarities in shape and structure so numerous that they can’t be the result of accident.
The constructal law makes “design” a concept in science. It reveals that scientists have been digging in the wrong patch when they ignored configuration or simply took it for granted. Design is, in fact, a spontaneously arising and evolving phenomenon in nature. Design happens all the time everywhere, not as the result of one mechanism but as the expression of a law of physics like Galileo’s principle of gravitational fall and the laws of thermodynamics.
Language can make this hard to grasp. The constructal law uses “design” as a noun that describes a configuration, which is known by many other names: image, pattern, rhythm, drawing, motif, etc. This sense, however, has been conflated with the verb “to design” that refers to the power of the human brain to contrive and to project images and linkages to new, higher planes. To design is human. It is human to absorb images that invade us, to reflect upon them in our minds, and to use them as personal catapults to make our drawings and devices so that we become a better and better species moving more easily on the landscape. In fact, we are so tied to the technologies that enhance our movement that we have evolved into a human-and-machine species (more on this later).
The verb “to design” has been monumentally unproductive in our quest to understand design in nature for three main reasons. First, it led to the common view that the things humans design are “artificial,” in contrast to the “natural” designs that surround us. This is wrong, because we are part of nature and our designs are governed by the same principle as everything else, the constructal law. Second, it has led some of us to search for “the designer”—God, or an individual, who must be behind every design. Science is not and never was the search for “the designer.” The name for that much older search is religion. Finally, it has led other, more scientifically minded people to reject the idea of design in nature as part of a broader repudiation of the traditional idea of a designer.
The constructal law tells us to stop looking for a phantom designer—there is no single mechanism or design-generating entity that can be found in river basins, blood vessels, transportation systems, etc. It teaches us, instead, that design is a phenomenon that emerges naturally as patterns. It also tells us that this evolving shape and structure is predictable. That is, if we know what is moving through a flow system, we can predict the sequence of designs that will emerge and evolve to facilitate the currents that run through it.
This starts with a drawing, or to use a better metaphor, the first frame of a movie—with what something looks like at a given moment. But nature does not exist in freeze-frame; it is dynamic, ever evolving. As the film rolls, the drawing changes over time in one direction: to flow more easily. I’m tempted to give this never-ending movie a grand and catchy title like Gone with the Flow or I, Constructal. This thrilling blockbuster details how flow systems configure and reconfigure themselves to overcome the friction and other forms of resistance that hinder them. Faster, easier, cheaper in terms of fuel (useful energy, exergy) used and materials required for movement: that is the flow system’s mantra.
In this chapter we show that evolving design in accordance with the constructal law is a universal phenomenon by focusing on three flow systems that would seem to have little in common. The first comprises the man-made cooling systems designed to remove heat from electronic devices. The second is the river basin that represents inanimate, nonbiological systems. The third is the system of blood vessels that carry oxygen and energy throughout our bodies. Each of these systems has been explored in great depth through the years; we know a tremendous amount about their shape and structure. But the systems have also been studied in isolation. This approach has led researchers to consider them not just apples and oranges, but apples and sports cars, oranges and shoes. The constructal law reveals that these flow systems generate strikingly similar designs in order to facilitate their own movement.
All three examples have at least two things in common. First, they are steady-state systems, that is, the currents that run through them (heat, water, blood) do not change much. Second, all three systems face one of the most common challenges in nature: how to move currents (of heat, fluid, people, goods, it doesn’t matter) from a point to an area or from an area to a point. This may sound like an abstract idea, but it is one that affects all of us every day. The movement of water from the reservoir (a point) to the various faucets and taps throughout our community (the area) is one example. So is the movement of sewage from each home and business (the area) to the treatment plant (a point). When we leave our homes each morning to go to work or the mall or to take the kids to school we become part of the volume of people flowing from the area (our neighborhoods) to various points within our local communities. We travel along networks of roads designed to get us where we want to go in the most efficient manner: faster, easier, cheaper. When we zoom along to our destination, obstacles have been mitigated if not eliminated. When we are stuck in traffic because of bottlenecks, we pay the price for outdated design.
I faced an area-to-point problem earlier in my career when I was designing cooling systems for electronics. My objective was to install as much circuitry as possible into the fixed space of a machine. Like everything else that moves, electronic components generate heat as they function. The heat is the result of dissipating (destroying) in the electrical resistances of the circuitry the electrical work taken from the wall outlet, in order to push all the electric currents through the circuitry. The more electronics you squeeze into a confined space, the hotter it gets.
The modern world of multifunctional cell phones and laptop computers hundreds of times more powerful than the room-size units that represented cutting-edge technology during the 1950s would not be possible if engineers hadn’t figured out how to channel away the heat, making these devices smaller, cheaper, and faster all at once. The burgeoning era of nanotechnology—which promises machines smaller than an eyelash—depends in great part on our ability to make those tiny workhorses operate without melting. Most people don’t give it much thought, but countless things we take for granted depend on our ability to remove heat.
There are many ways to cool a system. You can blow air on it, as a fan does inside your personal computer, or you can run coolant through it, as the tubes of Freon in many refrigerators and air conditioners do. Both approaches are effective, but they involve various costs—just as there’s no free lunch, there’s no free cooling. Blowers and cooling tubes take up lots of space. This doesn’t matter much with large appliances. But when we are measuring things in micrometers (a millionth of a meter), we need a better way.
My challenge while doing theoretical research in the early 1990s was to find a way to cool a solid block of circuits so small that it had no space for coolant coils or air. I had to find a way to cool, without a moving fluid, the inside of an electronic rock that was constantly generating intense heat.
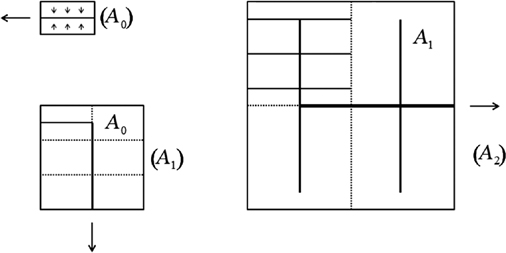
I began with pencil and paper. I drew a rectangle filled with circuits that produced heat at a fixed rate. This heat was the moving current in the system. My goal was to create a flow design that would pull the heat most efficiently from the entire area of the rectangle. After all, the heat does not stay within the circuit but travels to its environment. Remember, flow occurs in the physical world; thus, it is always tied to space, to geography. It is always mixing with and churning all around it, as we saw in chapter 1 when the warmer and faster-moving water on the ocean surface entrains the colder, slower-moving water below it. In my work, the best way to move the heat current was through solid-body conduction—by channeling the heat out of the core, solid region closer to the perimeter. I made two key decisions. First, I posited that the circuits are mounted on a structural material that is a relatively poor conductor of heat. Then, I imagined that I placed a slender strip of highly heat-conducting material—such as graphite, gold, or diamond—down the center of the rectangle (A0 in Figure 11). This would channel the heat from the surrounding area. There were no moving parts, so how would the heat leave the system? High temperatures drive heat currents to low temperatures. This natural flow would lead the heat to the cooler space first inside, near the perimeter, and then outside the system.
Through this design, I hit upon the seminal ideas that govern the design of everything that moves and flows, ideas that I would express a few years later as the constructal law. The first breakthrough arose from my decision to use two kinds of material—pieces of low and high conductivity. This choice proved to be a stroke of luck, because it encompassed the two major elements that cover the entire area of every flow structure: the channels and the finite-size spaces between adjacent channels (called “interstices”). In all designs, currents move slowly over relatively short distances through the interstices, and faster over longer distances through the channels. Because the constructal law is about pulsing, morphing things on the move, the channels and interstices are not static objects. They are not paintings or rocks that just sit there. They are designs that emerge and evolve to facilitate the flowing of the whole. It takes two to tango and this is the dance of flow design.

Figure 11. How to bathe an area with area-to-point flow. Start with an elemental system (A0) and shape it such that the resistance along the channel (the black centerline) is matched by the resistance above and below it. Next, the architecture of the first construct (A1) is discovered in the same fashion. Note that A1 is an assembly of elemental systems centered on a main channel (flowing downward), while the nerves of the elemental systems serve as tributaries to the main channel. The second construct (A2) is an assembly of first constructs (A1), and its architecture is discovered along the same mental route as from many A0s to a single A1.
To see how, let’s return to the circuits shown in Figure 11. The heat they generate is diffuse and disorganized. It moves slowly over the relatively short distance of the interstice to the highly conductive center strip. We cannot see diffusion. Once the heat is absorbed into this central channel, its flow becomes organized and it moves quickly down the channel and out of the system. We can see the channel.
Now consider rain that falls on a hillside and seeps into the ground. Like the heat given off by the circuits, its initial flow is diffuse, disorganized—the water seeping into the ground encounters a large resistivity as it moves through the porous soil (the interstices). Eventually the seeping water coalesces to form a rivulet, the first tiny channel. It does this by displacing the existing soil grains and connecting the pores between them. Because the rivulets evolve from what had been in place before they arose, the tiniest rivulet has the same thickness as the pore and the grain. Here’s the key point: By generating this design, its flow becomes organized and visible; it moves faster, more easily toward the quicker streams and eventually the running river.
We see the same thing in our circulatory system. We start in the heart, which pumps the blood through the aorta that branches off into ever-smaller channels (arteries) and very narrow rivulets (capillaries) that spread oxygen and useful energy to every cell (the interstice) through diffusion. The tiniest capillary has the same thickness as the “grain” that existed before it, the cell. Similarly, the system that carries the blood back to the heart goes from the small capillaries to larger veins and finally to the large vena cava, where the blood will begin its journey once again. In this case, too, design emerges because it facilitates flow.
The efficiency of this design is clear when we see how this architecture guides our morning commute. It usually begins with a walk to our cars, which we drive down small streets; just as capillaries are necessary for blood to reach every cell, local roads are needed to reach everyone in the community. If we had only local roads, it would take a great deal of time and fuel to travel long distances. So we construct highways into which the local roads flow. Once we leave the highway, we again travel on local roads to get where we’re going.
Highways offer obvious benefits, but this does not mean that they are the best option everywhere, because they cannot accommodate every commuter on the area they serve—just as the Danube cannot reach every seeping hillside on the continent and the aorta cannot move blood to every cell in our bodies. The slower, shorter paths are better for this. Thus, the slow and short flow works with the fast and long flow to move currents efficiently.
What flows through the system—heat, water, blood, people—is not nearly as important as the fact that every tree-shaped flow architecture is defined by these two flow regimes. It is this phenomenon that leads to design in nature. To see how, let’s imagine once again rain falling on a hillside. Initially the rain covers the ground evenly; when the rainwater moves, it flows like a sheet over the entire hill. How would you draw the movement of this water? You couldn’t, because it has no discernible pattern. Design starts to appear when the rainwater on the ground coalesces to form a rivulet. It is this transition to a new way of flowing that provides the contrast, which is the essence of design. This transition is the birth of design.
To think about water flow, take a white sheet of paper and imagine that it is a picture of wet ground. As the rain hits the ground and seeps into or flows evenly over it, nothing changes. To have something to draw, something must happen.
Draw a short line in black ink on the paper. This is the first rivulet formed by the water. Now we have black and white: channels and interstices. We have pattern. We have not only drawn the first rivulet but also have given structure to the white space that represents the rain flowing over the ground. As you add more black lines, representing the streams and rivers that evolve from the rivulets, your drawing becomes more complex.
The necessity and interdependence of channels and interstices is a point that was not fully appreciated before the constructal law. Design emerges over the entire area: It is the white space of oozing water that sustains and nourishes the black lines of the evolving channels that move that water more easily. It is important to remember this as we consider other flow systems. When we look at the circulatory system, for example, the eye focuses on the intricate, treelike structure as the aorta branches off into arteries and capillaries. But we can recognize this design (the channels) only because it stands in contrast to the surrounding tissue (the interstices) that is being fed.
This phenomenon also tells us something else. In order to move more easily, the flow system acquires geometry, design. It creates a path, many paths, connected in certain ways. Before the constructal law, we could see that rainwater coalesces to form rivulets, but we did not know why.
The constructal law accounts not only for the emergence of design but also its evolution. To see how, let’s return to the cooling system I was designing in the early 1990s. I had great freedom; I could design the path, write and direct the movie of morphing flow. The question we can ask now is: Would the designs I made when every solution was possible, using mathematics and engineering, resemble those that arise spontaneously in nature?
I began with the fact that all my circuits were giving off heat. If I left things as is, the heat would move out of the system too slowly, leading to a meltdown. So I placed that strip of high-conductivity material down the middle, to create a better, faster flow. I, of course, had an objective when I did this. The rainwater, by contrast, has no mind of its own. But two natural phenomena are part of its being. The first is gravity, which pulls the water to lower ground. The second is the constructal law, which accounts for the fact that rain will form the first rivulet when the flow of water becomes large and rapid enough. That is, when the flow is slow and short, diffusion is the way to go. But when the flow intensifies, an organized structure with streams and channels is better.
I called my first drawing the elemental construct. Then I got more ambitious. I thought of cooling a larger area. My objective remained the same: to facilitate the flow of heat toward the sink so that the entire area was cooled efficiently. As I added circuits, I increased the amount of heat in the system. A single strip of high-conductivity material, or cooling blade, would no longer be sufficient to handle the extra load—just as a small road cannot handle all the cars in a city. In simple terms, the heat would back up, riddling the area with congestion, causing overheating.
One possible solution was to place a cooling blade next to each circuit. This would have cooled the system, but it also would have made a heavy machine. Efficiency, including lightness, is a hallmark of good design. So I changed the positions and thicknesses of my blades and of the adjacent interstices to put the right-size blades in the right places.
I did not know it at the time, but this is the same thing that happens in a river basin. Even as my circuits were bombarding my rectangle with heat, so, too, does rain cover a hillside with water. In time the right-size channels emerge to handle the flow over the entire area efficiently. Just as I did not place a cooling blade next to every circuit, nature does not place a main river channel next to every hillside. Instead, we find a hierarchical pattern of many small rivulets, streams, etc. and a few large channels. And, while all river basins have the same basic design, they are all different in that they have evolved their own combination of small and large channels to serve the particularities of their location.
This intricate design does not evolve at once. At first, seeping is a good way to flow. The first rivulet forms when resistance builds to the point—which we can predict mathematically if we understand the environment in which it is emerging—that this becomes an easier way to flow. This is the elemental construct. As the volume of water increases, the rivulet coalesces with other rivulets, making a larger channel. This is the first construct. The process continues, creating a series of larger and larger constructs until a river basin emerges that serves the flow of water over the entire area through the right balance of multiscale channels.
Although these various-sized channels emerge in response to the specific resistance encountered by the flowing water, the overall balance of the system is achieved through a universal design balance we will explore in greater detail in chapter 7. It is this: The resistance to moving slow and short should be comparable with the resistance to moving fast and long. That is, when we look at the evolving river basin, we find that the time water spends seeping through the ground (moving slow and short) should be roughly equivalent to the time it spends flowing long and fast in the channels.
I used pen and paper, and later computers, to design and test the performance of various ways to cool the entire area. One solution was to place a strip of high-conductivity material down the center of each rectangle, producing a design of parallel lines. This proved to be less efficient than having a smaller branch run off the single main channel at a slightly less than 90-degree angle. This was my first construct (see Figure 11, (A1)). To dissipate the heat generated in areas even farther away, it was best to shoot other branches off these. When I looked at the drawing, I saw that I had created a treelike pattern. It did not occur by accident. It was completely deterministic. That was why, a few months later in France, I knew Prigogine was wrong when he proclaimed that the treelike patterns we see in nature are the result of chance.
It didn’t strike me until much later—after I had discovered the constructal law—that as I did this work I was engaged in a version of that old riddle: Which came first, the chicken or the egg? As I sat at my drawing board, I was essentially playing the role of the constructal law for my rectangles of heat flows: I was the clock and the evolutionary mechanism morphing the design for better flow. Just as in nature, I did this by changing the geometry freely: the drawing of the streams and channels. That is, I improved the performance of the whole system by changing its design. When resistance to heat flow by conduction built up in one channel, I reduced it by adding a branch or by bringing branches together. I could not eliminate any of the resistances. Imperfection is an inevitable phenomenon and a necessary part of design. As we will see in more detail throughout this book, good design involves the nearly uniform distribution of imperfection throughout the entire flow system.
Here’s another key point: I was not trying to mimic nature. I was not even looking at nature. I was living in my mind, working from pure theory of how things should be—better flow through the reduction of global imperfection. My approach corresponded with the one in nature, because this is the way to provide access to flow. The natural way is “anything goes.” Call that the egg part. The chicken comes in because I realized my efforts stemmed from the constructal tendency of everything to find better ways to flow. Thus, even as I was acting as the constructal law, I was governed by it. My “artificial” designs were completely natural.
Four subsequent experiments illustrate this. In the first, Sylvie Lorente of the Institut National des Sciences Appliquées de Toulouse, Wishsanuruk Wechsatol of King Mongkut’s University of Technology Thonburi in Bangkok, and I asked a computer to move a steady stream of water with less and less resistance out of the center of a disk to six users equidistant from one another on the perimeter. We gave the computer total freedom to solve this problem—it could use any material of any shape and size. Figure 12 illustrates that it generated a treelike structure.

Figure 12. The constructal flow pattern that provides easiest access for laminar flow between the center and six equidistant points on the circle. The bifurcations are located on the concentric circle indicated with a dashed line.
Then we ramped it up, asking the computer to serve twelve and then twenty-four users on the perimeter—that is, to morph the design to serve a larger area. As we see in Figure 13, it once again offered more elaborate treelike patterns, which are actually quite regular and simple, that is, easy to remember.
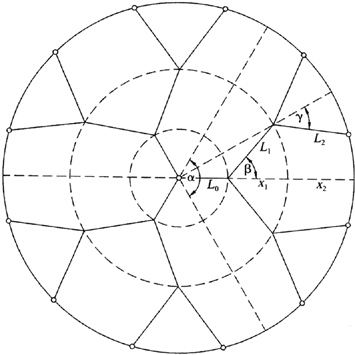
Figure 13. The constructal flow pattern for laminar flow between the center and twelve points on the circle. Note the two levels of bifurcation.
In the second experiment, J. D. Chen of the oilfield services company Schlumberger-Doll Research took two thin pieces of glass roughened with evenly spaced dimples. He covered one side of each piece with glycerin, a viscous fluid. He sandwiched them by putting the roughened sides together and laid them down on a table. Then he took a syringe filled with dyed water that he injected through a central hole in the top plate. The dyed water displaced the glycerin and created the now-familiar treelike pattern predicted by our computer simulation and pencil-and-paper calculations. That is, the water flow organized itself into a predictable pattern that evolved into a treelike structure in order to flow more easily (Figure 14). The less viscous fluid (water) flowed through the channels, while the more viscous one (glycerin) flowed through the interstices, not the other way around. The river basin cannot be a tree-shaped structure of wet mud surrounded by flowing lakes of water.

Figure 14. Tree-shaped patterns obtained by injecting colored water into a layer of glycerin between two glass plates.
The third experiment was one that you can easily duplicate at home. Grind some coffee beans finely and put them in a pot. Add water and bring it to a boil. You want the finest sediment that is still emulsified in the liquid, not the coarse grounds that settle in the bottom of the pot. Take the pot off the heat, wait three minutes, then carefully pour off the liquid. Wait another 30 minutes to allow more of the grounds to settle to the bottom. After that, pour out almost all the liquid, so that the remaining sediment has the consistency of soft honey or paint. Use this liquid to wet the entire area of a concave surface, such as the inside of a funnel (see Figure 15).
At first it doesn’t seem like anything is happening. In fact, the water is flowing volumetrically (diffusely) over the entire area and it is encountering a great deal of resistance. Then patterns start to emerge as the seeping water coalesces to form rivulets and then branches as it organizes itself into a predictable geometric pattern—an evolving treelike design—to reduce resistance and flow more easily as a whole. You can actually see how the water pushes the coffee grounds out of the way to form the first rivulets.
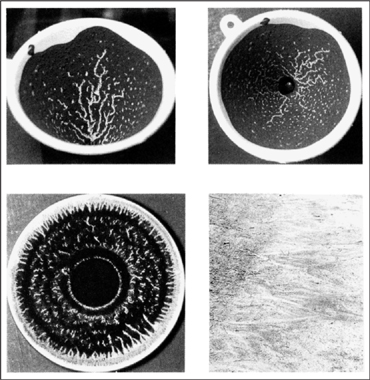
Figure 15. The formation of the smallest rivers in the drainage basin of a funnel coated with unfiltered coffee sediment. The funnel was held vertically upward, and the photograph was taken at an angle and from above. Note the marriage of shapeless flow (disorganization, diffusion) and flow with tree shape and structure (organization, streams) at the smallest, finite scale. Trees form all around the funnel and are visible from above. Bottom right: the first rivulets after the rain, on a sloped, sandy terrain.
Finally, to show how river basins evolve in time, several of us made “movies” documenting how they generate their area-to-point tree-shaped designs in accordance with the constructal law. In the first, Stanley A. Schumm of Colorado State University and his student R. S. Parker covered a 15-by-9-meter area with sand in a laboratory. Then they pelted it with a steady and uniform artificial rain. To mimic a natural hillside, the surface was flat and tilted slightly so that the water would drain to one side. The rain wet the sand uniformly, yet channels developed nonuniformly, in treelike fashion. Their development never ends. The tree shape keeps changing so that the collected water gets out of the area more and more easily (Figure 16). This is evolution, reproduced in the laboratory.
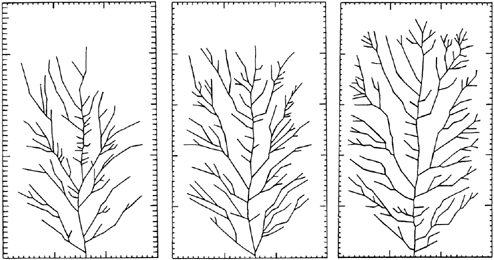
Figure 16. The evolution of an artificial river basin under uniform rain on the floor of the laboratory.
The second movie was a computer simulation based on the same scenario of steady uniform rain on a square territory, in a model of soil erosion in which grains are removed from spots where the local seepage velocity is high enough. The dislodged grains created channels with markedly higher permeability, and the channels formed a tree shape that grew into better and better tree shapes for moving more water more easily. The soil is uniform, with the same erosion characteristics everywhere. The velocity threshold needed to remove one grain was the same over the territory. This is why the flow structure that emerges is a symmetric tree (Figure 17).
The third movie was generated on the computer with the same erosion model, except that the soil structure and properties were not uniform. This time, the erosion threshold velocity had values distributed randomly over the square basin. The resulting shapes had a random appearance (Figure 18). This is due to the assumed random geological properties of the terrain, not to a presumably random tendency of generating configuration. This is the origin of the erroneous view that tree-shaped river designs are the result of chance. The geology and the conditions are, but the constructal law is not acting capriciously.
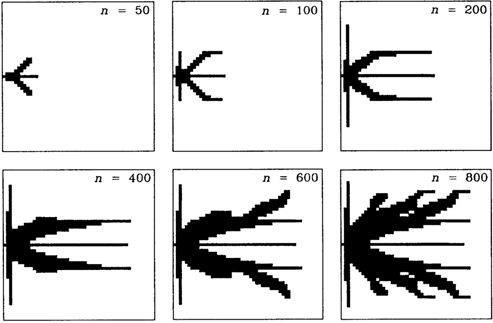
Figure 17. The evolution (persistence, survival) of a river basin in a porous layer with uniform resistance to erosion (n is the number of grains removed by the erosion process, that is, the measure of time).
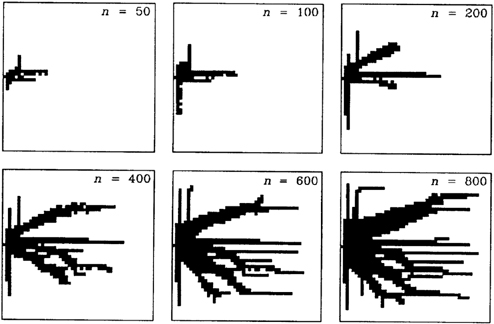
Figure 18. The evolution of a river basin in a porous layer with unknown (random) distribution of resistance to erosion. Compare this to Figure 17.
The principle that generated all these configurations was the same and it was deterministic. The second and third movies were reproduced in every frame of the movie, when the erosion simulation process was repeated on the same basins, with the same geological erosion characteristics. These experiments confirmed the fact that natural river basins of all sizes acquire evolving design. Lightning bolts; trees; the air passages in the lungs; the arteries, veins, and capillaries in the circulatory system; and every other point-to-area or area-to-point flow in nature always generate predictable patterns in order to flow more easily.
The treelike pattern isn’t the only configuration we see in such systems. River basins and blood vessels exhibit other design features that reflect their tendency to seek greater flow access. Several of these are well known, but until the constructal law we did not have a single explanation that predicts and unites these phenomena.
River basins reflect firmly established rules that relate their channel numbers and lengths. These include the fact that rivers meander—that is, they have a snakelike pattern whose wavelength is proportional to the width of the channel. In addition, the width of the channel is about five to ten times greater than its depth. For example, standing at the widest point of the Danube River, which is about one kilometer, we know the water there is quite deep. By contrast, we know that the rivulet that forms under a faucet in the garden is not deep because it is not wide.
Other scaling patterns—known as the rules of Horton, Melton, and Hack—have been known since the 1930s and are based on extensive measurements of river basin geometries all over the world. As we noted, these include Robert Horton’s descriptive finding that the number of daughter streams connected to a mother stream is between 3 and 5, and that the length of the longest daughter stream should be roughly proportional to that of the mother stream—a proportionality factor between 1.5 and 3.5.
Instead of cataloging streams in the wild, three colleagues and I used pencil, paper, and the constructal law to predict these scaling rules and to answer the fundamental question of why they emerge at all. We imagined a river basin and asked: What should it look like in order to reduce its flow resistance globally? We considered possible configurations and found that the proportion of daughter to mother streams should be 4 to 1 (not 2 to 1 or 8 to 1). Using this same approach we also predicted that their width and depth should be proportional, and that the length of the mother stream divided by the length of the daughter stream should be 2.
“Hold on,” shouts the careful reader—and by that I mean you. “You derived specific values through your work—the 1-to-4 ratio of mother to daughter streams—while Horton’s empirical observations unearthed a narrow range (between 3 and 5).” Good point. How do we reconcile the lack of precision and the unpredictability of finer details of a natural pattern with the deterministic constructal law that led us to our theoretical drawings? How do we account for this gap between theory and reality?
The short answer is that nature is filled with accident and variation all the time and everywhere. The same can be said of our pencil-and-paper fun; we considered 2 to 1, 4 to 1, and 8 to 1, not every daughter-to-mother ratio imaginable. More obvious is that a river basin in the Amazon forms under much different geological and meteorological conditions than one in Alaska—differences in climate, rainfall history, soil types, vegetation, and a host of other local factors affect the flow. Our knowledge of the developing internal structure of any flow system depends on two entirely different concepts: the generating principle (the constructal law) that is unique and deterministic, and the properties and external forcing of the natural flow medium that are not known predicatively and accurately at every point. The principle (that a flow system with freedom to evolve will generate designs that flow more and more easily) describes the direction of change over time in a natural world with varying conditions and constraints. If nature were a laboratory with a perfectly stable and unchanging environment, then every river basin would be identical. Instead, the river basins of nature are strikingly similar, because they have the same governing principle, which means the same rules of design and the same performance level, even though they look different. In nature, we find numbers varying between 3 and 5; given the immense diversity out there that means roughly 4. This also reminds us why flow systems continue to evolve, why there is always room for improvement.
To underscore this observation, let’s return to the circulatory system. It is one of the marvels of nature that this system is so exquisitely complex that no cell is far from a life-sustaining capillary. It transports blood from the heart to this vast volume by reconfiguring its design through branching. The same with the lung: The trachea begets two bronchi, each of which branches off into smaller tubes, which branch off into two smaller tubes, etc.
Thus we see the same design we witnessed in rivers—the creation of streams and channels to improve access for flow—but with much greater precision. Instead of a range of between 3 and 5, we find the number 2 every time (until the very smallest scales). We see then that the inanimate system of the river basin and the animate system of blood vessels and air passages evolve toward the same design structure. We should add that the structure of the circulatory system might indeed be imprinted in our DNA so that the entire structure emerges in toto. But the DNA chemistry alone cannot account for the fact that the same phenomenon governs the evolution of river basins, lightning, and city traffic. The answer is the constructal law.
In addition, just as Horton found that the length of the longest daughter stream is proportional to the length of the mother stream, the Swiss physiologist Walter Rudolf Hess demonstrated in 1913 the proportionality between the diameters of the mother and daughter blood vessels, which is a factor of 2 raised to the 1/3 power. This was extended in 1926 by the American physiologist Cecil D. Murray, after whom this design rule is known as Murray’s law. The ratio Hess and Murray discovered is in fact the one that reduced the flow resistance of the Y-shaped fork of the vessels and is also what we find in the real world.
Using the constructal law, our group predicted that the pairing of blood vessels (dichotomy) should occur in order to reduce imperfection when the flow is laminar. Similarly, it allowed us to predict that rivers should use the 4-to-1 ratio (quadrupling) because their flow is not smooth but turbulent. This is because the type of flow (laminar or turbulent) has an impact on the design of the branching. Most blood vessels and bronchial tubes are small enough so that the flow through them is smooth, or what we refer to as laminar flow. The branching into two (or dichotomy) should occur in this instance to reduce flow imperfection. The flow through river channels with rushing water is much bigger and faster, and consequently their flows are turbulent. Thus rivers tend to branch with a 4-to-1 ratio.
So we see in the constructal law the never-ending movie of life in action. From the man-made flows to all the other animate and inanimate flows of nature, it provides, for the first time, an understanding of how seemingly disparate phenomena are governed and united by a single principle of physics. By refocusing our attention on how things look—on their evolving designs that are the morphing boundaries of their flow systems—the constructal law reveals, predicts, and explains design in nature. It shows us how the governing laws of the universe, such as the laws of thermodynamics, work with the universal tendency to flow with configuration in order to create the pulsating, evolving designs we see all around us. It allows us to see the predictable pattern in what we had long considered just cosmic coincidence.
I have not only discovered this fact, I’ve lived it. When meat began to disappear from shelves in Romania during the 1960s, my father, a veterinarian, had a solution. He hatched chickens. He had a light box that illuminated the inside of the egg so we could make sure the embryo was developing. As a teenager, I stared in awe and wonder at the growth that unrolled before my eyes each day, as the vasculature grew and spread tightly on the inside surface of the shell. I also noticed that the design I was seeing was the same as that of the river basins on the colored maps I was drawing in school. Where the chicken embryo was evolving on the inside of the sphere, the Danube basin had evolved on the outside of the spherical Earth.
Back then, I considered these similarities cool correspondences, nice ideas. Now I recognize that my father’s light box was illuminating the design all around us. I am also able to see that the Earth with its river basins and other “basins”—of atmospheric, ocean, and air traffic circulation—is a vasculature woven on top of and through another spherical surface of life. So life is flow, life is movement, life is design.