
Most people don’t like airports. Worse than the overpriced sandwiches and “unforeseen delays due to weather conditions” is the feeling of being stuck, boxed in among the confining crowds.
But the Hartsfield-Jackson Atlanta International Airport is different. It may be one of the world’s busiest hubs, serving almost 90 million passengers each year, but when we walk down its corridors and ride its underground train, we seem to flow. This natural ease of motion is one reason the airport is consistently named among (and usually the) most efficient in the world by the Air Transport Research Society. Architects, engineers, and passengers can easily see that the Atlanta airport is a masterpiece of design. The more interesting question is: Why does it work?
The traditional approach to finding the answer sends us back to the drawing board. By poring over the airport’s blueprints, we can determine the placement of each corridor, escalator, elevator, and concourse train. By examining the relationship between these spaces and the travelers rushing across them, and then performing thousands of other calculations, we can understand how all the parts of this giant jigsaw puzzle fit together so neatly.
After doing all that, we could build a model to help us construct our own efficient airport. This is how much of science works. Researchers and engineers catalog the elements in play in any given situation, whether it’s the many components that comprise a modern airport or the complex interplay of solar heating with oceanic and atmospheric currents that contributes to global climate. Like master chefs, they continuously tweak their recipes, adding and subtracting features to their models, assigning them different weights, to come up with a model that “works.”
This ad hoc approach is laborious but effective, enabling us to fathom a wide range of phenomena. It is also limited because it reflects the absence of principle. We must slice and dice the variables because we do not know the law governing their interaction and selection. It is akin to finding that our cake tastes just right when we add one cup of sugar, without truly understanding why half a cup or two cups are not the right amounts. It is like seeing the tree-shaped pattern of lightning bolts and river basins and not knowing why they look the same.
The constructal law offers a better approach. Instead of forcing us to rely almost exclusively on rejiggering variables, it is a principle we can use to build better things.
For example, the relationship between mass and speed we discussed in chapter 3, and the discovery that biological creatures should evolve to cover longer distances per unit of useful energy consumed, can help us create better cars, ships, and airplanes. The fact that the design of trees and other vegetation should facilitate the flows of water and stresses described in chapter 5 can inform our construction of mechanical structures (from beams and bridges to self-healing metals) that are also vascularized. And the insights about hierarchy detailed in chapter 6 help us understand why some social systems perish and others thrive.
These findings do not provide templates from the natural world that we can copy in our own designs. Instead, they illuminate the principle that already governs that work. Just as the discovery of the laws of motion allowed us to build better flying objects, the constructal law will jump-start our own efforts today. In this chapter we will explore how we can design better airports, roads, and cities by taking an even more dynamic look at hierarchy and the evolution of technology.
Until now we have focused on size, including the fact that all vascular flow systems generate multiscale channels because this is a good design for spreading a current from a point to an area or an area to a point. But that raises several questions: Where should those channels be placed? And in what combination? Is there a principle we can use to predict not just the fact of hierarchy but its design?
The answers emerge when we remember that the constructal law concerns movement, access, and speed. Flow designs—from lightning bolts and trees to scientific laws—emerge and evolve to facilitate flowing currents. Although these designs are what grab the eye and command attention, they are not the main attraction. Like trains and planes, they are a means to an end. They are global engines that have arisen for one reason: to enable the currents that flow through them to move more easily across the landscape.
In the hierarchy of sizes and numbers, the size of the main channel (the Mississippi, the aorta, the president) is less important than the fact that it moves the most current quicker and over a longer distance. The smaller channels of varying sizes and the interstices move less current, less rapidly, over shorter distances. As we will see in this chapter, the emergence of multiscale design hinges on the balancing of these two flow regimes. The key design principle is this: The time to move fast and long should be roughly equal to the time to move slow and short. When this occurs, currents flow with ease over the area inhabited by the entire flow structure. This is the foundation of all constructal designs, including the Atlanta airport.
Using this principle, we no longer have to rely on ad hoc models to determine the foundations of good design. Suddenly, we see the connection between seemingly unrelated phenomena, between the design of snowflakes and river basins, of flowing lava and bacterial colonies. It predicts how dogs should run along the beach; the path of your morning commute; as well as the development of Rome, Paris, and other cities.
All these connections begin with the prediction that given freedom, entities on the move should generate and seek paths that allow them to move faster and farther per unit of useful energy. Because flow is governed by this principle, this is true for the simplest forms of movement and the most complex.
In addition—and this is key—because the constructal law summarizes an evolutionary tendency, simple and complex designs are not discrete phenomena. They are part of a continuum in which smaller structures should morph inside and along with larger ones. This means two things. First, the complex designs are rooted in the simplest—the intricate air transport routes followed by all the planes flowing over the globe (Figure 42) grow out of the basic movement of people walking from here to there. Second, even as each component of the flow system evolves to flow more easily, it is also part of a larger system whose shape and structure are also evolving to strike the right balance among all its components to enhance its flow. To put this in human terms, we could say that the constructal law finds the nexus between individual self-interest and collective action.
To see how, start with a drawing of a straight line. It is the most direct path from one point to another when only one type of movement is involved. Unobstructed light, for example, follows a straight line between two points. Given freedom, so do people. If a man walks from A to B, and if the surface under his feet is paved uniformly, as in a parking lot, then the urge to have access inspires him to follow the straight line AB.
The broken line is more complicated and an even more prevalent drawing in the nature of flowing things. We see it whenever the straight-line path is unavailable, which is often the case for wingless people who cannot zip across the clear sky. Nevertheless, we seek special paths and we find them, zigging around a tree here, zagging to the shortest path around a body of water there, to get where we are going.

Figure 42. Where aircraft flew in 2002 (top) and where aircraft will fly in 2050 (bottom). The figure shows the density and paths of all aircraft, which are visible because of the trails of condensation left behind every aircraft.
The broken line is also the way to go when the flow between points A and B involves two kinds of movement, such as running and swimming. Tim Pennings, professor of mathematics at Hope College in Michigan, demonstrated this through a clever experiment involving his Welsh corgi named Elvis. While playing ball on a beach at Lake Michigan, Pennings noticed that when Elvis started running from point A on the beach to fetch a stick floating in the water at point B, he always chose a special point on the water’s edge, point J, to jump into the water and swim to B (Figure 43). The jumping point was such that the segments AJ and JB were almost, but not exactly, perpendicular. Why? Because it is easier for Elvis to run than to swim.
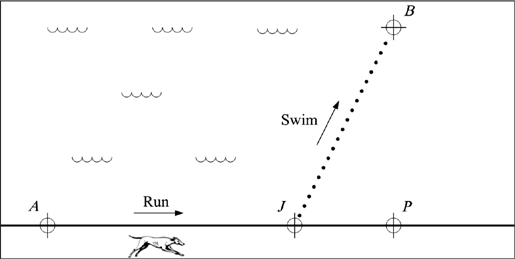
Figure 43. The dog (A) reaches the floating stick (B) by combining two very different kinds of movement, running and swimming. The dog runs on the beach from A to J, then swims from J to B. The refracted path AJB can be predicted by minimizing the total travel time from A to B. The same refracted path is predicted by minimizing the work done by the dog from A to B.
This does not mean that the shortest swim is the answer: That would have been the case if Elvis always jumped into the water at point P, which he did not. The run and the swim should be balanced against each other such that the entire effort of getting from A to B is reduced. In this way, Elvis solved one of the basic problems in constructal theory: finding the quickest way to get from point A to point B when two forms of movement are involved. The answer he intuitively discerned was that the best route is not always the shortest. Dogs of innumerable generations before Elvis learned this the hard way by catching the food floating at B, starving, or drowning. The same instinct is in us. If we start running in order to save a person drowning in the ocean, each of us will run only partially along the edge of the beach before jumping in, for example, from A to J in Figure 43, not from A to P.
The mind is a wonderful thing because it can imagine many variants of the movie that we just watched. Instead of a stick floating on the water, we see an imperiled person caught in a riptide. A woman leaps into action. Not just any woman, but the world-record holder in the 100-meter dash. Problem is, she is a terrible swimmer. She will follow instinctively a broken line that maximizes her running time and minimizes that spent in the water. Similarly, if our would-be hero is a champion swimmer who runs like a tortoise, she will jump into the water sooner because this is a better route for her.
The constructal law does not command a one-size-fits-all design. It proclaims that everything should seek greater and greater access in an environment booby-trapped with constraints, obstacles, and surprises. These countless constraints—such as the relative running and swimming skills of people, the topography encountered by ground water—account for much of the diversity we find in nature without violating the principle. This means that we can use the constructal law and simple geometry to predict what every path should look like to reduce global effort.
We do this by recognizing that all lines involving forward motion form angles between 90 and 180 degrees; anything less than 90 degrees is moving backward. The straight-line path, for example, is a 180-degree angle. When this path is not available, the line is bent or broken. How much? The answer depends on the ratio between the speeds of the two types of movement involved—V0 (slow) and V1 (fast). The greater the discrepancy, the smaller the angle. To determine the broken line that Elvis should follow, we divide his running speed by his swimming speed. If they are identical, he should follow a straight-line path to the stick. As they diverge, his angle of “refraction” should decrease. The extreme design—the 90-degree angle of refraction—is the natural way to flow when the two flowing modes differ significantly. We see this most clearly in modern cities, where there is a vast difference in the speeds of the two most common forms of movement, walking and riding in cars. Thus, the avenues and side streets meet at 90-degree angles.
Elvis the dog had not crossed my radar in the early 1990s when I was designing advanced cooling systems for electronics. But it turns out that he had found a solution to a simple version of the far more complex and prevalent challenge that confronted me. With all due respect to Elvis, he had to worry only about himself, how he should combine running and swimming to fetch his stick. My work addressed the far more common broken-line problem in nature of how to minimize the travel time involving two flow regimes and innumerable currents over an entire area.
Put another way, my work did not just concern Elvis but all the dogs and all the sticks on the same area. Or, more precisely, how to ferry all the heat generated by all the electronic circuits out of a tiny, confined space—just as the Atlanta airport must accommodate all the people traveling across its concourse, and the air transport system must facilitate the flow of all the planes around the world. As we saw in chapter 2, I accomplished this by placing the circuits on material that did not conduct heat well (a slow way of moving akin to swimming) and then placed a strip of highly conductive material down the middle (a faster way of moving, like running).
The heat generated by the circuits spread diffusely—slowly in a disorganized, patternless movement—over the short distance perpendicular to the center strip, where it moved relatively quickly over the long distance to the heat sink. I found that I could cool a larger area by adding more strips of high-conductivity material in a treelike pattern. How many trees? My answer provided the breakthrough that illuminated a central principle of good design: Just as Elvis balanced the time he spent swimming and running, the right answer was one that balanced the resistances that all the heat encountered while moving in these two flow regimes.
The fact that Elvis and I derived the same answer to a similar problem offers further proof that a principle is at work. As we have seen, when a straight-line path is available, nature embraces that. It is only when that ideal path is not available that we find a broken line—not just any broken line, but a special one that still bends toward the fastest route. When that broken line involves two types of movement, its shape will strike a balance between them in a configuration that provides better access for whatever is flowing. These three scenarios generate simple drawings because they concern the movement of a single current between two points. Flow in nature, however, is almost always more complex because it usually involves vast quantities of mass—all the water in a river basin, all the elephant mass over land, all the goods and services produced by a local or global economy. Thus, the design generated is not a single straight or broken line but a system of multiscale channels with hierarchy, that is, a superposition of broken lines. It, too, is governed by the constructal law.
So far we have focused on the evolving design of the channels that carry that current. But the constructal law governs all flows over an area or throughout a volume. Think of a river basin. The eye is drawn to the vascular structure of its channels. But that is only part of the drawing. Equally important is the area between those branches that feeds water to them. Just as airports do not generate passengers but channel them from surrounding areas, and banks do not generate money but collect it from thousands of depositors, the river basin must collect its water from the surrounding ground. Similarly, my strips of high-conductivity material did not generate heat but attracted it from the surrounding area or volume.
In terms of a drawing, then, the entire area of a flow system is both the black (the lines of channels that emerge) and the white (the rest of the area—the interstices—that serves or is served by those black lines). When we take a global view, we see that everything that moves over an entire area has two ways to flow—short and slow (the white), or long and fast (the black).
The constructal law predicts that currents should move slow and short when that is the better way to flow, and fast and long when this improves movement. That is, in every instance the flowing current should “select” the better mode for flowing. As we saw in chapter 2, in many cases this involves the transition from laminar to turbulent flow in water, air, or other fluid. In larger designs, this means that current will flow diffusely until it can move more easily by coalescing into channels, and vice versa. Water seeps through the ground until it encounters more water; the water then can move more easily by forming rivulets and larger streams.
As these hierarchical designs evolve, generating multiscale channels (few large, many small) to cover more ground, they should strike a balance between these two flow regimes every step of the way.
The river basin does not begin with the Mississippi but with water seeping diffusely in the ground that forms the first rivulets; the evolution of our circulatory system did not begin with the aorta but with the diffuse flow of blood in tiny organisms that eventually generated capillaries and larger blood vessels; our transportation systems did not begin with highways and airports but with the flow of people across untamed ground that created the first footpaths.
The water in the river basin combines the slow seepage down the hill with the fast flow along the river channel. The slow flow is perpendicular to the fast, just as the access lanes from the concourses in the Atlanta airport are perpendicular to the trains they lead to. Scientists who study the movement of chemically marked water flowing down a river basin are finding that the seepage time down the hill is essentially the same as the time spent in all the river channels. This occurs in all the river basins on Earth.
As we detailed in chapter 1, it also happens in the design of animal lungs. Take a breath, a nice deep one. The time needed by the air to flow quickly down the airways from your mouth to the alveoli is the same time required by the oxygen to diffuse slowly across each alveolus and into the tissue where it is absorbed by the blood. Notice, too, that this rhythm, this design—these two times in balance—remains in place no matter how quickly you are breathing; the time spent inhaling is always the same as the time spent exhaling. The same rhythmic design characterizes the beating heart, blood circulation, digestion, excretion, ejaculation, etc., and is predictable based on the constructal law.
In fact, this design happens everywhere. The surface of the Earth is a tissue woven of all these flowing things. It is covered by an extremely diverse number of things that flow and move in these two different ways. There are, of course, many poor designs, especially in the man-made world, whose evolutionary history is much shorter than that which we find in older, more entrenched systems. More telling is the fact that so many of them strike the same balance between the two flow regimes we find in other natural designs.
Now we will see how, by looking at an array of engineered designs in history. We begin with one of the oldest and most famous structures, the Pyramids in Egypt, and other ancient sites that still intrigue us with their size and geometric form. Even by today’s standards, their size is immense and their form is perfect. These designs are so impressive that our culture tends to attribute them to an ancient scientific base of knowledge that was lost, and to presumed links between ancient peoples living on opposite sides of the globe.
The constructal law solves the mystery of the Pyramids in a surprisingly direct way: They are the result of a universal natural phenomenon that governs the movement of all materials on Earth. This view does not take anything away from the achievements of the ancient builders. Rather, like the evolution of the wheel described in chapter 4, it is a physics argument that what our ancestors chose to do is natural, that to engineer is natural, to tend to migrate on the globe is natural, and that the geometry of all material flows (animate and inanimate) can be reasoned based on a single principle.
In the making of a Pyramid, the constructal law calls for the expenditure of less work by striking a balance between the time to move slow and short and the time to move fast and long. This principle accounts for the location and shape of the edifice. First, the location is in the middle of the quarry, because less work means a shorter sliding distance between the place where stones are mined and the construction site. (As technology has evolved, work sites have moved farther from the sources of material because it takes less effort to transport them.)
This same phenomenon also accounts for the shape of the Pyramid. The French architect Pierre Crozat demonstrated that builders used the Pyramid slope to move the stones upward using wood levers and ropes. Each stone was lifted, moved horizontally, and then dropped at the next higher level. In a pile of stones held together by gravity (dry-stone construction), shape means the base angle. A good angle is one in which the work spent on moving the stone horizontally is roughly the same as the work spent on moving it on the incline.
If the flow of stones is configured such that the edifice is constructed with less and less expenditure of useful energy, then the shape of the pyramid (the angle at the base) is unique, size independent, and dictated by the technology of the era. The prediction is that the pyramid construction must proceed layer by layer such that the pyramid is geometrically similar to itself during its growth (in layers, like an onion).
Put another way, there are two “media” through which the streams of stones flow—two mechanisms—one with low resistivity (moving the stone horizontally, which is relatively easy) and the other with high resistivity (moving on the incline, which is much harder). When the two media are highly dissimilar, the angle at the base (that is, the angle of refraction of the ray of moving stones) approaches 90 degrees. Rivers, stones, and animals flow with configurations that come from the same principle. We should also note that the law of refraction governs the movement of goods in economics, where it is known as the law of parsimony. For example, to ship Lucky Strike cigarettes from Durham, North Carolina, to soldiers in Dunkirk is not to send them on the shortest (geodesic) line that links the two cities. It is to send the goods along a less expensive path if possible, which could be the refracted ray consisting of the short and high unit price (land route, by truck from Durham to Savannah), followed by the long and low unit price (by ship, from Savannah to Dunkirk).
The history of the development of trade routes documents this constructal design tendency. We often hear that a city or harbor grew because “it found itself” at the crossroads—at the intersection of trade routes. In fact, it works the other way around; the efficient refracted routes defined their intersection, the city, the port, the loading and unloading site, etc. More complicated flows are bundles of paths, refracted such that local and global flow is enhanced. A river basin under falling rain is like an area inhabited by people: Every point of the area must have greater and greater access to a common point on the perimeter. There are two media, one with low resistivity (channel flow; vehicles on the street) and the other with high resistivity (seepage through wet riverbanks; walking). The shape comes from the tendency to facilitate flow access.
The Atlanta airport is a more complex design than the Pyramids. Instead of just balancing the movement of stones, it must accommodate all the passengers and their goods (Figure 44). Movement in the airport is between a point and an area—for example, from the airport entrance to all the gates, or from one of the arrival gates to all the other gates and the exit. To cover its entire area, passengers must combine two movements. They travel slowly over a short distance as they walk down the concourses. Then they proceed quickly over longer distances by riding the train that links the concourses.
With these parameters in mind, Lorente and I used the constructal law to predict what shape the Atlanta airport—and all such designs—should have to provide the most access to the currents that flow through them. Through this work, we developed a formula that can be used to determine a good design for areas covered by two flow regimes, and thereby reduce our reliance on models.
The airport area can be shaped so that it facilitates access for every body and every thing that moves. We reasoned that in the sketch shown in Figure 44, the rectangular area (H × L) is fixed, but the shape of the rectangle (the ratio H/L) may change in the minds of the designers who are seeking to facilitate flow access. These minds are numerous, not one. They visualize all sorts of flows—people, luggage, food, waste, services, etc.

Figure 44. Two ways to flow are better than one. A large airport without trains, or without walking, cannot compete on the same area with the design that combines walking with riding in a vehicle. The Atlanta airport is a modern illustration of the seed from which all forms of urban and natural flow networks have grown. On a fixed area (A = HL) with variable shape (H/L) and two speeds (walking V0 and train V1), the time of travel from P to M (or from all points Q to M, averaged over A) is minimum when the shape is H/L = 2V0/V1. The walking time (PR) is equal to the riding time (RM). The long and fast travel is balanced with the short and slow travel.
But for now we will just consider passengers. What is the best ratio for H/L? Consider the travel between the farthest gate (P) and the terminal (M). Think of P as the least advantageous position because it is the farthest. The passenger from P must combine some walking at speed V0, on the short side, with some riding on the train, at speed V1. This passenger needs the time t0 = (H/2)/V0 to walk, and the time t1 = L/V1 to ride. The total time needed by this passenger is t0 + t1, and it is minimal when the shape of the area is H/L = 2V0/V1. The ratio of V0/V1 is the walking speed divided by train speed and is considerably smaller than 1. Consequently, the aspect ratio H/L must be smaller than 1 (as shown in Figure 44).
It is especially telling that we also discover this special shape if we take all the passengers into account. If we calculate the time to walk and ride for the arbitrary passenger Q, and if we average this total time over all the passengers (that is, over the rectangular area), we find also that the averaged time is minimal when H/L = 2V0/V1. The aspect ratio of the rectangle is a number comparable with 1 but smaller than 1, for example 1/2, because the V0/V1 ratio for the walker and the train is a number of order 1/4. This shape is evident in the actual layout of the Atlanta airport.
The coincidence that the best airport shape for the farthest traveler (P) is the same as the best shape for a community of travelers as a whole is worth thinking about. It raises the question of whether the airport designers behaved altruistically by shaping the airport to help the passengers who must use the most peripheral gates, or the same designers as a group behaved egotistically by imagining themselves in that airport, at every possible gate position Q. The more plausible interpretation of the final design is the egotistical route. Configurations emerge naturally in areas and volumes where there are large numbers of moving individuals and each individual has the same tendency, the same drive, as his or her neighbors: to seek and find access, and go with the flow. The urge to organize is selfish.
Even more amazing is that when the airport shape is the one that everybody likes, then the average time needed between the area and the point (M) is divided roughly equally between the time spent walking and the time spent riding on the train. The genius of the airport’s design is this: The time to walk along half a concourse is about the same as the time to ride quickly on the train, end to end—about five minutes. That is, the time we move slowly (walking) is equal to the time we move fast (riding the train). Passengers do this through a design that should be familiar by now: It is shaped like a tree.
It is no surprise, then, that the newest design found in the world’s leading airports—the most recent evolution of the flow systems we call airports—look more and more like the Atlanta airport. The facilities in Singapore, South Korea (Incheon), Hong Kong, and Tokyo (Narita Terminal 2) are all characterized by the right combination of pedestrian concourses and perpendicular trains. Through the constructal law, the evolution of airport architecture and technology is predictable. This is not copying the Atlanta airport. This is natural evolution, in accord with the constructal law.
We see a similar balance in the transport systems connected to airports. The time to fly along one of the air routes of Europe is comparable with the time to travel on land, perpendicular to the route (Figure 45). It takes roughly two hours to fly from Paris to Madrid and about two hours to drive from the Madrid airport to a locality on the entire area served by the airport. A fast train in Europe links two neighboring cities within one hour or less. This is also the time needed to travel between home and the more numerous train stations. Inside the city the areas covered are smaller but the principle still reigns. The minutes needed to get to the train station should be comparable to the minutes spent on the train. In other words, you would be less likely to drive two hours to a train station to take a half-hour train trip. Even if it saves you a little time in the long run, you would probably just continue driving the full distance to avoid expending the effort to find a parking space, buy a ticket, and overcome other forms of resistance. In a well-designed transportation system, we spend equal times on our feet and on our bottoms. Just as in the Atlanta airport. In a poorly designed system, these times are out of balance.

Figure 45. Tapestry of air mass transit over Europe. The burning of jet fuel is for moving people and goods on the whole area: This flow is hierarchical and nonuniformly distributed. Large centers and thick channels are allocated to numerous smaller channels. The fine channels are allocated to area elements (between the channels) that are covered by ground movement—people, and all the animate and the inanimate flows of the environment. The time to travel long and fast (along the channels) is comparable with the time to travel short and slow (across the areas between channels).
As the TV ad says: Individual results will vary, depending on the person’s starting location. The principle applies to the average time it takes everyone to complete his or her journey; it describes the flow design of huge numbers of people, not the experience of each person. The constructal law is the big picture, but it is also the small one. It is the forest and the tree. It is all the animal mass that moves on Earth and the athlete that runs quickly.
The shaping of the airport area is a template for the shaping of all the other slow and fast loops in the flow tapestry of nature. For instance, we can use it to predict the design of cities—which serve many functions but whose shapes and structures are determined by the need to enable people and goods to move easily. Anywhere, and everywhere, it’s all about flow.
The smallest street with its houses, lawns, and yards on both sides is just like the airport area (H × L). This is the smallest building block of the city design. The shape of the smallest city block is dictated by the ratio 2V0/V1, where V0 is fixed (the walking across the lawn), and V1 increases in time because vehicles become faster in time.
The entire fabric of city design evolves in time because of technology evolution, which has reduced the time it takes to cover an area. With pure theory in our minds, we can look back at the evolution of city designs and marvel at how continuous the running of this movie has been. In antiquity, the speed of the heavy cart pulled by the ox was about twice the speed of the human. This means that the smallest street would have emerged naturally on a square city block—an area with a shape H/L comparable with 1. Given the fact that the simplest drawing for the individual house and yard is a nearly square rectangle, this means that in antiquity the smallest city block must have had one or two but not many more houses on one side of the street. Today this holds true for all the other rural and urban areas where the fast mode on the tiny street is the ox and cart.
Fast-forwarding to the present, in the design of cities, where the car speed is more than ten times the walking speed, we should expect more houses on the smallest streets. In addition, city blocks should become more elongated as the technology of transportation evolves. This is in agreement with designs of modern urban developments.
The two ends of this movie are illustrated beautifully in one map of modern Rome (Figure 46), the birthplace of Western civilization (city living, literally). The center of Rome is the ancient city, and here the streets are considerably shorter than in the more recently built, peripheral areas (for example, the upper corners). History begins to make sense now that the principle of the evolution of design is known.

Figure 46. The plan of modern Rome, showing that in the ancient city (the center) the street length scales are considerably shorter than in the new outskirts.
All roads lead to Rome. This is how the population moving from the countryside (the area) was connected to Rome (the point). Not a radial pattern with roads in all directions, but a tree-shaped one with only a few major arteries leaving the city. This natural design connects every large and small city to its allocated area, and all city and area units are connected to Rome. The same design connects every river basin and delta to their points of discharge and supply.
As the human settlement becomes larger in time, streets and patterns of streets emerge. Small villages have only two or three streets that touch the main square and branch outward into more roads that cross the land. Larger towns and cities have grids. The reason is that in larger settlements there are many more points of interest that must be connected by tree-shaped flows of humanity to the surrounding area.
The street design is a plaid: A few broad streets form a grid that is superimposed on a grid formed by narrower streets. To see this, imagine that inside the city area the entire population (all the Qs in Figure 44) must have access to one destination, M (for example, a church). The design that serves the population is a combination of slow and fast movement (small and large streets), as in the Atlanta airport. The movement of this population between the area, H × L, and the point, M, is tree shaped.
Next, imagine another destination point, perhaps a market, in the same area. The area-to-point flow must be another tree-shaped flow, but this new tree will be superimposed on the preceding tree flow. More points of flow attraction on the same area will require more tree flows superimposed on the preceding ones. The infrastructure of solid channels that facilitates all these possible (superimposed) tree flows of humanity—whenever they may occur—is the grid of streets.
All the individual area-to-point movements through the grid, however, are tree shaped, not grid shaped. But, through the superposition of many area-to-point movements, it begins to look like a grid. Imagine the movement of the city population to a political rally in the main square. Citizens converge in river-basin fashion, the many from the small streets becoming groups and columns on the avenues. Another tree-shaped flow is the morning migration of commuters from their homes to the train station. In the network of air routes over Europe (Figure 45), the flow of passengers from (or to) a city is tree shaped, not grid shaped. How do the streets and the air routes accommodate all these superimposed tree-shaped flows? By evolving into a superposition of trees, which is a grid, that is, a network.
Lovers of truth in language will note that we are not calling the airport and river-basin flows “networks.” A tree is not a net. One does not catch fish with a fork or a broom. A grid is a network because it has loops, as if it were woven into a net. The grid is a net because it is a superposition of actual flows, which are shaped like trees.
As the city evolves, its population increases and the street pattern evolves to serve the growing population. The grid is a sign of the evolution of civilization: living inside a walled area with many objectives distributed as discrete points on that area (markets, churches, schools, government buildings, train stations, etc.). The grid of streets is the architectural invention of Hippodamus of Miletus, who designed the city of Rhodes in 408 BCE.
City designs continue to evolve as populations increase and transportation technology improves. Because highways and automobiles have become much faster and more economical (per kilogram transported) than their predecessors in the era when the city center was built, the city population finds itself in agreement on adding two modern features to the design. Suspended highways and underground tunnels are built across the city, passing through the center. Circular highways are built around the slow-moving center, famous examples being Le Boulevard Périphérique around Paris, and the Beltway around Washington, D.C.
Theory empowers us to expect these signs of evolution in the future. As the large city expands significantly beyond its beltway, and as highway and automobile technologies improve, a second beltway (wider, faster, with a radius twice the original radius) will emerge around the city and the first beltway.
Taking a step back, we see that these designs have emerged naturally as humans have been maintaining, on the whole, a balance between movements that are slow and short and fast and long, every step of the way. When we recognize and use this principle, we can fast-forward our efforts to design better transportation systems. To see how, consider a broad sketch of all the people who travel only on local roads to get to work. For them, the time they spend walking from their house to the curb (1) and driving out of their cul-de-sac (2) is their short and slow movement. Their time speeding down the avenue (3) is their fast and long.
For all the people who must also travel on the highway (4), those first three movements are their short and slow movement while their time barreling down the interstate is their fast and long. Similarly, for all the travelers taking to the skies, those first four movements become the slow and short while their time on the plane is the fast and long. As urban planners design new plans for multimodal forms of transportation—networks of interconnected sidewalks, bike paths, roads, trains, ferries, airports, etc.—they will build better systems by keeping all these modes in balance.
Knowing the principle also warns the designer about what not to do. On the East Coast of the United States, there is much talk from proponents of high-speed trains like the TGV in France, and the light-rail trains like the RER in Paris. These ideas sound good, but on the design of the American landscape they make as much sense as the military saying “hurry up and wait.” Why use a bullet train when at the other end you have to wait one hour for a bus, and where there are no sidewalks and safety at night? This underscores the folly of trying to impose a design that has not evolved naturally. Building a high-speed train where there is little supporting infrastructure makes as much sense as placing a larger river near a hillside without streams to feed it.
There must be a balance between the time spent traveling long and fast and the time of moving short and slow. When this balance is reached, large numbers of citizens (future users) vote for the design. They vote in the booth, telling the city to build it. They vote with their wallets when they pay city taxes and buy tickets. This is why the flight from Washington, D.C., to Raleigh-Durham takes half an hour—the same time that most of us need to drive home from the airport.
The balancing of times, and the search for greater flow access for everybody, are mental viewings that take the designer well beyond the two-dimensional (on an area) examples discussed in this chapter. The same ideas work in three dimensions. A tall building works well when its elevators are fast enough so that the time spent on the vertical is comparable with the time walking in the corridors. Security checkpoints in the airport and in war zones work best when the time and effort spent in the bottlenecks are comparable to what is spent en route to them. The infrastructure and security of a previously virgin or newly liberated area owe their design to the same principle as all other design phenomena.
The designs of the Atlanta airport, Rhodes, and Rome were not copied from nature. Their emergence and persistence as living flow systems are nature itself. Now we know the principle that underlies their repeated occurrences, scaling rules, and longevity.
Who designed and who built the patterns is not the question. Science is not the search for a designer. Huge numbers worked and continue to work on the design, and they use time and freedom to make changes, and memory to construct it. Culture serves as memory in the evolution of urban design. The dry riverbed and the seismic fault are memory for river-basin evolution. The new scientific aspect that unites all flow systems is that they possess design (pattern, configuration, shape, structure), and the design-generation phenomenon is universal and anticipated by the constructal law.
Now we see why it is useful to know the principle. Designers are empowered by it. Their imagination leaps ahead, over the territory that would have been littered with tried and rejected designs. The traditional first move on a designer’s table is to look and to copy. Looking at nature and copying what millions of flow systems have built is called “biomimetics.” It works only when the person who looks understands the phenomenon that generated the natural drawing.
Thus we render biomimetics obsolete because the constructal law allows us to predict and explain the designs that emerge naturally. Looking at the drawings in a handbook is the most common approach, and it leads to marching in place, not to leaping forward. Copying an inventor’s revolutionary design is much more effective, but such leaps are either costly or illegal. With the constructal law we are the inventors.