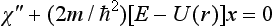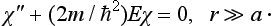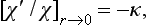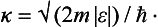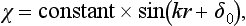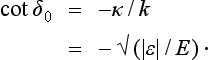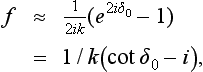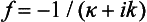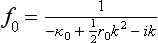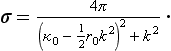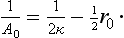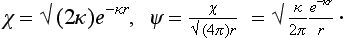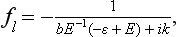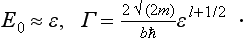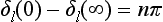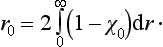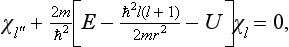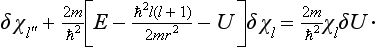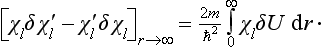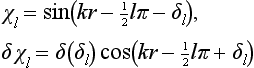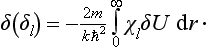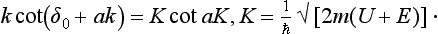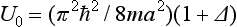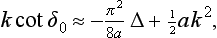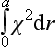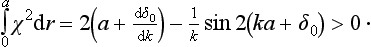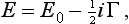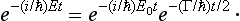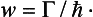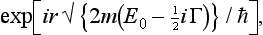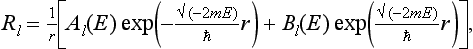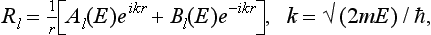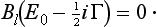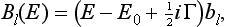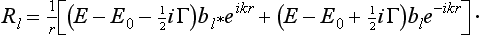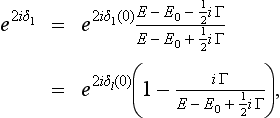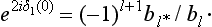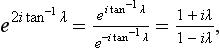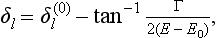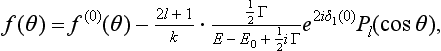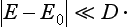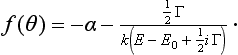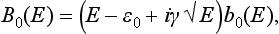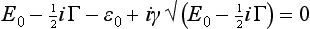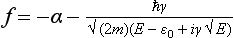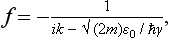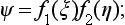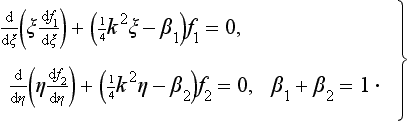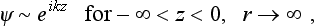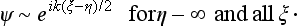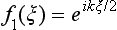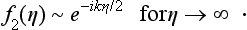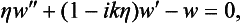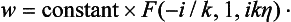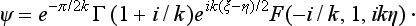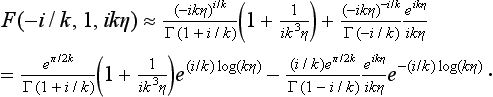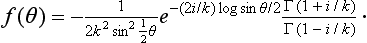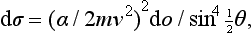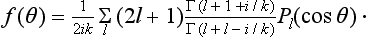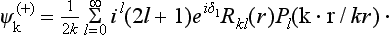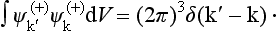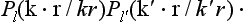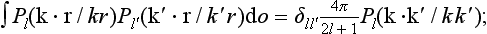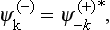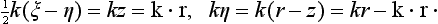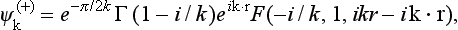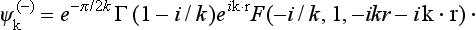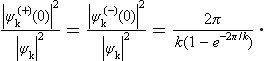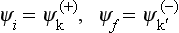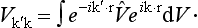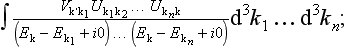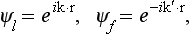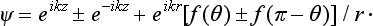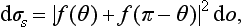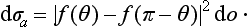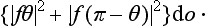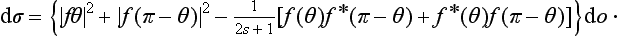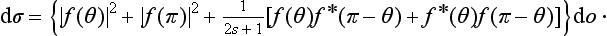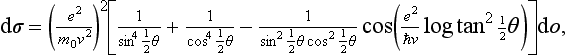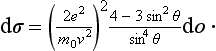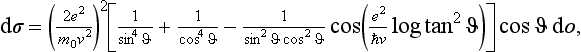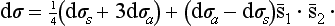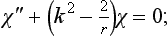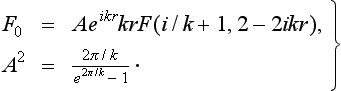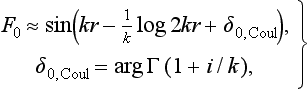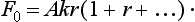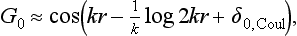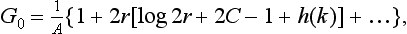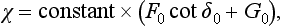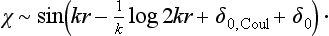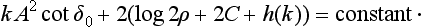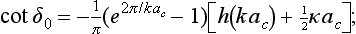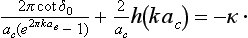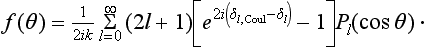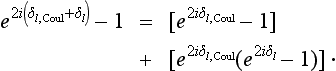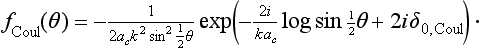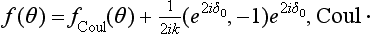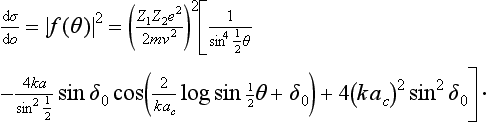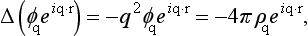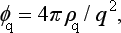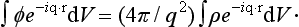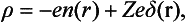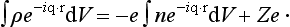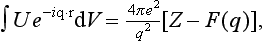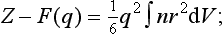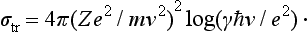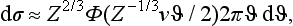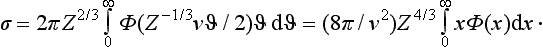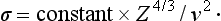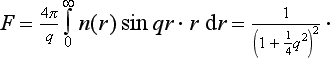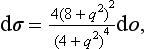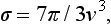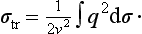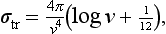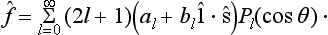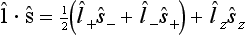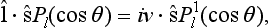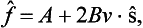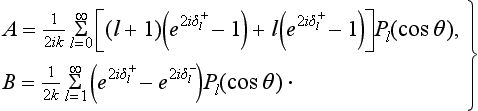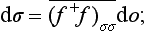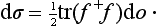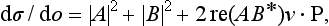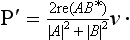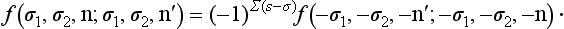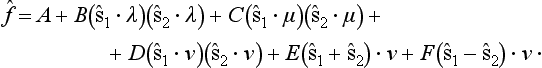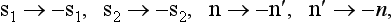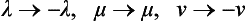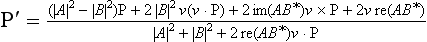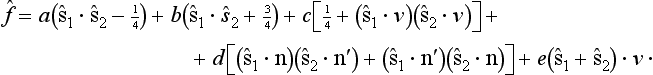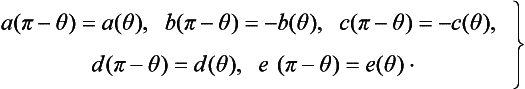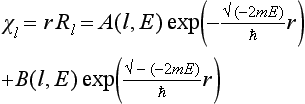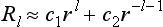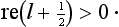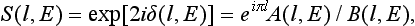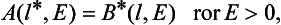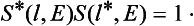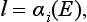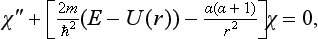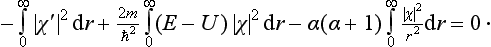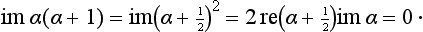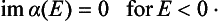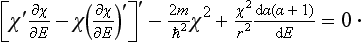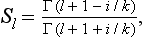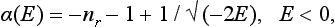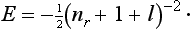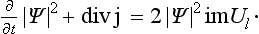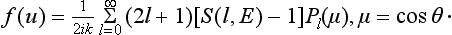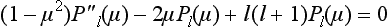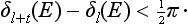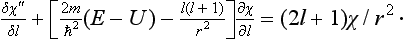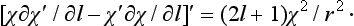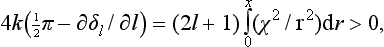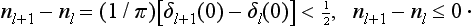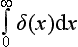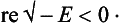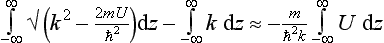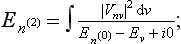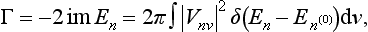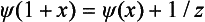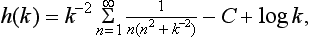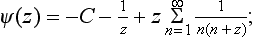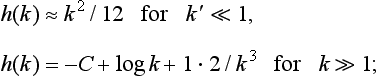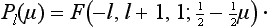§133 Resonance scattering at low energies
Particular consideration must be given to the scattering of slow particles (ka 
1) in an attractive field when the discrete spectrum of negative energy levels includes an s state whose energy is small compared with the value of the field U within its range of action a. We denote this level by ∈ (∈ > 0). The energy E of the particle undergoing scattering, being small, is close to ∈, i.e. it is, as we say, almost in resonance with the level. This leads, as we shall see, to a considerable increase in the scattering cross-section.
The existence of the shallow level can be taken into account in scattering theory by means of a formal method based on the following arguments.
In the exact Schrödinger’s equation for the function χ = rR0 (with l = 0),
in the “inner” region of the field (r ≤ a) we can neglect E in comparison with U:
In the “outer” region (r 
a), on the other hand, we can neglect U:
The solution of equation (133.2) must be “joined” at some r1 (such that 1/k r1 a) to the solution of equation (133.1) which satisfies the boundary condition χ(0) = 0; the joining condition is that the ratio χ′/χ should be continuous. This ratio does not depend on the normalization factor in the wave function.
However, instead of considering the motion in the region r ∼ a, we apply to the solution in the outer region a suitably chosen boundary condition on χ′/χ for small r; since the solution in the outer region varies only slowly as r → 0, we can formally apply this condition at the point r = 0. The equation (133.1) for the region r ∼ a does not contain E; the boundary condition which replaces it must therefore also be independent of the energy of the particle. In other words, it must be of the form
where κ is some constant. But, κ being independent of E, the same condition (133.3) must also apply to the solution of Schrödinger’s equation for small negative energy E = − |∈|, i.e. to the wave function of the corresponding stationary state of the particle. For E = − |∈| we have from (133.2)
where A0 is a constant, and substitution of this function in (133.3) shows that κ is a positive quantity,
Let us now apply the boundary condition (133.3) to the wave equation for free motion,
which is the exact general solution of equation (133.2) for E > 0. Thus we have for the required phase δ0
Since the energy E is here restricted only by the condition ka 1, and need not be small compared with |∈|, the phase δ0 and the s-wave scattering amplitude may not be small.
The phases δl with l > 0 and the corresponding partial amplitudes are again small. Hence we can again regard the total amplitude as being equal to the s-wave scattering amplitude
Substituting (133.6) we obtain
and for the total scattering cross-section
Thus the scattering is again isotropic, but the cross-section depends on the energy, and in the resonance region (E ∼ |∈|) is large compared with the squared range of action of the field a2 (since ka 1). The form of (133.8) is not affected by the details of the interaction of the particles at small distances, and depends only on the value of the resonance level.†
The above formula is somewhat more general than the assumption made in its derivation. Let the function U (r) be slightly modified; this alters also the value of the constant κ in the boundary condition (133.3). By an appropriate change in U (r), κ can be made to vanish, and then to become small and negative. This gives the same formulae (133.7) for the scattering amplitude and (133.8) for the cross-section. In the latter, however, the quantity |∈| = ħ2κ2/2m is now simply a constant characteristic of the field U (r), and not an energy level in that field. In such cases the field is said to have a virtual level, since, although there is no actual level close to zero, a slight change in the field would be sufficient to cause one to appear.
In the analytical continuation of the function (133.7) in the complex plane of E, ik becomes − √(− 2mE)/ħ on the left half of the real axis (see §128), and we see that the scattering amplitude has a pole at E = − |∈|, in accordance with the general results of §128. On the other hand, the virtual level corresponds, as we should expect, to no singularity of the scattering amplitude on the physical sheet. (The scattering amplitude has a pole at E = − |∈| on the non-physical sheet; see the first footnote to §128.)
Formally, the expression (133.7) corresponds to the case where in the expression (125.15),
the first term in the expansion of the function g0(k) is negative and anomalously small. To refine the formula, we can take account of the second term in the expansion:
(L. D. Landau and Ya. A. Smorodinskii 1944); it may be recalled that, when the field decreases sufficiently rapidly, the functions gl(k) can be expanded in even powers of k (see §132). In (133.9) we have denoted by − κ0 the value of g0(0), in order to retain the notation κ for the quantity (133.5), which is related to the energy level ∈. According to the above discussion, κ is given by the value of − ik which makes the denominator in (133.9) equal to zero, i.e. by the root of the equation
The correction term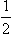 
r0k2 in the denominator in (133.9) is small compared with κ0 since k is assumed small, but it is itself of “normal” order of magnitude: the coefficient r0 ∼ a and is always positive (see Problem 1). It should be emphasized that the inclusion of this term is a legitimate refinement in the formula for the scattering amplitude when contributions from angular momenta l ≠ 0 are neglected; it gives a correction to f of relative order ka, whereas the contribution from scattering with l = 1 is of relative order (ka)3. When k → 0, the amplitude f0 → 1/κ0, i.e. 1/κ0 is equal to the scattering length α defined in §132. The coefficient r0 in the formula
is called the effective range of the interaction.†
For the cross-section we have, from (133.9),
If we neglect the term in k4 in the denominator (though it may legitimately be included), this formula can be written (using (133.10)) in the form
Let us return to the expression (133.4) for the wave function of the bound state in the “outer” region, and relate the normalization coefficient to the parameters defined above. On calculating the residue of the function (133.9) at its pole E = ∈ and comparing with (128.11), we find
The second term is a small correction to the first, since κr0 ∼ κa 1. Without this correction, A02 = 2κ, i.e.
corresponding to the normalization that would occur if (133.14) were valid in all space.
We shall briefly discuss resonance in scattering with non-zero orbital angular momenta. The expansion of the function gl(k) begins with a term ∼k−2l; retaining the first two terms in the expansion, we write the partial scattering amplitude as
where b and ∈ are two constants, with b > 0 (see below). The case of resonance corresponds to an anomalously low value of the coefficient of E−l, i.e. an anomalously small ∈. However, since E is small, the term b∈E−l may still be large in comparison with k.
If ∈ < 0, the denominator in the expression (133.15) has a real root E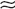 
− |∈|, so that ∈ is a discrete energy level (with angular momentum l),†but in contrast to resonance in s-wave scattering the amplitude (133.15) is never large compared with a; the amplitude of resonance scattering with angular momentum l + 1 is only of the same order of magnitude as that of non-resonance scattering with angular momentum l.
If ∈ > 0, however, the amplitude (133.15) becomes of the order of 1/k in the region E ∼ ∈, i.e. large compared with a. The relative width of this region is small: ΔE/∈ ∼ (ka)2l−1. Thus in this case there is a sharp resonance. This type of resonance scattering occurs because a positive level with l ≠ 0, though not a true discrete level, is quasi-discrete: owing to the presence of the centrifugal potential barrier, the probability that a particle of low energy will escape from this state to infinity is small, so that the “lifetime” of the state is long (see §134). This is the reason why resonance scattering with l ≠ 0 is different in nature from that in the s state, where there is no centrifugal barrier. The denominator in (133.15) with ∈ > 0 vanishes when E = E0−i.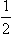 
Γ, where
This pole of the scattering amplitude is, however, on the non-physical sheet. The small quantity Γ is the width of the quasi-discrete level (see §134).
Finally, we may mention an interesting property of the phases δ1 which is easily derived from the above results. We shall regard the phases δl(E) as continuous functions of the energy, and not restrict them to the range from 0 to π (cf. the footnote following (33.20)). We shall show that the equation
then holds, where n is the number of discrete levels with angular momentum l in the attractive field U (r) (N. Levinson 1949).
To prove this, we note that, in a field which satisfies the condition |U| ħ2/ma2, the Born approximation is valid at all energies, so that δl(E) 1 for all E, and δl(∞) = 0, since for E → ∞ the scattering amplitude tends to zero, while δl(0) = 0 in accordance with the general results of §132. In such a field there are no discrete levels (see §45), and so n = 0. We now consider the variation of the difference δl(Δ) − δl(∞), where Δ is some given small quantity, as the potential well U (r) gradually becomes deeper. As this occurs, the first, second etc. levels successively appear at the top of the well, and the phases δl(Δ) are increased by π each time.† On reaching the given U (r) and then making Δ → 0, we obtain formula (133.17).
PROBLEMS
Express the effective interaction range r0 in terms of the wave function of the stationary state E = ∈ in the “inner” region r∼a (Ya. A. Smorodinskii 1948).
SOLUTION
Let χ0 be the wave function in the region r∼a, normalized by the condition that χ0 →1 as r →∞. Then the square of the wave function can be written in all space in the form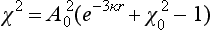 
; this expression becomes 
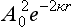for κr 1 and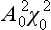 
for κr 1. It must be normalized by the condition
and a comparison with (133.13) gives
From equation (133.1) with U (r)<0, the solution of which is χ0, it follows that χ0(r) < χ0(∞) = 1. Hence we always have r0 < 0.
SOLUTION
Varying U (r) in Schrödinger’s equation
we obtain
Multiplying the first equation by δχl, the second by χl, subtracting, and integrating with respect to r, we find
Substituting on the left-hand side the asymptotic expressions
(the choice of the coefficient 1 in this expression determining the normalization used), we obtain
From this formula we can draw certain conclusions regarding the sign of the phases δl, considered as continuous functions of energy. To avoid the ambiguity in the definition of these functions (an additive multiple of π) we shall normalize them by the condition δl(∞) = 0.
Starting from U = 0, when all the δl are zero, and gradually increasing |U|, we find that in a repulsive field (U > 0) all the δl < 0, and in an attractive field (U < 0) δl > 0. In a repulsive field δl(0) = 0 and therefore, for small energies, the δl are small; the scattering amplitude is therefore negative: f 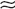δ0/k < 0. In an attractive field the corresponding deduction that f is positive can be made only if there are no discrete levels. Otherwise, when E is small, the phases δl are close to nπ, not to zero (see (133.17)), and no conclusion can be drawn concerning the sign of f.
PROBLEM 3
Find the scattering length α and the effective range of interaction r0 for a spherical square potential well of radius a and depth U0 containing a single discrete energy level near zero.
SOLUTION
We proceed as in §132, Problem 1, except that in the region within the well we do not neglect the particle energy E = ħ2k2/2m in comparison with U0. The equation to determine the phase δ0 is found to be
In order that the well should contain only one level, close to zero, it is necessary that
with Δ 1; see §33, Problem 1. Expanding the above equation in powers of ka And Δ, we find that
whence α = 1/κ0 = 8a/π2Δ, r0 = a. The value of κ0 coincides, as it should, with that of √(2m|E1|)/ħ, where E1 is the energy of the level in the well; see §33, Problem 1.
PROBLEM 4
of the squared wave function of the s state in terms of the phase δ0(k) for a field U (r) that is zero outside a sphere of radius a (G. Lüders 1955).
SOLUTION
According to (128.10),
where the prime denotes differentiation with respect to r (and the derivatives with respect to E in (128.10) are replaced by those with respect to k = √(2mE)/ħ). Since, at r = a, there is no field, we can use on the right-hand side the wave function of free motion, χ = 2 sin (kr + δ0) (normalized as in (33.20)). The result is
Since the integral of χ2 is certainly positive, the expression on the right must also be positive.†
§134 Resonance at a quasi-discrete level
A system which can disintegrate does not, strictly speaking, have a discrete energy spectrum. The particle leaving it when it disintegrates recedes to infinity; in this sense, the motion of the system is infinite, and hence the energy spectrum is continuous.
It may happen, however, that the disintegration probability of the system is very small. The simplest example of this kind is given by a particle surrounded by a fairly high and wide potential barrier. Another possible reason for metastability of a state is that the spin of the system must change in a disintegration due to a weak spin-orbit interaction.
For such systems with a small disintegration probability, we can introduce the concept of quasi-stationary states, in which the particles move “inside the system” for a considerable period of time, leaving it only when a fairly long time interval τ has elapsed; τ may be called the lifetime of the almost stationary state concerned (τ ∼ 1/w, where w is the disintegration probability per unit time). The energy spectrum of these states will be quasi-discrete; it consists of a series of broadened levels, whose width is related to the lifetime by Γ ∼ ħ/τ (see (44.7)). The widths of the quasi-discrete levels are small compared with the distances between them.
In discussing the quasi-stationary states, we can use the following formal method. Until now we have always considered solutions of Schrödinger’s equation with a boundary condition requiring the finiteness of the wave function at infinity. Instead of this, we shall now look for solutions which represent an outgoing spherical wave at infinity; this corresponds to the particle finally leaving the system when it disintegrates. Since such a boundary condition is complex, we cannot assert that the eigenvalues of the energy must be real. On the contrary, by solving Schrödinger’s equation, we obtain a set of complex values, which we write in the form
where E0 and Γ are two constants, which are positive (see below).
It is easy to see the physical significance of the complex energy values. The time factor in the wave function of a quasi-stationary state is of the form
Hence all the probabilities given by the squared modulus of the wave function decrease with time as e−(Σ/ħ)t.† In particular, the probability of finding the particle “inside the system” decreases according to this law. Thus Γ determines the lifetime of the state; the disintegration probability per unit time is
At large distances the wave function of the quasi-stationary state (the outgoing wave) contains the factor
which increases exponentially as r → ∞ (the imaginary part of the root is negative). Hence the normalization integral ∫ |ψ|2 dV for these functions diverges. It may be noted, incidentally, that this resolves the apparent contradiction between the decrease with time of |ψ|2 and the fact that the normalization integral can be shown from the wave equation to be a constant.
Let us ascertain the form of the wave function which describes the motion of a particle with energy close to one of the quasi-discrete levels of the system.
As in §128, we write down the asymptotic form (at large distances) of the radial part of the wave function in the form (128.1):
and regard E as a complex variable. For real positive E,
and Al(E) = Bl*(E) (see (128.3), (128.4)); the function Bl(E) is here taken on the upper edge of a cut along the right half of the real axis.
The condition which determines the complex eigenvalues of the energy consists in the absence of an ingoing wave from the asymptotic expression (134.3). This means that for E = E0 −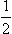 
iΓ the coefficient Bl(E) must vanish:
Thus the quasi-discrete energy levels, like the true discrete levels, are zeros of the function Bl(E). However, unlike the zeros which correspond to true levels, they do not lie on the physical sheet: in writing the condition (134.5) we have assumed that the required wave function of the quasi-stationary state arises from the same term in (134.3), which is an outgoing wave (∼eikr) when E > 0 also (in (134.4)). But the point E = E0 −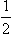 
iΓ lies below the positive real axis. This point can be reached from the upper edge of the cut (where the coefficients in (134.4) are defined), without leaving the physical sheet, only by passing round the point E = 0. Then √ − E changes sign, so that the outgoing wave becomes an ingoing one. Consequently, to preserve the outgoing wave the point must be reached by going directly down through the cut, on to another, non-physical, sheet.
Let us now consider real positive energy values close to the quasi-discrete level (assuming, of course, that Γ is small, since otherwise no such close values could exist). Expanding the function Bl(E) in powers of the difference E-(E0 − 
iΓ) and taking only the first-order term, we have
where bl is a constant. Substituting in (134.4), we obtain the following expression for the wave function of a state close to the quasi-stationary state:
The phase δl of this function is given by
For |E − E0| Γ, the phase δl is equal to δl(0), so that δl(0) is the value of the phase far from the resonance.
In the resonance region δl varies considerably with energy. If we rewrite formula (134.8), using the result
in the form
we see that the phase changes by π in a passage through the whole resonance region (from E E0 to E E0).
For E = E0 −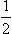 
iΓ, the function (134.7) becomes Rl = −(1/r)iΓbl*eikr. If the wave function is normalized by the condition that the integral of |ψ|2 over the region within the system is unity, the total current in this outgoing wave, equal to v|iΓbl*|2, must be equal to the disintegration probability (134.2). Hence we find
These results enable us to determine the amplitude of elastic scattering of a particle with energy E close to some quasi-discrete level E0 of the compound system consisting of the scattering system together with the particle undergoing scattering. In the general formula (123.11) we must substitute the expression (134.8) in the term with the value of l which corresponds to the level E0 This gives
where f(0)(θ) is the scattering amplitude far from the resonance, which is independent of the properties of the quasi-stationary state (it is given by formula (123.11) with δl = δl(0) in each term of the sum).† The amplitude f(0)(θ) is called the potential scattering amplitude, and the second term in (134.12) the resonance scattering amplitude. The latter has a pole at E = E0 −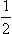 
iΓ, which, as shown above, is not on the physical sheet.‡
Formula (134.12) determines the elastic scattering near resonance at one of the quasi-discrete levels of the compound system. Its range of validity is defined by the requirement that the difference |E − E0| should be small compared with the distance D to the adjoining quasi-discrete levels:
This formula is somewhat simplified if the scattering of slow particles is being considered, i.e. if the wavelength of the particles in the resonance region is large compared with the dimensions of the scattering system. Here only s-wave scattering is important; we shall suppose that the level E0 does in fact belong to motion with l = 0. The potential scattering amplitude then reduces to a real constant − α (see §132).† In the resonance scattering amplitude we put l = 0 and replace 
by unity, since δ0(0) = − αk 1. Thus we find
In a narrow range |E − E0| ∼ Γ the second term is large compared with the amplitude α, and the latter may be omitted. Farther from the resonance, however, the two terms may be comparable.
In the above derivations it has been tacitly assumed that the value E0 of the level itself is not too small, and that the resonance region is not in the neighbourhood of the point E = 0. If resonance at the first quasi-discrete level of the compound system is considered, which lies at a distance from E = 0 small compared with the distance to the next level (E0 D), the expansion (134.6) may be no longer permissible. This is seen from the fact that the amplitude (134.14) does not tend to a constant limit as E → 0, as would be necessary for s-wave scattering according to the general theory.
Let us consider the case of a quasi-discrete level close to zero, again assuming that in the resonance region the particles undergoing scattering are so slow that only s-wave scattering is of importance.
The expansion of the coefficients Bl(E) in the wave function must now be made in powers of the energy E itself. The point E = 0 is a branch point of the functions Bl(E), and a passage round this point from the upper to the lower edge of the cut changes Bl(E) into Bl*(E). This means that the expansion is in powers of √ − E, which changes sign on the above-mentioned passage. We write the first terms in the expansion of the function B0(E) for real positive E in the form
where ∈0 and γ are real constants, and b0(E) a function of energy, which can also be expanded in powers of √E but has no zero near the point E = 0.‡ The quasi-discrete level E = E0 − 
iΓ corresponds to the vanishing of the factor E − ∈0 + iγ√E, continued into the lower half-plane of the non-physical sheet; we therefore have for the determination of E0 and Γ the equation
(the constants ∈0 and γ must be positive in order that E0 and Γ should be positive). For example, a level with width Γ E0 corresponds to the relation ∈0 γ2 between these constants, and from (134.16) we have E0 = ∈0, = Γ = 2γ√∈0.
The expression (134.15) replaces in this case formula (134.6); the subsequent formulae must be correspondingly modified (everywhere replacing E0 by ∈0 and Γ by 2γ√E), Hence we obtain for the scattering amplitude, instead of (134.14), the expression
(where we have put k = √(2mE)/ħ, m being the reduced mass of the particle and the scattering system). For E √ 0 this amplitude tends to a constant limit, as it should, thus confirming the form of the expansion (134.15).
It may be noted that the expression (134.17) also covers the case of a true discrete level of the compound system close to zero, which is given by an appropriate relation between the constants ∈0 and γ. If |∈0| γ2, the first term E may be neglected in the denominator of the resonance term for energies E , γ2.
Neglecting also the potential scattering amplitude α, we obtain the formula
which is the same as formula (133.7) (with κ = − √(2m)∈0/ħγ). This corresponds to resonance at the level E = ∈02/γ2, which is a true or virtual discrete level according as the constant κ is positive or negative.
§135 Rutherford’s formula
Scattering in a Coulomb field is of interest from the point of view of physical applications. It is also of interest in that, for this case, the quantum-mechanical collision problem can be solved exactly.
When there is a direction (in this case, the direction of incidence of the particle) which can be distinguished from the remainder, Schrödinger’s equation in the Coulomb field is conveniently solved in parabolic coordinates ξ, η, φ (§37). The problem of the scattering of a particle in a central field is axially symmetric. Hence the wave function φ is independent of the angle φ. We write the particular solution of Schrödinger’s equation (37.6) in the form
this is † equations (37.8) with m = 0:
The energy of the particle scattered is, of course, positive; we have put E = 
K2. The signs in equations (135.2) are for the case of a repulsive field; exactly the same final result is obtained for the scattering cross-section in an attractive field.
We have to find that solution of Schrödinger’s equation which, for negative z and large r, has the form of a plane wave:
corresponding to a particle incident in the positive direction of the z-axis. We shall see from what follows that the condition imposed can be satisfied by a single particular integral (135.1); a sum of integrals with various values of β, β2 is not needed.
In parabolic coordinates, this condition takes the form
This can be satisfied only if
and f2(η) is subject to the condition
Substituting (135.3) in the first of equations (135.2), we see that this function does in fact satisfy the equation, provided that the constant β1 =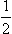 
ik. The second equation (135.2), with β2 = 1 − β1, then takes the form
Let us seek its solution in the form
where the function w (η) tends to a constant as η → ∞. For w (η) we have the equation
which, by introducing the new variable η1 = ikη, can be reduced to the equation for a confluent hypergeometric function with parameters α = − i/k, γ = 1. We have to choose that solution of equation (135.6) which, on being multiplied by f1(ξ), contains only an outgoing (i.e. scattered) and not an ingoing spherical wave. This solution is the function
Thus, on assembling the expressions obtained, we find the following exact solution of Schrödinger’s equation, describing the scattering:
We have chosen the normalization constant in ψ such that the incident plane wave has unit amplitude (see below).
In order to separate the incident and scattered waves in this function, we must consider its form at large distances from the scattering centre. Using the first two terms of the asymptotic expansion (formula (d.14)) for the confluent hypergeometric function, we have for large η
Substituting this in (135.7) and changing to spherical polar coordinates (ξ − η = 2z, η = r − z = r (1 − cos θ)), we have the following final asymptotic expression for the wave function:
where
The first term in (135.8) represents the incident wave. We see that, in consequence of the slow decrease of the Coulomb field, the plane wave is distorted even at large distances from the centre, as is shown by the presence of the logarithmic term in the phase and of the 1/r term in the amplitude.† The distorting logarithmic term in the phase is found also in the scattered spherical wave given by the second term in (135.8). These differences from the usual asymptotic form of the wave function (123.3) are unimportant, however, since they give a correction to the current density which tends to zero as r → ∞.
Thus we obtain for the scattering cross-section dσ = / f (θ)|2 do the formula
or, in ordinary units,
where the velocity v of the particle = kħ/m. This is the familiar Rutherford’s formula given by classical mechanics. Thus, for scattering in a Coulomb field, quantum and classical mechanics give the same result (N. Mott, and W. Gordon, 1928). Bora’s formula (126.12) naturally leads to the same expression (135.10) also.
We shall give for reference the expression for the scattering amplitude (135.9), written as a sum of spherical harmonics. This is obtained by substituting in (124.5) the phases from (36.28), i.e.†
Thus we find
The signs in the scattering amplitude (135.9) correspond to a repulsive field. In an attractive Coulomb field, formula (135.9) is replaced by the complex conjugate expression. f (θ) then becomes infinite at the poles of the function Γ(1 − i/k), i.e. at points where the argument of the gamma function is a negative integer or zero (when im k > 0 and the function rψ decreases at infinity). The corresponding energy values are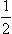 
k2 = − 
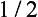n2 (n = 1, 2, 3, …), and coincide with the discrete energy levels in the Coulomb field (cf. §128).
§136 The system of wave functions of the continuous spectrum
In the analysis of motion in a centrally symmetric field (Chapter V) we have considered stationary states in which the particle has definite values of the energy, the orbital angular momentum l, and the component m of this angular momentum. The wave functions of such states of the discrete spectrum (ψnlm) and the continuous spectrum (ψklm, energy ħ2k2/2m) together form a complete set in terms of which the wave function of any state may be expanded. Such a set of functions is, however, not appropriate for problems in scattering theory. Here another set is convenient, in which the wave functions of the continuous spectrum are described by a particular asymptotic behaviour: at infinity there is a plane wave and an outgoing spherical wave. In these states the particle has a definite energy, but no definite angular momentum magnitude or component.
According to (123.6) and (123.7), such wave functions, here denoted by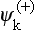 
, are given by
The argument of the Legendre polynomials is written as cos θ = k. r/kr, and the expression therefore does not involve any particular choice of the coordinate axes as it did in (123.6) (where the z-axis was the direction of propagation of the plane wave). By giving the vector k all possible values, we obtain a set of wave functions, which, as we shall now show, are orthogonal and normalized by the usual rule for the continuous spectrum:
To prove this,† we note that the product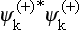 
is expressed by a double sum over l and l′ of terms containing the products
The integration over the directions of r is effected by means of the formula
cf. (c.12) in the Mathematical Appendices. This leaves
where γ is the angle between k and k.’ The-radial functions Rkl are orthogonal; however, and are normalized by
Hence we can put k = k′ in the coefficients in front of the integrals; using also the relation (124.3), we have
The expression on the right is zero for k ≠ k′; on being multiplied by 2πk2 sin γ dk dγ/(2π)3 and integrated over all k-space it gives 1, and this proves formula (136.2).
Together with the system of functions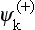 
, we can also introduce a system corresponding to states in which there are at infinity a plane wave and an ingoing spherical wave. These functions, which we denote by 
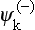, are obtained directly from the 
:
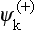since the complex conjugate of eikr/r (outgoing wave) is e−ikr/r (ingoing wave), and the plane wave becomes e−ik, r, so that, in order to retain the previous definition of k (plane wave eik, r), we must replace k by − k, as in (136.4). Noticing that Pl(− cos θ) = (−1)lPl(cos θ), we obtain from (136.1)
The case of a Coulomb field is of great importance. Here the functions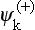 
(and 
) can be written in a closed form, which is obtained directly from formula (135.7). We express the parabolic coordinates by
Thus we obtain for a repulsive Coulomb field†
The wave functions for an attractive Coulomb field are found by simultaneously changing the signs of k and r:
The action of the Coulomb field on the motion of the particle near the origin may be characterized by the ratio of the squared modulus of 
or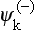 
at the point r = 0 to the squared modulus of the wave function ψk = eik, r for free motion. Using the formula
we easily find, for a repulsive field,
and for an attractive field,
The functions 
and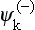 
play an important part in problems relating to the application of perturbation theory in the continuous spectrum. Let us suppose that, as a result of some perturbation 
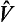, the particle makes a transition between states of the continuous spectrum. The transition probability is determined by the matrix element
The question arises of which solutions of the wave equation are to be taken as the initial (ψi) and final (ψf) wave functions, in order to obtain the amplitude for a transition of the particle from a state with momentum ħk to one with momentum ħk′ at infinity.† We shall show that this requires that
(A. Sommerfeld 1931).
This becomes clear if we consider how the problem would be solved by perturbation theory applied not only as regards the perturbation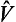 
but also as regards the field U (r) in which the particle is moving. In the zero-order approximation (with respect to U), the matrix element (136.12) is
In subsequent approximations with respect to U, this integral is replaced by a series of which each term is an integral
cf. §§43 and 130. The numerator contains the matrix elements (in varying order) with respect to the unperturbed plane waves, and all poles are avoided in the integrations, according to one fixed rule. On the other hand, this series can be obtained as the matrix element (136.12) with the wave functions ψi and ψf as perturbation-theory series with respect to the field U. The fact that the result must be a sum of integrals in which all poles are avoided by the same rule means, therefore, that the poles in the terms of the series representing ψi and ψf* must be avoided by a similar rule. But if the wave equation is solved by perturbation theory with this avoidance rule, we necessarily obtain a solution whose asymptotic form includes an outgoing (as well as a plane) wave. In other words, the wave functions, which in the zero-order approximation (with respect to U) have the form
must be replaced by exact solutions of the wave equation, respectively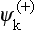 
and 
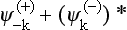. This proves the rule (136.13).
The choice of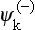 
as the final wave function applies also to transitions from the discrete to the continuous spectrum; here there is, of course, no problem of choosing ψi.
§137 Collisions of like particles
The case where two identical particles collide requires special consideration. The identity of the particles leads in quantum mechanics to the appearance of a peculiar exchange interaction between them. This has an important effect on scattering also (N. F. Mott 1930).†
The orbital wave function of a system of two particles must be symmetric or antisymmetric with respect to the particles, according as their total spin is even or odd (see §62). The wave function which describes the scattering, and which is obtained by solving the usual Schrödinger’s equation, must therefore be symmetrized or antisymmetrized with respect to the particles. An interchange of the particles is equivalent to reversing the direction of the radius vector joining them. In the coordinate system in which the centre of mass is at rest, this means that r remains unchanged, while the angle θ is replaced by π − θ (and so z = r cos θ becomes − z). Hence, instead of the asymptotic expression (123.3) for the wave function, we must write
By virtue of the identity of the particles it is, of course, impossible to say which of them scatters and which is scattered. In the coordinate system in which the centre of mass is at rest, we have two equal incident plane waves, propagated in opposite directions (eikz and e−ikz). The outgoing spherical wave in (137.1) takes into account the scattering of both particles, and the probability current calculated from it gives the probability that either of the particles will be scattered into the element do of solid angle considered. The scattering cross-section is the ratio of this current to the current density in either of the incident plane waves, i.e. it is given, as before, by the squared modulus of the coefficient of eikr/r in the wave function (137.1).
Thus, if the total spin of the colliding particles is even, the scattering cross-section is of the form
while if the total spin is odd, it is
The appearance of the interference term f (θ) f* (π − θ) + f*(θ) f (π − θ) characterizes the exchange interaction. If the particles were different, as they are in classical mechanics, the probability that either of them would be scattered into a given element of solid angle do would simply be equal to the sum of the probabilities that one particle is deviated through an angle θ and the other through π − θ; in other words, the cross-section would be
In the limiting case of low velocities, the scattering amplitude tends to a constant value independent of the angle (§132) if the interaction of the particles decreases sufficiently rapidly with increasing distance. It is seen from (137.3) that dσa is then zero, i.e. only particles with even total spin scatter each other.
In formulae (137.2), (137.3) it is supposed that the total spin of the colliding particles has a definite value. If the particles are not in definite spin states, then to determine the cross-section it is necessary to average, assuming all possible spin states to be all equally probable. We have shown in §62 that, of the total number of (2s + 1)2 different spin states of a system of two particles with spin s, s (2s + 1) states correspond to an even total spin and (s + 1)(2s + 1) to an odd total spin (if s is half-integral), or vice versa if s is integral. Let us first suppose that the spin s of the particles is half-integral. Then the probability that the system of two colliding particles will have even S is s (2s + 1)/(2s + 1)2 = s/(2s + 1), while the probability of odd S is (s + 1)/(2s + 1). Hence the cross-section is
Substituting here (137.2), (137.3), we obtain
Similarly, we find for integral s
As an example, we shall write out the formulae for the collision of two electrons interacting by Coulomb’s law (U = e2/r). Substitution of the expression (135.9) in the formula (137.5) with s = 
gives (in ordinary units), after a simple calculation,
where we have introduced the mass m0 of the electron in place of the reduced mass m =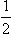 
m0. This formula is considerably simplified if the velocity is so large that e2 vħ; we notice that this is just the condition for perturbation theory to be applicable to a Coulomb field. Then the cosine in the third term can be replaced by unity, and we have
The opposite limiting case, e2 vħ, corresponds to the passage to the limit of classical mechanics (see the end of §127). In formula (137.7) this transition occurs in a very curious way. For e2 vħ, the cosine in the third term in the square brackets is a rapidly oscillating function. For any given θ, formula (137.7) gives for the scattering cross-section a value which in general differs considerably from the Rutherford value. However, on averaging over even a small range of values of θ, the oscillating term in (137.7) vanishes, and we obtain the classical formula.
All the above formulae for the cross-section refer to a system of coordinates in which the centre of mass is at rest. The transition to a system in which one of the particles is at rest before the collision is effected (according to (123.2)) simply by replacing θ by 2ϑ. Thus, for a collision of electrons we have from (137.7)
where d0 is the element of solid angle in the new system of coordinates. In replacing θ by 2ϑ, the element of solid angle do must be replaced by 4 cos ϑ do, since sin θ dθdφ = 4 cos ϑ sin ϑdϑdφ.
PROBLEM
Determine the scattering cross-section for two identical particles of spin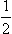 
, with given mean spin values 
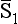and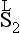 
.
SOLUTION
The dependence of the cross-section on the polarizations of the particles must be expressed by a term proportional to the scalar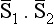 
. We look for dσ in the form 
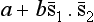. For unpolarized particles 
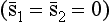, the second term is absent, and according to (137.4)
. If both particles are completely polarized in the same direction 
, the system is certainly in a state with S = 1; in this case, therefore, dσ = a +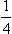 
b = dσa. With a and b determined from these two equations, we have
§138 Resonance scattering of charged particles
In the scattering of charged nuclear particles (e.g. of protons by protons), as well as the short-range nuclear forces there is the Coulomb interaction, which decreases only slowly. The theory of resonance scattering in this case is developed by the same method as that described in §133. The only difference is that the wave function in the region outside the range of action of the nuclear forces (r a) must be, instead of the solution of the equation of free motion (133.2), the exact general solution of Schrödinger’s equation in a Coulomb field. Here the velocity of the particles is again assumed only so small that ka 1; the relation between 1/k and the Coulomb unit of length ac = ħ2/mZ1Z2e2 (where m is the reduced mass of the colliding particles) is left arbitrary.†
For motion with l = 0 in a repulsive Coulomb field, Schrödinger’s equation for the radial function χ = rR0 is
here we use Coulomb units. In §36 the solution of this equation has been found, subject to the requirement that χ/r is finite at r = 0. This solution, which we here denote by F0, has the form (see (36.27) and (36.28))
The asymptotic expression for this function at large distances is
and the leading terms of the expansion for small r (kr 1, r , 1) are
Now, however, with the changed boundary condition, the behaviour of the function at the origin becomes unimportant, and we need the general solution of equation (138.1), which is a linear combination of two independent integrals.
The parameters of the confluent hypergeometric function in (138.2) are such (the value of γ = 2 being integral) that the case described at the end of §d of the Mathematical Appendices occurs. In accordance with the discussion given there, we obtain the second integral of equation (138.1) by replacing the function F in (138.2) by some other linear combination of two terms whose sum is, according to (d.14), the confluent hypergeometric function. Taking the difference of these terms as the combination in question, we find the second independent solution of equation (138.1) (denoted by G0) in the form†
the function F0 is the real part of the same expression. The asymptotic form at large distances is
and the leading terms of the expansion for small r are
where C = 0·577… is Euler’s constant, and h (k) denotes the function
ψ(z) = Γ′(z)/Γ(z) being the logarithmic derivative of the Γ function.†
The general integral of equation (138.1) may be written as the sum
where cot δ0 is a constant. The notation is chosen so that the asymptotic form of this solution is
Thus δ0 is the additional phase shift of the wave function due to the short-range forces. We have to relate it to the constant appearing in the boundary condition [χ′/χ]r→0 = constant, which replaces the treatment of the wave function in the region where nuclear forces act. Owing to the logarithmic divergence of the logarithmic derivative χ′/χ as r → 0, this condition must be applied at some arbitrarily small but finite value r = χ, not at r = 0. Calculating by means of formulae (138.4) and (138.7) the derivative χ′(ρ)/χ(ρ) and equating it to a constant, we obtain the boundary condition in the form
The expression on the left-hand side of the equation contains the constants 2 log 2ρ and 4C, which are independent of k; we include these in the constant on the right, and then denote it by − κ. The final expression for cot δ0 is, in ordinary units,
in the limit 1/ac → 0, i.e. for uncharged particles, formula (138.11) becomes the relation cot δ0 = − κ/k, i.e. (133.6).
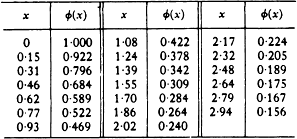
Figure 49 shows a graph of the function h (x).†
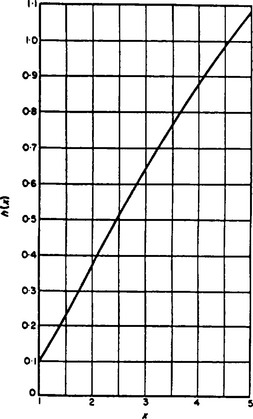
FIG. 49
Thus, when there is a Coulomb interaction, the “constant” is
We have put the word “constant” in quotation marks, since K is actually the first term in an expansion in powers of the small quantity ka of some function which depends on the properties of the short-range forces. As stated in §133, resonance at low energies corresponds to the case where the value of the constant κ is anomalously small. Consequently, in order to improve the accuracy, we must take account also of the next term (∼ k2) in the expansion, which contains a coefficient of “normal” magnitude, i.e. in (138.12) − κ must be replaced by − κ0 +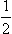 
r0k2.†
The existence of resonance may, as stated in §133, be due to either a true or a virtual discrete bound state of the system. It can be shown‡ that the sign of the constant κ is again the criterion which determines whether the level is true or virtual.
The total phase shifts of the wave functions are, according to (138.10), the sums δl, Coul + δl. The scattering cross-section is therefore
The difference in the brackets may be written
The Coulomb phases δl, Coul contribute equally, in order of magnitude, to the scattering amplitude for all l. The phases δl relating to the short-range forces are small for l ≠ 0 at low energies. Hence, in substituting (138.14) in (138.13), we retain the first bracket in every term of the sum; the sum of these terms is the Coulomb scattering amplitude (135.9)
The second bracket in (138.14) is retained only in the term with l = 0. Thus the total scattering amplitude is
The second term in this expression may be called the nuclear scattering amplitude. It should be emphasized, however, that the division is arbitrary: in view of the definition of δ0 in (138.11), the presence of the Coulomb interaction has a considerable effect on this term also, which is quite different from the corresponding term with the same short-range forces for uncharged particles. In particular, when kac →0 the phase δ0, and therefore the whole of the second term in (138.16), tend exponentially to zero as e−2π/kac, i.e. the nuclear scattering is entirely masked by the Coulomb repulsion.
In the scattering cross-section the two parts of the amplitude interfere:
Here it is assumed that the colliding particles are different; for like particles, the scattering amplitude must be symmetrized before being squared (cf. §137).
§139 Elastic collisions between fast electrons and atoms
Elastic collisions between fast electrons and atoms can be treated by means of the Born approximation if the velocity of the incident electron is large compared with those of the atomic electrons.
Owing to the large difference in mass between the electron and the atom, the latter may be regarded as at rest during the collision, and the system of coordinates in which the centre of mass is fixed is the same as that in which the atom is fixed. Then p and p′ in formula (126.7) denote the momenta of the electron before and after the collision, m the mass of the electron, and the angle θ is the same as the angle of deviation ϑ of the electron. The potential energy U (r) in formula (126.7) must be defined appropriately.
In §126 we have calculated the matrix element Upp of the interaction energy with respect to the wave functions of a free particle before and after the collision. In a collision with an atom it is necessary to take into account also the wave functions describing the internal state of the atom. In an elastic collision, the state of the atom is left unchanged. Hence Up, p must be determined as the matrix element with respect to the wave functions ψp and ψp, of the electron; it is diagonal with respect to the wave function of the atom. In other words, U (r) in formula (126.7) must be taken to be the potential energy of the interaction of the electron with the atom, averaged with respect to the wave function of the latter. It is eφ(r), where φ(r) is the potential of the field at the point r due to the mean distribution of charges in the atom.
Denoting the density of the charge distribution in the atom by ρ(r), we have, for the potential φ, Poisson’s equation:
The required matrix element Up, p is essentially the Fourier component of U (i.e. of φ) corresponding to the wave vector q = k′ − k. Applying Poisson’s equation to each Fourier component separately, we have
i.e.
The charge density ρ(r) consists of the electron charges and the charge on the nucleus:
where en (r) is the electron charge density in the atom. Multiplying by e−iq.r and integrating, we have
Thus we obtain for the integral in question the expression
where F (q) is defined by the formula
and is called the atomic form factor. It is a function of the scattering angle and of the velocity of the incident electron.
Finally, substituting (139.2) in (126.7), we obtain the following expression for the cross-section for the elastic scattering of fast electrons by an atom†
Let us consider the limiting case qa0 1, where a0 is of the order of magnitude of the dimensions of the atom. Small scattering angles correspond to small q: ϑ v0/v, where v0∼ħ/ma0 is of the order of magnitude of the velocities of the atomic electrons.
Let us expand F (q) as a series of powers of q. The zero-order term is ∫ ndV, which is the total number Z of electrons in the atom. The first-order term is proportional to ∫ rn (r) dV, i.e. to the mean value of the dipole moment of the atom; this vanishes identically (see §75). We must therefore continue the expansion up to the second-order term, obtaining
substituting in (139.4), we obtain
Thus, in the range of small angles, the cross-section is independent of the scattering angle, and is given by the mean square distance of the atomic electrons from the nucleus.
In the opposite limiting case of large q (qa0 1, i.e. ϑ v0/v), the factore−iq.r in the integrand in (139.3) is a rapidly oscillating function, and therefore the whole integral is nearly zero. Consequently, we can neglect F (q) in comparison with Z, so that
i.e., we have Rutherford scattering at the nucleus of the atom.
We may also calculate the transport cross-section
In the range of angles ϑ v0/v we have, according to (139.5), dσ = constant × sin ϑ dϑ = constant × ϑ dϑ, where the constant is independent of ϑ. Hence, in this region, the integrand in the above integral is proportional to ϑ, so that the integral converges rapidly at the lower limit. In the region 1 ϑ v0/v we have dσ 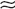constant × dϑ/ϑ3; the integrand is proportional to 1/ϑ, and the integral (139.7) diverges logarithmically. Hence we see that this range of angles plays the chief part in the integral, and we need integrate only over this range. The lower limit of integration must be taken as of the order of v0/v; we shall write it in the form e2/γħv, where γ is a dimensionless constant. As a result we have the formula
An exact calculation of the constant γ requires a consideration of scattering through angles ϑ > v0/v, and cannot be carried out in a general form; σtr depends only slightly on the choice of this constant, since it enters only in a logarithm, and multiplied by the large quantity ħv/e2.
For a numerical calculation of the atomic form factor for heavy atoms, we can use the Thomas—Fermi distribution of the density n (r). We have seen that, in the Thomas–Fermi model, n (r) has the form
all quantities in this and the following formulae are measured in atomic units. It is easy to see that the integral (139.3), when calculated with such a function n (r), will contain q only in the combination qZ−1/3:
Table 11 gives, for reference, the values of the function φ(x), which holds for all atoms.†
With the atomic form factor (139.9), the cross-section (139.4) wall have the form
where Φ(x) is a new function holding for all atoms. The total cross-section may be obtained by integration. The chief part in the integral is played by the range of small ϑ. Hence we can write
and extend the integration over ϑ to infinity:
Thus σ is of the form
Similarly, it is easy to see that the constant γ in formula (139.8) will be proportional to Z−1/3.
PROBLEM
Calculate the cross-section for the elastic scattering of fast electrons by a hydrogen atom in the ground state.
SOLUTION
The wave function of the normal state of the hydrogen atom is (in atomic units) ϕ = π−1/2 e−r, so that n = e−2r/π. The integration over angles in (139.3) is effected as in the derivation of formula (126.12); we have
Substituting in (139.4), we obtain
where q = 2v sin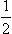 
ϑ. The total cross-section is calculated by putting do = 2π sin ϑ d ϑ = (2π/v2)q dq and integrating over q from 0 to 2v; since v is assumed large and the integral converges, the upper limit may be replaced by infinity. The result is
The transport cross-section is calculated as
Changing the variable of integration by putting u = 4 + q2, and taking the upper limit as infinity everywhere except in the term du/u, we obtain
in accordance with (139.8).
§140 Scattering with spin—orbit interaction
Hitherto we have considered only collisions of particles whose interaction does not depend on their spins. Under these conditions the spins either do not affect the scattering process at all, or have an indirect influence due to exchange effects (§137).
Let us now examine the generalization of the theory of scattering given in §123 to the case where the interaction of the particles depends significantly on their spins, as occurs in collisions of nuclear particles.
We shall discuss in detail the simplest case, where one of the colliding particles (for definiteness taken to be the particle in the incident beam) has spin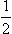 
, and the other (the target particle) has spin zero.
For a given (half-integral) angular momentum j of the system, the orbital angular momentum can have only the two values l = j ±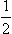 
, corresponding to states of different parities. In this case, therefore, the conservation of the absolute magnitude of the orbital angular momentum follows from that of j and the parity.
The operator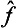 
(§125) now acts not only on the orbital variables but also on the spin variables of the wave function of the system. It must commute with the operator of the conserved quantity 12. The most general form of such an operator is
where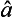 
and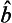 
are orbital operators depending only on 12.
The S-matrix, and therefore the matrix of the operator f, are diagonal with respect to the wave functions of states with definite values of the conserved quantities l and j (and the component m of the total angular momentum), and the diagonal elements are expressed in terms of the phases δ of the wave functions by formula (123.15). Forgiven l and given total angular momentum j = l + 
or l −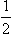 
the eigenvalues of 1. s are 
l and − 
(l+1) respectively (see (118.5)). Hence, to determine the diagonal matrix elements of the operators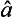 
and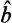 
(denoted by al and bl), we have the relations
where the phases δl+ and δl− correspond to states with j = l +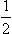 
and j = l − 
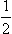respectively.
We are interested, however, not in the diagonal elements themselves of the operator f with respect to the states with given l and j, but in the scattering amplitude as a function of the directions of the incident and scattered waves. This amplitude is still an operator, but only with respect to the spin variables—an operator which is non-diagonal with respect to the spin component σ. In the rest of this section f will denote this operator.
To derive this operator we must apply the operator (140.1) to the function (125.17) which corresponds to a plane wave incident along the z-axis. Thus
Here we must also calculate the result of the action of the operator 1.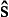 
on the function Pl(cos θ). This can be done by writing
(see (29.11)) and using formulae (27.12) for the matrix elements of the operators l±, or still more simply by using the operator expressions (26.14), (26.15). The result is
where Pl1 is the associated Legendre polynomial and ν a unit vector in the direction n × n′ which is perpendicular to the plane of scattering (n being the direction of incidence (the z-axis) and n′ the direction of scattering, defined by the spherical polar angles θ, φ).
On determining al and bl from (140.2) and substituting in (140.3), we have finally
The matrix elements of this operator give the scattering amplitude for definite values of the spin component in the initial (σ) and final (σ′) states. Let us consider the cross-section summed over all possible values of σ′ and averaged with respect to the probabilities of various values σ in the initial state (in the incident beam). The cross-section is given by
by taking the diagonal matrix elements of the product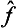 
+ 
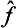we effect the summation over final states, and the bar denotes the averaging with respect to initial states.† If all spin directions are equally probable in the initial state, this averaging reduces to taking the trace of the matrix, divided by the number of possible values of the spin component σ:
On substitution of (140.4) in (140.6) the mean value of the square (ν.s)2 is calculated as 
. The result is
where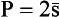 
is the initial polarization of the beam, defined as the ratio of the mean spin in the initial state to its maximum possible value (
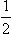). In the case of spin 
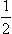the vector 
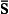completely describes the spin state (§59).
It may be pointed out that the polarization of the incident beam leads to an azimuthal asymmetry of the scattering: owing to the factor ν.P in the last term, the cross-section (140.8) depends not only on the polar angle θ but also on the azimuth φ of the vector n′ relative to n (if the polarization is not perpendicular to ν, so that ν.P ≠ 0).
The polarization of the scattered particles can be calculated from the formula
For example, if the initial state is unpolarized (P = 0), a simple calculation gives
Thus scattering leads, in general, to the appearance of a polarization perpendicular to the plane of scattering. This effect is, however, absent in the Born approximation: if all the phases δ are small, the coefficient A is real in the first approximation with respect to the phases, and B is purely imaginary, so that re(AB*) = 0.
The fact that the polarization P′ (140.10) is in the direction of ν is obvious a priori. P′ is an axial vector, and ν is the only axial vector which can be constructed from the available polar vectors n and n′. It is therefore evident that this property will also be possessed by the polarization resulting from the scattering of an unpolarized beam of particles with spin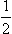 
by an unpolarized target composed of nuclei with any spin (not necessarily zero).†
In formulating the reciprocity theorem for scattering in the presence of spins it must be borne in mind that time reversal changes the signs not only of the momenta but also of the angular momenta. Hence the symmetry of scattering with respect to time reversal must in this case be expressed by the equality of amplitudes for processes which differ not only in the interchange of the initial and final states and the reversal of the directions of motion but also in that the signs of the spin components of the particles are changed in both states. Here, however, the signs of these amplitudes may differ because, according to (60.3), time reversal introduces a factor (−1)δ − σ in the spin wave function. This has the result that the reciprocity theorem must be formulated as follows:‡
Here f (σ1, σ2, n; σ1′, σ2′, n′) is the amplitude of scattering with change in the spin components of the colliding particles from σ1, σ2 to σ1′, σ2′. The sum in the exponent is taken over both particles before and after scattering.
In the Born approximation, the scattering has a further symmetry; the probabilities of processes differing by the interchange of the initial and final states, without change in the signs of the momenta and spin components of the particles as in time reversal, are the same (see §126). Combining this property with the reciprocity theorem, we find that the scattering is symmetrical with respect to a change in sign of all the momenta and spin components, without interchange. Hence we easily conclude that in the Born approximation there can be no polarization in the scattering of any unpolarized beam by an unpolarized target. For, under the transformation mentioned, the polarization vector P changes sign, while the unit vector k × k′, whose direction must be the same as that of P, remains unaltered. Thus the property noted above for the scattering of particles with spin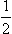 
by particles with spin zero is actually a general one.
In the case of arbitrary spins of the colliding particles, the general formulae for the angular distributions are very complicated, and we shall not pause to derive them here, but merely calculate the number of parameters by which these distributions must be determined.
The case considered above of a collision between particles of spin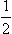 
and 0 has, in particular, the property that to given values of j and the parity there corresponds only one state of the system of two particles (apart from the unimportant orientation of the total angular momentum in space). Each such state leads to one real parameter (the phase σ) in the scattering amplitude. For other spins there are in general several different states with the same total angular momentum J and parity; these states differ in the values of the total spin S of the particles and the orbital angular momentum l of their relative motion. Let the number of such states be n. It is easy to see that each such group of states contributes 
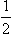n (n + 1) real parameters in the scattering amplitude. For the S-matrix is, with respect to these states, a matrix having unitary symmetry (owing to the reciprocity theorem), with n. n complex elements. The number of independent quantities in this matrix is conveniently calculated by noting that, if the operator 
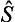is written in the form 
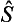= exp(i
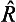), the unitarity condition is automatically satisfied when 
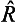is any Hermitian operator (see (12.13)). If the matrix 
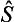is symmetrical, so is the matrix 
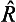, which, being Hermitian, is therefore real, and a real symmetrical matrix has 
n (n + 1) independent components.
As an example, for two particles with spins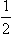 
the number n = 2: for given J there are in all four states, two with l = J and total spin S = 0 or 1, and two with l = J ± 1, S = 1. It is evident that two of these states are even (l is even) and two are odd (l is odd).
The general form of the scattering amplitude for particles with spin 
, as an operator relating to the spin variables of the two particles, is easily written down from the necessary invariance conditions: it must be a scalar invariant under time reversal. To construct this expression we have the two axial vectors s1 and s2 of the particle spins and two ordinary (polar) vectors n and n′. Each of the operators 
1 and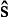 
2 must appear linearly in the amplitude, since any function of an operator of spin 
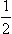can be reduced to a linear function. The most general form of operator satisfying these conditions can be written as
The coefficients A, B, … are scalar quantities, which can depend only on the scalar n. n′, i.e. on the scattering angle θ (and on the energy); λ, μ, ν are three mutually perpendicular unit vectors along n + n′, n − n′ and n × n′ respectively. The operations of time reversal correspond to the changes
so that
and the invariance of the operator (140.12) is obvious.
In the mutual scattering of nucleons (protons and neutrons) the last term in (140.12) does not appear. This is evident from the fact that the nuclear forces acting between nucleons conserve the absolute magnitude of the total spin S of the system; the operator 
1 − 
2, however, does not commute with the operator 
2. (The remaining terms in (140.12) are expressed, according to (117.4), in terms of the total spin operator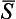 
, and therefore commute with 
2.) In the scattering of like nucleons (pp or nn), the coefficients A, B,… as functions of the angle of scattering also satisfy certain symmetry relations as a result of the identity of the two particles (see Problem 2).
PROBLEMS
Determine the polarization after the scattering of particles with spin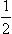 
by particles with spin zero when the polarization before scattering is non-zero.
SOLUTION
A calculation using formula (140.9) is conveniently effected in components, with the z-axis in the direction of v. The result is
PROBLEM 2
Find the symmetry conditions satisfied by the coefficients in the scattering amplitude for two like nucleons, as functions of the angle θ (R. Oehme 1955).
SOLUTION
We regroup the terms in (140.12) in such a way that each is non-zero only for singlet (S = 0) or triplet (S = 1) states of the system of two nucleons:
Using formulae (117.4), we easily see that the first term is non-zero only for S = 0 and the remainder only for S = 1. Owing to the identity of the particles, the scattering amplitude must be symmetric with respect to interchange of the particle coordinates for S = 0, and antisymmetric for S = 1. This transformation is equivalent to θ → π − θ, or to a change in sign of one of the vectors n and n′ (cf. §137). From these conditions we obtain the relations
Owing to isotopic invariance, the scattering amplitude is the same for nn and pp scattering and for np scattering in the isotopic state with T = 1, For the np system, however, the state with T = 0 is also possible, and the np scattering amplitude is therefore described by other coefficients a, b,… in (1), which do not possess the symmetry properties (2).
§141 Regge poles
In §128 we have considered the analytical properties of the scattering amplitude as a function of the complex variable E, the energy of the particle; the orbital angular momentum l acted as a parameter having real integral values. Further properties of the scattering amplitude that are of methodological importance appear if we now regard l as a continuous complex variable for real values of the energy E.†
As in §128, we shall take radial wave functions whose asymptotic form (as r → ∞) is
These functions are solutions of Schrödinger’s equation (32.8) (in which l is now regarded as a complex parameter); the choice from the two independent solutions is governed by the condition
It is immediately evident that this condition places a certain limitation on the permissible values of the parameter l: the general form of the solution of equation (32.8) for small r is
(see the end of §32). In order for the second solution to be clearly distinguished from the first solution and eliminated, the term in r−l−1 must exceed that in rl as r → 0. For complex l, this leads to the condition re l > re (−l − 1), or
In the following, we shall consider only this half of the complex l-plane, to the right of the vertical line l = − 
.
The wave function R (r; l, E), being a solution of a differential equation with coefficients analytic in the parameter l, is an analytic function of l, having no singularities in the half-plane (141.3). This applies, in particular, to the asymptotic expression (141.1), and the functions A (l, E) and B (l, E) therefore have no singularities with respect to l. Here, however, it is assumed that the retention of both terms in (141.1) as r → ∞ is in fact legitimate. When E > 0 this is always true; when E < 0 it is true if the field U (r) satisfies the condition (128.6) or (128.13). In these arguments it is important that the form of the asymptotic behaviour (with respect to r) of the wave function depends on E but not on l. The approach to the asymptotic form is therefore unaffected by the fact that l is complex.
Comparing (141.1) with the asymptotic formula (128.15), we find the S-matrix element in the form
which is valid for complex l also (although the “phase shift” δ is of course then not real).
For real l, and E > 0, the functions A and B are related by (128.4): A (l, E) = B*(l, E). Hence it follows that, for complex l,
and S (l, E) therefore satisfies the complex unitarity condition
Since A (l, E) and B (l, E) have no singularities as functions of l, the function S (l, E) and thus the partial scattering amplitude f (l, E) have singularities (poles) only at the zeros of the function B (l, E). The poles of the scattering amplitude in the complex l-plane are called Regge poles. Their position depends, of course, on the value of the real parameter E. The functions
which determine the positions of the poles, are called Regge trajectories; when E varies, the poles move along certain lines in the l-plane. The subscript i which labels the poles will be omitted henceforward.
Going on now to study the properties of the Regge trajectories, we shall show first of all that for E < 0 all the α(E) are real functions. To do so, let us consider the equation
which is satisfied by the wave function with l = α. Multiplying this equation by χ* and integrating with respect to r (with integration by parts in the first term), we obtain
Here we have used the fact that for B = 0 (the condition determining the Regge poles) the wave function decreases exponentially as r → ∞, so that all the integrals converge. The first two terms in the above equation are real, and so is the integral in the last term. Hence we must have
But, since we are considering only poles in the half-plane (141.3), we certainly have re (α + 
) > 0, and this gives the desired result
Next, we proceed as follows with (141.7), in a similar manner to the derivation of equation (128.10): differentiate with respect to E, multiply by χ, and multiply (141.7) by ∂χ/∂E, and subtract. This gives the identity
Integration with respect to r from 0 to ∞, again using the fact that χ → 0 as r → ∞, shows that the integral of the first term is zero, and we have
Since we know that α is real, the wave function is also real, and both integrals in (141.9) are therefore positive. Hence
and, since α + 
> 0,
Thus, for E < 0, the functions α(E) increase monotonically with E.
The negative values of E for which the functions α(E) take “physical” values (i.e. are integers l = 0, 1, 2, …) correspond to the discrete energy levels of the system. Note that this gives rise to a new principle of classification of bound states, according to the Regge trajectories on which they lie.
As an example, let us consider Regge trajectories for motion in an attractive Coulomb field. The scattering matrix elements are then given by†
with k in Coulomb units. The poles of this expression are at points where the argument of Γ(l + 1 − i/k) is a negative integer or zero. For E < 0 we have k = i√(−2E), so that
where nr = 0, 1, 2, … is the number of the Regge trajectory. Equating α(E) to an integer l = 0, 1, 2, …, we obtain the familiar Bohr formula for discrete energy levels in a Coulomb field:
The number nr here coincides with the radial quantum number which determines the number of nodes of the radial wave function. Each Regge trajectory (i.e. each given value of nr) corresponds to an infinity of levels with different values of the orbital angular momentum.
Let us now consider the properties of the functions α(E) for E > 0. The functions A (l, E) and B (l, E) of the complex variable E in (141.1) are defined on a plane with a cut along the right half of the real axis (see §128). Correspondingly, the functions l = α(E), for which B (l, E) = 0, have a similar cut. On the upper and lower edges of the cut, α(E) has complex conjugate values, with im α > 0 on the upper edge. Without pausing to give a formal proof of this, we shall present a more physical explanation of the reason.
When l is complex, so is the centrifugal energy and therefore the effective potential energy Ul = U + l (l + 1)/2mr2. Repeating the derivation in §19, we now have instead of (19.6)
When l = α, and im α > 0, we also have im Ul > 0. Then the right-hand side of the equation is positive, signifying an emission of new particles in the field volume. Accordingly, the asymptotic expression for the wave function (which, when B = 0, contains only the first term in (141.1)) must represent an outgoing wave, and this occurs on the upper edge of the cut, cf. the derivation of (128.3) from (128.1).
Since, for E > 0, the functions α(E) are complex, they cannot here take their “physical” values l = 0, 1, 2, …. They may, however, be close to these values in the complex l-plane. We shall show that there is then a resonance in the partial scattering amplitude (corresponding to the integral value of l in question).
Let l0 be the integral value close to the function α(E), and let E0 be the (real and positive) value of the energy for which re α(E0) = l0. Then, near this value, we have
where η = im α(E0) is a real constant. We shall consider values α(E) on the upper edge of the cut; according to the preceding discussion, η > 0 in that case (and η 1, from the assumption that α is close to l0). It is easy to see that the constant β (i.e. the derivative dα/dE for E = E0) may be regarded as real and positive: since α(E) is almost real, so is the wave function χ(r; α, E). Neglecting quantities of a higher order of smallness with respect to η, we can neglect the imaginary part of χ, and then it follows that β is positive, since the integrals in (141.9) are positive.†
Since l = α(E) is a zero of B (l, E), the latter is proportional to α − l near the point α, E0. Using (141.12), we therefore have
The form of this expression is the same as that of (134.6), with E0 the energy and Γ = 2η/a > 0 the width of the quasi-discrete level. Thus the closeness of the Regge trajectory (for E > 0) to integral values of l corresponds to quasi-stationary states of the system. For these states, therefore, there exists the same principle of classification as for strictly stationary states: each Regge trajectory can correspond to a family of discrete and quasi-discrete levels.
The treatment of l as a complex variable enables us to derive a useful integral form of the total scattering amplitude (for E > 0), given by the series (123.11):
To obtain this, we must first define the functions Pl(μ) not only for integral l ≥ 0 but also for complex l. This can be done by taking Pi(μ) as the solution of equation (c.2):
with the boundary condition Pl(1) = 1. The Pl(μ) thus defined as a function of l has no singularities for finite values of l.†
It is easily seen that the series (141.14) is equal to the integral
taken along a contour C that passes in a negative direction (clockwise) round all the points l = 0, 1, 2, … on the real axis and is closed at infinity:
All the poles l = α1, α2, … of the function S (l, E) (which are not on the real axis if E > 0) must remain outside the contour C. The integral (141.16) reduces to − 2πi times the sum of the residues of the integrand at the points l = 0, 1, 2, …, which are poles of the function 1/sin πl, and the residues of this function itself are (−1)l/π. Since for integral l we have Pl(−μ) = (−1)l Pl(μ), we arrive at (141.14) from (141.16)‡
PROBLEM
Show that the phase shifts corresponding to successive integral values of l satisfy the inequality
SOLUTION
We will regard l as a continuous real variable, and differentiate (32.10) with respect to it:
Multiplication of this by χ and the original equation by ∂χ/∂l, and subtraction, gives
We integrate this over r from 0 to ∞. For r = 0 the expression in the square brackets is zero, and for r → ∞ we can use for χ the asymptotic expression (33.20). The result is
so that ∂δl/∂l < 
π. Integration over l from l to l + 1 gives the required inequality. Together with 1133.17), it shows that the number nl of discrete levels does not increase with l. As E → ∞ and the Born approximation becomes valid, the scattering phases tend to zero, so that δl(∞) = 0. Then
†Here we neglect the spin—orbit interaction of the particles (if they have spin). By assuming the field to be centrally symmetric, we exclude from consideration also processes such as the scattering of electrons by molecules.
†It is supposed that the incident beam of particles is defined by a wide (to avoid diffraction effects) but finite diaphragm, as happens in actual experiments on scattering. There is therefore no interference between the two terms of the expression (123.3); the squared modulus |ψ|2 is taken at points where there is no incident wave.
†The problem of recovering the form of the scattering potential from the phases δl (assumed known) is of fundamental interest. This has been solved by I. M. Gel’fand, B. M. Levitan and V. A. Marchenko. It is found that, to determine U (r), it is in principle sufficient to know δ0(k) as a function of the wave number throughout the range from k = 0 to k = ∞, together with the coefficients an in the asymptotic expressions (for r → ∞) Rn0 (an/r)e−κnr (κn = √(2m|En|)/ħ) of the wave functions of states corresponding to the discrete (negative) energy levels En (if any). The determination of U (r) from these data requires the solution of a certain linear integral equation. This topic is fully discussed by V. de Alfaro and T. Regge, Potential Scattering, North-Holland, Amsterdam, 1965.
†This is seen from the divergence of the integral ∫ 2πρ d ρ which gives the total cross-section in classical mechanics.
†† This formula is the expansion of the delta function in Legendre polynomials, and can be immediately verified by multiplying both sides by sin θ Pl(cos θ) and integrating over θ. Here the integral
of the even function δ(x) is taken to be 
.
†To calculate the integral, we displace the path of integration with respect to the variable μ = cos θ (θ being the angle between n and n′) in the complex μ-plane in such a way that it bends into the upper half-plane, the end points μ = ±1 being kept fixed. Then the function eikrμ decreases rapidly as we move away from these end points.
†In the general theory derived in §123 this approximation corresponds to the case where all the phases δl are small; it is also necessary that these phases can be calculated from Schrödinger’s equation with the potential energy regarded as a perturbation (see Problem 4).
†Hence it is clear that this property no longer holds in even the second approximation of perturbation theory. This will be proved directly in §130; cf. (130.13).
†The inapplicability of perturbation theory in this case is easily seen by calculating the scattering amplitude in the second approximation (see (130.13)); although the coefficient of the exponential is small in comparison with the coefficient in the first-approximation term, the magnitude of the negative exponent is only half as great.
†The relation between θ and ρ given by (127.5) may not be one-to-one; more than one value of ρ may correspond to the same value of θ. In such a case, the amplitude f (θ) is given by the sum of (127.6) with the appropriate values of l0. At extrema of θ(ρ) the derivative dp/dθ and therefore the classical differential cross-section dσ/do become infinite; near such an angle, the classical approximation is of course invalid (see Problem 2).
†This type of scattering occurs in the theory of the rainbow, and it is therefore called rainbow scattering.
‡Strictly speaking, the amplitude should include a term representing the contribution to small-angle scattering from impact parameters ρ → ∞. This contribution, however, is in general small in comparison with that shown
This type of scattering is called luminescence, from its occurrence in the theory of certain meteorological phenomena.
†In the rest of this section we shall be considering the properties of the scattering amplitude on the physical sheet. Later, however, it will sometimes be necessary to consider another “non-physical” sheet of the Riemann surface (see §134), On this sheet
The passage from the right half of the axis to the non-physical sheet is made directly down through the cut.
†Except the point E = 0, which is singular, because of the singularity of A (E) and B (E) previously mentioned. The scattering amplitude, however, remains finite as E → 0 (see §132). In future we shall, for brevity, omit this qualification.
†Since U (r) is real on the real axis U (r*) = U*(r); thus the condition (128.13) is satisfied throughout the right half-plane if it is satisfied in the lower right quadrant.
†The limiting form (33.17) of these functions can be used only for E > 0; in the rest of the E-plane, where the two terms in χ are of different orders of magnitude, the use of these limiting expressions would involve an error in χ which is in general greater than that which arises from neglecting U in Schrödinger’s equation.
†It is assumed, of course, that the field U (r) decreases, as r → ∞, sufficiently rapidly for f (0, E) to exist (when E > 0); see §124.
†To avoid misunderstanding, we should emphasize that here we are discussing the complete wave function ψ of the system, normalized by the condition that the coefficient of the plane wave in its asymptotic expression should be equal to unity (cf. 123.3)). In the previous section we were considering the parts ψl of the wave function which correspond to definite values of l, and ψl was assumed to be normalized in some arbitrary manner. If we expand the complete function ψ in terms of the functions ψl, the latter will appear in ψ with coefficients proportional to 1/Bl. For example, the function (128.3) with l = 0 must appear in ψ in the form
Hence ψ becomes infinite at the zeros of the functions Bl(E), i.e. at the discrete energy levels.
‡The idea of the foregoing proof is due to L. D. Faddeev (1958).
†For convenience of notation, we write q as an argument of the Fourier component instead of as a subscript.
‡According to the properties of the delta function, the product (q2 − k2)δ(q − k) gives zero when multiplied by any function f (q) (not having a singularity at q = k) and integrated over d3q. In this sense, (q2−k2)δ(q − k) ≡ 0.
†This result can, of course, also be easily obtained without recourse to the momentum representation: the fact that the second-approximation formula differs from the first-approximation formula by the replacement of U (k′ − k) by the expression in the braces in (130.13) is evident from a comparison of (43.1) and (43.6).
†This method of determining the scattering amplitude is analogous to the one used in the discussion of Fraunhofer diffraction (Fields, §61). Diffraction effects make formula (131.4) inapplicable for z ≥ ka2.
†In the two-dimensional case, the scattering amplitude in the field U (x, z) is determined, as in §123, Problem, by the analogous formula
The square |f|2 dφ is the scattering cross-section per unit length along the y-axis, and φ is the angle of scattering in the xz-plane; cf. also §126, Problem 6.
‡In §152 a generalization of formulae (131.7) and (131.8) to the case of scattering by ft system of particles will be given.
†The quasi-classical function 2ħδ(ρ) is the change in the action, caused by the field U, when the particle traverses a classical path. For a fast particle, this path may be taken as a straight line, and 2δ(ρ) is then the difference of the classical action integrals
In this sense, the function 2δ(ρ) here acts like the eikonal in geometrical optics. The approximation in scattering theory is therefore often called the eikonal approximation. It must be emphasized, however, that the scattering amplitude does not reduce to its quasi-classical value, since the conditions θ1 1, δl 1 are not in general satisfied.
†A discussion of the coefficient of the exponential is given by A. Z. Patashinskii, V. L. Pokrovskii and I. M. Khalatnikov, Soviet Physics JETP 18, 683, 1964.
‡The method described here is valid not only for large E but generally for all cases of exponentially small scattering.
||It may be recalled (see §126) that, if U (r) has a singularity for real r, the decrease of the cross-section is not exponential.
†Formula (3), like (131.4), is not applicable for very large z, when diffraction effects become important.
‡This formula (for q ≠ 0) can, as already mentioned, also be derived without using Schrödinger’s equation in the potential field.
†In the scattering of electrons by atoms, the length a with which 1/k must be compared (the condition ka 1) is represented by the radius of the atom, which is several times the Bohr radius (several times ħ2/me2) for complex atoms. Owing to the large value of this radius, the constancy of the effective cross-section actually applies here only up to energies of the order of fractions of an electron-volt; at greater electron energies there is a marked energy dependence of the cross-section (called the Ramsauer effect).
‡For small E, the condition (128.6) is satisfied even when U decreases as e−r/a.
†The scattering at low velocities is in this case nowhere quasi-classical, since the inequality (132.11) is incompatible with the simultaneous requirement that U (ρ)| ≤ E.
†If n is an odd integer 2p + 1, then n − 3 = 2p − 2 is an even number. In this case also, however, the integral (132.14) has an “anomalous” part, which gives a contribution to the scattering amplitude proportional to q2p−2 log q.
‡This formula becomes inapplicable if the width and depth of the well are such that κa is close to an odd multiple of 
π. For such values of κa the discrete spectrum of negative energy levels includes one which is close to zero (see §33, Problem 1), and the scattering is described by formulae which we shall derive in the next section.
†Formula (133.8) was first derived by E. Wigner (1933); the idea of the derivation given here is due to H. A. Bethe and R. E. Peierls (1935).
†The values of the constants α and r0 may be mentioned for the important case of the interaction of two nucleons. For a neutron and a proton with parallel spins (isotopic state with T = 0), α = 5·4 × 10−13 cm, r0 = 1·7 × 10−13cm; these correspond to a true level with energy |∈| = 2·23 MeV, the ground state of the deuteron. For a neutron and a proton with antiparallel spins (isotopic state with T = 1), α = −24 × 10−13 cm, r0 = 2·7 × 10−13 cm; these values correspond to a virtual level with |∈| = 0·067 MeV. Owing to isotopic invariance, the latter values must apply also to a system of two neutrons with antiparallel spins; parallel spins of the nn system in the s state are prohibited by Pauli’s principle.
†For ∈ < 0, and E close to |∈|,
A comparison with (128.17) shows that 6 > 0.
†In formula (133.6) this corresponds to a change of δ0 from 0 to π when, for a given small value of k, the quantity κ changes from a negative value (− κ k) to a positive value κ k. When l ≠ 0, the same follows from the formula k cot δl = − bE−l(E − ∈) when, for a given E = Δ, ∈ varies from ∈ Δ to −∈ Δ.
†This inequality had previously been derived in a different manner by Wigner (1955).
†We may note that this shows the physical necessity for Σ to be positive, a condition which is automatically satisfied on account of the boundary condition imposed at infinity on the solution of the wave equation, or by the equivalent (see §130) rule of passage round poles in the formulae of perturbation theory. Let transitions from the discrete level n to the states v of the continuous spectrum be caused by a constant perturbation V. Then the second-order correction to the energy level is
cf. (38.10) The rule (43.10) gives
in agreement with (43.1) for the transition probability.
†If scattering of a charged particle by a system of charged particles is considered, the expression (135.11) must be used for the phases φl(0).
‡It may be noted that formula (133.15) for resonance scattering of slow particles by a positive energy level ∈ with l ≠ 0, with E close to ∈, is in exact correspondence with the resonance term in (134.12). The values of E0 and Γ are given by formulae (133.16), and since E is small the phase δl(0) is small, so that e2iδl(0) 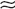1.
†It is assumed that the scattering field decreases sufficiently rapidly with increasing distance. In §145 the results given here will be applied to the scattering of slow neutrons by nuclei.
‡The function b0(E) determines, according to (134.9), the phase of the potential scattering. In the scattering of slow particles, the first terms in its expansion are b0(E) = constant i (1 + iαk).
†In this section we use Coulomb units (see §36).
†The origin of this distortion may be elucidated classically. If we consider a family of classical Coulomb hyperbolic paths with the same direction of incidence (parallel to the z-axis), the equation of the surface normal to them at large distances from the scattering centre (z → − ∞) is easily shown to tend to z + k−2 log k (r − z) = constant, not z = constant. This is the surface of constant phase of the incident wave in (135.8).
†The value of δl, Coul in this formula differs from the true (divergent) Coulomb phase by a quantity which is the same for all l.
†Essentially, only the orthogonality of the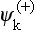 
needs to be proved separately; the normalization could be derived directly from the asymptotic form of the functions (cf. §21). In this sense, the validity of (136.2) is evident from the fact that, as r − ∞, the only non-decreasing term in these functions is 
.
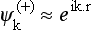†Using Coulomb units.
†An example of such a process is an electron colliding with a heavy nucleus at rest and emitting a photon, thereby changing its energy and its direction of motion; the perturbation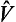 
is the interaction between the electron and the radiation field, and the Coulomb field of the nucleus is the field U for which the functions ψk(+) and 
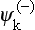are defined (see RQT, §§92 and 96). Another example is a collision of an electron with an atom, accompanied by ionization of the latter; sec §148, Problem 4.
†Here the direct spin—orbit interaction is again ignored.
†The theory given below is due to L. D. Landau and Ya. A. Smorodinskil (1944).
†The functions F0 and G0 (and the correspondingly defined functions Fl and Gl with l ≠ 0) are called regular and irregular Coulomb functions respectively.
†The expansion (138.7) is obtained from (138.5) by means of the expansion (d.17), using the well-known relation
(which is easily derived from Γ(z + 1) = zΓ(z)) and the values ψ(1) = −C, ψ(2) = −C + 1.
†To calculate the function h (k), we can use the formula
which is easily obtained by means of the formula
see Whittaker and Watson, Course of Modern Analysis, Cambridge, 1944, §12.16. The limiting expressions for h (k) are
the latter formula gives values of h (k) which are correct to within 4% even for k > 2·5.
†The values of the constants α = 1/κ0 and r0 for proton—proton scattering are α = − 7·8 × 10−13 cm, r0 = 2·8 × 10−13 cm (Coulomb unit of length 2ħ2/mpe2 = 57·6 × 10−13 cm). These values relate to a pair of protons with antiparallel spins; when the spins are parallel a system of two protons cannot be in the s state, by Pauli’s principle.
‡See L. Landau and Ya. A. Smorodinskii, Zhurnal éksperimental’noi i teoriticheskoi fiziki 14, 269, 1944.
†We are neglecting exchange effects between the fast electron which undergoes scattering and the atomic electrons, i.e. we do not symmetrize the wave function of the system. The legitimacy of this procedure is evident: the interference between the rapidly oscillating wave function of the free particle and the wave function of the atomic electrons in the “exchange integral” has the result that the corresponding contribution to the scattering amplitude is small.
†It must be borne in mind that this formula is not applicable for small q, since the integral of nr2 cannot in practice be calculated by the Thomas—Fermi method (see the third note to §113). It should also be mentioned that the Thomas—Fermi model does not represent the individual properties of atoms or their systematic variation with atomic number.
†If the squared modulus |f0n|2 of the matrix element of some operator for the transition 0 → n is summed over final states n, we have
To avoid misunderstanding, it should be emphasized that the sign + denoting the conjugate refers in (140.6) and henceforward to f as a spin operator; in particular, the transposition of n and n′ is not implied.
†Here we have in mind a target with a completely random distribution of spin directions. For s >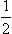 
, it will be recalled, the mean value of the spin vector does not fully determine the spin state, and if this mean value is zero there is not necessarily a complete absence of ordering of the spins.
‡‡ The derivation of this relation is similar to that of formula (125.12). The amplitudes c the ingoing and outgoing waves must contain spin factors, and instead of (125.10) we have the condition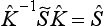 
, where 
is an operator which not only effects inversion but also changes the spin state in accordance with (60.3).
†These properties were first investigated by T. Regge (1958).
†Cf. (135.11), in which the sign of k must be changed to convert from repulsion to attraction.
†To elucidate the structure of these integrals, we note that the asymptotic region r a (where a is the range of action of the field), in which the expression (141.1) for the wave function is valid, makes only a small contribution to the integrals if η is small. For, if l = α(E) is a zero of B (l, E), then by (141.5) l = α* is a zero of A (l, E). Hence A (α, E) and therefore χ(r;α, E) in the region r a, are small quantities ∼η1/2; see (134.11). In estimating the integrals, it is also important that, on the upper edge of the cut (in relation to E), the wave function contains a factor eikr: χ(r;α, E) = A (α, E)eikr. On this edge, we can regard E as E + iδ (δ → +0); then k also has a small positive imaginary part, which ensures the convergence of the integrals in (141.9). Physically, the smallness of the contribution to the integrals from the region r a is due to the fact that the energy E0 corresponds to a quasi-stationary state (see below); the particle therefore reaches this region only as a result of an improbable decay “of the state The principal contribution to the integrals comes from the region r ∼ a, in which the wave function is almost real.
†By comparison of (141.15) with (e.2) we can express Pl(μ) as a hypergeometric function:
‡A more detailed account of the ideas discussed in this section (for non-relativistic theory) is given in the book by de Alfaro and Regge quoted in §123.