 , of real numbers and properties of various subsets of it.
, of real numbers and properties of various subsets of it.When you read advanced mathematics books you will see the word “set” show up with great frequency. Since the late 1800s, set theory has been a fundamental approach to describing mathematical objects. For example, if you study abstract algebra you will encounter a statement that begins
Similarly, in real analysis you study the set,  , of real numbers and properties of various subsets of it.
, of real numbers and properties of various subsets of it.
A set is nothing more than a collection of objects, and the objects are referred to as its elements. When a set is quite small, it is usually described by listing its elements inside of squiggly braces. For example, 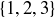 is a set whose elements are the first three natural numbers. One very small yet very important set is the empty set. This is a set that has no elements, and it is commonly denoted by
is a set whose elements are the first three natural numbers. One very small yet very important set is the empty set. This is a set that has no elements, and it is commonly denoted by 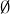 or
or  .
.
Sets are often described using set builder notation. For example, the set of positive “perfect squares,” which we give the temporary name S, can be described as
![]()
The initial statement, 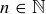 , describes what sort of objects are being considered for membership in S, while the second half describes all of the conditions that are placed on membership. The vertical bar that separates the two halves can be read as “such that,” so that as a sentence we have “S is the set of all natural numbers n such that n is equal to
, describes what sort of objects are being considered for membership in S, while the second half describes all of the conditions that are placed on membership. The vertical bar that separates the two halves can be read as “such that,” so that as a sentence we have “S is the set of all natural numbers n such that n is equal to 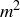 for some natural number m.”
for some natural number m.”
Exercise 3.1 Complete the statement: 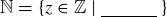 .
.
We will let 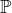 denote the set of all prime numbers:
denote the set of all prime numbers:
![]()
(Unlike  and
and  , there is no standard notation for the primes.) This set can be defined using set builder notation:
, there is no standard notation for the primes.) This set can be defined using set builder notation:
![]()
Here is an example of a “family” of sets defined using set builder notation. For any  , we can define
, we can define
![]()
In other words, 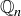 consists of those rational numbers that can be expressed with a denominator that is a power of n. For example
consists of those rational numbers that can be expressed with a denominator that is a power of n. For example 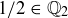 ; on the other hand,
; on the other hand,  for the following reason. Suppose that
for the following reason. Suppose that
![]()
for some integers m and k. If 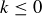 you would have
you would have 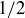 equaling an integer, so k must be positive. But then cross-multiplying would yield
equaling an integer, so k must be positive. But then cross-multiplying would yield 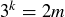 , and hence
, and hence 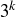 would be even for some
would be even for some 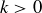 , a contradiction.
, a contradiction.
Exercise 3.2 Explain why modifying the definition of 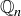 to become
to become
![]()
does not change its contents.
Exercise 3.3 Prove that 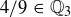 ,
,  , and
, and 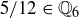 . We will return to the sets
. We will return to the sets 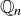 at several points, so it is worth spending some time now to understand what elements they contain.
at several points, so it is worth spending some time now to understand what elements they contain.
Exercise 3.4 You can explain the existential quantifier usingset theory. If A is a set and P(a) is a statement about 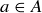 , explain why
, explain why
![]()
are either both true or both false. Then do the same for the universal quantifier
![]()
If S is a set with finitely many different elements, then 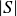 denotes the number of different elements in S. For example,
denotes the number of different elements in S. For example,
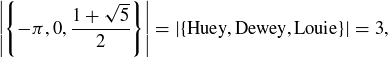
and
![]()
as well. If S is not finite then we simply say that S is an infinite set.
We say that A is a subset of B, and we write 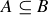 , if every
, if every 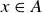 is also an element of B. For example,
is also an element of B. For example,
![]()
If 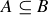 , and it is known that there is a
, and it is known that there is a  with
with  , then we write
, then we write 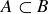 and say that A is a proper subset of B. Thus,
and say that A is a proper subset of B. Thus,  and
and 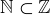 . As with
. As with 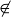 , we use the symbols
, we use the symbols  and
and 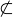 , so that we may write
, so that we may write  .1
.1
A Hasse diagram is sometimes used to display subset relationships in a finite collection of sets, with 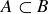 if you can follow an ascending path of edges from A to B. For example, Figure 1 shows the subset relationships among all eight possible subsets of
if you can follow an ascending path of edges from A to B. For example, Figure 1 shows the subset relationships among all eight possible subsets of 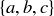 .
.
Exercise 3.5 Show that if  , then
, then  . Then, explain why
. Then, explain why 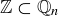 for
for 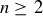 .
.
EXAMPLE 3.1. It is important to understand that 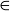 and
and  correspond to different concepts. Let
correspond to different concepts. Let  be the 4-element set whose members consist of three integers and a set of two integers. Then the following are true statements:
be the 4-element set whose members consist of three integers and a set of two integers. Then the following are true statements:
(a) 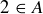
(b) 
(c) 
(d) 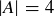
Exercise 3.6 Referring to Example 3.1, explain why the following statements are false:
(a) 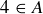
(b) 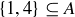
(c) 
(d) 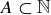
Two sets are equal if they contain exactly the same elements. That is, 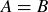 if both of the following are true:
if both of the following are true: 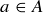 implies
implies 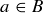 , and
, and  implies
implies 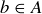 . Alternatively, using subset notation we say that
. Alternatively, using subset notation we say that 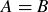 if both
if both 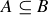 and
and  .
.
In the proof of the proposition below, we show that two sets are equal in a standard way. Notice that the word “let” begins both halves of the argument, as you need to start each half with any possible element of the given set.
PROOF. We will first show that 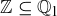 , and then that
, and then that  .
.
To show that 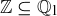 , let
, let  . If we set
. If we set 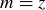 and
and  , then we know that
, then we know that 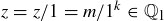 as well.
as well.
To show that  , let
, let 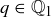 . By the definition of
. By the definition of 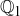 , there exist integers m and k such that
, there exist integers m and k such that  . Since
. Since 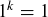 for any k, we know that
for any k, we know that 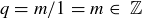 .
.

Exercise 3.7 Determine all of the subset and proper subset relationships among the famous sets  ,
, 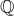 ,
,  , and
, and  .
.
Exercise 3.8 Determine all sets S such that 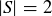 and
and  .
.
For  , we define
, we define
![]()
In this definition, the two vertical bars have different meanings that should be clear from context: “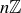 equals the set of all integers m such that n divides m.” For example,
equals the set of all integers m such that n divides m.” For example,  .
.
Given two sets A and B, you can combine them into one set:
![]()
The resulting set is called the union of A and B. Similarly, you can restrict to common elements:
![]()
The resulting set is the intersection of A and B.
These operations are commonly visualized using Venn diagrams. A 2-set Venn diagram is a way of illustrating how two sets may interact with each other, as in Figure 2. The entire shaded region represents 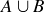 while the smaller, darker region is
while the smaller, darker region is  . The rectangle acts as a “universal” set containing both A and B as subsets; we will say more about universal sets later in this section.
. The rectangle acts as a “universal” set containing both A and B as subsets; we will say more about universal sets later in this section.
You can also have a set that is the difference of two sets:
![]()
Notice that in this definition of set difference we do not assume that 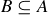 . Another common way to write
. Another common way to write  is
is  .
.
REMARK 3.3. We emphasize that this type of “subtraction” has absolutely nothing to do with the difference of real numbers. For example,
![]()
doesn’t involve the calculation of 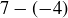 , and certainly not
, and certainly not 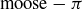 !
!
The symmetric difference of two sets is
![]()
Put another way,  . This set is illustrated in Figure 2 by the two somewhat crescent-shaped regions that are lightly shaded.
. This set is illustrated in Figure 2 by the two somewhat crescent-shaped regions that are lightly shaded.
(a) 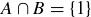
(b) 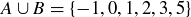
(c) 
(d) 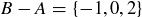
(e) 
Exercise 3.10 If  and
and 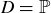 , the set of primes, determine the following sets.
, the set of primes, determine the following sets.
(a) 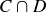
(b) 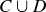
(c) 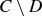
(d) 
(e) 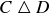
Exercise 3.11 Two sets A and B are said to be disjoint if they have no common elements; that is,  . Explain whether each of the following statements is logically equivalent to
. Explain whether each of the following statements is logically equivalent to 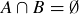 .
.
(a) 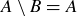 and
and 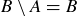
(b) 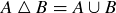
We often want to talk about the things that are not in a set A. However, there is a small problem. For example, you might want to point out that
![]()
but it would be rather silly to point out that
![]()
In a less silly vain, suppose someone says “Pick a number not equal to 1.” Are you allowed to pick  ? the golden ratio ϕ? or maybe the imaginary number
? the golden ratio ϕ? or maybe the imaginary number  ? The term “number” hasn’t described a specific domain of discourse, making the request vague.
? The term “number” hasn’t described a specific domain of discourse, making the request vague.
When talking about elements that are not in a given set, it is always best to make sure that a universal set, the set of elements under consideration, has been made explicit. If U is the universal set, and if 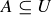 , then the complement of A consists of all of the elements in U that aren’t in A:
, then the complement of A consists of all of the elements in U that aren’t in A:
![]()
For example, if we let  be the universal set, then
be the universal set, then 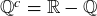 is the set of irrational numbers.
is the set of irrational numbers.
REMARK 3.5. Because the universal set is not always clear in a given situation, some mathematicians avoid referring to complements of sets, preferring to always write  instead of
instead of  .
.
Exercise 3.13 In this exercise you’ll examine the identity:
![]()
(a) Explain why 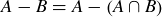 by appealing to a Venn diagram.
by appealing to a Venn diagram.
(b) Now prove that  without referring to a Venn diagram. Instead argue that any element of
without referring to a Venn diagram. Instead argue that any element of  is an element of
is an element of  , and vice versa.
, and vice versa.
There are many elementary facts about set operations that are used quite frequently. The following theorem lists a number of these essentially arithmetic identities. Proofs of two of these identities are presented below; finding proofs for the rest is Exercise 3.51.
THEOREM 3.6. Let A, B and C be sets. Then the following formulas hold.
(1) 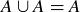
(2) 
(3) 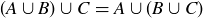
(4) 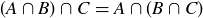
(5) 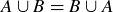
(6) 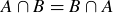
(7) 
(8) 
PROOF OF (3). We first show that 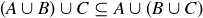 . To do this, let
. To do this, let 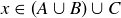 . By the definition of the union of two sets, this implies that
. By the definition of the union of two sets, this implies that 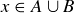 or
or 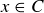 , which (again by the definition of union) means that
, which (again by the definition of union) means that 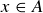 or
or 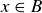 or
or 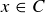 . This in turn means that
. This in turn means that 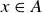 or
or 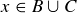 , which implies that
, which implies that  . Thus, we have shown that
. Thus, we have shown that 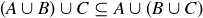 .
.
The other half of the proof is Exercise 3.14.

Exercise 3.14 Prove that 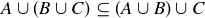 , which completes the proof of (3).
, which completes the proof of (3).
PROOF OF (8). We first show that 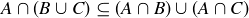 . Let
. Let 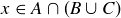 . This implies, by the definition of intersection, that
. This implies, by the definition of intersection, that 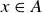 and
and 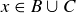 . In particular,
. In particular, 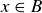 or
or 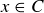 . If
. If 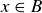 , then
, then  , so
, so 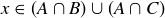 . If
. If 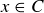 , then
, then  , and thus
, and thus 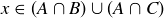 . The conclusion is that
. The conclusion is that 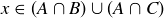 , proving that
, proving that 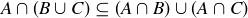 .
.
The other half of the proof is Exercise 3.15.

Exercise 3.15 Prove that  , which completes the proof of (8).
, which completes the proof of (8).
The associative laws tell us that the manner in which we build the unions and intersections of three sets, two-at-a-time, doesn’t matter. Section 3.5 gives definitions of the union and intersection of an arbitrary number of sets, in a way that is consistent with the associative laws we have just proven and that leads to more general versions of the distributive and other laws.
The following theorem is stated in terms of complements; a complement-free version can be found in Exercise 3.53.
PROOF OF (3). To prove the “only if” half, we use the assumption that 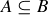 to prove that
to prove that  . Since we want to show that
. Since we want to show that 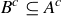 , we let
, we let 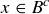 ; our goal is to conclude that
; our goal is to conclude that  .
.
Since
![]()
we know that 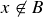 . We are assuming that
. We are assuming that 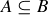 , so we know that
, so we know that 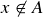 as well. Since
as well. Since 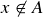 , x is in the set
, x is in the set 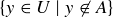 , which is exactly the statement that
, which is exactly the statement that  .
.
As you might have expected, the proof of the “if” half is Exercise 3.16.

Exercise 3.16 Finish the proof of (3) in Theorem 3.7.
Figure 3 shows a Venn diagram for three sets A, B, and C. When dealing with two or three sets at a time, Venn diagrams are very useful for helping you build instinct and then verify claims; these are important parts of the process of mathematical exploration and explanation. However, Venn diagrams have their limitations, as they might not be helpful for situations involving more than three sets (see Section 3.5 and Exercises 3.57, 3.65, and 3.88). The proofs given so far in this section are the type of general “element” arguments already seen in the proof of Proposition 3.2 and in part (b) of Exercise 3.13. These types of arguments are ubiquitous in many mathematical settings and require practice.
Exercise 3.17 Use a 3-set Venn diagram to investigate the claim that symmetric difference is associative: for any sets A, B, and C,
![]()
Exercise 3.18 Let A and B be finite sets. Venn diagrams may be useful for investigating the following:
(a) Prove 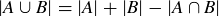 .
.
(b) If C is another finite set, is there an analogous formula for 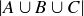 ? If so, prove that your formula is correct.
? If so, prove that your formula is correct.
Section 3.3 discussed the intersection and union of two sets, and Section 3.4 extended these to three sets. What if we want to discuss intersections and unions of more than three sets? In particular, how could we discuss intersections and unions of an infinite number of sets? As an example to motivate these general questions, we look first at a specific infinite collection of nested open intervals on the real number line  .
.
Recall that 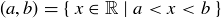 . For each
. For each 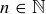 define an associated open interval
define an associated open interval
![]()
For instance, 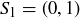 ,
, 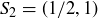 , and
, and 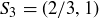 .
.
Exercise 3.19 Indicate the first five of these sets on a number line to see why we call them “nested.”
What is the union of all of these intervals? Generalizing the definition of union in Section 3.3, it should consist of all real numbers that are in at least one of the sets 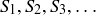 Notationally, we write
Notationally, we write
![]()
which can be read as “the union of the 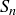 s, taken over all natural numbers n.”
s, taken over all natural numbers n.”
![]()
PROOF. We prove that the two sides of the equation are equal by showing that each is a subset of the other.
Let  . This means that
. This means that 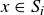 for some
for some  . Since
. Since  for each
for each  , we know that
, we know that  .
.
Alternatively, let 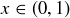 . Since
. Since 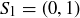 , we know that
, we know that 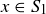 , and therefore
, and therefore  .
.

What is the intersection of these intervals? It should consist of all of the real numbers that are in every one of the sets 
![]()
PROOF. In trying to prove that a set is empty, it is a common tactic to begin by assuming to the contrary that the set is not empty. So to establish the equation we begin by assuming to the contrary that there is some 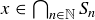 . Then this x must satisfy
. Then this x must satisfy
![]()
for all  . In particular, if we consider all n of the form
. In particular, if we consider all n of the form 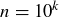 for natural numbers k, then we must have
for natural numbers k, then we must have 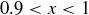 , and
, and 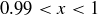 , and
, and  , and so on. Can any such x exist? The answer is “no”; but a rigorous proof must be postponed until we encounter the Archimedean Property in Section 8.2.
, and so on. Can any such x exist? The answer is “no”; but a rigorous proof must be postponed until we encounter the Archimedean Property in Section 8.2.

Now let’s define the general concept of indexing. An index set is simply a set I that helps describe a collection of mathematical objects. In the case of sets, the individual sets are written as 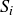 , where
, where  . In the example above, the index set
. In the example above, the index set 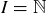 , because there is one set for each natural number. Other options for index sets are
, because there is one set for each natural number. Other options for index sets are 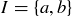 when there are only two sets involved, and
when there are only two sets involved, and 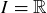 when there’s a set corresponding to each real number.
when there’s a set corresponding to each real number.
We can now define unions and intersections of any indexed collection of sets:
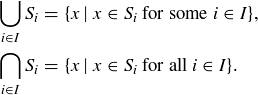
Exercise 3.20 Convince yourself that, in the case when I has two elements, these new definitions of union and intersection express the same concept as the definitions given in Section 3.3.
For example, let 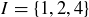 , and define
, and define 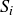 to be the set of points in the plane
to be the set of points in the plane 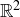 that lie on the graph of
that lie on the graph of  for
for 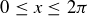 . Then
. Then
![]()
consists of all of the points on the curves shown in Figure 4, while the intersection contains only three of them:
![]()
Exercise 3.21 Let 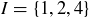 , and define
, and define 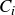 to be the set of points in
to be the set of points in 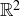 that lie on the graph of
that lie on the graph of 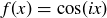 for
for 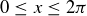 . Draw a graph of the indexed union of the sets
. Draw a graph of the indexed union of the sets 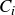 , and determine their intersection.
, and determine their intersection.
REMARK 3.10. In Section 3.4 we presented a number of results about intersections and unions in the context of two or three sets. You are asked to prove versions of these results in the context of indexed sets in Exercise 3.57 at the end of this chapter. Even if you decide not to prove the results, it would be worth your time to glance at the statements in that exercise.
In this section, we define the Cartesian product of two sets, a concept that will be essential when we discuss functions and relations.
The elements of 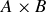 are ordered pairs, with the first element in the pair from A and the second element from B. For example, if
are ordered pairs, with the first element in the pair from A and the second element from B. For example, if 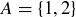 and
and 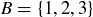 , then
, then 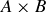 has six elements:
has six elements:
![]()
Ordered pairs are different than 2-element sets since the order of the listed elements matters: for example, 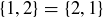 as sets, but
as sets, but  .2
.2
You are no doubt familiar with the use of ordered pairs of real numbers for graphing points in the “Cartesian” plane  , where
, where 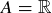 and
and 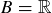 form the horizontal and vertical axes, respectively. For example, the graph of
form the horizontal and vertical axes, respectively. For example, the graph of 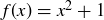 is the subset of
is the subset of 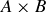 defined by the set of ordered pairs
defined by the set of ordered pairs
![]()
However, many of the sets A and B that you may encounter won’t allow for a similar 2-dimensional graphical representation.
Exercise 3.22 If  and B is any set, what is
and B is any set, what is  ?
?
Exercise 3.23 What is  in terms of
in terms of 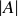 and
and 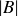 ? Does your answer hold if one of A and B is infinite, or empty?
? Does your answer hold if one of A and B is infinite, or empty?
REMARK 3.12. It would be nice to be able to define the concept of an ordered pair in terms of sets, since sets are our building blocks; and in fact we can do this by defining  to be the set
to be the set 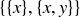 . However, most of the time when we’re dealing with the Cartesian product of two sets, we write the elements in the standard ordered pair notation
. However, most of the time when we’re dealing with the Cartesian product of two sets, we write the elements in the standard ordered pair notation  .
.
Exercise 3.24 Prove that  using the technical definition given above that
using the technical definition given above that 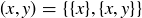 .
.
Given a set A, the collection of all subsets of A is called the power set of A. We will write this set as 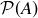 ; another common notation is
; another common notation is  , for reasons made apparent in Theorem 3.14.
, for reasons made apparent in Theorem 3.14.
(a) If 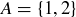 , then
, then 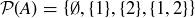 .
.
(b) The power set of the empty set is a set whose only element is the empty set: 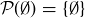 , which can also be written
, which can also be written  . This set is not equal to the empty set itself because
. This set is not equal to the empty set itself because  but
but 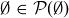 .
.
(c) When dealing with power sets, be careful with 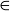 and
and  . Check that
. Check that 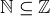 , while
, while 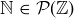 .
.
Exercise 3.25 The empty set 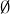 is the only set A with
is the only set A with 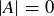 , and we have seen that
, and we have seen that 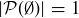 .
.
(a) Show that if A is any set with  , then
, then  .
.
(b) Show that if A is any set with 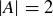 , then
, then 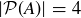 .
.
(c) Determine the size of  if
if  .
.
Exercise 3.26 What is 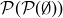 ? How about
? How about  ?
?
We hope that by now you’ve conjectured a formula for 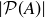 in terms of
in terms of 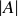 when A is a finite set. We provide two proofs of the theorem below, the first using induction and the second using the counting principle stated in Proposition 2.13.
when A is a finite set. We provide two proofs of the theorem below, the first using induction and the second using the counting principle stated in Proposition 2.13.
INDUCTIVE PROOF. The base case was established in Exercise 3.25: if 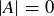 , then we must have
, then we must have 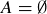 , so
, so
![]()
Thus the theorem is true for 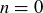 .
.
For the inductive step, we assume that the theorem statement is true for all sets of size at most n. Let A be any set with 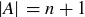 , and let α be any element of A. Then A can be expressed as
, and let α be any element of A. Then A can be expressed as
![]()
where 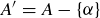 is a set with n elements.
is a set with n elements.
Every 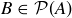 is in exactly one of the following two cases:
is in exactly one of the following two cases:
(a)  , in which case
, in which case  ,
,
(b) 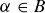 , in which case
, in which case 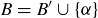 for some
for some  .
.
The subsets B in case (a) are exactly the elements of 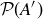 , and so by induction there are
, and so by induction there are 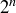 such subsets. The subsets B in case (b) also correspond to the elements of
such subsets. The subsets B in case (b) also correspond to the elements of 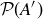 : every such
: every such 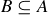 corresponds to a unique
corresponds to a unique  , and vice versa. Thus, we conclude that
, and vice versa. Thus, we conclude that
![]()

DIRECT PROOF. Since A is finite we can list its elements in some particular order:
![]()
Any subset of A can be uniquely described by a sequence of yes/no answers to the n questions, “Is 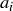 in A?” As examples: the empty set corresponds to a sequence of length n where each answer is “no”; the set A corresponds to each answer being “yes”; and if
in A?” As examples: the empty set corresponds to a sequence of length n where each answer is “no”; the set A corresponds to each answer being “yes”; and if 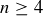 , the subset
, the subset 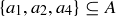 corresponds to “yes, yes, no, yes, no, no, no, …, no.”
corresponds to “yes, yes, no, yes, no, no, no, …, no.”
By Proposition 2.13, the total number of such yes/no sequences is 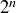 , so
, so  has
has 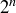 elements.
elements.

Exercise 3.27 Let 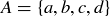 and
and 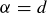 . Referring to the inductive proof above, verify that there are eight elements in each of the two cases, and determine all of the sets
. Referring to the inductive proof above, verify that there are eight elements in each of the two cases, and determine all of the sets 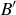 in case (b).
in case (b).
Figure 5 is a visual aid that might help you better understand the inductive step in the first proof of Theorem 3.14. It is an enhanced Hasse diagram showing  as the disjoint union of two bold “cubes,” each the size of
as the disjoint union of two bold “cubes,” each the size of  . With
. With 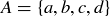 ,
, 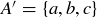 , and
, and 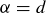 , it is clear that the size of
, it is clear that the size of  is twice the size of
is twice the size of 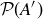 : a thin edge connects a subset B that contains d with its corresponding subset
: a thin edge connects a subset B that contains d with its corresponding subset  .
.
For even moderately sized n, the power set of an n-element set S contains an enormous number of different subsets. Applying Theorem 3.14 to  , we see that
, we see that 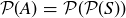 has
has  subsets, which is greater than 30 million when
subsets, which is greater than 30 million when  . Among these many subsets are those of a special type that we will consider again in Chapters 5 and 6:
. Among these many subsets are those of a special type that we will consider again in Chapters 5 and 6:
DEFINITION 3.15. Given a set S and an index set I, a collection  of non-empty subsets of S is a partition of S if the following two conditions hold:
of non-empty subsets of S is a partition of S if the following two conditions hold:
(a)  when
when  .
.
(b) 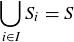 .
.
EXAMPLE 3.16. The blocks of a partition of a set S “cover” the set without overlap. If 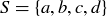 , then the following subsets of
, then the following subsets of 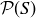 are two of many possible partitions of S:
are two of many possible partitions of S:
![]()
The first partition has three blocks, of sizes 1, 2 and 1; the second has two blocks.
Exercise 3.28 The set  has five partitions. Find them.
has five partitions. Find them.
Exercise 3.29 This problem explores some partitions of  .
.
(a) Show that  can be partitioned into two blocks, using “even” and “odd.”
can be partitioned into two blocks, using “even” and “odd.”
(b) Find a partition of  into infinitely many blocks.
into infinitely many blocks.
(c) Find a partition of  into three blocks, each of infinite size.
into three blocks, each of infinite size.
(d) Find a partition of  into infinitely many blocks, each of size 2.
into infinitely many blocks, each of size 2.
In this chapter, we have already presented arguments that help us determine the sizes of certain finite sets:  in Exercise 3.18,
in Exercise 3.18, 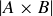 in Exercise 3.23, and
in Exercise 3.23, and 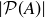 in Section 3.7. The goal of this section is to determine the sizes of two subsets of
in Section 3.7. The goal of this section is to determine the sizes of two subsets of 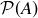 : the set of all k-element subsets of A, and the set of partitions of A into k blocks. For example, Exercise 3.8 and the middle level of Figure 5 show that the number of 2-element subsets of a 4-element set is 6. We begin by first developing several basic enumeration techniques with wide applicability beyond sets.
: the set of all k-element subsets of A, and the set of partitions of A into k blocks. For example, Exercise 3.8 and the middle level of Figure 5 show that the number of 2-element subsets of a 4-element set is 6. We begin by first developing several basic enumeration techniques with wide applicability beyond sets.
3.8.1. Sampling. Let S be a set of n elements. We might wish to select, or sample, k elements from S, one element at a time, keeping track of the order of our choices. We then have two natural possibilities: after an element is selected, it is either still available for future selection (“sampling with replacement”), or it is removed from future consideration (“sampling without replacement”). For example, if 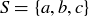 , then the sequence
, then the sequence 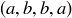 is one ordered sample of size
is one ordered sample of size 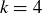 , but only if we are sampling with replacement.
, but only if we are sampling with replacement.
Exercise 3.30 Use the counting principle of Proposition 2.13 to prove that the number of ways to sample k times with replacement from an n-element set S is equal to 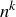 .
.
Let  be the number of ways to sample k times from an n-element set S without replacement. Recall that if m is any positive integer, m factorial is defined as
be the number of ways to sample k times from an n-element set S without replacement. Recall that if m is any positive integer, m factorial is defined as
![]()
and we set 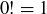 .
.
![]()
PROOF. If 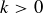 , there are n ways to select a first element from S. Once it is chosen, there are
, there are n ways to select a first element from S. Once it is chosen, there are  ways to select the second element from S. With the first two elements chosen, there are
ways to select the second element from S. With the first two elements chosen, there are  ways to select the third element from S. This process continues until the kth element is chosen from among
ways to select the third element from S. This process continues until the kth element is chosen from among  options. By Proposition 2.13, the product of these values is
options. By Proposition 2.13, the product of these values is  , giving the first equality above. The second equality follows from rewriting
, giving the first equality above. The second equality follows from rewriting 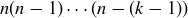 as
as
![]()
If we define 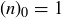 for all non-negative integers n, then the equalities hold for
for all non-negative integers n, then the equalities hold for 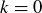 as well: the expression
as well: the expression  is an empty product and so equals 1, and there’s only one way to pick nothing.
is an empty product and so equals 1, and there’s only one way to pick nothing.

Exercise 3.31 Compute 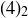 , and explain what it counts in terms of the set
, and explain what it counts in terms of the set 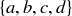 .
.
A permutation of S is the special case of sampling without replacement when 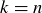 . In this case, we are ordering all of the elements of S, and we get the formula
. In this case, we are ordering all of the elements of S, and we get the formula
![]()
Exercise 3.32 There are many ascending paths of four edges from 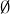 to
to 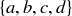 in the Hasse diagram of Figure 5; for example,
in the Hasse diagram of Figure 5; for example,
![]()
How many different such paths are there?
3.8.2 Combinations. What if instead of an ordered sample, we wish to choose a subset of size k from the elements of S? In this context, the subset is often called a combination, or a k-combination. A combination is by definition unordered; but we can use ordered sampling without replacement to prove the following formula for 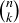 , which counts k-combinations.
, which counts k-combinations.
PROOF. Every ordered sample of size k can be produced in two steps: first choose the corresponding k-element subset of S, and then permute those k elements. Moreover, every selection of a k-element subset of S and a permutation of its elements determines a unique ordered sample of size k. Since there are  ways to permute any k elements, we must have
ways to permute any k elements, we must have
![]()
which immediately leads to the desired formula for 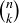 .
.

The symbol  is referred to as “n choose k” because it counts the number of ways of choosing k elements from among n possible options.
is referred to as “n choose k” because it counts the number of ways of choosing k elements from among n possible options.
Exercise 3.33 Explain the relationship between  ,
, 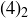 , and
, and 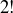 in terms of the set
in terms of the set 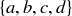 , referring back to Exercise 3.31.
, referring back to Exercise 3.31.
Exercise 3.34 Prove that the formula
![]()
holds for all 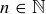 by explaining why the left-hand side counts all of the subsets of an n-element set.
by explaining why the left-hand side counts all of the subsets of an n-element set.
Several end-of-chapter exercises give you practice with permutations and combinations. For further discussion and application, you can then proceed directly to Section 9.3 if you wish, where the common terminology “binomial coefficient” for 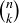 is explained and Pascal’s Triangle is presented.
is explained and Pascal’s Triangle is presented.
3.8.3. Partitions. Let  represent the number of partitions of an n-element set S into k blocks, with n and
represent the number of partitions of an n-element set S into k blocks, with n and 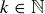 . There is no formula for
. There is no formula for 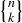 akin to the one given in Theorem 3.18 for
akin to the one given in Theorem 3.18 for 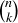 . However, some cases are not too difficult to analyze. For instance,
. However, some cases are not too difficult to analyze. For instance, 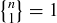 , because the only possible partition of S into one block has S as the only block. And
, because the only possible partition of S into one block has S as the only block. And 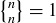 as well, because the only possible partition of S into n blocks has a single element of S in each block.
as well, because the only possible partition of S into n blocks has a single element of S in each block.
A more interesting case is 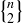 for
for 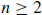 . Every partition of S into two blocks can be obtained by letting
. Every partition of S into two blocks can be obtained by letting 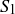 be a subset of S and then setting
be a subset of S and then setting 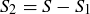 . However, if you do this for every subset
. However, if you do this for every subset  , two issues arise:
, two issues arise:
(a) Every partition is generated twice.
(b) In two instances, 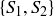 is not a legitimate partition.
is not a legitimate partition.
Exercise 3.35 Explain the two issues above, and prove that  .
.
Exercise 3.36 Prove that 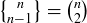 for
for 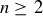 .
.
The numbers  are called Stirling numbers of the second kind. A partial table of values is given in Figure 6, and a recursive formula is presented in Exercise 3.84. The total number of partitions of an n-element set S is called the nth Bell number,
are called Stirling numbers of the second kind. A partial table of values is given in Figure 6, and a recursive formula is presented in Exercise 3.84. The total number of partitions of an n-element set S is called the nth Bell number, 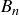 ; thus,
; thus,
![]()
The first six Bell numbers are 1, 2, 5, 15, 52, and 203. You showed that 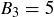 in Exercise 3.28.
in Exercise 3.28.
In this section we provide a cautionary tale about set theory.
Let’s attempt to define a set whose elements are themselves sets:
![]()
An appropriate response at first glance is “Hunh?” But then you can start finding elements of 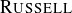 . For instance,
. For instance, 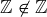 so
so 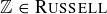 ; and
; and  , so
, so 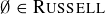 . At this point you might think that every set is an element of RUSSELL. However, consider the set:
. At this point you might think that every set is an element of RUSSELL. However, consider the set:
![]()
If you have a sufficiently robust notion of what is implied by the ellipses in the definition of 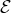 , then it might appear that
, then it might appear that 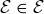 .
.
Let’s try to determine if  . Well, if we assume that
. Well, if we assume that  , then by the definition of
, then by the definition of 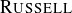 we know that
we know that 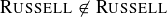 , which contradicts our assumption. On the other hand, if we assume that
, which contradicts our assumption. On the other hand, if we assume that  , then by the definition of
, then by the definition of  we know that
we know that  , which again is a contradiction. Thus it is neither possible for
, which again is a contradiction. Thus it is neither possible for 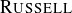 to be in
to be in 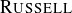 nor for
nor for  not to be in
not to be in 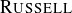 . (If your head hurts at this point, that’s okay. Step away from the book and take a stroll outside until the pain subsides.)
. (If your head hurts at this point, that’s okay. Step away from the book and take a stroll outside until the pain subsides.)
This example was introduced to the mathematics community around the turn of the last century by Bertrand Russell. It pointed out that a naive3 treatment of set theory, similar to what is occurring in this chapter, may initially appear to be benign but is in fact not logically consistent. This led to a number of axiomatic approaches to set theory, the most famous of which is the Zermelo–Fraenkel set theory.
GOING BEYOND THIS BOOK. If you are interested in the fact that set theory is considerably more complicated than our toolkit approach in this chapter indicates, then you have a number of options. You might investigate topics like “Zermelo Fraenkel” and “Axiom of Choice.” You might read a more extensive treatment; we recommend Cunningham’s book [Cun16] and Hajnal and Hamburger’s text [HH99]. And if you are interested in the history around Russell’s Paradox, we recommend Grattan-Guinness’ article [GG78], but caution that this paper will be easier to follow after you have learned Cantor’s Diagonal Argument (see the proof of Theorem 7.15).
Exercises you can work on after Sections 3.1 and 3.2
3.37 List every element in each of the following sets.
(a) 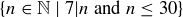
(b) 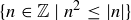
(c) 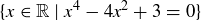
3.38 Determine all of the subset and proper subset relationships among the following sets.
(a) 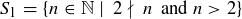
(b) 
(c) 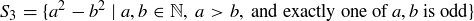
3.39 Which, if any, of the following statements are true?
(a) 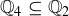
(b) 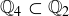
(c) 
(d) 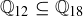
3.40 For any natural number n, is there any difference between the set 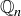 and the set
and the set
![]()
3.41 Find three different elements that are in both 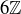 and
and 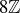 . Is there a convenient way to describe the set of all elements that are in both
. Is there a convenient way to describe the set of all elements that are in both 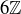 and
and 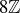 ?
?
3.42 What conditions on a and b guarantee that 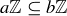 ? Is your condition logically equivalent to
? Is your condition logically equivalent to 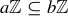 ?
?
3.43 For 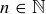 , let
, let  . Is this set equal to
. Is this set equal to 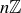 ?
?
![]()
Find a formula expressing 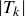 in terms of the value of k.
in terms of the value of k.
Exercises you can work on after Section 3.3
3.45 Let  and define
and define  . Determine each of the following.
. Determine each of the following.
(a) 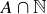
(b) 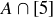
(c) 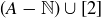
(d) 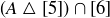
(e) 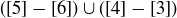
3.46 Describe the following sets.
(a) 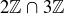
(b) 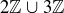
3.47 One way to develop an instinct for logical connectives is through their parallel constructions in set theory. For example, when thinking of P 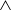 Q you can imagine a Venn diagram with sets P and Q containing those situations where P is true and those situations where Q is true. Thus P
Q you can imagine a Venn diagram with sets P and Q containing those situations where P is true and those situations where Q is true. Thus P 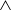 Q would correspond to the intersection of P and Q:
Q would correspond to the intersection of P and Q: 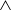 is analogous to
is analogous to  . Similarly,
. Similarly, 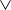 is analogous to
is analogous to 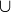 .
.
(a) Explain why 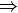 is analogous to
is analogous to  .
.
(b) What is 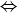 analogous to?
analogous to?
(c) What is exclusive-or analogous to?
3.48 Considering the three sets
![]()
![]()
as subsets of the universal set  , determine the following.
, determine the following.
(a) 
(b) 
(c) 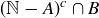
3.49 Figure 7 shows a 3-set Venn diagram for the sets 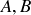 , and C. Using only the processes of intersection, union, and complement, find expressions that specify certain regions. For example, the connected region labelled 0 is
, and C. Using only the processes of intersection, union, and complement, find expressions that specify certain regions. For example, the connected region labelled 0 is
![]()
Find expressions for:
(a) the region labelled 1,
(b) the region labelled 2,
(c) the union of the shaded regions.
3.50 Let U be an infinite set with 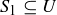 and
and 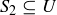 . How many different possible subsets of U can be constructed using the sets
. How many different possible subsets of U can be constructed using the sets 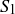 and
and 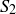 and the symbols
and the symbols 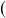 ,
, 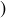 ,
, 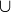 ,
,  , and c? Each set and symbol can be used a finite number of times.
, and c? Each set and symbol can be used a finite number of times.
Exercises you can work on after Section 3.4
3.51 Prove the remaining six items in Theorem 3.6.
3.52 Prove the remaining three items in Theorem 3.7.
3.53 Prove the following generalization of Theorem 3.7.
Let A, B, and C be sets. Then the following hold.
(1) 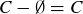
(2) 
(3) 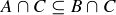 if and only if
if and only if 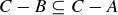
(4) DeMorgan’s Laws
(a) 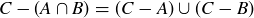
(b) 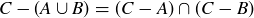
3.54 Is the following claim correct:
![]()
If so, prove it; and, if not, provide a counterexample.
3.55 Let A and B be two sets. Prove that the following are equivalent.
(a) 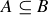
(b) 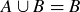
(c) 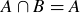
(d) 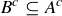
The claim that “the following are equivalent” means that you need to show that each statement is logically equivalent to every other statement in the list above. This can be done in any number of ways, one of which is to establish the following cycle of implications:
![]()
Exercises you can work on after Sections 3.5 and 3.6
3.56 For each natural number n, let 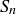 be an infinite set.
be an infinite set.
(a) What can you conclude about the size of 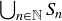 , and why?
, and why?
(b) What can you conclude about the size of 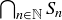 , and why?
, and why?
3.57 Verify the following generalizations of results from Section 3.4. Here I is an arbitrary index set for the collection of sets 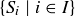 .
.
(1) 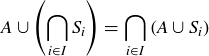
(2) 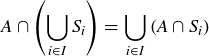
(3) 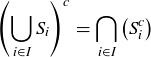
(4) 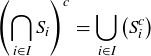
3.58 Let  be the disk of radius 1 centered at the point
be the disk of radius 1 centered at the point 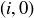 in
in 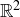 :
:
![]()
(a) Plot the points in 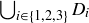 .
.
(b) Plot the points in 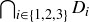 .
.
(c) Plot the points in 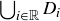 .
.
3.59 For each 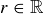 let
let 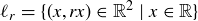 . Each
. Each 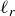 is a line in the plane that goes through the origin.
is a line in the plane that goes through the origin.
(a) Plot the points in the sets 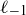 ,
,  ,
, 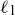 , and
, and  .
.
(b) Show that  .
.
(c) What is  ?
?
(d) What is 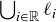 ?
?
3.60 (This exercise assumes you have studied the equations of lines and planes in  .) For each
.) For each 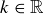 let
let 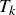 be the set of all points
be the set of all points 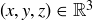 satisfying the equation
satisfying the equation  . Describe the sets
. Describe the sets 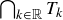 and
and  .
.
3.61 For each 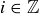 let
let 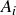 be the half-open interval
be the half-open interval 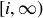 on the real line.
on the real line.
(a) What is  ?
?
(b) What is 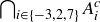 ?
?
We emphasize that this means 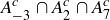 , not
, not 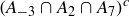 . Part (4) of Exercise 3.57 reinforces this.
. Part (4) of Exercise 3.57 reinforces this.
(c) What is  ?
?
(d) What is 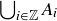 ?
?
3.62 Either explicitly describe a collection of sets 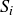 ,
, 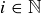 , so that the following conditions are all true simultaneously, or prove that this is impossible.
, so that the following conditions are all true simultaneously, or prove that this is impossible.
(a) For each  ,
, 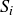 is an infinite subset of
is an infinite subset of  .
.
(b) 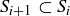 for each
for each  .
.
(c)  is an infinite set.
is an infinite set.
(a) Show that if 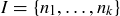 is any finite subset of
is any finite subset of  , then
, then  is an infinite set.
is an infinite set.
(b) Show that 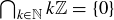 .
.
3.64 Draw each of the following Cartesian products as a subset of 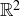 , where
, where 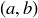 and
and 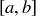 are open and closed intervals of real numbers.
are open and closed intervals of real numbers.
(a) 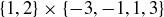
(b) 
(c) 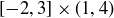
(d) 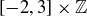
(e) 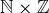
(f) 
Admittedly, for each of the last few products you can’t easily depict the entire set, but you should demonstrate that you know exactly which points in 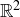 are elements of the product.
are elements of the product.
3.65 For sets A, B, C, and D, prove the following.
(a) 
(b) 
(c) 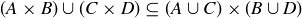
Further, show by example that for (c) the containment can be proper.
3.66 Let A and B be subsets of a universal set U. Then 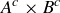 and
and  are both subsets of
are both subsets of  . How are they related to each other?
. How are they related to each other?
3.67 Consider the following subset of 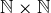 :
:
![]()
The set S can be represented as a subset of the lattice of integer points contained inside the first quadrant in 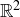 , as in Figure 8. In this exercise you will use this graphical representation to illustrate various claims.
, as in Figure 8. In this exercise you will use this graphical representation to illustrate various claims.
(a) Show how Figure 8 can be used to illustrate why this statement is false:
![]()
(b) Show how Figure 8 can be used to illustrate the truth of
![]()
(c) Is the following claim true or false? How does Figure 8 illustrate your answer?
![]()
(d) Is the following claim true or false? How does Figure 8 illustrate your answer?
![]()
Exercises you can work on after Section 3.7
3.68 Which of the following statements about the power set of the real numbers are true, and which are false?
(a) 
(b) 
(c) 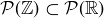
3.69 Let A and B be arbitrary sets, and consider the following pairs of sets. Is one always contained in the other? Are they always equal? Provide proofs or counterexamples.
(a) 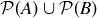 and
and 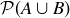
(b)  and
and 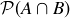
(c)  and
and 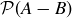
3.70 Is there a set A and an element a such that 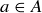 and
and 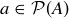 ?
?
3.72 In this exercise you will consider power sets of certain subsets of the natural numbers. As in Exercise 3.45, for each  let
let 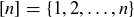 .
.
(a) Prove that  if and only if
if and only if 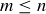 .
.
(b) Prove that
![]()
To show the containment is proper, you must exhibit an explicit member of 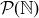 that is not contained in the union of the
that is not contained in the union of the 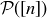 s.
s.
3.73 Which of the following are partitions of the set 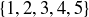 ?
?
(a) 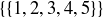
(b) 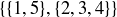
(c) 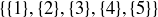
3.74 This problem explores partitions of  .
.
(a) Find a partition of  into blocks of finite size, where no two blocks have the same size.
into blocks of finite size, where no two blocks have the same size.
(b) Find a partition of  into infinitely many blocks, each of infinite size.
into infinitely many blocks, each of infinite size.
3.75 Let  and
and 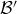 be two partitions of a set S. Then
be two partitions of a set S. Then 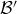 is said to be a refinement of
is said to be a refinement of  if every block of
if every block of 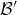 is a subset of a block of
is a subset of a block of  .
.
(a) Explain why 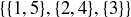 is a refinement of
is a refinement of 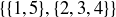 .
.
(b) Explain why 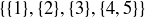 is not a refinement of
is not a refinement of 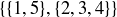 .
.
(c) Find all of the refinements of 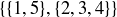 .
.
3.76 Let S be any set and let  be the partition of S into single elements,
be the partition of S into single elements,
![]()
The notion of a refinement is defined in Exercise 3.75. Prove that  is a refinement of every partition of S.
is a refinement of every partition of S.
Exercises you can work on after Section 3.8
3.77 0010011 is an example of a binary sequence of length 7 containing four 0s and three 1s. How many different binary sequences of length 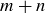 contain m 0s and n 1s?
contain m 0s and n 1s?
3.78 Four balls labeled a, b, c, and d are to be thrown into seven baskets numbered  . How many ways can this be done if …
. How many ways can this be done if …
(a) …no two balls can end up in the same basket?
(b) …there is no restriction on the number of balls in the same basket?
(c) …the only restriction is that at least two baskets must be occupied?
3.79 As in Exercise 3.78, suppose that four balls are to be thrown into seven baskets numbered  ; but now the balls are unlabeled and indistinguishable from each other. “Stars and bars” is one approach to counting the number of different possibilities. Consider all of the different ways that you can create a sequence of six bars and four stars, such as
; but now the balls are unlabeled and indistinguishable from each other. “Stars and bars” is one approach to counting the number of different possibilities. Consider all of the different ways that you can create a sequence of six bars and four stars, such as
![]()
Each  represents a ball, and each bar separates two adjacent baskets, so that the example just given puts two balls in basket 3, one ball in basket 4, and one ball in basket 7.
represents a ball, and each bar separates two adjacent baskets, so that the example just given puts two balls in basket 3, one ball in basket 4, and one ball in basket 7.
How many different assignments of balls to baskets are possible?
3.80 A subset S of 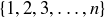 is diffuse if it does not contain any two consecutive integers. Prove that the number of k-element diffuse subsets of
is diffuse if it does not contain any two consecutive integers. Prove that the number of k-element diffuse subsets of  is
is 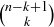 .
.
If you enjoy this problem, take a look at Exercise 3.87.
3.81 Suppose that A and B are disjoint sets, with 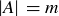 and
and 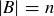 .
.
(a) What’s 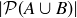 ?
?
(b) Express the number of k-combinations of 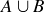 as a single binomial coefficient.
as a single binomial coefficient.
(c) In the case when  and
and 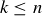 , explain why the number of k-combinations of
, explain why the number of k-combinations of 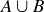 can also be expressed as
can also be expressed as
![]()
(d) In fact, the expression in part (c) gives the correct count even when 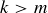 or
or 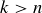 , as long as you have the appropriate definition for
, as long as you have the appropriate definition for 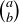 when
when 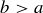 . What is the correct approach?
. What is the correct approach?
3.82 Each card in a standard deck has one of 13 values (Ace, 2, 3, …, 10, Jack, Queen, King) and one of four suits ( ,
,  ,
,  ,
,  ).
).
(a) How many cards are in a standard deck?
(b) The deck is shuffled well, and five cards are dealt face-up in order on a table. How many different ways can this be done?
(c) In games like poker, the order of the cards in your hand doesn’t matter. How many different 5-card hands can be dealt from a standard deck?
(d) One particularly powerful hand in poker is four-of-a-kind, where four of the five cards match in value. How many different four-of-a-kind hands are possible?
(e) Another powerful hand in poker is called a full house: it contains three cards of one value and two cards of a different value. How many different ways can you create a full house?
3.83 How would you define the values of 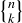 when
when  or
or 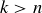 ?
?
![]()
for natural numbers n and k ( ). As a hint, focus on which partitions contain element
). As a hint, focus on which partitions contain element 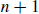 .
.
3.85 Use the results of Exercises 3.35, 3.36, and 3.84 to compute the next row in the table of Stirling numbers of the second kind (those with entries of “?” in Figure 9).
More Exercises!
3.86 The game of Chomp, explored more generally in Project 11.2, is a 2-player game that can be played on a 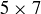 board. On each turn in this game, a player takes a right-angled “bite” from the northeast: a square is removed along with all other squares to the north and east of it. An example is shown in Figure 10, where we have illustrated two moves in the game.
board. On each turn in this game, a player takes a right-angled “bite” from the northeast: a square is removed along with all other squares to the north and east of it. An example is shown in Figure 10, where we have illustrated two moves in the game.
(a) Prove that the possible stages of the game correspond to edge paths from the northwest corner of the board to the southeast corner that are only allowed to move down or right with each step.
(b) Prove that the number of possible stages in 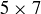 Chomp is
Chomp is 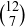 .
.
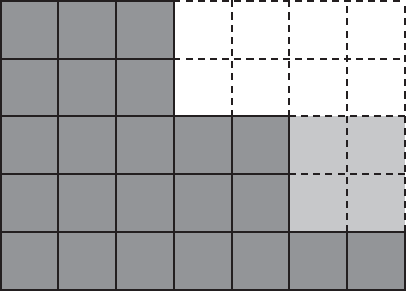
Figure 10. Two plays into the game Chomp. The eight unshaded squares were eaten first; the four lightly shaded squares were eaten second.
3.87 Let 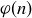 be the number of subsets of
be the number of subsets of  that do not contain consecutive integers.
that do not contain consecutive integers.
(a) Compute 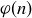 for
for 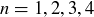 and 5. (Do not forget about the empty set.)
and 5. (Do not forget about the empty set.)
(b) Conjecture a connection between 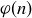 and the Fibonacci numbers, and prove that your conjecture is correct.
and the Fibonacci numbers, and prove that your conjecture is correct.
3.88 We’ve seen Venn diagrams for two and three sets at a time. Is it possible to draw a Venn diagram to represent four or more sets? (If you get frustrated, you might consult “The search for simple symmetric Venn diagrams” by Ruskey, Savage, and Wagon [RSW06].)
3.89 Call a subset 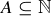 cofinite if
cofinite if 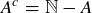 is a finite set.
is a finite set.
(a) Prove that the union of any two cofinite sets is cofinite.
(b) Prove that the intersection of any two cofinite sets is cofinite.
(c) Let 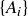 be an indexed family of cofinite sets
be an indexed family of cofinite sets 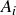 . Prove that the union
. Prove that the union 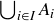 is cofinite.
is cofinite.
(d) Let  be an indexed family of cofinite sets
be an indexed family of cofinite sets 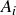 . Show by example that the intersection
. Show by example that the intersection 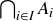 may not be cofinite.
may not be cofinite.
(e) Construct a family of cofinite sets 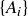 , where
, where  , such that
, such that
(1) 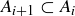 ,
,
(2) 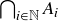 is infinite.
is infinite.
(f) Prove or disprove: Every 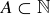 is the intersection of cofinite subsets of
is the intersection of cofinite subsets of  .
.
1 There is an alternate notational convention for subsets. In this notation, 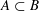 allows for the possibility that A and B are equal, and the notation
allows for the possibility that A and B are equal, and the notation 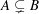 indicates that A is a proper subset of B.
indicates that A is a proper subset of B.
2 The ordered pair notation is not to be confused with open interval notation  . Context should make the distinction clear.
. Context should make the distinction clear.
3 There is a branch of set theory, called “naive set theory,” which we are not referencing here! By “naive” we mean “lacking experience or understanding.”