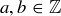 are related if they have the same parity. The idea of “less than” is another relation, where we could write
are related if they have the same parity. The idea of “less than” is another relation, where we could write 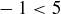 but not
but not 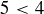 . As in the case of functions, we can capture this very general notion using ordered pairs.
. As in the case of functions, we can capture this very general notion using ordered pairs.In this chapter we introduce the concept of relations on a given set, quickly moving to equivalence relations and their key properties. Modular arithmetic is one of the best known and widely applicable examples of an equivalence relation, and this is the focus of the second half of the chapter.
Sometimes elements of a set are related by a mathematical property. For example, we might want to emphasize that the integers come in two types, even and odd, so we could say that  are related if they have the same parity. The idea of “less than” is another relation, where we could write
are related if they have the same parity. The idea of “less than” is another relation, where we could write 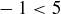 but not
but not 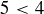 . As in the case of functions, we can capture this very general notion using ordered pairs.
. As in the case of functions, we can capture this very general notion using ordered pairs.
Here are nine example relations, in three groups of three.
EXAMPLE 6.2. These are three relations on  :
:
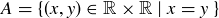 ,
,
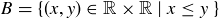 ,
,
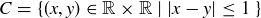 .
.
Because  ,
, 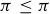 , and
, and 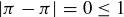 , we know that
, we know that 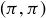 is in all three of these relations. You should check that
is in all three of these relations. You should check that 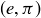 is in exactly two of them, and
is in exactly two of them, and 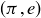 is in only one.
is in only one.
Exercise 6.1 In the plane, sketch the set of points  that are in each of the relations in Example 6.2.
that are in each of the relations in Example 6.2.
EXAMPLE 6.3. Here are three relations on  :
:
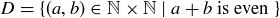 ,
,
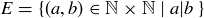 ,
,
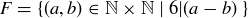 .
.
You should check that 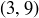 is in all three of these relations,
is in all three of these relations, 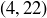 is in exactly two of them, and
is in exactly two of them, and 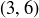 is in only one.
is in only one.
EXAMPLE 6.4. The following are three relations on 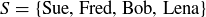 :
:
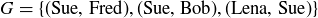 ,
,
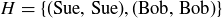 ,
,
the empty set, 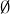 .
.
Relation G might correspond to a concept like “admiration,” where Sue admires both Fred and Bob, while Bob admires no one. But just as functions are best defined without “rules,” relations don’t need descriptions or meanings in order to exist: the definition says that any subset of 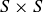 is a relation on S.
is a relation on S.
Also like functions, there is a useful notation for relations that often replaces ordered pairs: it is common to write xRy to mean that 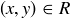 , or to connect x and y with a symbol like
, or to connect x and y with a symbol like 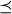 or ~. Thus
or ~. Thus 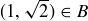 could also be expressed as
could also be expressed as 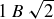 , but most often you will just see
, but most often you will just see 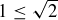 .
.
Just as adjectives like “injective” and “surjective” are part of the language of functions, the following adjectives describe certain relations.
Consider the relation E on  defined in Example 6.3. It is a reflexive relation because
defined in Example 6.3. It is a reflexive relation because 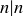 for any
for any  . It is not a symmetric relation: it’s true that
. It is not a symmetric relation: it’s true that 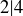 , but it’s not true that
, but it’s not true that 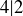 . Finally, the transitive property follows from part (c) of Exercise 1.10.
. Finally, the transitive property follows from part (c) of Exercise 1.10.
Exercise 6.2 Determine whether each of the relations in Example 6.2 is reflexive, symmetric, and/or transitive.
Exercise 6.3 In this exercise you should construct a relation with specified properties.
(a) Flip a coin three times to determine if your relation should be reflexive, symmetric, and/or transitive. Then construct a relation on a non-empty set of your choice that agrees with your list of properties.
(b) Repeat the process, re-flipping the coin if needed to get a different list of properties.
Exercise 6.4 Explain why any function 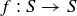 is a relation on S. Then give a function
is a relation on S. Then give a function 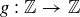 that is neither reflexive, symmetric, nor transitive.
that is neither reflexive, symmetric, nor transitive.
Many well-known relations are orderings. The real numbers are ordered by 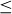 and
and 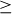 , and subsets of a set S are ordered by
, and subsets of a set S are ordered by  and
and  . All four of these relations are reflexive and transitive. These relations are not symmetric, though, and in fact the notion of symmetry runs counter to the notion of an ordering.
. All four of these relations are reflexive and transitive. These relations are not symmetric, though, and in fact the notion of symmetry runs counter to the notion of an ordering.
For example, the less than or equal relation 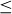 on
on  is antisymmetric, since
is antisymmetric, since 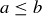 and
and 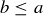 implies that
implies that 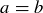 .
.
DEFINITION 6.7. A relation is a partial order if it is reflexive, antisymmetric, and transitive. A partially ordered set, or poset, consists of a set S and a partial order 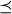 on S. Posets are often represented as pairs,
on S. Posets are often represented as pairs, 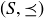 , so as to be clear about the set and the ordering under discussion.
, so as to be clear about the set and the ordering under discussion.
By the results of Exercise 6.2, you already know that 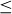 is a reflexive and transitive relation on
is a reflexive and transitive relation on  , so
, so 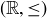 is a poset. In Exercise 6.37, you are asked to show that
is a poset. In Exercise 6.37, you are asked to show that  is an antisymmetric relation on
is an antisymmetric relation on 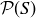 , the power set of any set S, which along with Exercise 6.33 shows that
, the power set of any set S, which along with Exercise 6.33 shows that 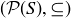 is a poset.
is a poset.
Exercise 6.5 In the previous section we noted that divisibility  is a reflexive and transitive relation on
is a reflexive and transitive relation on  . Prove that divisibility is antisymmetric, and therefore it is a partial order on
. Prove that divisibility is antisymmetric, and therefore it is a partial order on  , which we can write
, which we can write 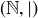 .
.
Let 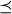 be a partial order on a finite set S. If a and b are distinct elements with
be a partial order on a finite set S. If a and b are distinct elements with 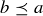 , and there is no third element such that
, and there is no third element such that 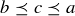 , then a is said to cover b. Just as we saw in Chapter 3 with set inclusion, a Hasse diagram is a method for representing a partial order on a finite set, where line segments indicate covering. Figure 1 is a Hasse diagram for the set
, then a is said to cover b. Just as we saw in Chapter 3 with set inclusion, a Hasse diagram is a method for representing a partial order on a finite set, where line segments indicate covering. Figure 1 is a Hasse diagram for the set 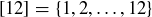 , where the partial order is given by divisibility; Exercise 6.38 asks you to verify that
, where the partial order is given by divisibility; Exercise 6.38 asks you to verify that 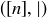 is a poset for any natural number n. Figure 1 in Chapter 3 shows a Hasse diagram for the power set of
is a poset for any natural number n. Figure 1 in Chapter 3 shows a Hasse diagram for the power set of 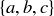 ordered by set inclusion.
ordered by set inclusion.
Exercise 6.6 Can you redraw the Hasse diagram in Figure 1 to avoid crossing line segments?
DEFINITION 6.8. A maximal element in a poset 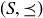 is an element M such that if
is an element M such that if  , then
, then 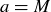 . Similarly a minimal element is an element m where if
. Similarly a minimal element is an element m where if  , then
, then  .
.
The poset 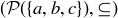 has
has 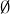 as the unique minimal element and
as the unique minimal element and 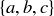 as the unique maximal element. Figure 1 shows that the natural number 1 is the unique minimal element in the poset
as the unique maximal element. Figure 1 shows that the natural number 1 is the unique minimal element in the poset 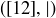 , while there are six maximal elements: 7, 8, 9, 10, 11 and 12. Notice that this is the second time we have defined minimal element, the first occurring in Section 4.1 in the context of
, while there are six maximal elements: 7, 8, 9, 10, 11 and 12. Notice that this is the second time we have defined minimal element, the first occurring in Section 4.1 in the context of  and
and 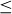 . Exercise 6.41 asks you to show that the earlier definition is consistent with Definition 6.8.
. Exercise 6.41 asks you to show that the earlier definition is consistent with Definition 6.8.
Exercise 6.7 Recalling the introduction to Fibonacci numbers in Section 1.2, let 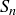 be the set of rabbit pairs born in the first n months,which becomes a poset
be the set of rabbit pairs born in the first n months,which becomes a poset 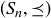 if we define
if we define 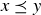 when rabbit pair x either is the same as rabbit pair y or is a descendant of rabbit pair y. Explain why
when rabbit pair x either is the same as rabbit pair y or is a descendant of rabbit pair y. Explain why 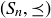 is a poset, and draw the Hasse diagram for
is a poset, and draw the Hasse diagram for 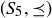 . What are the minimal and maximal elements of
. What are the minimal and maximal elements of 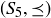 ? Feel free to give the rabbits cute or useful names.
? Feel free to give the rabbits cute or useful names.
Exercise 6.8 Let  be the set of all closed intervals
be the set of all closed intervals 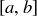 where
where 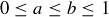 . For example,
. For example, 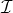 contains
contains 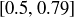 ,
, 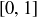 , and the point
, and the point 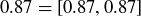 . Order the elements of
. Order the elements of 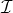 by saying
by saying 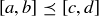 if
if 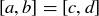 or
or 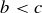 .
.
(a) Explain why 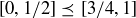 , but
, but 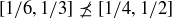 .
.
(b) Verify that 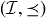 is a poset.
is a poset.
(c) Prove that the maximal elements in this poset are the intervals 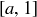 where
where 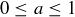 .
.
(d) Prove that the minimal elements in this poset are the intervals 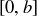 where
where 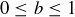 .
.
(e) Show by example that it is possible for an element to be both maximal and minimal.
DEFINITION 6.9. In a poset, we say that two elements x and y are comparable if 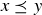 or
or 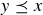 . Figure 1 shows that not all pairs of elements in a poset need to be comparable; for example, neither
. Figure 1 shows that not all pairs of elements in a poset need to be comparable; for example, neither 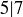 nor
nor 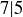 is true.
is true.
A poset is totally ordered1 if every pair of elements is comparable. For example, the poset 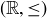 is a totally ordered set: if a and b are any two real numbers, then
is a totally ordered set: if a and b are any two real numbers, then 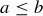 or
or 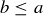 .
.
A poset is well ordered2 if it is a totally ordered set such that every non-empty subset contains a minimal element. This definition should remind you of the Well-Ordering Principle for  (Theorem 4.3), which states that
(Theorem 4.3), which states that 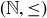 is well ordered.
is well ordered.
Exercise 6.9 Which of the following posets are totally ordered?
(a) 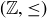
(b) 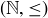
(c) 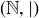
(d) 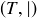 , where
, where 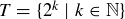
Exercise 6.10 Which of the totally ordered sets from Exercise 6.9 are well ordered?
Many end-of-chapter exercises help you further explore the structure of posets, including the problem of determining the largest totally ordered subsets in a poset, its maximal chains. This leads naturally to the study of antichains and Mirsky’s Theorem in Project 11.6. Also, Exercise 6.76 explains how certain partial orders can be refined to total orders.
There are many contexts in mathematics where you might think of two mathematical objects as being “equivalent,” even when they are not identical. For example, two triangles in the plane are congruent if their edges have the same lengths. Another example is similarity: two triangles in the plane are similar if they have the same angles. In both cases the triangles share important features, and in that sense they are equivalent. This informal notion is captured by equivalence relations.
DEFINITION 6.10. A relation R on a set S is an equivalence relation if it is reflexive, symmetric, and transitive. Equivalence relations are often denoted with the symbol ~ or some other variation on an equals sign, like 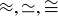 , or
, or  .
.
Out of the six relations described in Examples 6.2 and 6.3, three are equivalence relations: A, D, and F. It shouldn’t be surprising that A is an equivalence relation; it’s hard to be more “equivalent” than being equal! Having mentioned this, we want to immediately comment that the concept of equivalence relation is intended to allow different elements to be related without necessarily being equal, even if equality is part of the definition of the relation. As an example, let 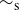 be the relation on
be the relation on  that says
that says 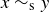 when
when 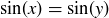 . We can have
. We can have 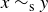 without
without 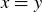 ; as examples,
; as examples, 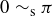 and
and 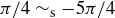 .
.
PROPOSITION 6.11. The relation 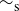 is an equivalence relation on
is an equivalence relation on  .
.
PROOF. We need to establish that 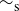 has three properties.
has three properties.
Reflexive: This follows since 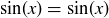 for all
for all 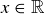 .
.
Symmetric: If 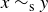 , then
, then 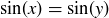 . But then it is also true that
. But then it is also true that 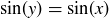 , so
, so 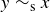 .
.
Transitive: If 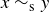 and
and 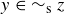 , then
, then
![]()
Thus 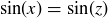 , so
, so 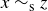 .
.

A generalization of 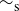 and Proposition 6.11 is explored in Exercise 6.57 at the end of this chapter.
and Proposition 6.11 is explored in Exercise 6.57 at the end of this chapter.
Exercise 6.11 In Example 6.3 we defined the relation D on the natural numbers,  . Consider the extension of this relation to the integers:
. Consider the extension of this relation to the integers:
![]()
Prove that 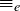 is an equivalence relation on
is an equivalence relation on  .
.
If R is an equivalence relation on a set S, there is an important subset of S associated to each 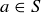 :
:
DEFINITION 6.12. If R is an equivalence relation on a set S, the equivalence class of 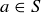 is the set of all elements related to a:
is the set of all elements related to a:
![]()
For example, you have just shown that 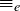 is an equivalence relation on
is an equivalence relation on  . The equivalence class of 0 is
. The equivalence class of 0 is
![]()
and the equivalence class of 1 is
![]()
Figure 2 shows that every integer is in exactly one of these two equivalence classes.
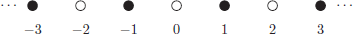
Figure 2. The two equivalence classes for 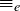 . The class
. The class 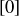 is indicated by hollow circles, and
is indicated by hollow circles, and 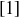 has filled circles.
has filled circles.
Exercise 6.12 Let 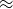 be the relation on
be the relation on  defined by having
defined by having 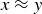 when x and y have the same integer part, that is, when
when x and y have the same integer part, that is, when 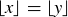 . Prove that this is an equivalence relation, and prove that the equivalence class of each element is a half-open interval of the form
. Prove that this is an equivalence relation, and prove that the equivalence class of each element is a half-open interval of the form 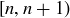 , where
, where 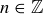 .
.
With 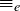 and
and 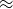 from the previous two exercises, you might have noticed that the equivalence classes of two elements are either the same or they are disjoint. This is not a coincidence, as you may begin to believe after working through the next exercise.
from the previous two exercises, you might have noticed that the equivalence classes of two elements are either the same or they are disjoint. This is not a coincidence, as you may begin to believe after working through the next exercise.
Exercise 6.13 Consider the equivalence relation 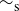 on
on  from Proposition 6.11.
from Proposition 6.11.
(a) Show that the equivalence class of 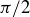 is
is
![]()
(b) Show that the equivalence class of 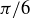 is
is
![]()
(c) Prove that for any two equivalence classes 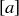 and
and 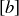 for
for 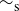 , either
, either 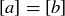 or
or 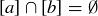 .
.
What you proved in the exercise above is a special case of the following general result.
Before presenting a proof of this result, we should think about the logic of the theorem. The statement of the theorem is of the form 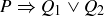 , namely
, namely
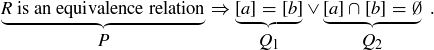
This is equivalent to 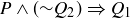 . (You might have proven this logical equivalence if you worked on Exercise 2.46.) This restatement of what needs to be proven makes intuitive sense: if you are being asked to show that at least one of two possibilities is true, and one of the possibilities is false, then the other one had better be true! This is the approach we take in the proof.
. (You might have proven this logical equivalence if you worked on Exercise 2.46.) This restatement of what needs to be proven makes intuitive sense: if you are being asked to show that at least one of two possibilities is true, and one of the possibilities is false, then the other one had better be true! This is the approach we take in the proof.
PROOF OF THEOREM 6.13. Let R be an equivalence relation on S, and assume there are elements 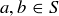 with
with 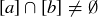 . Thus there must be some
. Thus there must be some 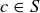 that is in both
that is in both 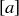 and
and 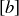 . So aRc and bRc. Since R is symmetric, we also know cRb. Since R is transitive, aRc and cRb imply that aRb; the symmetric property then implies that bRa as well.
. So aRc and bRc. Since R is symmetric, we also know cRb. Since R is transitive, aRc and cRb imply that aRb; the symmetric property then implies that bRa as well.
Now that we know that a and b are related, we show that 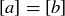 by proving that each equivalence class contains the other. If d is any element of
by proving that each equivalence class contains the other. If d is any element of 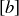 , then bRd. Since aRb, the transitive property shows that aRd, and thus
, then bRd. Since aRb, the transitive property shows that aRd, and thus 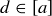 . So we know that
. So we know that 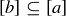 . A similar argument starting with
. A similar argument starting with 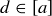 shows that
shows that 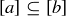 , and thus
, and thus 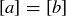 .
.

The result of Theorem 6.13, that 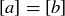 or
or 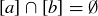 , suggests a relationship between equivalence classes and partitions, which were defined in Section 3.7. The blocks of a partition of a set S are non-overlapping, and their union is all of S, just as we have seen with examples of equivalence classes. The following theorem says that for every set S there is a bijection between the set of equivalence relations on S and the set of partitions of S.
, suggests a relationship between equivalence classes and partitions, which were defined in Section 3.7. The blocks of a partition of a set S are non-overlapping, and their union is all of S, just as we have seen with examples of equivalence classes. The following theorem says that for every set S there is a bijection between the set of equivalence relations on S and the set of partitions of S.
THEOREM 6.14. Let S be a set. If 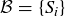 is a partition of S, then the relation defined by
is a partition of S, then the relation defined by
![]()
is an equivalence relation on S. Conversely, if ~ is an equivalence relation on S, then the equivalence classes induced by ~ form a partition of S.
PROOF. If you look back at the statement of Theorem 6.13 and the definition of partition, you will see that we have already proven that equivalence relations give rise to partitions: Theorem 6.13 says that two distinct equivalence classes cannot intersect (requirement (a) for a partition), and requirement (b) follows because every element is in an equivalence class, namely 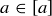 .
.
Now, let  be a partition of S, and let
be a partition of S, and let 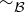 be the relation given in the statement of the theorem. Is this relation …
be the relation given in the statement of the theorem. Is this relation …
…reflexive? Yes, because 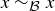 simply states that x and x are in the same block of
simply states that x and x are in the same block of  .
.
…symmetric? Yes, because 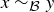 means that x and y are in the same block of the partition. But then y and x are in the same block of the partition, so
means that x and y are in the same block of the partition. But then y and x are in the same block of the partition, so 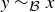 .
.
…transitive? Yes, because if 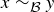 and
and 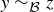 , then x and y are in the same block
, then x and y are in the same block 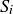 of the partition, and y and z are in the same block
of the partition, and y and z are in the same block 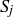 . Since
. Since 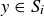 and
and 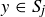 , we know that
, we know that 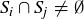 . Since these are blocks in a partition, it follows that
. Since these are blocks in a partition, it follows that 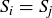 . Thus this block contains both x and z, meaning that
. Thus this block contains both x and z, meaning that 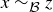 .
.

Exercise 6.14 If S is any set, then the set of singleton sets 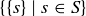 forms a partition. Describe the corresponding equivalence relation on S.
forms a partition. Describe the corresponding equivalence relation on S.
Exercise 6.15 How many equivalence relations are there on the set 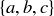 ?
?
In Sections 6.1 and 6.3 you encountered the equivalence relation F, which was originally defined on  but can be extended to
but can be extended to  :
:
![]()
You have also encountered a number of earlier exercises where the concept of even and odd mattered, and other exercises where it matters if an integer n is of the form 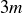 ,
, 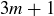 , or
, or 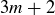 . In 1801, having had a number of similar things occur earlier in his work, Carl Friedrich Gauss introduced the idea of congruence modulo m.
. In 1801, having had a number of similar things occur earlier in his work, Carl Friedrich Gauss introduced the idea of congruence modulo m.
DEFINITION 6.15. If 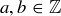 and
and 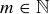 , we say a is congruent to b modulo m when
, we say a is congruent to b modulo m when 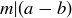 . The notation is
. The notation is
![]()
The extra “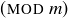 ” in the relation notation may seem cumbersome at first, but its usage is common. You may also see
” in the relation notation may seem cumbersome at first, but its usage is common. You may also see 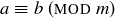 denoted by the more compact notation
denoted by the more compact notation 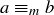 . The equivalence class of
. The equivalence class of 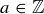 is denoted
is denoted 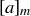 . The number m is called the modulus, and when the value of the modulus is clear, the subscript is sometimes dropped from these notations.
. The number m is called the modulus, and when the value of the modulus is clear, the subscript is sometimes dropped from these notations.
PROPOSITION 6.16. For any 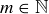 , the
, the 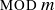 relation is an equivalence relation on
relation is an equivalence relation on  .
.
PROOF. We need to establish the three required properties.
Reflexive: For any 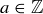 ,
, 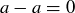 . Since
. Since 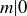 , it follows that
, it follows that 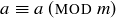 .
.
Symmetric: Assume that 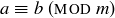 . By the definition this means
. By the definition this means 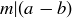 . But
. But 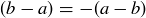 , and so
, and so 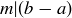 as well. Hence
as well. Hence 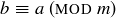 .
.
Transitive: If 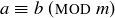 and
and 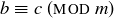 , then
, then 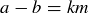 and
and 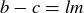 for some integers
for some integers 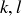 . Since
. Since 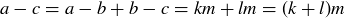 implies
implies 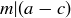 , we know that
, we know that 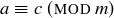 .
.

Exercise 6.16 What are the equivalence classes of  with respect to the equivalence relation MOD 2? What are the equivalence classes for MOD 3?
with respect to the equivalence relation MOD 2? What are the equivalence classes for MOD 3?
For each 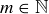 define the set of remainders (or the residues) to be
define the set of remainders (or the residues) to be
![]()
For example, 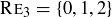 .
.
PROPOSITION 6.17. For any 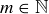 , let
, let 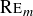 be as defined above. Then for every
be as defined above. Then for every 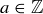 there is a unique
there is a unique 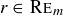 such that
such that 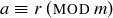 .
.
Exercise 6.17 Use the Division Algorithm from Section 1.6 to prove Proposition 6.17.
PROOF. Assume first that 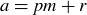 and
and 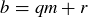 . Then
. Then 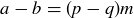 , so
, so 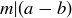 , which implies that
, which implies that 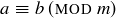 .
.
Now assume that 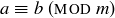 . We know that
. We know that 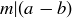 , so
, so 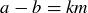 for some
for some 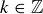 . We also know by Proposition 6.17 that there is an
. We also know by Proposition 6.17 that there is an 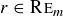 such that
such that 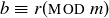 , so
, so 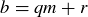 for some
for some 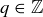 . Thus
. Thus
![]()
if we set 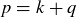 .
.

Exercise 6.18 Prove that 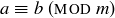 if and only if
if and only if 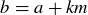 for some
for some 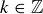 .
.
Exercise 6.19 Prove that the set of equivalence classes of  with respect to congruence
with respect to congruence 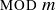 is
is  .
.
GOING BEYOND THIS BOOK. It is known that there are true statements of arithmetic that cannot be proven. In [Con13] John Conway describes a number of examples of elementary arithmetic functions, whose definitions are based on remainders modulo an integer m, that appear to be true but are not yet proven. The functions are interesting in their own right, and the possibility that they lead to elementary true but not provable statements is certainly intriguing.
In this section we will explore modular arithmetic. Let 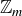 denote the set of equivalence classes of
denote the set of equivalence classes of  modulo m. For example,
modulo m. For example, 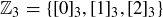 , which is also equal to
, which is also equal to 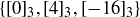 but not
but not 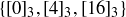 .
.
The fact that 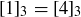 means that you need to use great care when defining operations or functions in terms of equivalence classes. Any element of an equivalence class is called a representative of that class, so 1, 4, and
means that you need to use great care when defining operations or functions in terms of equivalence classes. Any element of an equivalence class is called a representative of that class, so 1, 4, and 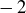 are just three of infinitely many representatives of the class
are just three of infinitely many representatives of the class 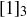 . This is similar to the familiar case of fractions like
. This is similar to the familiar case of fractions like 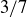 and
and 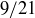 both representing the same value. In the case of fractions, we know that any representative is equally valid for use in computations. We would, however, be concerned if someone defined a function
both representing the same value. In the case of fractions, we know that any representative is equally valid for use in computations. We would, however, be concerned if someone defined a function 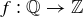 by saying
by saying 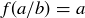 , as then
, as then 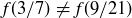 , but
, but 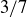 and
and 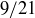 represent the same rational number.
represent the same rational number.
A CAUTIONARY TALE: Derek is working at the board, and he’s written down what he thinks is a function from 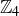 to
to 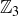 :
:
![]()
As an aside he’s written
![]()
John, however, is made a bit nervous by this, and he says “Wait a minute, Derek. The numbers 2 and 6 are in the same equivalence class modulo 4, so 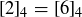 . Why shouldn’t it be the case that
. Why shouldn’t it be the case that
![]()
Exercise 6.20 Explain why this poses a problem for f being a function from 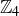 to
to 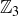 .
.
MORAL OF THE STORY: If you define a mathematical object in terms of representatives of an equivalence class, you need to make sure that your definition does not depend on which representative you pick. Mathematicians say that an object defined on equivalence classes is well defined when it has the same value regardless of which representative is used from a given equivalence class.
Our Cautionary Tale partly explains why we need to present a proof of the following theorem, stating that addition and multiplication can be defined on 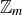 in terms of representatives of the equivalence classes, and that these operations are well defined.
in terms of representatives of the equivalence classes, and that these operations are well defined.
PROOF. We know that if 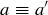 , then
, then 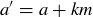 for some
for some 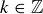 ; similarly we know that
; similarly we know that 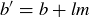 for some
for some 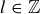 . Thus
. Thus 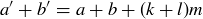 , so by Exercise 6.18 we have
, so by Exercise 6.18 we have 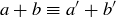 . Further,
. Further, 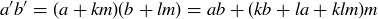 , so
, so  as well.
as well.

We can now define modular arithmetic: There are functions 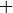 and
and  from
from 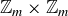 to
to 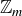 which are defined by
which are defined by
![]()
We emphasize that Theorem 6.19 says that the choice of representatives doesn’t affect the result of addition or multiplication, so each of these is a legitimate function from 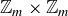 to
to 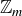 : each element of
: each element of 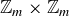 is mapped to a unique element of
is mapped to a unique element of 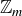 .
.
Because of the connection between equivalence classes and equivalence relations, we have two ways of expressing addition modulo m. In terms of equivalence relations we can make a statement like:
![]()
What we have shown is that we can also make the exact same claim using the language of equivalence classes by writing:
![]()
Notice that in this second statement we are discussing sets (the equivalence classes) and so we should use the symbol  in this context, while we should use
in this context, while we should use 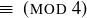 when discussing individual numbers. The same situation arises for multiplication modulo m.
when discussing individual numbers. The same situation arises for multiplication modulo m.
Exercise 6.21 The equivalence classes 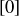 and
and 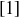 in
in 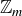 have some of the fundamental properties of 0 and 1 in
have some of the fundamental properties of 0 and 1 in  .
.
(a) Prove that 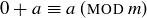 for any integer a and any modulus
for any integer a and any modulus 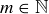 .
.
(b) Prove that 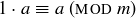 for any integer a and any modulus
for any integer a and any modulus  .
.
Because of the properties above,  is said to be an additive identity in
is said to be an additive identity in  and
and 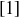 is a multiplicative identity in
is a multiplicative identity in 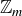 .
.
It is common to display the results of modular arithmetic in tables. For example, the tables for arithmetic in 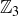 are shown in Figure 3. The connection with
are shown in Figure 3. The connection with 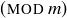 notation is easy to see. For example, since
notation is easy to see. For example, since 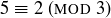 and
and 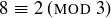 , we know that
, we know that 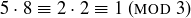 , as displayed in the lower-right entry of the multiplication table.
, as displayed in the lower-right entry of the multiplication table.
Exercise 6.22 It is time for you to practice modular arithmetic.
(a) Create the addition and multiplication tables for 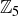 .
.
(b) Create the addition and multiplication tables for 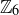 .
.
(c) You should now be able to check that the product of non-zero entries in 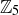 is never zero, just like in ordinary arithmetic. But in
is never zero, just like in ordinary arithmetic. But in 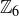 , the product of non-zero entries can be zero. Why do you think this happens in
, the product of non-zero entries can be zero. Why do you think this happens in 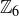 but not in
but not in 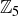 ?
?
Exercise 6.23 State a version of Theorem 6.19 that involves n terms, and use mathematical induction to prove it.
Here is one example of the utility of being able to do arithmetic modulo a number m. Trying to find the remainder of 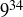 divided by 11 sounds quite hard. But
divided by 11 sounds quite hard. But 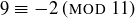 , so
, so 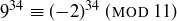 . Further, since
. Further, since 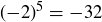 and
and 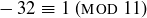 , we have
, we have
![]()
Thus the remainder is 5.
Here is another example of the utility of modular arithmetic. Exercise 4.23 asks you to use induction and a minimal criminal argument to prove that, for all  ,
, 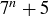 is divisible by 3. Using modular arithmetic, this is now a computation. Being divisible by 3 is equivalent to being congruent to 0 modulo 3. And we can establish the result by applying the fact that
is divisible by 3. Using modular arithmetic, this is now a computation. Being divisible by 3 is equivalent to being congruent to 0 modulo 3. And we can establish the result by applying the fact that 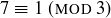 and
and 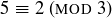 :
:
![]()
Exercise 6.24 What’s the last digit of 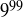 ? Notice that if you just want the last digit, you can work with the integers modulo 10.
? Notice that if you just want the last digit, you can work with the integers modulo 10.
In our Cautionary Tale, we attempted to define a function from 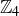 to
to 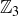 by squaring representatives. The definition did not actually make sense, as it was not consistent across all elements in an equivalence class. Given that example, it may seem a bit daft for us to now consider the following proposed definition for a function from
by squaring representatives. The definition did not actually make sense, as it was not consistent across all elements in an equivalence class. Given that example, it may seem a bit daft for us to now consider the following proposed definition for a function from 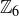 to
to 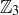 :
:
![]()
To see if this function is well defined, we need to check if the answer is the same regardless of the representative we choose for any given equivalence class. By Exercise 6.18 we know that 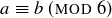 if and only if
if and only if 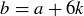 for some
for some 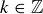 . Notice that
. Notice that
![]()
Since 3 divides 12 and 36 we know 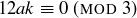 and
and 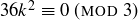 . Theorem 6.19 allows us to replace these terms by zeros, yielding
. Theorem 6.19 allows us to replace these terms by zeros, yielding
![]()
Thus 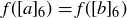 whenever
whenever 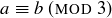 , so the function is well defined.
, so the function is well defined.
Exercise 6.25 Find a step in the argument given above for 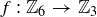 that fails when applied to the supposed function in the Cautionary Tale.
that fails when applied to the supposed function in the Cautionary Tale.
Exercise 6.26 Show that the following functions are well defined, where  .
.
(a) 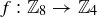 given by
given by 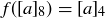 .
.
(b) 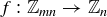 given by
given by 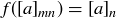 .
.
(c) 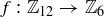 given by
given by 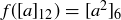 .
.
(d) 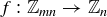 given by
given by 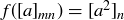 .
.
REMARK 6.20. In section 5.7.4 we discussed a common abuse of notation that occurs in the context of functions. There are many places in mathematics where one abuses notation by giving a single symbol multiple meanings or by simplifying notation. The expectation is that the context makes clear what the notation does not.
There are many abuses of notation that occur in the context of modular arithmetic. For example, when the modulus is clear or unimportant, you will often see 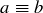 instead of the more complete
instead of the more complete 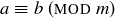 . Similarly in denoting equivalence classes you might see
. Similarly in denoting equivalence classes you might see 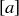 instead of
instead of 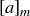 . Perhaps even more confusing, one often drops the square bracket notation and lets a stand for
. Perhaps even more confusing, one often drops the square bracket notation and lets a stand for 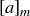 . This occurs most commonly in addition and multiplication tables, where the square brackets make for a rather cluttered diagram.
. This occurs most commonly in addition and multiplication tables, where the square brackets make for a rather cluttered diagram.
This section makes use of material from Sections 4.4 and 4.5. Theorem 6.19 shows that addition and multiplication make sense in 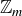 ; it is also the case that subtraction is well defined.
; it is also the case that subtraction is well defined.
Exercise 6.27 Prove Theorem 6.21.
It is less clear that you can divide in 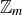 , and given that we are working with integers, you might guess that this is not always possible. Let’s experiment with
, and given that we are working with integers, you might guess that this is not always possible. Let’s experiment with 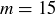 and see if we can solve
and see if we can solve
![]()
If we can, then whatever x might be it deserves to be considered as “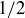 ” within
” within 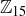 . Having no better plan available to us, we form the row of the multiplication table for
. Having no better plan available to us, we form the row of the multiplication table for 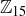 corresponding to
corresponding to 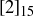 . We’ll also start to abuse notation and write k instead of
. We’ll also start to abuse notation and write k instead of 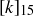 .
.
![]()
The highlighted column shows us that 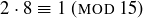 , so 8 plays the role of
, so 8 plays the role of 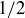 in
in 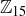 . We can use this fact to solve an equation like
. We can use this fact to solve an equation like
![]()
as follows:
![]()
In this calculation, we used both parts of Theorem 6.19: part (a) to add 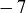 to both sides of a congruence, and part (b) to multiply both sides by 8. We can verify that we did not make an error by plugging our answer of
to both sides of a congruence, and part (b) to multiply both sides by 8. We can verify that we did not make an error by plugging our answer of 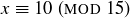 back into the original congruence:
back into the original congruence:
![]()
Exercise 6.28 What element of 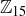 deserves to be called “1/4”?
deserves to be called “1/4”?
DEFINITION 6.22. If 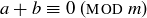 , we say that a and b are additive inverses.
, we say that a and b are additive inverses.
If 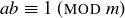 , we say that a and b are multiplicative inverses modulo m, and
, we say that a and b are multiplicative inverses modulo m, and 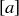 and
and 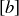 are multiplicative inverses in
are multiplicative inverses in 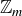 .
.
We can express 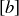 as
as 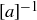 , notation that is similar to what we used for an inverse function in Chapter 5. But, as with functions, the concept of inverse requires great care.
, notation that is similar to what we used for an inverse function in Chapter 5. But, as with functions, the concept of inverse requires great care.
Since 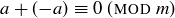 we know that
we know that 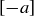 is an additive inverse of
is an additive inverse of 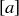 , and so additive inverses always exist in
, and so additive inverses always exist in 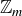 . The situation is more complicated for multiplicative inverses. You have seen that
. The situation is more complicated for multiplicative inverses. You have seen that 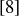 is a multiplicative inverse of
is a multiplicative inverse of  in
in 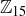 , and you should have discovered that
, and you should have discovered that 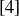 is its own multiplicative inverse in
is its own multiplicative inverse in 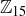 , so you can write
, so you can write 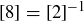 and
and 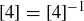 in
in  . Having now realized that at times you can do division in
. Having now realized that at times you can do division in 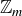 , an unreasonably optimistic individual might conjecture that every non-zero element in
, an unreasonably optimistic individual might conjecture that every non-zero element in 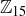 has a multiplicative inverse. The truly careful person would say, “Let’s try to find multiplicative inverses for other values, like [3], before we get too excited.” To do this, we once again produce the relevant row in the multiplication table for
has a multiplicative inverse. The truly careful person would say, “Let’s try to find multiplicative inverses for other values, like [3], before we get too excited.” To do this, we once again produce the relevant row in the multiplication table for 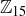 :
:
![]()
The number 1 does not appear anywhere in this row, so there is no number a such that 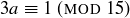 . You might now be sad, since
. You might now be sad, since 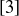 does not have a multiplicative inverse in
does not have a multiplicative inverse in 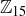 . But instead you really ought to be intrigued. Why does
. But instead you really ought to be intrigued. Why does  have an inverse in
have an inverse in 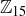 but not
but not 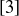 ? Is there a satisfactory condition that describes when an element of
? Is there a satisfactory condition that describes when an element of 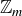 has a multiplicative inverse?
has a multiplicative inverse?
Exercise 6.29 Show that in 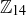 the elements
the elements  and
and 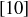 do not have multiplicative inverses, but
do not have multiplicative inverses, but 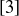 and
and 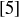 do.
do.
The following theorem should sound plausible, given your results from working on the exercise above.
PROOF. We have to establish two implications, both of which rely on the characterization of relatively prime integers given in Theorem 4.8.
(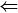 ) If k and m are relatively prime, then there are integers s and t such that
) If k and m are relatively prime, then there are integers s and t such that
![]()
But then 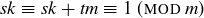 , so
, so 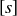 is a multiplicative inverse of
is a multiplicative inverse of 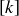 in
in 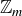 .
.
(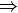 ) If
) If 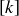 has a multiplicative inverse, then there exists an
has a multiplicative inverse, then there exists an 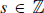 such that
such that 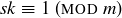 . But this means that there is some
. But this means that there is some 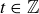 such that
such that 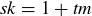 , and therefore
, and therefore 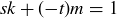 . Thus
. Thus 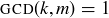 .
.

DEFINITION 6.24. Define 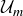 to be the subset of
to be the subset of 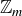 consisting of equivalence classes whose representatives are relatively prime to m:
consisting of equivalence classes whose representatives are relatively prime to m:
![]()
In the study of arithmetic systems, elements that have multiplicative inverses are called units. The notation 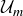 comes from the fact that we are looking at
comes from the fact that we are looking at 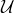 nits in
nits in 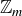 .
.
Exercise 6.30 Show that if  , then
, then 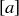 has exactly one multiplicative inverse.
has exactly one multiplicative inverse.
The set of units in 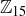 is
is 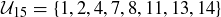 , where we are abusing notation by dropping the brackets. The fact that all of these elements are units is verified by the multiplication table for
, where we are abusing notation by dropping the brackets. The fact that all of these elements are units is verified by the multiplication table for 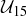 shown in Figure 4, as every row contains a 1.
shown in Figure 4, as every row contains a 1.
Exercise 6.31 What elements are in 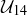 ? Once you’ve found them, make a multiplication table for
? Once you’ve found them, make a multiplication table for 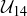 .
.
The following proposition explains why the multiplication tables for 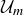 don’t contain any other elements of
don’t contain any other elements of 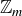 .
.
PROPOSITION 6.25. The set 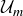 is closed under multiplication and taking multiplicative inverses.
is closed under multiplication and taking multiplicative inverses.
Exercise 6.32 Prove Proposition 6.25. To do this, you will have to show that if 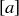 and
and 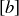 are both in
are both in 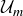 , then so is
, then so is 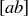 . You will also have to show that if
. You will also have to show that if  , then
, then 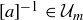 .
.
REMARK 6.26. Exercise 6.19 shows that 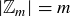 , but what can you say about
, but what can you say about 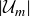 , the number of units modulo m? The answer takes some work to discover and justify; it is the topic of Project 11.7 on Euler’s totient function. If this is of interest, we recommend starting with a couple of warm-up problems that can be found in Exercise 6.71.
, the number of units modulo m? The answer takes some work to discover and justify; it is the topic of Project 11.7 on Euler’s totient function. If this is of interest, we recommend starting with a couple of warm-up problems that can be found in Exercise 6.71.
Exercises you can work on after Section 6.1
6.33 Let A be a non-empty set and consider the relation  on
on 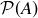 .
.
(a) Prove that  is reflexive.
is reflexive.
(b) Prove that  is transitive.
is transitive.
(c) Show that  is not symmetric.
is not symmetric.
6.34 Example 6.3 presents three relations on  . Since any relation on
. Since any relation on  is a subset of
is a subset of 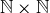 , you can visualize relations on
, you can visualize relations on  as a subset of the points in the first quadrant whose coordinates are natural numbers. For example, a portion of relation D from Example 6.3 is shown in Figure 5. Make similar illustrations for the relations E and F. You may need to include more points from
as a subset of the points in the first quadrant whose coordinates are natural numbers. For example, a portion of relation D from Example 6.3 is shown in Figure 5. Make similar illustrations for the relations E and F. You may need to include more points from 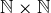 than we did in Figure 5 in order for your figure to genuinely illustrate these relations.
than we did in Figure 5 in order for your figure to genuinely illustrate these relations.
6.35 Since a relation on S is a subset of 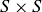 , you can often look at the “graph” of the relation, which is the obvious extension of the graph of a function. For example, in Figure 6 we illustrate the relation
, you can often look at the “graph” of the relation, which is the obvious extension of the graph of a function. For example, in Figure 6 we illustrate the relation
![]()
on the set 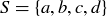 .
.
(a) What geometric property of the graph of a relation corresponds to the property of being reflexive?
(b) What geometric property of the graph of a relation corresponds to the property of being symmetric?
6.36 Consider a finite set S with 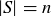 .
.
(a) How many different relations exist on S?
(b) How many different reflexive relations exist on S?
(c) How many different symmetric relations exist on S?
Exercises you can work on after Section 6.2
6.37 Continuing Exercise 6.33, prove that  is an antisymmetric relation on
is an antisymmetric relation on 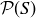 , and thus
, and thus 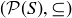 is a poset for any set S.
is a poset for any set S.
6.38 Prove that for any 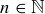 ,
, 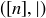 is a poset, where
is a poset, where 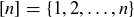 and
and  is divisibility.
is divisibility.
6.39 Draw a Hasse diagram for the poset 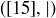 . How does the diagram change if you add 0 as a new element to this set?
. How does the diagram change if you add 0 as a new element to this set?
6.40 For any  , define
, define 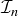 to be the partially ordered set whose elements are closed intervals in
to be the partially ordered set whose elements are closed intervals in 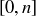 with integer endpoints, with
with integer endpoints, with  the same relation defined in Exercise 6.8.
the same relation defined in Exercise 6.8.
(a) Draw a Hasse diagram for 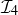 .
.
(b) What are the maximal elements of 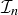 ?
?
(c) What are the minimal elements of 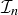 ?
?
6.41 Show that the definition of minimal element given in Section 4.1 agrees with Definition 6.8 when applied to the totally ordered set 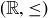 .
.
6.42 Prove that any finite poset that is totally ordered is also well ordered.
6.43 Let R and 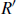 be partial orders on a set S. Recalling that R and
be partial orders on a set S. Recalling that R and 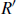 are subsets of
are subsets of 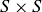 , we may define
, we may define 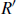 to be a refinement of R if whenever
to be a refinement of R if whenever 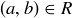 , then
, then 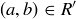 as well.
as well.
(a) Consider the poset  . Create a refinement
. Create a refinement 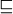 of
of  where
where 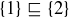 .
.
(b) Consider the poset 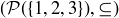 . Create a refinement
. Create a refinement 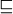 of
of  where
where 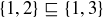 .
.
6.44 Show that there is a refinement of 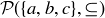 that is a total order. For a generalization of this result, see Exercise 6.76.
that is a total order. For a generalization of this result, see Exercise 6.76.
The remaining exercises in this section require the following definition.
DEFINITION 6.27. A chain in a poset 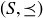 is a subset of elements where
is a subset of elements where
![]()
Put another way, a chain is a totally ordered subset of S. A maximal chain is one that is not properly contained in any other. The height of a poset is the number of elements in a largest chain, when such a value exists.
For example, in the poset 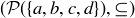 , the subsets
, the subsets
![]()
form a chain, and
![]()
is a maximal chain. As can be seen in Figure 5 in Chapter 3, all of the maximal chains in this poset contain 5 elements, so the height of the poset is 5.
6.45 How would you rewrite Exercise 3.32 in terms of maximal chains?
6.46 Consider the poset on 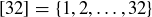 , ordered by divisibility.
, ordered by divisibility.
(a) Verify that 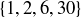 is a maximal chain.
is a maximal chain.
(b) Verify that 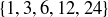 is also a maximal chain.
is also a maximal chain.
(c) Prove that this poset has height 6.
6.47 Consider the poset of subsets of 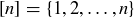 ordered by containment.
ordered by containment.
(a) Prove that this poset has height 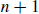 .
.
(b) Prove that this poset contains exactly 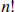 maximal chains.
maximal chains.
6.48 Construct a poset that, for every 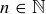 , has a maximal chain with n elements. That is, there is a maximal chain with only one element, there is a maximal chain with exactly two elements, and so on.
, has a maximal chain with n elements. That is, there is a maximal chain with only one element, there is a maximal chain with exactly two elements, and so on.
6.49 A zigzag poset, or fence, is a poset where the elements can be listed so that the order relation is alternating. An example of a zigzag poset on seven elements is shown in Figure 7. Using zigzag posets as an inspiration, prove that for any  there is an infinite poset, where all the maximal chains have n elements.
there is an infinite poset, where all the maximal chains have n elements.
Exercises you can work on after Section 6.3
6.50 Prove that same magnitude,
![]()
is an equivalence relation on  .
.
![]()
for 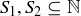 .
.
(a) Prove that 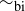 is an equivalence relation on
is an equivalence relation on 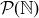 .
.
(b) Describe two distinct equivalence classes for 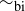 .
.
6.52 For any pair of subsets 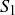 and
and 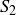 of
of  , define
, define
![]()
when the symmetric difference  is finite.
is finite.
(a) Prove that 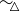 is an equivalence relation on
is an equivalence relation on 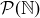 .
.
(b) Describe two distinct equivalence classes for 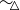 .
.
6.53 Consider the following relation on 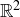 . We say
. We say 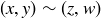 if
if 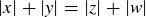 .
.
(a) Prove that ~ is an equivalence relation.
(b) Which elements are in the equivalence class of 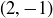 ? A graph may be useful here.
? A graph may be useful here.
6.54 Determine which of the following relations are equivalence relations. For those that are, describe the elements of two different equivalence classes.
(a)  , and
, and 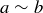 if either
if either 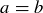 or the line in
or the line in 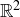 through a and b also goes through the origin.
through a and b also goes through the origin.
(b) 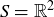 , and
, and  if either
if either  or the perpendicular bisector of the line segment joining a to b in
or the perpendicular bisector of the line segment joining a to b in  goes through the origin.
goes through the origin.
(c) S is the set of lines in  , and
, and  when the lines
when the lines 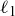 and
and 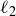 are parallel.
are parallel.
6.55 Determine which of the following relations are equivalence relations. For those that are, describe the elements of two different equivalence classes.
(a) 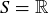 and
and 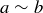 if
if 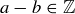 .
.
(b) 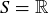 and
and 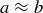 if
if 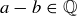 .
.
(c) 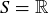 and
and 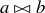 if
if 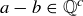 .
.
6.56 Let ~ and 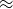 be equivalence relations on a set S.
be equivalence relations on a set S.
(a) Prove that the intersection  is an equivalence relation.
is an equivalence relation.
(b) Give a counterexample to the following claim: The union 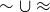 is an equivalence relation.
is an equivalence relation.
Remember, both ~ and 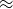 are subsets of
are subsets of 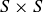 .
.
6.57 Let 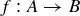 , and define
, and define 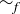 to be the relation on A defined by
to be the relation on A defined by
![]()
(a) Prove that 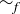 is an equivalence relation.
is an equivalence relation.
(b) Describe the equivalence classes of 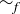 in the language of functions.
in the language of functions.
6.58 Let  and define a relation on A by
and define a relation on A by 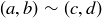 when
when 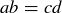 . For example,
. For example, 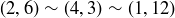 .
.
(a) Show that ~ is an equivalence relation.
(b) Find an equivalence class with exactly one element.
(c) Prove that for every 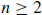 there is an equivalence class with exactly n elements.
there is an equivalence class with exactly n elements.
(d) Prove there are no equivalence classes with infinitely many elements.
(e) Which equivalence classes contain exactly two elements?
(f) Which equivalence classes contain exactly three elements?
6.59 Let  , and let ~ be the relation on
, and let ~ be the relation on 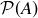 defined by
defined by
![]()
where  is the symmetric difference. Prove that ~ is an equivalence relation on
is the symmetric difference. Prove that ~ is an equivalence relation on  , and describe the equivalence class
, and describe the equivalence class 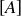 .
.
6.60 Let 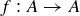 be a bijection. If
be a bijection. If  , we have already seen in Exercise 5.48 that
, we have already seen in Exercise 5.48 that
![]()
It is natural to similarly define
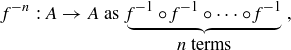
and also
![]()
(a) Explain why 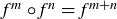 for any
for any 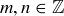 .
.
(b) If 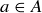 , then the orbit of a is
, then the orbit of a is
![]()
Prove that if 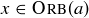 , then
, then 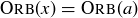 .
.
(c) Prove that 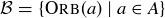 is a partition of A.
is a partition of A.
Exercises you can work on after Sections 6.4 and 6.5
6.61 Solve the following for x, or prove that no solution exists.
(a) 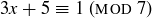
(b) 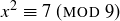
(c) 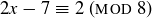
(d) 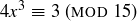
6.62 In Theorem 2.12, we used induction to show that, for all non-negative integers n,  is a multiple of 6.
is a multiple of 6.
(a) Use modular arithmetic to offer a simple and non-inductive proof of this theorem.
(b) Prove that, for all non-negative integers n, 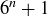 is divisible by 7 if and only if n is odd.
is divisible by 7 if and only if n is odd.
6.63 Let  be written in decimal notation as
be written in decimal notation as
![]()
Use modular arithmetic to …
(a) …prove that n is divisible by 3 if and only if 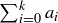 is divisible by 3,
is divisible by 3,
(b) …prove that n is divisible by 9 if and only if 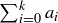 is divisible by 9.
is divisible by 9.
(c) …prove that n is divisible by 11 if and only if the alternating sum
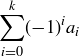
is divisible by 11.
If you did Exercise 1.47, compare your answer to that problem with your new solutions to parts (a) and (b) above.
6.64 Show that the following functions are not well defined.
(a) 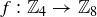 is given by
is given by 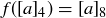 .
.
(b) 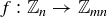 is given by
is given by 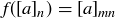 , where
, where 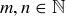 and
and 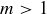 .
.
(c) 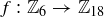 is given by
is given by 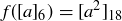 .
.
6.65 Show that 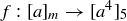 is well defined for any
is well defined for any 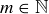 .
.
6.66 For any integer 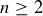 , what is the value of the binomial coefficient
, what is the value of the binomial coefficient 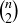 modulo n?
modulo n?
Exercises you can work on after Section 6.6
6.67 The integers modulo 7, 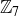 , consists of the equivalence classes
, consists of the equivalence classes 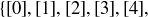
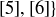 . Which pairs of equivalence classes are additive inverses of each other? Which pairs of equivalence classes are multiplicative inverses of each other? Are there any equivalence classes that do not “pair” nicely? Explain!
. Which pairs of equivalence classes are additive inverses of each other? Which pairs of equivalence classes are multiplicative inverses of each other? Are there any equivalence classes that do not “pair” nicely? Explain!
6.68 Recalling that you found the multiplicative inverses of 3 and 5 in 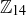 as part of Exercise 6.29, solve the following for x.
as part of Exercise 6.29, solve the following for x.
(a) 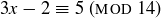
(b) 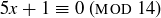
6.69 Recall that 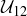 is the set of units in
is the set of units in 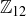 .
.
(a) What elements of 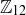 are in
are in 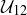 ?
?
(b) Create the multiplication table for 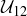 .
.
6.70 Show that each element of 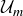 occurs once and only once in each row (or column) of the multiplication table for
occurs once and only once in each row (or column) of the multiplication table for 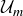 .
.
6.71 Determine the number of units in 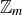 when m is prime, and when m is the square of a prime.
when m is prime, and when m is the square of a prime.
More Exercises!
6.72 In Exercise 4.11, you were asked to commit to memory an outline of the proof of the Fundamental Theorem of Arithmetic. Prove that you have!
6.73 Let R be a relation on any set S.
(a) Prove there is at least one equivalence relation on S that contains R.
(b) Let 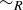 be the intersection of all equivalence relations on S that contain R. Prove that
be the intersection of all equivalence relations on S that contain R. Prove that 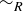 is itself an equivalence relation containing R.
is itself an equivalence relation containing R.
(c) Prove that if 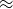 is an equivalence relation containing R, then
is an equivalence relation containing R, then 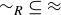 .
.
The relation 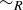 is often called the equivalence relation generated by R.
is often called the equivalence relation generated by R.
(d) Let T be the relation on 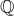 given by
given by 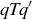 when
when 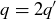 . Describe the equivalence relation
. Describe the equivalence relation 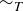 generated by T, and describe the equivalence class
generated by T, and describe the equivalence class 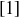 .
.
6.74 Here’s the result you will ultimately want to prove in this exercise:
Let S be a set of n integers. Then there is a subset of S that sums to a number divisible by n.
Here are some questions intended to help you develop a proof:
(a) Prove that the statement is true when 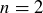 . (This should be easy.)
. (This should be easy.)
(b) Prove that the statement is true when 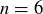 . (This might help you find an approach to the general result.)
. (This might help you find an approach to the general result.)
(c) Prove that the statement is true when 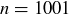 . (This tests if your approach really works!)
. (This tests if your approach really works!)
(d) Prove the general result.
6.75 In this problem we outline how you can construct the rational numbers from the integers using an appropriate equivalence relation.
Let Q be the set 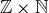 , and let ~ be the relation
, and let ~ be the relation
![]()
For example, 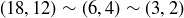 .
.
(a) Prove that ~ is an equivalence relation on the set Q.
Denote the equivalence class of 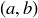 by
by 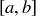 . We can define addition and multiplication on equivalence classes using the following formulas:
. We can define addition and multiplication on equivalence classes using the following formulas:
![]()
Denote the set of equivalence classes by 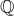 .
.
(b) Verify that these formulas are well defined, that is, the answers do not depend on the choice of representatives from the equivalence classes.
(c) Show that 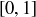 is an additive identity. That is,
is an additive identity. That is, 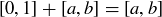 for all
for all 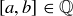 .
.
(d) Show that 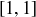 is a multiplicative identity, that is,
is a multiplicative identity, that is, 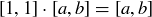 for all
for all 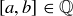 .
.
(e) Show that 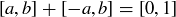 for all
for all 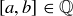 .
.
(f) Show that if 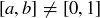 , there is a
, there is a 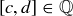 such that
such that 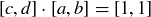 .
.
At this point you have probably already guessed that the set 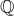 with these arithmetic operations is the same thing as the rational numbers. We have simply replaced the more standard notations of
with these arithmetic operations is the same thing as the rational numbers. We have simply replaced the more standard notations of 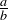 and
and 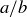 by
by 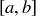 , and we have highlighted that there is an equivalence relation underlying the multiple ways you can write the same number via fractions.
, and we have highlighted that there is an equivalence relation underlying the multiple ways you can write the same number via fractions.
6.76 The goal of this exercise is to construct a proof of the following theorem:
For the definition of refinement, see Exercise 6.43. The proof we outline uses induction on the number of pairs of incomparable elements. The base case is when there are no incomparable elements, meaning that the original partial order is already a total order on S.
For the inductive step, we assume that the theorem holds whenever there are n or fewer pairs of incomparable elements. Let R be a partial order on a finite set S, with 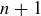 incomparable pairs, and let a and b be incomparable elements. That is,
incomparable pairs, and let a and b be incomparable elements. That is, 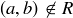 and
and 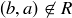 . In the steps below you will be asked to prove there is a refinement of R that contains
. In the steps below you will be asked to prove there is a refinement of R that contains 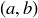 .
.
Define the set 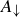 to consist of those elements that precede a with respect to the partial order R:
to consist of those elements that precede a with respect to the partial order R:
![]()
Similarly define the set 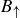 as those elements that b precedes with respect to the partial order R:
as those elements that b precedes with respect to the partial order R:
![]()
(a) Prove that 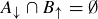 .
.
(b) Define a new relation on S: 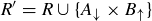 . Prove that
. Prove that 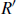 is a reflexive relation.
is a reflexive relation.
(c) Prove that 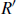 is antisymmetric. Note: This requires checking a number of cases, because a pair
is antisymmetric. Note: This requires checking a number of cases, because a pair  can be in
can be in 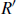 either because it is a pair in R or because it is in
either because it is a pair in R or because it is in 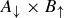 .
.
Proving that 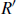 is transitive also requires the checking of a number of cases.
is transitive also requires the checking of a number of cases.
Transitivity: Assume that  and
and 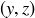 are both in
are both in 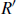 ; we need to prove that this implies
; we need to prove that this implies 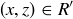 . It cannot be the case that both pairs come from
. It cannot be the case that both pairs come from 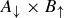 . If they did, then y would be in both
. If they did, then y would be in both 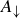 and
and 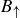 but we have already noted that
but we have already noted that 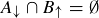 . If both pairs were already in R then the result follows since R is transitive.
. If both pairs were already in R then the result follows since R is transitive.
Assume that 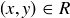 and
and 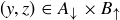 . Then from the definition of
. Then from the definition of 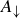 we know
we know 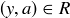 . Therefore
. Therefore 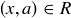 , since R is transitive. Thus
, since R is transitive. Thus 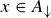 , and so
, and so
![]()
If instead we have 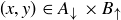 and
and 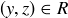 , then we know that
, then we know that 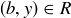 and so
and so 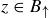 . Thus
. Thus
![]()
(d) It follows from the work above that 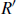 is a partial order on S. Verify that
is a partial order on S. Verify that 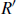 has n or fewer incomparable pairs, and so induction implies that
has n or fewer incomparable pairs, and so induction implies that 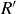 can be refined to a total order
can be refined to a total order 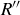 on S.
on S.
(e) Prove that 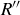 is also a total order that refines R.
is also a total order that refines R.
Having now worked through the details of this argument, write up a proof of Theorem 6.28 that reads well from beginning to end.
1 For some reason, no one calls it a “toset” …
2 …or a “woset.”