DEFINITION 4.1. A set 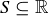 is said to have a minimal element if there is an
is said to have a minimal element if there is an 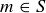 such that
such that  for all
for all 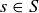 . That is, m is smaller than all other elements of S.
. That is, m is smaller than all other elements of S.
In this chapter, you will preview a few topics that you otherwise might first see in a course in algebra. The focal point of this chapter is a proof of the Fundamental Theorem of Arithmetic (Theorem 4.11), which says that the natural numbers greater than 1 have unique prime decompositions, up to the ordering of the terms.
We begin with a proof of an important property of the natural numbers, the Well-Ordering Principle, which guarantees the existence of minimal elements in sets of natural numbers. The concept of a minimal element, though, makes sense for any set of numbers.
DEFINITION 4.1. A set 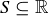 is said to have a minimal element if there is an
is said to have a minimal element if there is an 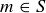 such that
such that  for all
for all 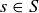 . That is, m is smaller than all other elements of S.
. That is, m is smaller than all other elements of S.
PROPOSITION 4.2. If 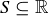 has a minimal element, then it has a unique minimal element.
has a minimal element, then it has a unique minimal element.
PROOF. If m and 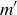 are both minimal elements of S, then we know
are both minimal elements of S, then we know 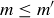 because m must be less than or equal to every element in S. However, it is also true that
because m must be less than or equal to every element in S. However, it is also true that 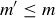 because
because 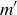 must be less than or equal to every element in S. Thus
must be less than or equal to every element in S. Thus 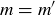 .
.

Here are a few examples illustrating the idea of minimal elements in sets of numbers.
(a) The minimal element of 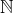 is the number 1.
is the number 1.
(b) The integers 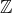 have no minimal element.
have no minimal element.
(c) The minimal element of the closed interval 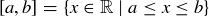 is a.
is a.
(d) The open interval 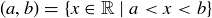 has no minimal element. To prove this, assume to the contrary that there is some
has no minimal element. To prove this, assume to the contrary that there is some 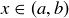 that is minimal. Then
that is minimal. Then 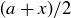 is still in the open interval
is still in the open interval 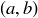 , and
, and 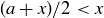 . This contradicts the claim that x is the minimal element.
. This contradicts the claim that x is the minimal element.
(e) The set of positive rational numbers is
![]()
The set 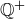 has no minimal element. For assume to the contrary that there is some q that is a minimal element in
has no minimal element. For assume to the contrary that there is some q that is a minimal element in 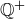 . Then the number
. Then the number 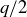 is also a rational number and greater than 0, and so
is also a rational number and greater than 0, and so 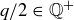 . But
. But 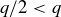 , contradicting the claim that q is smaller than all other elements of
, contradicting the claim that q is smaller than all other elements of 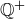 .
.
Exercise 4.1 Recall the definition of 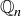 in Chapter 3, and define
in Chapter 3, and define
![]()
Does 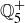 have a minimal element?
have a minimal element?
PROOF. Let 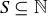 be a non-empty subset. Our proof that S contains a minimal element is by induction, with the base case being the situation where S contains the number 1. Since
be a non-empty subset. Our proof that S contains a minimal element is by induction, with the base case being the situation where S contains the number 1. Since 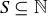 and 1 is minimal in
and 1 is minimal in 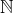 , it must also be the minimal element of S.
, it must also be the minimal element of S.
Our inductive hypothesis is that every subset 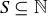 where
where
![]()
contains a minimal element. Assume then that
![]()
If S contains a natural number less than 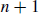 , then by our inductive hypothesis, S contains a minimal element. Otherwise S contains no natural number less than
, then by our inductive hypothesis, S contains a minimal element. Otherwise S contains no natural number less than 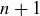 , but it must contain
, but it must contain 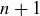 , in which case
, in which case 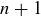 is the minimal element of S.
is the minimal element of S.

A powerful proof technique combines the Well-Ordering Principle with a proof by contradiction. As a first example, we can prove that the inequality
![]()
holds for all 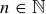 using this method. The argument begins by assuming to the contrary that there is some n where
using this method. The argument begins by assuming to the contrary that there is some n where  . That is, we are assuming the set of counterexamples is a non-empty subset of
. That is, we are assuming the set of counterexamples is a non-empty subset of 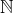 . Then by the Well-Ordering Principle there is a minimal counterexample, which we denote by m. Because
. Then by the Well-Ordering Principle there is a minimal counterexample, which we denote by m. Because 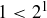 we know that
we know that 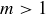 . This leads to a contradiction, because
. This leads to a contradiction, because
![]()
So  is also a counterexample, contradicting the fact that m was the smallest counterexample.
is also a counterexample, contradicting the fact that m was the smallest counterexample.
EXAMPLE 4.4. Here is a question inspired by the scoring in American football: what integers can be expressed in the form 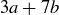 , where a and b are non-negative integers? The best first step is to consider examples, and after checking non-negative integers up to 15, we conjecture that the set of all such integers is
, where a and b are non-negative integers? The best first step is to consider examples, and after checking non-negative integers up to 15, we conjecture that the set of all such integers is
![]()
To prove this, assume to the contrary that there are counterexamples in
![]()
By the Well-Ordering Principle there must be a minimal counterexample, m, which we know by our earlier computations must be greater than 15. Since m is the minimal counterexample and 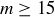 , it must be the case that
, it must be the case that 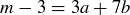 for some non-negative integers a and b, because
for some non-negative integers a and b, because 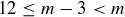 . But then we have
. But then we have 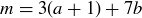 , which contradicts the claim that m is a counter- example.
, which contradicts the claim that m is a counter- example.
Exercise 4.2 What postage can you make using only 10 cent stamps and 4 cent stamps?
This proof strategy is sometimes referred to as the minimal criminal strategy. This basic structure is to first assume to the contrary that there are counterexamples to a given claim. Then by the Well-Ordering Principle you can discuss the smallest counterexample – the minimal criminal. You then derive a contradiction, thereby proving that the set of counterexamples is empty.
GOING BEYOND THIS BOOK. Minimal criminal arguments often employ steps that are reminiscent of standard proofs by induction, and indeed it is often simply a matter of stylistic preference as to whether to use a minimal criminal argument or induction. We use the minimal criminal strategy in the proof of the Fundamental Theorem of Arithmetic (Theorem 4.11). It also arises in work related to the four-color theorem, an important result in graph theory that is nicely described in Robin Wilson’s Four Colors Suffice [Wil14].
The Well-Ordering Principle is directly related to the principle of induction, each implying the other, and the connections between such topics is developed nicely in [Cun16].
The “easy” part of the Fundamental Theorem of Arithmetic was proved by induction as Theorem 2.11 in Section 2.6:
Every natural number 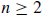 is either prime or it can be written as a product of primes.
is either prime or it can be written as a product of primes.
We are now left to show that the factorization of n into the product of primes is unique up to the order of the factors. To facilitate this part of the proof, we will first develop a relationship between two mathematical concepts that are important on their own: integer combinations and relatively prime integers.
DEFINITION 4.5. If a and b are real numbers, an integer combination of a and b is an expression of the form 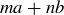 , where
, where 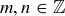 .
.
For example, 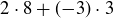 is an integer combination of 8 and 3 that equals 7. Also, Example 4.4 considers integer combinations of 3 and 7, but with restrictions on the values of m and n.
is an integer combination of 8 and 3 that equals 7. Also, Example 4.4 considers integer combinations of 3 and 7, but with restrictions on the values of m and n.
Exercise 4.3 Find an integer combination of 8 and 3 that equals 1. (It is possible to do this in many different ways.) Then try to find an integer combination of 8 and 6 that equals 1, or explain why this is impossible. What is the essential difference between these two cases?
DEFINITION 4.6. The integers a and b are said to be relatively prime if the only positive integer d such that 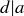 and
and 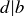 is
is 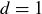 .
.
For example, 48 and 35 are relatively prime, while 5802 and 6111 are not.
Exercise 4.4 Verify that pairs of consecutive Fibonacci numbers 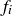 and
and 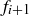 are relatively prime for
are relatively prime for 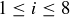 . Why do we need to specify consecutive Fibonacci numbers?
. Why do we need to specify consecutive Fibonacci numbers?
Exercise 4.5 Which integers are relatively prime to 0?
It is important to notice a fundamental difference between the definitions of “prime” and “relatively prime”: the term “prime” can only be applied to a single integer, while “relatively prime” applies to a pair of integers. For example, 3 is prime, as is 7, while 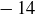 and 21 are not. The set
and 21 are not. The set 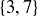 contains a relatively prime pair of integers, as does
contains a relatively prime pair of integers, as does 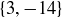 , while
, while 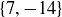 and
and 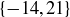 do not.
do not.
Here’s a result that will be used in the proof of Lemma 4.9 below.
PROOF. This proof is by contradiction. Suppose that a and b are relatively prime but  and b are not. Then there is some positive integer d greater than 1 such that
and b are not. Then there is some positive integer d greater than 1 such that 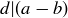 and
and 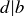 . By Exercise 1.17 we know that
. By Exercise 1.17 we know that 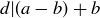 , which means that
, which means that 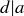 . Since
. Since 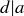 and
and 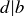 , a and b are not relatively prime, contradicting our original supposition.
, a and b are not relatively prime, contradicting our original supposition.

Exercise 4.6 For each of the following statements about integers a, b, and c, either prove the statement is true in general or provide a specific counterexample.
(a) If a and b are relatively prime, so are 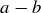 and
and 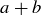 .
.
(b) If a and b are relatively prime, so are a and 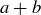 .
.
(c) If a and b are relatively prime, so are a and 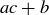 .
.
(d) If a and b are relatively prime, so are a and 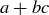 .
.
You saw in Exercise 4.3 that there’s an integer combination of 8 and 3 that equals 1, but no such integer combination of 8 and 6; the reason is that 8 and 3 are relatively prime but 8 and 6, having a common factor of 2, are not. We now prove the general result about this correspondence. The second half of the proof uses mathematical induction quite cleverly: we have two positive integers a and b, but we induct on the single value 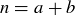 .
.
THEOREM 4.8. Let a and b be positive integers. There is an integer combination of a and b that equals 1 if and only if a and b are relatively prime.
PROOF. We first prove the “only if” part, namely
![]()
by proving the contrapositive: assuming that a and b are not relatively prime, we will show that no integer combination can be equal to 1.
If a and b are not relatively prime, there must exist some positive integer d greater than 1 such that 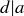 and
and 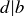 . This means that
. This means that 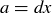 and
and 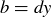 for some integers x and y, which implies that any integer combination
for some integers x and y, which implies that any integer combination 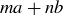 of a and b can be written as
of a and b can be written as
![]()
Thus any integer combination of a and b is divisible by d, so no integer combination can be equal to 1.
We now prove the “if” part of the theorem,
![]()
using induction on 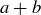 .
.
Suppose a and b are relatively prime positive integers. The smallest possible value of 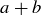 is 2, when
is 2, when 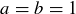 . In this base case for the induction argument, there is certainly an integer combination of a and b that equals 1:
. In this base case for the induction argument, there is certainly an integer combination of a and b that equals 1:
![]()
To show that the inductive step also holds, we consider any relatively prime positive integers a and b with 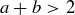 . Since a and b are assumed to be relatively prime, and since
. Since a and b are assumed to be relatively prime, and since 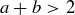 implies that at least one of a and b is greater than 1, they cannot be equal to each other. Therefore we know that either
implies that at least one of a and b is greater than 1, they cannot be equal to each other. Therefore we know that either 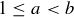 or
or 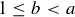 . Since the definition of relatively prime given above is symmetric with respect to a and b, these two cases are really no different, so without loss of generality we may assume that
. Since the definition of relatively prime given above is symmetric with respect to a and b, these two cases are really no different, so without loss of generality we may assume that 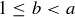 .
.
The key to the inductive step is to apply it to 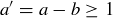 and
and 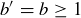 , which represents a “smaller” case since
, which represents a “smaller” case since 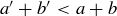 . Since
. Since 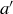 and
and 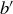 are relatively prime by Lemma 4.7, we may assume that there are integers m and n such that
are relatively prime by Lemma 4.7, we may assume that there are integers m and n such that 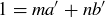 . A calculation now shows how this leads directly to an integer combination of a and b that equals 1, as desired:
. A calculation now shows how this leads directly to an integer combination of a and b that equals 1, as desired:
![]()

Exercise 4.7 Is Theorem 4.8 true if at least one of a and b equals 0?
Exercise 4.8 Is Theorem 4.8 true for all integers a and b?
Exercise 4.9 For each of the following triples of numbers, find specific integer combinations of a and b that equal c. For parts (a) and (b), you may find it helpful to first find a combination of a and b that equals 1.
(a) 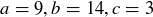
(b) 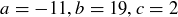
(c) 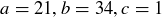
We now return to the Fundamental Theorem of Arithmetic, with the goal of finally completing a full proof of this well-known fact. We first use the main result of the previous section to prove an important lemma.
The structure of this proof will be to show that if 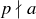 then
then 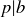 , which is equivalent to showing that
, which is equivalent to showing that 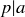 or
or 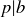 .1
.1
PROOF. Suppose that p is a prime, 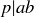 , and
, and 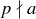 . Since
. Since 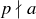 and the only positive integers dividing the prime p are 1 and p, we conclude that p and a must be relatively prime. By Theorem 4.8, this means that there are integers m and n such that
and the only positive integers dividing the prime p are 1 and p, we conclude that p and a must be relatively prime. By Theorem 4.8, this means that there are integers m and n such that 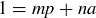 . Multiplying both sides of this equation by b gives
. Multiplying both sides of this equation by b gives
![]()
Notice that p divides both terms on the right-hand side of the equation because 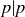 and
and 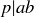 , so by Exercise 1.17 we know that p divides their sum, b, as desired.
, so by Exercise 1.17 we know that p divides their sum, b, as desired.

To prove the Fundamental Theorem of Arithmetic, it will be best to use a more general version of Lemma 4.9.
LEMMA 4.10. Let p be a prime number, and let 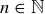 . If
. If 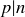 and n can be written as a product of natural numbers
and n can be written as a product of natural numbers
![]()
then 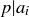 for some i.
for some i.
Exercise 4.10 Prove Lemma 4.10 by induction on k.
THEOREM 4.11 (Fundamental Theorem of Arithmetic). There is a unique way, up to the order of the terms, to express a natural number 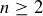 as a product of primes.
as a product of primes.
PROOF. Theorem 2.11 states that any integer greater than 1 can be expressed as some product of primes, including the case when the product contains only one prime, so we only need to show the uniqueness of the expression. An equivalent way to state this part of the theorem uses an efficient “standard form” for prime factorizations: any product of primes can be written as
![]()
where the distinct primes appearing in the product are listed in strictly increasing order 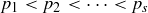 , and each exponent
, and each exponent 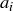 is a positive integer telling how many times the prime
is a positive integer telling how many times the prime 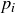 appears in the product. For example,
appears in the product. For example, 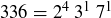 . Using this notion of standard form, the uniqueness part of the theorem states that if n is an integer greater than 1 such that both
. Using this notion of standard form, the uniqueness part of the theorem states that if n is an integer greater than 1 such that both
![]()
and
![]()
where 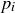 and
and 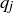 are sequences of increasing primes, then
are sequences of increasing primes, then  , and
, and 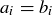 and
and 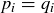 for all i.
for all i.
Suppose there is some natural number that has two distinct factorizations. Then by the Well-Ordering Principle (Theorem 4.3), there is a minimal natural number n that has at least two distinct factorizations. Let the standard form of any two such factorizations be the ones just given above.
We know that n is not prime, because then we must have 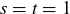 ,
, 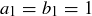 , and
, and 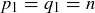 . So any standard form expression of n must involve at least two prime factors (which might not be distinct). Since
. So any standard form expression of n must involve at least two prime factors (which might not be distinct). Since 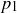 divides n, it must divide
divides n, it must divide 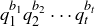 . By Lemma 4.10,
. By Lemma 4.10, 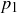 must divide
must divide 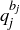 for some j; and so by Lemma 4.10 again, it divides
for some j; and so by Lemma 4.10 again, it divides 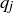 . Since
. Since 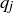 is itself prime, it must be the case that
is itself prime, it must be the case that 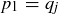 . Thus
. Thus 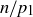 can be factored in two distinct ways, the expressions being
can be factored in two distinct ways, the expressions being
![]()
and
![]()
where if 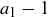 or
or 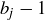 is zero we simply remove this term from our expression. These two expressions are distinct if the original expressions are distinct, because the exponent of the same prime simply decreased by 1. Thus we see that
is zero we simply remove this term from our expression. These two expressions are distinct if the original expressions are distinct, because the exponent of the same prime simply decreased by 1. Thus we see that 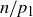 can be factored in distinct ways, contradicting the claim that n is the smallest such integer. Thus there cannot be a non-empty set of counterexamples, and therefore all natural numbers
can be factored in distinct ways, contradicting the claim that n is the smallest such integer. Thus there cannot be a non-empty set of counterexamples, and therefore all natural numbers 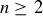 have unique factorizations up to the order of the terms.
have unique factorizations up to the order of the terms.

At this point you should pause and reflect on quite an accomplishment: you have worked your way through a proof of a very important number theoretical result, a proof that required induction, direct arguments, indirect arguments, and the support of several lemmas and simpler theorems.
Exercise 4.11 Outline the proof of the Fundamental Theorem of Arithmetic, including the “easy” part, on a single page (and remember it forever).
With the Fundamental Theorem of Arithmetic in hand, we are in a great position to generalize Theorem 4.8 by introducing two important concepts: the “greatest common divisor” and the “least common multiple” of a pair of integers.
DEFINITION 4.12. Let a and 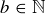 . The greatest common divisor of a and b, written
. The greatest common divisor of a and b, written 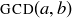 , is the largest positive integer d such that
, is the largest positive integer d such that 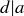 and
and 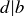 . The least common multiple of a and b, written
. The least common multiple of a and b, written 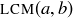 , is the smallest positive integer m such that
, is the smallest positive integer m such that 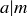 and
and 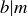 .
.
It is immediate from the definition of 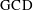 that two natural numbers a and b are relatively prime if and only if
that two natural numbers a and b are relatively prime if and only if 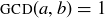 .
.
EXAMPLE 4.13. If 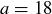 and
and 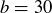 , the set of all positive common divisors of a and b is
, the set of all positive common divisors of a and b is 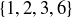 , so
, so 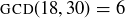 . The set of all positive common multiples of 18 and 30 is the infinite set
. The set of all positive common multiples of 18 and 30 is the infinite set 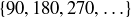 , so
, so 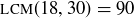 .
.
Exercise 4.12 Find two natural numbers a and b such that 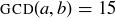 and
and 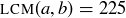 . Is the pair of numbers unique? Could you have
. Is the pair of numbers unique? Could you have 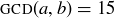 and
and 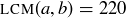 instead?
instead?
It is important to make sure that concepts like 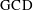 and
and  are “well defined.” Could there be some positive integers a and b for which
are “well defined.” Could there be some positive integers a and b for which 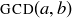 and
and 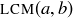 don’t exist or don’t give unique answers? We’ll leave the question for
don’t exist or don’t give unique answers? We’ll leave the question for  to Exercise 4.13 and answer the question for
to Exercise 4.13 and answer the question for 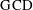 here. Since 1 is a common divisor of both a and b, and since no positive common divisor can be greater than
here. Since 1 is a common divisor of both a and b, and since no positive common divisor can be greater than 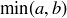 , the minimum of a and b, the set of positive common divisors is a non-empty and finite subset of
, the minimum of a and b, the set of positive common divisors is a non-empty and finite subset of 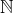 . Since a finite, non-empty subset of
. Since a finite, non-empty subset of 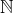 must have a single largest element, the
must have a single largest element, the 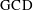 of a and b exists and is unique.
of a and b exists and is unique.
Exercise 4.13 Show that the concept of  is well defined.
is well defined.
A simple variant of the standard form of prime factorizations introduced in the proof of the Fundamental Theorem of Arithmetic gives us a quick way to compute 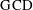 s and
s and 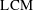 s. Suppose that a and b are positive integers greater than 1, so that there is a unique prime factorization of each. If we let
s. Suppose that a and b are positive integers greater than 1, so that there is a unique prime factorization of each. If we let 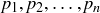 list all of the primes that are divisors of a or b, we can write
list all of the primes that are divisors of a or b, we can write
![]()
where all of the exponents are non-negative but some may be equal to 0. Then
![]()
and
![]()
For example, the primes that divide 18 and 30 are 2, 3, and 5, so we write 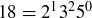 and
and 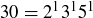 and compute
and compute
![]()
matching our earlier answers.
Exercise 4.14 Prove that this method really does compute 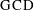 s and
s and  s.
s.
Exercise 4.15 Let 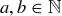 . Prove that
. Prove that 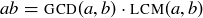 .
.
We end this section by examining an important relationship between integer combinations and 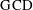 s. You were asked in an earlier section to show that it was possible to write 1 as an integer combination of 8 and 3, but you could not do the same for 8 and 6. The problem with 8 and 6 is that 2 is a common divisor, and so 2 is a common divisor of
s. You were asked in an earlier section to show that it was possible to write 1 as an integer combination of 8 and 3, but you could not do the same for 8 and 6. The problem with 8 and 6 is that 2 is a common divisor, and so 2 is a common divisor of 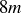 and
and 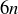 for any
for any 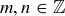 , and of
, and of 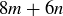 by Exercise 1.17. The following theorem is the appropriate generalization of Theorem 4.8.
by Exercise 1.17. The following theorem is the appropriate generalization of Theorem 4.8.
THEOREM 4.14. Let a and b be positive integers. The smallest positive integer combination of a and b is 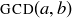 , and every integer combination of a and b is a multiple of
, and every integer combination of a and b is a multiple of 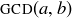 .
.
PROOF. Let 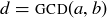 . The fact that every integer combination of a and b is a multiple of d follows from an argument just like that given above for 8 and 6: since
. The fact that every integer combination of a and b is a multiple of d follows from an argument just like that given above for 8 and 6: since 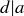 and
and 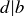 , for any integers m and n we find that
, for any integers m and n we find that 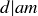 and
and 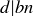 , so by Exercise 1.17 we know that
, so by Exercise 1.17 we know that 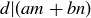 .
.
To prove that the smallest positive integer combination of a and b is d, we will first show that 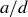 and
and 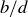 are relatively prime integers. They are certainly integers, since
are relatively prime integers. They are certainly integers, since 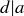 and
and 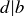 . They are also relatively prime, as the following short proof by contradiction shows. If
. They are also relatively prime, as the following short proof by contradiction shows. If 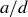 and
and 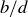 are not relatively prime, an integer c greater than 1 would divide both
are not relatively prime, an integer c greater than 1 would divide both 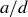 and
and 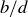 , which would mean that both
, which would mean that both 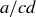 and
and 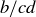 are integers. But this would mean that cd is a common divisor of a and b that is larger than d, a contradiction.
are integers. But this would mean that cd is a common divisor of a and b that is larger than d, a contradiction.
Since 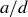 and
and 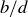 are relatively prime positive integers, by Theorem 4.8 there are integers m and n such that
are relatively prime positive integers, by Theorem 4.8 there are integers m and n such that 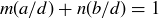 . Multiplying through by d gives us
. Multiplying through by d gives us 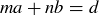 , as desired.
, as desired.

Exercise 4.16 Find an integer combination of 21 and 33 that equals 3.
In the spirit of the mathematical process described in Section 2.8, we encourage you to end your study of this section with generalizations of 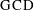 and
and  to more than two natural numbers at a time. If
to more than two natural numbers at a time. If 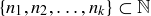 is a finite subset of natural numbers, define
is a finite subset of natural numbers, define 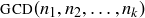 to be the largest
to be the largest 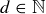 such that
such that 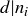 for all i, and define
for all i, and define 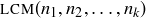 to be the smallest
to be the smallest 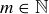 such that
such that 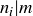 for all i. The following exercise asks you to explore several of the concepts introduced earlier in this section, to determine whether they might apply in this more general setting.
for all i. The following exercise asks you to explore several of the concepts introduced earlier in this section, to determine whether they might apply in this more general setting.
Exercise 4.17 There are a number of things to prove or refute in considering the extension of the concept of 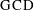 and
and  to more than two natural numbers.
to more than two natural numbers.
(a) Explain why the more general definitions of 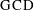 and
and  given above are well-defined.
given above are well-defined.
(b) Show that the most direct generalization of the “min” and “max” functions gives you a quick way to compute 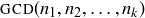 and
and 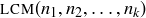 .
.
(c) Compute 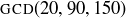 and
and 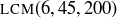 .
.
(d) Does
![]()
hold for all natural numbers a, b, and c? If not, can you characterize the triples for which it does hold?
Extending Theorem 4.14 to more than two numbers is the focus of Exercises 4.53 and 4.54.
The set of natural numbers 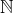 has the very nice property that it is “closed under addition.” This means that whenever
has the very nice property that it is “closed under addition.” This means that whenever 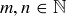 , then
, then 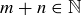 as well. For instance, 3 is a natural number and so is 17, as is 20, their sum. In general, we say that a set S of numbers is closed under addition if
as well. For instance, 3 is a natural number and so is 17, as is 20, their sum. In general, we say that a set S of numbers is closed under addition if 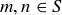 implies that
implies that 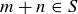 as well. Similarly, a set S of numbers is closed under multiplication if
as well. Similarly, a set S of numbers is closed under multiplication if 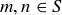 implies that
implies that 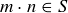 as well. The sets
as well. The sets 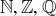 , and
, and  are all closed under addition and multiplication.
are all closed under addition and multiplication.
It is possible for finite sets of numbers to be closed under multiplication. For example, the set 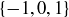 is closed under multiplication. It is not, however, closed under addition, as
is closed under multiplication. It is not, however, closed under addition, as 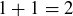 and
and 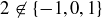 .
.
Exercise 4.18 Is any non-empty finite set closed under addition?
Let 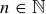 be at least 2, and define
be at least 2, and define 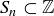 to be the set of all integers that leave a remainder of 1 when divided by n:
to be the set of all integers that leave a remainder of 1 when divided by n:
![]()
The set 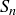 is not closed under addition: the numbers 1 and 1 are both in
is not closed under addition: the numbers 1 and 1 are both in 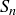 , but
, but 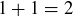 is not in
is not in 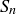 . However, these sets are closed under multiplication.
. However, these sets are closed under multiplication.
PROPOSITION 4.15. Each of the sets 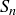 is closed under multiplication.
is closed under multiplication.
PROOF. Fix 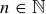 , and let a and b be elements of
, and let a and b be elements of 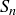 . Then
. Then 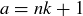 and
and 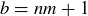 , for some
, for some 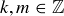 . A bit of arithmetic shows that
. A bit of arithmetic shows that
![]()
Since 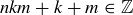 , it follows that
, it follows that 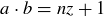 for some
for some 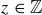 , and so
, and so 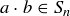 .
.

A set of numbers S is closed under subtraction if 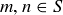 implies that
implies that 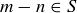 as well. The numbers 3 and 17 provide just one of many possible counterexamples to the claim that
as well. The numbers 3 and 17 provide just one of many possible counterexamples to the claim that 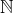 is closed under subtraction: 3 and 17 are both natural numbers, but
is closed under subtraction: 3 and 17 are both natural numbers, but 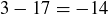 is not. The larger set of all integers,
is not. The larger set of all integers, 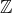 , is closed under subtraction.
, is closed under subtraction.
The notion of being closed under division is perhaps the most complicated, as 0 is an exceptional number. Thus a set S is said to be closed under division if given 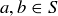 with
with 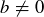 , the number
, the number 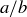 is also in S. The sets
is also in S. The sets 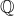 and
and  are closed under division, while
are closed under division, while 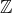 is not.
is not.
Exercise 4.19 Is 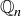 closed under addition? subtraction? multiplication? division?
closed under addition? subtraction? multiplication? division?
We end this section with a discussion of a set of numbers based on the golden ratio 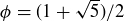 . We first discussed ϕ in Section 1.2, where we noted that it is a root of the polynomial
. We first discussed ϕ in Section 1.2, where we noted that it is a root of the polynomial 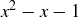 . In Exercise 4.36 we ask you to prove (in three ways!) that ϕ is irrational, a fact we will assume in this discussion.
. In Exercise 4.36 we ask you to prove (in three ways!) that ϕ is irrational, a fact we will assume in this discussion.
Let 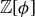 be the set of all integer combinations of 1 and ϕ:
be the set of all integer combinations of 1 and ϕ:
![]()
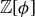 is a set of numbers satisfying
is a set of numbers satisfying 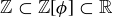 . (The inclusion
. (The inclusion 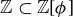 is proper as
is proper as 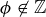 ; the claim that the inclusion
; the claim that the inclusion 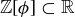 is proper is intuitive but is a bit more delicate to establish.) This set is called “
is proper is intuitive but is a bit more delicate to establish.) This set is called “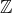 adjoined by ϕ” or “
adjoined by ϕ” or “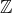 adjoined by the golden ratio.”
adjoined by the golden ratio.”
PROPOSITION 4.16. The set of numbers 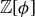 is closed under addition, subtraction, and multiplication.
is closed under addition, subtraction, and multiplication.
PROOF. Let 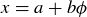 and
and 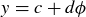 be numbers in
be numbers in 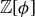 . Then
. Then
![]()
Since 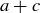 and
and 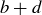 are in
are in 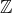 , it follows by the definition that
, it follows by the definition that 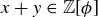 .
.
The same argument, with some minus signs replacing plus signs, shows that 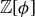 is closed under subtraction.
is closed under subtraction.
In proving that 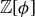 is closed under multiplication we will appeal to the fact that ϕ is a root of
is closed under multiplication we will appeal to the fact that ϕ is a root of 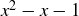 , which implies that
, which implies that 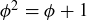 . Thus we have
. Thus we have
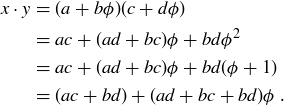
Since 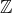 is closed under addition and multiplication,
is closed under addition and multiplication, 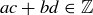 and
and 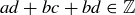 , hence
, hence 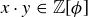 .
.

The set 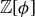 is not closed under division, though. For example, 1 and
is not closed under division, though. For example, 1 and 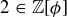 , but
, but 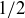 is not in
is not in 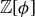 . To prove this, start by assuming to the contrary that
. To prove this, start by assuming to the contrary that 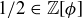 . Thus
. Thus 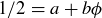 with
with 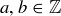 . If
. If 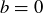 then
then 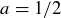 , which contradicts
, which contradicts 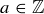 . However, if
. However, if 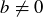 then
then 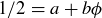 implies
implies
![]()
which contradicts the fact that 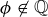 .
.
On the other hand, 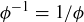 is in
is in 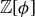 . We can take the identity
. We can take the identity 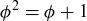 , divide every term by ϕ, and then rearrange the equation to show
, divide every term by ϕ, and then rearrange the equation to show
![]()
Since 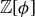 is closed under multiplication we immediately get the following result:
is closed under multiplication we immediately get the following result:
![]()
is contained in 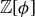 .
.
We hope that the example of 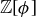 inspires an inclination to ask if similar results hold when you extend the integers using other irrational numbers. The exercise below gives you the chance to explore a similar situation, this time focused on
inspires an inclination to ask if similar results hold when you extend the integers using other irrational numbers. The exercise below gives you the chance to explore a similar situation, this time focused on 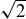 . You might even ask about using
. You might even ask about using 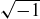 , which appears in Project 11.4 on the Gaussian integers.
, which appears in Project 11.4 on the Gaussian integers.
Exercise 4.20 The set of numbers 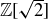 is a subset of
is a subset of  consisting of all integer combinations of 1 and
consisting of all integer combinations of 1 and 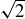 . That is,
. That is,
![]()
This set is called “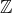 adjoined by
adjoined by 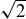 .” Determine whether
.” Determine whether 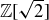 is closed under addition, subtraction, and multiplication.
is closed under addition, subtraction, and multiplication.
The sets of numbers 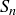 ,
,  , and
, and 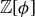 are all closed under multiplication, and so you can ask about decompositions of given elements as products of the others. Is there a notion of “prime numbers” for these systems? Unique factorization? The cases of
are all closed under multiplication, and so you can ask about decompositions of given elements as products of the others. Is there a notion of “prime numbers” for these systems? Unique factorization? The cases of 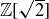 and
and 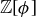 are beyond the scope of this book. They are often discussed in courses in abstract algebra and number theory, where you will find that sometimes adjoining square roots to the integers results in a system (called a “ring”) with unique factorization, and sometimes unique factorization fails. Perhaps the easiest example to present comes from
are beyond the scope of this book. They are often discussed in courses in abstract algebra and number theory, where you will find that sometimes adjoining square roots to the integers results in a system (called a “ring”) with unique factorization, and sometimes unique factorization fails. Perhaps the easiest example to present comes from 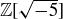 , where
, where
![]()
and none of the four factors shown can be further decomposed. Unique factorization in 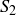 ,
, 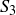 , and
, and 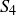 is explored in Exercises 4.48, 4.49, and 4.50.
is explored in Exercises 4.48, 4.49, and 4.50.
Exercises you can work on after Section 4.1
4.21 Let 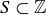 be a subset of the integers that has a minimal element. Prove that S has the well-ordering property, that is, every non-empty subset of S contains a minimal element.
be a subset of the integers that has a minimal element. Prove that S has the well-ordering property, that is, every non-empty subset of S contains a minimal element.
4.22 Prove that postage of 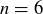 cents or more can be achieved by using only 2-cent and 7-cent stamps.
cents or more can be achieved by using only 2-cent and 7-cent stamps.
4.23 In this exercise you will construct two proofs of the fact that 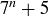 is divisible by 3 for all
is divisible by 3 for all 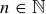 .
.
(a) Prove this result using a standard induction argument.
(b) Prove this result using a minimal criminal argument. As a hint, if 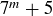 is the minimal criminal then 3 divides
is the minimal criminal then 3 divides 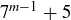 , and it also divides
, and it also divides 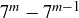 .
.
Modular arithmetic (Chapter 6) will offer another method for proving this fact.
![]()
for all 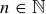 using a minimal criminal argument.
using a minimal criminal argument.
![]()
for all 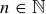 using a minimal criminal argument.
using a minimal criminal argument.
4.26 Return to the induction exercises at the end of Chapter 2, and prove some of them using a minimal criminal argument instead.
Exercises you can work on after Section 4.2
4.27 Use one of the results of Exercise 4.6 and mathematical induction to prove that any two consecutive Fibonacci numbers 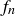 and
and 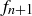 are relatively prime.
are relatively prime.
4.28 What would it mean to say that three integers a, b, and c are relatively prime? Try to come up with a reasonable mathematical definition for this concept. Make sure that your definition allows an example where the three integers a, b, and c are relatively prime as a triple, yet each of 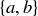 ,
, 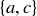 , and
, and 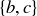 is not a relatively prime pair of integers.
is not a relatively prime pair of integers.
4.29 Let a, b, and c be natural numbers. Prove that if a and b are relatively prime and if a and c are also relatively prime, then a and bc are relatively prime.
4.30 The set of integer combinations of 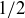 and
and 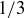 is
is
![]()
(a) Prove that the following inclusions are proper: 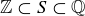 .
.
(b) Conjecture a relationship between S and
![]()
(c) Prove your conjecture.
4.31 Let a and b be relatively prime. Prove that for any 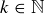 there are integers m and n such that
there are integers m and n such that
![]()
Exercises you can work on after Sections 4.3 and 4.4
4.32 What proportion of the integers in  can be expressed as
can be expressed as 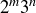 for non-negative integers m and n?
for non-negative integers m and n?
4.33 A natural number 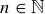 is awesome if whenever
is awesome if whenever 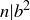 , then
, then 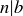 . Or, said a bit more carefully and using notation from Chapter 2, n is awesome if
. Or, said a bit more carefully and using notation from Chapter 2, n is awesome if 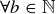 ,
, 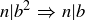 .
.
(a) Show that 1 and all the prime numbers are awesome.
(b) Show by an example that not all natural numbers are awesome.
(c) Show by an example that there are non-prime numbers that are awesome.
(d) Formulate a conjecture that identifies in a simple and precise way exactly which numbers are awesome.
(e) Prove your conjecture.
4.34 In this exercise we return to the sets 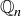 defined at the beginning of Chapter 3 and in Exercise 3.2.
defined at the beginning of Chapter 3 and in Exercise 3.2.
(a) Characterize when 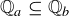 .
.
(b) Characterize when 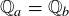 .
.
(c) Characterize when 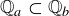 .
.
If it wasn’t understood already, you should prove your characterizations are correct!
4.35 Recall that 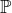 is the set of primes.
is the set of primes.
(a) Explain why
![]()
(b) Explain why
![]()
(c) Explain why
![]()
is an infinite set if 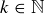 and
and 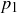 ,
, 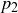 , …,
, …, 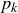 are any k primes. Then contrast this statement with the one in part (b).
are any k primes. Then contrast this statement with the one in part (b).
4.36 Here we outline three proofs that the golden ratio ϕ is irrational. It is your job to fill in the gaps in these arguments.
Proof 1: A variation on the 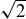 -argument presented in Section 1.7
-argument presented in Section 1.7
(a) Modify the argument that proves 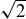 is irrational to show that
is irrational to show that 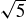 is irrational.
is irrational.
(b) Assume that ϕ is a rational number, and show that this implies 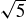 is also rational.
is also rational.
(c) Conclude that the assumption that ϕ is rational must be false.
Proof 2: Using the definition of ϕ
(a) Assume that 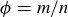 , in lowest terms. Show that
, in lowest terms. Show that 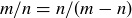 by recalling that ϕ is related to dividing segments into “extreme and mean ratio.”
by recalling that ϕ is related to dividing segments into “extreme and mean ratio.”
(b) Conclude that the assumption that 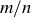 is in lowest terms is false, and therefore that no such expression exists for ϕ.
is in lowest terms is false, and therefore that no such expression exists for ϕ.
Proof 3: Using the quadratic equation it satisfies
(a) Assume that 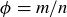 , in lowest terms. Show that the equation
, in lowest terms. Show that the equation 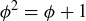 implies
implies 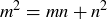 .
.
(b) Conclude that 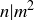 and that this contradicts the assumption that
and that this contradicts the assumption that 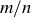 is in lowest terms. (Be careful here: see Exercise 4.33.)
is in lowest terms. (Be careful here: see Exercise 4.33.)
4.37 Use the Fundamental Theorem of Arithmetic to prove that 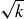 is irrational for each positive integer k that is not a perfect square.
is irrational for each positive integer k that is not a perfect square.
4.38 For which pairs of natural numbers a and b is 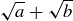 rational?
rational?
4.39 Generalize the statement and proof in Exercise 4.37 to 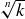 .
.
4.40 Find all pairs of natural numbers a and b with 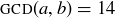 and
and 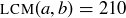 .
.
4.41 Let m and n be natural numbers where 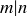 . What is
. What is 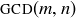 ? What is
? What is 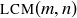 ?
?
4.42 Let m and n both divide k. Prove that 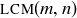 also divides k.
also divides k.
4.43 Let m and n be natural numbers with 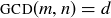 . Let e be a divisor of both m and n. Prove that
. Let e be a divisor of both m and n. Prove that 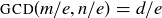 .
.
4.44 Prove that if m and n are relatively prime natural numbers and their product mn is a perfect square, then m and n must both be perfect squares.
4.45 Write a rational number 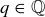 in lowest terms and take the product of its numerator and denominator. For how many rational numbers strictly between 0 and 1 will
in lowest terms and take the product of its numerator and denominator. For how many rational numbers strictly between 0 and 1 will 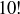 be the resulting product?
be the resulting product?
4.46 Is the following formula true?
![]()
Either prove it or find a counterexample.
Exercises you can work on after Section 4.5
The Fundamental Theorem of Arithmetic is so well known that people might take it for granted. The following two exercises show that we shouldn’t be so cavalier.
4.47 Consider the set 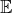 of even integers.
of even integers.
(a) Show that 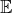 is closed under addition and multiplication.
is closed under addition and multiplication.
(b) Call a number 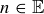 an even-prime if
an even-prime if 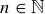 and n cannot be expressed as a product of two elements in
and n cannot be expressed as a product of two elements in 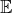 . Prove that an even number is an even-prime if and only if it can be written as
. Prove that an even number is an even-prime if and only if it can be written as 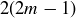 for some
for some 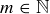 .
.
(c) Prove that every positive 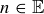 is an even-prime or can be expressed as a product of even-primes.
is an even-prime or can be expressed as a product of even-primes.
(d) Show by an example that there are numbers 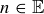 that can be expressed in two different ways as a product of even-primes.
that can be expressed in two different ways as a product of even-primes.
(e) Theorem 4.11 proves the uniqueness of prime decompositions for all 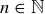 with
with 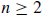 . By your work above you have shown that this proof cannot apply to
. By your work above you have shown that this proof cannot apply to 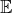 . Can you find a claim in the proof of Theorem 4.11 that is false when applied to
. Can you find a claim in the proof of Theorem 4.11 that is false when applied to 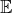 ?
?
4.48 Let 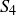 be the set of all integers giving a remainder of 1 when divided by 4. Thus
be the set of all integers giving a remainder of 1 when divided by 4. Thus
![]()
Proposition 4.15 shows that 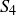 is closed under multiplication, and so it is reasonable to discuss the ways in which elements in
is closed under multiplication, and so it is reasonable to discuss the ways in which elements in 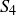 can be written as products of elements in
can be written as products of elements in 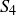 . For example, working in
. For example, working in 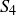 we can write
we can write 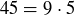 , but we cannot write
, but we cannot write 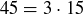 because 3 and 15 are not elements of
because 3 and 15 are not elements of 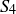 . Similarly, 9 has no non-trivial factorizations within
. Similarly, 9 has no non-trivial factorizations within 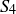 , as the prime decomposition of 9 is
, as the prime decomposition of 9 is  , and
, and 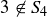 .
.
(a) Call a positive integer 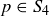 a 4-prime if its only positive factors in
a 4-prime if its only positive factors in 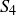 are 1 and p. Show that if p is an actual prime number in
are 1 and p. Show that if p is an actual prime number in 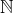 , and p is also in
, and p is also in 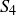 , then p is a 4-prime as well.
, then p is a 4-prime as well.
(b) Show that 21 and 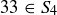 are 4-primes.
are 4-primes.
(c) Show that 693 can be written as a product of 4-primes in two distinct ways.
If you found this exercise interesting, you might look at the article “Unique factorization in multiplicative systems” by James and Niven [JN54].
4.49 Let 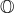 be the set of odd natural numbers.
be the set of odd natural numbers.
(a) Prove that 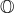 is closed under multiplication.
is closed under multiplication.
(b) Describe a notion of primes within 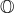 , and prove that
, and prove that 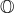 has the same unique factorization property as
has the same unique factorization property as 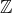 .
.
4.50 Recall that for a given integer 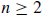 ,
,  consists of those integers that leave a remainder of 1 when divided by n. In Exercise 4.49 you proved that
consists of those integers that leave a remainder of 1 when divided by n. In Exercise 4.49 you proved that 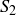 (the odd natural numbers) has the unique factorization property. In Exercise 4.48 you proved that
(the odd natural numbers) has the unique factorization property. In Exercise 4.48 you proved that 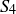 does not. This leaves an obvious question: does
does not. This leaves an obvious question: does 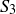 have the unique factorization property? Develop a conjecture, and then prove it!
have the unique factorization property? Develop a conjecture, and then prove it!
4.51 We could extend the definition presented in Exercise 4.20 by letting 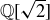 consist of all rational combinations of 1 and
consist of all rational combinations of 1 and 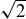 . That is,
. That is,
![]()
Determine whether “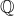 adjoined by
adjoined by 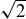 ” is closed under addition, subtraction, multiplication, and division by non-zero elements.
” is closed under addition, subtraction, multiplication, and division by non-zero elements.
4.52 Given your experience with 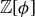 and
and 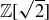 , you might be tempted to define “
, you might be tempted to define “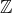 adjoin
adjoin 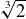 ” to be:
” to be:
![]()
(a) Show by an example that this set is not closed under multiplication.
(b) Prove that the set
![]()
is closed under multiplication.
More Exercises!
4.53 Let 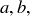 and c be real numbers. Any sum of the form
and c be real numbers. Any sum of the form
![]()
with 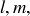 and
and 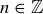 , is called an integer combination of
, is called an integer combination of 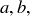 and c. Is it true that
and c. Is it true that 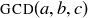 is the smallest positive integer combination of the natural numbers
is the smallest positive integer combination of the natural numbers 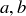 and c? Is every linear combination of a, b, and c a multiple of
and c? Is every linear combination of a, b, and c a multiple of 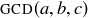 ?
?
4.54 Extend the ideas and questions in Exercise 4.53 from three terms to n terms.
4.55 Let 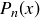 represent the set of polynomials in the variable x of degree less than or equal to n. For example,
represent the set of polynomials in the variable x of degree less than or equal to n. For example, 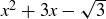 is in
is in 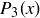 , but
, but 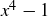 is not. Determine whether
is not. Determine whether 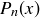 is closed under addition, subtraction, and multiplication.
is closed under addition, subtraction, and multiplication.