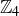 and multiplication in
and multiplication in 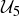 (the invertible elements modulo 5). Each of these involve four equivalence classes, but little else looks similar. In particular, the equivalence classes are different:
(the invertible elements modulo 5). Each of these involve four equivalence classes, but little else looks similar. In particular, the equivalence classes are different:Algebra and geometry are two of the oldest branches of mathematics. These two topics come together in the study of groups, algebraic objects that can be used to describe symmetry. In this chapter we introduce group theory, following a narrow and carefully chosen path toward the idea of isomorphism.
Modular arithmetic was introduced in Section 6.5 where we discussed addition, subtraction, and multiplication modulo n; in Section 6.6 we then determined that you can divide by m modulo n only when m and n are relatively prime. In this short introductory section, we examine addition in 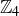 and multiplication in
and multiplication in 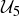 (the invertible elements modulo 5). Each of these involve four equivalence classes, but little else looks similar. In particular, the equivalence classes are different:
(the invertible elements modulo 5). Each of these involve four equivalence classes, but little else looks similar. In particular, the equivalence classes are different:
![]()
To emphasize the differences, we note that
![]()
In addition to the fact that the equivalence classes are different, a quick inspection of the addition table for 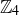 and the multiplication table for
and the multiplication table for 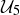 seems to indicate that addition modulo 4 and multiplication modulo 5 are not related, as seen in Figure 1.
seems to indicate that addition modulo 4 and multiplication modulo 5 are not related, as seen in Figure 1.
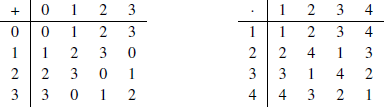
Figure 1. Addition in  and multiplication in
and multiplication in 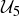 . In both tables we have dropped the equivalence class notation to avoid clutter.
. In both tables we have dropped the equivalence class notation to avoid clutter.
However, after reorganizing the order in which we list the elements of 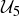 , we see that the resulting arithmetic tables look remarkably similar. As one example, look at the positions for 2 in the table for
, we see that the resulting arithmetic tables look remarkably similar. As one example, look at the positions for 2 in the table for 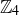 and 4 in the table for
and 4 in the table for 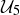 in Figure 2. The locations for
in Figure 2. The locations for 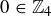 and
and 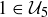 are also the exact same; the locations of
are also the exact same; the locations of 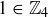 and
and 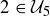 are the same; and the locations of
are the same; and the locations of 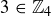 and
and 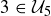 are the same. Overall, both tables follow the pattern illustrated by the card suit table on the right in Figure 2.
are the same. Overall, both tables follow the pattern illustrated by the card suit table on the right in Figure 2.

Figure 2. The tables on the left and in the middle are the same as in Figure 1, but with the elements of 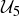 listed in a different order. The general pattern for both tables is shown by the card suits in the table on the right.
listed in a different order. The general pattern for both tables is shown by the card suits in the table on the right.
This small example hints at an idea worthy of further exploration, as it now appears that these two different mathematical objects may have some underlying structural similarity. Introducing the algebraic notion of groups and exploring how to describe this notion of similarity are the objectives of this chapter.
We have constructed tables to display the structure of modular arithmetic. In this section we develop a similar table, but in a quite different context. Let  denote a square, which in order to keep things concrete, we can think of as the
denote a square, which in order to keep things concrete, we can think of as the 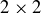 square
square
![]()
The corners of  are the four points in
are the four points in
![]()
At an informal level, a symmetry of  consists of any motion that does not change the square. In other words, if you look at the square, close your eyes while a symmetry is being performed, and then open them again, you would not see any difference. One example would be a 90
consists of any motion that does not change the square. In other words, if you look at the square, close your eyes while a symmetry is being performed, and then open them again, you would not see any difference. One example would be a 90 rotation of
rotation of  , and another would be the reflection across the diagonal, both shown in Figure 3.
, and another would be the reflection across the diagonal, both shown in Figure 3.
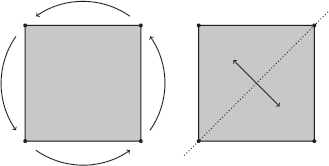
Figure 3. Two symmetries of  are the counterclockwise rotation shown on the left and a reflection across the diagonal shown on the right.
are the counterclockwise rotation shown on the left and a reflection across the diagonal shown on the right.
While this characterization has some intuitive appeal, its lack of rigor makes it fairly useless for proving theorems. Therefore we define a symmetry of  to be a function
to be a function 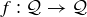 that preserves distances: if the distance from
that preserves distances: if the distance from 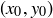 to
to 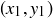 is d, then the distance from
is d, then the distance from 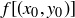 to
to 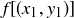 is also d.
is also d.
We would like to describe all the functions in 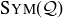 , and the following lemma is key to being able to do this.
, and the following lemma is key to being able to do this.
LEMMA 10.2. Any symmetry of  is determined by what it does to the adjacent corners
is determined by what it does to the adjacent corners 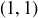 and
and 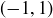 . That is, if f and
. That is, if f and 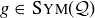 , where
, where 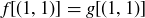 and
and 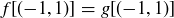 , then f and g are the same function.
, then f and g are the same function.
The idea behind our proof is that the location of any point in  is determined by its distance from two adjacent corners; and by our definition, symmetries preserve distances. Thus if we know where the corners are moved by f or g, then we can determine the image of any point under f or g.
is determined by its distance from two adjacent corners; and by our definition, symmetries preserve distances. Thus if we know where the corners are moved by f or g, then we can determine the image of any point under f or g.
PROOF. A symmetry of  has to take corners of
has to take corners of  to corners of
to corners of  because the distance between opposite corners is the maximum distance between any two points in
because the distance between opposite corners is the maximum distance between any two points in  , and symmetries preserve distances. Adjacent corners, which are pairs of corners separated by a distance of 2, must then be mapped to adjacent corners.
, and symmetries preserve distances. Adjacent corners, which are pairs of corners separated by a distance of 2, must then be mapped to adjacent corners.
Assume that 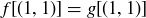 and
and 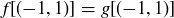 , and let
, and let 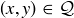 be an arbitrary point. Our goal is to show that
be an arbitrary point. Our goal is to show that 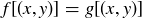 .
.
Let 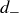 be the distance from
be the distance from 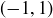 to
to 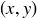 , and let
, and let 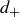 be the distance from
be the distance from 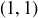 to
to  . Then
. Then  is on the circle of radius
is on the circle of radius 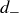 centered at
centered at 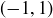 and is on the circle of radius
and is on the circle of radius 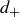 centered at
centered at 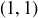 . Further,
. Further, 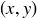 is the only point in
is the only point in  that sits on both circles; the circles may intersect twice, but only one of those intersections is contained in
that sits on both circles; the circles may intersect twice, but only one of those intersections is contained in  , as seen in Figure 4. In general, every point in
, as seen in Figure 4. In general, every point in  is determined by its distances to any two adjacent corners of
is determined by its distances to any two adjacent corners of  .
.
Since 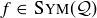 , the distance from
, the distance from 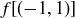 to
to 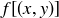 is
is 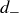 , and the distance from
, and the distance from 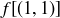 to
to 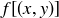 is
is 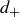 . Since
. Since 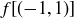 and
and 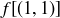 are adjacent corners of
are adjacent corners of  , it follows that there is only one possible location for
, it follows that there is only one possible location for 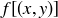 . Since the same conditions hold for
. Since the same conditions hold for 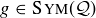 , we conclude that
, we conclude that 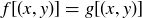 .
.

PROOF. In the proof of Lemma 10.2, we showed that the corner 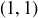 has to go to one of the four corners of
has to go to one of the four corners of  . Thus if
. Thus if 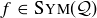 , there are four possibilities for
, there are four possibilities for 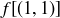 . The image of the corner
. The image of the corner 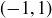 must then be a corner of
must then be a corner of  that is adjacent to
that is adjacent to 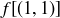 , so there are two possible locations for
, so there are two possible locations for 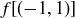 . By Lemma 10.2, once we know the location of
. By Lemma 10.2, once we know the location of 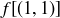 and
and 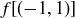 , we have determined
, we have determined 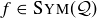 . Thus there are at most
. Thus there are at most 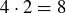 functions in the set
functions in the set 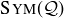 .
.

As was shown in Figure 3, a counterclockwise rotation through 90 , with the center of the rotation at
, with the center of the rotation at 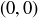 , is one example of a symmetry of
, is one example of a symmetry of  . We denote this symmetry as ρ and note that there is a simple formula for this function:
. We denote this symmetry as ρ and note that there is a simple formula for this function:
![]()
Exercise 10.1 Prove that the formula for ρ is correct by showing that it is distance-preserving and sends two adjacent corners of  to the correct locations.
to the correct locations.
Counterclockwise rotations through 180 and 270
and 270 are also symmetries of
are also symmetries of  . A counterclockwise rotation through an angle of 180
. A counterclockwise rotation through an angle of 180 can be produced by applying ρ twice. Hence we may express this symmetry as
can be produced by applying ρ twice. Hence we may express this symmetry as 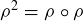 . Similarly, a counterclockwise rotation through 270
. Similarly, a counterclockwise rotation through 270 can be expressed as
can be expressed as 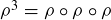 .
.
Exercise 10.2 Show that the symmetry 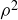 can be expressed by the formula
can be expressed by the formula
![]()
and the symmetry 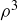 can be expressed by the formula
can be expressed by the formula
![]()
We do not need to introduce separate notation for clockwise rotations, as each clockwise rotation is equivalent to a counterclockwise rotation. For example, let ϱ denote a 90 clockwise rotation of
clockwise rotation of  . We then have
. We then have 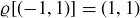 and
and 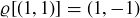 . But
. But 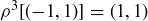 and
and 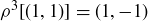 , so by Lemma 10.2,
, so by Lemma 10.2, 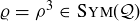 . In the study of symmetry, it is the destination, not the journey, that matters!
. In the study of symmetry, it is the destination, not the journey, that matters!
In addition to the rotations described above, there are four reflections of  . In general, a reflection in the Euclidean plane is defined via a line
. In general, a reflection in the Euclidean plane is defined via a line 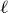 in the plane, called the axis of the reflection. Each point
in the plane, called the axis of the reflection. Each point 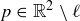 has a corresponding point
has a corresponding point 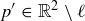 such that the segment joining p to
such that the segment joining p to 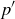 is perpendicular to
is perpendicular to 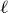 , and the distances from p to
, and the distances from p to 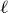 and from
and from 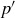 to
to 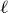 are the same. The reflection associated to the axis
are the same. The reflection associated to the axis 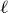 exchanges p and
exchanges p and 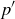 (for all such pairs), and it leaves the points on
(for all such pairs), and it leaves the points on 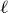 fixed.
fixed.
The set 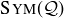 contains reflections across the x-axis, the y-axis, and across the two diagonals of
contains reflections across the x-axis, the y-axis, and across the two diagonals of  . Denote the main diagonal by
. Denote the main diagonal by
![]()
and the off-diagonal by
![]()
We name these four reflections using subscripts corresponding to their axes: the reflection across the y-axis is 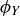 , the reflection across the x-axis is
, the reflection across the x-axis is 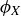 ; and the reflections across the diagonals are
; and the reflections across the diagonals are 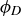 and
and 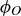 .
.
Exercise 10.3 Find formulas for 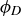 and
and 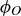 , similar to the formulas you found in Exercise 10.2.
, similar to the formulas you found in Exercise 10.2.
Finally, there is one more very important symmetry of  that is easy to miss on first examination: the “do nothing” identity function
that is easy to miss on first examination: the “do nothing” identity function 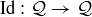 , given by
, given by 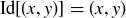 .
.
PROPOSITION 10.4. The set 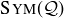 consists of the eight functions described above.
consists of the eight functions described above.
PROOF. By Corollary 10.3, we know that there are at most eight functions in 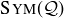 . The eight functions described above are all in
. The eight functions described above are all in 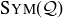 , and they are all distinct, as can be verified by applying the functions to the corners
, and they are all distinct, as can be verified by applying the functions to the corners 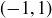 and
and 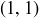 .
.

Now, knowing that we have described all the symmetries of  , we can create a table that displays the result of function composition; see Table 1. For example, the second row is labeled by ρ and the fifth column by
, we can create a table that displays the result of function composition; see Table 1. For example, the second row is labeled by ρ and the fifth column by 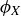 , so the entry in the table is then
, so the entry in the table is then 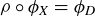 . (If you think the answer should be
. (If you think the answer should be 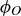 then you composed your functions in the wrong order!)
then you composed your functions in the wrong order!)
Table 1 A table describing the composition of symmetries in 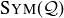 .
.
 |
Id | ρ | 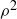 |
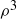 |
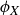 |
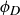 |
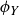 |
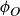 |
| Id | Id | ρ | 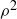 |
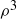 |
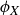 |
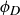 |
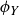 |
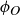 |
| ρ | ρ | 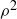 |
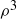 |
Id | 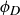 |
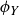 |
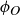 |
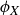 |
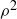 |
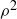 |
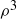 |
Id | ρ | 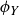 |
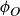 |
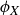 |
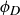 |
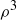 |
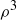 |
Id | ρ | 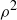 |
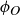 |
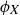 |
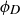 |
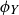 |
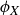 |
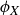 |
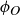 |
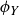 |
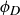 |
Id | 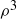 |
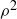 |
ρ |
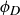 |
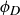 |
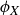 |
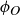 |
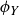 |
ρ | Id | 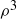 |
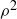 |
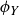 |
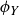 |
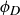 |
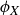 |
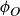 |
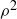 |
ρ | Id | 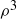 |
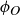 |
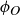 |
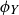 |
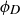 |
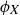 |
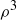 |
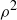 |
ρ | Id |
Exercise 10.4 Verify that the entry in Table 1 in the row corresponding to 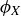 and the column corresponding to
and the column corresponding to 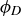 should be
should be 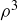 .
.
There are other  tables we already know. We could make the table describing addition modulo 8, and in Figure 4 (page 154) we displayed the table for multiplication of the eight invertible elements in
tables we already know. We could make the table describing addition modulo 8, and in Figure 4 (page 154) we displayed the table for multiplication of the eight invertible elements in 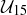 . No two of these three tables – the one for
. No two of these three tables – the one for 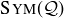 , the one for
, the one for 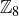 , and the one for
, and the one for 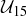 – appear to be the same. However, in the previous section we saw how simply permuting the elements can make two seemingly different tables become essentially identical. Checking that one table can or cannot be permuted to produce the other could well require all
– appear to be the same. However, in the previous section we saw how simply permuting the elements can make two seemingly different tables become essentially identical. Checking that one table can or cannot be permuted to produce the other could well require all 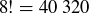 permutations of the eight elements, which is one indication that blind permutation is not a good strategy.
permutations of the eight elements, which is one indication that blind permutation is not a good strategy.
GOING BEYOND THIS BOOK. Herman Weyl’s classic book Symmetrie, translated into English as Symmetry [Wey89], provides an extended introduction to geometric symmetry by exploring the symmetry inherent in works of art and architecture, and then extending these ideas into the natural sciences.
The language and viewpoint of group theory is central in mathematics. Mathematical groups have proven to be a useful means of describing the symmetry of mathematical objects, from the sorts of geometric symmetries we have already seen, to notions of symmetry that are more subtle.
Many of the mathematical objects we have studied are groups, including those based on the associative operations from modular arithmetic.
EXAMPLE 10.6. For any  ,
, 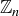 and addition modulo n forms a group
and addition modulo n forms a group 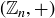 . As we saw in Sections 6.5 and 6.6, the identity element is
. As we saw in Sections 6.5 and 6.6, the identity element is 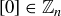 and the inverse of
and the inverse of 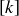 is
is 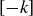 . The integers themselves,
. The integers themselves,  , also form a group under addition.
, also form a group under addition.
EXAMPLE 10.7. For any 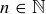 , the set
, the set 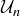 of units modulo n, with the binary operation of multiplication modulo n, forms a group
of units modulo n, with the binary operation of multiplication modulo n, forms a group 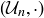 . You can see the Cayley table for
. You can see the Cayley table for 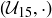 in Section 6.6.
in Section 6.6.
EXAMPLE 10.8. Finally, let’s look at an example that is not based on a number system. Let S be a non-empty set, and let 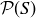 be its power set. Then the symmetric difference provides us with a binary operation
be its power set. Then the symmetric difference provides us with a binary operation 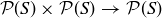 , since the symmetric difference of two subsets of S is another subset of S. You proved that the symmetric difference is associative in Exercise 3.17. The empty set is an identity element, as
, since the symmetric difference of two subsets of S is another subset of S. You proved that the symmetric difference is associative in Exercise 3.17. The empty set is an identity element, as
![]()
for all 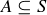 . Finally, because
. Finally, because 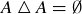 , each subset of S is its own inverse. Thus
, each subset of S is its own inverse. Thus 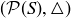 is a group.
is a group.
REMARK 10.9. The notation 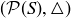 represents a group, while the similar notation
represents a group, while the similar notation 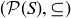 from Section 6.2 represents a partially ordered set. The context makes things clear; in particular,
from Section 6.2 represents a partially ordered set. The context makes things clear; in particular,  is a relation, not a binary operation. To simplify notation, a group
is a relation, not a binary operation. To simplify notation, a group 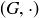 is often called G when the operation is apparent.
is often called G when the operation is apparent.
Exercise 10.5 There are many binary operations on subsets of a non-empty set S; 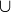 and
and  are two examples. In this exercise you will show that
are two examples. In this exercise you will show that 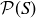 with
with 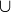 and
and 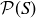 with
with  do not provide examples of groups.
do not provide examples of groups.
(a) Show that the empty set 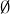 is the only element of
is the only element of 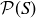 that can serve as the identity element for
that can serve as the identity element for 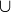 .
.
(b) Show that there are elements of 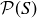 that do not have inverses with respect to
that do not have inverses with respect to 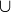 .
.
(c) Show that the full set S is the only element of 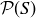 that can serve as the identity element for
that can serve as the identity element for  .
.
(d) Show that, as long as S is non-empty, there are elements of 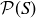 that do not have inverses with respect to
that do not have inverses with respect to  .
.
The symmetries of a square, 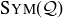 , form a group. The elements are symmetries of the square
, form a group. The elements are symmetries of the square  and the binary operation is function composition. In fact, much more is true.
and the binary operation is function composition. In fact, much more is true.
DEFINITION 10.10. Given any subset  , the set of all distance-preserving functions
, the set of all distance-preserving functions 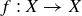 is the symmetry group of X, denoted
is the symmetry group of X, denoted 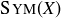 .1
.1
THEOREM 10.11. Let 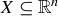 and let
and let 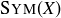 be the collection of all symmetries of X. Then
be the collection of all symmetries of X. Then 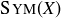 is closed under composition and the taking of inverses, and the set of symmetries along with function composition forms a group.
is closed under composition and the taking of inverses, and the set of symmetries along with function composition forms a group.
Given our work developing 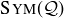 , Theorem 10.11 is not surprising, and we ask you to prove it in Exercise 10.27. You can find even more general results along these lines in [Mei08].
, Theorem 10.11 is not surprising, and we ask you to prove it in Exercise 10.27. You can find even more general results along these lines in [Mei08].
Given any two groups, we can use the Cartesian product to create a new group.
DEFINITION 10.12. In order to be very clear about the product structure, we let 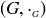 be a group where “
be a group where “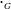 ” is the operation and
” is the operation and 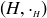 be another group with “
be another group with “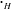 ” as the operation. The Cartesian product of these two groups has as its underlying set the Cartesian product
” as the operation. The Cartesian product of these two groups has as its underlying set the Cartesian product 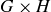 ; the binary operation for
; the binary operation for 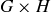 is defined component-by-component:
is defined component-by-component:
![]()
For example, consider 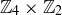 , where the two operations are addition modulo 4 and addition modulo 2. In this group, we would have
, where the two operations are addition modulo 4 and addition modulo 2. In this group, we would have
![]()
where we have included all the notation for elements of 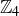 and
and 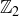 .
.
Exercise 10.6 Prove Lemma 10.13.
You may have noticed that the definition of a group demands that there is “an identity” instead of “the identity,” and that every element has “an inverse” and not necessarily a unique inverse.
PROPOSITION 10.14. Let G be a group. Then there is only one identity element in G.
PROOF. Assume to the contrary that both e and 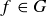 are identities for G. Then
are identities for G. Then 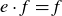 , since e is an identity element. But it is also true that
, since e is an identity element. But it is also true that 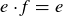 since f is an identity element. Thus
since f is an identity element. Thus 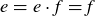 .
.

PROPOSITION 10.15. Let G be a group. Then each 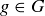 has exactly one inverse.
has exactly one inverse.
PROOF. Let g be any element of G, and assume to the contrary that both h and k are inverses of g. Thus 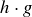 and
and 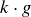 are both equal to the identity
are both equal to the identity 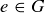 . Right multiplying both expressions by h then gives
. Right multiplying both expressions by h then gives
![]()
But 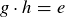 , since h is an inverse of g. So we have
, since h is an inverse of g. So we have 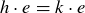 , hence
, hence 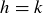 .
.

Given a group G, we can make a table that displays all of the products of elements of G; the addition and multiplication tables we made for modular arithmetic are examples. The rows and columns of the table correspond to the elements of G, and the entry in the row corresponding to g and the column corresponding to h is the product 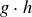 . This is exactly what we did in constructing Table 1 for
. This is exactly what we did in constructing Table 1 for 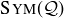 . A table displaying a group in this fashion is called a Cayley table.
. A table displaying a group in this fashion is called a Cayley table.
Exercise 10.7 Construct the Cayley table for 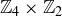 .
.
Here we introduce another group and use it to construct an additional example of a Cayley table. Let 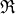 be a rectangular box with three different side lengths. It may, for example, have length
be a rectangular box with three different side lengths. It may, for example, have length 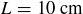 , width
, width 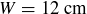 , and height
, and height 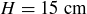 . As in the case of the square, let
. As in the case of the square, let 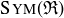 be the collection of all functions from
be the collection of all functions from 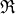 back to
back to 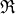 that preserve distances.
that preserve distances.
We can quickly identify a number of elements that are in 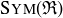 . There is an identity element. There are three reflections, where instead of reflecting across a fixed line, we reflect across a fixed plane that divides
. There is an identity element. There are three reflections, where instead of reflecting across a fixed line, we reflect across a fixed plane that divides 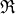 into two congruent pieces; the box and one such plane are depicted in Figure 5. And there are three 180
into two congruent pieces; the box and one such plane are depicted in Figure 5. And there are three 180 rotations where the axis of rotation is a line that passes through the center of a rectangular face of
rotations where the axis of rotation is a line that passes through the center of a rectangular face of 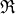 . We can denote the reflections by
. We can denote the reflections by 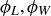 , and
, and 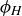 , where we let the subscript denote the orientation of the reflecting plane. For example, the reflecting plane for
, where we let the subscript denote the orientation of the reflecting plane. For example, the reflecting plane for 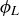 is orthogonal to the four edges corresponding to the length
is orthogonal to the four edges corresponding to the length 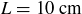 . Similarly we can denote the three rotations by
. Similarly we can denote the three rotations by 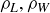 , and
, and 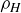 , where for example the axis of rotation for
, where for example the axis of rotation for 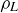 is parallel to the four edges corresponding to the length L.
is parallel to the four edges corresponding to the length L.
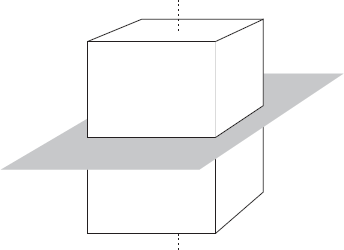
Figure 5. Two symmetries of an irregular box 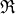 . The 180
. The 180 rotation about the “height” axis is denoted
rotation about the “height” axis is denoted 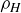 ; the reflection across the plane perpendicular to this axis is denoted
; the reflection across the plane perpendicular to this axis is denoted 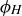 . As shown in Table 2, the composition
. As shown in Table 2, the composition 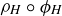 is the antipodal map we call α.
is the antipodal map we call α.
Our census of symmetries might lead you to guess that 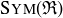 contains only these seven elements, and in order to verify this guess, you would like to have a result like Corollary 10.3. Because
contains only these seven elements, and in order to verify this guess, you would like to have a result like Corollary 10.3. Because 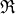 is irregular – having different length, width, and height – we get a slightly stronger result.
is irregular – having different length, width, and height – we get a slightly stronger result.
Exercise 10.8 Prove Lemma 10.16.
Since 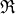 has eight corners, Lemma 10.16 immediately implies the following.
has eight corners, Lemma 10.16 immediately implies the following.
There is a small gap between the maximum number of functions in 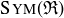 and the number we have found. There is indeed one symmetry that we have not already described.
and the number we have found. There is indeed one symmetry that we have not already described.
Exercise 10.9 Let 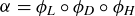 . Prove that
. Prove that 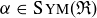 and that it is not one of the seven symmetries we previously identified.
and that it is not one of the seven symmetries we previously identified.
We now know the eight elements in 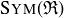 :
:
![]()
The Cayley table for this group of symmetries is shown in Table 2.
Table 2 Cayley table for the symmetries of the irregular box  .
.
| Id | 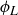 |
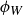 |
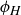 |
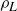 |
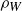 |
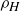 |
α | |
| Id | Id | 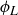 |
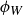 |
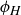 |
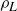 |
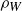 |
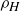 |
α |
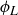 |
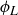 |
Id | 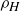 |
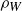 |
α | 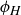 |
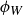 |
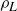 |
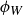 |
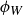 |
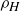 |
Id | 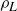 |
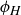 |
α | 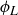 |
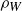 |
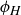 |
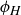 |
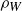 |
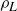 |
Id | 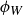 |
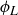 |
α | 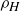 |
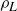 |
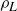 |
α | 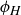 |
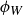 |
Id | 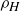 |
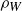 |
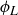 |
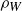 |
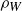 |
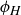 |
α | 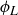 |
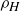 |
Id | 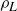 |
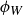 |
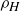 |
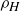 |
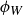 |
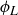 |
α | 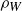 |
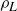 |
Id | 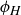 |
| α | α | 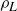 |
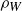 |
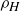 |
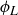 |
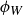 |
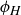 |
Id |
Exercise 10.10 Verify three entries in the Cayley table for 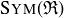 , keeping in mind that using the identity element is a lazy strategy.
, keeping in mind that using the identity element is a lazy strategy.
GOING BEYOND THIS BOOK. Arthur Cayley was an early advocate of studying groups like 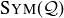 ; he frequently constructed composition tables like the one we have been exploring. For this reason such tables are often referred to as Cayley tables. Groups and Their Graphs by Grossman and Magnus [GM64] is an excellent text describing Cayley tables and geometric structures associated with groups, as is Nathan Carter’s Visual Group Theory [Car09].
; he frequently constructed composition tables like the one we have been exploring. For this reason such tables are often referred to as Cayley tables. Groups and Their Graphs by Grossman and Magnus [GM64] is an excellent text describing Cayley tables and geometric structures associated with groups, as is Nathan Carter’s Visual Group Theory [Car09].
There are a handful of elementary properties which can be used to distinguish one group from another.
10.5.1. Abelian Groups. Not all groups have commutative operations; for example, 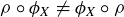 in
in 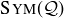 .2 However, many groups do have operations that are commutative.
.2 However, many groups do have operations that are commutative.
DEFINITION 10.18. An Abelian group is a group where the binary operation is commutative. That is, for every g and 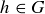 you have
you have 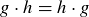 .
.
REMARK 10.19. The adjective Abelian is used, instead of commutative, in honor of the pioneering mathematics of Niels Abel. Because the term is derived from his last name, it is often capitalized.
We have already seen a number of examples of Abelian groups. Addition in 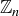 is a commutative operation, so
is a commutative operation, so 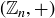 is an Abelian group. Similarly multiplication modulo n is commutative, hence
is an Abelian group. Similarly multiplication modulo n is commutative, hence 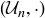 is an Abelian group. There are also infinite Abelian groups. The most accessible examples would be
is an Abelian group. There are also infinite Abelian groups. The most accessible examples would be  ,
, 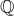 , and
, and  , with
, with 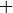 as the binary operation. The sets
as the binary operation. The sets 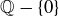 and
and 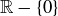 with multiplication as the binary operation form Abelian groups as well.
with multiplication as the binary operation form Abelian groups as well.
Exercise 10.11 Verify some of the claims we have just made. At a minimum you should consider the following two items.
(a) Prove that 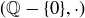 is an Abelian group.
is an Abelian group.
(b) Why is 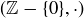 not an Abelian group?
not an Abelian group?
Exercise 10.12 Is the symmetry group of the irregular box 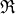 in Section 10.4 Abelian?
in Section 10.4 Abelian?
10.5.2. Cyclic Groups. In some groups, a single element can be used to express every element.
DEFINITION 10.20. If 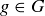 , then for
, then for  define
define
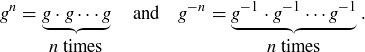
A group G is cyclic if there is some 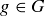 such that
such that 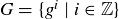 . The element g is called a cyclic generator of G.
. The element g is called a cyclic generator of G.
PROPOSITION 10.21. For any  the group
the group 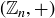 is cyclic.
is cyclic.
PROOF. The element 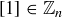 is a cyclic generator of
is a cyclic generator of 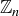 since for any
since for any 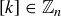
![]()
Thus every element in 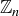 can be written as a power3 of
can be written as a power3 of 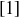 .
.

Exercise 10.13 Show that cyclic generators may not be unique. That is, find a cyclic group G and distinct elements g and 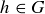 where g and h are both cyclic generators of G.
where g and h are both cyclic generators of G.
While the groups 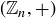 are all cyclic groups, the situation for
are all cyclic groups, the situation for 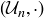 is a bit more complicated. As an example, the group
is a bit more complicated. As an example, the group 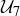 is cyclic, since
is cyclic, since 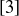 is a cyclic generator:
is a cyclic generator:
![]()
However, 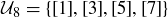 is not cyclic. To verify this, we simply check the possibilities:
is not cyclic. To verify this, we simply check the possibilities:
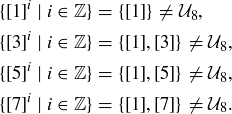
Exercise 10.14 Find two more examples like those shown above, one where 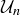 is cyclic and the other where
is cyclic and the other where 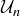 is not cyclic.
is not cyclic.
10.5.3. Order of a Group and an Element. The word “order” has two meanings in group theory, which context makes clear.
DEFINITION 10.22. If a group G has a finite number of elements, then this number is the order of G. It is denoted 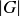 . If G is not finite, we say that G is an infinite group.
. If G is not finite, we say that G is an infinite group.
For example, 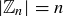 and
and 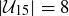 , while
, while 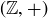 is an infinite group.
is an infinite group.
DEFINITION 10.23. If there is an  such that
such that 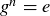 , then we say that g has finite order. In this case, the order of g is
, then we say that g has finite order. In this case, the order of g is
![]()
For example, the order of 1 in 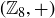 is 8, while the order of 2 in
is 8, while the order of 2 in 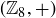 is 4, and the order of 4 in
is 4, and the order of 4 in 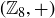 is 2. Notice that stating “
is 2. Notice that stating “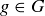 has order 1” is the same thing as saying “
has order 1” is the same thing as saying “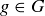 is the identity.”
is the identity.”
Exercise 10.15 Consider the Abelian group 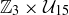 , where addition modulo 3 is the operation in the first coordinate and multiplication modulo 15 is the operation in the second coordinate.
, where addition modulo 3 is the operation in the first coordinate and multiplication modulo 15 is the operation in the second coordinate.
(a) What is the order of 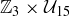 ?
?
(b) What is the order of the element 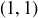 ?
?
(c) What is the order of the element 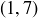 ?
?
In Section 10.1 we showed that the Cayley tables for 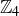 and
and 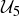 have the same underlying form, even though the names of the elements and the binary operations are different. The differences, though, are simply cosmetic and are not part of the algebraic structure of either group.
have the same underlying form, even though the names of the elements and the binary operations are different. The differences, though, are simply cosmetic and are not part of the algebraic structure of either group.
DEFINITION 10.24. Two groups G and H are isomorphic if there exists a bijection 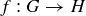 such that
such that
![]()
for each 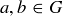 . We write
. We write 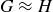 when G and H are isomorphic.
when G and H are isomorphic.
Notice that the product on the left side of the equation above comes from G while the product on the right side comes from H; the subscripts on the operations are presented here for emphasis but are unnecessary in practice. Thus the equation is essentially saying that you can apply the binary operation from G and then f, and you’ll get the same result as when you first apply f to the individual elements and then the operation from H. The phrase associated to this equation is “f respects the binary operations.” A bijection 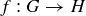 that respects the binary operations is an isomorphism.
that respects the binary operations is an isomorphism.
An isomorphism between 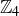 and
and 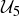 is given by the function
is given by the function
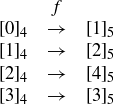
The fact that f is a bijection is clear from its description. What remains to be shown is that 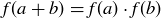 for any
for any 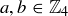 . As just one example, we can establish that
. As just one example, we can establish that
![]()
which holds because
![]()
Going through a similar computation for all sixteen possible choices of a and b is a numbing proposition. In most situations, however, you do not need to do this. For this example we can use the fact that 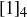 is a cyclic generator of
is a cyclic generator of 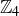 and
and 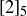 is a cyclic generator of
is a cyclic generator of 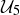 . In fact, the function f has been defined by beginning with
. In fact, the function f has been defined by beginning with 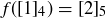 and then extending this via
and then extending this via
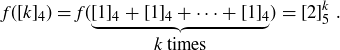
To show 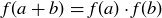 , we note that
, we note that
![]()
and
![]()
Since 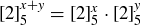 , the claim follows.
, the claim follows.
Exercise 10.16 Construct an isomorphism between 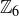 and
and 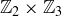 .
.
Exercise 10.17 Let 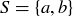 , and let
, and let 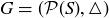 as in Example 10.8. The order of G is 4. Prove that
as in Example 10.8. The order of G is 4. Prove that 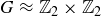 .
.
We close with a useful lemma.
PROOF. We know that  is a bijection, so it remains only to prove the fundamental identity
is a bijection, so it remains only to prove the fundamental identity
![]()
for every 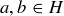 . By applying the fact that f is an isomorphism and that
. By applying the fact that f is an isomorphism and that 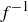 is its inverse function, we see
is its inverse function, we see
![]()
and applying 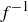 to the first and last terms then gives us
to the first and last terms then gives us 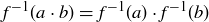 .
.

In this section we describe ways in which isomorphic groups share key properties. We begin with the following result, which follows immediately from the requirement that an isomorphism from G to H is a bijection.
PROPOSITION 10.26. If G and H are isomorphic finite groups, then 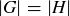 .
.
More interesting is that every isomorphism takes the identity element to the identity element.
LEMMA 10.27. Let 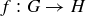 be an isomorphism, and let
be an isomorphism, and let 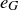 and
and 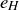 be the identity elements of G and H respectively. Then
be the identity elements of G and H respectively. Then 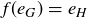 .
.
PROOF. Since 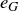 is the identity in G, we know
is the identity in G, we know 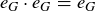 . Applying f to just the left side of this equation we get
. Applying f to just the left side of this equation we get
![]()
We also know that 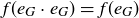 , so
, so
![]()
Multiplying both sides of this equation on the left by 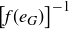 gives us
gives us
These multiplications are occurring in the group H, so
![]()
Applying this to both sides of (10.1) then gives
![]()

It is also the case that isomorphisms take inverses to inverses:
PROOF. The proof is similar to the prior argument, in that we will start by applying f to an equation involving inverses. Namely, since 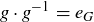 , we know:
, we know:
![]()
Thus 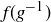 is the inverse4 of
is the inverse4 of 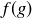 . Said symbolically, we conclude that
. Said symbolically, we conclude that 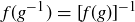 .
.

LEMMA 10.29. If 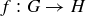 is an isomorphism, then
is an isomorphism, then 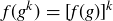 for any
for any 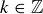 . Here we are using the convention that
. Here we are using the convention that 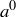 is the identity element for any group element a.
is the identity element for any group element a.
Exercise 10.18 Prove Lemma 10.29. To do this, you may want to consider three cases.
(a) Prove that, for each 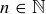 ,
, 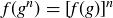 using an induction argument.
using an induction argument.
(b) Prove that 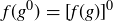 by quoting a previous result.
by quoting a previous result.
(c) Prove that, for each  ,
, 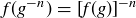 using Lemma 10.28 and an induction argument.
using Lemma 10.28 and an induction argument.
PROOF. In this argument we assume that both elements have finite order. We leave the case where they might be of infinite order as Exercise 10.41.
We first show that 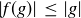 . By Lemma 10.29 we know that
. By Lemma 10.29 we know that
![]()
for any 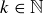 . If
. If 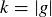 then
then 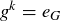 . It follows that
. It follows that 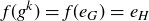 . Thus
. Thus 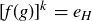 and so
and so 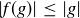 .
.
It is also true that 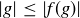 . To prove this, let
. To prove this, let 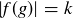 , so that
, so that 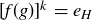 and thus
and thus 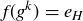 . Since f is a bijection and f takes the identity element of G to the identity element of H (by Lemma 10.27),
. Since f is a bijection and f takes the identity element of G to the identity element of H (by Lemma 10.27), 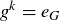 and so
and so 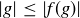 .
.
The only way we can have 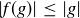 and
and 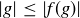 is if
is if 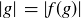 .
.

Exercise 10.19 In the proof of Theorem 10.30 we appealed to the fact that if 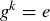 , then
, then 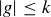 . Why can’t we claim that if
. Why can’t we claim that if 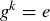 then
then 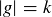 ?
?
In Exercise 10.43 we ask you to prove the following corollary.
COROLLARY 10.31. Let 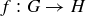 be an isomorphism. Then, for any
be an isomorphism. Then, for any 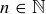 , f induces a bijection between the elements of order n in G and the elements of order n in H.
, f induces a bijection between the elements of order n in G and the elements of order n in H.
PROOF. It suffices to prove that G being cyclic implies H is cyclic, as that argument can then be used with 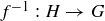 to show that when H is cyclic, G must be cyclic as well.
to show that when H is cyclic, G must be cyclic as well.
Let x be a cyclic generator of G. Given any 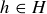 there is a
there is a 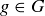 such that
such that 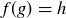 , and so there must be an n such that
, and so there must be an n such that 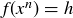 . But
. But 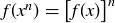 by Lemma 10.29. Thus given any
by Lemma 10.29. Thus given any 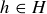 there is an n such that
there is an n such that 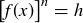 , and so
, and so 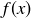 is a cyclic generator of H.
is a cyclic generator of H.

Exercise 10.20 Prove Theorem 10.33.
Discovering that two groups are isomorphic usually entails understanding how those groups are connected to each other, with a benefit often being that additional insights are gained for at least one if not both of the groups. Proving that two groups are not isomorphic also involves discovery, this time of group-theoretic properties that are not the same for the two groups. In this section we provide some examples to help illustrate these ideas.
In Exercise 10.16 you showed that 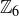 is isomorphic to
is isomorphic to 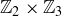 . The key is to realize that
. The key is to realize that 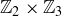 is also a cyclic group, with
is also a cyclic group, with 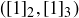 being one example of a cyclic generator. From this it is easy to see that the map sending
being one example of a cyclic generator. From this it is easy to see that the map sending 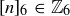 to
to
![]()
is an isomorphism.
The following result generalizes Exercise 10.17.
PROPOSITION 10.34. Let 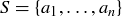 be a finite set with n elements, and let
be a finite set with n elements, and let 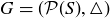 . Then
. Then
![]()
PROOF. For convenience and following standard conventions, we denote
![]()
by 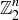 . An arbitrary element of
. An arbitrary element of 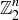 can be written in coordinate notation as
can be written in coordinate notation as  with each
with each 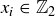 . Our putative isomorphism from
. Our putative isomorphism from 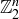 to G is then defined by
to G is then defined by
![]()
If  and
and  are distinct elements of
are distinct elements of 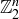 , then they must differ in at least one coordinate, hence
, then they must differ in at least one coordinate, hence  and
and  are distinct subsets of S. Thus f is injective. To show that f is surjective, note that, given any subset
are distinct subsets of S. Thus f is injective. To show that f is surjective, note that, given any subset 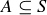 , the element
, the element 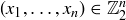 defined by
defined by
![]()
is mapped to A by f.
Finally, we need to establish that f respects the binary operations. First note that if  , then
, then 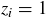 if and only if exactly one of
if and only if exactly one of 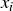 and
and 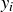 is 1 (and the other is 0). So
is 1 (and the other is 0). So
![]()
Let the images of  and
and  be
be
![]()
and
![]()
Then
![]()
Since this is the exact same description given for 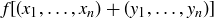 , we see that f respects the binary operations.
, we see that f respects the binary operations.

These two examples give some suggestions as to how you might create an isomorphism between two groups. Establishing that two groups are not isomorphic requires finding distinguishing properties of the groups. For example, 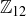 and
and 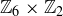 are both Abelian groups of order 12, but they are not isomorphic. Theorem 10.32 tells us that the property of being cyclic is preserved by isomorphisms, and
are both Abelian groups of order 12, but they are not isomorphic. Theorem 10.32 tells us that the property of being cyclic is preserved by isomorphisms, and 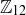 is cyclic while
is cyclic while 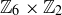 is not.
is not.
Let 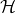 be a regular hexagon and let
be a regular hexagon and let 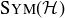 be its symmetry group. Like the symmetry group of a square discussed earlier in this chapter, any symmetry of
be its symmetry group. Like the symmetry group of a square discussed earlier in this chapter, any symmetry of 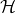 is determined by what it does to adjacent corners. An analysis almost exactly like that building up to Proposition 10.4 shows that
is determined by what it does to adjacent corners. An analysis almost exactly like that building up to Proposition 10.4 shows that 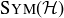 has twelve elements: six reflections, five non-trivial rotations, and the identity element.
has twelve elements: six reflections, five non-trivial rotations, and the identity element.
Exercise 10.21 Find two elements of 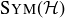 that do not commute.
that do not commute.
Like 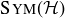 , the groups
, the groups 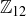 and
and 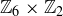 have order 12. But
have order 12. But 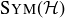 cannot be isomorphic to
cannot be isomorphic to 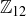 or
or 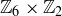 or any other Abelian group of order 12, because you have just shown that
or any other Abelian group of order 12, because you have just shown that 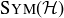 is not Abelian, and in Exercise 10.20 you proved that isomorphic groups are either both Abelian or both non-Abelian.
is not Abelian, and in Exercise 10.20 you proved that isomorphic groups are either both Abelian or both non-Abelian.
Thus the properties of being cyclic and Abelian are sufficient to distinguish these three groups of order 12.
REMARK 10.35. If you enjoyed seeing how to distinguish these three groups of order 12, you should tackle Project 11.11, where you will identify and distinguish all of the groups of order 8.
GOING BEYOND THIS BOOK. Marcia Ascher’s book Ethnomathematics [Asc91] contains two chapters that describe ways that groups arise in the context of anthropology. One is on “The logic of kin relations” and the other is “Symmetric strip patterns.” These chapters, and the whole book in fact, are fascinating.
Exercises you can work on after Sections 10.1 and 10.2
10.22 Lemma 10.2 states that symmetries in 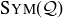 are determined by what they do to the points
are determined by what they do to the points 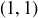 and
and 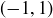 . Prove or disprove the following variations on the statement of this lemma.
. Prove or disprove the following variations on the statement of this lemma.
(a) Any symmetry of  is determined by what it does to the points
is determined by what it does to the points 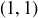 and
and 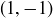 .
.
(b) Any symmetry of  is determined by what it does to the points
is determined by what it does to the points 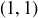 and
and 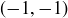 .
.
(c) Any symmetry of  is determined by what it does to the points
is determined by what it does to the points 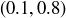 and
and 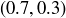 .
.
10.23 In Section 10.2 we described the eight symmetries of a square. The rotation ρ was shown to be given by the formula 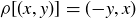 . If you are familiar with matrix multiplication you could also describe ρ as being given by the matrix
. If you are familiar with matrix multiplication you could also describe ρ as being given by the matrix
![]()
and the function is then given by matrix multiplication
![]()
Determine the matrices associated with the other seven symmetries, and verify in at least two interesting cases that matrix multiplication yields the same results as function composition.
10.24 Let Δ be an equilateral triangle. The goal of this exercise is to show that 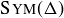 contains six functions.
contains six functions.
(a) Prove there are at most six symmetries of Δ.
(b) Find three reflections in 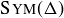 and name them.
and name them.
(c) Find two rotations in 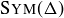 and name them.
and name them.
(d) Show that you now have a collection of six distinct symmetries of Δ, meaning that you have identified all of the elements in 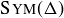 .
.
10.25 Let  be a regular octagon, and consider the group of symmetries
be a regular octagon, and consider the group of symmetries 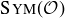 .
.
(a) Describe all the elements of 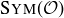 , and prove that your list is complete.
, and prove that your list is complete.
(b) Let ρ be a counterclockwise rotation through 45 and let f be any reflection in
and let f be any reflection in 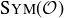 . Prove that
. Prove that 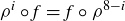 for all i.
for all i.
Exercises you can work on after Sections 10.3 and 10.4
10.26 In this problem you will describe the symmetries of a cube 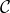 .
.
(a) Prove that a symmetry of 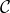 is determined by what it does to any face of
is determined by what it does to any face of 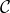 .
.
(b) Prove that 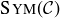 consists of 48 functions.
consists of 48 functions.
(c) Describe the 48 symmetries of  .
.
10.27 Prove Theorem 10.11.
10.28 There is a group with only one element, called the trivial group. Describe the structure of the trivial group, and verify that it is indeed a group.
10.29 Let 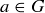 be an element of a group G, and let
be an element of a group G, and let 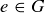 be the identity element. Show that if there are elements g and h in G such that
be the identity element. Show that if there are elements g and h in G such that
![]()
then 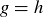 . Thus there is no reason to distinguish “left inverses” and “right inverses.”
. Thus there is no reason to distinguish “left inverses” and “right inverses.”
10.30 Create the Cayley table for 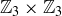 .
.
10.31 Create the Cayley table for 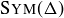 , described in Exercise 10.24.
, described in Exercise 10.24.
10.32 Let G be any group. Prove that every element of G shows up once and only once in each row and each column of its Cayley table.
Exercises you can work on after Section 10.5
(a) Prove that if G and H are both Abelian, then their Cartesian product 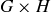 is also Abelian.
is also Abelian.
(b) Prove the converse: If 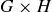 is Abelian, then G and H are Abelian.
is Abelian, then G and H are Abelian.
10.34 Prove that 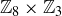 is a cyclic group.
is a cyclic group.
10.35 Prove or disprove: 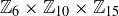 is a cyclic group.
is a cyclic group.
(a) What is 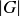 ?
?
(b) Find an element in G whose order is 10.
(c) Find an element in G whose order is 20.
(d) Prove that G is not cyclic.
10.37 Let G be an Abelian group of even order. Prove that some non-identity element must be its own inverse. That is, there is some 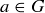 with
with 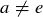 and
and 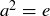 .
.
10.38 Here are some examples where 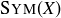 is infinite.
is infinite.
(a) Let X be the set of integer points inside of  . Prove that
. Prove that 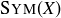 is a countably infinite group.
is a countably infinite group.
(b) Is 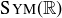 countable or uncountable?
countable or uncountable?
(c) Let 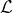 be the integer grid in
be the integer grid in 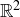 , that is,
, that is,
![]()
Is 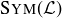 countable or uncountable?
countable or uncountable?
This problem continues with Exercise 10.50.
10.39 Let Δ be a regular tetrahedron – one where all the edges have the same length – with vertices 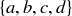 , as shown in Figure 6. The line segments joining vertices are referred to as the edges of Δ; the four triangles associated to triples of vertices are the faces of Δ.
, as shown in Figure 6. The line segments joining vertices are referred to as the edges of Δ; the four triangles associated to triples of vertices are the faces of Δ.
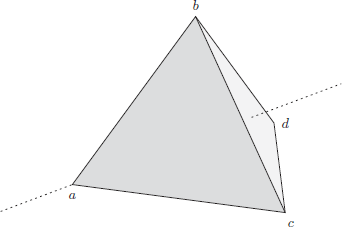
Figure 6. A 120 rotation around the axis passing through vertex a produces a symmetry of the regular tetrahedron.
rotation around the axis passing through vertex a produces a symmetry of the regular tetrahedron.
Let 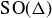 be all of the rotational symmetries of Δ that you can perform on a solid, physical model of Δ.5 For example, you can hold the vertex a fixed and rotate the face of Δ opposite of a by 120
be all of the rotational symmetries of Δ that you can perform on a solid, physical model of Δ.5 For example, you can hold the vertex a fixed and rotate the face of Δ opposite of a by 120 , which has the effect of permuting the vertices b, c, and d.
, which has the effect of permuting the vertices b, c, and d.
(a) Prove that 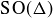 contains at most 12 elements.
contains at most 12 elements.
(b) Find 12 distinct elements in 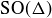 , thus proving that
, thus proving that 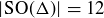 .
.
(c) Create the Cayley table for 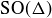 , and highlight entries that demonstrate that
, and highlight entries that demonstrate that 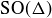 is not Abelian.
is not Abelian.
Exercises you can work on after Sections 10.6–10.8
![]()
10.41 Assume that 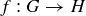 is an isomorphism. Prove that if
is an isomorphism. Prove that if 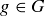 is an element of infinite order, then so is
is an element of infinite order, then so is 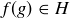 .
.
10.42 Let Δ be a tetrahedron where two non-intersecting edges of Δ have length 2, while the remaining four edges have length 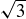 . (See Figure 7.) If you would like a particular set of coordinates for the vertices, use
. (See Figure 7.) If you would like a particular set of coordinates for the vertices, use 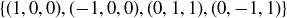 . Since this tetrahedron was pointed out to us by Jon McCammond, we will refer to it as McCammond’s Tetrahedron. Prove that the symmetry group of McCammond’s Tetrahedron is isomorphic to the symmetry group of the square
. Since this tetrahedron was pointed out to us by Jon McCammond, we will refer to it as McCammond’s Tetrahedron. Prove that the symmetry group of McCammond’s Tetrahedron is isomorphic to the symmetry group of the square  .
.
10.43 Prove Corollary 10.31.
10.44 Use Corollary 10.31 to prove that 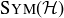 and
and 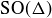 – the symmetries of a regular hexagon and the rotations of a regular tetrahedron – are not isomorphic.
– the symmetries of a regular hexagon and the rotations of a regular tetrahedron – are not isomorphic.
10.45 Let 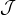 be the toy jack shown in Figure 8.
be the toy jack shown in Figure 8.
(a) Prove that the order of 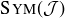 is 16.
is 16.
(b) The symmetry group of a toy jack and the symmetry group of an octagon are both non-Abelian groups of order 16. Prove that these two groups are not isomorphic.
More Exercises!
10.46 Let 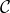 be the circle
be the circle 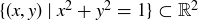 . Prove that
. Prove that 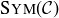 is an uncountable, non-Abelian group.
is an uncountable, non-Abelian group.
10.47 Prove that “isomorphic” is an equivalence relation on the set of all groups.
10.48 There are five Abelian groups of order 16. List them, and prove that no two groups on your list are isomorphic.
10.49 In this problem we focus on the collection of all finite groups.
(a) For a fixed  , prove there can be only finitely many groups of order n.
, prove there can be only finitely many groups of order n.
(b) Prove that the collection of all finite groups is countably infinite.
10.50 In this problem we explore elements of the groups introduced in Exercise 10.38.
(a) Let X be the set of integer points inside of  . Prove that if
. Prove that if 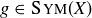 , then
, then 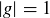 or 2, or g has infinite order.
or 2, or g has infinite order.
(b) Let 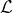 be the integer grid in
be the integer grid in 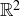 , that is,
, that is,
![]()
What can you say about the orders of the elements in 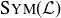 ?
?
1 Distance-preserving functions 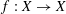 are called isometries of X, and in this terminology we are defining the isometry group of X. That said, there is a lot of terminology to absorb in this chapter, so we will not use the term isometry.
are called isometries of X, and in this terminology we are defining the isometry group of X. That said, there is a lot of terminology to absorb in this chapter, so we will not use the term isometry.
2 If you have studied matrix arithmetic, you have encountered non-commutative multiplication when you learned how to multiply square matrices (and you might be interested in Exercise 10.23 in the end-of-chapter exercises).
3 It seems odd to say “product” or “power” when the binary operation is addition, but this is the accepted way to phrase such statements.
4 If you are concerned that we might have found only the “right inverse,” congratulations! But see Exercise 10.29.
5 The name we have chosen for this group, 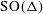 , references a general class of groups including the “rotation group” that is commonly denoted
, references a general class of groups including the “rotation group” that is commonly denoted 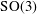 . The group
. The group 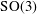 is the group of all rotations in
is the group of all rotations in 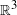 that fix the origin.
that fix the origin.