
E pur si muove!
(And nonetheless it moves!)
Giordano Bruno’s last cry from the burning stake, 16th February, 1600.50
THE classification of history into ancient, mediaeval and modern is but a symptom of the white man’s arrogance; for while Europe was suffering the imbecility of the Dark Ages, the rest of the world went on living. Yet in the struggles of oriental science we find the same type of patterns and tendencies as in Europe, though not necessarily at corresponding times. Just as the torch of Alexandria was extinguished by militaristic Rome, so the intellectual life of Babylon was wiped out by the militaristic Assyrians, and the golden age of Muslim science was stifled by the militaristic Turks; in India and China the story is similar. And again; we find the confrontations between religion and science. In the vein of Tertullian, the Muslim philosopher al-Ghazzali (1058-1111) wrote that scientific studies shake men’s faith in God and undermine religion, and that they lead to loss of belief in the origin of the world and the Creator;51 and several Muslim fanatics, like their Christian counterparts, proved their piety by burning libraries. In China, too, the emperor Tsin Shi Hwang-di (3rd century B.C.) was warned by his advisors of the idling scholars whose influence was founded on books; and he ordered all literature in China burned, excepting only books on medicine, husbandry and divination, and those in the hands of the seventy official scholars. And again, we find the quaint mixture of mathematics and mumbo-jumbo that can be found in the mysticism of the Pythagoreans. For example, the able Chinese mathematician Sun-Tsu (probably 1st century A.D.) wrote a textbook containing, for the most part, sound mathematics; but it also contains this problem:
A pregnant woman, who is 29 years of age, is expected to give birth to a child in the 9th month of the year. Which shall be her child, a son or a daughter?
The solution is truly Pythagorean:
Take 49; add the month of her child-bearing; subtract her age. From what remains, subtract the heaven 1, subtract the earth 2, subtract the man 3, subtract the four seasons 4, subtract the five elements 5, subtract the six laws 6, subtract the seven stars 7, subtract the eight winds 8, subtract the nine provinces 9. If the remainder be odd, the child shall be a son; and if even, a daughter.
Note that the remainder is negative, so that a Chinese student of the 1st century would be stunned, because he could scarcely know the concept of a negative number, let alone its parity. To say very impressively nothing at all is the secret of all such oracles; it is also the secret of computerized astrology and the trumpets of Madison Avenue.
* * *
AS we have seen, European mathematics was far behind that of the Muslim world. Yet as the Middle Ages ended, Europe was catching up, and by the 17th century it was so far ahead that the rest of the world never caught up with it again, and to Europe we now return.
The end of the Middle Ages was heralded by three events, all of which took part in the latter half of the 15th century.
First, in 1453 the Turks captured Constantinople. The significance of this event is not that they grabbed and sacked a city ruled by those who had grabbed and sacked it before them, but that they had breached its walls with guns. The era of gun powder mean the end of the feudal fiefs who often defied their kings behind the walls of their castles. The local tyranny of the feudal aristocracy was replaced by the centralized tyranny of the divine kings and emperors. And the absolute power of the Church was broken; where the Church had patronized the nominal ruler, the central and powerful ruler was now patronizing the Church.

Christopher Columbus (1451–1506)

Vasco da Gama (1469–1525)

Ferdinand Magellan (1480–1521)
Second, the turn of the fifteenth century saw the great discoveries of the rest of the world. Christopher Columbus discovered America; Vasco da Gama rounded the Cape of Good Hope (1499) on his voyage to India; and Ferdinand Magellan’s flotilla circumnavigated the globe (1519-1522). The far-reaching consequences of these events included the need for better clocks, better astronomy, better trigonometry, and the resulting stimulation of the exact sciences. It is probably not accidental that the mathematicians appearing on the scene come increasingly from England, France and Holland, countries that suddenly found themselves in the center of the maritime world, and where (unlike Spain and Portugal) the influence of the Church was rapidly waning.
Third, and perhaps most important, the 15th century saw the revolution in the dissemination of information brought about by printing from movable and reusable type. This had been used in China since the 9th century (mostly for printing charms), but in the 15th century several Europeans started experimenting with it, and though no single man is usually responsible for an epoch-making invention of this kind, credit is traditionally given to Johannes Gutenberg of Mainz, who printed an edition of the Bible by this method in 1456. Until then, manuscripts were usually copied by hand, as a rule by monks in monasteries, one of them dictating from a master copy to an assembly of scribes, or by the painstaking process of carving a wooden block for an entire page to be printed.
More than anything else, the invention of the letterpress broke the Church’s monopoly of learning. Henceforth, books were available to ever wider sections of the population, and the subversive little invention eventually tumbled the thrones of Europe’s tyrants. (No tyrants were ever more acutely aware of this than the Jenghis Khans in the Kremlin: In the USSR, not only presses, but even little mimeographs are jealously guarded by a multiple net of security regulations such as civilized countries do not even use for presses printing currency.) Like other books, mathematical textbooks could now be mass produced. It was a sign of the times that mathematical textbooks were no longer published only in Latin, the language of the educated, but also in the national languages. Advanced mathematics continued to be written in Latin until the beginning of the 19th century, but textbooks of elementary mathematics began to appear in English, French, German, Italian, Dutch and other languages (some of them even before the invention of the letterpress).
The invention of the letterpress affected mathematical works in yet another way. In the late Middle Ages, mathematicians would meet in challenge disputes, often for considerable sums of money, in which mathematicians posed problems to each other. University positions were subject to renewal, and the university authorities would be influenced by the outcome of these contests. In 1535, for example, a contest between Antonio Fiore and Niccolo Tartaglia in Venice involved 30 banquets that the loser was to give for the winner and his friends. Naturally, these mathematical prizefighters jealously guarded the secrets of their trade. The contest above, for example, centered around the equation
![]()
Tartaglia knew how to solve it and confided the secret to the colorful founder of probability theory Gerolamo Cardano (1501-1576), but swore him to secrecy, and there was much intrigue, polemics and unpleasantness when Cardano, who later found the solution of the general cubic equation, published his results, even though he gave credit to Tartaglia (who had himself obtained the trick through an intermediary from Scipione del Ferro of Bologna, the latter having discovered it some time between 1500 and 1515).52 The letterpress changed all this; for mathematicians found a surer road to renown than prizefighting: Publish or perish was the name of the new game.
* * *
THE story of π during this age of the Renaissance was mainly one of ever more accurate numerical values of the constant; the theory was still essentially based on the Archimedean polygons. Apart from the Hindu-Arabic numerals and decimal fractions that had filtered from the Arabs into Europe during the Middle Ages, there were now two new instruments for numerical calculations at the disposal of the circle squareres: trigonometric functions and logarithms.

Nicolas Copernicus (1473–1543)

Tycho Brahe (1546–1601)

Johann Kepler (1571–1630)
Trigonometric functions (in one form or another) had already been used by Ptolemy and the other scientists at the University of Alexandria, but accurate tables now became available through the works of the Renaissance astronomers, foremost among whom were Nicolas Copernicus (1473-1543) and Johann Kepler (1571-1630). Both these trailblaizing astronomers are connected with tables of trigonometric functions. Copernicus introduced the secant into trigonometry and was apparently the first to calculate a table; Kepler popularized, refined and explained Napier’s logarithms of trigonometric functions. From 1600 to 1612 Kepler worked at the Royal Castle of Prague for the king of Bohemia and emperor of Austria Rudolf II of Hapsburg, where he succeeded the Danish astronomer Tycho Brahe. Rudolf II surrounded himself with astrologers and alchemists, whom he hired to find the Stone of the Wise, by whose magic one could make gold. Kepler was not the last scientist hired to produce gold, and who produced something of more lasting value instead; the tradition continues among the scientists of our day.
Logarithms were discovered at the beginning of the 17th century indpendently by Jobst Bürgi, a Swiss clockmaker working in Prague, and John Napier, a Scottish nobleman and amateur mathematician, whose many activities included the publication of The Plaine Discouery of the whole Reuelation of Saint John (in which he argued that the Pope was the Anti-Christ), contracting for the discovery of treasure, devising warlike machines for the defense of Britain against Philip of Spain, promoting astrology, and recommending salt as a fertilizer. Napier’s book Mirifici logarithmorum canonis descriptio (A Description of the Wonderful Rule of Logarithms) was published earlier (1614) than Bürgi’s (1620), and he is generally regarded as the discoverer of logarithms.
These developments, naturally, facilitated the calculation of π by the Archimedean method or its modifications, and accuracies far beyond any possible practical use were obtained. We shall come back to this point in the next chapter, but first we shall examine the theoretical progress made during this period. The main achievement was that of another amateur mathematician, François Viète, Seigneur de la Bigotière (1540-1603). He was a lawyer by profession and rose to the position of councillor of the Parlement of Brittany, until forced to flee during the persecution of the Huguenots. The next six years or so during which he was out of favor, he spent largely on mathematics. With the accession of Henry IV, a former Huguenot, Viète was restored to office, becoming Master of Requests (1580) and a Royal Privy Councillor (1589). He endeared himself to the king by breaking the Spanish code made up of some 500 cyphers, thus enabling the French to read all secret enemy dispatches. Thereupon the Spanish, with singular one-track-mindedness, accused him of being in league with the devil.
Viète made important contributions to arithmetic, algebra, trigonometry and geometry. He also introduced a number of new words into mathematical terminology, some of which, such as negative and coefficient, have survived. His attack on π, though still proceeding along general Archimedean lines, started with a square rather than a hexagon, and resulted in the first analytical expression giving π as an infinite sequence of algebraic operations.
His procedure consisted (essentially) of relating the area of an n-sided polygon to that of a 2n-sided polygon (see figure here). The area of an n-sided polygon is

Similarly,
![]()
so that from (2) and (3),
![]()
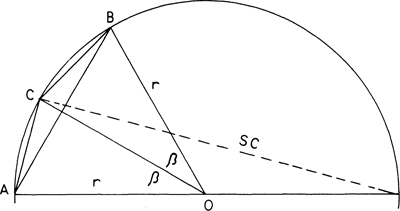
Viète’s method of finding π.
and if we double the sides of the polygon again, we have
![]()
Continuing like this k times, we obtain
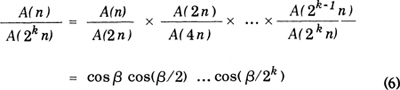
But if k tends to infinity, the area of a regular polygon with 2k sides is indistinguishable from that of a circle, so that
![]()
Substituting (7) and (2) in (6), we have
![]()
Viète chose a square to start with, so that n = 4, β = 45°, cos β = sin β = √½.
Also, each of the cosine factors in (8) is expressible in terms of the preceding factor through the half-angle formula
![]()
so that we finally have
![]()
and this is Viète’s expression, published in 1593 in his Variorum de rebus mathematicis responsorum liber VIII (Various mathematical problems, vol. 8). Actually, his derivation used the supplementary chord of a polygon, that is, the chord joining a point of a polygon on a circle to the other end of the diameter, marked SC in the figure here. (Note that this is the supplementary chord of a 2n-sided, not of an n-sided polygon.) Viète showed that the supplementary chord of n-sided polygon is to the diameter as the area of the polygon with n sides is to that of the polygon with 2n sides. But since that ratio is simply cos β , the derivation given above conveys the essence of Viète’s procedure.
Viète’s result represents one of the milestones in the history of π, and it is also the high point of renaissance mathematics connected with π; therefore it deserves a few comments.
First, we note that Viète was still imprisoned by the idea of the Archimedean polygon; he is, in fact, one of the last men to use a polygon in furthering the theory of calculating π (the others were Descartes, Snellius and Huygens, as we shall see in Chapter 11), though he was far from last in using it for numerical evaluation.
Second, Viète was the first in history to represent π by an analytical expression of an infinite sequence of algebraic operations. (As a matter of fact, he was also the first to use the term “analytical” in mathematical terminology, and the term has survived.) The idea of continuing certain operations ad infinitum was of course much older. Archimedes had used it, and before him Antiphon expressed the principle of exhaustion, as we have seen here. Viète was familiar with the Greek classics, and he refers to Antiphon in his treatment; his approach executed Antiphon’s idea mathematically. However, there is a vast difference between expressing an idea qualitatively and giving quantitative instructions how to execute it, and Viète was the first to achieve this. Viète’s expression, in fact, is the first known use of an infinite product, whether connected with π or not.
Third, Viète was a typical child of the Renaissance in that he freeley mixed the methods of classical Greek geometry with the new Arabic art of algebra and trigonometry. The idea of substitution is algebraic, and the square roots in his expression come from the trigonometric half-angle formula for the cosine, but otherwise his treatment is entirely Greek, based on considerations of area ratios involving the supplementary chord. Had he tried to express the mouthful ratio of the supplementary chord to the diameter trigonometrically, he would have found that it equals cos β , a much more easily manipulated quantity. He would then have obtained our formula (8) above, and a man of Viète’s stature could hardly have overlooked that by expressing β in radian measure and setting θ = 2π/n, he would have obtained the formula
![]()
which Leonard Euler obtained in a quite different way almost 200 years later. Viète’s result (10) is a special case of (11) for θ = π/2.
Fourth, Viète did not yet know the concept of convergence and did not worry whether his infinite sequence of operations would “blow up” or not. We need not worry either, because as far as the formula for π is concerned, it is sufficient to take k arbitrarily large, but finite. However, if you are a friend of mathematical rigor and this kind of “sloppy engineering mathematics” disgusts you, rest assured: The convergence of Viète’s formula was proved by F. Rudio in 1891.53
Fifth, it should be noted that Viète’s formula is of almost no use for numerical calculations of π; the square roots are much too cumbersome, and the convergence is slow. Viète himself did not use it for his calculation correct to 9 decimal places; he used the Archimedean method without substantial modification by taking a polygon of 393,216 sides (the number is obtained by 16 successive doublings of the original hexagon). This enabled him to reduce the Archimedean bounds to
![]()
but this is only a minor success compared with the formula (10) which he derived. In the vast majority of practical applications, π = 22/7 is good enough, and to obtain better and better approximations is only a matter of drudgery. In contrast, Viète’s formula (10) is an entirely new formulation, one that can be manipulated and investigated. Indeed, if no better expressions had been discovered since then, this one could have served for investigating some of the properties of π that no number of decimal places can reveal.
Finally, the fact that Viète introduced a number of mathematical terms that have survived to the present is a point of interest. Terminology and symbolism cannot, by themselves, solve anything; but if not conveniently chosen, they can spoil a lot. The long sentence for the circle ratio (here) could not be squared or subjected to other mathematical operations as the symbol π can, and Viète’s example shows that one can miss an important turning to a wide new field by using Greek geometry instead of the concise symbolism of trigonometry. In Viète’s time, mathematical notation was still a long way from what it is now. The operator symbols +, –, = had only very recently been introduced, and algebra often described an equation in words rather than symbols. The unknown quantity (our “x”) had a strange name. The Italians, through whom algebra mostly came to Europe from the Arabs, called it cosa, the “thing” (the same word as the Mafia uses in cosa nostra), and the word went into other languages, e.g., in German it became die Coss, and in Latin it became numerus cossicus; in English, algebra was known as the Cossike arte. Robert Recorde (1510-1558) tells us that in nombers Cossike, all nombers haue not rootes; but soche only emongest simple cossike nombers are rooted, whose nomber hath a roote, agreable to the figure of his denomination.
There are other quaint little tid-bits in mathematical terminology. For example, the origin of the words tangent and secant are clear enough, but where does sine come from? It comes from a translator’s error in the Toledo translation center (here). Arabic script, like Hebrew script, consists of consonants, with the vowels punctuated underneath, and the latter are often omitted. The sine, which one would expect to be called “half-chord” in analogy with the secant and tangent, was given a name by the Hindus, which the Arabs took over, and which they spelled by the consonants jb. When Robert of Chester, one of the Toledo translators, translated al-Khowarizmi’s Algebra from Arabic into Latin in 1145, he encountered this word without knowing its Hindu origin; supplying the missing vowels, he found the Arabic word for bay or inlet, and the Latin for bay, inlet or cavity is sinus.
But back to π. The Renaissance was a golden age of the amateur mathematician. Viète was Royal Privy Councillor, Bürgi a clockmaker, Napier a landowner and theologist, Cardano a physician. Two more amateur mathematicians of the Renaissance deserve mention. Their mathematical achievements were not very impressive, but they were great artists: Albrecht Dürer (1471-1528) and Leonardo da Vinci (1452-1519). Dürer studied geometry, or what today would more closely be described as descriptive geometry, because as an artist he was interested in perspective and the proportions of the human form. Leonardo da Vinci was interested in mathematics for the simple reason that he was interested in everything; or at least so one would judge on reading the copious material which he entrusted to his notebooks and other manuscripts. Dürer, in his Underweysung der messung mit dem zirckel und richtsheyt (Instruction for mensuration with compasses and straightedge), 1525, uses the Babylonian value π = 3 1/8. Leonardo’s voluminous manuscripts contain at least two entries directly connected with the squaring of the circle. One is the construction by rearrangement of circular segments which has already been discussed (here); the other is an original idea of how to square the circle: Take a wheel (cylinder) whose thickness (height) equals half the radius of the wheel; roll it one revolution, and the area of the rectangular track it leaves is equal to the area of the circle of the wheel (base of the cylinder). Leonardo’s words are La intera revolutione della rota quala la grossezza sia equale al suo semidiamitro lasscia di se vesstigio equale alla quadratura del suo cierchio. The “semidiamitro” is evidently an oversight, for half the radius, not half the diameter, must be used; in that case the track left by the wheel is indeed 2πr × ½r = πr2.
Viète’s result of finding π accurately to 9 decimal digits was preceded and followed by similar calculations, all based on the Archimedean polygons; they did not bring anything significantly new, and we delay the discussion of these indefatigable digit hunters to the next chapter; in the meantime we pause to note some interesting oddities of the history of π in the Renaissance.
There is, for example, the earliest of my several competitors, a French scholar by the name of Johannes Buteo (1492-1572); in 1559 he published a book De quadratura circuli, which seems to be the first book that amounts to a history of π and related problems. Buteo, unlike many of his contemporaries, was thoroughly familiar with the Archimedean method, and gives a survey of the methods used in antiquity and the Middle Ages.
Then there is Joseph Scaliger (1540-1609; not to be confused with Julius Scaliger, 1484-1558, who first published a book abusing and ridiculing Gerolamo Cardano, and mistakenly believing it had caused him to die, followed it by a grandiose and heartrending eulogy, heaping lavish praise on the supposed victim54). Joseph Scaliger was a famous philologist at the University of Leyden, who in 1594 published a work Cyclometria elementa in which he purports to demonstrate that already the perimeter of a 12-sided polygon is greater than the circumference of the circumscribed circle, so that it is to no purpose to use polygons with more than 12 sides for the calculation of π. It was possible, maintained Scaliger, for something to be geometrically true, but arithmetically false.
It is to be hoped that Scaliger was a better philologist than mathematician.
Unlike Scaliger, Michael Stifel (ca. 1487-1567) was a significant mathematician, the most important German algebraist of the 16th century. He was a former monk, turned itinerant Lutheran preacher, and for a time professor of mathematics at the University of Jena. Although he was mainly interested in algebra, he also dabbled in circle squaring, but came to the conclusion that attempts to square the circle were futile. Although he was right, his opinion, at the time, could have been little more than a lucky guess, probably with an admixture of sour grapes.