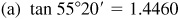 . Read up the page since
. Read up the page since 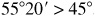 .
.The solution of right triangles depends on using approximate values for trigonometric functions of acute angles. An important part of the solution is determining the appropriate value to use for a trigonometric function. This part of the solution is different when you are using tables (as in Secs. 4.2 to 4.4) from when you are using a scientific calculator (as in Secs. 4.5 and 4.6.)
In general, the procedure will be to use the given data to write an equation using a trigonometric function and then to solve for the unknown value in the equation. The given data will consist either of two sides of a right triangle or of one side and an acute angle. Once one value has been found, a second acute angle and the remaining side can be found. The second acute angle is found using the fact that the acute angles of a right triangle are complementary (add up to 90°). The third side is found by using a definition of a second trigonometric function or by using the Pythagorean theorem (see App. 1, Geometry).
App. 2, Tables, has three different four-decimal-place tables of values for trigonometric functions, with Table 1 giving angles in 10′ intervals, Table 2 giving angles in 0.1° intervals, and Table 3 giving angles in 0.01-rad intervals. Tables published in texts differ in several ways, such as in the number of digits listed, the number of decimal places in each value, whether or not secant and cosecant values are listed, and the measurement unit of the angles.
The angles in Tables 1 and 2 are listed in the left- and right-hand columns. Angles less than 45° are located in the left-hand column, and the function is read from the top of the page. Angles greater than 45° are located in the right-hand column, and the function is read from the bottom of the page. In each row, the sum of the angles in the left- and right-hand columns is 90°, and the tables are based on the fact that cofunctions of complementary angles are equal.
In Table 3, the angles in radians are listed in the left-hand column only, and the function is read from the top of the page.
In this chapter, Table 1 or Table 2 will be used to find values of trigonometric functions whenever a manual solution is used. If the angle contains a number of degrees only or a number of degrees and a multiple of 10′, the value of the function is read directly from the table.
Opposite 24°40′ (< 45°) in the left-hand column read the entry 0.4173 in the column labeled sin A at the top.
Opposite 72° (>45°) in the right-hand column read the entry 0.3090 in the column labeled cos A at the bottom.
EXAMPLE 4.3 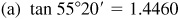 . Read up the page since
. Read up the page since 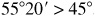 .
.
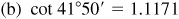 . Read down the page since
. Read down the page since 
If the number of minutes in the given angle is not a multiple of 10, as in 24°43′, interpolate between the values of the functions of the two nearest angles (24°40′ and 24°50′) using the method of proportional parts.
We find
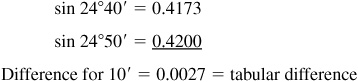
Correction = difference for 3′ = 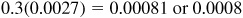 when rounded off to four decimal places.
when rounded off to four decimal places.
As the angle increases, the sine of the angle increases; thus,
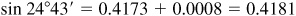
If a five-place table is available, the value 0.41813 can be read directly from the table and then rounded off to 0.4181.
We find
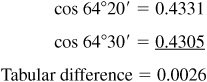
Correction = 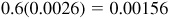 or 0.0016 to four decimal places.
or 0.0016 to four decimal places.
As the angle increases, the cosine of the angle decreases. Thus
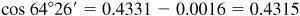
To save time, we should proceed as follows in Example 4.4:
(a) Locate sin 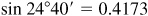 . For the moment, disregard the decimal point and use only the sequence 4173.
. For the moment, disregard the decimal point and use only the sequence 4173.
(b) Find (mentally) the tabular difference 27, that is, the difference between the sequence 4173 corresponding to 24°40′ and the sequence 4200 corresponding to 24°50′.
(c) Find 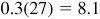 and round off to the nearest integer. This is the correction.
and round off to the nearest integer. This is the correction.
(d) Add (since sine) the correction to 4173 and obtain 4181. Then
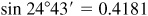
When, as in Example 4.4, we interpolate from the smaller angle to the larger, (1) the correction is added in finding the sine, tangent, and secant; and (2) the correction is subtracted in finding the cosine, cotangent, and cosecant.
We find
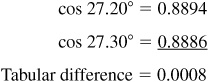
Correction =  or 0.0002 to four decimal places.
or 0.0002 to four decimal places.
As the angle increases, the cosine decreases, and thus

We find

Correction = 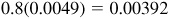 or 0.0039 to four decimal places.
or 0.0039 to four decimal places.
As the angle increases, the secant increases, and thus

(See Probs. 4.1 and 4.2.)
The process is a reversal of that given above.
EXAMPLE 4.8 Reading directly from Table 1, we find
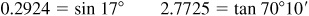
EXAMPLE 4.9 Find A, given sin  . (Use Table 1.)
. (Use Table 1.)
The given value is not an entry in the table. We find, however,
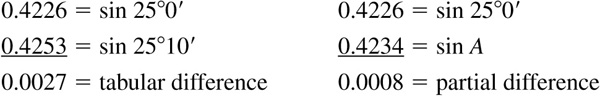
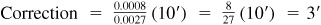 , to the nearest minute.
, to the nearest minute.
Adding (since sine) the correction, we have 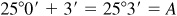 .
.
EXAMPLE 4.10 Find A, given 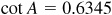 . (Use Table 1.)
. (Use Table 1.)
We find

Subtracting (since cotangent) the correction, we have 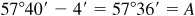 .
.
To save time, we should proceed as follows in Example 4.9:
(a) Locate the next smaller entry:  . For the moment, use only the sequence 4226.
. For the moment, use only the sequence 4226.
(b) Find the tabular difference, 27.
(c) Find the partial difference, 8, between 4226 and the given sequence 4234.
(d) Find 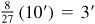 and add to 25°0′.
and add to 25°0′.
EXAMPLE 4.11 Find A, given  . (Use Table 2.)
. (Use Table 2.)
The given value is not an entry in the table. We find

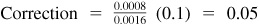 , to the nearest hundredth.
, to the nearest hundredth.
Adding (since sine) the correction, we have 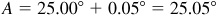 .
.
EXAMPLE 4.12 Find A, given 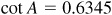 . (Use Table 2.)
. (Use Table 2.)
We find

 , to the nearest hundredth.
, to the nearest hundredth.
Subtracting (since cotangent) the correction, we have  .
.
(See Prob. 4.4.)
Calculators give values of trigonometric functions based on the number of digits that can be displayed, usually 8, 10, or 12. The number of decimal places shown varies with the size of the number but is usually at least four. When a calculator is used in this book, all trigonometric function values shown will be rounded to six digits unless the value is exact using fewer digits.
(a) Put the calculator in degree mode.
(b) Press (() key, enter 24, press (+) key, enter 40, press (÷) key, enter 60, press ()) key, and press (sin) key.
 rounded to six digits.
rounded to six digits.
(a) Put the calculator in degree mode.
(b) Press (() key, enter 48, press (+) key, enter 23, press (÷) key, enter 60, press ()) key, and press (tan) key.
 rounded to six digits.
rounded to six digits.
This procedure will be indicated in calculator solutions by showing  .
.
(See Prob. 4.3)
(a) Put the calculator in degree mode.
(b) Enter 53.28.
(c) Press (cos) key.
 rounded to six digits.
rounded to six digits.
For values of cotangent, secant, and cosecant, the reciprocal of the value of the reciprocal function is used. (See Sec. 2.4.)
(a) Put the calculator in degree mode.
(b) Press (() key, enter 37, press (+) key, enter 20, press (÷) key, enter 60, press ()) key, and press (tan) key.
(c) Press (1/x) key or divide 1 by the value of tan 37°20′ from (b).
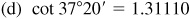 rounded to six digits.
rounded to six digits.
The values of angles can easily be found as a number of degrees plus a decimal. If angles are wanted in minutes, then the decimal part of the angle measure is multiplied by 60′ and this result is rounded to the nearest 10′, 1′, or 0.1′, as desired.
(a) Put the calculator in degree mode.
(b) Enter 0.4234, press (inv) key, and press (sin) key.
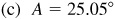 to the nearest hundredth degree OR
to the nearest hundredth degree OR
(d) Record the whole number of degrees, 25°.
(e) Press (–) key, enter 25, press (=) key, press (×) key, enter 60, and press (=) key.
(f) To the nearest minute, the displayed value is 3′.
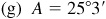 to the nearest minute.
to the nearest minute.
(a) Put the calculator in degree mode.
(b) Enter 0.8163, press (inv) key, and press (cos) key.
 to the nearest hundredth degree OR
to the nearest hundredth degree OR
(d) Record the whole number of degrees, 35°.
(e) Press (–) key, enter 35, press (=) key, press (×) key, enter 60, and press (=) key.
(f) To the nearest minute, the displayed value is 17′.
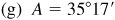 to the nearest minute.
to the nearest minute.
When values of cotangent, secant, or cosecant are given, the reciprocal of the given function value is found, and then the reciprocal function is used.
(a) Put the calculator in degree mode.
(b) Enter 3.4172 and press (1/x) key or enter 1, press (÷) key, enter 3.4172, and press (=) key.
(c) Press (inv) key and press (cos) key.
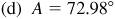 to the nearest hundredth degree OR
to the nearest hundredth degree OR
(e) Record the whole number of degrees, 72°.
(f) Press (-) key, enter 72, press (=) key, press (×) key, enter 60, and press (=) key.
(g) To the nearest minute, the displayed value is 59′.
 to the nearest minute.
to the nearest minute.
Errors in computed results arise from:
(a) Errors in the given data. These errors are always present in data resulting from measurements.
(b) The use of values of trigonometric functions, whether from a table or a calculator, that are usually approximations of infinite decimals.
A measurement recorded as 35 m means that the result is correct to the nearest meter; that is, the true length is between 34.5 and 35.5 m. Similarly, a recorded length of 35.0 m means that the true length is between 34.95 and 35.05 m; a recorded length of 35.8 m means that the true length is between 35.75 and 35.85 m; a recorded length of 35.80 m means that the true length is between 35.795 and 35.805 m; and so on.
In the number 35 there are two significant digits, 3 and 5. They are also two significant digits in 3.5, 0.35, 0.035, 0.0035 but not in 35.0, 3.50, 0.350, 0.0350. In the numbers 35.0, 3.50, 0.350, 0.0350 there are three significant digits, 3, 5, and 0. This is another way of saying that 35 and 35.0 are not the same measurement.
It is impossible to determine the significant figures in a measurement recorded as 350, 3500, 35,000,.... For example, 350 may mean that the true result is between 345 and 355 or between 349.5 and 350.5. One way to indicate that a whole number ending in a zero has units as its digit of accuracy is to insert a decimal point; thus 3500. has four significant digits. Zeros included between nonzero significant digits are significant digits.
A computed result should not show more decimal places than that shown in the least accurate of the measured data. Of importance here are the following relations giving comparable degrees of accuracy in lengths and angles:
(a) Distances expressed to 2 significant digits and angles expressed to the nearest degree.
(b) Distances expressed to 3 significant digits and angles expressed to the nearest 10′ or to the nearest 0.1°.
(c) Distances expressed to 4 significant digits and angles expressed to the nearest 1′ or to the nearest 0.01°.
(d) Distances expressed to 5 significant digits and angles expressed to the nearest 0.1′ or to the nearest 0.001°.
(NOTE: If several approximations are used when finding an answer, each intermediate step should use at least one more significant digit than is required for the accuracy of the final result.)
SOLVED PROBLEMS
4.1 Find the function value using tables.
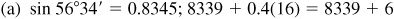



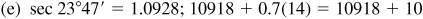
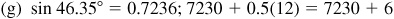

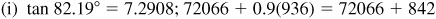
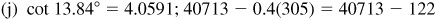


4.2 In the manual solution, if the correction is 6.5, 13.5, 10.5, etc., we will round off so that the final result is an even number.

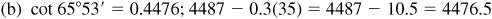

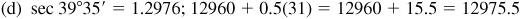
4.3 Find the function value using a calculator.
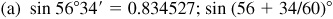



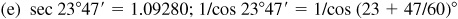
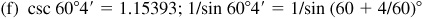

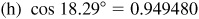



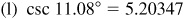
4.4 Find A to the nearest minute and to the nearest hundredth of a degree.




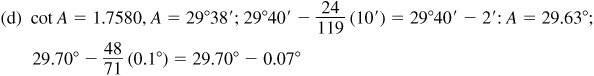

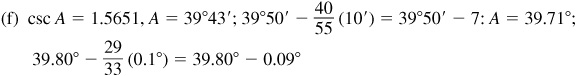
4.5 Solve the right triangle in which 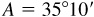 and
and  .
.
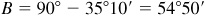 . (See Fig. 4.1.)
. (See Fig. 4.1.)

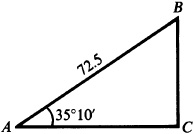
4.6 Solve the right triangle in which  and
and 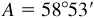 .
.
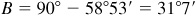 . (See Fig. 4.2.)
. (See Fig. 4.2.)
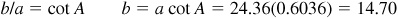
or
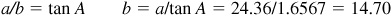

or


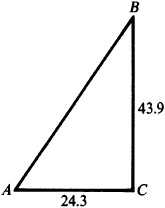
4.7 Solve the right triangle ABC in which  and
and 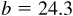 . (See Fig. 4.3.)
. (See Fig. 4.3.)
 ;
; 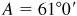 and
and  , or
, or  and
and 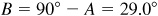 .
.
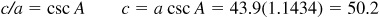
or
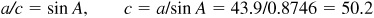
4.8 Solve the right triangle ABC in which  and
and  . (See Fig. 4.4.)
. (See Fig. 4.4.)
 ;
;  and
and 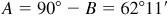 , or
, or  and
and 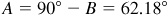 .
.
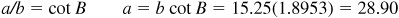
or

(NOTE: See App. 1, Geometry, for properties used in Probs. 4.9 to 4.11.)
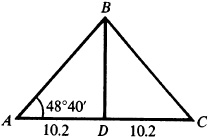
4.9 The base of an isosceles triangle is 20.4 and the base angles are 48°40′. Find the equal sides and the altitude of the triangle.
In Fig. 4.5, BD is perpendicular to AC and bisects it.
In the right triangle ABD,

or

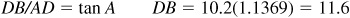
4.10 Considering the earth as a sphere of radius 3960 mi, find the radius r of the 40th parallel of latitude. Refer to Fig. 4.6.
In the right triangle OCB,  and
and  .
.
Then

Manual: 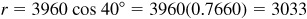 .
.
Calculator:  .
.
To three significant digits, the radius r of the 40th parallel is 3030 mi.

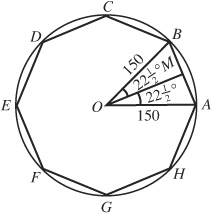
4.11 Find the perimeter of a regular octagon inscribed in a circle of radius 150 cm.
In Fig. 4.7, two consecutive vertices A and B of the octagon are joined to the center O of the circle. The triangle OAB is isosceles with equal sides 150 and 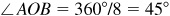 . As in Prob. 4.9, we bisect ∠AOB to form the right triangle MOB.
. As in Prob. 4.9, we bisect ∠AOB to form the right triangle MOB.
Then 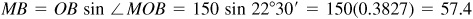 , and the perimeter of the octagon is
, and the perimeter of the octagon is 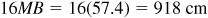 .
.
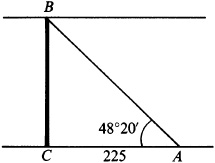
4.12 To find the width of a river, a surveyor set up his surveying equipment at C on one bank and sighted across to a point B on the opposite bank; then, turning through an angle of 90°, he laid off a distance  . Finally, setting the equipment at A, he measured ∠CAB as 48°20′. Find the width of the river.
. Finally, setting the equipment at A, he measured ∠CAB as 48°20′. Find the width of the river.
See Fig. 4.8. In the right triangle ACB,
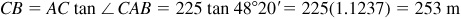
4.13 In Fig. 4.9, the line AD crosses a swamp. In order to locate a point on this line, a surveyor turned through an angle 51°16′ at A and measured 1585 feet to a point C. He then turned through an angle of 90° at C and ran a line CB. If B is on AD, how far must he measure from C to reach B ?

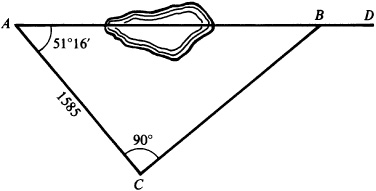
4.14 From a point A on level ground, the angles of elevation of the top D and bottom B of a flagpole situated on the top of a hill are measured as 47°54′ and 39°45′. Find the height of the hill if the height of the flagpole is 115.5 ft. (See Fig. 4.10.)
Manual: Let the line of the pole meet the horizontal through A in C.
In the right triangle ACD, .
.
In the right triangle ACB, .
.
Then
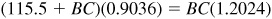
and
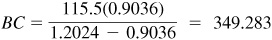
Calculator: In the right triangle ACD, .
.
In the right triangle ACB, .
.

Then
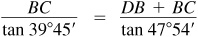

The height of the hill is 349.3 ft.
4.15 From the top of a lighthouse, 175 ft above the water, the angle of depression of a boat due south is 18°50′. Calculate the speed of the boat if, after it moves due west for 2 min, the angle of depression is 14°20′.
In Fig. 4.11, AD is the lighthouse, C is the position of the boat when due south of the lighthouse, and B is the position 2 min later.
Manual: In the right triangle CAD,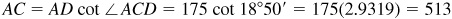
In the right triangle BAD,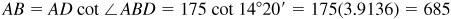 .
.
In the right triangle ABC, 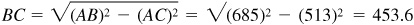 .
.
Calculator: In the right triangle CAD,  .
.
In the right triangle BAD, .
.
In the right triangle ABC,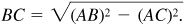

The boat travels 454 ft in 2 min; its speed is 227 ft/min.
SUPPLEMENTARY PROBLEMS
4.16 Find, to four decimal places, the values of the six trigonometric functions of each of the following angles:
(a) 18°47′,
(b) 32°13′,
(c) 58°24′,
(d) 79°45′

[NOTE: With a calculator, the values are the same except for  ,
,  ,
,  , and
, and  .]
.]
4.17 Find, to four decimal places, the values of the six trigonometric functions of each of the following angles:
(a) 29.43°,
(b) 73.67°,
(c) 61.72°,
(d) 12.08°

[NOTE: With a calculator, the values are the same except for 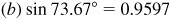 ,
,  , and
, and 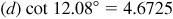 .]
.]
4.18 Find (acute) angle A, given:

4.19 Solve each of the right triangles ABC, given:

4.20 Find the base and altitude of an isosceles triangle whose vertical angle is 65° and whose equal sides are 415 cm.
Ans. Base = 446 cm, altitude = 350 cm
4.21 The base of an isosceles triangle is 15.90 in and the base angles are 54°28′. Find the equal sides and the altitude.
Ans. Side = 13.68 in, altitude = 11.13 in
4.22 The radius of a circle is 21.4 m. Find (a) the length of the chord subtended by a central angle of 110°40′ and (b) the distance between two parallel chords on the same side of the center subtended by central angles 118°40′ and 52°20′.
Ans. (a) 35.2 m, (b) 8.29 m
4.23 Show that the base b of an isosceles triangle whose equal sides are a and whose vertex angle is θ is given by  .
.
4.24 Show that the perimeter P of a regular polygon of n sides inscribed in a circle of radius r is given by  .
.
4.25 A wheel 5 ft in diameter rolls up an incline of 18°20′. What is the height of the center of the wheel above the base of the incline when the wheel has rolled 5 ft up the incline?
Ans. 3.95 ft
4.26 A wall is 10 feet tall and is 15 feet from a house. A window in the house is 30.5 feet above the ground. A fire escape slide attaches to the bottom of the window and to the top of the wall opposite the window. How long a slide must be purchased?
Ans. 25.4 ft
4.27 A parked car is spotted from a hotel window which is 100 m above the car. If the angle of depression from the window to the car is 15.4°, how far is the car from the window?
Ans. 377 m
4.28 A tower 45 m high casts a shadow of 12 m. What is the angle of elevation of the sun?
Ans. 75°
4.29 A rectangle is 48 cm long and 34 cm wide. What is the angle the diagonal makes with the longer side?
Ans. 35°
4.30 A railroad track makes an angle of 4.8° with the horizontal. How far must the train go up the track for it to gain 30 m in altitude?
Ans. 359 m