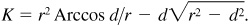The equation

defines a unique value of x for each given angle y. But when x is given, the equation may have no solution or many solutions. For example: if 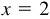 , there is no solution, since the sine of an angle never exceeds 1. If
, there is no solution, since the sine of an angle never exceeds 1. If 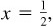 there are many solutions
there are many solutions 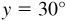 , 150°, 390°, 510°, –210°, –330°, ….
, 150°, 390°, 510°, –210°, –330°, ….

In spite of the use of the word arc, (2) is to be interpreted as stating that “y is an angle whose sine is x.” Similarly we shall write y = arccos x if x = cos y, y = arctan x if x = tan y, etc.
The notation y = sin -1 x, y = cos -1 x, etc. (to be read “inverse sine of x, inverse cosine of x,” etc.) is also used but sin -1 x may be confused with 1/sin x = (sin x)-1, so care in writing negative exponents for trigonometric functions is needed.
The graph of y = arcsin x = is the graph of x sin y and differs from the graph of y = sin x of Chap. 7 in that the roles of x and y are interchanged. Thus, the graph of y = arcsin x is a sine curve drawn on the y axis instead of the x axis.
Similarly the graphs of the remaining inverse trigonometric relations are those of the corresponding trigonometric functions, except that the roles of x and y are interchanged. (See Fig. 13.1)
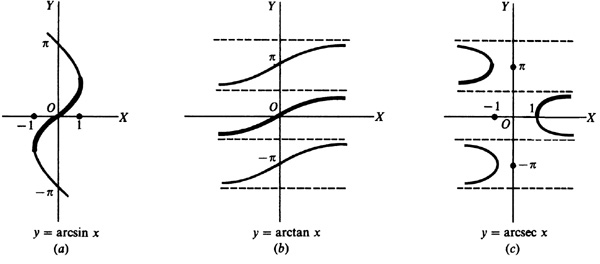
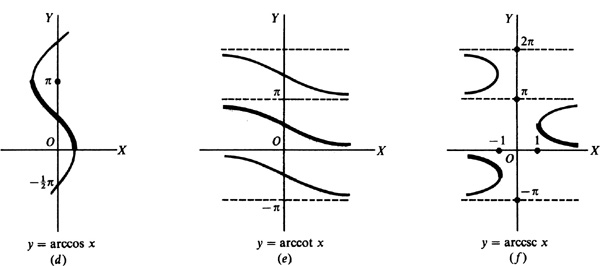
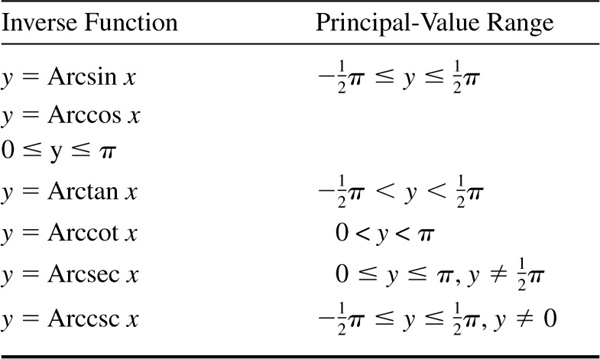
It is sometimes necessary to consider the inverse trigonometric relations as functions (i.e., one value of y corresponding to each admissible value of x). To do this, we agree to select one out of the many angles corresponding to the given value of x. For example, when 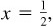 we agree to select the value
we agree to select the value 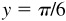 , and when
, and when 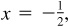 we agree to select the value
we agree to select the value 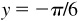 . This selected value is called the principal value of arcsin x. When only the principal value is called for, we write Arcsin x, Arccos x, etc. Alternative notation for the principal value of the inverses of the trigonometric functions is Sin-1 x, Cos -1 x, Tan -1 x, etc. The portions of the graphs on which the principal values of each of the inverse trigonometric relations lie are shown in Fig. 13.1(a) to (f) by a heavier line.
. This selected value is called the principal value of arcsin x. When only the principal value is called for, we write Arcsin x, Arccos x, etc. Alternative notation for the principal value of the inverses of the trigonometric functions is Sin-1 x, Cos -1 x, Tan -1 x, etc. The portions of the graphs on which the principal values of each of the inverse trigonometric relations lie are shown in Fig. 13.1(a) to (f) by a heavier line.
When x is positive or zero and the inverse function exists, the principal value is defined as that value of y which lies between 0 and 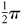 inclusive.
inclusive.
EXAMPLE 13.1 (a) Arcsin 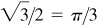 since
since 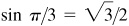 and
and 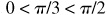 .
.
(b) Arccos 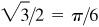 since
since 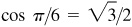 and
and 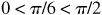 .
.
(c) Arctan 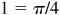 since
since 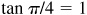 and
and 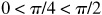 .
.
When x is negative and the inverse function exists, the principal value is defined as follows:
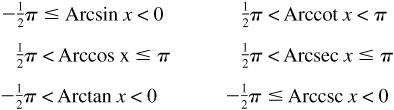
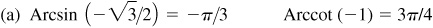

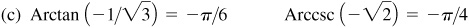
Authors vary in defining the principal values of the inverse functions when x is negative. The definitions given are the most convenient for calculus. In many calculus textbooks, the inverse of a trigonometric function is defined as the principal-valued inverse, and no capital letter is used in the notation. This generally causes no problem in a calculus class.
Let y be an inverse trigonometric relation of x. Since the value of a trigonometric relation of y is known, two positions are determined in general for the terminal side of the angle y (see Chap. 2). Let y1 and y2 be angles determined by the two positions of the terminal side. Then the totality of values of y consists of the angles y1 and y2, together with all angles coterminal with them, that is,
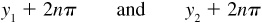
where n is any positive or negative integer or zero.
One of the values y1 or y2 may always be taken as the principal value of the inverse trigonometric function.
EXAMPLE 13.3 Write expressions for the general value of (a) arcsin 1/2, (b) arccos (–1), and (c) arctan (–1).
(a) The principal value of arcsin 1/2 is π/6, and a second value (not coterminal with the principal value) is 5π/6. The general value of arcsin 1/2 is given by

where n is any positive or negative integer or zero.
(b) The principal value is π and there is no other value not coterminal with it. Thus, the general value is given by 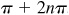 , where n is a positive or negative integer or zero.
, where n is a positive or negative integer or zero.
(c) The principal value is –π/4, and a second value (not coterminal with the principal value) is 3π/4. Thus, the general value is given by

where n is a positive or negative integer or zero.
SOLVED PROBLEMS
13.1 Find the principal value of each of the following.
(a) Arcsin 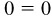
(b) Arccos 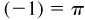
(c) Arctan 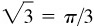
(d) Arccot 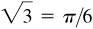
(e) Arccos 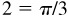
(f) Arccsc 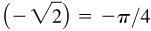
(g) Arccos 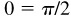
(h) Arcsin 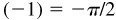
(i) Arctan 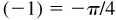
(j) Arccot 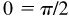
(k) Arccos 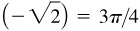
(l) Arccsc 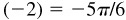
13.2 Express the principal value of each of the following to the nearest minute or to the nearest hundredth of a degree.
(a) Arcsin 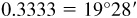 or 19.47°
or 19.47°
(b) Arccos 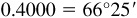 or 66.42°
or 66.42°
(c) Arctan 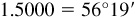 or 56.31°
or 56.31°
(d) Arccot 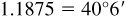 or 40.10°
or 40.10°
(e) Arccos 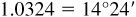 or 14.39°
or 14.39°
(f) Arccsc 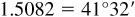 or 41.53°
or 41.53°
(g) Arcsin 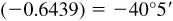 or –40.08°
or –40.08°
(h) Arccos 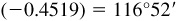 or 116.87°
or 116.87°
(i) Arctan 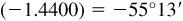 or –55.22°
or –55.22°
(j) Arccot 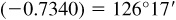 or 126.28°
or 126.28°
(k) Arccos 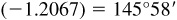 or 145.97°
or 145.97°
(l) Arccsc 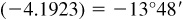 or –13.80°
or –13.80°
13.3 Verify each of the following.
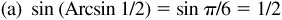
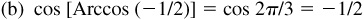
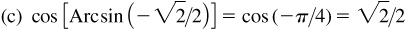
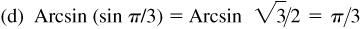
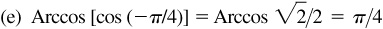
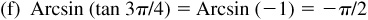
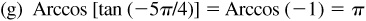
13.4 Verify each of the following.
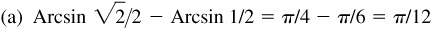
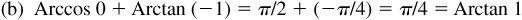
13.5 Evaluate each of the following:
(a) cos (Arcsin 3/5),
(b) sin [Arccos (–2/3)],
(c) tan [Arcsin (–3/4)]
(a) Let 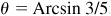 ; then
; then 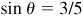 , θ being a first-quadrant angle. From Fig. 13.2(a),
, θ being a first-quadrant angle. From Fig. 13.2(a),

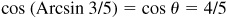
(b) Let 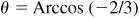 ; then
; then 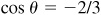 , θ being a second-quadrant angle. From Fig. 13.2(b),
, θ being a second-quadrant angle. From Fig. 13.2(b),
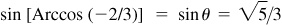
(c) Let 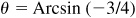 ; then
; then 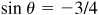 , θ being a fourth-quadrant angle. From Fig. 13.2(c),
, θ being a fourth-quadrant angle. From Fig. 13.2(c),
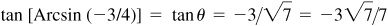
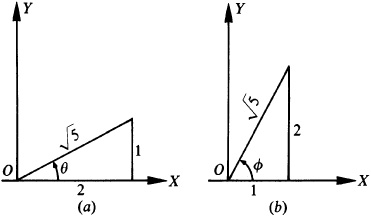
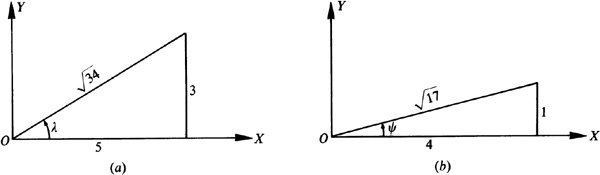
Let
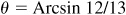
and
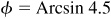
Then 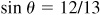 and
and 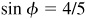 , θ and φ being first-quadrant angles. From Fig. 13.3(a) and (b),
, θ and φ being first-quadrant angles. From Fig. 13.3(a) and (b),
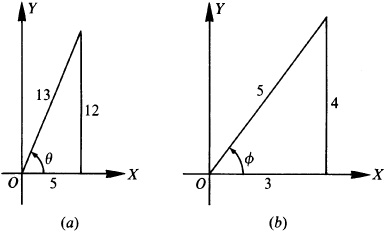
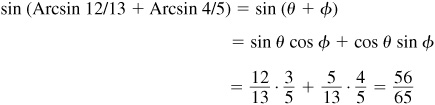
Let
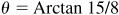
and
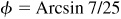
Then 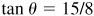 and
and 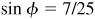 , θ and φ being first-quadrant angles. From Fig. 13.4(a) and (b),
, θ and φ being first-quadrant angles. From Fig. 13.4(a) and (b),
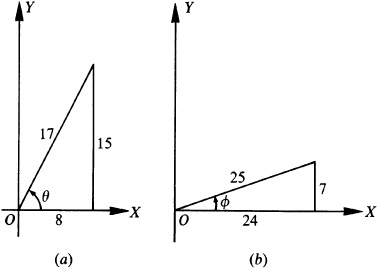
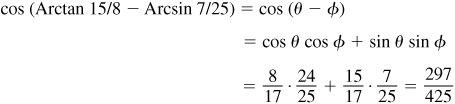
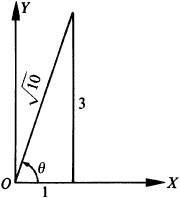
13.8 Evaluate sin (2 Arctan 3).
Let 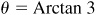 ; then
; then 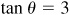 , θ being a first-quadrant angle. From Fig. 13.5,
, θ being a first-quadrant angle. From Fig. 13.5,
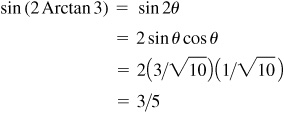
Let 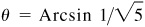 and
and 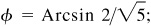 then
then 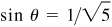 and
and 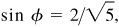 each angle terminating in the first quadrant. We are to show that
each angle terminating in the first quadrant. We are to show that 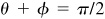 or, taking the sines of both members, that
or, taking the sines of both members, that 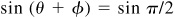 .
.
From Fig. 13.6(a) and (b),
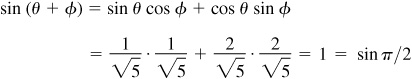
Let θ = Arctan 1/2 and φ = Arctan 4/3; then 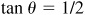 and
and 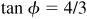 .
.
We are to show that 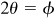 or, taking the tangents of both members, that
or, taking the tangents of both members, that 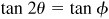 .
.
Now 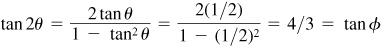 .
.
Let θ = Arcsin 77/85, φ = Arcsin 3/5, and ψ = Arccos 15/17; then 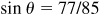 ,
,  , and
, and 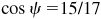 , each angle terminating in the first-quadrant. Taking the sine of both members of the given relation, we are to show that
, each angle terminating in the first-quadrant. Taking the sine of both members of the given relation, we are to show that 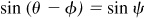 . From Fig. 13.7(a), (b), and (c),
. From Fig. 13.7(a), (b), and (c),
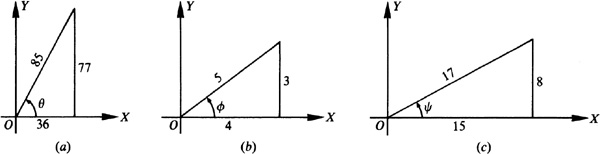
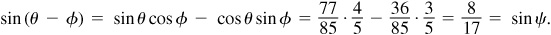
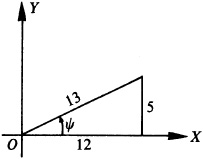
13.12 Show that Arccot 43/32 - Arctan 1/4 = Arccos 12/13.
Let θ = Arccot 43/32, φ = Arctan 1/4, and ψ = Arccos 12/13; then 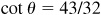 ,
, 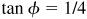 , and
, and 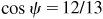 , each angle terminating in the first-quadrant. Taking the tangent of both members of the given relation, we are to show that
, each angle terminating in the first-quadrant. Taking the tangent of both members of the given relation, we are to show that 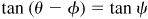 . From Fig. 13.8,
. From Fig. 13.8, 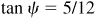 .
.
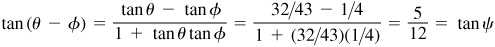
13.13 Show that Arctan 1/2 + Arctan 1/5 + Arctan 1/8 = π/4.
We shall show that Arctan 1/2 + Arctan 1/5 = π/4 – Arctan 1/8.
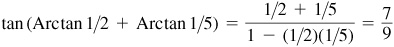
and
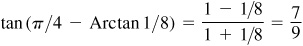
Let θ = Arctan 1/3, φ = Arctan 1/7, 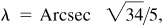 , and
, and 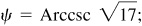 then
then 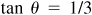 ,
, 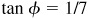 ,
, 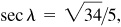 and
and 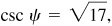 each angle terminating in the first quadrant.
each angle terminating in the first quadrant.
Taking the tangent of both members of the given relation, we are to show that
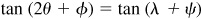
Now
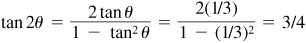
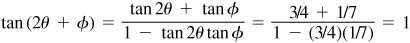
and, using Fig. 13.9(a) and (b), 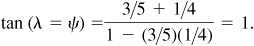
13.15 Find the general value of each of the following.
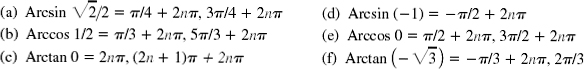
where n is a positive or negative integer or zero.
13.16 Show that the general value of (a) Arcsin 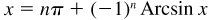
(b) 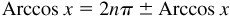
(c) Arctan 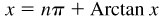
where n is any positive or negative integer or zero.
(a) Let θ = Arcsin x. Then since 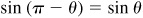 , all values of Arcsin x are given by
, all values of Arcsin x are given by
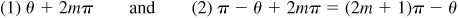
Now, when 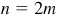 (that is, n is an even integer), (1) may be written as
(that is, n is an even integer), (1) may be written as 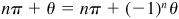 ; and when
; and when 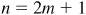 , (that is, n is an odd integer), (2) may be written as
, (that is, n is an odd integer), (2) may be written as 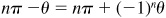 . Thus, Arcsin
. Thus, Arcsin 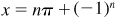 Arcsin x, where n is any positive or negative integer or zero.
Arcsin x, where n is any positive or negative integer or zero.
(b) Let θ = Arccos x. Then since 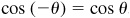 , all values of Arccos x are given by
, all values of Arccos x are given by 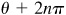 and
and 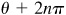 or
or 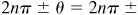 Arccos x, where n is any positive or negative integer or zero.
Arccos x, where n is any positive or negative integer or zero.
(c) Let θ = Arctan x. Then since 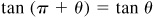 , all values of Arctan x are given by
, all values of Arctan x are given by 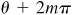 and
and 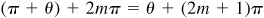 or, as in (a), by nπ + Arctan x, where n is any positive or negative integer or zero.
or, as in (a), by nπ + Arctan x, where n is any positive or negative integer or zero.
13.17 Express the general value of each of the functions of Prob. 13.15, using the form of Prob. 13.16.
(a) Arcsin 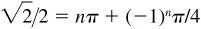
(b) Arccos 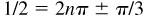
(c) Arctan 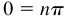
(d) Arcsin 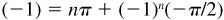
(e) Arccos 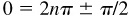
(f) Arctan 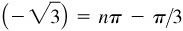
where n is any positive or negative integer or zero.
13.18 Write the following in inverse-relation notation.
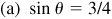 ,
,
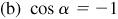 ,
,
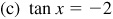 ,
,
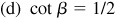
Ans.
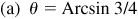 ,
,
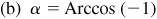 ,
,
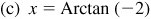 ,
,
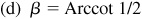
13.19 Find the principal value of each of the following.
(a) Arcsin 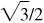
(b) Arccos 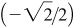
(c) Arctan 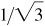
(d) Arccot 1
(e) Arcsin (–1/2)
(f) Arccos (–1/2)
(g) Arctan 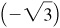
(h) Arccot 0
(i) Arccos 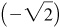
(j) Arccos (–1)
Ans. (a) π/3,
(b) 3π/4,
(c) π/6,
(d) π/4,
(e) –π/6,
(f) 2π/3,
(g) –π/3,
(h) π/2,
(i) 3π/4,
(j) –π/2
13.20 Evaluate each of the following.
(a) sin [Arcsin (–1/2)]
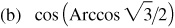
(c) tan [Arctan (–1)]
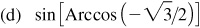
(e) tan (Arcsin 0)
(f) sin (Arccos 4/5)
(g) cos [Arcsin (–12/13)]
(h) sin (Arctan 2)
(i) Arccos (sin 220°)
(j) Arcsin [cos (–105°)]
(k) Arctan (cot 230°)
(l) Arccot (tan 100°)
(m) sin (2 Arcsin 2/3)
(n) cos (2 Arcsin 3/5)
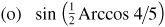
Ans.
(a) –1/2,
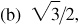 ,
,
(c) –1,
(d) 1/2,
(e) 0,
(f) 3/5,
(g) 5/13,
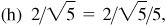
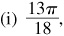

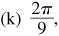
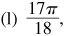
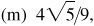
(n) 7/25,
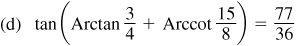
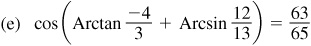
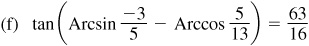
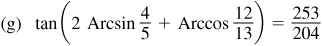
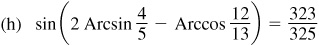
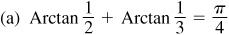
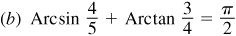
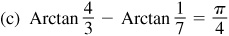
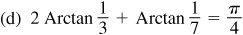

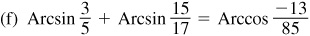
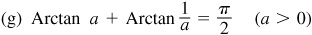
13.23 Prove: The area of the segment cut from a circle of radius r by a chord at a distance d from the center is given by