Any motion that regularly repeats is referred to as periodic or harmonic motion. Common examples include an object undergoing uniform circular motion, a mass oscillating on a spring and a pendulum. This type of motion can be characterized by its period or frequency.
The time it takes an object to move through one full cycle of motion is called the period. For an object undergoing uniform circular motion, the period is the time it takes to make one revolution. For a mass on a spring or a pendulum, it is the time it takes to make a round trip (i.e., the final position and velocity must be the same as the initial values). The period is denoted by T and is measured in seconds.
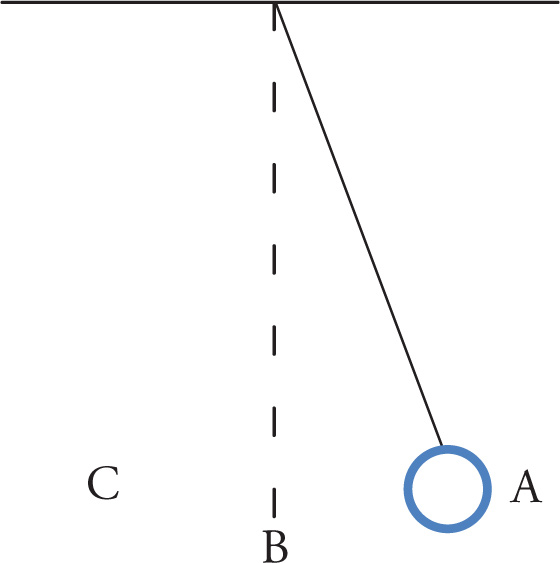
Example 11-1: The bob on a pendulum moves from point A to point B in 0.5 seconds. What is the period of oscillation?
Solution: A to B represents one-quarter of a period. A full period is the time it takes for the bob to move from A to B to C to B and back to A. So T = 4(0.5 s) = 2 s.
Rather than timing one cycle to find the period, we can instead count the number of cycles that occur in one second. This is known as the frequency, denoted by f. The units of f are cycles per second, or hertz (Hz).
Now the first thing we notice is that period and frequency are reciprocals. After all, the period is “the number of seconds per cycle,” and the frequency is “the number of cycles per second.” So, we have these fundamental relationships:
Period and Frequency
f = 
and T = 
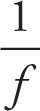
Every type of oscillation has a period and a frequency, but there is a special class of oscillations in which these quantities have a unique property. This “ideal” type of oscillatory motion is referred to as simple harmonic motion (often abbreviated SHM). A mass oscillating on a spring exhibits SHM.
The spring in the series of diagrams below is fixed at its left end and has a block attached to its right end. When the spring is neither stretched nor compressed (i.e., when it’s at its natural length, as shown in Diagram 1 below) we say the spring is at its equilibrium position. In general, the point at which the net force on the block is zero, which in this case is when the spring is at its natural length, is called the equilibrium position, and we label it x = 0.
Now, imagine that we stretch the spring (Diagram 1 to Diagram 2), and let go. Once released, the spring pulls back to the left, going through its equilibrium position and then to the point of maximum compression. From here, the spring pushes back to the right, passing again through its equilibrium position, and returning to the point of maximum extension. If friction is negligible, this back-and-forth motion will continue indefinitely, and the time it takes for the block to go through one period, for example, from Diagram 2 to Diagram 6, is a constant.
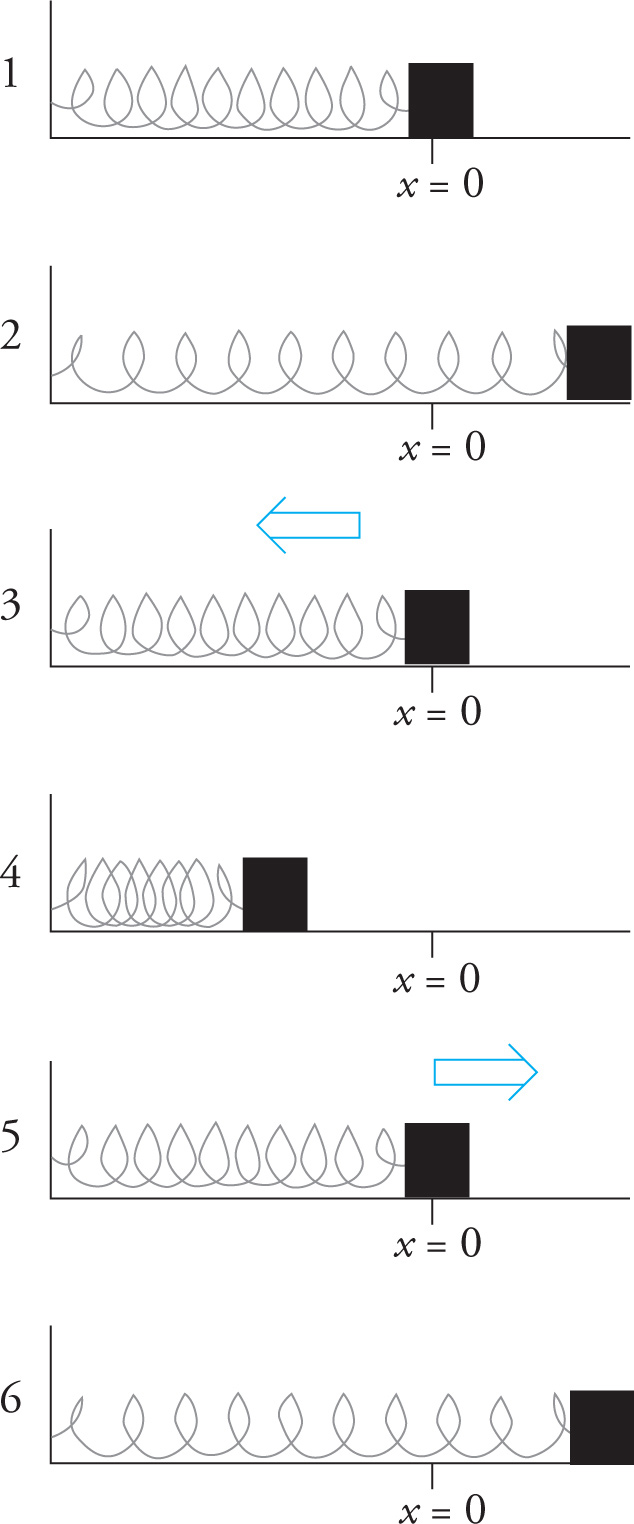
Let’s first describe the motion of the block attached to the spring from the point of view of the force it feels. The spring exerts a force on the block that’s proportional to its displacement. If we call the equilibrium position x = 0, then the force exerted by the spring is given by
Hooke’s Law
F = −kx
The proportionality constant, k, called the spring constant, tells us how strong the spring is; the greater the value of k, the stiffer (and stronger) the spring.
As we can see from Hooke’s Law, the units of k are newton/meter. Since a meter is a large distance to stretch or compression a spring, the values for k are often large.
What is the role of the minus sign in Hooke’s law? Look back at the diagrams on the previous page. Since we’re calling the equilibrium position x = 0, when the block is to the right of equilibrium, its position, x, is positive. At this point, the stretched spring wants to pull back to the left; because the direction of the force of the spring is to the left, we indicate this direction by calling it negative. Similarly, when the block is to the left of equilibrium, its position, x, is negative. At this point, the compressed spring wants to push back to the right; because the direction of the force of the spring is to the right, we indicate this direction by calling it positive. We see that the direction of the spring force is always directed opposite to its displacement from equilibrium, and for this reason, the minus sign is needed in Hooke’s law. Furthermore, because the spring is always trying to restore the block to equilibrium, we say that spring provides the restoring force; it’s this force that maintains the oscillations. The fact that the restoring force exerted by the spring obeys Hooke’s Law (i.e., the force is directly proportional to the distance from equilibrium) is the reason why the block undergoes simple harmonic motion.
Unfortunately, knowing an equation for the force doesn’t allow us to solve directly for other things, such as the speed of the block at some later time or the work done by or against the spring: The force changes as the block moves, so acceleration is not uniform. However, there is a way to figure out these quantities by using energy. When we pull on the spring to get the oscillations started, we’re exerting a force over a distance; that is, we’re doing work. Because we’re doing work against the spring, the spring stores potential energy, called elastic potential energy. If we once again call the equilibrium position of the spring x = 0, then the potential energy of a stretched or compressed spring is given by this equation:
Elastic Potential Energy
PEelastic = 
kx2
It follows that Wby spring = –ΔPEelastic and Wagainst spring = ΔPEelastic. To justify this, imagine an external force is stretching a spring from x = 0 to x = X. The minimum force required to do this is opposite the spring force: +kx. From mechanics, we learned that the work done by a variable force is equal to the area under the force vs. position graph.
The area under curve is the area of a triangle with base equal to X and height equal to kX. So PE = Wagainst spring = (1/2)bh = (1/2)(X)(kX) = (1/2)kX2.
We can also use conservation of energy to find the speed of a oscillating mass on a spring at any given position.
When we release the block from rest in Diagram 2, the spring is stretched and the block isn’t moving, so all the energy is in the form of elastic potential energy. This potential energy turns into kinetic energy, until at x = 0 (equilibrium), all the energy has been converted to kinetic energy. As the block rushes past equilibrium, this kinetic energy gradually turns back into elastic potential energy until the point where the spring is at maximum compression and it’s all transformed back to potential energy. The compressed spring then pushes outward, converting its potential energy back to kinetic; the block rushes through equilibrium again, and kinetic energy is transformed back to potential energy, until it reaches its starting point (Diagram 6) at maximum extension. At this instant, we’re back to our full reserve of elastic potential energy (and no kinetic energy), and the process is ready to repeat.
As a result, we can look at the motion of the block from the point of view of the back-and-forth transfer between elastic potential energy and kinetic energy.
The maximum displacement of the block from equilibrium is called the amplitude, denoted by A. This positive number tells us how far to the left and right of equilibrium the block will travel. So, in the series of diagrams above, the block’s position at maximum extension is x = +A, and its position at maximum compression is x = –A.
We can summarize the dynamics of the oscillations in this table:
Because we’re ignoring any frictional forces during the oscillations of the block, total mechanical energy will be conserved. That is, the sum of the block’s kinetic energy, mv2, and the spring’s potential energy, kx2, will be a constant. We can use this fact to figure out the maximum speed of the block. At the instant the block is passing through equilibrium, all the potential energy of the spring has been transformed into kinetic energy of the block. If the amplitude of the oscillations is A, then the maximum elastic potential energy, kA2 (the value of kx2 when x = ± A), is completely converted to maximum kinetic energy at x = 0. This gives us:
PEelastic, max → KEmax
kA2 = mv2
∴ vmax = A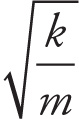
Example 11-2: A block of mass m attached to a spring with constant k oscillates horizontally on a frictionless surface with amplitude A. In which case does the spring do more work, moving the mass from x = A to x = A/2 or from x = A/2 to x = 0?
Solution: In both cases the spring does positive work, since the restoring force is in the same direction as the motion of the block. Since the force is not constant, we cannot use the formula W = Fd cosθ. Instead, the work done by the spring is given by W = –ΔPEelastic = –(PEfinal – PEinitial).
W = −(k[A/2]2 − kA2) = −(
kA2 − kA2) = 
kA2
From x = A/2 to x = 0:
W = −(k[0]2 − k[A/2]2) = −(0 − kA2) = kA2
Notice that even though the distance travelled is the same in each case, the average force exerted by the spring is greater from x = A to x = A/2 than it is from x = A/2 to x = 0, and therefore the work done by the spring is also greater.
Example 11-3: A block of mass 200 g is oscillating on the end of a horizontal spring of spring constant 100 N/m and natural length 12 cm. When the spring is stretched to a length of 14 cm, what is the acceleration of the block?
Solution: When the spring is stretched by 2 cm, Hooke’s law tells us that the force exerted by the spring has a magnitude of F = kx = (100 N/m)(0.02 m) = 2 N. Therefore, by Newton’s second law, the acceleration of the block will have a magnitude of a = F/m = (2 N)/(0.2 kg) = 10 m/s2.
Example 11-4: If the block in Example 11-3 above were replaced with a block of mass 800 g, how would its maximum speed change?
Solution: The equation derived above, vmax = A
, tells us that vmax is inversely proportional to the square root of the mass of the oscillator. Therefore, if m increases by a factor of 4, vmax will decrease by a factor of 2.
Earlier it was mentioned that a mass oscillating on a spring exhibits “ideal” oscillatory motion, which is called simple harmonic motion, and that this motion is the result of Hooke’s Law (i.e., the restoring force is directly proportional to the distance from equilibrium). But what makes this motion different than non-ideal oscillations? It turns out (using calculus) that the frequency and period only depend on the spring constant, k, and the mass of the block, m.
f = 
and T = 2π
Notice that neither f nor T depends on A, the amplitude. This is why we call the motion of the block on the spring simple harmonic motion. This is not an obvious statement. If a mass on a spring is pulled back 1 cm or pulled back 10 cm (assuming the spring is still within its elastic limit), the time it takes to complete one cycle is exactly the same. As an example of an oscillating system that does not exhibit simple harmonic motion, imaging a ball bouncing. Removing air resistance and assuming that the bounces are completely elastic, the ball will continue to bounce to the same height from which it was released. However, dropping the ball from 1 cm will take less time to fall and rise than dropping it from 10 cm (which can be proven with the Big 5 equations).
It’s possible for a system to oscillate because of a restoring force that is not directly proportional to the displacement. If this were the case, the frequency and period would depend on the amplitude; we’d still call the motion harmonic, which just means back-and-forth, but we wouldn’t call it simple harmonic.
Example 11-5: Suppose that the block shown in the series of diagrams on the first page of this chapter requires 0.25 sec to move from Diagram 4 to Diagram 6. What is the frequency of the oscillations?
Solution: The interval from Diagram 4 to Diagram 6 represents half a cycle, which requires half a period to complete. If half a period is 0.25 sec, then the period is 0.5 sec. Therefore, the frequency, f, is 1/T = 1/(0.5 s) = 2 Hz.
So far we have examined the simple harmonic motion of a mass on a horizontal spring, where the system is in equilibrium when the spring is at its rest length. If the spring is now rotated so that it is suspended vertically and a mass is attached, will the oscillations still be simple harmonic? The answer is yes. The formulas for period and frequency are exactly the same. The force of gravity, however, does affect the situation. The weight of the block will naturally stretch the spring so that equilibrium (Fnet = 0) no longer occurs when the spring is at its rest length. The new equilibrium position is when the upward force of the spring exactly balances the weight: kx = mg. When the spring is stretched beyond this point and released, the mass will oscillate around the new equilibrium position. It is often convenient to rename the new equilibrium position x = 0. This enables us to “ignore gravity”. In other words, measuring x from equilibrium instead of measuring from the rest length of the spring, it becomes exactly like a horizontal spring, but with a longer rest length. We can therefore still use the equations
–kx = ma and vmax = A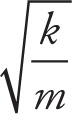
Besides the spring-block simple harmonic oscillator, there’s another oscillator that the MCAT will expect you to know about: the simple pendulum. If the connecting rod or string between the suspension point and the object at the end of a pendulum has negligible mass (so that all the mass is in the object at the end of the rod or string), and if there is no friction at the suspension point during oscillation, we say the pendulum is a simple pendulum.
The displacement of the mass is not taken as a distance from equilibrium (as in the spring-block case), but rather as the angle it makes with the vertical. The vertical (shown as a dashed line in the figure below) is the equilibrium position, θ = 0. The restoring force here is gravity; specifically, it’s equal to mg sinθ, which is the component of the object’s weight in the direction toward equilibrium.
Strictly speaking, a pendulum does not undergo simple harmonic motion because the restoring force is not proportional to the displacement (mg sinθ is not exactly proportional to θ). However, if the angle is small, then sinθ ≈ θ (in radians), so the restoring force can be approximated as mgθ, which is proportional to θ.1 In this case, we can treat the motion as simple harmonic, and the frequency and period are given by the following equations:
f =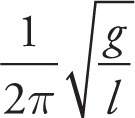 
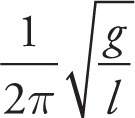and T = 2π
where l is the length of the pendulum and g is the acceleration due to gravity. Observe that in the case of simple harmonic motion of a simple pendulum, the mass of the swinging object does not affect the frequency or period of oscillation.
Example 11-6: The bob (mass = m) of a simple pendulum is raised to a height h above its lowest point and released. Find an expression for the maximum speed of the pendulum.
Solution: When the bob is at height h above its lowest point, it has gravitational potential energy equal to mgh (relative to its lowest point). As it passes through the equilibrium position, all this potential energy is converted to kinetic energy. Therefore, mgh = mv2max, and we get vmax =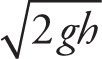 
. This is the speed of the bob as it passes through equilibrium, which is where it attains its maximum speed.
A mechanical wave is a series of disturbances (i.e., oscillations) within a medium that transfers energy from one place to another. The medium itself is not transported, just the energy. Examples included a vibrating string or sound. Mechanical waves cannot exist without a medium. In a later chapter we will discuss electromagnetic waves, which do not need a medium. This is because the electric and magnetic fields oscillate rather than physical matter.
Perhaps the simplest example of wave is one we can create by wiggling one end of a long rope:
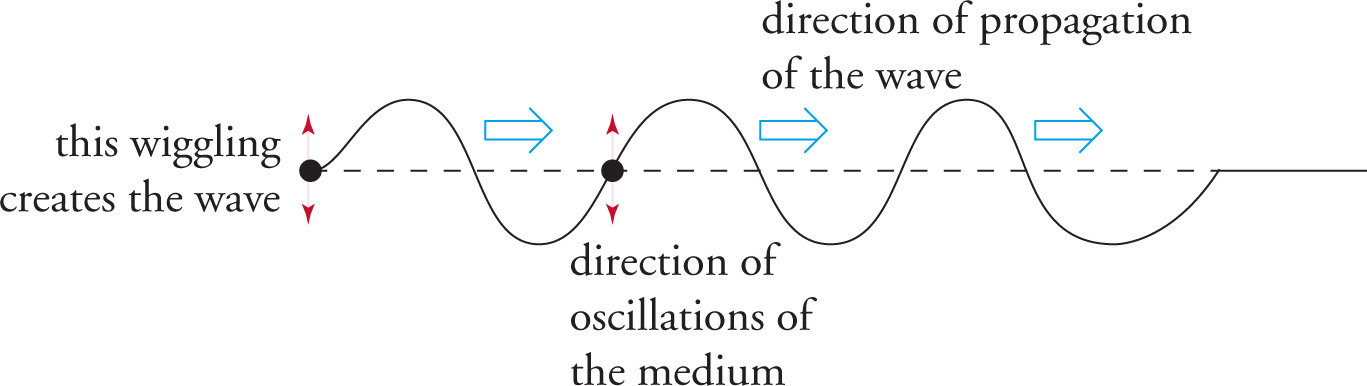
This wave uses the rope as the medium, traveling from one end to the other. Notice that the wave is moving horizontally, but the rope itself is moving up and down. That’s why this is called a transverse wave: The wave travels (propagates) in a direction that’s perpendicular to the direction in which the medium is vibrating.
The most fundamental characteristic of a wave is its frequency. If we pick a spot on the rope and count how many times it moves up and down (the number of round trips it makes) in one second, we’ve just measured the frequency, f, which we express in hertz (cycles per second).
The period of a wave, T, is the reciprocal of the frequency, and is the amount of time it takes any spot on the rope to complete one cycle (in this case, one up-and-down round trip).
These definitions for frequency and period are same as for a mass on a spring or a pendulum. Each particle of rope oscillates up and down with simple harmonic motion. However, we can also think of the frequency and period of a wave in a different way. Instead of focusing on the oscillations, we can observe “pulses” moving the right. Frequency can be thought as the number of pulses that pass a given point per unit time and period is the time it takes between pulses.
The figure below identifies the crests (peaks) and troughs of the wave. The distance from one crest to the next (i.e., the length of one cycle of the wave) is called the wavelength, denoted by λ, the Greek letter lambda. We can also measure the wavelength by measuring the distance from one trough to the next, or, in fact, between any two consecutive corresponding points along the wave.
The amplitude of a wave, A, is the maximum displacement from equilibrium that any point in the medium makes as the wave goes by. In the case of a wave on a rope, the amplitude is the distance from the original horizontal position of the rope up to a crest; it’s also the distance from the horizontal position down to a trough.
To figure out how fast the wave travels, we just notice that the wave travels a distance of λ in time T; that is, λ is the length of one wave cycle, and T, the period, is the time required for one wave cycle to go by. Since distance = rate × time, we get λ = vT. Solving this for v gives us λ(1/T) = v and since f = 1/T, the equation becomes v = λf. This is the most important equation for waves and one of the most important equations for the MCAT.
Wave Equation
v = λf
For a transverse wave on a rope, there’s another equation we can use to figure out the wave speed:
The linear density of a rope is its mass per unit length.
Notice that the second equation for the wave speed shows that v does not depend on f (or λ). While this may seem to contradict the first equation, v = λf, it really doesn’t. The speed of the wave depends on the characteristics of the rope; how tense it is, and what it’s made of. We can wiggle the end at any frequency we want, and the speed of the wave we create will be a constant. However, because λf = v must always be true, a higher f will mean a shorter λ (and a lower f will mean a longer λ). Thus, changing f doesn’t change v: It changes λ. This brings up our first big rule for waves:
Big Rule 1: The speed of a wave is determined by the type of wave and the characteristics of the medium, not by the frequency.
Notice that two different types of wave can move with different speeds through the same medium; for example, sound and light move through air with very different speeds. There are exceptions to Big Rule 1, but the only one the MCAT will expect you to know about is dispersion, which is discussed in Chapter 13, on Optics. Any other exception would be discussed in the passage; otherwise, you can assume the rule applies.
Our second big rule for waves concerns what happens when a wave passes from one medium into another. Because wave speed is determined by the characteristics of the medium, a change in the medium implies a change in wave speed, but the frequency won’t change.
Big Rule 2: When a wave passes into another medium, its speed changes, but its frequency does not.
The reasoning behind this makes sense if you focus on a wave as a series of pulses. Frequency is the number of pulses that pass by per unit time. It stands to reason that, if a certain number of pulses per second arrives at the boundary between two different media, then the same number of pulses per second must leave, passing into the new medium. In other words, rate in = rate out. This is similar to the Equation of Continuity in fluids and the rule for electric current passing through resistors in series.
Because f is constant, Rule 2 tells us that the wavelength is proportional to wave speed.
Notice that Rule 1 applies to different waves in one medium, while Rule 2 applies to a single wave in different media. Memorize these rules. The MCAT loves waves.
Example 11-7: A transverse wave of frequency 4 Hz travels at a speed of 6 m/s along a rope. What would be the speed of a 12 Hz wave along this same rope?
Solution: Big Rule 1 for waves says that the speed of a wave is determined by the type of wave and the characteristics of the medium, not by the frequency. If all we do is change the frequency, the wave speed will not change: The wave speed will still be 6 m/s. (What will change? The wavelength. Because λ = v/f, a change in f with no change in v will change λ.)
Example 11-8: Which one of the following statements is true concerning the amplitude of a wave?
A. Amplitude increases with increasing frequency.
B. Amplitude increases with increasing wavelength.
C. Amplitude increases with increasing wave speed.
D. None of the above.
Solution: The amplitude is determined by how much energy we put into the wave to get it started. If we wiggle the rope up and down through a large distance (a large amplitude). This takes more energy on our part, and as a result, the wave carries more energy. However, the amplitude doesn’t depend on f, λ, or v. The answer is D.
Example 11-9: A wave of frequency 12 Hz has a wavelength of 3 m. What is the speed of this wave?
Solution: Using the equation v = λf, we find that v = (3 m)(12 Hz) = 36 m/s.
Example 11-10: The horizontal distance between each crest and the closest trough of a transverse traveling wave along a long horizontal rope is 2 m. If the wave speed is 8 m/s, what is the period of this wave?
Solution: If the horizontal distance between each crest and the closest trough for a transverse traveling wave is 2 m, then the wavelength is 4 m. Now, using v = λf, we find that f = v/λ = (8 m/s)/(4 m) = 2 Hz, so T = 1/f = 1/(2 Hz) = 0.5 sec.
Example 11-11: What happens when the wave shown below passes from the thick, heavy rope into the thinner, lighter rope?
Solution: According to Big Rule 2 for waves, when a wave passes into another medium, its speed changes, but its frequency does not. How does the speed change? Because the rope is lighter (i.e., it has a lower linear density), the equation for wave speed on a string (given above) tells us that v will increase. So, if v increases but f doesn’t change, then λ will also increase because λ = v/f.
Example 11-12: A certain rope transmits a 2 Hz transverse wave of amplitude 10 cm with a speed of 1 m/s. What would be the wavelength of a 5 Hz transverse wave of amplitude 8 cm on this same rope?
Solution: First, ignore the amplitudes; they’re included in the question only to make things seem more complicated than they are. The amplitude of a wave indicates how much energy the wave transports, but it has nothing to do with wavelength, period, frequency, or wave speed (recall Example 11-8 above). Now, if a 2 Hz transverse wave has a speed of 1 m/s on this rope, then a transverse wave of any frequency will have a speed of 1 m/s on this rope; that’s what Big Rule 1 for waves tells us. Thus, if f = 5 Hz and v = 1 m/s, then
Example 11-13: How long will it take a wave of wavelength λ and period T to travel a distance d?
A. λTd
B.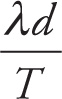 
C. 
D. 
Solution: First, let’s see if we can eliminate any choices because the units don’t work out correctly. We’re being asked for an amount of time, so the answer must have the dimension (and units) of time. Choice A can’t be correct, since it has units of [λ][T][d] = m·sec·m = m2·sec. Notice that both λ and d have units of meters, which we don’t want in the answer, so these units must cancel. Therefore, B can’t be correct either since λ and d are multiplied by each other, rather than being divided as they should to make their units cancel.
One difference between the two remaining choices is that in C, the distance d is in the numerator, while in D, the distance d is in the denominator. Now, let’s think about this: More time will be required for the wave to travel a greater distance. In other words, the bigger d is, the greater the travel time should be. Therefore, we can eliminate D; after all, since d is in the denominator in choice D, a larger d will result in a smaller amount of time, which doesn’t make sense. Thus, the answer must be C.
Here’s an alternate solution using equations. Because distance = speed × time (d = vt), we know that t = d/v. We can find v using the wave equation v = λf, and since f = 1/T, we find that
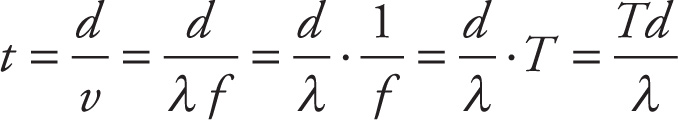
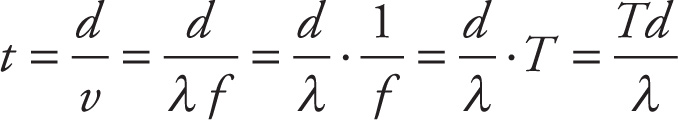
The answer is indeed C, just as we figured out by checking units and using logic.
When two or more waves are superimposed on each other, they will combine to form a single resultant wave. This is called interference. The amplitude of the resultant wave will depend on the amplitudes of the combining waves and on how these waves travel relative to each other.
If crest meets crest, and trough meets trough, we say that the waves are in phase with each other. Their amplitudes will add, and we say the waves interfere constructively. However, if the crest of one wave coincides with the trough of the other (and vice versa), we say that the waves are exactly out of phase with each other. In this case, their amplitudes subtract, and we say that the waves interfere destructively.
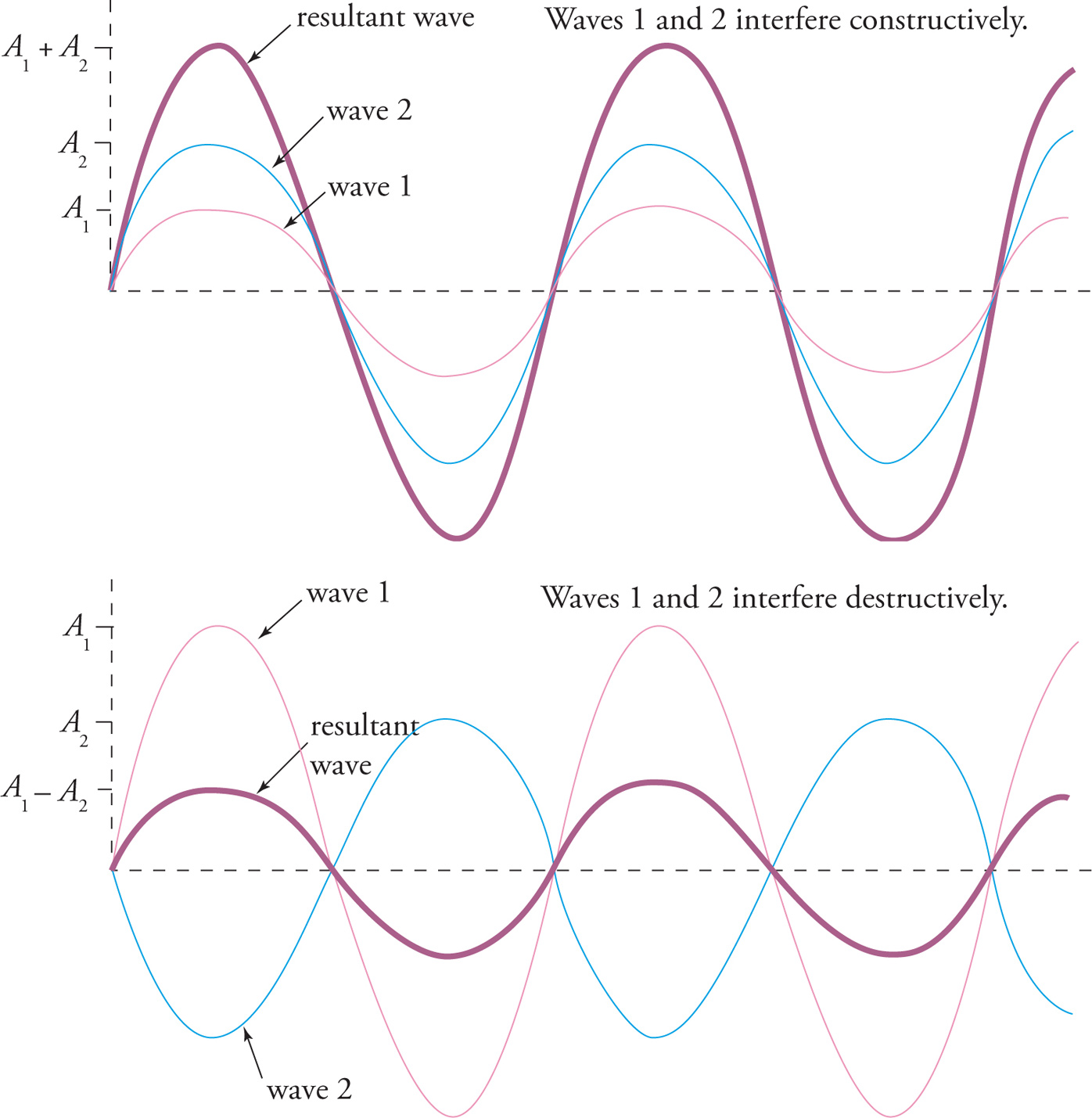
A passage might also say that waves that are directly opposite each other in amplitude are 180 degrees out of phase, or π radians out of phase; it is common to refer to a whole cycle or wave as being 360 degrees or 2π radians, as if it were a circle. If the waves aren’t exactly in phase (0°, 360°, or 2π radians) or exactly out of phase (180° or π radians), the amplitude of the resultant wave will be somewhere between the difference and the sum of the amplitudes of the interfering waves.
The interfering waves may also have different wavelengths. These waves will produce a more complicated-looking resultant wave, but we’d still say the waves interfere constructively where they reinforce each other, and destructively where they tend to cancel each other out.
The preceding pictures of waves that are in phase and out of phase can also be thought of graphs representing the displacement at a fixed location as a function of time. As example, imagine a cork floating in calm water. Source 1 creates a wave, which travels through the water, causing the cork to bob up and down. A graph of the cork’s motion as a function of time would be sinusoidal (i.e., it looks like a Wave 1 in the picture except that the distance from maximum to maximum is the period rather than the wavelength).
Similarly, if Source 2 were acting alone, Wave 2 would cause the cork to bob up and down. The graph of this motion as a function of time would look similar to the picture of Wave 2. If Wave 1 and Wave 2 both arrive at the cork, they will interfere. If the waves are in phase when they arrive at the cork (i.e., crests arrive at the same time, troughs arrive at the same time, etc.) or if they are 180° out of phase when they arrive at the cork (i.e., the crest of one wave arrives simultaneously with the trough of the other), the graph of the cork’s motion as a function of time would like the resultant waves in the picture. Note that if the waves have different frequencies (and wavelengths), then the graph of the cork’s motion will not look like a sine or cosine, but will be more complicated. An example of this is beats, which are discussed in the next chapter.
Be careful on the MCAT. If you see a picture of a sine or cosine, make sure you can determine whether it is an actual wave (pictured at a fixed time), or a graph of one particle’s motion as a function of time.
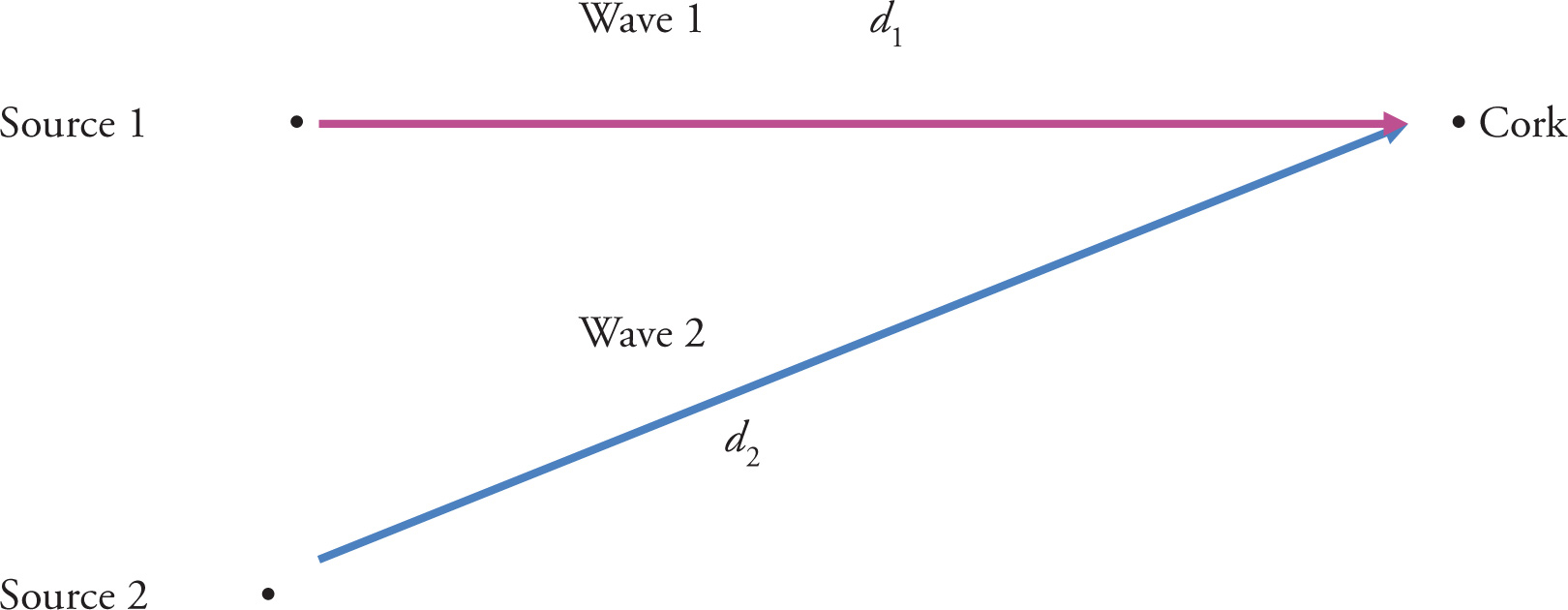
How can you determine whether two waves are in phase, 180° out of phase or something in between? One way is to look at path difference. In the above picture, imagine Source 1 and Source 2 emit identical waves that are exactly in phase. Just because they are initially in phase does not mean they will be in phase when they arrive at the cork. The reason is because Wave 2 had to travel a larger distance than Wave 1. The path difference = d2 – d1. The general rule is:
• If the path difference = nλ and, (n = 0, 1, 2, …), the waves will be in phase and will therefore constructively interfere.
• If the path difference = (n + ½)λ, the waves will be 180° out of phase and will therefore destructively interfere.
If Wave 2 travels an integer number of wavelengths farther than Wave 1, the crests from each will still arrive at the same time. If Wave 2 travels λ/2, 3λ/2, 5λ/2, etc. farther than Wave 1, the crest from one wave will arrive simultaneously with a trough from the other wave. Note that if the cork in the picture experiences constructive interference, it does not mean than neighboring corks will. The distance from the sources to the other corks would be different. An example of this is Young’s Double-Slit experiment, where the two sources are small holes in a screen emitting light that is in phase. On the opposite wall is a screen that features alternating bright and dark fringes. Bright fringes are the result of constructive interference and dark fringes are the result of destructive interference. They alternate, since the path difference changes as you move up or down the screen.
Let’s say that we have a long rope with one end in our fingers and the other end attached to a wall. We wiggle the rope up and down at a certain frequency, f, and create waves of frequency f that travel down the length of the rope. When they hit the wall, they’ll be reflected. We now have two waves on the same rope (the wave we continue to generate plus the reflected wave) with the same frequency and amplitude but traveling in opposite directions. These waves will interfere. If the frequency is just right, the resulting wave seems to stand still; the rope continues to vibrate up and down, but the resultant wave no longer travels. The combination of these traveling waves produces a standing wave, with the horizontal positions of the crests and troughs remaining fixed.
Notice that each point along the rope has its own amplitude. Some points don’t vibrate up and down at all; these points are called nodes (points of no displacement). Halfway between any two consecutive nodes are points where the amplitude is maximized; these positions are called antinodes. Every other point has an amplitude that’s smaller than the amplitude at the antinode positions.
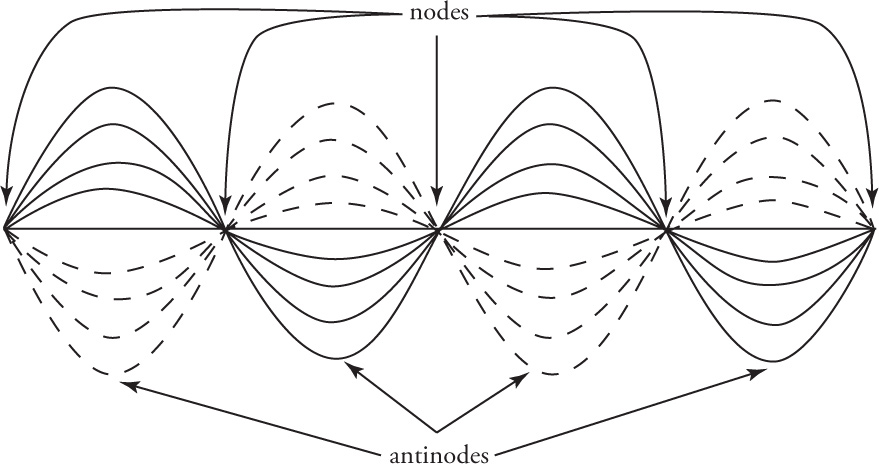
To figure out the conditions under which a standing wave will be formed, we’ll look at the three simplest standing waves. In the figure at the top of the next page, we have a rope of length L. The first picture shows the simplest standing wave that can form if we have nodes at the two ends; the second and third pictures show the next simplest standing waves that the rope could support.
The distance between any two consecutive nodes is always one-half of the wavelength. The first picture shows us that one of these half-wavelengths is equal to L; in the second picture, two half-wavelengths are equal to L; and in the third picture, three half-wavelengths are equal to L.
Notice the pattern that emerges relating the length of the rope and the wavelength of the standing wave.
Standing-Wave Wavelengths for Two Fixed Ends
λn =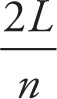 
where n = 1, 2, 3…
The only standing waves that can be supported are those for which the length of the rope is equal to a whole number of half-wavelengths, so the wavelength must be twice the length of the rope divided by a whole number:
The number n is called the harmonic number. The first harmonic is usually called the fundamental because once we know the fundamental wavelength, λ1, we automatically know all the other harmonic wavelengths, because we can write λn in terms of λ1, like this: λn = λ1/n.
Because the equation v = λf must always be true, and only certain wavelengths are allowed for a standing wave, then only certain frequencies will give standing waves. To find the harmonic frequencies, we just write λnfn = v, and solve for fn:
Standing-Wave Frequencies for Two Fixed Ends
Fn =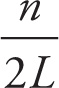 
v where n = 1, 2, 3…
In the same way that the fundamental wavelength can be used to figure out all the other harmonic wavelengths, the fundamental frequency can be used to figure out all the other harmonic frequencies: fn = nf1. Memorizing this equation is helpful for the MCAT.
It is possible to create standing waves with only one fixed end (node) and one non-fixed end (antinode), but the appropriate formulas to find frequency and wavelength for this situation are discussed in Chapter 12. Regardless of the type of standing wave, the formula to find the appropriate harmonic from the fundamental frequency still holds (fn = nf1).
Example 11-14: If a rope of length 6 m supports a standing wave with exactly four nodes (which includes the ends of the rope), what is the wavelength of the standing wave?
Solution: Draw the standing wave. It should look just like the third harmonic drawn on the previous page. Therefore, the wavelength is λ3 = 2L/3 = 2(6 m)/3 = 4 m.
Example 11-15: The speed of a transverse traveling wave along a certain 4-meter-long rope is 24 m/s. Which of the following frequencies could cause a standing wave to form on this rope, assuming both ends of the rope are fixed?
A. 32 Hz
B. 33 Hz
C. 34 Hz
D. 35 Hz
Solution: The fundamental frequency for this rope is f1 = (1/2L)v = 3 Hz. All harmonic frequencies are whole-number multiples of the fundamental, so any frequency that could cause a standing wave to form on the rope must be a multiple of 3 Hz. Of the choices given, only choice B, 33 Hz, is a multiple of 3 Hz.
Example 11-16: For a particular rope, it’s found that the fundamental frequency is 6 Hz. What’s the third-harmonic frequency?
Solution: From the equation fn = nf1, we get f3 = 3f1 = 3(6 Hz) = 18 Hz.
Example 11-17: For a particular rope, it’s found that the second-harmonic frequency is 8 Hz. What’s the fifth-harmonic frequency?
Solution: The equation fn = nf1 gives us f2 = 2f1. This means that f1 = f2/2 = (8 Hz)/2 = 4 Hz. Therefore, f5 = 5f1 = 5(4 Hz) = 20 Hz.
Example 11-18: The second-harmonic wavelength for a rope fixed at both ends is 0.5 m. How fast do transverse waves travel along this rope if the fundamental frequency is 4 Hz?
Solution: Using the equation λn = λ1/n, we get λ2 = λ1/2. This means that λ1 = 2λ2 = 2(0.5 m) = 1 m. Now, multiplying any harmonic wavelength by its corresponding harmonic frequency will give us the wave speed. In particular, we have v = λ1f1, so v = (1 m)(4 Hz) = 4 m/s.
Simple Harmonic Motion (SHM) requires:
− dynamics condition: restoring force is directly proportional to displacement from equilibrium (x = 0) and points towards that equilibrium point
− kinematics condition: frequency and period are independent of the amplitude of oscillations
Hooke’s law (spring): F = –kx
Elastic potential energy (spring): PEelastic = 
kx2
Spring-block oscillator frequency: f =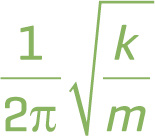 
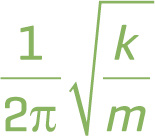
Simple pendulum frequency (small oscillations): f = 
Period/frequency
(all harmonic motion and waves): T = 1/f
Wave equation: v = λf
Two Big Rules for Waves to be used with wave equation:
1) Wave speed v depends on wave type and the medium, not on frequency
2) A single wave passing between media maintains a constant frequency
Standing wave on a rope (both ends fixed nodes)
| Standing-wave wavelengths: | λn =  (n = 1, 2, 3, …) |
 |
|
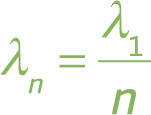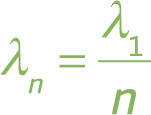| Standing-wave frequencies: | fn = 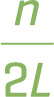 v (n = 1, 2, 3, …) |
| fn = nf1 |
1. A 2 kg mass is attached to a massless, 0.5 m string and is used as a simple pendulum by extending it to an angle θ = 5° and allowing it to oscillate. Which of the following changes will increase the period of the pendulum?
A) Replacing the mass with a 1 kg mass
B) Changing the initial extension of the pendulum to a 10° angle
C) Replacing the string with a 0.25 m string
D) Moving the pendulum to the surface of the moon
2. A 100 kg bungee jumper attached to a bungee cord jumps off a bridge. The bungee cord stretches and the man reaches the lowest spot in his descent before beginning to rise. The force of the stretched bungee cord can be approximated using Hooke’s law, where the value of the spring constant is replaced by an elasticity constant, in this case, 100 kg/s2. If the cord is stretched by 30 m at the lowest spot of the man’s descent, then what his acceleration at the lowest spot?
A) 0 m/s2
B) 10 m/s2
C) 20 m/s2
D) 30 m/s2
3. A physics student is doing a wave experiment with a 1 m long cord stretched across the lab table. In the middle of the cord, a 1 cm section is painted red. A specially designed machine creates vibrations so that a sine wave will travel on the cord from the east side of the table to the west side of the table. The vibrations of the sine wave are parallel to the table and peak at the north side of the table and the south side of the table. Which of the following best describes the motion of the red spot?
A) The spot moves from east to west along the sine wave.
B) The spot moves from west to east along the sine wave.
C) The spot remains in a fixed location on the table.
D) The spot vibrates between the north side and south side of the table.
4. A parent is pushing a young child on a swing at the playground. When the parent stops pushing, the child’s swinging motion continues without assistance. Assume the chain on the swing has negligible mass and any friction is negligible. Which of the following would need to be true in order for the child’s motion on the swing to be considered simple harmonic motion?
I. The mass of the child is not too large
II. The child is not swinging too high, so the angle between the swing and the vertical is not too big
III. The tension in the chain of the swing is negligible
A) I only
B) II only
C) I and III
D) I, II, and III
5. Immediately before a performance, a musician breaks a guitar string. The only string available to repair the guitar is twice the linear density of the string normally used. How can the musician adjust the new string so that it will still have the correct frequency? (Note: v = (Tension/µ)0.5, where µ = linear mass density.)
A) The tension of the new string should be twice the tension of the old string.
B) The tension of the new string should be half the tension of the old string.
C) The amplitude of the new string should be twice the amplitude of the old string.
D) The amplitude of the new string should be half the amplitude of the old string.
6. The speed of a 2 kg mass on a spring is 4 m/s as it passes through its equilibrium position. What is its frequency if the amplitude is 2 m?
A) 1/5 Hz
B) 1/3 Hz
C) 3 Hz
D) 5 Hz
7. The distance from a trough to a crest is 20 cm on a 3 m rope of 1 kg. If the tension in the rope is 3 N, what is the period? (Note: v = [tension/linear density]0.5)
A) 1/15 s
B) 2/15 s
C) 15/2 s
D) 15 s
A physics student conducts an experiment to study pendulums and momentum. Using an apparatus known as Newton’s cradle, the student conducts two different trials. The Newton’s cradle apparatus consists of five identical steel balls of equal size and mass. Each ball is suspended from two wires that connect it to a frame, so that the ball is in the air and can move side to side in a single plane. The balls are suspended so that they are touching each other and are free to move individually or as a group. Each ball can be considered a simple pendulum since the hanging wires have negligible mass. Assume there is no friction in the pendulum mechanism.
For the first trial, Ball A is raised at an angle, θ, from the vertical and let go. The ball swings down and hits Ball B. Momentum is transferred through Balls B, C, and D to Ball E, causing Ball E to swing up to a maximum angle, θ, from the vertical on the right while Balls A, B, C, and D are stationary. Then Ball E swings down and hits Ball D, transferring momentum through Balls D, C, and B to Ball A, causing Ball A to swing up again to the same maximum angle, θ, from the vertical while Balls E, D, C, and B are stationary. The period for this motion is measured to be 1.5 seconds.
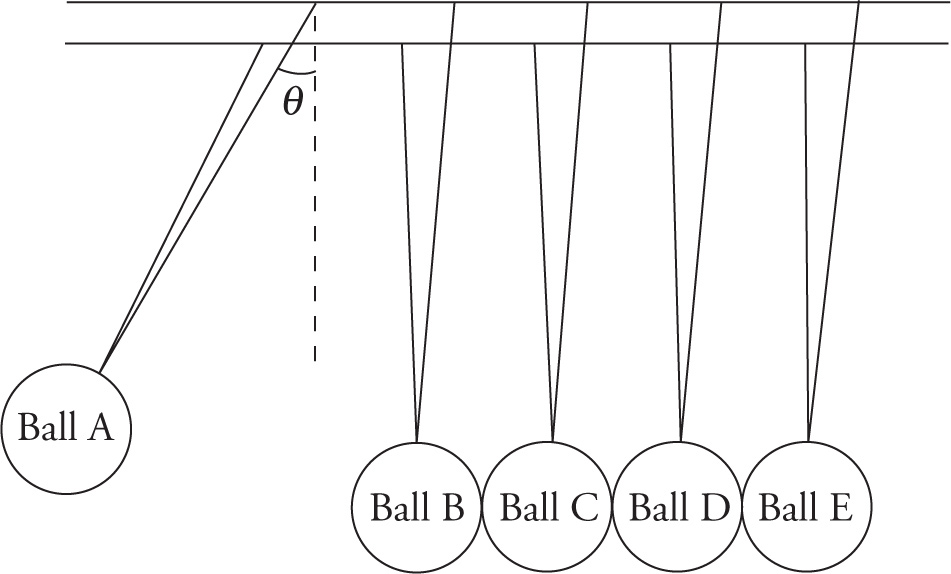
Figure 1 Newton’s Cradle Apparatus with Ball A raised at the start of Trial 1
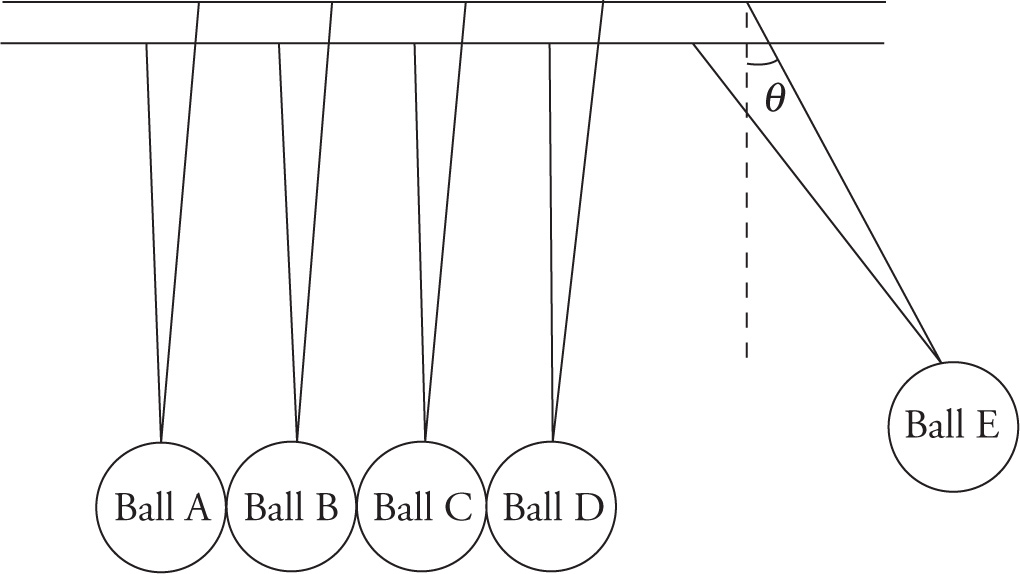
Figure 2 Newton’s Cradle Apparatus after transfer of momentum to Ball E during Trial 1
For the second trial, both Ball A and Ball B are lifted together to the same angle, θ, as in the first trial. The result of the swing is that both Ball D and Ball E swing up on the right with the same displacement angle, θ. As in the first trial, momentum is conserved.
1. Which of the following is true during the experiment?
A) Kinetic energy is not conserved and the collisions are inelastic.
B) Kinetic energy is not conserved and the collisions are elastic.
C) Kinetic energy is conserved and the collisions are inelastic.
D) Kinetic energy is conserved and the collisions are elastic.
2. Which of the following is true when Ball E is at half of its maximum height as measured from its lowest point?
I. The kinetic energy is half of the total mechanical energy.
II. The velocity is half of the maximum velocity of the ball.
III. The time elapsed from the time Ball E started in motion to the time it reached half of its maximum height is half of the period.
A) I only
B) I and III
C) II and III
D) I, II, and III
3. What should be the measured period in Trial 2?
A) 1.0 seconds
B) 1.5 seconds
C) 2.0 seconds
D) 3.0 seconds
4. For Ball E, how does the maximum velocity in Trial 2, v2, compare to the maximum velocity in Trial 1, v1?
A) v2 = (1/2)v1
B) v2 = (1/
)v1
C) v2 = v1
D) v2 = 2v1
5. To help record results, the student attached pens of negligible mass to each ball and scrolled paper perpendicular to the axis of motion of the Newton’s cradle. The paper scrolls at a rate of 20 cm/s underneath the pens during the trials. What is the wavelength of the resulting wave graphed in Trial 1?
A) 13 cm
B) 20 cm
C) 30 cm
D) 33 cm
6. If L is the length of each string, what is the maximum height of Ball E in Trial 1 above its lowest position?
A) L − cos θ
B) L − L cos θ
C) L + L cos θ
D) L cos θ
7. In both Trial 1 and Trial 2 of the experiment, the number of balls that moved on the right side was the same as the number of balls lifted on the left side to start the motion, while all the central balls remained stationary. Which of the following changes to the experiment would most likely result in not having the same number of balls swing on each side of the apparatus?
A) Raise three balls on the left side to start the motion.
B) Increase the length of the wires holding the balls.
C) Change the masses of the balls so that each mass is different from the others.
D) Add a small space between each of the balls as they hang on the apparatus.
1. D Based on the equation T, = 2π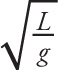 
, we know that the period does not depend on either the mass or the initial angle of extension, eliminating choices A and B. Furthermore, we know that decreasing the length of the string will decrease the period, eliminating choice C. Moving the pendulum to the surface of the moon will lower the gravitational acceleration, which would increase the period. Therefore, choice D is correct.
2. C A force diagram of the jumper at the lowest spot is shown below.
Fbungee = (100 kg/s2)(30 m) = 3000 N
Fg = (100 kg)(10 m/s2) = 1000 N
Since the force up is greater than the force down, there is a net upward force of 2000 N on the jumper and an upward acceleration. Acceleration = F/m = (2000 N)/(100 kg) = 20 m/s2.
3. D A sine wave is a transverse wave, so the vibration direction is perpendicular to the direction of propagation. The question states that the wave vibrates between the north and south and propagates from east to west. The red spot is simply a part of the cord and will vibrate in the same direction the cord is vibrating (choice C is wrong), namely between the north and south. Since a wave only transports energy, not material, it would be impossible for the spot to propagate along the wave, eliminating choices A and B and leaving choice D as the correct answer.
4. B Simple harmonic motion is by definition when the restoring force is proportional to the displacement of the object. In this case, the swing is similar to a simple pendulum (a simple pendulum has no mass in the material connecting the end of the pendulum to the rotation point, and the question states the chain has negligible mass). For a simple pendulum to experience simple harmonic motion, the restoring force must be proportional to the displacement. In this case, the displacement is the angle, θ, between the swing and the vertical. The restoring force is the component of the weight directed toward the vertical. For a child of mass, m, the restoring force is mg sin θ. If the angle is small, then sin θ approximates θ, so the motion is considered simple harmonic motion. Thus, Item II is true, eliminating choices A and C. Item I is false: The mass of the child will impact the magnitude of the restoring force, but will not indicate whether the motion is simple harmonic motion (choice D can be eliminated and choice B is correct). Item III is also false: The tension in the chain will have a variable value that is equal to the component of the weight directed along the chain, but it will have no impact on whether the motion is simple harmonic motion.
5. A The amplitude of the wave on the string will not impact the frequency of the wave or the wave speed, eliminating choices C and D. Since the frequency = wave speed/wavelength, in order to keep the frequency constant, the wave speed should be kept constant. Wave speed is proportional to the square root of tension/linear density (v = (Tension/μ)0.5) and since linear density is doubled, then tension should also be doubled in order to keep wave speed constant. The correct answer is choice A.
6. B The kinetic energy is at a maximum at the equilibrium position, and is equal to the potential energy at the amplitude: kA2 = mv2max. This equation can be solved for the spring constant, k = 8 N/m. The spring constant and the mass are all you need to determine the frequency from f =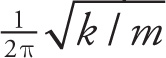 
, giving a frequency of approximately 0.33 Hz.
7. B The speed of the wave is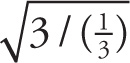 
= 3 m/s. From v = fλ, and knowing that the wavelength is 40 cm =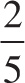 
m, the frequency is 15/2 Hz, making the period 
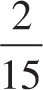
s.
1. D By definition, if a collision is elastic then kinetic energy is conserved and if a collision is inelastic then energy is not conserved, eliminating choices B and C. Momentum is always conserved during a collision. Before the collision, all the momentum is with Ball A, so pbefore = mvA. After the collision, all the momentum is with Ball E, so pafter = mvE = pbefore so vA = vE. Since the masses and velocities are the same for Ball A and Ball E, the kinetic energy of Ball A before the collision = the kinetic energy of Ball E after the collision, so kinetic energy is conserved and the collision is elastic. The correct answer is choice D.
2. A When Ball E is at its maximum height, all of its energy is potential energy and Etotal = PEmax = mghmax. When Ball E is at half of its maximum height, its potential energy is mg()hmax = ()PEmax = ()Etotal. Since the total mechanical energy is the sum of the potential energy and the kinetic energy, then the other half of the total energy must be kinetic energy. Item I is true (choice C can be eliminated). When the ball is at its lowest point, all of its mechanical energy will be kinetic energy and Etotal = KEmax = mv2max. As discussed above, at half the maximum height, half the total mechanical energy is kinetic energy. So Etotal = KEmax = 
mv2max = KEhalf. The kinetic energy can also be calculated using the velocity at the half height, vhalf. So KEhalf = mv2half = mv2max and vhalf = 
vmax. Item II is false (choice D can be eliminated). The period is the time for one full cycle. This is the time from Ball A dropping, through Ball E rising, Ball E dropping, and Ball A rising again. The entire time Ball E is moving is half of the period. The time for it to rise half way is approximately 1/8 of the entire period. Item III is false (choice B can be eliminated). The correct answer is choice A.
3. B Period depends on the length of the wire and the acceleration due to gravity T = 2π
. Neither of these changed between Trial 1 and Trial 2, so the period should be the same in Trial 2 as in Trial 1. The correct answer is choice B.
4. C For a pendulum, the maximum velocity is at the lowest point (when θ = 0). For Ball E, this occurs after the collision of Ball A, and again after falling from its maximum height. For both trials, since the angle of displacement is the same for Ball E, then the height of the ball is the same, the maximum potential energy is the same, the maximum kinetic energy is the same, and the maximum velocity is the same. The correct answer is choice C. (Note: The total mechanical energy for the system will be doubled in Trial 2 compared to Trial 1, but the question is asking specifically about Ball E, not the whole system.)
5. C The rate of the paper is the rate of propagation of the wave. Since v = f λ, and f = 1/T, we have that λ = vT. Then, λ = (20 cm/s)(1.5 s) = 30 cm. The correct answer is choice C.
6. B The easiest way to solve this is to remember that at θ = 0° the height = 0. Plugging in 0° for the angle in each of the answer choices, only choice B gives the correct value of height = 0, eliminating choices A, C, and D. Another (longer) way solve the question is using a sketch like the one below.
Using the sketch and basic trigonometry the equation is cos θ = (L − h)/L and h = L − L cos θ. The correct answer is choice B.
7. C Momentum is always conserved, so the momentum before the collision must equal the momentum after the collision. Since the balls all have the same mass, momentum is conserved when the number of balls in motion before the collision equals the number in motion after the collision. It seems likely that raising three balls to start the motion would result in three balls moving on the right side to conserve momentum (in fact, this is what happens), which is the pattern the question seeks to avoid, eliminating choice A. Changing the length of the wires will change the period of motion, but will not affect the collisions and the number of balls in motion, eliminating choice B. A small space between the balls does not affect their momentum, momentum will still be conserved, and the same number of balls will still move on each side of the apparatus, eliminating choice D. Changing the masses of the balls so that each is different means that a different combination of balls needs to move at potentially different speeds in order to conserve momentum, and a different number of balls would move on each side of the apparatus. The correct answer is choice C.
1 The conversion between degrees and radians is as follows: 180 degrees = π radians. If the angle is given in degrees, the restoring force is approximately mg θ(π/180°), which is still proportional to θ.
