Chapter 5

Membrane Potential and Action Potential

David A. McCormick

The communication of information between neurons and between neurons and muscles or peripheral organs requires that signals travel over considerable distances. A number of notable scientists have contemplated the nature of this communication through the ages. In the second century A.D., the great Greek physician Claudius Galen proposed that “humors” flowed from the brain to the muscles along hollow nerves. A true electrophysiological understanding of nerve and muscle, however, depended on the discovery and understanding of electricity itself. The precise nature of nerve and muscle action became clearer with the advent of new experimental techniques by a number of European scientists, including Luigi Galvini, Emil Du Bois-Reymond, Carlo Matteucci, and Hermann von Helmholtz, to name a few (McComas, 2011). Through the application of electrical stimulation to nerves and muscles, these early electrophysiologists demonstrated that the conduction of commands from the brain to the muscle for the generation of movement was mediated by the flow of electricity along nerve fibers.

With the advancement of electrophysiological techniques, electrical activity recorded from nerves revealed that the conduction of information along the axon was mediated by the active generation of an electrical potential, called the action potential. But what precisely was the nature of these action potentials? To know this in detail required not only a preparation from which to obtain intracellular recordings but also one that could survive in vitro. The squid giant axon provided precisely such a preparation. Many invertebrates contain unusually large axons for the generation of escape reflexes; large axons conduct more quickly than small ones and so the response time for escape is reduced. The squid possesses an axon approximately 0.5 mm in diameter, large enough to be impaled by even a course micropipette (Fig. 5.1). By inserting a glass micropipette filled with a salt solution into the squid giant axon, Alan Hodgkin and Andrew Huxley demonstrated in 1939 that axons at rest are electrically polarized, exhibiting a resting membrane potential of approximately −60 mV inside versus outside. In the generation of an action potential, the polarization of the membrane is removed (referred to as depolarization) and exhibits a rapid swing toward, and even past, 0 mV (Fig. 5.1). This depolarization is followed by a rapid swing in the membrane potential to more negative values, a process referred to as hyperpolarization. The membrane potential following an action potential typically becomes even more negative than the original value of approximately −60 mV. This period of increased polarization is referred to as the after-hyperpolarization or the undershoot.

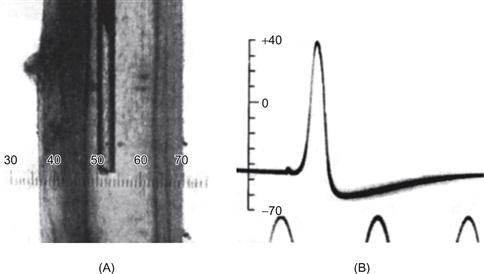
Figure 5.1 Intracellular recording of the membrane potential and action potential generation in the squid giant axon. (A) A glass micropipette, about 100 μm in diameter, was filled with seawater and lowered into the giant axon of the squid after it had been dissected free. The axon is about 1 mm in diameter and is transilluminated from behind. (B) One action potential recorded between the inside and the outside of the axon. Peaks of a sine wave at the bottom provided a scale for timing, with 2 ms between peaks.

From Hodgkin and Huxley (1939).

The development of electrophysiological techniques to the point that intracellular recordings could be obtained from the small cells of the mammalian nervous system revealed that action potentials in these neurons are generated through mechanisms similar to that of the squid giant axon.

It is now known that action potential generation in nearly all types of neurons and muscle cells is accomplished through mechanisms similar to those first detailed in the squid giant axon by Hodgkin and Huxley. This chapter considers the cellular mechanisms by which neurons and axons generate a resting membrane potential, how signals passively propagate through neuronal processes, and finally, how active propagation of electrical signals is achieved through generation of the action potential.

Membrane Potential

Membrane Potential Is Generated by the Differential Distribution of Ions

Through the operation of ionic pumps and special ionic buffering mechanisms, neurons actively maintain precise internal concentrations of several important ions, including Na⁺, K⁺, Cl⁻, and Ca²⁺. The mechanisms by which they do so are illustrated in Figures 5.2 and 5.3. The intracellular and extracellular concentrations of Na⁺, K⁺, Cl⁻, and Ca²⁺ differ markedly (Fig. 5.2); K⁺ is actively concentrated inside the cell, and Na⁺, Cl⁻, and Ca²⁺ are actively extruded to the extracellular space. However, this does not mean that the cell is filled only with positive charge; anions to which the plasma membrane is impermeant are also present inside the cell and almost balance the high concentration of K⁺. The osmolarity inside the cell is approximately equal to that outside the cell.

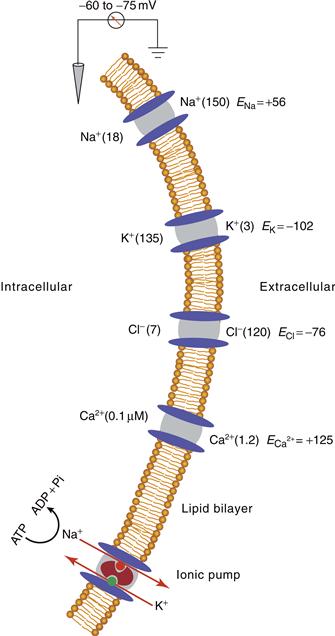
Figure 5.2 Differential distribution of ions inside and outside plasma membrane of neurons and neuronal processes, showing ionic channels for Na⁺, K⁺, Cl⁻, and Ca²⁺, as well as an electrogenic Na⁺–K⁺ ionic pump (also known as Na⁺, K⁺-ATPase). Concentrations (in millimoles except that for intracellular Ca²⁺) of the ions are given in parentheses; their equilibrium potentials (E) for a typical mammalian neuron are indicated.

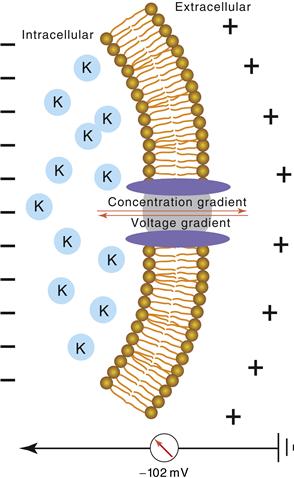
Figure 5.3 The equilibrium potential is influenced by the concentration gradient and the voltage difference across the membrane. Neurons actively concentrate K⁺ inside the cell. These K⁺ ions tend to flow down their concentration gradient from inside to outside the cell. However, the negative membrane potential inside the cell provides an attraction for K⁺ ions to enter or remain within the cell. These two factors balance one another at the equilibrium potential, which in a typical mammalian neuron is −102 mV for K⁺.

Electrical and Thermodynamic Forces Determine the Passive Distribution of Ions

Ions tend to move down their concentration gradients through specialized ionic pores, known as ionic channels, in the plasma membrane. Through simple laws of thermodynamics, the high concentration of K⁺ inside glial cells, neurons, and axons results in a tendency for K⁺ ions to diffuse down their concentration gradient and leave the cell or cell process (Fig. 5.3). However, the movement of ions across the membrane also results in a redistribution of electrical charge. As K⁺ ions move down their concentration gradient, the intracellular voltage becomes more negative, and this increased negativity results in an electrical attraction between the negative potential inside the cell and the positively charged, K⁺ ions, thus offsetting the outward flow of these ions. The membrane is selectively permeable—that is, it is impermeable to the large anions inside the cell, which cannot follow the potassium ions across the membrane. At some membrane potential, the “force” of the electrostatic attraction between the negative membrane potential inside the cell and the positively charged K⁺ ions will exactly balance the thermal “forces” by which K⁺ ions tend to flow down their concentration gradient (Fig. 5.3). In this circumstance, it is equally likely that a K⁺ ion exits the cell by movement down the concentration gradient as it is that a K⁺ ion enters the cell due to the attraction between the negative membrane potential and the positive charge of this ion. At this membrane potential, there is no net flow of K⁺ (the same number of K⁺ ions enter the cell as leave the cell per unit time) and these ions are said to be in equilibrium. The membrane potential at which this occurs is known as the equilibrium potential. (See Box 5.1 for calculation of the equilibrium potential.)

Box 5.1 Nernst Equation

The equilibrium potential is determined by (1) the concentration of the ion inside and outside the cell, (2) the temperature of the solution, (3) the valence of the ion, and (4) the amount of work required to separate a given quantity of charge. The equation that describes the equilibrium potential was formulated by a German physical chemist named Walter Nernst in 1888:

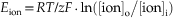
Here, E_ion is the membrane potential at which the ionic species is at equilibrium, R is the gas constant [8.315 J per Kelvin per mole (J K⁻¹ mol⁻¹)], T is the temperature in Kelvins (T_Kelvin = 273.16 + T_Celcius), F is Faraday’s constant [96,485 coulombs per mole (C mol⁻¹)], z is the valence of the ion, and [ion]_o and [ion]_i are the concentrations of the ion outside and inside the cell, respectively. For a monovalent, positively charged ion (cation) at room temperature (20°C), substituting the appropriate numbers and converting natural log (ln) into log base 10 (log₁₀) result in

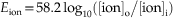
at a body temperature of 37°C, the Nernst equation is

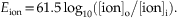
David A. McCormick

To illustrate, let us consider the passive distribution of K⁺ ions in the squid giant axon as studied by Hodgkin and Huxley. The K⁺ concentration [K⁺] inside the squid giant axon is about 400 mM, whereas the [K⁺] outside the axon is about 20 mM. Because [K⁺]_i is greater than [K⁺]_o, potassium ions will tend to flow down their concentration gradient, from inside to outside the axon, taking positive charge with them. The equilibrium potential (at which the tendency for K⁺ ions to flow down their concentration gradient will be exactly offset by the attraction for K⁺ ions to enter the cell because of the negative charge inside the cell) at a room temperature of 20°C can be calculated by the Nernst equation as such:

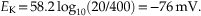
Therefore, at a membrane potential of −76 mV, K⁺ ions have an equal tendency to flow either into or out of the axon. The concentrations of K⁺ in mammalian neurons and glial cells differ considerably from that in the squid giant axon, which is adapted to live in seawater. By substituting 3.1 mM for [K⁺]_o and 140 mM for [K⁺]_i in the Nernst equation, with mammalian body temperature, T = 37°C, we obtain

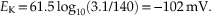
Movements of Ions Can Cause Either Hyperpolarization or Depolarization

In mammalian cells, at membrane potentials positive to −102 mV, K⁺ ions tend to flow out of the cell. Increasing the ability of K⁺ ions to flow across the membrane—that is, increasing the conductance of the membrane to K⁺ (gK) causes the membrane potential to become more negative, or hyperpolarized, due to the exiting of positively charged ions from inside the cell (Fig. 5.4).

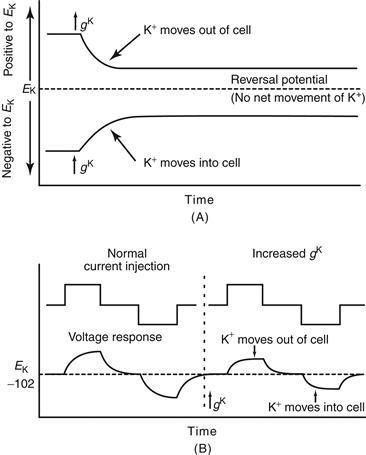
Figure 5.4 Increases in K⁺ conductance can result in hyper-polarization, depolarization, or no change in membrane potential. (A) Opening K⁺ channels increases the conductance of the membrane to K⁺, denoted gK. If the membrane potential is positive to the equilibrium potential (also known as the reversal potential) for K⁺, then increasing gK will cause some K⁺ ions to leave the cell, and the cell will become hyperpolarized. If the membrane potential is negative to E_K when gK is increased, then K⁺ ions will enter the cell, therefore making the inside more positive (more depolarized). If the membrane potential is exactly E_K when gK is increased, then there will be no net movement of K⁺ ions. (B) Opening K⁺ channels when the membrane potential is at E_K does not change the membrane potential; however, it reduces the ability of other ionic currents to move the membrane potential away from E_K. For example, a comparison of the ability of the injection of two pulses of current, one depolarizing and one hyperpolarizing, to change the membrane potential before and after opening K⁺ channels reveals that increases in gK decrease the responses of the cell noticeably.

At membrane potentials negative to −102 mV, K⁺ ions tend to flow into the cell; increasing the membrane conductance to K⁺ causes the membrane potential to become more positive, or depolarized, due to the flow of positive charge into the cell. The membrane potential at which the net current “flips” direction is referred to as the reversal potential. If the channels conduct only one type of ion (e.g., K⁺ ions), then the reversal potential and the Nernst equilibrium potential for that ion coincide (Fig. 5.4A). Increasing the membrane conductance to K⁺ ions while the membrane potential is at the equilibrium potential for K⁺ (E_K) does not change the membrane potential because no net driving force causes K⁺ ions to either exit or enter the cell. However, this increase in membrane conductance to K⁺ decreases the ability of other species of ions to change the membrane potential because any deviation of the potential from E_K increases the drive for K⁺ ions to either exit or enter the cell, thereby drawing the membrane potential back toward E_K (Fig. 5.4B). This effect is known as a “shunt” and is important for some effects of inhibitory synaptic transmission.

The exiting and entering of the cell by K⁺ ions during generation of the membrane potential give rise to a curious problem. When K⁺ ions leave the cell to generate a membrane potential, the concentration of K⁺ changes both inside and outside the cell. Why does this change in concentration not alter the equilibrium potential, thus changing the tendency for K⁺ ions to flow down their concentration gradient? The reason is that the number of K⁺ ions required to leave the cell to achieve the equilibrium potential is quite small. For example, if a cell were at 0 mV and the membrane suddenly became permeable to K⁺ ions, only about 10⁻¹² mol of K⁺ ions per square centimeter of membrane would move from inside to outside the cell in bringing the membrane potential to the equilibrium potential for K⁺. In a spherical cell of 25 μm diameter, this would amount to an average decrease in intracellular K⁺ of only about 4 μM (e.g., from 140 to 139.996 mM). However, there are instances when significant changes in the concentrations of K⁺ may occur, particularly during the generation of pronounced activity, such as an epileptic seizure. During the occurrence of a tonic–clonic generalized (grand mal) seizure, large numbers of neurons discharge throughout the cerebral cortex in a synchronized manner. This synchronous discharge of large numbers of neurons significantly increases the extracellular K⁺ concentration, by as much as a couple of millimoles, resulting in a commensurate positive shift in the equilibrium potential for K⁺. This shift in the equilibrium potential can increase the excitability of affected neurons and neuronal processes and thus promote the spread of the seizure activity. Fortunately, the extracellular concentration of K⁺ is tightly regulated and is kept at normal levels through uptake by glial cells, as well as by diffusion through the fluid of the extracellular space.

As is true for K⁺ ions, each of the membrane-permeable species of ions possesses an equilibrium potential that depends on the concentration of that ion inside and outside the cell. Thus, equilibrium potentials may vary between different cell types, such as those found in animals adapted to live in salt water versus mammalian neurons. In mammalian neurons, the equilibrium potential is approximately 56 mV for Na⁺, approximately −76 mV for Cl⁻, and about 125 mV for Ca²⁺ (see Fig. 5.2). Thus, increasing the membrane conductance to Na⁺ (gNa) through the opening of Na⁺ channels depolarizes the membrane potential toward 56 mV; increasing the membrane conductance to Cl⁻ brings the membrane potential closer to −76 mV; and finally increasing the membrane conductance to Ca²⁺ depolarizes the cell toward 125 mV.

Na⁺, K⁺, and Cl⁻ Contribute to the Determination of the Resting Membrane Potential

If a membrane is permeable to only one ion and no electrogenic ionic pumps are operating (see next section), then the membrane potential is necessarily at the equilibrium potential for that ion. At rest, the plasma membrane of most cell types is not at the equilibrium potential for K⁺ ions, indicating that the membrane is also permeable to other types of ions. For example, the resting membrane of the squid giant axon is permeable to Cl⁻ and Na⁺, as well as K⁺, due to the presence of ionic channels that not only allow these ions to pass but also are open at the resting membrane potential. Because the membrane is permeable to K⁺, Cl⁻, and Na⁺, the resting potential of the squid giant axon is not equal to E_K, E_Na, or E_Cl, but is somewhere in between these three. A membrane permeable to more than one ion has a steady-state membrane potential whose value is between those of the equilibrium potentials for each of the permeant ions (Box 5.2).

Box 5.2 Goldman-Hodgkin-Katz Equation

An equation developed by Goldman and later used by Alan Hodgkin and Bernard Katz describes the steady-state membrane potential for a given set of ionic concentrations inside and outside the cell and the relative permeabilities of the membrane to each of those ions:

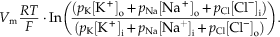
The relative contribution of each ion is determined by its concentration differences across the membrane and the relative permeability (p_K, p_Na, p_Cl) of the membrane to each type of ion. If a membrane is permeable to only one ion, then the Goldman–Hodgkin–Katz equation reduces to the Nernst equation. In the squid giant axon, at resting membrane potential, the permeability ratios are

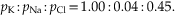
The membrane of the squid giant axon, at rest, is most permeable to K⁺ ions, less so to Cl⁻, and least permeable to Na⁺. (Chloride appears to contribute considerably less to the determination of the resting potential of mammalian neurons.) These results indicate that the resting membrane potential is determined by the resting permeability of the membrane to K⁺, Na⁺, and Cl⁻. In theory, this resting membrane potential may be anywhere between E_K (e.g., −76 mV) and E_Na (55 mV). For the three ions at 20°C, the equation is

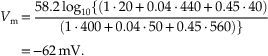
This suggests that the squid giant axon should have a resting membrane potential of −62 mV. In fact, the resting membrane potential may be a few millivolts hyperpolarized to this value through the operation of the electrogenic Na⁺–K⁺ pump.

David A. McCormick

Different Types of Neurons Have Different Resting Potentials

Intracellular recordings from neurons in the mammalian central nervous system (CNS) reveal that different types of neurons exhibit different resting membrane potentials. Indeed, some types of neurons do not even exhibit a true “resting” membrane potential; they spontaneously and continuously generate action potentials even in the total lack of synaptic input. In the visual system, intracellular recordings have shown that photoreceptor cells of the retina—the rods and cones—have a membrane potential of approximately −40 mV at rest and are hyperpolarized when activated by light. Cells in the dorsal lateral geniculate nucleus, which receive axonal input from the retina and project to the visual cortex, have a resting membrane potential of approximately −70 mV during sleep and −55 mV during waking, whereas pyramidal neurons of the visual cortex have a resting membrane potential of about −75 mV. Presumably, the resting membrane potentials of different cell types in the central and peripheral nervous system are highly regulated and are functionally important. For example, the depolarized membrane potential of photoreceptors presumably allows the membrane potential to move in both negative and positive directions in response to changes in light intensity. The hyper-polarized membrane potential of thalamic neurons during sleep (−70 mV) dramatically decreases the flow of information from the sensory periphery to the cerebral cortex, presumably to allow the cortex to be relatively undisturbed during sleep, and the 20 mV membrane potential between the resting potential and the action potential threshold in cortical pyramidal cells allows these cells to be strongly influenced by subthreshold barrages of synaptic potentials from other cortical neurons, which provide the context under which we think and behave (see Chapter 9).

Ionic Pumps Actively Maintain Ionic Gradients

Because the resting membrane potential of a neuron is not at the equilibrium potential for any particular ion, ions constantly flow down their concentration gradients. This flux becomes considerably larger with the generation of electrical and synaptic potentials because ionic channels are opened by these events. Although the absolute number of ions traversing the plasma membrane during each action potential or synaptic potential may be small in individual cells, the collective influence of a large neural network of cells, such as in the brain, and the presence of ion fluxes even at rest can substantially change the distribution of ions inside and outside neurons. Cells have solved this problem with the use of active transport of ions against their concentration gradients. The proteins that actively transport ions are referred to as ionic pumps, of which the Na⁺–K⁺ pump is perhaps the most thoroughly understood (Lauger, 1991). The Na⁺–K⁺ pump is stimulated by increases in the intracellular concentration of Na⁺ and moves Na⁺ out of the cell while moving K⁺ into it, achieving this task through the hydrolysis of ATP (Fig. 5.2). Three Na⁺ ions are extruded for every two K⁺ ions transported into the cell. Because of the unequal transport of ions, the operation of this pump generates a hyper-polarizing electrical potential and is said to be electrogenic. The Na⁺–K⁺ pump typically results in the membrane potential of the cell being a few millivolts more negative than it would be otherwise.

The Na⁺–K⁺ pump consists of two subunits, α and β, arranged in a tetramer (αβ)₂. The Na⁺–K⁺ pump is believed to operate through conformational changes that alternatively bind Na⁺ ions from the inside of the cell and release them to the extracellular space, while binding K⁺ ions from outside the cell and releasing them into the intracellular mileau (Fig. 5.2). Such a conformation change is due to the phosphorylation and dephosphorylation of the protein.

The membranes of neurons and glia contain multiple types of ionic pumps, used to maintain the proper distribution of each ionic species important for cellular signaling (Reithmeier, 1994). Many of these pumps are operated by the Na⁺ gradient across the cell, whereas others operate through a mechanism similar to that of the Na⁺–K⁺ pump (i.e., the hydrolysis of ATP). For example, the calcium concentration inside neurons is kept to very low levels (typically 50–100 nM) through the operation of both types of ionic pumps, as well as special intracellular Ca²⁺ buffering mechanisms. Ca²⁺ is extruded from neurons through both a Ca²⁺, Mg²⁺-ATPase and a Na⁺–Ca²⁺ exchanger. The Na⁺–Ca²⁺ exchanger is driven by the Na⁺ gradient across the membrane and extrudes one Ca²⁺ ion for each Na⁺ ion allowed to enter the cell.

The Cl⁻ concentration in neurons is actively maintained at a low level through operation of a chloride-bicarbonate exchanger, which brings in one ion of Na⁺ and one ion of HCO₃⁻ for each ion of Cl⁻ extruded. Intracellular pH can also markedly affect neuronal excitability and is therefore tightly regulated, in part by a Na⁺–H⁺ exchanger that extrudes one proton for each Na⁺ allowed to enter the cell.

Summary

The membrane potential is generated by the unequal distribution of ions, particularly K⁺, Na⁺, and Cl⁻, across the plasma membrane. This unequal distribution of ions is maintained by ionic pumps and exchangers. K⁺ ions are concentrated inside the neuron and tend to flow down their concentration gradient, leading to a hyperpolarization of the cell. At the equilibrium potential, the tendency of K⁺ ions to flow out of the cell will be exactly offset by the tendency of K⁺ ions to enter the cell due to the attraction of the negative potential inside the cell. The resting membrane is also permeable to Na⁺ and Cl⁻ and therefore the resting membrane potential is approximately −75 to −40 mV, in other words, substantially positive to E_K.

Passive Electrical Properties of the Neuron

Electrical activity in the nervous system not only conducts actively along neuronal processes, owing to the opening and closing of ion channels, but also moves passively, with electrical charges pushing or pulling other charges both inside and outside thin neuronal elements. How electrical charge moves passively through neurons shapes how these cells process synaptic inputs and generate action potential outputs, and thus interact with other neurons. Three properties that strongly influence the passive response properties of neuronal elements are: membrane resistance, axial resistance, and membrane capacitance (Fig. 5.5A). These three properties not only determine the amplitude of the neuron’s passive response to a synaptic input, but also the amplitude and speed of spread of this input to other parts of the neuron and the properties of the action potential response.

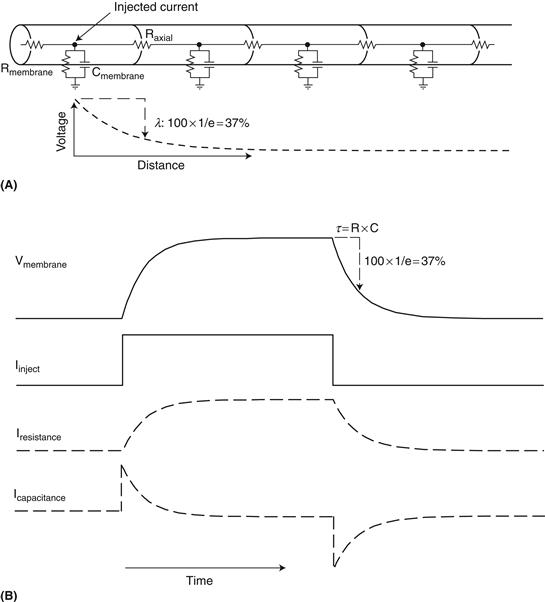
Figure 5.5 Passive response properties of neuronal element. (A) Idealized cylindrical neuronal process. The injection of current into a particular point in the process will result in the flow of ions across three paths: down the process through the axial resistance (R_axial) and across the membrane through the membrane resistance (R_membrane) and capacitance (C_membrane). The leak of current out of the process as it flows down the process and across the membrane will result in an exponential decrease in voltage. The point at which the voltage has reduced to 1/e (37%) of its original value is known as the length constant (λ). (B) Response of the membrane to the injection of a constant current pulse. Initially the injected current flows readily through the membrane capacitance (bottom trace). As this capacitative current (I_capacitance) decreases (bottom trace), there is a rise in charge inside the membrane and thus the voltage rises (V_membrane; top trace). This increase in voltage inside the cell results in an increase in current flow across the membrane resistance (I_resistance). Turning off the current pulse will result in the opposite flow of current through the capacitance, and the membrane potential will return to it’s previous level with an exponential time course. The time it takes to move to 1/e (37%) of the steady state change in membrane potential is known as the membrane time constant (τ).

The outer membrane of the neuron, being composed of phosholipids and ion channels, offers resistance to the flow of charged ions and thus exhibits a specific membrane resistance, R_m. Conversely, the cell membrane can be considered to exhibit a specific level of conductivity (G_m; conductance) to electrical currents, which is mathematically described as 1/R_m. The amount of current that flows across a given conductance is proportional to the voltage applied, in what is known as Ohm’s law:

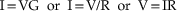
This is a linear relationship that states that the larger the voltage that is applied to a fixed conductance, the greater the current that will flow. Likewise, increasing membrane conductance (e.g., opening ion channels) increases the current that flows across the membrane in the presence of a fixed voltage. Imagine measuring the flow of water through a pipe. The rate of flow of the water (current) is proportional to the pressure applied (voltage) as well as the size of the pipe (conductance or resistance). Increasing the diameter of the pipe increases the rate at which water flows as long as the pressure doesn’t change. The change in voltage (pressure) that occurs with a fixed current flow against a resistance can also be determined (V = IR). In a neuron, for example, the opening of enough ion channels to produce 100 pA of current in a cell that is 100 Megohms in resistance will result in a change in membrane potential of 10 mV at the point of entry of the ionic current and at steady state. The qualifiers “at the point of entry” and “at steady state” are given because neurons have two properties that strongly shape the response to ionic currents: Current flows down processes and not just across membranes, and membranes not only have resistance but also capacitance (Fig. 5.5A).

Capacitance is the ability to store electrical charge and occurs whenever two electrical conductors (e.g., cytoplasm and extracellular fluid) are separated by a nonconductor (e.g., lipid membrane). The gathering of ions near one side of the membrane will push like charges away, and attract opposite charges toward, the other side of the membrane. For example, the entry of positive charge into a neuron will result in an increase in positive ions under the membrane. These positive ions on the inside of the cell membrane will repel positive ions away from the outside of the membrane, resulting in a capacitative current (I_c). In a way, capacitors conduct electricity, just as conductors do. However, there are marked differences. While a resistor conducts a constant flow of current (e.g., charges/second) with a constant voltage (I = V/R), a capacitor requires an ever increasing voltage (e.g., volts/second) in order to deliver a constant flow of current. In other words, the ability of a capacitor to provide a conduit for current flow is dependent upon the rate of change of membrane potential; it is frequency dependent. In fact, one way of thinking of a capacitor is that it is a variable resistor in which the resistance depends on frequency: at high frequencies (i.e., volts/sec is high), the resistance is low and current flows readily, while at low frequencies, the resistance is high and current flow is limited. Let’s consider why this is so and how this affects the manner in which neurons behave.

A capacitor is defined by the amount of charge (measured in coulombs; Q = 6.24 × 10¹⁸ electrons or protons) that are stored on the opposing plates per volt (C = Q/V). The current flowing through a capacitor (I_c), measured in amperes, is dQ/dt (coulombs/sec), which is equal to CdV/dt (i.e., the time differential of Q = CV). Thus, the greater the rate of change of membrane potential, the greater the flow of current through the membrane capacitance. Likewise, when the membrane potential is steady, there is no current flow through the capacitance. A second big difference between current flow through capacitance versus resistance is that the capacitative current is made up of the movement of different ions on each side of the membrane; the gathering of ions on one side influences the distribution of ions on the other. In contrast, the movement of ions through the membrane resistance, which is made up largely of ionic pores, consists of the actual movement of ions across the membrane and therefore can result in changes in ion concentrations inside and outside the cell.

Membranes are characterized by a capacitance and resistance in parallel (Fig. 5.5). If we apply a steady current to the inside of the membrane, at first the capacitance acts as a low-resistance pathway and there is a large flow of current (initially equal to that of the applied current) through the membrane capacitance (Fig. 5.5B; I_capacitance). The change in distribution of charge across the membrane will alter the membrane potential, and this will provide a new driving force for ions to move through the ionic pores that make up the membrane resistance/conductance (Fig. 5.5B; I_resistance). As ions move through the membrane resistance/conductance, the rate at which they accumulate under the membrane will slow down, resulting in a decreased rate of change of membrane potential (dV/dt) and consequently a decrease in current flow through the membrane capacitance. Eventually, the membrane potential will settle at a value dictated by the magnitude of the current injected and the membrane resistance, according to Ohm’s law.

Figure 5.6 The voltage-clamp technique keeps the voltage across the membrane constant so that the amplitude and time course of ionic currents can be measured. In the two-electrode voltage-clamp technique, one electrode measures the voltage across the membrane while the other injects current into the cell to keep the voltage constant. The experimenter sets a voltage to which the axon or neuron is to be stepped (the command potential). Current is then injected into the cell in proportion to the difference between the present membrane potential and the command potential. This feedback cycle occurs continuously, thereby clamping the membrane potential to the command potential. By measuring the amount of current injected, the experimenter can determine the amplitude and time course of the ionic currents flowing across the membrane.

The time course over which the change in membrane potential occurs in response to a step change in current is described by an exponential function in which the time constant τ_m, is determined by the product of the specific membrane resistance and membrane capacitance per unit area (τ_m = RC) and is equal to the time it takes for the membrane potential to reach 37% (100 * 1/e) of its steady-state value (Fig. 5.5B). Once the current step is turned off, current will then flow across the capacitor in the opposite direction. In the example of Figure 5.5B, the removal of the positive current step leaves the inner membrane with a buildup of positive charge (and the outer membrane with an excess of negative charge). As the inner positive and outer negative charges move away from the membrane, the membrane potential will decrease exponentially, and thus the current through the membrane resistance (conductance) will also decrease exponentially (Fig. 5.5B).

Let’s consider the hydraulic analogy again. Imagine two parallel pipes connected together on both ends. One pipe contains a chamber with a diaphragm inside (a capacitor), and the other contains a constriction (a resistor). Applying a steady flow of water to one end of the two parallel connected pipes will at first cause an equal movement of water at the other end by distending the diaphragm (capacitor). However, as the diaphragm stretches, it will start to resist further movement, and thus the water pressure inside the pipes will begin to rise. This rise in pressure will force water through the parallel (resistor) pipe at a rate determined by the pressure/resistance. Since water is now flowing through the “resistor” pipe, there is less further accumulation of water against the diaphragm, resulting in a decreased rate of water flow through the “capacitor” path. Eventually, all of the water flow will be through the “resistive” pipe and none will be through further distension of the diaphragm. Once the steady flow of water is removed, however, the diaphragm will provide a temporary source for water to flow once again, resulting in the slow dissipation of the “capacitive current” and a slow return to the precurrent water pressure (e.g., Fig. 5.5B).

An important consideration in passive properties of membrane responses, owing in part to the parallel capacitance/resistance properties of the membrane, is their frequency filtering properties. In the example in Figure 5.5B, a square pulse of current was applied, yet the membrane responded with a gradual increase (at the onset of current) and then decrease (at the offset of current) in membrane potential; the high-frequency components of the current step were filtered out by the capacitive/resistive properties of the membrane. Neuronal membranes naturally respond to some frequencies (e.g., low frequencies) better than others (e.g., high frequencies). Since conductance through the membrane capacitance is frequency dependent, being highest with rapid changes in current, the membrane capacitor, in parallel with membrane resistance, acts as a low-pass filter for changes in membrane potential (voltage across the membrane). Higher frequencies are decreased in amplitude, while low frequencies are preserved (in other words, the high-frequency currents escape from the neuron passing easily through the capacitance of the membrane, thereby reducing the ability of high-frequency current entry into the neuron to build up voltage [“pressure”] inside the cell). For a neuron with a membrane time constant of 20 msec, the “cutoff” frequency (defined as f_c = 1/(2πRC)) of the filtering properties of the membrane will be 8 Hz, meaning that increasing frequency above 8 Hz will result in a larger and larger decrease in the membrane voltage response. One often overlooked property of filters is that they not only change the amplitude but also the phase (timing) of an input in a frequency-dependent manner.

Next let’s consider how current flows along a neuronal process. The entry of ions into the cell at one point will result not only in the flow of current across the membrane resistance and capacitance but also the movement of current away from the entry point along the neuronal process. This movement of charge along the inner part of the neuron is known as “axial current.” The resistance to the movement of axial current, owing to the properties of cytoplasm and organelles within the neuron, is referred to as axial resistance (Fig. 5.5A). Axial resistance in neurons is usually small in comparison to membrane resistance, allowing current to flow readily down neuronal processes. However, as the current flows, some of it escapes through the local membrane resistance and capacitance of each neuronal compartment that it enters. Imagine a garden hose that not only is elastic (can bulge, representing capacitance) but also has small holes in it all along its length. The application of a given value of water pressure at the end of the hose will result in a gradient of pressure along the hose, owing to the local reduction in water pressure through the leaking and bulging of the hose. Likewise, in a neuronal process, the voltage (e.g., “pressure”) decreases exponentially as the current spreads across the axial resistance and leaks out through the resistance and capacitance of the membrane (Fig. 5.5A). The point at which the membrane potential has fallen to 1/e (or 37%) of its original value is known as the length constant (λ) of the process (Fig. 5.5A). Neuronal processes such as dendrites and axons have characteristic length constants in the range of 0.1 to 1 mm at steady state, depending on their diameter. Larger-diameter processes, such as the squid giant axon, have lower axial resistance (higher axial conductance) and therefore a longer length constant, allowing electrical current to have a broader influence and to flow quickly. The length constant also depends upon the frequency of the input, since the outer membrane acts as a frequency dependent filter. This filtering property not only affects the amplitude of electrical events as they propagate, but also their phase. Since the dendritic processes of many neurons are within the 0.1–1 mm length constant, voltage changes at one part of a dendrite can passively spread to a significant portion of the local dendritic arbor. For the vast majority of axons, a length constant of 0.1–1 mm is insufficient to spread information to synaptic boutons, resulting in the need of action potentials to propagate information over long distances. It is interesting to note, however, that a length constant of 0.2–0.4 mm, even in the fine axons of the brain, suggests that local changes in membrane potential at the soma can actually propagate to nearby synaptic terminals and potentially influence synaptic transmission (Shu, Hasenstaub, Duque, Yu, & McCormick, 2006).

The flow of current in actual neurons is complex, owing to both the complicated geometries of dendritic and axonal arbors and the presence of ionic channels that actively open and close in response to changes in membrane voltage. These active properties of neurons result not only in the ability of the cell to communicate over long distances, but they also allow each cell type to exhibit its own unique electrophysiological properties that are useful for achieving its specific task in brain function.

Action Potential

An Increase in Na⁺ and K⁺ Conductance Generates Action Potentials

Hodgkin and Huxley not only recorded the action potential with an intracellular microelectrode (Fig. 5.1), but they also went on to perform a remarkable series of experiments that explained qualitatively and quantitatively the ionic mechanisms by which the action potential is generated (Hodgkin & Huxley, 1952a, 1952b). As mentioned earlier, these investigators found that during the action potential, the membrane potential of the cell rapidly overshoots 0 mV and approaches the equilibrium potential for Na⁺. After generation of the action potential, the membrane potential repolarizes and becomes more negative than before, generating an after-hyperpolarization. These changes in membrane potential during generation of the action potential were associated with a large increase in conductance of the plasma membrane, but to what does the membrane become conductive in order to generate the action potential? The prevailing hypothesis was that there was a nonselective increase in conductance causing the negative resting potential to increase toward 0 mV. Since publication of the experiments of E. Overton in 1902, the action potential had been known to depend on the presence of extracellular Na⁺. Reducing the concentration of Na⁺ in the artificial seawater bathing the axon resulted in a marked reduction in the amplitude of the action potential. On the basis of these and other data, Hodgkin and Katz proposed that the action potential is generated through a rapid increase in the conductance of the membrane to Na⁺ ions. A quantitative proof of this theory was lacking, however, because ionic currents could not be observed directly. Development of the voltage-clamp technique by Kenneth Cole at the Marine Biological Laboratory in Massachusetts resolved this problem and allowed quantitative measurement of the Na⁺ and K⁺ currents underlying the action potential (Cole, 1949; Box 5.3).

Box 5.3 Voltage-Clamp Technique

In the voltage-clamp technique, two independent electrodes are inserted into the squid giant axon: one for recording the voltage difference across the membrane and the other for intracellularly injecting the current (Fig. 5.6). These electrodes are then connected to a feedback circuit that compares the measured voltage across the membrane with the voltage desired by the experimenter. If these two values differ, then current is injected into the axon to compensate for this difference. This continuous feedback cycle, in which the voltage is measured and current is injected, effectively “clamps” the membrane at a particular voltage. If ionic channels were to open, then the resultant flow of ions into or out of the axon would be compensated for by the injection of positive or negative current into the axon through the current-injection electrode. The current injected through this electrode is necessarily equal to the current flowing through the ionic channels. It is this injected current that is measured by the experimenter. The benefits of the voltage-clamp technique are twofold. First, the current injected into the axon to keep the membrane potential “clamped” is necessarily equal to the current flowing through the ionic channels in the membrane, thereby giving a direct measurement of this current. Second, ionic currents are both voltage and time dependent; they become active at certain membrane potentials and do so at a particular rate. Keeping the voltage constant in the voltage clamp allows these two variables to be separated; the voltage dependence and the kinetics of the ionic currents flowing through the plasma membrane can be measured directly.

David A. McCormick

Hodgkin and Huxley used the voltage-clamp technique to investigate the mechanisms of generation of the action potential in the squid giant axon. Axons and neurons have a threshold for the initialization of an action potential of about −45 to −55 mV. Increasing the voltage from −60 to 0 mV produces a large, but transient, flow of positive charge into the cell (known as inward current). This transient inward current is followed by a sustained flow of positive charge out of the cell (the outward current). By voltage clamping the cell and substituting different ions inside or outside the axon or both, Hodgkin, Huxley, and colleagues demonstrated that the transient inward current is carried by Na⁺ ions flowing into the cell, and the sustained outward current is mediated by a sustained flux of K⁺ ions moving out of the cell (Fig. 5.7) (Hille, 1977; Hodgkin & Huxley, 1952a, 1952b).

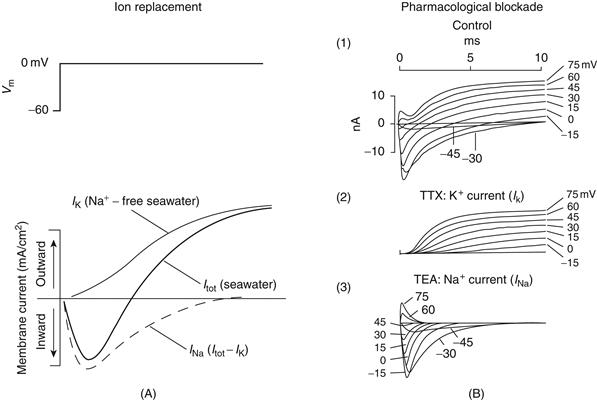
Figure 5.7 Voltage-clamp analysis reveals ionic currents underlying action potential generation. (A) Increasing the potential from −60 to 0 mV across the membrane of the squid giant axon activates an inward current followed by an outward current. If the Na⁺ in seawater is replaced by choline (which does not pass through Na⁺ channels), then increasing the membrane potential from −60 to 0 mV results in only the outward current, which corresponds to I_K. Subtracting I_K from the recording in normal seawater illustrates the amplitude–time course of the inward Na⁺ current, I_Na. Note that I_K activates more slowly than I_Na and that I_Na inactivates with time. From Hodgkin and Huxley (1952). (B) These two ionic currents can also be isolated from one another through the use of pharmacological blockers. (1) Increasing the membrane potential from −45 to 75 mV in 15-mV steps reveals the amplitude–time course of inward Na⁺ and outward K⁺ currents. (2) After the block of I_Na with the poison tetrodotoxin (TTX), increasing the membrane potential to positive levels activates I_K only. (3) After the block of I_K with tetraethylammonium (TEA), increasing the membrane potential to positive levels activates I_Na only.

From Hille (1977).

Na⁺ and K⁺ currents (I_Na and I_K, respectively) can be blocked, allowing each current to be examined in isolation (Fig. 5.7B). Tetrodotoxin (TTX), a powerful poison found in the puffer fish Spheroides rubripes, selectively blocks voltage-dependent Na⁺ currents (the puffer fish remains a delicacy in Japan and must be prepared with the utmost care by the chef). Using TTX, one can selectively isolate I_K and examine its voltage dependence and time course (Fig. 5.7B).

Another compound, tetraethylammonium (TEA), is a useful pharmacological tool for selectively blocking I_K (Fig. 5.7B). The use of TEA to examine the voltage dependence and time course of the Na⁺ current underlying action-potential generation (Fig. 5.7B) reveals some fundamental differences between Na⁺ and K⁺ currents. First, the inward Na⁺ current activates, or “turns on,” much more rapidly than the K⁺ current (giving rise to the name “delayed rectifier” for this K⁺ current). Second, the Na⁺ current is transient; it inactivates, even if the membrane potential is maintained at 0 mV (Fig. 5.7A). In contrast, the outward K⁺ current, once activated, remains “on” as long as the membrane potential is clamped to positive levels; that is, the K⁺ current does not inactivate but is sustained. Remarkably, from one experiment, we see that the Na⁺ current both activates and inactivates rapidly, whereas the K⁺ current only activates slowly. These fundamental properties of the underlying Na⁺ and K⁺ channels allow the generation of action potentials.

Hodgkin and Huxley proposed that K⁺ channels possess a voltage-sensitive “gate” that opens by depolarization and closes by the subsequent repolarization of the membrane potential. This process of “turning on” and “turning off” the K⁺ current came to be known as activation and deactivation. The Na⁺ current also exhibits voltage-dependent activation and deactivation (Fig. 5.7), but the Na⁺ channels also become inactive despite maintained depolarization. Thus, the Na⁺ current not only activates and deactivates, but it also exhibits a separate process known as inactivation, whereby the channels become blocked even though they are activated. Removal of this inactivation is achieved by removal of depolarization and is a process known as deinactivation. Thus, Na⁺ channels possess two voltage-sensitive processes: activation−deactivation and inactivation–deinactivation.

The kinetics of these two properties of Na⁺ channels are different; inactivation takes place at a slower rate than activation. The functional consequence of the two mechanisms is that Na⁺ ions are allowed to flow across the membrane only when the current is activated but not inactivated. Accordingly, Na⁺ ions do not flow at resting membrane potentials because the activation gate is closed (even though the inactivation gate is not). Upon depolarization, the activation gate opens, allowing Na⁺ ions to flow into the cell. However, this depolarization also results in closure (at a slower rate) of the inactivation gate, which then blocks the flow of Na⁺ ions. Upon repolarization of the membrane potential, the activation gate once again closes and the inactivation gate once again opens, preparing the axon for generation of the next action potential (Fig. 5.8)

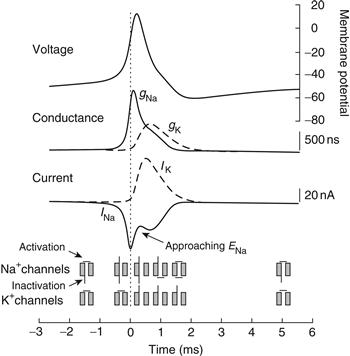
Figure 5.8 Generation of the action potential is associated with an increase in membrane Na⁺ conductance and Na⁺ current followed by an increase in K⁺ conductance and K⁺ current. Before action potential generation, Na⁺ channels are neither activated nor inactivated (illustrated at the bottom of the figure). Activation of Na⁺ channels allows Na⁺ ions to enter the cell, depolarizing the membrane potential. This depolarization also activates K⁺ channels. After activation and depolarization, the inactivation particle on the Na⁺ channels closes and the membrane potential repolarizes. The persistence of the activation of K⁺ channels (and other membrane properties) generates an after-hyperpolarization. During this period, the inactivation particle of the Na⁺ channel is removed and the K⁺ channels close.

Depolarization allows ionic current to flow by virtue of activation of the channel. The rush of Na⁺ ions into the cell further depolarizes the membrane potential and more Na⁺ channels become activated, forming a positive feedback loop that rapidly (within 100 μs or so) brings the membrane potential toward E_Na. However, the depolarization associated with generation of the action potential also inactivates Na⁺ channels, and, as a larger and larger percentage of Na⁺ channels become inactivated, the rush of Na⁺ into the cell diminishes. This inactivation of Na⁺ channels and the activation of K⁺ channels result in the repolarization of the action potential. This repolarization deactivates the Na⁺ channels. Then, the inactivation of the channel is slowly removed, and the channels are ready, once again, for the generation of another action potential (Fig. 5.8).

By measuring the voltage sensitivity and kinetics of these two processes, activation–deactivation and inactivation–deinactivation of the Na⁺ current, as well as the activation–deactivation of the delayed rectifier K⁺ current, Hodgkin and Huxley generated a series of mathematical equations that quantitatively described the generation of the action potential (calculation of the propagation of a single action potential required an entire week of cranking a mechanical calculator). According to these early experimental and computational neuroscientists, the action potential is generated as follows. Depolarization of the membrane potential increases the probability of Na⁺ channels being in the activated but not yet inactivated, state. At a particular membrane potential, the resulting inflow of Na⁺ ions tips the balance of the net ionic current from outward to inward (remember that depolarization will also increase K⁺ and Cl⁻ currents by moving the membrane potential away from E_K and E_Cl). At this membrane potential, known as the action potential threshold (typically about −55 mV), the movement of Na⁺ ions into the cell depolarizes the axon and opens more Na⁺ channels, causing yet more depolarization of the membrane; repetition of this process yields a rapid, positive feedback loop that brings the axon close to E_Na. However, even as more and more Na⁺ channels are becoming activated, some of these channels are also inactivating and therefore no longer conducting Na⁺ ions. In addition, the delayed rectifier K⁺ channels are also opening, due to the depolarization of the membrane potential, and allowing positive charge to exit the cell. At some point, close to the peak of the action potential, the inward movement of Na⁺ ions into the cell is exactly offset by the outward movement of K⁺ ions out of the cell. After this point, the outward movement of K⁺ ions dominates, and the membrane potential is repolarized, corresponding to the fall of the action potential. The persistence of the K⁺ current for a few milliseconds following the action potential generates the after-hyperpolarization. During this after-hyperpolarization, which is lengthened by the membrane time constant, inactivation of the Na⁺ channels is removed, preparing the axon for generation of the next action potential (Fig. 5.8).

The occurrence of an action potential is not associated with substantial changes in the intracellular or extracellular concentrations of Na⁺ or K⁺, as shown earlier for the generation of the resting membrane potential. For example, generation of a single action potential in a 25-μm-diameter hypothetical spherical cell should increase the intracellular concentration of Na⁺ by only approximately 6 μM (from about 18 to 18.006 mM). Thus, the action potential is an electrical event generated by a change in the distribution of charge across the membrane and not by a marked change in the intracellular or extracellular concentration of Na⁺ or K⁺.

Action Potentials Typically Initiate in the Axon Initial Segment and Propagate Down the Axon and Backwards Through the Dendrites

Neurons have complex morphologies, including dendritic arbors, a cell body, and typically one axonal output that branches extensively. In many cells, all of these parts of the neuron are capable of independently generating action potentials. The activity of most neurons is dictated by barrages of synaptic potentials generated at each moment by a variable subset of the thousands of synapses impinging upon the cell’s dendrites and soma. Where, then, is the action potential initiated? In most cells, each action potential is initiated in the initial portion of the axon, known as the axon initial segment (Coombs, Curtis, & Eccles, 1957; Popovic, Foust, McCormick, & Zecevic, 2011; Stuart, Spruston, Sakmann, & Hausser, 1997). The initial segment of the axon has the lowest threshold for action potential generation because it typically contains a moderately high density of Na⁺ channels that have a more negative activation threshold and it is a small compartment that is easily depolarized by the in-rush of Na⁺ ions. Once a spike is initiated (e.g., about 30−50 μm down the axon from the cell body in cortical pyramidal cells), this action potential then propagates orthodromically down the axon to the synaptic terminals, where it causes release of transmitter, as well as antidromically back through the cell body and into the cell dendrites, where it can modulate intracellular processes.

Refractory Periods Prevent “Reverberation”

The ability of depolarization to activate an action potential varies as a function of the time since the last generation of an action potential, due to the inactivation of Na⁺ channels and the activation of K⁺ channels. Immediately after the generation of an action potential, another action potential usually cannot be generated regardless of the amount of current injected into the axon. This period corresponds to the absolute refractory period and is largely mediated by the inactivation of Na⁺ channels. The relative refractory period occurs during the action potential after-hyperpolarization and follows the absolute refractory period. The relative refractory period is characterized by a requirement for the increased injection of ionic current into the cell to generate another action potential and results from persistence of the outward K⁺ current. The practical implication of refractory periods is that action potentials are not allowed to “reverberate” between the soma and the axon terminals.

The Speed of Action Potential Propagation Is Affected by Myelination

Axons may be either myelinated or unmyelinated. Invertebrate axons or small vertebrate axons are typically unmyelinated, whereas larger vertebrate axons are often myelinated. As described in Chapter 3, sensory and motor axons of the peripheral nervous system are myelinated by specialized cells (Schwann cells) that form a spiral wrapping of multiple layers of myelin around the axon (Fig. 5.9). Several Schwann cells wrap around an axon along its length; between the ends of successive Schwann cells are small gaps (nodes of Ranvier). In the central nervous system, a single oligodendrocyte, a special type of glial cell, typically ensheaths several axonal processes.

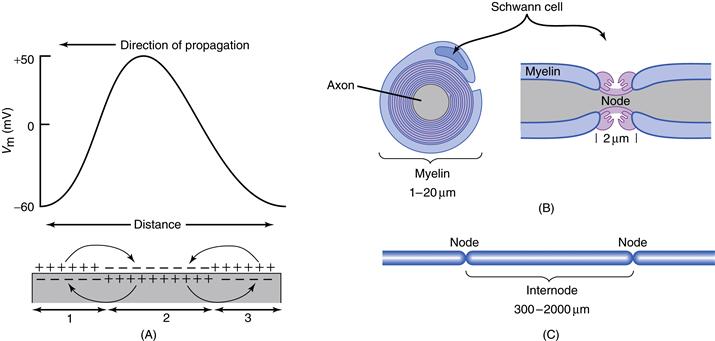
Figure 5.9 Propagation of the action potential in unmyelinated and myelinated axons. (A) Action potentials propagate in unmyelinated axons through the depolarization of adjacent regions of membrane. In the illustrated axon, region 2 is undergoing depolarization during the generation of the action potential, whereas region 3 has already generated the action potential and is now hyperpolarized. The action potential will propagate further by depolarizing region 1. (B) Vertebrate myelinated axons have a specialized Schwann cell that wraps around them in many spiral turns. The axon is exposed to the external medium at the nodes of Ranvier (Node). (C) Action potentials in myelinated fibers are regenerated at the nodes of Ranvier, where there is a high density of Na⁺ channels. Action potentials are induced at each node through the depolarizing influence of the generation of an action potential at adjacent nodes, thereby increasing conduction velocity.

In unmyelinated axons, the Na⁺ and K⁺ channels taking part in action potential generation are distributed along the axon, and the action potential propagates along the length of the axon through local depolarization of each neighboring patch of membrane, causing that patch of membrane to also generate an action potential (Fig. 5.9). Myelination of the axon reduces its membrane capacitance by moving the electrical charge differences between the inside and outside of the axon further apart and thus reducing their influence on each other. This has the effect of significantly increasing the passive length constant (λ) of the axon. In myelinated axons, however, the Na⁺ channels are concentrated at the nodes of Ranvier. The generation of an action potential at each node results in depolarization of several adjacent nodes (owing to the long length constant of the myelinated axon) and subsequently generation of an action potential with an internode delay of only about 20 μs, referred to as saltatory conduction (from the Latin saltare, “to leap”). Interestingly, since action potentials are typically 1 msec or longer in duration, many adjacent nodes of Ranvier are in the process of generating action potentials at the same time (Popovic et al., 2011). Growing evidence indicates that, near the nodes of Ranvier and underneath the myelin covering, K⁺ channels may play a role in determining the resting membrane potential and repolarization of the action potential. A cause of some neurological disorders, such as multiple sclerosis and Guillain-Barre syndrome, is the demyelination of axons, resulting in a block of conduction of the action potentials.

Ion Channels are Membrane-Spanning Proteins with Water-Filled Pores

The generation of ionic currents useful for the propagation of action potentials requires the movement of significant numbers of ions across the membrane in a relatively short time. The rate of ionic flow during the generation of an action potential is far too high to be achieved by an active transport mechanism and results instead from the opening of ion channels. Although the existence of ionic channels in the membrane has been postulated for decades, their properties and structure have only recently become known in detail. The powerful combination of electrophysiological and molecular techniques has enhanced our knowledge of the structure–function relations of ionic channels greatly (Box 5.4).

Box 5.4 Ion Channels and Disease

Cells cannot survive without functional ion channels. It is therefore not surprising that an ever-increasing number of diseases have been found to be associated with defective ion channel function. There are a number of different mechanisms by which this may occur.

1. Mutations in the coding region of ion channel genes may lead to gain or loss of channel function, either of which may have deleterious consequences. For example, mutations producing enhanced activity of the epithelial Na⁺ channel are responsible for Liddle’s syndrome, an inherited form of hypertension, whereas other mutations in the same protein that cause reduced channel activity give rise to hypotension. The most common inherited disease in Caucasians is also an ion channel mutation. This disease is cystic fibrosis (CF), which results from mutations in the epithelial chloride channel, known as CFTR. The most common mutation, deletion of a phenylalanine at position 508, results in defective processing of the protein and prevents it from reaching the surface membrane. CFTR regulates chloride fluxes across epithelial cell membranes, and this loss of CFTR activity leads to reduced fluid secretion in the lung, resulting in potentially fatal lung infections.

2. Mutations in the promoter region of the gene may cause under- or overexpression of a given ion channel.

3. Other diseases result from defective regulation of channel activity by cellular constituents or extracellular ligands. This defective regulation may be caused by mutations in the genes encoding the regulatory molecules themselves or defects in the pathways leading to their production. Some forms of maturity-onset diabetes of the young (MODY) may be attributed to such a mechanism. ATP-sensitive potassium (K-ATP) channels play a key role in the glucose-induced insulin secretion from pancreatic β cells, and their defective regulation is responsible for one form of MODY.

4. Autoantibodies to channel proteins may cause disease by downregulating channel function—often by causing internalization of the channel protein itself. Well-known examples are myasthenia gravis, which results from antibodies to skeletal muscle acetylcholine channels, and Lambert–Eaton myasthenic syndrome, in which patients produce antibodies against presynaptic Ca²⁺ channels.

5. Finally, a number of ion channels are secreted by cells as toxic agents. They insert into the membrane of the target cell and form large nonselective pores, leading to cell lysis and death. The hemolytic toxin produced by the bacterium Staphylococcus aureus and the toxin secreted by the protozoan Entamoeba histolytica, which causes amebic dysentery, are examples.

Natural mutations in ion channels have been invaluable for studying the relationship between channel structure and function. In many cases, genetic analysis of a disease has led to the cloning of the relevant ion channel. The first K⁺ channel to be identified (Shaker), for example, came from the cloning of the gene that caused Drosophila to shake when exposed to ether. Likewise, the gene encoding the primary subunit of a cardiac potassium channel (KCNQ1) was identified by positional cloning in families carrying mutations that caused a cardiac disorder known as long QT syndrome (see later). Conversely, the large number of studies on the relationship between Na⁺ channel structure and function has greatly assisted our understanding of how mutations in Na⁺ channels produce their clinical phenotypes.

Many diseases are genetically heterogeneous, and the same clinical phenotype may be caused by mutations in different genes. Long QT syndrome is a relatively rare inherited cardiac disorder that causes abrupt loss of consciousness, seizures, and sudden death from ventricular arrhythmia in young people. Mutations in five different genes, two types of cardiac muscle K⁺ channels (HERG, KCNQ1, KCNE1, KCNE2) and the cardiac muscle sodium channel (SCN1A), give rise to long QT syndrome. The disorder is characterized by a long QT interval in the electrocardiogram, which reflects the delayed repolarization of the cardiac action potential. As might therefore be expected, mutations in the cardiac Na⁺ channel gene that cause long QT syndrome enhance the Na⁺ current (by reducing Na⁺ channel inactivation), whereas those in potassium channel genes cause loss of function and reduce the K⁺ current.

Mutations in many different types of ion channels have been shown to cause human diseases. In addition to the examples listed earlier, mutations in water channels cause nephrogenic diabetes insipidus; mutations in gap junction channels cause Charcot–Marie–Tooth disease (a form of peripheral neuropathy) and hereditary deafness; mutations in the skeletal muscle Na⁺ channel cause a range of disorders known as periodic paralyses; mutations in intracellular Ca²⁺-release channels cause malignant hyperthermia (a disease in which inhalation anesthetics trigger a potentially fatal rise in body temperature); and mutations in neuronal voltage-gated Ca²⁺ channels cause migraine and episodic ataxia. The list increases daily. As is the case with all single gene disorders, the frequency of these diseases in the general population is very low. However, the insight they have provided into the relationship between ion channel structure and function, and into the physiological role of the different ion channels, has been invaluable. As William Harvey said in 1657, “Nor is there any better way to advance the proper practice of medicine than to give our minds to the discovery of the usual form of nature, by careful investigation of the rarer forms of disease.”

Frances M. Ashcroft

Various neural toxins were particularly useful in the initial isolation of ionic channels. For example, three subunits (α, β1, β2) of the voltage-dependent Na⁺ channel were isolated with the use of a derivative of a scorpion toxin. The α subunit of the Na⁺ channel is a large glycoprotein with a molecular mass of 270 kDa, whereas the β1 and β2 subunits are smaller polypeptides of molecular masses 39 and 37 kDa, respectively (Fig. 5.10). The α subunit, of which there are at least nine different isoforms, is the building block of the water-filled pore of the ionic channel, whereas the β subunits have some other role, such as in the regulation or structure of the native channel (Catterall, 2000a).

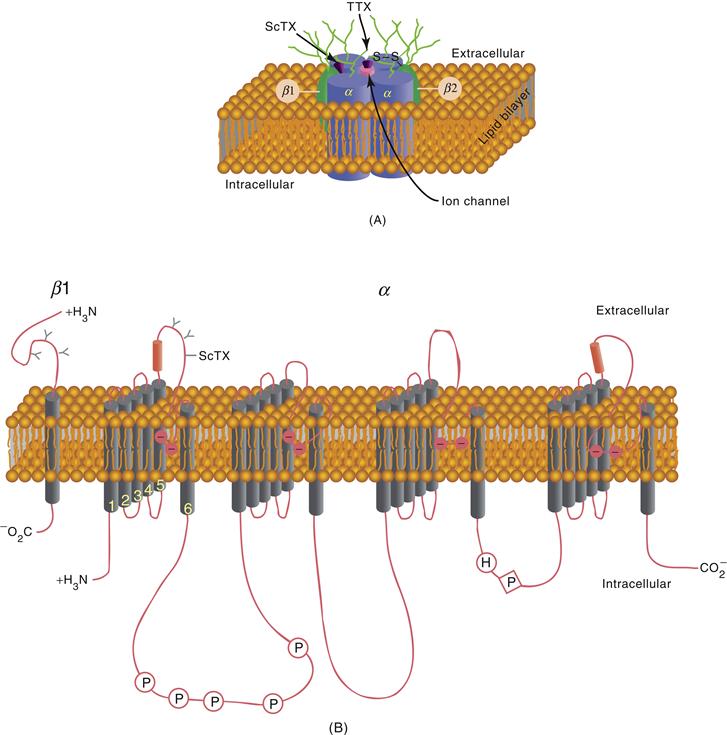
Figure 5.10 Structure of the sodium channel. (A) Cross section of a hypothetical sodium channel consisting of a single transmembrane α subunit in association with a β1 subunit and a β2 subunit. The α subunit has receptor sites for α-scorpion toxins (ScTX) and tetrodotoxin (TTX). (B) Primary structures of α and β1 subunits of sodium channel illustrated as transmembrane-folding diagrams. Cylinders represent probable transmembrane α-helices.

The α subunit of the Na⁺ channel contains four internal repetitions (Fig. 5.10B). Hydrophobicity analysis of these four components reveals that each contains six hydrophobic domains that may span the membrane as an α-helix. Of these six membrane-spanning components, the fourth (S4) has been proposed to be critical to the voltage sensitivity of the Na⁺ channels. Voltage-sensitive gating of Na⁺ channels is accomplished by the redistribution of ionic charge (“gating charge”) in the channel. Positive charges in the S4 region may act as voltage sensors such that an increase in the positivity of the inside of the cell results in a conformational change of the ionic channel. In support of this hypothesis, site-directed mutagenesis of the S4 region of the Na⁺ channel to reduce the positive charge of this portion of the pore also reduces the voltage sensitivity of activation of the ionic channel.

The mechanisms of inactivation of ionic channels have been analyzed with a combination of molecular and electrophysiological techniques. The most convincing hypothesis is that inactivation is achieved by a block of the inner mouth of the aqueous pore. Ionic channels are inactivated without detectable movement of ionic current through the membrane; thus inactivation is probably not directly gated by changes in the membrane potential alone. Rather, inactivation is triggered or facilitated as a secondary consequence of activation. Site-directed mutagenesis or the use of antibodies has shown that the part of the molecule between regions III and IV may be allowed to move to block the cytoplasmic side of the ionic pore after the conformational change associated with activation.

Neurons of the Central Nervous System Exhibit a Wide Variety of Electrophysiological Properties

The first intracellular recordings of action potentials in mammalian neurons by Sir John Eccles and colleagues revealed a remarkable similarity to those of the squid giant axon and gave rise to the assumption that the electrophysiology of neurons in the CNS was really rather simple: when synaptic potentials brought the membrane potential positive to action potential threshold, action potentials were produced through an increase in Na⁺ conductance followed by an increase in K⁺ conductance, as in the squid giant axon. The assumption, therefore, was that the complicated patterns of activity generated by the brain during the resting, sleeping, or active states were brought about as an interaction of the very large numbers of neurons present in the mammalian CNS. However, intracellular recordings of invertebrate neurons revealed that different cell types exhibit a wide variety of different electrophysiological behaviors, indicating that neurons may be significantly more complicated than the squid giant axon.

Elucidation of the basic electrophysiology and synaptic physiology of different types of neurons and neuronal pathways within the mammalian CNS was facilitated by the in vitro slice technique, in which thin (~0.5 mm) slices of brain can be maintained for several hours. Intracellular recordings from identified cells revealed that neurons of the mammalian nervous system, such as those of invertebrate networks, can generate complex patterns of action potentials entirely through intrinsic ionic mechanisms and without synaptic interaction with other cell types. For example, Rodolfo Llinás and colleagues discovered that Purkinje cells of the cerebellum can generate high-frequency trains (>200 Hz) of Na⁺- and K⁺-mediated action potentials interrupted by Ca²⁺ spikes in the dendrites, whereas a major afferent to these neurons, the inferior olivary cell, can generate rhythmic sequences of broad action potentials only at low frequencies (<15 Hz) through an interaction between various Ca²⁺, Na⁺, and K⁺ conductances (Fig. 5.11). These in vitro recordings confirmed a major finding obtained with earlier intracellular recordings in vivo: each morphologically distinct class of neuron in the brain exhibits distinct electrophysiological features. Just as cortical pyramidal cells are morphologically distinct from cerebellar Purkinje cells, which are distinct from thalamic relay cells, the electrophysiological properties of each of these different cell types are also markedly distinct (Llinás, 1988).

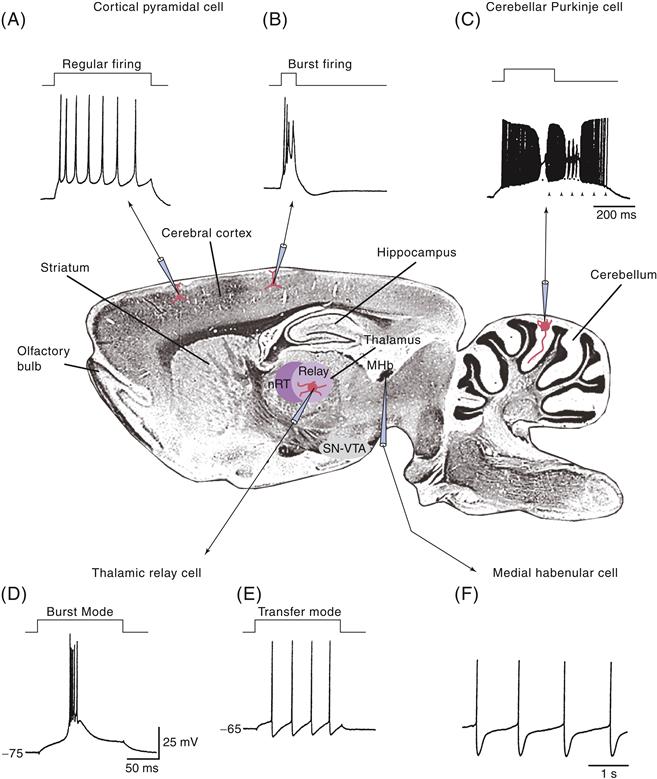
Figure 5.11 Neurons in the mammalian brain exhibit widely varying electrophysiological properties. (A) Intracellular injection of a depolarizing current pulse in a cortical pyramidal cell results in a train of action potentials that slow down in frequency. This pattern of activity is known as “regular firing.” (B) Some cortical cells generated bursts of three or more action potentials, even when depolarized only for a short period of time. (C) Cerebellar Purkinje cells generate high-frequency trains of action potentials in their cell bodies that are disrupted by the generation of Ca²⁺ spikes in their dendrites. These cells can also generate “plateau potentials” from the persistent activation of Na⁺ conductances (arrowheads). Thalamic relay cells may generate action potentials either as bursts (D) or as tonic trains of action potentials (E) due to the presence of a large low-threshold Ca²⁺ current. (F) Medial habenular cells generate action potentials at a steady and slow rate in a “pacemaker” fashion.

Although no uniform classification scheme has been formulated in which all the different types of neurons of the brain can be classified, a few characteristic patterns of activity seem to recur. The first general class of action potential generation is characterized by those cells that generate trains of action potentials one spike at a time. The more prolonged the depolarization of these cells, the more prolonged their discharge. The more intensely these cells are depolarized, the higher the frequency of action potential generation. This type of relatively linear behavior is typical for brainstem and spinal cord motor neurons functioning in muscle contraction. A modification of this basic pattern of “regular firing” is characterized by the generation of trains of action potentials that exhibit a marked tendency to slow down in frequency with time, a process known as spike frequency adaptation. Examples of cells that discharge in this manner are cortical and hippocampal pyramidal cells.

In addition to these regular firing cells, many neurons in the central nervous system exhibit the intrinsic propensity to generate rhythmic bursts of action potentials (Fig. 5.11). Examples of such neurons are thalamic relay neurons, inferior olivary neurons, and some types of cortical and hippocampal pyramidal cells. In these cells, clusters of action potentials can occur together when the membrane is brought above the firing threshold. These clusters of action potentials are typically generated through the activation of specialized Ca²⁺ currents that, through their slower kinetics, allow the membrane potential to be depolarized for a sufficient period to result in the generation of a burst of regular, Na⁺- and K⁺-dependent action potentials (discussed in the next section).

Yet another general category of neurons in the brain comprises cells that generate relatively short duration (<1 ms) action potentials and can discharge at relatively high frequencies (>300 Hz). Such electrophysiological properties are often found in neurons that release the inhibitory amino acid γ-aminobutyric acid (Fig. 5.11), including Purkinje cells of the cerebellum and some types of interneurons in the cerebral cortex, thalamus, and hippocampus. Finally, the last general category of neurons consists of those that spontaneously generate action potentials at relatively slow frequencies (e.g., 1–10 Hz). This type of electrophysiological behavior is often associated with neurons that release neuromodulatory transmitters, such as acetylcholine, norepinephrine, serotonin, and histamine. Neurons that release these neuromodulatory substances often innervate wide regions of the brain and appear to set the “state” of the different neural networks of the CNS in a manner similar to the modulation of the different organs of the body by the sympathetic and parasympathetic nervous systems.

Each of these unique intrinsic patterns of activity in the nervous system is due to the presence of a distinct mixture and distribution of different ionic currents in the cells. As in classical studies of the squid giant axon, these different ionic currents have been characterized, at least in part, with voltage-clamp and pharmacological techniques, and the basic electrophysiological properties have been replicated with computational simulations (Figs. 5.8 and 5.13).

Neurons Have Multiple Active Conductances

The search for the electrophysiological basis of the varying intrinsic properties of different types of neurons of vertebrates and invertebrates revealed a wide variety of ionic currents. Each type of ionic current is characterized by several features: (1) the type of ions conducted by the underlying ionic channels (e.g., Na⁺, K⁺, Ca²⁺, Cl⁻, or mixed cations), (2) their voltage and time dependence, and (3) their sensitivity to second messengers. In vertebrate neurons, two distinct Na⁺ currents have been identified and six distinct Ca²⁺ currents and more than seven distinct K⁺ currents are known (Fig. 5.12). This is a minimal number, since these currents are formed from a much greater pool of channel subunits. The following sections briefly review these classes of ionic currents and their ionic channels, relating them to the different patterns of behavior mentioned earlier for neurons in the mammalian CNS.

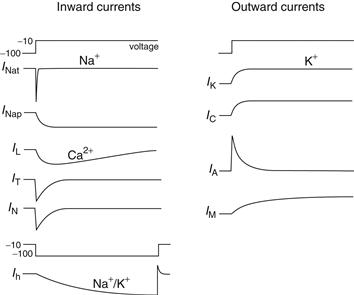
Figure 5.12 Voltage dependence and kinetics of different ionic currents in the mammalian brain. Depolarization of the membrane potential from −100 to −10 mV results in the activation of currents entering or leaving neurons.

Na⁺ Currents are Both Transient and Persistent

Depolarization of many different types of vertebrate neurons results not only in the activation of the rapidly activating and inactivating Na⁺ current (I_Nat) underlying action potential generation, but also in the rapid activation of a Na⁺ current that does not inactivate and is therefore known as the “persistent” Na⁺ current (I_Nap). The threshold for activation of the persistent Na⁺ current is typically about −65 mV—that is, below the threshold for the generation of action potentials. This property gives this current the interesting ability to enhance or facilitate the response of the neuron to depolarizing, yet subthreshold, inputs. For example, synaptic events that depolarize the cell will activate I_Nap, resulting in an extra influx of positive charge and therefore a larger depolarization than otherwise would occur. Likewise, hyper-polarizations may result in deactivation of I_Nap, again resulting in larger hyperpolarizations than would otherwise occur. In this manner, the persistent Na⁺ current may play an important regulatory function in the control of the functional responsiveness of the neuron to synaptic inputs and may contribute to the dynamic coupling of the dendrites to the soma.

Persistent activation of I_Nap may also contribute to another electrophysiological feature of neurons: the generation of plateau potentials. A plateau potential refers to the ability of many different types of neurons to generate, through intrinsic ionic mechanisms, a prolonged (from tens of milliseconds to seconds) depolarization and action potential discharge in response to a short-lasting depolarization (Fig. 5.11C). One can wonder whether such plateau potentials contribute to persistent firing in neurons during the performance of working memory tasks, where groups of neurons have to retain information for brief (seconds) periods of time.

K⁺ Currents Vary in Their Voltage Sensitivity and Kinetics

Potassium currents that contribute to the electrophysiological properties of neurons are numerous and exhibit a wide range of voltage-dependent and kinetic properties (reviewed in Coetzee et al., 1999). Perhaps the simplest K⁺ current is that characterized by Hodgkin and Huxley: this K⁺ current, I_K, activates rapidly on depolarization and does not inactivate (Fig. 5.12). Other K⁺ currents activate with depolarization but also inactivate with time. For example, the rapid activation and inactivation of I_A give this current a transient appearance (Fig. 5.12), and I_A is believed to be important in controlling the rate of action potential generation, particularly at low frequencies (Fig. 5.13). Like the Na⁺ channel, I_A channels are inactivated by the plugging of the inner mouth of the pore through movement of an inactivation particle.

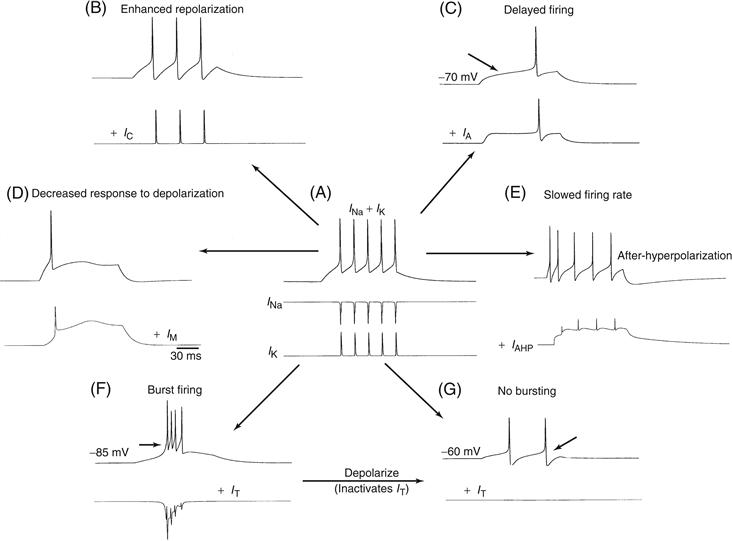
Figure 5.13 Simulation of the effects of the addition of various ionic currents to the pattern of activity generated by neurons in the mammalian CNS. (A) The repetitive impulse response of the classical Hodgkin–Huxley model (voltage recordings above, current traces below). With only I_Na and I_K, the neuron generates a train of five action potentials in response to depolarization. Addition of I_C (B) enhances action potential repolarization. Addition of I_A (C) delays the onset of action potential generation. Addition of I_M (D) decreases the ability of the cell to generate a train of action potentials. Addition of I_AHP (E) slows the firing rate and generates a slow after-hyperpolarization. Finally, addition of the transient Ca²⁺ current I_T results in two states of action potential firing: (F) burst firing at −85 mV and (G) tonic firing at −60 mV.

From Huguenard and McCormick (1994).

Another broad class of K⁺ channels consists of those that are sensitive to changes in the intracellular concentration of Ca²⁺. These K⁺ currents are collectively referred to as I_KCa (Fig. 5.12). Still other K⁺ channels are not only activated by voltage but are also modulated by the activation of various modulatory neurotransmitter receptors (e.g., I_M; Fig. 5.12). Between these classic examples of K⁺ currents are a variety of other types that have not been fully characterized, including K⁺ currents that vary from one another in their voltage sensitivity, kinetics, and response to various second messengers.

Molecular biological studies of voltage-sensitive K⁺ channels, first done in Drosophila and later in mammals, have revealed the presence of a large number of genes that generate K⁺ channels. The voltage-gated K⁺ channel subunits are contained within nine distinct subfamilies: Kv1-9 (reviewed in Coetzee et al., 1999). These genes generate a wide variety of different K⁺ channels, not only due to the large number of genes involved, but also due to alternative RNA splicing, gene duplication, and other mechanisms. Functional expression of different K⁺ channels reveals remarkable variation in the rate of inactivation, such that some are rapidly inactivating (A-current like), whereas others inactivate more slowly and, finally, some K⁺ channels do not inactivate, such as I_K. One of the largest subfamilies of K⁺ channels are those that give rise to the resting membrane potential, so-called “leak channels.” Interestingly, these channels appear to be opened by gaseous anesthetics, indicating that hyperpolarization of central neurons is a major component of general anesthesia. It is now clear that each type of neuron in the nervous system contains a unique set of functional voltage-sensitive K⁺ channels, selected, modified, and placed in particular spatial locations in the cell in a manner that facilitates the unique role of that cell type in neuronal processing.

An additional current that also regulates the responsiveness of neurons to depolarizing inputs is the voltage-sensitive K⁺ current known as the M current (Figs. 5.12 and 5.13D) (Brown & Passmore, 2009). By investigating the ionic mechanisms by which the release of acetylcholine from preganglionic neurons in the brain results in prolonged changes in the excitability of neurons of the sympathetic ganglia, Brown and Adams (1980) discovered a unique K⁺ current that slowly (over tens of milliseconds) turns on with depolarization of the neuron (Fig. 5.13D). The slow activation of this K⁺ current results in a decrease in the responsiveness of the cell to depolarization and therefore regulates how the cell responds to excitation. This K⁺ current, like I_AHP, is reduced by the activation of a wide variety of receptors, including muscarinic receptors, for which it is named. Reduction of I_M results in a marked increase in responsiveness of the affected cell to depolarizing inputs and again may contribute to the mechanisms by which neuromodulatory systems control the state of activity in cortical and hippocampal networks (reviewed in McCormick, 1992; Nicoll, 1988).

Ca²⁺ Currents Control Electrophysiological Properties and Ca²⁺-Dependent Second-Messenger Systems

Ionic channels that conduct Ca²⁺ are present in all neurons. These channels are special in that they serve two important functions. First, Ca²⁺ channels are present throughout the different parts of the neuron (dendrites, soma, synaptic terminals) and contribute greatly to the electrophysiological properties of these processes. Second, Ca²⁺ channels are unique in that Ca²⁺ is an important second messenger in neurons, and entry of Ca²⁺ into the cell can affect numerous physiological functions, including neurotransmitter release, synaptic plasticity, neurite outgrowth during development, and even gene expression. On the bases of their voltage sensitivity, their kinetics of activation and inactivation, and their ability to be blocked by various pharmacological agents, Ca²⁺ currents can be separated into at least six separate categories, three of which are I_T (“transient”), I_L (“long lasting”), and I_N (“neither”), illustrated in Figure 5.12A. A fourth, I_P, is found in Purkinje cells of the cerebellum, as well as in many different cell types of the CNS. These Ca²⁺ channels are formed from at least 10 different α subunits as well as a variety of β and γ subunits, indicating that an even greater number of Ca²⁺ currents are yet to be characterized.

Neurons Possess Multiple Subtypes of High-Threshold Ca²⁺ Currents

High-voltage-activated Ca²⁺ channels are activated at membrane potentials positive to approximately −40 mV and include the currents I_L, I_N, and I_P. L-type calcium currents exhibit a high threshold for activation (about −10 mV) and give rise to rather persistent, or long-lasting, ionic currents (Fig. 5.12A). Dihydropyridines, Ca²⁺ channel antagonists, are clinically useful for their effects on the heart and vascular smooth muscle (e.g., for the treatment of arrhythmias, angina, and migraine headaches) and selectively block L-type Ca²⁺ channels. In contrast with I_L, I_N is not blocked by dihydropyridines: it is blocked selectively by a toxin found in Pacific cone shells (ω-conotoxin-GVIA). N-type Ca²⁺ channels have a threshold for activation of about −20 mV, inactivate with maintained depolarization, and are modulated by a variety of neurotransmitters. In some cell types, I_N has a role in the Ca²⁺-dependent release of neurotransmitters at presynaptic terminals. The P-type calcium channel is distinct from N and L types in that it is not blocked by either dihydropyridines or ω-conotoxin-GVIA but is blocked by a toxin (ω-agatoxin-IVA) present in the venom of the Funnel web spider. This type of calcium channel activates at relatively high thresholds and does not inactivate. Prevalent in Purkinje cells, as well as other cell types, as mentioned earlier, the P-type Ca²⁺ channel participates in the generation of dendritic Ca²⁺ spikes, which can strongly modulate the firing pattern of the neuron in which it resides (Fig. 5.11C; Llinás, 1988).

Collectively, high-threshold-activated Ca²⁺ channels contribute to the generation of action potentials in mammalian neurons. The activation of Ca²⁺ currents adds somewhat to the depolarizing part of the action potential, but, more importantly, these channels allow Ca²⁺ to enter the cell, which has the secondary consequence of activation of various Ca²⁺-activated K⁺ currents and protein kinases (see Chapter 8). As mentioned earlier, activation of these K⁺ currents modifies the pattern of action potentials generated in the cell (Figs. 5.11 and 5.13).

High-threshold Ca²⁺ channels are similar to the Na⁺ channel in that they are composed of a central α1 subunit that forms the aqueous pore and several regulatory or auxiliary subunits. As in the Na⁺ channel, the primary structure of the α1 subunit of the Ca²⁺ channel consists of four homologous domains (I–IV), each containing six regions (S1–S6) that may generate transmembrane α-helices. Genes for at least 10 different Ca²⁺ channel α subunits have been cloned and are separated into three subfamilies (Cav1, Cav2, and Cav3). The properties of the products of these genes indicate that I_L is likely to correspond to the Cav1 subfamily, whereas I_N corresponds to Cav2.2 and I_T is formed from the Cav3 subfamily (see Catterall, 2000b).

Low-Threshold Ca²⁺ Currents Generate Bursts of Action Potentials

Low-threshold Ca²⁺ currents (Fig. 5.12A) often take part in the generation of rhythmic bursts of action potentials (Figs. 5.11 and 5.13). The low-threshold Ca²⁺ current is characterized by a threshold for activation of about −65 mV, which is below the threshold for generation of typical Na⁺–K⁺-dependent action potentials (−55 mV). This current inactivates with maintained depolarization. Because of these properties, the role of low-threshold Ca²⁺ currents differs markedly from that of the high-threshold Ca²⁺ currents. Through activation and inactivation of the low-threshold Ca²⁺ current, neurons can generate slow (about 100 ms) Ca²⁺ spikes, which can result, due to their prolonged duration, in generation of a high-frequency “burst” of short-duration Na⁺–K⁺ action potentials (Fig. 5.11).

In the mammalian brain, this pattern is especially well exemplified by the activity of thalamic relay neurons; in the visual system, these neurons receive direct input from the retina and transmit this information to the visual cortex. During periods of slow wave sleep, the membrane potential of these relay neurons is relatively hyperpolarized, resulting in the removal of inactivation (deinactivation) of the low-threshold Ca²⁺ current. This deinactivation allows these cells to spontaneously generate low-threshold Ca²⁺ spikes and bursts of from two to five action potentials (Fig. 5.14). The large number of thalamic relay cells bursting during sleep in part gives rise to the spontaneous synchronized activity that early investigators were so surprised to find during recordings from the brains of sleeping animals. It has even proved possible to maintain one of the sleep-related brain rhythms (spindle waves) intact in slices of thalamic tissue maintained in vitro, due to the generation of this rhythm by the interaction of a local network of thalamic cells and their electrophysiological properties.

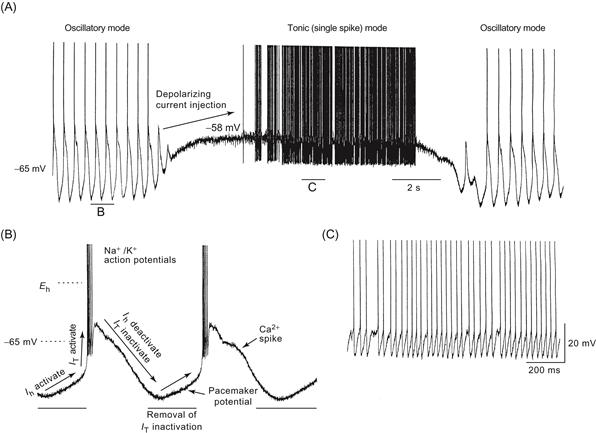
Figure 5.14 Two different patterns of activity generated in the same neuron, depending on membrane potential. (A) The thalamic neuron spontaneously generates rhythmic bursts of action potentials due to the interaction of the Ca²⁺ current I_T and the inward “pacemaker” current I_h. Depolarization of the neuron changes the firing mode from rhythmic burst firing to tonic action potential generation in which spikes are generated one at a time. Removal of this depolarization reinstates rhythmic burst firing. This transition from rhythmic burst firing to tonic activity is similar to that which occurs in the transition from sleep to waking. (B) Expansion of detail of rhythmic burst firing. (C) Expansion of detail of tonic firing.

From McCormick and Pape (1990).

The transition to waking or the period of sleep when dreams are prevalent (rapid eye movement sleep) is associated with a maintained depolarization of thalamic relay cells to membrane potentials ranging from about −60 to −55 mV. The low-threshold Ca²⁺ current is inactivated and therefore the burst discharges are abolished. In this way, the properties of a single ionic current (I_T) help explain in part the remarkable changes in brain activity taking place in the transition from sleep to waking (Fig. 5.14).

Hyperpolarization-Activated Ionic Currents Are Involved in Rhythmic Activity

In most types of neurons, hyperpolarization negative to approximately −60 mV activates an ionic current, known as I_h, that conducts both Na⁺ and K⁺ ions (Fig. 5.12). This current typically has very slow kinetics, turning on with a time constant on the order of tens of milliseconds to seconds. Because the channels underlying this current allow the passage of both Na⁺ and K⁺ ions, the reversal potential of I_h is typically about −35 mV—between E_Na and E_K. Because this current is activated by hyperpolarization below approximately −60 mV, it is typically dominated by the inward movement of Na⁺ ions and is therefore depolarizing. For what purpose could neurons use a depolarizing current that activates when the cell is hyperpolarized? A clue comes from cardiac cells in which this current, known as I_f for “funny,” is important for determining heart rate. Activation of I_f results in a slow depolarization of the membrane potential between adjacent cardiac action potentials. The more that I_f is activated, the faster the membrane depolarizes between beats, and therefore the sooner the threshold for the next action potential is reached and the next beat is generated. In this manner, the amplitude, or sensitivity to voltage, of I_f can modify the heart rate. Interestingly, the sensitivity of I_f to voltage is adjusted by the release of noradrenaline and acetylcholine; the activation of adrenoceptors by noradrenaline increases I_f and therefore increases the heart rate, whereas the activation of muscarinic receptors decreases I_f, thereby decreasing the heart rate (see DiFrancesco, 2005). This continual adjustment of I_f results from a “push–pull” arrangement between β-adrenergic and muscarinic cholinergic receptors and is mediated by the adjustment of intracellular levels of cyclic AMP. Indeed, the recent cloning of H channels reveals that their structure is similar to that of cyclic nucleotide-gated channels.

Could I_h play a role in neurons similar to that of I_f in the heart? Possibly. Synchronized rhythmic oscillations in the membrane potential of large numbers of neurons, in some respects similar to those of the heart, are characteristic of the mammalian brain. Oscillations of this type are particularly prevalent in thalamic relay neurons during some periods of sleep, as mentioned earlier. Intracellular recordings from these thalamic neurons reveal that they often generate rhythmic “bursts” of action potentials mediated by the activation of a slow spike that is generated through the activation of the low-threshold, or transient, Ca²⁺ current, I_T (Fig. 5.14). Between the occurrence of each low-threshold Ca²⁺ spike is a slowly depolarizing membrane potential generated by activation of the mixed Na⁺–K⁺ current I_h, as with I_f in the heart. The amplitude, or voltage sensitivity, of I_h adjusts the rate at which the thalamic cells oscillate, and, as with the heart, this sensitivity is adjusted by the release of modulatory neurotransmitters. In a sense, the thalamic neurons are “beating” in a manner similar to that of the heart.

Summary

An action potential is generated by the rapid influx of Na⁺ ions followed by a slightly slower efflux of K⁺ ions. Although the generation of an action potential does not disrupt the concentration gradients of these ions across the membrane, the movement of charge is sufficient to generate a large and brief deviation in the membrane potential. Action potentials are typically initiated in the axon initial segment and the propagation of the action potential along the axon allows communication of the output of the cell to its distant synapses. Neurons possess many different types of ionic channels in their membranes, allowing complex patterns of action potentials to be generated and complex synaptic computations to occur within single neurons.

References

1. Brown DA, Adams PR. Muscarinic suppression of a novel voltage sensitive K⁺ current in a vertebrate neurone. Nature (London). 1980;283:673–676.

2. Brown DA, Passmore GM. Neural KCNQ (Kv7) channels. British Journal of Pharmacology. 2009;156:1185–1195.

3. Catterall WA. From ionic currents to molecular mechanisms, The structure and function of voltage-gated sodium currents. Neuron. 2000a;26:13–25.

4. Catterall WA. Structure and regulation of voltage-gated Ca²⁺ channels. Annual Review of Cell and Developmental Biology. 2000b;16:521–555.

5. Coetzee WA, Amarillo Y, Chui J, et al. Molecular diversity of K⁺ channels. Annals of the New York Academy of Sciences. 1999;868:233–285.

6. Cole KS. Dynamic electrical characteristics of the squid axon membrane. Archives des Sciences Physiologiques. 1949;3:253–258.

7. Coombs JS, Curtis DR, Eccles JC. The interpretation of spike potentials of motoneurons. Journal of Physiology. 1957;139:198–231.

8. DiFrancesco D. Physiology and pharmacology of the cardiac pacemaker (“funny”) current. Pharmacology and Therapeutics. 2005;107:59–79.

9. Hille B. Ionic basis of resting potentials and action potentials. In: Kandel ER, ed. Bethesda, MD: American Physiological Society; 1977;99–136. Handbook of physiology. Sect. 1, Vol. 1.

10. Hodgkin AL. Chance and design in electrophysiology An informal account of certain experiments on nerve carried out between 1934 and 1952. Journal of Physiology (Landon). 1976;263:1–21.

11. Hodgkin AL, Huxley AF. Action potentials recorded from inside a nerve fiber. Nature (London). 1939;144:710–711.

12. Hodgkin AL, Huxley AF. Currents carried by sodium and potassium ions through the membrane of the giant axon of Loligo. Journal of Physiology (London). 1952a;116:449–472.

13. Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. Journal of Physiology (London). 1952b;117:500–544.

14. Huguenard J, McCormick DA. Electrophysiology of the Neuron An Interative Tutorial Oxford: Oxford University Press; 1991.

15. Lauger P. Electrogenic ion pumps Sunderland, MA: Sinauer; 1991.

16. Llinás RR. The intrinsic electrophysiological properties of mammalian neurons: Insights into central nervous system function. Science. 1988;242:1654–1664.

17. McComas AJ. Galvani’s spark Oxford: Oxford University Press; 2011.

18. McCormick DA. Neurotransmitter actions in the thalamus and cerebral cortex and their role in neuromodulation of thala-mocortical activity. Progress in Neurobiology. 1992;39:337–388.

19. McCormick DA, Pape H-C. Properties of a hyperpolarization-activated cation current and its role in rhythmic oscillation in thalamic relay neurones. Journal of Physiology (London). 1990;431:291–318.

20. Nicoll RA. The coupling of neurotransmitter receptors to ion channels in the brain. Science. 1988;241:545–551.

21. Popovic MA, Foust AJ, McCormick DA, Zecevic D. The spatio-temporal characteristics of action potential initiation in layer 5 pyramidal neurons: A voltage imaging study. Journal of Physiology. 2011;589:4167–4187.

22. Reithmeier RAF. Mammalian exchangers and co-transporters. Current Opinion in Cell Biology. 1994;6:583–594.

23. Shu Y, Hasenstaub A, Duque A, Yu Y, McCormick DA. Modulation of intracortical synaptic potentials by presynaptic somatic membrane potential. Nature. 2006;441:761–765.

24. Stuart G, Spruston N, Sakmann B, Hausser M. Action potential initiation and backpropagation in neurons of the mammalian CNS. Trends in Neurosciences. 1997;10:125–131.

Suggested Readings

1. Hille B. Ionic channels of excitable membranes 3rd ed. Sunderland, MA: Sinauer; 2001.

2. Hodgkin AL. Chance and design Cambridge: Cambridge Univ. Press; 1992.

3. Huguenard J, McCormick DA. Electrophysiology of the neuron New York: Oxford Univ. Press; 1994.

4. Johnston D, Wu SM-S. Foundations of cellular neurophysiology Cambridge, MA: MIT Press; 1995.

5. Koch C. Biophysics of computation New York: Oxford Univ. Press; 1999.