

in which all the armaments
of theoretical physics
cannot ward off the conclusion:
implosion produces black holes
The confrontation was inevitable. These two intellectual giants, J. Robert Oppenheimer and John Archibald Wheeler, had such different views of the Universe and of the human condition that time after time they found themselves on opposite sides of deep issues: national security, nuclear weapons policy—and now black holes.
The scene was a lecture hall at the University of Brussels in Belgium. Oppenheimer and Wheeler, neighbors in Princeton, New Jersey, had journeyed there along with thirty-one other leading physicists and astronomers from around the world for a full week of discussions on the structure and evolution of the Universe.
It was Tuesday, 10 June 1958. Wheeler had just finished presenting, to the assembled savants, the results of his recent calculations with Kent Harrison and Masami Wakano—the calculations that had identified, unequivocally, the masses and circumferences of all possible cold, dead stars (Chapter 5). He had filled in the missing gaps in the Chandrasekhar and Oppenheimer–Volkoff calculations, and had confirmed their conclusions: Implosion is compulsory when a star more massive than about 2 Suns dies, and the implosion cannot produce a white dwarf, or a neutron star, or any other kind of cold, dead star, unless the dying star ejects enough mass to pull itself below the maximum-mass limit of about 2 Suns.
“Of all the implications of general relativity for the structure and evolution of the Universe, this question of the fate of great masses of matter is one of the most challenging,” Wheeler asserted. On this his audience could agree. Wheeler then, in a near replay of Arthur Eddington’s attack on Chandrasekhar twenty-four years earlier (Chapter 4), described Oppenheimer’s view that massive stars must die by imploding to form black holes, and then he opposed it: Such implosion “does not give an acceptable answer,” Wheeler asserted. Why not? For essentially the same reason as Eddington had rejected it; in Eddington’s words, “there should be a law of Nature to prevent a star from behaving in this absurd way.” But there was a deep difference between Eddington and Wheeler: Whereas Eddington’s 1935 speculative mechanism to save the Universe from black holes was immediately branded as wrong by such experts as Niels Bohr, Wheeler’s 1958 speculative mechanism could not at the time be proved or disproved—and fifteen years later it would turn out to be partially right (Chapter 12).
Wheeler’s speculation was this. Since (in his view) implosion to a black hole must be rejected as physically implausible, “there seems no escape from the conclusion that the nucleons [neutrons and protons] at the center of an imploding star must necessarily dissolve away into radiation, and that this radiation must escape from the star fast enough to reduce its mass [below about 2 Suns]” and permit it to wind up in the neutron-star graveyard. Wheeler readily acknowledged that such a conversion of nucleons into escaping radiation was outside the bounds of the known laws of physics. However, such conversion might result from the as yet ill-understood “marriage” of the laws of general relativity with the laws of quantum mechanics (Chapters 12–14). This, to Wheeler, was the most enticing aspect of “the problem of great masses”: The absurdity of implosion to form a black hole forced him to contemplate an entirely new physical process. (See Figure 6.1.)
Oppenheimer was not impressed. When Wheeler finished speaking, he was the first to take the floor. Maintaining a politeness that he had not displayed as a younger man, he affirmed his own view: “I do not know whether non-rotating masses much heavier than the sun really occur in the course of stellar evolution; but if they do, I believe their implosion can be described in the framework of general relativity [without asserting new laws of physics]. Would not the simplest assumption be that such masses undergo continued gravitational contraction and ultimately cut themselves off more and more from the rest of the Universe [that is, form black holes]?” (See Figure 6.1.)
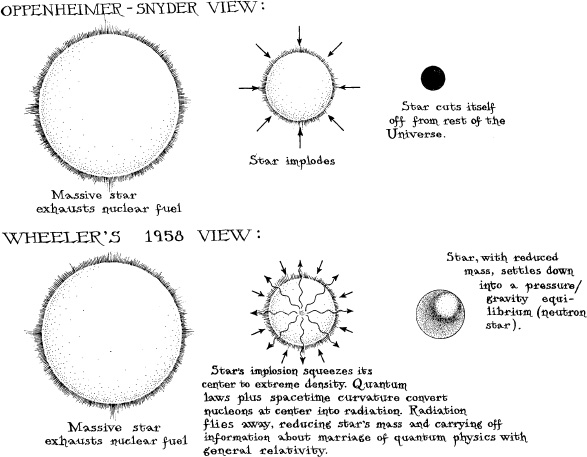
6.1 Contrast of Oppenheimer’s view of the fates of large masses (upper sequence) with Wheeler’s 1958 view (lower sequence).
Wheeler was equally polite, but held his ground. “It is very difficult to believe ‘gravitational cutoff is a satisfactory answer,” he asserted.
Oppenheimer’s confidence in black holes grew out of detailed calculations he had done nineteen years earlier:
Black-Hole Birth: A First Glimpse
In the winter of 1938–39, having just completed his computation with George Volkoff of the masses and circumferences of neutron stars (Chapter 5), Oppenheimer was firmly convinced that massive stars, when they die, must implode. The next challenge was obvious: use the laws of physics to compute the details of the implosion. What would the implosion look like as seen by people in orbit around the star? What would it look like as seen by people riding on the star’s surface? What would be the final state of the imploded star, thousands of years after the implosion?
This computation would not be easy. Its mathematical manipulations would be the most challenging that Oppenheimer and his students had yet tackled: The imploding star would change its properties rapidly as time passes, whereas the Oppenheimer-Volkoff neutron stars had been static, unchanging. Spacetime curvature would become enormous inside the imploding star, whereas it had been much more modest in neutron stars. To deal with these complexities would require a very special student. The choice was obvious: Hartland Snyder.
Snyder was different from Oppenheimer’s other students. The others came from middle-class families; Snyder gave the impression of working class, though his father was actually an engineer. It was rumored (incorrectly) that he was a truck driver in Utah before turning physicist. As Robert Serber recalls, “Hartland pooh-poohed a lot of things that were standard for Oppie’s students, like appreciating Bach and Mozart and going to string quartets and liking fine food and liberal politics.”
The Caltech nuclear physicists were a more rowdy bunch than Oppenheimer’s entourage; on Oppenheimer’s annual spring trek to Pasadena, Hartland fit right in. Says Caltech’s William Fowler, “Oppie was extremely cultured; knew literature, art, music, Sanskrit. But Hartland—he was like the rest of us bums. He loved the Kellogg Lab parties, where Tommy Lauritsen played the piano and Charlie Lauritsen [leader of the lab] played the fiddle and we sang college songs and drinking songs. Of all of Oppie’s students, Hartland was the most independent.”
Hartland was also different mentally. “Hartland had more talent for difficult mathematics than the rest of us,” recalls Serber. “He was very good at improving the cruder calculations that the rest of us did.” It was this talent that made him a natural for the implosion calculation.
Before embarking on the full, complicated calculation, Oppenheimer insisted (as always) on making a first, quick survey of the problem. How much could be learned with only a little effort? The key to this first survey was Schwarzschild’s geometry for the curved space-time outside a star (Chapter 3).
Schwarzschild had discovered his spacetime geometry as a solution to Einstein’s general relativistic field equation. It was the solution for the exterior of a static star, one that neither implodes nor explodes nor pulsates. However, in 1923 George Birkhoff, a mathematician at Harvard, had proved a remarkable mathematical theorem: Schwarzschild’s geometry describes the exterior of any star that is spherical, including not only static stars but also imploding, exploding, and pulsating ones.
For their quick calculation, then, Oppenheimer and Snyder simply assumed that a spherical star, upon exhausting its nuclear fuel, would implode indefinitely, and without probing what happens inside the star, they computed what the imploding star would look like to somebody far away. With ease they inferred that, since the spacetime geometry outside the imploding star is the same as outside any static star, the imploding star would look very much like a sequence of static stars, each one more compact than the previous one.
Now, the external appearance of such static stars had been studied two decades earlier, around 1920. Figure 6.2 reproduces the embedding diagrams that we used in Chapter 3 to discuss that appearance. Recall that each embedding diagram depicts the curvature of space inside and near a star. To make the depiction comprehensible, the diagram displays the curvature of only two of the three dimensions of space: the two dimensions on a sheet that lies precisely in the star’s equatorial “plane” (left half of the figure). The curvature of space on this sheet is visualized by imagining that we pull the sheet out of the star and out of the physical space in which we and the star live, and move it into a flat (uncurved), fictitious hyperspace. In the uncurved hyperspace, the sheet can maintain its curved geometry only by bending downward like a bowl (right half of the figure).
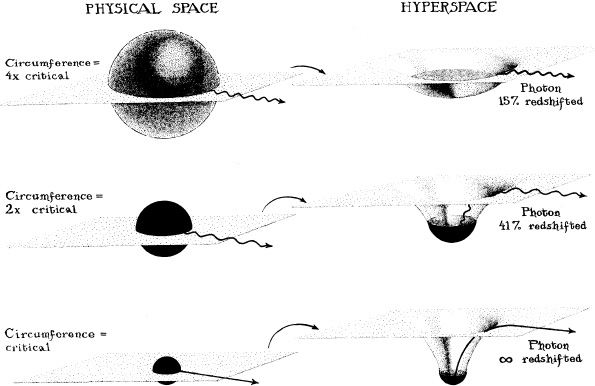
6.2 (Same as Figure 3.4.) General relativity’s predictions for the curvature of space and the redshift of light from a sequence of three highly compact, static (non-imploding) stars that all have the same mass but have different circumferences.
The figure shows a sequence of three static stars that mimic the implosion that Oppenheimer and Snyder were preparing to analyze. Each star has the same mass, but they have different circumferences. The first is four times bigger around than the critical circumference (four times bigger than the circumference at which the star’s gravity would become so strong that it forms a black hole). The second is twice the critical circumference, and the third is precisely at the critical circumference. The embedding diagrams show that the closer the star is to its critical circumference, the more extreme is the curvature of space around the star. However, the curvature does not become infinitely extreme. The bowl-like geometry is smooth everywhere with no sharp cusps or points or creases, even when the star is at its critical circumference; that is, the spacetime curvature is not infinite, and, correspondingly, since tidal gravitational forces (the kinds of forces that stretch one from head to foot and produce the tides on the Earth) are the physical manifestation of spacetime curvature, tidal gravity is not infinite at the critical circumference.
In Chapter 3 we also discussed the fate of light emitted from the surfaces of static stars. We learned that because time flows more slowly at the stellar surface than far away (gravitational time dilation), light waves emitted from the star’s surface and received far away will have a lengthened period of oscillation and correspondingly a lengthened wavelength and a redder color. The light’s wavelength gets shifted toward the red end of the spectrum as the light climbs out of the star’s intense gravitational field (gravitational redshift). When the static star is four times larger than its critical circumference, the light’s wavelength is lengthened by 15 percent (see the photon of light in the upper right part of the figure); when the star is at twice its critical circumference, the redshift is 41 percent (middle right); and when the star is precisely at its critical circumference, the light’s wavelength is infinitely redshifted, which means that the light has no energy left at all and therefore has ceased to exist.
Oppenheimer and Snyder, in their quick calculation, inferred two things from this sequence of static stars: First, an imploding star, like these static stars, would probably develop strong spacetime curvature as it nears its critical circumference, but not infinite curvature and therefore not infinite tidal gravitational forces. Second, as the star implodes, light from its surface should get more and more redshifted, and when it reaches the critical circumference, the redshift should become infinite, making the star become completely invisible. In Oppenheimer’s words, the star should “cut itself off’ visually from our external Universe.
Was there any way, Oppenheimer and Snyder asked themselves, that the star’s internal properties—ignored in this quick calculation—could save the star from this cutoff fate? For example, might the implosion be forced to go so slowly that never, even after an infinite time, would the critical circumference actually be reached?
Oppenheimer and Snyder would have liked to answer these questions by calculating the details of a realistic stellar implosion, as depicted in the left half of Figure 6.3. Any real star will spin, as does the Earth, at least a little bit. Centrifugal forces due to that spin will force the star’s equator to bulge out at least a little bit, as does Earth’s equator. Thus, the star cannot be precisely spherical. As it implodes, the star must spin faster and faster like a figure skater pulling in his arms; and its faster spin will cause centrifugal forces inside the star to grow, making the equatorial bulge more pronounced—sufficiently pronounced, perhaps, that it even halts the implosion, with the outward centrifugal forces then fully balancing gravity’s pull. Any real star has high density and pressure in its center, and lower density and pressure in its outer layers; as it implodes, high-density lumps will develop here and there like blueberries in a blueberry muffin. Moreover, the star’s gaseous matter, as it implodes, will form shock waves—analogues of breaking ocean waves—and these shocks may eject matter and mass from some parts of the star’s surface just as an ocean wave can eject droplets of water into the air. Finally, radiation (electromagnetic waves, gravitational waves, neutrinos) will pour out of the star, carrying away mass.
All these effects Oppenheimer and Snyder would have liked to include in their calculations, but to do so was a formidable task, far beyond the capabilities of any physicist or computing machine in 1939. It would not become feasible until the advent of supercomputers in the 1980s. Thus, to make any progress at all, it was necessary to build an idealized model of the imploding star and then compute the predictions of the laws of physics for that model.
Such idealizations were Oppenheimer’s forte: When confronted with a horrendously complex situation such as this one, he could discern almost unerringly which phenomena were of crucial importance and which were peripheral.
For the imploding star, one feature was crucial above all others, Oppenheimer believed: gravity as described by Einstein’s general relativistic laws. It, and only it, must not be compromised when formulating a calculation that could be done. By contrast, the star’s spin and its nonspherical shape could be ignored; they might be crucially important for some imploding stars, but for stars that spin slowly, they probably would have no strong effect. Oppenheimer could not really prove this mathematically, but intuitively it seemed clear, and indeed it has turned out to be true. Similarly, his intuition said, the outpouring of radiation was an unimportant detail, as were shock waves and density lumps. Moreover, since (as Oppenheimer and Volkoff had shown) gravity could overwhelm all pressure in massive, dead stars, it seemed safe to pretend (incorrectly, of course) that the imploding star has no internal pressure whatsoever—neither thermal pressure, nor pressure arising from the electrons’ or neutrons’ claustrophobic degeneracy motions, nor pressure arising from the nuclear force. A real star, with its real pressure, might implode in a different manner from an idealized, pressureless star; but the differences of implosion should be only modest, not great, Oppenheimer’s intuition insisted.
Thus it was that Oppenheimer suggested to Snyder an idealized computational problem: Study, using the precise laws of general relativity, the implosion of a star that is idealized as precisely spherical, nonspinning, and nonradiating, a star with uniform density (the same near its surface as at its center) and with no internal pressure whatsoever; see Figure 6.3.
Even with all these idealizations—idealizations that would generate skepticism in other physicists for thirty years to come—the calculation was exceedingly difficult. Fortunately, Richard Tolman was available in Pasadena for help. Leaning heavily on Tolman and Oppenheimer for advice, Snyder worked out the equations governing the entire implosion—and in a tour de force, he managed to solve them. He now had the full details of the implosion, expressed in formulas! By scrutinizing those formulas, first from one direction and then another, physicists could read off whatever aspect of the implosion they wished—how it looks from outside the star, how it looks from inside, how it looks on the star’s surface, and so forth.
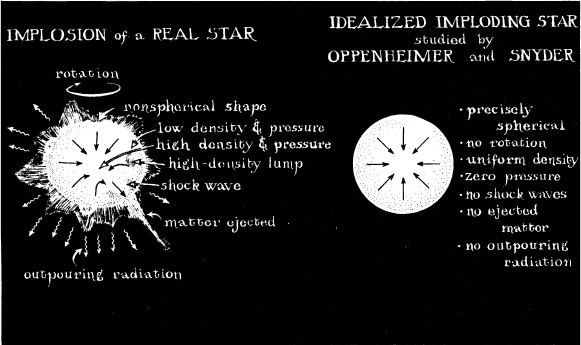
6.3 Left: Physical phenomena in a realistic, imploding star. Right: The idealizations that Oppenheimer and Snyder made in order to compute stellar implosion.
Especially intriguing is the appearance of the imploding star as observed from a static, external reference frame, that is, as seen by observers outside the star who remain always at the same fixed circumference instead of riding inward with the star’s imploding matter. The star, as seen in a static, external frame, begins its implosion in just the way one would expect. Like a rock dropped from a rooftop, the star’s surface falls downward (shrinks inward) slowly at first, then more and more rapidly. Had Newton’s laws of gravity been correct, this acceleration of the implosion would continue inexorably until the star, lacking any internal pressure, is crushed to a point at high speed. Not so according to Oppenheimer and Snyder’s relativistic formulas. Instead, as the star nears its critical circumference, its shrinkage slows to a crawl. The smaller the star gets, the more slowly it implodes, until it becomes frozen precisely at the critical circumference. No matter how long a time one waits, if one is at rest outside the star (that is, at rest in the static, external reference frame), one will never be able to see the star implode through the critical circumference. That is the unequivocal message of Oppenheimer and Snyder’s formulas.
Is this freezing of the implosion caused by some unexpected, general relativistic force inside the star? No, not at all, Oppenheimer and Snyder realized. Rather, it is caused by gravitational time dilation (the slowing of the flow of time) near the critical circumference. Time on the imploding star’s surface, as seen by static external observers, must flow more and more slowly when the star approaches the critical circumference, and correspondingly everything occurring on or inside the star including its implosion must appear to go into slow motion and then gradually freeze.
As peculiar as this might seem, even more peculiar was another prediction made by Oppenheimer and Snyder’s formulas: Although, as seen by static external observers, the implosion freezes at the critical circumference, it does not freeze at all as viewed by observers riding inward on the star’s surface. If the star weighs a few solar masses and begins about the size of the Sun, then as observed from its own surface, it implodes to the critical circumference in about an hour’s time, and then keeps right on imploding past criticality and on in to smaller circumferences.
By 1939, when Oppenheimer and Snyder discovered these things, physicists had become accustomed to the fact that time is relative; the flow of time is different as measured in different reference frames that move in different ways through the Universe. But never before had anyone encountered such an extreme difference between reference frames. That the implosion freezes forever as measured in the static, external frame but continues rapidly on past the freezing point as measured in the frame of the star’s surface was extremely hard to comprehend. Nobody who studied Oppenheimer and Snyder’s mathematics felt comfortable with such an extreme warpage of time. Yet there it was in their formulas. One might wave one’s arms with heuristic explanations, but no explanation seemed very satisfying. It would not be fully understood until the late 1950s (near the end of this chapter).
By looking at Oppenheimer and Snyder’s formulas from the viewpoint of an observer on the star’s surface, one can deduce the details of the implosion even after the star sinks within its critical circumference; that is, one can discover that the star gets crunched to infinite density and zero volume, and one can deduce the details of the spacetime curvature at the crunch. However, in their article describing their calculations, Oppenheimer and Snyder avoided any discussion of the crunch whatsoever. Presumably Oppenheimer was prevented from discussing it by his own innate scientific conservatism, his unwillingness to speculate (see the last two paragraphs of Chapter 5).
If reading the star’s final crunch off their formulas was too much for Oppenheimer and Snyder to face, even the details outside and at the critical circumference were too bizarre for most physicists in 1939. At Caltech, for example, Tolman was a believer; after all, the predictions were unequivocal consequences of general relativity. But nobody else at Caltech was very convinced. General relativity had been tested experimentally only in the solar system, where gravity is so weak that Newton’s laws give almost the same predictions as general relativity. By contrast, the bizarre Oppenheimer–Snyder predictions relied on ultra-strong gravity. General relativity might well fail before gravity ever became so strong, most physicists thought; and even if it did not fail, Oppenheimer and Snyder might be misinterpreting what their mathematics was trying to say; and even if they were not misinterpreting their mathematics, their calculation was so idealized, so devoid of spin, lumps, shocks, and radiation, that it should not be taken seriously.
Such skepticism held sway throughout the United States and Western Europe, but not in the U.S.S.R. There Lev Landau, still recuperating from his year in prison, kept a “Golden List” of the most important physics research articles published anywhere in the world. Upon reading the Oppenheimer–Snyder paper, Landau entered it in his List, and he proclaimed to his friends and associates that these latest Oppenheimer revelations had to be right, even though they were extremely difficult for the human mind to comprehend. So great was Landau’s influence that his view took hold among leading Soviet theoretical physicists from that day forward.
Nuclear Interlude
Were Oppenheimer and Snyder right, or were they wrong? The answer would likely have been learned definitively during the 1940s had World War 11 and then crash programs to develop the hydrogen bomb not intervened. But the war and the bomb did intervene, and research on impractical, esoteric issues like black holes became frozen in time as physicists turned their full energies to weapons design.
Only in the late 1950s did the weapons efforts wind down enough to bring stellar implosion back into physicists’ consciousness. Only then did the skeptics launch their first serious attack on the Oppenheimer–Snyder predictions. Carrying the banner of the skeptics at first, but not for long, was John Archibald Wheeler. From the outset, a leader of the believers was Wheeler’s Soviet counterpart, Yakov Borisovich Zel’-dovich.
The characters of Wheeler and Zel’dovich were shaped in the fire of nuclear weapons projects during the nearly two decades that black-hole research was frozen in time, the decades of the 1940s and 1950s. From their weapons work, Wheeler and Zel’dovich emerged with crucial tools for analyzing black holes: powerful computational techniques, a deep understanding of the laws of physics, and interactive research styles in which they would continually stimulate younger colleagues. They also emerged carrying difficult baggage—a set of complex relationships with some of their key colleagues: Wheeler with Oppenheimer; Zel’dovich with Landau and with Andrei Sakharov.
John Wheeler, fresh out of graduate school in 1933, and the winner of a Rockefeller-financed National Research Council postdoctoral fellowship, had a choice of where and with whom to do his postdoctoral study. He could have chosen Berkeley and Oppenheimer, as did most NRC theoretical physics postdocs in those days; instead he chose New York University and Gregory Breit. “In personality they [Oppenheimer and Breit] were utterly different,” Wheeler says. “Oppenheimer saw things in black and white and was a quick decider. Breit worked in shades of grey. Attracted to issues that require long reflection, I chose Breit.”
From New York University in 1933, Wheeler moved on to Copenhagen to study with Niels Bohr, then to an assistant professorship at the University of North Carolina, followed by one at Princeton University, in New Jersey. In 1939, while Oppenheimer and students in California were probing neutron stars and black holes, Wheeler and Bohr at Princeton (where Bohr was visiting) were developing the theory of nuclear fission: the breakup of heavy atomic nuclei such as uranium into smaller pieces, when the nuclei are bombarded by neutrons (Box 6.1). Fission had just been discovered quite unexpectedly by Otto Hahn and Fritz Strassman in Germany, and its implications were ominous: By a chain reaction of fissions a weapon of unprecedented power might be made. But Bohr and Wheeler did not concern themselves with chain reactions or weapons; they just wanted to understand how fission comes about. What is the underlying mechanism? How do the laws of physics produce it?
Fusion, Fission, and Chain Reactions
The fusion of very light nuclei to form medium-sized nuclei releases huge amounts of energy. A simple example from Box 5.3 is the fusion of a deuterium nucleus (“heavy hydrogen,” with one proton and one neutron) and an ordinary hydrogen nucleus (a single proton) to form a helium-3 nucleus (two protons and one neutron): Such fusion reactions keep the Sun hot and power the hydrogen bomb (the “superbomb” as it was called in the 1940s and 1950s).
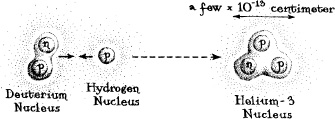
The fission (splitting apart) of a very heavy nucleus to form two medium-sized nuclei releases a large amount of energy—far more than comes from chemical reactions (since the nuclear force which governs nuclei is far stronger than the electromagnetic force which governs chemically reacting atoms), but much less energy than comes from the fusion of light nuclei. A few very heavy nuclei undergo fission naturally, without any outside help. More interesting for this chapter are fission reactions in which a neutron hits a very heavy nucleus such as uranium-235 (a uranium nucleus with 235 protons and neutrons) and splits it roughly in half:
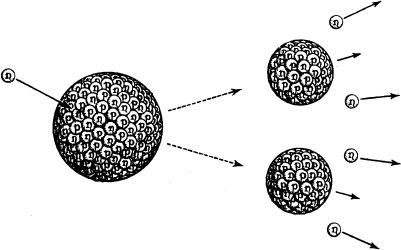
There are two special, heavy nuclei, uranium-235 and plutonium-239, with the property that their fission produces not only two medium-sized nuclei, but also a handful of neutrons (as in the drawing above). These neutrons make possible a chain reaction: If one concentrates enough uranium-235 or plutonium-239 into a small enough package, then the neutrons released from one fission will hit other uranium or plutonium nuclei and fission them, producing more neutrons that fission more nuclei, producing still more neutrons that fission still more nuclei, and so on. The result of this chain reaction, if uncontrolled, is a huge explosion (an atomic bomb blast); if controlled in a reactor, the result can be highly efficient electric power.
Bohr and Wheeler were remarkably successful. They discovered how the laws of physics produce fission, and they predicted which nuclei would be the most effective at sustaining chain reactions: uranium-235 (which would become the fuel for the bomb to destroy Hiroshima) and plutonium-239 (a type of nucleus that does not exist in nature but that the American physicists would soon learn how to make in nuclear reactors and would use to fuel the bomb to destroy Nagasaki). However, Bohr and Wheeler were not thinking of bombs in 1939; they only wanted to understand.
The Bohr–Wheeler article explaining nuclear fission was published in the same issue of the Physical Review as the Oppenheimer–Snyder article describing the implosion of a star. The publication date was 1 September 1939, the very day that Hitler’s troops invaded Poland, triggering World War 11.
Yakov Borisovich Zel’dovich was bom into a Jewish family in Minsk in 1914; later that year his family moved to Saint Petersburg (renamed Leningrad in the 1920s, then restored to Saint Petersburg in the 1990s). Zel’-dovich completed high school at age fifteen and then, instead of entering university, went to work as a laboratory assistant at the Physicotechnical Institute in Leningrad. There he taught himself so much physics and chemistry and did such impressive research that, without any formal university training, he was awarded a Ph.D. in 1934, at age twenty.
In 1939, while Wheeler and Bohr were developing the theory of nuclear fission, Zel’dovich and a close friend, Yuli Borisovich Khariton, were developing the theory of chain reactions produced by nuclear fission: Their research was triggered by an intriguing (incorrect) suggestion from French physicist Francis Perrin that volcanic eruptions might be powered by natural, underground nuclear explosions, which result from a chain reaction of fissions of atomic nuclei. However, nobody including Perrin had worked out the details of such a chain reaction. Zel’dovich and Khariton—already among the world’s best experts on chemical explosions—leaped on the problem. Within a few months they had shown (as, in parallel, did others in the West) that such an explosion cannot occur in nature, because naturally occurring uranium consists mostly of uranium-238 and not enough uranium-235. However, they concluded, if one were to artificially separate out uranium-235 and concentrate it, then one could make a chain-reaction explosion. (The Americans would soon embark on such separation to make the fuel for their Hiroshima bomb.) The curtain of secrecy had not yet descended around nuclear research, so Zel’dovich and Khariton published their calculations in the most prestigious of Soviet physics journals, the Journal of Experimental and Theoretical Physics, for all the world to see.
During the six years of World War II, physicists of the warring nations developed sonar, mine sweepers, rockets, radar, and, most fatefully, the atomic bomb. Oppenheimer led the “Manhattan Project” at Los Alamos, New Mexico, to design and build the American bombs. Wheeler was the lead scientist in the design and construction of the world’s first production-scale nuclear reactors, in Hanford, Washington, which made the plutonium-239 for the Nagasaki bomb.
After the bombs’ decimation of Hiroshima and Nagasaki and the deaths of several hundred thousand people, Oppenheimer was in anguish: “If atomic bombs are to be added to the arsenals of a warring world, or to the arsenals of nations preparing for war, then the time will come when mankind will curse the name of Los Alamos and Hiroshima.” “In some sort of crude sense which no vulgarity, no humor, no overstatement can quite extinguish, the physicists have known sin; and this is a knowledge which they cannot lose.”
But Wheeler had the opposite kind of regret: “As I look back on [1939 and my fission theory work with Bohr], I feel a great sadness. How did it come about that I looked on fission first as a physicist [simply curious to know how fission works], and only secondarily as a citizen [intent on defending my country]? Why did I not look at it first as a citizen and only secondarily as a physicist? A simple survey of the records shows that between twenty and twenty-five million people perished in World War 11 and more of them in the later years than in the earlier years. Every month by which the war was shortened would have meant a saving of the order of half a million to a million lives. Among those granted life would have been my brother Joe, killed in October 1944 in the Battle for Italy. What a difference it would have made if the critical date [of the atomic bomb’s first use in the war] had been not August 6, 1945, but August 6, 1943.”
In the U.S.S.R., physicists abandoned all nuclear research in June 1941, when Germany attacked Russia, since other physics would produce quicker payoffs for national defense. As the German army marched on and surrounded Leningrad, Zel’dovich and his friend Khariton were evacuated to Kazan, where they worked intensely on the theory of the explosion of ordinary types of bombs, trying to improve the bombs’ explosive power. Then, in 1943, they were summoned to Moscow. It had become clear, they were told, that both the Americans and the Germans were mounting efforts to construct an atomic bomb. They were to be part of a small, elite, Soviet bomb development effort under the leadership of Igor V. Kurchatov.
By two years later, when the Americans bombed Hiroshima and Nagasaki, Kurchatov’s team had developed a thorough theoretical understanding of nuclear reactors for making plutonium-239, and had developed several possible bomb designs—and Khariton and Zel’-dovich had become the lead theorists on the project.
When Stalin learned of the American atomic bomb explosions, he angrily berated Kurchatov for the Soviet team’s slowness. Kurchatov defended his team: Amidst the war’s devastation, and with its limited resources, the team could not move more rapidly. Stalin told him angrily that if a child doesn’t cry, its mother can’t know what it needs. Ask for anything you need, he commanded, nothing will be refused; and he then demanded a no-holds-barred, crash project to construct the bomb, a project under the ultimate authority of Lavrenty Pavlovich Beria, the fearsome head of the secret police.
The magnitude of the effort that Beria mounted is hard to imagine. He commandeered the forced labor of millions of Soviet citizens from Stalin’s prison camps. These zeks, as they were colloquially called, constructed uranium mines, uranium purification factories, nuclear reactors, theoretical research centers, weapons test centers, and self-contained, small cities to support these facilities. The facilities, scattered across the face of the nation, were surrounded by levels of security unheard of in the Americans’ Manhattan Project. Zel’dovich and Khariton were moved to one of these facilities, in “a far away place” whose location, though almost certainly well known to Western authorities by the late 1950s, was forbidden to be revealed by Soviet citizens until 1990.1 The facility was known simply as Obyekt (“the Installation”); Khariton became its director, and Zel’dovich the leader of one of its key bomb design teams. Under Beria’s authority, Kurchatov set up several teams of physicists to pursue, in parallel and completely independently, each aspect of the bomb project; redundancy brings security. The teams at the Installation fed design problems to the other teams, including a small one led by Lev Landau at the Institute of Physical Problems in Moscow.
While this massive effort was rolling inexorably forward, Soviet spies were acquiring, through Klaus Fuchs (a British physicist who had worked on the American bomb project), the design of the Americans’ plutonium-based bomb. It differed somewhat from the design that Zel’dovich and his colleagues had produced, so Kurchatov, Khariton, and company faced a tough decision: They were under excruciating pressure from Stalin and Beria for results, and they feared the consequences of an unsuccessful bomb test in an era when failure often meant execution; they knew that the American design had worked at Alamogordo and Nagasaki, but they could not be completely sure of their own design; and they possessed enough plutonium for only one bomb. The decision was clear but painful: They put their own design on hold2 and converted their crash program over to the American design.
At last, on 29 August 1949—after four years of crash effort, untold misery, untold deaths of slave-labor zeks, and the beginning of an accumulation of waste from nuclear reactors near Cheliabinsk that would explode ten years later, contaminating hundreds of square miles of countryside—the crash program reached fruition. The first Soviet atomic bomb was exploded near Semipalatinsk in Soviet Asia, in a test witnessed by the Supreme Command of the Soviet army and government leaders.
On 3 September 1949 an American WB-29 weather reconnaissance plane, on a routine flight from Japan to Alaska, discovered products of nuclear fission from the Soviet test. The data were given to a committee of experts, including Oppenheimer, for evaluation. The verdict was unequivocal. The Russians had tested an atomic bomb!
Amidst the panic that ensued (backyard bomb shelters; atomic bomb drills for schoolchildren; McCarthy’s “witch hunts” to root out spies, Communists, and their fellow travelers from government, army, media, and universities), a profound debate occurred amongst physicists and politicians. Edward Teller, one of the most innovative of the American atomic bomb design physicists, advocated a crash program to design and build the “superbomb” (or “hydrogen bomb”)—a weapon based on the fusion of hydrogen nuclei to form helium. The hydrogen bomb, if it could be built, would be awesome. There seemed no limit to its power. Did one want a bomb ten times more powerful than Hiroshima? a hundred times more powerful? a thousand? a million? If the bomb could be made to work at all, it could be made as powerful as one wished.
John Wheeler backed Teller: A crash program for the “super” was essential to counter the Soviet threat, he believed. Robert Oppenheimer and his General Advisory Committee to the D.S. Atomic Energy Commission were opposed. It was not at all obvious whether a superbomb as then conceived could ever be made to work, Oppenheimer and his committee argued. Moreover, even if it did work, any super that was vastly more powerful than an ordinary atomic bomb would likely be too heavy for delivery by airplane or rocket. And then there were the moral issues, which Oppenheimer and his committee addressed as follows. “We base our recommendations [against a crash program] on our belief that the extreme dangers to mankind inherent in the proposal wholly outweigh any military advantage that could come from this development. Let it be clearly realized that this is a super weapon; it is in a totally different category from an atomic bomb. The reason for developing such super bombs would be to have the capacity to devastate a vast area with a single bomb. Its use would involve a decision to slaughter a vast number of civilians. We are alarmed as to the possible global effects of the radioactivity generated by the explosion of a few super bombs of conceivable magnitude. If super bombs will work at all, there is no inherent limit in the destructive power that may be attained with them. Therefore, a super bomb might become a weapon of genocide.”
To Edward Teller and John Wheeler these arguments made no sense at all. The Russians surely would push forward with the hydrogen bomb; if America did not push forward as well, the free world could be put in enormous danger, they believed.
The Teller–Wheeler view prevailed. On 10 March 1950, President Truman ordered a crash program to develop the super.
The Americans’ 1949 design for the super appears in retrospect to have been a prescription for failure, just as Oppenheimer’s committee had suspected. However, since it was not certain to fail, and since nothing better was known, it was pursued intensely until March 1951, when Teller and Stanislaw Ulam invented a radically new design, one that showed bright promise.
The Teller–Ulam invention at first was just an idea for a design. As Hans Bethe has said, “Nine out of ten of Teller’s ideas are useless. He needs men with more judgement, even if they be less gifted, to select the tenth idea, which often is a stroke of genius.” To test whether this idea was a stroke of genius or a deceptive dud required turning it into a concrete and detailed bomb design, then carrying out extensive computations on the biggest available computers to see whether the design might work, and then, if the calculations predicted success, constructing and testing an actual bomb.
Two teams were set up to carry out the calculations: One at Los Alamos, the other at Princeton University. John Wheeler led the Princeton team. Wheeler’s team worked night and day for several months to develop a full bomb design based on the Teller–Ulam idea, and to test by computer calculations whether it would work. As Wheeler recalls, “We did an immense amount of calculation. We were using the computer facilities of New York, Philadelphia, and Washington—in fact, a very large fraction of the computer capacity of the United States. Larry Wilets, John Toll, Ken Ford, Louis Henyey, Carl Hausman, Dick l’Olivier, and others worked three six-hour stretches each day to get things out.”
When the calculations made it clear that the Teller–Ulam idea probably would work, a meeting was called, at the Institute for Advanced Study in Princeton (where Oppenheimer was the director), to present the idea to Oppenheimer’s General Advisory Committee and its parent U.S. Atomic Energy Commission. Teller described the idea, and then Wheeler described his team’s specific design and its predicted explosion. Wheeler recalls, “While I was starting to give my talk, Ken Ford rushed up to the window from outside, lifted it up, and passed in this big chart. I unrolled it and put it on the wall; it showed the progress of the thermonuclear combustion [as we had computed it.] ... The Committee had no option but to conclude that this thing made sense. . . . Our calculation turned Oppie around on the project.”

A portion of John Wheeler’s hydrogen bomb design team at Princeton University in 1952. Front row, left to right: Margaret Fellows, Margaret Murray, Dorothea Reiffel, Audrey Ojala, Christene Shack, Roberta Casey. Second row: Walter Aron, William Clendenin, Solomon Bochner, John Toll, John Wheeler, Kenneth Ford. Third and fourth rows: David Layzer, Lawrence Wilets, David Carter, Edward Frieman, Jay Berger, John Mclntosh, Ralph Pennington, unidentified, Robert Goerss. [Photo by Howard Schrader; courtesy Lawrence Wilets and John A Wheeler.]
Oppenheimer has described his own reaction: “The program we had in 1949 [the ‘prescription for failure’] was a tortured thing that you could well argue did not make a great deal of technical sense. It was therefore possible to argue also that you did not want it even if you could have it. The program in 1952 [the new design based on the Teller –Ulam idea] was technically so sweet that you could not argue about that. The issues became purely the military, the political and the humane problems of what you were going to do about it once you had it.” Suppressing his deep misgivings about the ethical issues, Oppenheimer, together with the other members of his committee, closed ranks with Teller, Wheeler, and the super’s proponents, and the project moved forward at an accelerated pace to construct and test the bomb. It worked as predicted by the combined calculations of Wheeler’s team and a cooperating team at Los Alamos.
Wheeler’s team’s extensive design calculations were ultimately written up as the secret Project Matterhorn Division B Report 31 or PMB-31. “I’m told,” says Wheeler, “that for at least ten years PMB-31 was the bible for design of thermonuclear devices” (hydrogen bombs).
In 1949–50, while America was in a state of panic, and Oppenheimer, Teller, and others were debating whether America should mount a crash program to develop the super, the Soviet Union was already in the midst of a crash superbomb project of its own.
In spring 1948, fifteen months before the first Soviet atomic bomb test, Zel’dovich and his team at the Installation had carried out theoretical calculations on a superbomb design similar to the Americans’ “prescription for failure.”3 In June 1948, a second superbomb team was established in Moscow under the leadership of Igor Tamm, one of the most eminent of Soviet theoretical physicists. Its members were Vitaly Ginzburg (of whom we shall hear much in Chapters 8 and 10), Andrei Sakharov (who would become a dissident in the 1970s, and then a hero and Soviet saint in the late 1980s and 1990s), Semyon Belen’ky, and Yuri Romanov. Tamm’s team was charged with the task of checking and refining the Zel’dovich team’s design calculations.
The Tamm team’s attitude toward this task is epitomized by a statement of Belen’ky’s at the time: “Our job is to lick Zel’dovich’s anus.” Zel’dovich, with his paradoxical combination of a forceful, demanding personality and extreme political timidity, was not among the most popular of Soviet physicists. But he was among the most brilliant. Landau, who as a leader of a small subsidiary design team occasionally received orders from Zel’dovich’s team to analyze this, that, or another facet of the bomb design, sometimes referred to him behind his back as “that bitch, Zel’dovich.” Zel’dovich, by contrast, revered Landau as a great judge of the correctness of physics ideas, and as his greatest teacher—though Zel’dovich had never taken a formal course from him.
It required only a few months for Sakharov and Ginzburg, in Tamm’s team, to come up with a far better design for a superbomb than the “prescription for failure” that Zel’dovich and the Americans were pursuing. Sakharov proposed constructing the bomb as a layered cake of alternating shells of a heavy fission fuel (uranium) and light fusion fuel, and Ginzburg proposed for the fusion fuel lithium deuteride (LiD). In the bomb’s intense blast, the LiD’s lithium nuclei would fission into tritium and helium nuclei, and the tritium would then fuse with the LiD’s deuterium to form helium nuclei, releasing enormous amounts of energy. The heavy uranium would strengthen the explosion by preventing its energy from leaking out too quickly, by helping compress the fusion fuel, and by adding fission energy to the fusion. When Sakharov presented these ideas, Zel’dovich grasped their promise immediately. Sakharov’s layered cake and Ginzburg’s LiD quickly became the focus of the Soviet superbomb effort.
To push the superbomb forward more rapidly, Sakharov, Tamm, Belen’ky, and Romanov were ordered transferred from Moscow to the Installation. But not Ginzburg. The reason seems obvious: Three years earlier, Ginzburg had married Nina Ivanovna, a vivacious, brilliant woman, who in the early 1940s had been thrown into prison on a trumped-up charge of plotting to kill Stalin. She and her fellow plotters supposedly were planning to shoot Stalin from a window in the room where she lived, as he passed by on Arbat Street below. When a troika of judges met to decide her fate, it was pointed out that her room did not have any windows at all looking out on Arbat Street, so in an unusual exhibition of mercy, her life was spared; she was merely sentenced to prison and then to exile, not death. Her imprisonment and exile presumably were enough to taint Ginzburg, the inventor of the LiD fuel for the bomb, and lock him out of the Installation. Ginzburg, preferring basic physics research over bomb design, was pleased, and the world of science reaped the rewards: While Zel’dovich, Sakharov, and Wheeler concentrated on bombs, Ginzburg solved the mystery of how cosmic rays propagate through our galaxy, and with Landau he used the laws of quantum mechanics to explain the origin of superconductivity.
In 1949, as the Soviet atomic bomb project reached fruition, Stalin ordered that the full resources of the Soviet state be switched over, without pause, to a superbomb effort. The slave labor of zeks, the theoretical research facilities, the manufacturing facilities, the test facilities, the multiple teams of physicists on each aspect of the design and construction, all must be focused on trying to beat the Americans to the hydrogen bomb. Of this the Americans, in the midst of their debate over whether to mount a crash effort on the super, knew nothing. However, the Americans had superior technology and a large head start.
On 1 November 1952, the Americans exploded a hydrogen bomb–type device code-named Mike. Mike was designed to test the 1951 Teller–Ulam invention and was based on the design computations of Wheeler’s team and tile cooperating team at Los Alamos. It used liquid deuterium as its principal fuel. To liquify the deuterium and pipe it into the explosion region required an enormous, factory-like apparatus. Thus, this was not the kind of bomb that one could deliver on any airplane or rocket. Nevertheless, it totally destroyed the island of Elugelab in the Eniwetok Atoll in the Pacific Ocean; it was 800 times more powerful than the bomb that killed over 100,000 people in Hiroshima.
On 5 March 1953, amidst somber music, Radio Moscow announced that Joseph Stalin had died. There was rejoicing in America, and grief in the U.S.S.R. Andrei Sakharov wrote to his wife, Klava, “I am under the influence of a great man’s death. I am thinking of his humanity.”
On 12 August 1953, at Semipalatinsk, the Soviets exploded their first hydrogen bomb. Dubbed Joe-4 by the Americans, it used Sakharov’s layered-cake design and Ginzburg’s LiD fusion fuel, and it was small enough to deliver in an airplane. However, the fuel in Joe-4 was not ignited by the Teller–Ulam method, and as a result Joe-4 was rather less powerful than the Americans’ Mike: “only” about 30 Hiroshimas, compared to Mike’s 800.
In fact, in the language of the American bomb design physicists, Joe-4 was not a hydrogen bomb at all; it was a boosted atomic bomb, that is, an atomic bomb whose power is boosted by the inclusion of some fusion fuel. Such boosted atomic bombs were already part of the American arsenal, and the Americans refused to regard them as hydrogen bombs because their layered-cake design did not enable them to ignite an arbitrarily large amount of fusion fuel. There was no way by this design to make, for example, a “doomsday weapon” thousands of times more powerful than Hiroshima.
But 30 Hiroshimas was not to be sneezed at, nor was deliverability. Joe-4 was an awesome weapon indeed, and Wheeler and other Americans heaved a sigh of relief that, thanks to their own, true superbomb, the new Soviet leader, Georgi Malenkov, could not threaten America with it.
On 1 March 1954, the Americans exploded their first LiD-fueled, deliverable superbomb. It was code named Bravo and like Mike, it relied on design calculations by the Wheeler and Los Alamos teams and used the Teller–Ulam invention. The explosive energy was 1300 Hiroshimas.
In March 1954, Sakharov and Zel’dovich jointly invented (independently of the Americans) the Teller–Ulam idea, and within a few months Soviet resources were focused on implementing it in a real superbomb, one that could have as large a destructive power as anyone might wish. It took just eighteen months to fully design and construct the bomb. On 23 November 1955, it was detonated, with an explosive energy of 300 Hiroshimas.
As Oppenheimer’s General Advisory Committee had suspected, in their opposition to the crash program for the super, these enormously powerful bombs—and the behemoth 5000-Hiroshima weapon exploded later by the Soviets in an attempt to intimidate John Kennedy—have not been very attractive to the military establishments of either the United States or the U.S.S.R. The weapons currently in Russian and American arsenals are around 30 Hiroshimas, not thousands. Although they are true hydrogen bombs, they are no more powerful than a large atomic bomb. The military neither needed nor wanted a “doomsday” device. The sole use of such a device would be psychological intimidation of the adversary—but intimidation can be a serious matter in a world with leaders like Joseph Stalin.
On 2 July 1953, Lewis Strauss, a member of the Atomic Energy Commission who had fought bitterly with Oppenheimer over the crash program for the super, became the Commission’s chairman. As one of his first acts in power, he ordered removal of all classified material from Oppenheimer’s Princeton office. Strauss and many others in Washington were deeply suspicious of Oppenheimer’s loyalty. How could a man loyal to America oppose the super effort, as he had before Wheeler’s team demonstrated that the Teller–Ulam invention would work? William Borden, who had been chief counsel of Congress’s Joint Committee on Atomic Energy during the super debate, sent a letter to J. Edgar Hoover saying, in part: “The purpose of this letter is to state my own exhaustively considered opinion, based upon years of study of the available classified evidence, that more probably than not J. Robert Oppenheimer is an agent of the Soviet Union.” Oppenheimer’s security clearance was canceled, and in April and May of 1954, simultaneous with the first American tests of deliverable hydrogen bombs, the Atomic Energy Commission conducted hearings to determine whether or not Oppenheimer was really a security risk.
Why Did Soviet Physicists Build the Bomb for Stalin?
Why did Zel’dovich, Sakharov, and other great Soviet physicists work so hard to build atomic bombs and hydrogen bombs for Joseph Stalin? Stalin was responsible for the deaths of millions of Soviet citizens: 6 million or 7 million peasants and kulaks in forced collectivization in the early 1930s, 2.5 million from the top strata of the military, government, and society in the Great Terror of 1937–39, 10 million from all strata of society in the prisons and labor camps of the 1930s through 1950s. How could any physicist, in good conscience, put the ultimate weapon into the hands of such an evil man?
Those who ask such questions forget or don’t know the conditions—physical and psychological—that pervaded the Soviet Union in the late 1940s and early 1950s:
1.The Soviet Union had just barely emerged from the bloodiest, most devastating war in its history—a war in which Germany, the aggressor, had killed 27 million Soviet people and had laid waste to their homeland—when Winston Churchill fired an early salvo of the cold war: In a 5 March 1946 speech in Fulton, Missouri, Churchill warned the West about a Soviet threat and coined the phrase “iron curtain” to describe the boundaries that Stalin had established around his empire. Stalin’s propaganda machinery milked Churchill’s speech for all it could, creating a deep fear among Soviet citizens that the British and Americans might attack. The Americans, the subsequent propaganda claimed,* were planning a nuclear war against the Soviet Union, with hundreds of atomic bombs, carried by airplanes, and targeted on hundreds of Soviet cities. Most Soviet physicists believed the propaganda and accepted the absolute necessity that the D.S.S.R. create nuclear weapons to protect against a repeat of Hitler’s devastation.
2.The machinery of Stalin’s state was so effective at controlling information and at brainwashing even the leading scientists that few of them understood the evil of the man. Stalin was revered by most Soviet physicists (even Sakharov), as by most Soviet citizens, as the Great Leader-—a harsh but benevolent dictator who had masterminded the victory over Germany and would protect his people against a hostile world. The Soviet physicists were frightfully aware that evil pervaded lower levels of the government: The flimsiest of denunciations by somebody one hardly knew could send one to prison, and often to death. (In the late 1960s, Zel’dovich recalled for me what it was like: “Life is so wonderful now,” he said; “the knocks no longer come in the middle of the night, and one’s friends no longer disappear, never to be heard from again.”) But the source of this evil, most physicists believed, could not be the Great Leader; it must be others below him. (Landau knew better; he had learned much in prison. But, psychologically devastated by his imprisonment, he rarely spoke of Stalin’s guilt, and when he did, his friends did not believe.)
3.Though one lived a life of fear, information was so tightly controlled that one could not deduce the enormity of the toll that Stalin had taken. That toll would only become known in Gorbachev’s epoch of glasnost, the late 1980s.
4.Many Soviet physicists were “fatalists.” They didn’t think about these issues at all. Life was so hard that one merely struggled to keep going, doing one’s job as best one could, whatever it might be. Besides, the technical challenge of figuring out how to make a bomb that works was fascinating, and there was some joy to be had in the camaraderie of the design team and the prestige and substantial salary that one’s work brought.
*Beginning in 1945, American strategic planning did, indeed, include an option—if the U.S.S.R initiated a conventional war—for a massive nuclear attack on Soviet cities and on military and industrial targets; see Brown (1978).
Wheeler was in Washington on other business at the time of the hearings. He was not involved in any way. However, Teller, a close personal friend, went to Wheeler’s hotel room the night before he was to testify, and paced the floor for hours. If Teller said what he really thought, it would severely damage Oppenheimer. But how could he not say it? Wheeler had no doubts; in his view, Teller’s integrity would force him to testify fully.
Wheeler was right. The next day Teller, espousing a viewpoint that Wheeler understood, said: “‘In a great number of cases I have seen Dr. Oppenheimer act ... in a way which for me was exceedingly hard to understand. I thoroughly disagreed with him in numerous issues and his actions frankly appeared to me confused and complicated. To this extent I feel that I would like to see the vital interests of the country in hands which I understand better, and therefore trust more. . . . I believe, and that is merely a question of belief and there is no expert-ness, no real information behind it, that Dr. Oppenheimer’s character is such that he would not knowingly and willingly do anything that is designed to endanger the safety of this country. To the extent, therefore, that your question is directed toward intent, I would say I do not see any reason to deny clearance. If it is a question of wisdom and judgment, as demonstrated by actions since 1945, then I would say one would be wiser not to grant clearance.”
Almost all the other physicists who testified were unequivocal in their support of Oppenheimer—and were aghast at Teller’s testimony. Despite this, and despite the absence of credible evidence that Oppenheimer was “an agent of the Soviet Union,” the climate of the times prevailed: Oppenheimer was declared a security risk and was denied restoration of his security clearance.
To most American physicists, Oppenheimer became an instant martyr and Teller an instant villain. Teller would be ostracized by the physics community for the rest of his life. But to Wheeler, it was Teller who was the martyr: Teller had “had the courage to express his honest judgment, putting his country’s security ahead of solidarity of the community of physicists,” Wheeler believed. Such testimony, in Wheeler’s view, “deserved consideration,” not ostracism. Andrei Sakharov, thirty-five years later, came to agree.4
Black-Hole Birth: Deeper Understanding
Not only did Wheeler and Oppenheimer differ profoundly on issues of national security, they also differed profoundly in their approach to theoretical physics. Where Oppenheimer hewed narrowly to the predictions of well-established physical law, Wheeler was driven by a deep yearning to know what lies beyond well-established law. He was continually reaching, mentally, toward the domain where known laws break down and new laws come into play. He tried to leapfrog his way into the twenty-first century, to catch a glimpse of what the laws of physics might be like beyond twentieth-century frontiers.
Of all the places that such a glimpse might be had, none looked more promising to Wheeler, from the 1950s onward, than the interface between general relativity (the domain of the large) and quantum mechanics (the domain of the small). General relativity and quantum mechanics did not mesh with each other in a logically consistent way. They were like the rows and columns of a crossword puzzle early in one’s attempts to solve it. One has a tentative set of words written along the rows and a tentative set written down the columns, and one discovers a logical inconsistency at some of the intersections of rows and columns: Where the row word GENERAL demands an E, the column word QUANTUM demands a U; where the row word RELATIVITY demands an E, the column word QUANTUM demands a T. Looking at the row and column, it is obvious that one or the other or both must be changed to get consistency. Similarly, looking at the laws of general relativity and the laws of quantum mechanics, it was obvious that one or the other or both must be changed to make them mesh logically. If such a mesh could be achieved, the resulting union of general relativity and quantum mechanics would produce a powerful new set of laws that physicists were calling quantum gravity. However, physicists’ understanding of how to marry general relativity with quantum mechanics was so primitive in the 1950s that, despite great effort, nobody was making much progress.

Progress was also slow on trying to understand the fundamental building blocks of atomic nuclei—the neutron, the proton, the electron, and the plethora of other elementary particles that were being created in particle accelerators.
Wheeler had a dream of leaping over these impasses and catching a simultaneous glimpse of the nature of quantum gravity and the nature of elementary particles. Such a glimpse, he thought, might come from seeking out those places in theoretical physics where paradoxes abound. From resolving a paradox comes deep understanding. The deeper the paradox, the more likely that the understanding would probe beyond twentieth-century frontiers.
It was in this spirit that, soon after emerging from the superbomb effort, Wheeler, with Harrison and Wakano, filled in the missing gaps in our knowledge of cold, dead stars (Chapter 5); and it was in this spirit that Wheeler contemplated the resulting “fate of great masses.” Here was a deep paradox of just the sort Wheeler was seeking: No cold, dead star can be more massive than about 2 Suns; and yet the heavens seem to abound in hot stars far more massive than that—stars which some day must cool and die. Oppenheimer, in his straightforward way, had asked the well-established laws of physics what happens to such stars, and had got (with Snyder) an answer that seemed outrageous to Wheeler. This reinforced Wheeler’s conviction that here, in the fates of great masses, he might catch a glimpse of physics beyond twentieth-century frontiers. Wheeler was right, as we shall see in Chapters 12 and 13.
Wheeler had fire in his belly—a deep, unremitting need to know the fate of great masses and learn whether their fate might unlock the mysteries of quantum gravity and elementary particles. Oppenheimer, by contrast, seemed not to care much in 1958. He believed his own calculations with Snyder but showed no need to push further, no drive for deeper understanding. Perhaps he was tired from the intense battles of the preceding two decades—weapons design battles, political battles, personal battles. Perhaps he was overawed by the mysteries of the unknown. In any event, he would never again contribute answers. The torch was being passed to a new generation. Oppenheimer’s legacy would become Wheeler’s foundation; and in the U.S.S.R., Landau’s legacy would become Zel’dovich’s foundation.
In his 1958 Brussels confrontation with Oppenheimer, Wheeler asserted that the Oppenheimer–Snyder calculations could not be trusted. Why? Because of their severe idealizations (Figure 6.3 above). Most especially, Oppenheimer had pretended from the outset that the imploding star has no pressure whatsoever. Without pressure, it was impossible for the imploding material to form shock waves (the analogue of breaking ocean waves, with their froth and foam). Without pressure and shock waves, there was no way the imploding material could heat up. Without heat and pressure, there was no way for nuclear reactions to be triggered and no way to emit radiation. Without outpouring radiation, and without the outward ejection of material by nuclear reactions, pressure, or shock waves, there was no way for the star to lose mass. With mass loss forbidden from the outset, there was no way the massive star could ever reduce itself below 2 Suns and become a cold, dead, neutron star. No wonder Oppenheimer’s imploding star had formed a black hole, Wheeler reasoned; his idealizations prevented it from doing anything else!
In 1939, when Oppenheimer and Snyder did their work, it had been hopeless to compute the details of implosion with realistic pressure (thermal pressure, degeneracy pressure, and pressure produced by the nuclear force) and with nuclear reactions, shock waves, heat, radiation, and mass ejection. However, the nuclear weapons design efforts of the intervening twenty years provided precisely the necessary tools. Pressure, nuclear reactions, shock waves, heat, radiation, and mass ejection are all central features of a hydrogen bomb; without them, the bomb won’t explode. To design a bomb, one had to incorporate all these things into one’s computer calculations. Wheeler’s team, of course, had done so. Thus, it would have been natural for Wheeler’s team now to rewrite their computer programs so that, instead of simulating the explosion of a hydrogen bomb, they simulated the implosion of a massive star.
It would have been natural, that is, if the team still existed. However, the team was now disbanded; they had written their PMB-31 report and had dispersed to teach, do physics research, and become administrators at a variety of universities and government laboratories.
America’s bomb design expertise was now concentrated at Los Alamos, and at a new government laboratory in Livermore, California. At Livermore in the late 1950s, Stirling Colgate became fascinated by the problem of stellar implosion. With encouragement from Edward Teller, and in collaboration with Richard White and later Michael May, Colgate set out to simulate such an implosion on a computer. The Colgate–White–May simulations kept some of Oppenheimer’s idealizations: They insisted from the outset that the imploding star be spherical and not rotate. Without this restriction, their computations would have been enormously more difficult. However, their simulations took account of all the things that worried Wheeler—pressure, nuclear reactions, shock waves, heat, radiation, mass ejection—and did so by relying heavily on bomb design expertise and computer codes. To perfect the simulations required several years of effort, but by the early 1960s they were working well.
One day in the early 1960s, John Wheeler rushed into a relativity class at Princeton University that I, as a graduate student, was taking from him. He was slightly late, but beaming with pleasure. He had just returned from a visit to Livermore, where he had seen the results of the most recent Colgate, White, and May simulations. With excitement in his voice, he drew diagram after diagram on the blackboard, explaining what his Livermore friends had learned:
When the imploding star had a small mass, it triggered a supernova explosion and formed a neutron star in just the manner that Fritz Zwicky had speculated thirty years earlier. When the mass of the star was much larger than the 2-Suns maximum for a neutron star, the implosion—despite its pressure, nuclear reactions, shock waves; heat, and radiation—produced a black hole. And the black hole’s birth was remarkably similar to the highly idealized one computed nearly twenty-five years earlier by Oppenheimer and Snyder. As seen from outside, the implosion slowed and became frozen at the critical circumference, but as seen by someone on the star’s surface, the implosion did not freeze at all. The star’s surface shrank right through the critical circumference and on inward, without hesitation.
Wheeler, in fact, had already come to expect this. Other insights (to be described below) had already transformed him from a critic of Oppenheimer’s black holes to an enthusiastic supporter. But here, for the first time, was a concrete proof from a realistic computer simulation: Implosion must produce black holes.
Was Oppenheimer pleased by Wheeler’s conversion? He showed little interest and little pleasure. At a December 1963 international conference in Dallas, Texas, on the occasion of the discovery of quasars (Chapter 9), Wheeler gave a long lecture on stellar implosion. In his lecture, he described with enthusiasm the 1939 calculations of Oppenheimer and Snyder. Oppenheimer attended the conference, but during Wheeler’s lecture he sat on a bench in the hallway chatting with friends about other things. Thirty years later, Wheeler recalls the scene with sadness in his eyes and voice.
In the late 1950s, Zel’dovich began to get bored with weapons design work. Most of the really interesting problems had been solved. In search of new challenges, he forayed, part time, into the theory of elementary particles and then into astrophysics, while keeping command of his bomb design team at the Installation and of another team that did subsidiary bomb calculations at the Institute of Applied Mathematics, in Moscow.
In his bomb design work, Zel’dovich would pummel his teams with ideas, and the team members would do calculations to see whether the ideas worked. “Zel’dovich’s sparks and his team’s gasoline” was the way Ginzburg described it. As he moved into astrophysics, Zel’dovich retained this style.
Stellar implosion was among the astrophysical problems that caught Zel’dovich’s fancy. It was obvious to him, as to Wheeler, Colgate, May, and White in America, that the tools of hydrogen bomb design were ideally suited to the mathematical simulation of imploding stars.
To puzzle out the details of realistic stellar implosion, Zel’dovich collared several young colleagues: Dmitri Nadezhin and Vladimir Imshennik at the Institute of Applied Mathematics, and Mikhail Podurets at the Installation. In a series of intense discussions, he gave them his vision of how the implosion could be simulated on a computer, including all the key effects that were so important for the hydrogen bomb: pressure, nuclear reactions, shock waves, heat, radiation, mass ejection.
Stimulated by these discussions, Imshennik and Nadezhin simulated the implosion of stars with small mass—and verified, independently of Colgate and White in America, Zwicky’s conjectures about supernovae. In parallel, Podurets simulated the implosion of a massive star. Podurets’s results, published almost simultaneously with those from May and White in America, were nearly identical to the Americans’. There could be no doubt. Implosion produces black holes, and does so in just the way that Oppenheimer and Snyder had claimed.
The adaptation of bomb design codes to simulate stellar implosion is just one of many intimate connections between nuclear weapons and astrophysics. These connections were obvious to Sakharov in 1948. Upon being ordered to join Tamm’s bomb design team, he embarked on a study of astrophysics to prepare himself. My own nose was rubbed into the connections unexpectedly in 1969.
I never really wanted to know what the Teller-Ulam/Sakharov–Zel’dovich idea was. The superbomb, one that by virtue of their idea could “be arbitrarily powerful,” seemed obscene to me, and I didn’t want even to speculate about how it worked. But my quest to understand the possible roles of neutron stars in the Universe forced the Teller–Ulam idea onto my consciousness.
Zel’dovich, several years earlier, had pointed out that gas from interstellar space or a nearby star, falling onto a neutron star, should heat up and shine brightly: It should become so hot, in fact, that it radiates mostly high-energy X-rays rather than less energetic light. The infalling gas controls the rate of outflow of X-rays, Zel’dovich argued, and conversely, the outflowing X-rays control the rate of infall of gas. Thereby, the two, gas and X-rays, working together, produce a steady, self-regulated flow. If the gas falls in at too high a rate, then it will produce lots of X-rays, and the outpouring X-rays will strike the infalling gas, producing an outward pressure that slows the gas’s fall (Figure 6.4a). On the other hand, if the gas falls in at too low a rate, then it produces so few X-rays that they are powerless to slow the infalling gas, so the infall rate increases. There is just one unique rate of gas infall, not too high and not too low, at which the X-rays and gas are in mutual equilibrium.
This picture of the flow of gas and X-rays disturbed me. I knew full well that if, on Earth, one tries to hold a dense fluid such as liquid mercury up by means of a less dense fluid such as water below it, tongues of mercury quickly eat their way down into the water, the mercury goes whooshing down, and the water goes whooshing up (Figure 6.4b). This phenomenon is called the Rayleigh–Taylor instability. In Zel’dovich’s picture, the X-rays were like the low-density water and the infalling gas was like the high-density mercury. Wouldn’t tongues of gas eat their way into the X-rays, and wouldn’t the gas then fall freely down those tongues, destroying Zel’dovich’s self-regulated flow (Figure 6.4c)? A detailed calculation with the laws of physics could tell me whether this happens, but such a calculation would be very complex and time consuming; so, rather than calculate, I asked Zel’dovich one afternoon in 1969, when we were discussing physics in his apartment in Moscow.
Zel’dovich looked a bit uncomfortable when I raised the question, hut his answer was firm: “No, Kip, that doesn’t happen. There are no tongues into the X-rays. The gas flow is stable.” “How do you know, Yakov Borisovich?” I asked. Amazingly, I could not get an answer. It seemed clear that Zel’dovich or somebody had done a detailed calculation or experiment showing that X-rays can push hard on gas without Rayleigh–Taylor tongues destroying the push, but Zel’dovich could not point me to any such calculation or experiment in the published literature, nor would he describe for me the detailed physics that goes on. How uncharacteristic of him!
A few months later I was hiking in the high Sierras in California with Stirling Colgate. (Colgate is one of the best American experts on the flows of fluids and radiation, he was deeply involved in the late stages of the American superbomb effort, and he was one of the three Livermore physicists who had simulated a star’s implosion on a computer.) As we hiked, I posed to Colgate the same question I had asked of Zel’dovich, and he gave me the same answer: The flow is stable; the gas cannot escape the force of the X-rays by developing tongues. “How do you know, Stirling?” I asked. “It has been shown,” he replied. “Where can I find the calculations or experiments?” I asked. “1 don’t know ...”
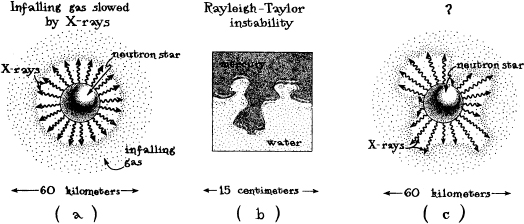
6.4 (a) Gas falling onto a neutron star is slowed by the pressure of outpouring X-rays. (b) Liquid mercury trying to fall in the Earth’s gravitational field is held back by water beneath it; a Rayleigh–Taylor instability results. (c) Is it possible that there is also a Rayleigh–Taylor instability for the infalling gas held back by a neutron star’s X-rays?
“That’s very peculiar,” I told Stirling. “Zel’dovich told me precisely the same thing—the flow is stable. But he, like you, would not point me to any proofs.” “Oh! That’s fascinating. So Zel’dovich really knew,” said Stirling.
And then I knew as well. I hadn’t wanted to know. But the conclusion was unavoidable. The Teller–Ulam idea must be the use of X-rays, emitted in the first microsecond of the fission (atomic bomb) trigger, to heat, help compress, and ignite the superbomb’s fusion fuel (Figure 6.5). That this is, indeed, part of the Teller–Ulam idea was confirmed in the 1980s in several unclassified American publications; otherwise I would not mention it here.
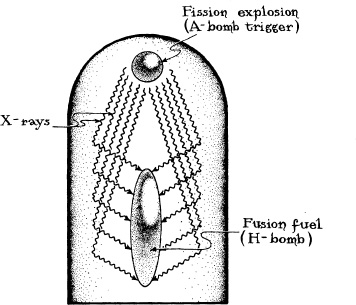
6.5 Schematic diagram showing one aspect of the Teller–Ulam/Sakharov–Zel’-dovich idea for the design of a hydrogen bomb: A fission-powered explosion (atomic bomb trigger) produces intense X-rays that somehow are focused onto the fusion fuel (lithium deuteride, LiD). The X-rays presumably heat the fusion fuel and help compress it long enough for fusion reactions to occur. The technology for focusing the X-rays and other practical problems are so formidable that by knowing this piece of the Teller–Ulam “secret,” one is only an infinitesimal distance along the way toward building a working superbomb.
What converted Wheeler from a skeptic of black holes to a believer and advocate? Computer simulations of imploding stars were only the final validation of his conversion. Far more important was the destruction of a mental block. This mental block pervaded the world’s community of theoretical physicists from the 1920s through the 1950s. It was fostered in part by the same Schwarzschild singularity that was then being used for a black hole. It was also fostered by the mysterious, seemingly paradoxical conclusion, from Oppenheimer and Snyder’s idealized calculations, that an imploding star becomes frozen forever at the critical circumference (“Schwarzschild singularity”) from the viewpoint of a static, external observer, but it implodes quickly through the freezing point and on inward from the viewpoint of an observer on the star’s surface.
In Moscow, Landau and his colleagues, while believing Oppenheimer and Snyder’s calculations, had severe trouble reconciling these two viewpoints. “You cannot appreciate how difficult it was for the human mind to understand how both viewpoints can be true simultaneously,” Landau’s closest friend, Evgeny Lifshitz, told me some years later.
Then one day in 1958, the same year as Wheeler was attacking Oppenheimer and Snyder’s conclusions, there arrived in Moscow an issue of the Physical Review with an article by David Finkelstein, an assistant professor at a little known American university, the Stevens Institute of Technology in Hoboken, New Jersey. Landau and Lifshitzread the article. It was a revelation. Suddenly everything was clear.5
Finkelstein visited England that year and lectured at Kings College in London. Roger Penrose (who later would revolutionize our understanding of what goes on inside black holes; see Chapter 13) took the train down to London to hear Finkelstein’s lecture, and returned to Cambridge enthusiastic.
In Princeton, Wheeler was intrigued at first, but was not fully convinced. He would become convinced only gradually, over the next several years. He was slower than Landau or Penrose, I believe, because he was looking deeper. He was fixated on his vision that quantum gravity must make nucleons (neutrons and protons) in an imploding star dissolve away into radiation and escape the implosion, and it seemed impossible to reconcile this vision with Finkelstein’s insight. Nevertheless, as we shall see later, in a certain deep sense both Wheeler’s vision and Finkelstein’s insight were correct.
So just what was Finkelstein’s insight? Finkelstein discovered, somewhat by chance and in just two lines of mathematics, a new reference frame in which to describe Schwarzschild’s spacetime geometry. Finkelstein was not motivated by the implosion of stars and he did not make the connection between his new reference frame and stellar implosion. However, to others the implication of his new reference frame was clear. It gave them a totally new perspective on stellar implosion.

David Finkelstein, ca. 1958. [Photo by Herbert S. Sonnenfeld; courtesy David Finkelstein.]
The geometry of spacetime outside an imploding star is that of Schwarzschild, and thus the star’s implosion could be described using Finkelstein’s new reference frame. Now, Finkelstein’s new frame was quite different from the reference frames we have met previously (Chapters 1 and 2). Most of those frames (imaginary laboratories) were small, and all portions of each frame (top, bottom, sides, middle) were at rest with respect to each other. By contrast, Finkelstein’s reference frame was large enough to cover simultaneously the regions of space-time far from the imploding star, the regions near it, and all regions in between. More important, the various parts of Finkelstein’s frame were in motion with respect to each other: The parts far from the star were static, that is, not imploding, while the parts near the star were falling inward along with the imploding star’s surface. Correspondingly, Finkelstein’s frame could be used to describe the star’s implosion simultaneously from the viewpoint of faraway static observers and from the viewpoint of observers who ride inward with the imploding star. The resulting description reconciled beautifully the freezing of the implosion as observed from far away with the continued implosion as observed from the star’s surface.
In 1962, two members of Wheeler’s Princeton research group, David Beckedorff and Charles Misner, constructed a set of embedding diagrams to illustrate this reconciliation, and in 1967 I converted their embedding diagrams into the following fanciful analogy for an article in Scientific American.
Once upon a time, six ants lived on a large rubber membrane (Figure 6.6). These ants, being highly intelligent, had learned to communicate using signal balls that roll with a constant speed (the “speed of light”) along the membrane’s surface. Regrettably, the ants had not calculated the membrane’s strength.
One day five of the ants happened to gather near the center of the membrane, and their weight made it begin to collapse. They were trapped; they could not crawl out fast enough to escape. The sixth ant—an astronomer ant—was a safe distance away with her signal-ball telescope. As the membrane collapsed, the trapped ants dispatched signal balls to the astronomer ant so she could follow their fate.
The membrane did two things as it collapsed: First, its surface contracted inward, dragging surrounding objects toward the center of the collapse in much the same manner as an imploding star’s gravity pulls objects toward its center. Second, the membrane sagged and became curved into a bowl-like shape analogous to the curved shape of space around an imploding star (compare with Figure 6.2).

6.6 Collapsing rubber membrane populated by ants provides a fanciful analogue of the gravitational implosion of a star to form a black hole. [Adapted from Thorne (1967)]
The membrane’s surface contracted faster and faster as the collapse proceeded. As a result, the signal balls, which were uniformly spaced in time when dispatched by the trapped ants, were received by the astronomer ant at more and more widely spaced time intervals. (This is analogous to the reddening of light from an imploding star.) Ball number 15 was dispatched 15 seconds after the collapse began, at the precise moment when the trapped ants were being sucked through the membrane’s critical circumference. Ball 15 stayed forever at the critical circumference because the membrane there was contracting with precisely the speed of the ball’s motion (speed of light). Just 0.001 second before reaching the critical circumference, the trapped ants dispatched ball number 14.999 (shown only in the last diagram). This ball, barely outracing the contracting membrane, did not reach the astronomer ant until 137 seconds after the collapse began. Ball number 15.001, sent out 0.001 second after the critical circumference, got inexorably sucked into the highly curved region and was crushed along with the five trapped ants.
But the astronomer ant could never learn about the crushing. She would never receive signal ball number 15, or any signal balls emitted after it; and those just before 15 would take so long to escape that to her the collapse would appear to slow and freeze right at the critical circumference.
This analogy is remarkably faithful in reproducing the behavior of an imploding star:
1.The shape of the membrane is precisely that of the curved space round the star—as embodied in an embedding diagram.
2.The motions of the signal balls on the membrane are precisely the same as the motions of photons of light in the imploding star’s curved space. In particular, the signal balls move with the speed of light as measured locally by any ant at rest on the membrane; yet balls emitted just before number 15 take a very long time to escape, so long that to the astronomer ant the collapse seems to freeze. Similarly, photons emitted from the star’s surface move with the speed of light as measured locally by anyone; yet the photons emitted just before the star shrinks inside its critical circumference (its horizon) take a very long time to escape, so long that to external observers the implosion must appear to freeze.
3.The trapped ants do not see any freezing whatsoever at the critical circumference. They are sucked through the critical circumference without hesitation, and crushed. Similarly, anyone on the surface of an imploding star will not see the implosion freeze. He will experience implosion with no hesitation, and get crushed by tidal gravity (Chapter 13).
This, translated into embedding diagrams, was the insight that came from Finkelstein’s new reference frame. With this way of thinking about the implosion, there was no more mystery. An imploding star really does shrink through the critical circumference without hesitation. That it appears to freeze as seen from far away is an illusion.
The embedding diagrams of the parable of the ants capture only some of the insight that came from Finkelstein’s new reference frame, not all. Further insight is embodied in Figure 6.7, which is a spacetime diagram for the imploding star.
Until now, the only spacetime diagrams we have met were in the flat spacetime of special relativity; for example, Figure 1.3. In Figure 1.3, we drew our diagrams from two different viewpoints: that of an inertial reference frame at rest in the city of Pasadena (with the downward pull of gravity ignored), Figure 1.3c; and that of an inertial frame attached to your high-speed sports car as you zoom down Pasadena’s, Colorado Boulevard, Figure 1.3b. In each diagram we plotted our chosen frame’s space horizontally, and its time vertically.
In Figure 6.7, the chosen reference frame is that of Finkelstein. Accordingly, we plot horizontally two of the three dimensions of space, as measured in Finkelstein’s frame (“Finkelstein’s space”), and we plot vertically time as measured in his frame (“Finkelstein’s time”). Since, far from the star, Finkelstein’s frame is static (not imploding), Finkelstein’s time there is that experienced by a static observer. And since, near the star, Finkelstein’s frame falls inward with the imploding stellar surface, Finkelstein’s time there is that experienced by an infalling observer.
Two horizontal slices are shown in the diagram. Each depicts two of the dimensions of space at a specific moment of time, but with the space’s curvature removed so the space looks flat. More specifically, circumferences around the star’s center are faithfully represented on these horizontal slices, but radii (distances from the center) are not. To represent both radii and circumferences faithfully, we would have to use embedding diagrams like those of Figure 6.2 or those of the parable of the ants, Figure 6.6. The space curvature would then show clearly: Circumferences would be less than 2π times radii. By drawing the horizontal slices flat, we are artificially removing their curvature. This incorrect flattening of the space is a price we pay to make the diagram legible. The payoff we gain is our ability to see space and time together on a single, legible diagram.
At the earliest time shown in the diagram (bottom horizontal slice), the star, with one spatial dimension absent, is the interior of a large circle; if the missing dimension were restored, the star would be the interior of a large sphere. At a later time (second slice), the star has shrunk; it is now the interior of a smaller circle. At a still later time, the star passes through its critical circumference, and still later it shrinks to zero circumference, creating there a singularity in which, according to general relativity, the star is crunched out of existence. We shall not discuss the details of this singularity until Chapter 13, but it is crucial to know that it is a completely different thing from the “Schwarzschild singularity” of which physicists spoke from the 1920s through the 1950s. The “Schwarzschild singularity” was their ill-conceived name for the critical circumference or for a black hole; this “singularity” is the object that resides at the black hole’s center.
The black hole itself is the region of spacetime that is shown black in the diagram, that is, the region inside the critical circumference and to the future of the imploding star’s surface. The hole’s surface (its horizon) is at the critical circumference.
Also shown in the diagram are the world lines (trajectories through spacetime) of some particles attached to the star’s surface. As one’s eye travels upward in the diagram (that is, as time passes), one sees these world lines move in closer and closer to the center of the star (to the central axis of the diagram). This motion exhibits the star’s shrinkage with time.
Of greatest interest are the world lines of four photons (four particles of light). These photons are the analogues of the signal balls in the parable of the ants. Photon A is emitted outward from the star’s surface at the moment when the star begins to implode (bottom slice). It travels outward with ease, to larger and larger circumferences, as time passes (as one’s eye travels upward in the diagram). Photon B, emitted shortly before the star reaches its critical circumference, requires a long time to escape; it is the analogue of signal ball number 14.999 in the parable of the ants. Photon C, emitted precisely at the critical circumference,. remains always there, just like signal ball number 15 And photon D, emitted from inside the critical circumference (inside the black hole), never escapes; it gets pulled into the singularity by the hole’s intense gravity, just like signal ball 15.001.
6.7 A spacetime diagram depicting the implosion of a star to form a black hole. Plotted upward is time as measured in Finkelstein’s reference frame. Plotted horizontally are two of the three dimensions of that frame’s space. Horizontal slices are two-dimensional “snapshots” of the imploding star and the black hole it creates at specific moments of Finkelstein’s time, but with the curvature of space suppressed.
It is interesting to contrast this modern understanding of the propagation of light from an imploding star with eighteenth-century predictions for light emitted from a star smaller than its critical circumference.
Recall (Chapter 3) that in the late eighteenth century John Michell in England and Pierre Simon Laplace in France used Newton’s laws of gravity and Newton’s corpuscular description of light to predict the existence of black holes. These “Newtonian black holes” were actually static stars with circumferences so small (less than the critical circumference) that gravity prevented light from escaping from the stars’ vicinities.
The left half of Figure 6.8 (a space diagram, not a spacetime diagram) depicts such a star inside its critical circumference, and depicts the spatial trajectory of a photon (light corpuscle) emitted from the star’s surface nearly vertically (radially). The outflying photon, like a thrown rock, is slowed by the pull of the star’s gravity, it draws to a halt, and it then falls back into the star.
The right half of the figure depicts in a spacetime diagram the motions of two such photons. Plotted upward is Newton’s universal time; plotted outward, his absolute space. With the passage of time, the circular star sweeps out the vertical cylinder; at any moment of time (horizontal slice through the diagram) the star is described by the same circle as in the left picture. As time passes, photon A flies out and then falls back into the star, and photon B, emitted a little later, does the same.
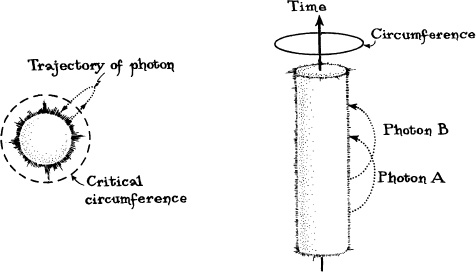
6.8 The predictions from Newton’s laws of physics for the motion of light corpuscles (photons) emitted by a star that is inside its critical circumference. Left: a spatial diagram (similar to Figure 3.1). Right: a spacetime diagram.
It is instructive to compare this (incorrect) Newtonian version of a star inside its critical circumference and the photons it emits with the (correct) relativistic version, Figure 6.7. The comparison shows two profound differences between the predictions of Newton’s laws and those of Einstein:
1.Newton’s laws (Figure 6.8) permit a star smaller than the critical circumference to live a happy, non-imploding life, with its gravitational squeeze forever counterbalanced by its internal pressure. Einstein’s laws (Figure 6.7) insist that when any star is smaller than its critical circumference, its gravitational squeeze will be so strong that no internal pressure can possibly counterbalance it. The star has no choice but to implode.
2.Newton’s laws (Figure 6.8) predict that photons emitted from the star’s surface at first will fly out to larger circumferences, even in some cases to circumferences larger than critical, and then will be pulled back in. Einstein’s laws (Figure 6.7) demand that any photon emitted from inside the critical circumference move always toward smaller and smaller circumferences. The only reason that such a photon can escape the star’s surface is that the star itself is shrinking faster than the outward-directed photon moves inward (Figure 6.7).
Although Finkelstein’s insight and the bomb code simulations fully convinced Wheeler that the implosion of a massive star must produce a black hole, the fate of the imploding stellar matter continued to disturb him in the 1960s, just as it had disturbed him in Brussels in his 1958 confrontation with Oppenheimer. General relativity insisted that the star’s matter will be crunched out of existence in the singularity at the hole’s center (Chapter 13), but such a prediction seemed physically unacceptable. To Wheeler it seemed clear that the laws of general relativity must fail at the hole’s center and be replaced by new laws of quantum gravity, and these new laws must halt the crunch. Perhaps, Wheeler speculated, building on views he had expounded in Brussels, the new laws would convert the imploding matter into radiation that quantum mechanically “tunnels” its way out of the hole and escapes into interstellar space. To test this speculation would require understanding in depth the marriage of quantum mechanics and general relativity. Therein lay the beauty of the speculation. It was a testbed to assist in discovering the new laws of quantum gravity.
As Wheeler’s student in the early 1960s, I thought that his speculation of matter being converted into radiation at the singularity and then tunneling its way out of the hole was outrageous. How could Wheeler believe such a thing? The new laws of quantum gravity would surely be important in the singularity at the hole’s center, as Wheeler asserted. But not near the critical circumference. The critical circumference was in the “domain of the large,” where general relativity must be highly accurate; and the general relativistic laws were unequivocal—nothing can escape out of the critical circumference. Gravity holds everything in. Thus, there can be no “quantum mechanical tunneling” (whatever that was) to let radiation out; I was firmly convinced of it.
In 1964 and 1965 Wheeler and I wrote a technical book, together with Kent Harrison and Masami Wakano, about cold, dead stars and stellar implosion. I was shocked when Wheeler insisted on including in the last chapter his speculation that radiation might tunnel its way out of the hole and escape into interstellar space. In a last-minute struggle to convince Wheeler to delete his speculation from the book, I called on David Sharp, one of Wheeler’s postdocs, for help. David and I argued vigorously with Wheeler in a three-way telephone call, and Wheeler finally capitulated.
Wheeler was right; David and I were wrong. Ten years later, Zel’-dovich and Stephen Hawking would use a newly developed partial marriage of general relativity and quantum mechanics to prove, mathematically, that radiation can tunnel its way out of a black hole—though very, very slowly (Chapter 12). In other words, black holes can evaporate, though they do it so slowly that a hole formed by the implosion of a star will require far longer than the age of our Universe to disappear.
The names that we give to things are important. The agents of movie stars, who change their clients’ names from Norma Jean Baker to Marilyn Monroe and from Béla Blasko to Béla Lugosi, know this well. So do physicists. In the movie industry a name helps set the tone, the frame of mind with which the viewer regards the star—glamour for Marilyn Monroe, horror for Béla Lugosi. In physics a name helps set the frame of mind with which we view a physical concept. A good name will conjure up a mental image that emphasizes the concept’s most important properties, and thereby it will help trigger, in a subconscious, intuitive sort of a way, good research. A bad name can produce mental blocks that hinder research.
Perhaps nothing was more influential in preventing physicists, between 1939 and 1958, from understanding the implosion of a star than the name they used for the critical circumference: “Schwarzschild singularity.” The word “singularity” conjured up an image of a region where gravity becomes infinitely strong, causing the laws of physics as we know them to break down—an image that we now understand is correct for the object at the center of a black hole, but not for the critical circumference. This image made it difficult for physicists to accept the Oppenheimer–Snyder conclusion that a person who rides through the Schwarzschild singularity (the critical circumference) on an imploding star will feel no infinite gravity and see no breakdown of physical law.
How truly nonsingular the Schwarzschild singularity (critical circumference) is did not become fully clear until David Finkelstein discovered his new reference frame and used it to show that the Schwarzschild singularity is nothing but a location into which things can fall but out of which nothing can come—and a location, therefore, into which we on the outside can never see. An imploding star continues to exist after it sinks through the Schwarzschild singularity, Finkelstein’s reference frame showed, just as the Sun continues to exist after it sinks below the horizon on Earth. But just as we, sitting on Earth, cannot see the Sun beyond our horizon, so observers far from an imploding star cannot see the star after it implodes through the Schwarzschild singularity. This analogy motivated Wolfgang Rindler, a physicist at Cornell University in the 1950s, to give the Schwarzschild singularity (critical circumference) a new name, a name that has since stuck: He called it the horizon.
There remained the issue of what to call the object created by the stellar implosion. From 1958 to 1968 different names were used in East and West: Soviet physicists used a name that emphasized a distant astronomer’s vision of the implosion. Recall that because of the enormous difficulty light has escaping gravity’s grip, as seen from afar the implosion seems to take forever; the star’s surface seems never quite to reach the critical circumference, and the horizon never quite forms. It looks to astronomers (or would if their telescopes were powerful enough to see the imploding star) as though the star becomes frozen just outside the critical circumference. For this reason, Soviet physicists called the object produced by implosion a frozen star—and this name helped set the tone and frame of mind for their implosion research in the 1960s.
In the West, by contrast, the emphasis was on the viewpoint of the person who rides inward on the imploding star’s surface, through the horizon and into the true singularity; and, accordingly, the object thereby created was called a collapsed star. This name helped focus physicists’ minds on the issue that became of greatest concern to John Wheeler: the nature of the singularity in which quantum physics and spacetime curvature would be married.
Neither name was satisfactory. Neither paid particular attention to the horizon which surrounds the collapsed star and which is responsible for the optical illusion of stellar “freezing.” During the 1960s, physicists’ calculations gradually revealed the enormous importance of the horizon, and gradually John Wheeler—the person who, more than anyone else, worries about using optimal names—became more and more dissatisfied.
It is Wheeler’s habit to meditate about the names we call things when relaxing in the bathtub or lying in bed at night. He sometimes will search for months in this way for just the right name for something. Such was his search for a replacement for “frozen star”/“collapsed star.” Finally, in late 1967, he found the perfect name.
In typical Wheeler style, he did not go to his colleagues and say, “I’ve got a great new name for these things; let’s call them da-de-da-de-da.” Rather, he simply started to use the name as though no other name had ever existed, as though everyone had already agreed that this was the right name. He tried it out at a conference on pulsars in New York City in the late fall of 1967, and he then firmly adopted it in a lecture in December 1967 to the American Association for the Advancement of Science, entitled “Our Universe, the Known and the Unknown.” Those of us not there encountered it first in the written version of his lecture: “[B]y reason of its faster and faster infall [the surface of the imploding star] moves away from the [distant] observer more and more rapidly. The light is shifted to the red. It becomes dimmer millisecond by millisecond, and in less than a second is too dark to see . . . [The star,] like the Cheshire cat, fades from view. One leaves behind only its grin, the other, only its gravitational attraction. Gravitational attraction, yes; light, no. No more than light do any particles emerge. Moreover, light and particles incident from outside ... [and] going down the black hole only add to its mass and increase its gravitational attraction.”
Black hole was Wheeler’s new name. Within months it was adopted enthusiastically by relativity physicists, astrophysicists, and the general public, in East as well as West—with one exception: In France, where the phrase trou noir (black hole) has obscene connotations, there was resistance for several years.
1. It is near the town of Arzimas, between Cheliabinsk and the Ural Mountains.
2. After their successful test of a bomb based on the American design, the Soviets returned to their own design, constructed a bomb based on it, and tested it successfully in 1951.
3. Sakharov has speculated that this design was directly inspired by information acquired from the Americans through espionage, perhaps via the spy Klaus Fuchs. Zel’dovich by contrast has asserted that neither Fuchs nor any other spy produced any significant information about the superbomb that his design team did not already know; the principal value of the Soviet superbomb espionage was to convince Soviet political authorities that their physicists knew what they were doing.
4. Just for the record, I strongly disagree with Wheeler (though he is one of my closest friends and my mentor) and with Sakharov. For thoughtful and knowledgeable insights into the Teller–Oppenheimer controversy and the pros and cons of the American debate over whether to build the superbomb, I recommend reading Bethe (1982) and York (1976). For Sakharov’s view, see Sakharov (1990); for a critique of Sakharov’s view, see Bethe (1990). For a transcript of the Oppenheimer hearings, see USAEC (1954).
5. Finkelstein’s insight had actually been found earlier, in other contexts by other physicists including Arthur Eddington; but they had not understood its significance and it was quickly forgotten.