LEARNING OBJECTIVES
■ Introduce the fundamental principles underpinning store location research
■ Using GIS to identify demand and supply-side factors for retail
■ GIS and localised marketing campaigns
■ Using GIS to identify store catchment areas and market shares
■ GIS and spatial interaction models for retail planning
■ The role of GIS for public sector retail planning
■ GIS for the identification, mapping and analysis of food deserts
The retail sector is a major commercial user of GIS software and spatial data. In this chapter we outline a series of examples of GIS for retail network planning and analysis. Many of these examples demonstrate that GIS is often coupled with spatial modelling tools in order to derive powerful insight into retail systems. Location-based decision making undoubtedly represents one of the most important functions within any retail organisation. Despite the rapid growth in internet retailing across the world (Clarke et al., 2015) it is through their network of stores that most contemporary retailers still interact most closely with their customers. In the highly competitive UK grocery sector, for example, one of the key battlegrounds during the ‘store-wars’ era of the 1970s and 1980s (Wrigley, 1987) involved the rapid acquisition of sites suitable for new store development and the diffusion of brands spatially from a core headquarter location. It was during this ‘store-wars’ era that we saw the development of site location teams within major grocery retailers and, embedded within them, a highly competitive strategy towards new store development. Today, most of the major UK grocery chains have specialised teams of in-house location analysts, who carry out sophisticated spatial analysis to identify new sites, estimate market areas associated with new and existing stores and forecast revenue in advance of new store investment (Birkin et al., 2002, 2017). Reynolds and Wood (2010) note that UK grocery retailers tend to carry out the most sophisticated site location research in the retail industry and are more likely to have their own specialised in-house teams than retailers in any other sector, managing some of the largest store portfolios. These retailers also benefit from some of the most powerful consumer insights driven by loyalty schemes, Electronic Point of Sale (EPOS) data and geodemographics (see the section on demand estimation, below).
A recent set of surveys of UK location planning teams identified their primary role as being to support the financial business case for new stores (Wood and Reynolds, 2011, 2012; Reynolds and Wood, 2010). An important component of their work thus involves an assessment of the trading potential of a proposed site and the prediction of store revenue in advance of investment. Site location teams are thus fundamental to many areas of a retailer’s operations and operate at both a strategic level (e.g. evaluating sites and generating revenue predictions in advance of major investment decisions) and an operational level (e.g. assisting marketing teams with store-based demographic information or monitoring store performance against forecast revenue predictions in day-to-day operations).
There are now many useful introductions to store location research spanning the different techniques as they have been fashionable over time (Davies, 1977; Fenwick, 1978; Davies and Rogers, 1984; Bowlby et al., 1984a, 1984b; Clarke, 1998; Birkin et al., 2002, 2017). Although we wish to concentrate here on the role of GIS it is necessary to also consider alternative methods, albeit more briefly. Early store location decisions were inevitably made by senior executives on gut feeling or retail nous accumulated over many years (Davies, 1977). But in the 1970s and 1980s the analogue technique became more widespread. Analogue techniques were (and still are) very common procedures for site location in the UK and the US especially. The basic approach involves attempting to forecast the potential sales of a new (or existing) store by drawing comparisons (or analogies) with other stores in the corporate chain that are alike in physical, locational and trade area circumstances. This can be done ‘manually’ or through regression techniques. Hence, if you are evaluating a new store site in, say, Cambridge, UK, can you find an existing store location around the UK that has the same (or similar) population and trading characteristics as Cambridge? Alternatively, the procedure might work by trying to find sites that are analogous with the top performing stores within the company. That is, if a store in, for example, Oxford, UK, is performing very strongly, can the analyst find sites elsewhere in the country that match the characteristics of the Oxford site? Additionally, a similar approach has been to follow the behaviour of other (larger) retailers and base store location decisions on whatever decisions they make. This has been labelled the ‘parasitic’ approach and is more common for smaller retailers.
The success of the analogue approach depends on whether or not you can find similar sites across the country and whether you believe you can successfully transfer the trading characteristics across geographical locations. In reality, a wide variation in performance is frequently found between ‘similar’ outlets in a retail chain. Moreover, even if a similar geographical catchment is found to the new store, what happens if the analogous store is currently over- or underperforming? Laing et al. (2003) provide an interesting discussion on the analogue procedure. If key drivers of success can be suggested by analogue, revenue predictions have increasingly utilised regression analysis across a broad set of variables (which can be compared across stores), such as total sales area, catchment demographics and the degree of competition (see Birkin et al. (2002, 2017) and below for more detail on the use of analogues and regression analysis for store revenue estimation).
During the 1980s, census data became available in electronic form and the introduction of GIS and desktop PCs allowed retail location planning teams to develop computerised spatial forecasting models to estimate store revenue. At the time, Wrigley (2014: 30) asserted that ‘never before have the skills of locational analysts, developed and practised by geographers and planners been so closely identified with the commercial imperatives of retailers’. Retailers were able to carry out analysis and visualisation, utilising the wealth of spatially referenced data at their disposal following the introduction of loyalty cards and the widespread availability of census and geodemographic data, allowing location analysis to grow in sophistication. GIS provided retailers with tools to undertake drive time analysis, allowing them to identify the size and characteristics of the population that live within thresholds of individual stores. Coupled with knowledge of competitor presence, store catchment population characteristics could now be used to predict sales and revenue.
Before we examine the use of GIS for retail analysis in more detail, it is useful to examine the fundamental principles which underpin store location research.
The building blocks for analysis
Whether developing new retail sites or ensuring current sites are making the most of their corporate brand, or planning what retail networks should look like in the future, the data used in the analysis are vitally important. As such, the following section looks at the various data needed for network planning and the issues impacting on the quality of those data.
Demand estimation
Fundamental to retail network planning is the use of demand data (e.g. population counts, understanding of different household types, expenditure estimates, etc.), for it is crucial to understand where people live and how much potential expenditure is available at a small-area level. However, for many retailers this information is difficult and expensive to obtain. For instance, some retailers have their own data collected through store cards (e.g. Tesco Clubcard) or store credit cards (e.g. Topshop, M&S and Debenhams). These data are used as a way to understand the location and characteristics of their consumers and the catchment area associated with a given store. Those retailers that do not have access to this sort of information have to collate information from other sources. These include information generated from official government surveys, market research or consumer data purchased from companies such as Experian and Acxiom Ltd. This might include geodemographic classifications – designed to segment the entire population of an area (e.g. the UK) according to the type of area in which they live. Such classifications are usually based on a broad range of indicator variables that cover housing tenure, socio-economic information and demographic characteristics. Examples in the UK include CAMEO by Callcredit, ACORN by CACI, Mosaic by Experian and OAC by the ONS (see Chapter 5 for a recap on geodemographics). However, these data can often be expensive to acquire and the methodologies behind their production are usually kept hidden. In addition, the journey to work can also be especially important to consider in certain geographical locations. Using straightforward population data, retail demand in Canary Wharf in London, for example, would be small whereas we know that with a large, predominately young professional daytime work population such demand is likely to be considerable (see Berry et al., 2016). So to reproduce market performance effectively we need to represent expenditure originating from the workplace as well as in relation to residential locations.
Alternatively, retailers also have the option of using data from the various censuses undertaken around the world. The census forms the most comprehensive and detailed data available in most countries and has been collected by the ONS in England and Wales every decade since 1801 (with the exception of 1941). The attributes collected form a comprehensive view of the population, comprising numerous demographic, social and economic characteristics. The data are geographically referenced and the finest area at which they are released is the Output Area (OA) level. However, the UK census data have no information on income or expenditure (as we discussed at length in Chapters 5 and 6) which is problematic when trying to estimate demand (although note that this information is present in other censuses around the world – e.g. in the US). If these data are missing, a combination of both small-area census data and up-to-date consumer data can be used to create a more up-to-date and robust data source. Mindful of the inadequacies of both commercially available data and available census variables, Birkin et al. (2002) discuss examples for the estimation of financial services expenditures in relation to diverse factors including age, gender, household size, dependent children, occupation, income and ethnicity.
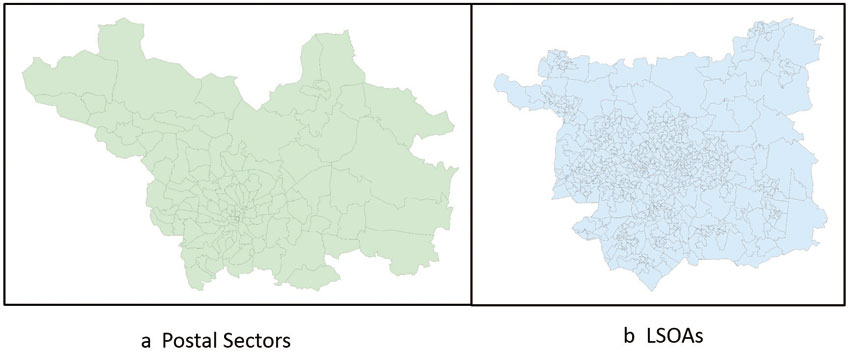
Another issue are the boundary data in which the demand data are produced. In commercial applications, postal geographies have long been a popular boundary data set for retail analysis due to the range of contextual geodemographic and behavioural indicators that were available using these geographies (which are also important for marketing). The standard hierarchical format from the lowest level is postcodes, postal sectors, postal districts and postal areas. Postal geographies can be problematic, however, as postcodes are continually moving and changing (Raper et al., 1992). Census output geographies used in England and Wales (coverage varies in Scotland and Northern Ireland) include OAs, Lower Layer Super Output Areas (LSOAs), Middle Layer Super Output Areas (MSOAs), alongside electoral wards and Local Authority Districts (LADs) or unitary authorities (UAs). Similarly to postal geographies, these geographies are hierarchical so that the smaller areas can be aggregated into larger ones. More recently, the release of specific geographies such as workplace zones (WZs), designed for the release of data related to workplace populations, recognises the importance of small-area geographies that are fit-for-purpose for the range of small-area analysis carried out by commercial users such as the retail sector. However, postal geographies and administrative boundaries do not match exactly. Figure 8.1 highlights the differences between the two for Leeds.
Figure 8.1 Differences between postal geographies and administrative boundaries in Leeds, UK
In addition, organising any data into discrete areal units presents a set of theoretical problems such as the MAUP and the ecological fallacy. First of all, the MAUP can create difficulties when analysing aggregate data for discrete geographical areas (Openshaw, 1984). The problem is dual faceted: the first relates to scale, the second to zoning. Essentially, the issue is that patterns identified in data at one scale of aggregation might not present themselves at a different level of aggregation. The ecological fallacy is a special case of the MAUP, whereby individual-level relationships inferred from relationships observed at the aggregate level might not be valid (see also the discussion in Chapter 2 on these issues).
Supply-side factors
In addition to demand data, a number of important choices regarding the representation of supply points have to be made in network planning. Whether retail facilities are identified as stand-alone outlets or they are grouped into centres is the first crucial decision. For many retail activities – automotive, petrol and supermarkets are all obvious examples – it looks natural to represent flows to individual outlets. In addition, the distinction between outlet-based systems and centre-based systems is becoming increasingly blurred. The incorporation of ‘stand-alone’ retail facilities into retail parks often means that such locations are, in fact, more akin to centres than stand-alone outlets (see Thomas et al., 2004): the presence of both competitors and complementary retailers adding to the overall ‘attractiveness’ of the outlet.
Table 8.1 Drivers of retail attractiveness in different retail markets
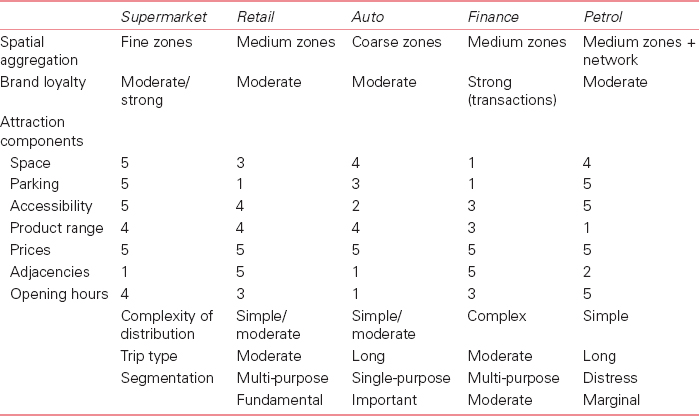
Note: 1 = Relatively unimportant; 5 = Very important.
Source: Birkin et al. (2010)
Most retailers will, of course, have information on their own stores (size, turnover, location, workforce, etc.). However, in order to gain information on the location of competitors, they might have to purchase data from private sector sources (if available). If detailed information can be obtained on store attributes, this information can then be used to measure the attractiveness of a given shopping destination to be used in a GIS or spatial modelling framework. Size and turnover have traditionally been used to measure the attractiveness of shopping centres; however, we know that other elements affect the attractiveness of a shopping centre, such as brand, parking facilities, price and consumers’ perception (Birkin et al., 2010). Table 8.1, taken from Birkin et al. (2010), highlights the various attributes required and their importance to each retail sector.
GIS for retail analysis and planning
The retail industry makes extensive and sophisticated use of GIS and the analysis of spatial data in order to understand consumers, evaluate store performance and develop store networks. Planning authorities and local government also make use of GIS to evaluate access to retail services and to assess proposals for new stores or retail centres. We shall discuss public sector GIS-based retail planning issues later in the chapter.
Major retail corporations employ large teams of analysts who routinely use GIS to support both operational and strategic decision making. Insight derived from GIS analysis of customer and store trading data includes:
■ understanding the characteristics and spatial distribution of consumers;
■ planning localised marketing campaigns;
■ identifying locations to launch new products or store formats;
■ using consumer characteristics to estimate likely retail spending;
■ identifying store catchment areas;
■ estimating market shares across small-area neighbourhoods;
■ forecasting new/proposed store revenue.
The first major advantage of GIS, as we have seen throughout the book so far, is visualisation. Data in spreadsheet or database management packages are impossible to analyse for spatial patterns. Once mapped the data are often said to be ‘brought to life’. GIS visualisation enables retailers to map any aspect of demand or supply, but also to identify the links between demand and supply by considering consumer flows (derived from loyalty card or survey data) and providing an indication of how and where people shop. Let us take each in turn. First, GIS can be useful for mapping all kinds of data relating to demand-side issues.
Figure 8.2 Mapping census variables in a retail GIS for Montreal, Canada
Source: Apparacio et al. (2007)
Figure 8.2 shows an example of mapping core census data for Montreal, Canada, as part of a wider retail GIS study of accessibility (see further discussion below). Here, Apparacio et al. (2007) plot income levels against a social deprivation index, to highlight a cluster of low-income areas in central Montreal. They later test the hypothesis that retail access is worse for residents of these areas compared to those in more affluent suburbs.
Second, we can use GIS to plot store location networks, to understand the spatial patterns of different types of stores and perhaps identify market gaps. Figure 8.3 shows the location of supermarkets in London, Ontario, Canada, in 1961 and 2005 (Larsen and Gilliland, 2008).
First, Figure 8.3 shows the expansion of stores into suburban neighbourhoods and the closure of many central stores since 1961. Second, buffers of one kilometre have been placed around each store to see which areas of the city might be poorly served and therefore possible commercial opportunities in the future. As we shall discuss later in the chapter, such maps are also useful for identifying potential ‘food deserts’ for public sector planners.
Figure 8.3 Mapping immediate retail catchments in London, Ontario, Canada, in 1961 and 2005
Source: Larsen and Gilliland (2008)
For retailers the most common use of the buffer procedure in GIS is to estimate the catchment area of existing or potential new stores. The first step might be to estimate the typical catchment area for their existing stores in the chain. Then a buffer of the average size could be placed around a potential new store location. Figure 8.4 shows the example presented by Russell and Heidkamp (2011) in their study of retail accessibility in New Haven, Connecticut, US (see also the section on GIS for public sector retail planning, below).
Figure 8.4 shows that buffers can be drawn either based on straight-line distance (Figure 8.4a) or on travel distance along a road network (Figure 8.4b). Suppose now we wish to overlay the population that lives in these buffers in order to work out some measure of potential demand or catchment size. The areas demarcated by the buffers in Figure 8.4 are likely to be made up of a number of small census zones or tracts or perhaps postal zones (or whatever spatial scale is being used). So a key question is how can the GIS be used to estimate the demand that lies within these buffers? Census tracts that fall entirely within a buffer are easy to deal with – we can simply take the total population in each zone and sum to give an overall total. However, towards the edge of a buffer the census zones or postal areas might only be partly included. The task of estimating demand within these divided census tracts is called interpolation. Figure 8.5 helps to explain and understand interpolation better.
In Figure 8.5, the buffer cuts the census zone at its eastern end. Let us assume that the census zone contains 10,000 people and that the buffer contains around 10% of the area of the census zone. The standard interpolation procedure would suggest we need to add 1,000 people into the buffer for this part of the intersection calculation. The problem with this procedure is that the population might not be evenly distributed across the census tract being split in this way, thus making the estimation of the population contained with the buffer problematic. If, for example, the population is actually clustered in the western area of the zone, the population living within the area cut by the buffer might be very small or even zero. Alternatively, if the population is concentrated in the eastern area of the census zone then perhaps most of the 10,000 people should realistically be allocated to the buffer.
The overlay procedure in GIS is useful in retail catchment analysis. Following Benoit and Clarke (1997) we can use GIS overlay procedures to search for ‘ideal zones’. Their example related to the search for a new site in Leeds, UK, for a discount retailer. GIS could be used as a type of sieve, removing layers of information not required. Thus, to find a new site for a discounter we could remove all postal sectors with a high social class background, all postal sectors containing young families (on the assumption that the more elderly might use discounters more) and all postal sectors containing an existing (competitor) discount retailer. By overlaying these characteristics one at a time we are left with zones that only contain older, low-income residents with no discount retailers within their locality. A population size threshold could also be added. Figure 8.6 shows the outcome of this type of analysis in Leeds where a number of ideal zones emerge, of which postal sector LS10 3 seems to be the most promising. The end product shows the location of large numbers of elderly and low-income households with little or no competitor locations.
Figure 8.4 Drawing a buffer around a potential new store in New Haven, Connecticut, US: (a) straight line; (b) drive times
Source: Russell and Heidkamp (2011)
Figure 8.5 Interpolation procedure within GIS
Source: Birkin et al. (2017)
Figure 8.6 The end result of ‘sieving’ data to find optimal or ideal zones
Source: Benoit and Clarke (1997), redrawn in Birkin et al. (2017)
Another way of overlaying or combining data is to turn variables into a standard indicator score based on a type of scoring system. The following example is taken from Spatial Insights’ (undated) study of potential new locations for additional pawnbrokers or pawn shops in the city of Houston, Texas, in the US. Pawn shops are retail outlets where typically low-income residents can sell goods and possibly buy them back later (usually after payday). Figure 8.7 plots the current distribution of pawn shops in Houston along with a supply/demand index which, in turn, is portrayed as a GIS ‘hot spot’ style indicator of demand. This index is formed by combining (or overlaying) five key census variables. The first is total population. The distribution of population across Houston is divided into five equal categories. Then, an individual census tract scores one point for a low population and (up to) 5 points if it falls within the top band. The second variable is household income. This time low = 5 points, high = 1 point, as low-income residents are more likely to use pawn shops. The third variable is the number of rented households (a proxy again for low social class: again low = 1 point, high = 5 points). The fourth variable is household size: large families again tend to come from the poorer backgrounds in US cities. So, again low = 1 point, high = 5 points. Finally, population density is also measured. A high population density is also associated with lower income groups, so low = 1 point, high = 5 points. Thus by overlaying the scores on all five variables a very low-income area can be identified by a very high score (maximum 25). This score was then factored for simplicity to a mark of zero to ten. These areas are plotted on Figure 8.7 as high hot spot areas and the retailers can quickly evaluate the current location of pawn shops against these high indicator scores (giving a type of index of potential).
Figure 8.7 Deriving hot spots of demand for potential new pawnbrokers in Houston, Texas, US
Source: Spatial Insights (undated)
So the buffer and overlay procedure seems to have a number of potentially useful applications in retail analysis. However, there are problems when this technique is used to try to estimate potential store revenues. This is a vital component of the store location planning exercise – yes, we can look for ideal zones or areas of high potential, but how much revenue will a new store actually attract? Let us introduce an example relating to a retailer operating in the US. So far in the methodology we have shown how such retailers estimate a buffer size which can then be drawn onto a potential new site location. Figure 8.8 illustrates an example where a US retailer has earmarked a new site in a typical US city. They have then estimated the catchment area as a buffer of one mile around this potential new store location. The key next question is how much of the demand within the buffer, which can be estimated by overlay and interpolation in total, will actually end up at the new store? If there are no competitors within the one-mile boundary then maybe the new store will be able to capture much of the demand that presently has to leave the catchment area. However, it is rare that one-mile buffers in large city regions contain no existing competitors (for most retail goods and services). If we suppose that in fact there are three existing competitor stores in the one-mile buffer then the picture is more complicated, but probably more realistic. According to a number of studies (e.g. Beaumont, 1991) the most likely allocation procedure is the fair share method. That is, the four retailers will each get approximately 25% of the business. This can be factored by brand or size so that the split is not quite so even. However, it remains a fairly crude solution methodology. One alternative is to assume the consumer will travel to the nearest store within the catchment area (dominant store analysis).
Figure 8.8 A one-mile buffer demarcated for a retailer in a US city
Source: Birkin et al. (2017)
To compound the problems it is possible to think of other flaws in this technique for estimating individual store revenues. The first is the rather arbitrary nature of the one-mile buffer. Although this might work generally across the store chain, trade might be more likely to be skewed in certain directions because of the location of the competitors, not only within the buffer but also outside it. For example if there were no competitors for two miles to the east of the new store location then in reality the store could get considerable trade from households outside the buffer boundary to the east (buffer inflow). Similarly, if there is a large competitor outlet just outside the buffer to the north, then perhaps the new store will get much less trade from the northern parts of the buffer as trade crosses the artificial boundary (buffer outflow). A second problem relates to the fact that there is no account taken of distance decay within the buffer. For example, the new store is actually far more likely to receive trade from nearby streets (which might or might not be very populous) and little from streets near the edge of the buffer. Hence the assumption of fair share allocation from within the whole buffer is likely to be problematic. This problem can be reduced by identifying a primary, secondary and tertiary catchment area within the one-mile buffer, but there will still be problems of assigning proportions of demand from each of these to the new store. Finally, in very densely populated areas with lots of competitors, the individual catchment areas will become so blurred as to make any attempts of allocating the demand almost impossible (the so-called overlapping catchment area problem).
Figure 8.9 Use of Thiessen polygons for trade area demarcation
Source: Pearson (2007)
A potential solution to this problem is to try to identify a unique buffer for every store. This will mean some having very small buffer sizes and others very large (depending on the amount of competition nearby). An effective way to do this in GIS is to use Thiessen polygons, also known as Voronoi polygons. Thiessen polygons can be constructed so that each polygon contains exactly one of the stores so that any location within the polygon is closer to that store than to a store within any other polygon. Figure 8.9 shows the plotting of Thiessen polygons for two rival grocery stores in a region of the US (Pearson, 2007). Using Thiessen polygons as trade areas, analysts can evaluate the retail outlets in terms of socio-economic and/or demographic attributes of each outlet’s trade area. However, the issue of trade flowing across Thiessen polygon boundaries is huge and again grave doubts might be given for using this technique to accurately forecast retail sales.
Adding a modelling capability to the GIS
As noted above, GIS is excellent for mapping data and exploring spatial patterns using buffer and overlay, sieve mapping, etc. However, it is less accurate and therefore less useful for new store revenue estimation. Thus in this section we look briefly at modelling techniques more commonly used for this purpose. Some modelling techniques are available directly in some proprietary GIS packages, such as regression modelling (as noted in Chapter 6). Even the spatial interaction models discussed below are available now in ArcGIS, although certainly in the case of these models it is hard to disaggregate the models within a GIS package and even harder to calibrate using statistical routines. Thus, more often than not, these models need to be run using specialist software and loose coupled back to the proprietary GIS for mapping and any further spatial analysis.
Statistical models
Regression modelling represents one of the more scientific methods of network planning and builds on the philosophy of the analogue procedure discussed in the first section of this chapter. Regression analysis works by defining a dependent variable such as store turnover and attempting to correlate this with a set of independent or explanatory variables (e.g. size, catchment population and brand). If there is a degree of correlation between these dependent and independent variables then the regression model can be used in a predictive context by using the independent variables as predictors of the dependent variable. Coefficients are also calculated to weight the importance of each independent variable in explaining the variation in the set of dependent variables. The model can be written as:
where Yi is turnover (the dependent variable) of store i, Xmi are independent variables, bm are regression coefficients estimated by calibrating against existing stores and a is the intercept term.
Although multiple regression allows for greater sophistication and objectivity than the more manual analogue techniques, there are still a number of problems. The primary weakness is that they evaluate sites in isolation, without considering the full impacts of the competition or the company’s own global network. As with the analogue method, a second major weakness is the problem of ‘heterogeneity of sample stores’. That is, how easy is it to find a sample of stores which have similar trading characteristics and catchment areas (see Ghosh and McLafferty, 1987)? Additionally, regression models assume that the explanatory variables in the models be independent of each other and uncorrelated. In many retail applications this is not the case. More specifically, independent variables such as floor-space and car parking spaces might be strongly correlated. This can lead to unreliable parameter estimates and severe problems of interpretation (multicollinearity). However, through careful analysis and interpretation many of these problems can be overcome. Perhaps the most important limitation is that regression models fail to handle adequately spatial interactions or customer flows. That is, they do not model the processes (spatial interactions) that generate the flows of expenditure between residential or workplace areas (demand zones) and retail outlets.
Mathematical modelling
During the 1980s and 1990s, as retail markets became more saturated and the competition for sites increased, there was an important shift towards the use of more sophisticated techniques in network planning. Improvements in information technology and the development of GIS software led to major improvements in spatial modelling techniques. One such modelling technique which became a core feature of retail network planning was the spatial interaction model (SIM). SIMs were originally developed from the gravity-based principles of Newton’s scientific theory of Universal Gravitation (hence they are most commonly called gravity models in the retail industry) and over time these principles have been refined to produce much more complex models (Birkin et al., 2010; Newing et al., 2015). By definition, SIMs are used to simulate or predict the interactions or flows (e.g. people, households, expenditure) between origins and destinations. Wilson (1974) defines four different variations of the SIM in his ‘family of SIMs’. With regard to the retail sector, the most commonly used SIM is the production constrained model, shown below:
where Sij is the flow of people (or expenditure) from residential area i to retail store j, Oi is a measure of demand (expenditure) in area i,Wj is a measure of attractiveness of retail store j, dij is a measure of the distance (e.g. time, miles) between i and j, β is the distance decay parameter and Ai is a balancing factor to ensure that all demand is allocated to grocery stores within the modelled region, written as:
The model allocates flows of expenditure between origin and destination zones on the basis of two main hypotheses: (i) Flows between an origin and destination will be proportional to the relative attractiveness of that destination vis-à-vis all other competing destinations. (ii) Flows between an origin and destination will be proportional to the relative accessibility of that destination vis-à-vis all other competing destinations. Furthermore, the model works on the assumption that in general, when choosing between centres that are equally accessible, shoppers will show a preference for the more attractive centre. When centres are equally attractive, shoppers will show a preference for the more accessible centre. Note, however, that these preferences are not deterministic. Thus when choosing between equally accessible centres, shoppers will not always choose the most attractive. The models are therefore able to represent well the stochastic nature of consumer behaviour. By summing the flows coming into each store or shopping centre the models can estimate the revenue of those outlets. This is a crucial output of the modelling procedure.
In the retail industry, SIMs can be calibrated to reproduce existing interaction patterns between populations and shopping centres from observed data (e.g. Tesco Clubcard data) to facilitate the estimation of store turnovers. Having allocated expenditures between all retailers, the models can be used to predict local market shares and compare actual turnovers to model predictions – that is, what would the model expect a certain outlet to be achieving in sales terms? For example, is a store that turns over £1 million per annum doing well or badly in relative rather than absolute terms? Having identified the variations in market share (or penetration) the retailer might then be keen to improve its performance by opening new outlets in the areas that currently have a low market share. The models can then be used to test the impact of new store openings through a variety of ‘what-if?’ scenarios. This powerful capability has meant many of the UK retailers (Tesco, Asda, Sainsbury’s, etc.) and UK consultancy firms (Callcredit, CACI, Experian and Javelin) have invested heavily in producing SIMs for market analysis. Figure 8.10 demonstrates how the individual market share figures for an example 70,000-square foot Asda store in Leeds can be calculated by a SIM similar to that in Equation 8.2.
Over time, a number of derivations of the SIM have been developed to ensure the technique is applicable in different sectors of the retail market. For example, Fotheringham (1983) presented the ‘competing destinations’ model, arguing that the standard SIM needed to be adapted to include a competing destinations term that recognised that outlets or centres in very close proximity to each other were really a single destination in the eyes of consumers. Ottensmann (1997) and Birkin et al. (2010) also introduced the concept of elastic demand into SIMs, a concept that replicates the increase in demand for a specific service in an area, if that service is introduced or increased. The theory is that increased access to a service will increase demand for that service. For example, the opening of a new cinema, bingo hall, fast food outlet, etc. will stimulate local demand from people who might not have bothered to travel longer distances to enjoy such services beforehand. In addition to these theoretical developments, it has become commonplace for modern SIMs to be highly disaggregated, to account for more complex behaviour in a given system. Wilson (1974) initially made attempts to more accurately represent different behaviour in commuting to work through the disaggregation of the SIM to represent different modes of travel in a transport model.
Figure 8.10 Estimated market share for an individual Asda store in East Leeds, UK
Nevertheless, despite the benefits associated with SIMs, care must still be taken when using them. For instance, SIMs are data intensive which means they require good quality data (demand and supply). Poor quality data cause issues with calibration and ultimately accuracy. In the retail sector, it is likely that firms would be very reluctant to divulge their own customer flow data. Conversely, even if one were to gain access to, say, Tesco’s Clubcard data, calibrating a model exclusively to one retailer’s customers rather than the whole market could create a bias that might manifest itself in a false value of a parameter for other competitor types (Birkin et al., 2010). Equally troublesome are missing real-world flows in the data and the way in which these are dealt with, as calibrating the model to a set of averages does not necessarily result in the correct patterns. In addition, boundary issues come through modelling a system that is enclosed within a boundary but, in real life, that boundary does not form an effective divide. In a given retail system, the outcome is that any stores near the boundary edge will have unrealistic and normally very high levels of market share. To deal with this problem, Birkin et al. (2010) suggest a boundary-free approach to spatial interaction modelling (i.e. entire regions or nations modelled concurrently), which is certainly more possible today with high performance PCs and super-computers.
GIS for public sector retail planning
Guy (2006) provides an excellent account of retail planning developments since the 1950s and 1960s, especially from a UK perspective. In the first chapter of his book, Guy discusses the purpose of retail planning, in terms of different economic, social and environmental issues. Interestingly, he reminds the reader that retail planners have an economic duty to promote retailing – so they should ‘allow the retail sector to grow and change whilst maintaining a significant level of profitability’ (Guy, 2006: 3). That said, there are a number of social issues which in turn raise spatial issues and which are therefore more significant perhaps for a GIS approach. In particular, Guy (2006) notes the importance of planners maintaining a good balance or mix of shop types, protecting the vitality of small shopkeepers and of the town centre (especially in Europe). Indeed, most European countries have seen a tightening of planning guidelines towards out-of-town developments, effectively making it more difficult to open such centres without proving a real need in the local communities affected, and providing equity in shopping provision such that no particular socioeconomic group should be disadvantaged.
In this section we shall explore the use of GIS to help this final goal in particular, although we will look at impact assessment as well as this also impinges on these social issues of protecting smaller retail centres and independents. GIS can be seen to be a key instrument in examining variations in retail provision and also accessibility by local residents. All such studies can also be couched in terms of a growing literature on ‘food deserts’ – the latter term referring to parts of our cities or regions where access to larger supermarkets in particular is poor.
The simplest measure of access is the distance to the nearest store, usually measured from the centre of an existing demand zone (census block or post code). This can be made more sophisticated by taking a population-weighted mean minimum distance along a street or road network. Smoyer-Tomic et al. (2006) provide a neat illustration of this for supermarket accessibility in Edmonton, Canada (see Figure 8.11).
There are many other methods for estimating access. Figure 8.12 shows a very good illustration of how simple nearest distances (in this case 1,000 metres) can be made more sophisticated by the overlay of different types of stores and some census data (in this case related to household income). Apparacio et al. (2007) show clearly that access to branded supermarket chains was even worse in the low-income central areas of Montreal, Canada, than access to supermarkets in general.
A number of other accessibility studies have examined the difficulties faced by certain types of consumers in accessing the larger, high-quality supermarket outlets. Building on Figure 8.11, Smoyer-Tomic et al. (2006) were able to look at distances needed to be travelled (estimated in a variety of ways) against population size, low-income households, households with no car and the population over 65. The resulting analysis revealed nine areas of concern within Edmonton (see Figure 8.13), which they could further disaggregate into areas of concern for ‘elderly residents’, ‘low-income residents’, ‘seniors and low-income residents’, ‘low-income residents and no car owners’.
While sieve mapping in GIS can be used to find ideal sites for making profits (see above) it can also be used to find ideal sites for new stores based on low existing access for certain groups of consumers. In addition to the above examples, Eckert and Shetty (2011) illustrate the combination of a large number of key variables to plot census blocks ‘of concern’ in Toledo, Ohio, US, in terms of poor accessibility. They overlay data to find census block groups with the following characteristics (a sieve map in effect as all zones that do not have these qualities can be eliminated):
■ Average accessibility to nearest food retailer is over one mile.
■ The percentage of the population below poverty level is above the city average.
■ The percentage of households without a car is above the city average.
■ The percentage of population receiving public assistance is above the city average.
■ Median household income of the block group is below the city average.
Figure 8.11 Neighbourhood-level population-weighted mean minimum street network travel distance to the nearest supermarket in Edmonton, Canada
Source: Smoyer-Tomic et al. (2006)
Figure 8.12 Spatial distribution of supermarket accessibility in Montreal, Canada, 2001
Source: Apparacio et al. (2007)
They found 28 blocks met those criteria (Eckert and Shetty, 2011). Figure 8.14 shows those 28 zones ‘of concern’.
Many of the studies in the literature on food deserts use some kind of distance measure based on straight-line or distance on a road/street network. Others have favoured an accessibility score based on an index, such as that derived by Hansen (1959). Clarke et al. (2002) developed this indicator approach by estimating accessibility based on the outcomes of a SIM as defined in the preceding section of this chapter. This is arguably more powerful than the Hansen style indicator as it takes into account the actual interactions that people are most likely to make rather than simply the set of opportunities in the area (Bertuglia et al., 1994). Figure 8.15 shows the resulting access scores for Cardiff in Wales in 2002. The low-scoring areas typically coincide with low-income housing estates such as Rhiwbina, Fairwater and Llanrumney.
Figure 8.13 Neighbourhoods in Edmonton, Canada, with high population need and low supermarket accessibility, disaggregated by consumer type
Source: Smoyer-Tomic et al. (2006)
Figure 8.14 Areas of concern regarding poor access to grocery retailing in Toledo, Ohio, US
Source: Eckert and Shetty (2011)
The identification of poor access or food deserts is of obvious interest to retail planners (see also Raja et al. (2008) for an interesting discussion of food deserts and potential ethnic disparities in access, and McEntee and Agyeman (2010) for the use of GIS to identify potential food deserts in rural areas). The question then arises – what can be done about the problem? Many of the papers cited above discuss policy alternatives. Retail planners could investigate the possibility of ‘spatial infill’ by encouraging small supermarkets (or convenience stores) to help plug the gaps in access. For retailers concerned about low revenue potential in low-income food deserts, planners could consider financial incentives such as tax breaks or help with costs of purchase and refurbishment. In the UK we have even seen the encouragement of large superstores in low-income food deserts – especially the Tesco Extra stores opened in collaboration with local authorities under a ‘social regeneration’ banner in the UK (Wrigley et al., 2003).
Finally in this chapter we briefly examine how GIS could be useful for planners to estimate the impacts of large-scale retail developments such as out-of-town retail parks, shopping centres or very large superstores. As we argued above in relation to the private sector, GIS is typically not enough on its own to handle estimating the impacts of such major developments, especially in relation to revenue estimation. Ironically in the 1960s and 1970s many local authorities in the UK used SIMs to help in this type of analysis. However, after a number of conflicting model results in a number of planning enquiries these models were effectively banned. Khawaldah et al. (2012) and Birkin et al. (2015) review the alternative methods adopted since the 1980s and compare the results against using SIMs. In the following discussion, we briefly discuss the likely stages in a UK planning enquiry (the analysis for which is normally undertaken by retail consultants acting on behalf of commercial developers). Here we follow the steps outlined by Drivers Jonas (1992; also see England, 2000).
Figure 8.15 Mapping food deserts in Cardiff, UK
Source: Clarke et al. (2002)
1 Identify the catchment area of the proposed retail development, the area from which the centre draws the majority of its revenue. The information about that ideally should come from a household survey to show the existing shopping patterns in the area, although often this information is not available. The catchment area might be subdivided into drive time isochrones, and these isochrones might be further subdivided into primary, secondary and tertiary zones for greater spatial accuracy in assessing impact.
2 Estimate the expenditure within the catchment area, derived from the population and its per capita expenditure.
3 Estimate the turnover of existing shopping centres. This information can be estimated by using national average turnover/floor-space ratios for individual firms (or the centre as a whole), or by using survey data and proportioning centre turn-over on the basis of the customer patronage seen in the survey (i.e. as a percentage of the total spend).
4 Estimate the turnover of the new shopping proposal. This is normally estimated on the basis of company average turnover/floor-space ratios for retailers known to be entering the centre (or trading performance of similar centres where such data are not available).
5 Estimate the amount of spending in each existing centre which will be diverted to make up the new centre’s turnover, and the locational source of that spending.
GIS might be typically used at all stages of this process. The main difficulties with this procedure are, first, that many smaller centres get omitted from the analysis. When consumers record their preferences for shopping destinations in surveys, they commonly overstate the importance of the larger centres in the area and underplay (or omit) the importance of smaller centres. Thus, when the analysis comes to impact assessment the smaller centres (probably most affected by new developments) can be completely ignored. Second, the estimation of potential revenue using national turnover/floor-space ratios is fraught with danger – smaller developments will clearly be estimated to take too much revenue based on national figures while very large new centres will be under-predicted. The conclusion of Khawaldah et al. (2012) and Birkin et al. (2015) is that SIMs would do a much better job more often than not.
In this chapter we have explored the use of GIS in retail location planning from the perspective of both the private and public sectors. It has been argued that GIS is a powerful tool for visualisation and catchment area analysis. Key data sets can be mapped and analysed using key analytical routines such as buffer and overlay. The illustrations throughout the chapter show the widespread use of GIS in many retail organisations and consultancies. Despite its usefulness, however, we have also argued that for certain operations GIS might not be currently powerful enough – especially, for example, for the estimation of store revenues. For this important task, we argue that spatial models (statistical and/or mathematical) are more powerful and have a better track record of success (see Birkin et al., 2016). If these models can be incorporated directly into a GIS package then there are advantages in terms of data linkage and visualisation. However, mathematical models in particular are harder to incorporate into black box systems where the models cannot be effectively disaggregated and calibrated to fit the system of interest. Thus loose coupling is probably the best solution for linking such models to the other spatial analysis routines in a GIS.
This chapter is accompanied by two practical activities.
Practical 4a: Retail site location analysis, provides hands-on experience of using GIS to evaluate outputs from a retail modelling exercise. Using a fictional (but realistic) retail network in the UK, we give you experience handling data related to both the demand and supply sides. We give you the opportunity to assess retail provision, retail demand and store performance. You also examine outputs from a SIM in order to assess impacts of a new store opening.
Practical 4b: Public sector retail planning, gives you the opportunity to consider concepts related to access to retail stores. Using an example from Washington, DC, you identify potential food deserts by considering access to food stores.
All website URLs accessed 30 May 2017.
Apparacio, P., Cloutier, M. S., & Shearmur, R. (2007) The case of Montreal’s missing food deserts: evaluation of accessibility to food supermarkets. International Journal of Health Geographics, 6(4). DOI: https://doi.org/10.1186/1476-072X-6-4.
Beaumont, J. R. (1991) GIS and market analysis, in D. J. Maguire, M. Goodchild, & D. W. Rhind (eds) Geographical Information Systems: Principles and Applications, Longman, London, vol. 2, 139–151.
Benoit, D., & Clarke, G. P. (1997) Assessing GIS for retail location analysis. Journal of Retailing and Consumer Services, 4(4), 239–258.
Berry, T., Newing, A., Davies, D., & Branch, K. (2016) Using workplace population statistics to understand retail store performance. The International Review of Retail, Distribution and Consumer Research, 26(4), 375–395.
Bertuglia, C. S., Clarke, G. P., & Wilson, A. G. (1994) Modelling the City: Planning, Performance and Policy, Routledge, London.
Birkin, M., Clarke, G. P., & Clarke, M. (2002) Retail Geography and Intelligent Network Planning, Wiley, Chichester.
Birkin, M., Clarke, G. P., & Clarke, M. (2010) Refining and operationalizing entropy-maximizing models for business applications. Geographical Analysis, 42(4), 422–445.
Birkin, M., Khawaldah, H., Clarke, M., & Clarke, G. P. (2015) Applied spatial interaction modelling in economic geography: an example of the use of models for public sector planning, in C. Karlsson, M. Andersson, & T. Norman (eds) Handbook of Research Methods and Applications in Economic Geography, Edward Elgar, Cheltenham, 491–512.
Birkin, M., Clarke, G. P., & Clarke, M. (2017) Retail Location Planning in an Era of Multi-Channel Growth, Routledge, London.
Bowlby, S., Breheny, M., & Foot, D. (1984a) Store location: problems and methods 1: Is locating a viable store becoming more difficult? Retail and Distribution Management, 12(5), 31–33.
Bowlby, S., Breheny, M., & Foot, D. (1984b) Store location: problems and methods 2: Expanding into new geographical areas. Retail and Distribution Management, 12(6), 41–46.
Clarke, G. P. (1998) Changing methods of location planning for retail companies. GeoJournal, 45, 289–298.
Clarke, G. P., Eyre, H., & Guy, C. (2002) Deriving indicators of access to food retail provision in British cities: studies of Cardiff, Leeds and Bradford. Urban Studies, 39(11), 2041–2060.
Clarke, G. P., Thompson, C., & Birkin, M. (2015) Exploring the geography of e-commerce in UK retailing. Regional Studies, Regional Science, 2(1), 370–390.
Davies, R. L. (1977) Store location and store assessment research: the integration of some new and traditional techniques. Transactions of the Institute of British Geographers, 141–157.
Davies, R. L., & Rogers, D. S. (1984) Store Location and Store Assessment Research, Wiley, Chichester.
Drivers Jonas (1992) Retail Impact Assessment Methodologies: Research Study for the Scottish Office, Scottish Office, Edinburgh.
Eckert, J., & Shetty, S. (2011) Food systems, planning and quantifying access: using GIS to plan for food retail. Applied Geography, 31(4), 1216–1223.
England, J. (2000) Retail Impact Assessment: A Guide to Best Practice. Routledge, London.
Fenwick, I. (1978) Techniques in Store Location Research: A Review and Applications, Retailing and Planning Associates, Corbridge.
Fotheringham, A. S. (1983) A new set of spatial-interaction models: the theory of competing destinations. Environment and Planning A, 15(1), 15–36.
Ghosh, A., & MacLafferty, S. (1987) Locational Strategies for Retail and Service Firms, Lexington Books, Lexington, MA.
Guy, C. (2006) Planning for Retail Development: A Critical View of the British Experience, Routledge, London.
Hansen, W. G. (1959) How accessibility shapes land use. Journal of the American Institute of Planners, 25(2), 73–76.
Khawaldah, H., Birkin, M., & Clarke, G. (2012) A review of two alternative retail impact assessment techniques: the case of Silverburn in Scotland. Town Planning Review, 83(2), 233–260.
Laing, R. D., Clarke, I., Mackaness, W., Ball, B., & Horita, M. (2003) The devil is in the detail: visualising analogical thought in retail location decisionmaking. Environment and Planning B: Planning and Design, 30, 15–36.
Larsen, K., & Gilliland, J. (2008) Mapping the evolution of food deserts in a Canadian city: supermarket accessibility in London, Ontario, 1961–2005. International Journal of Health Geographics, 7(16). DOI: https://doi.org/10.1186/1476-072X-7-16.
McEntee, J., & Agyeman, J. (2010) Towards the development of a GIS method for identifying rural food deserts: geographic access in Vermont, USA. Applied Geography, 30(1), 165–176.
Newing, A., Clarke, G. P., & Clarke, M. (2015) Developing and applying a disaggregated retail location model with extended retail demand estimations. Geographical Analysis, 47, 219–239.
Openshaw, S. (1984) The Modifiable Areal Unit Problem. Geo Books, Norwich.
Ottensmann, J. R. (1997) Partially constrained gravity models for predicting spatial interactions with elastic demand. Environment and Planning A, 29(6), 975–988.
Pearson, J. (2007) A comparative business site-location feasibility analysis using geographic information systems and the gravity model. Volume 9, Papers in Resource Analysis. Saint Mary’s University of Minnesota Central Services Press, Winona, MN. Available from: www.gis.smumn.edu.
Raja, S., Ma, C., & Yadav, P. (2008) Beyond food deserts: measuring and mapping racial disparities in neighborhood food environments. Journal of Planning Education and Research, 27(4), 469–482.
Raper, J., Rhind, D., & Shepherd, J. (1992) Postcodes: The New Geography, Longman, Harlow.
Reynolds, J., & Wood, S. (2010) Location decision making in retail firms: evolution and challenge. International Journal of Retail & Distribution Management, 38(11/12), 828–845.
Russell, S. E., & Heidkamp, C. P. (2011) ‘Food desertification’: the loss of a major supermarket in New Haven, Connecticut. Applied Geography, 31(4), 1197–1209.
189Smoyer-Tomic, K. E., Spence, J. C., & Amrhein, C. (2006) Food deserts in the prairies? Supermarket accessibility and neighborhood need in Edmonton, Canada. The Professional Geographer, 58(3), 307–326.
Spatial Insights (undated) Market Potential GIS Case Study: Market Potential Analysis using ReCAP Retail Location Data: Check Cashing and Pawn Brokers. Available from: www.directionsmag.com/entry/a-market-potential-gis-case-study-market-potential-analysis-for-check-cashi/122646.
Thomas, C. J., Bromley, R. D. F., & Tallon, R. (2004) Retail parks revisited: a growing competitive threat to traditional shopping centres? Environment and Planning A, 36, 647–666.
Wilson, A. G. (1974) Urban and Regional Models in Geography and Planning, Pion, London.
Wood, S., & Reynolds, J. (2011) The intra-firm context of retail expansion planning. Environment and Planning A, 43(10), 2468–2491.
Wood, S., & Reynolds, J. (2012) Managing communities and managing knowledge: strategic decision making and store network investment within retail multinationals. Journal of Economic Geography, 12(2), 539–565.
Wrigley, N. (1987) The concentration of capital in UK grocery retailing. Environment & Planning A, 19(10), 1283–1288.
Wrigley, N. (2014) Store Choice, Store Location and Market, Analysis (Routledge Revivals), Routledge, London.
Wrigley, N., Warm, D., & Margetts, B. (2003) Deprivation, diet, and food-retail access: findings from the Leeds ‘food deserts’ study. Environment and Planning A, 35, 151–188.