In the previous chapter we introduced the reader to some basic terminology and concepts that are important to understand in order to get started. In this chapter we provide an introduction to key GIS methods that can be used to address social science research questions that have a spatial nature. As noted in the previous chapter, GIS-based spatial analysis covers a very large number of methods ranging from computation of spatial variables, such as the distance from households to the nearest hospital, to measurements of area or density calculations. In this chapter we give more specific and detailed examples of how GIS-based spatial analysis can be conducted to address simple but powerful queries relating to social science issues and problems. In particular, we discuss ways in which GIS and spatial analysis techniques can be employed to provide information and intelligence in relation to the importance and role of geography in the actions and performance of private and public sector organisations. The following questions represent examples of the types of issues and problems typically faced by organisations in the private sector (questions 1 and 2) and the public sector (questions 3 and 4):
1 Retailers wish to use socio-economic data available for different areas to assess the likely demand for their products if they open or expand an outlet; how can these areas be classified?
2 The same retailers collect information on movements of shoppers from residential zones to stores. Can we build models of such flows? Can we predict changes in such flows if we expand an outlet or open a new one?
3 Local council policy makers want to know what the spatial impacts of a council policy would be – could they use small-area data for socio-economic impact assessment?
4 National government departments need information on geographical distributions of deprivation. How can deprivation be measured, mapped and analysed?
These are typical examples of social science issues that can be analysed with GIS. They also give a small flavour of the applicability of GIS in the social sciences and of the topics and case studies that are presented and discussed in Part II of this book.
Some of these questions will be addressed using appropriate and publicly available data throughout this chapter. In particular, in this chapter we show how GIS and spatial analysis can be used to perform simple but important queries and generate relevant information and intelligence that can be used to address the above issues, using publicly available data. We begin by considering some practical issues pertaining to data availability. We then discuss examples of attribute (aspatial) queries which can be addressed with simple descriptive statistics (alongside spatial thematic mapping). Asking, for example, how many people live in each region of a country is an aspatial type of query that does not necessarily require GIS capability to address it, but which can be easily answered using any database management system or spreadsheet software. We then move on to explicitly spatial queries which make more use of the geo-analytical capability of GIS and tools such as buffer analysis, point-in-polygon and spatial overlay, that take into account geographical distance, adjacency, containment and intersection (see again Chapter 1).
Before we begin, it is useful to consider again the four general questions/social science examples posed above in the context of the checklist presented in Chapter 1. Taking each item in the list in turn:
1 Identify your research question and how it is ‘spatial’. Review existing research in your field that uses a GIS or spatial analysis. This will help give you a better sense of how GIS can be useful to you.
Looking at the spatial nature of the question of likely demand for the products of retailers, we note that there is a combination of socio-economic and (geo)demographic factors such as age, lifestyle and household disposable income, but also where they live and how far from the location of different retail outlets.
Similarly, with regard to the question of travel-to-shop flows we might have a combination of socio-economic and demographic factors similar to the first question, coupled with actual geographical information on the shopping trips made (derived from surveys for example).
With regard to the question about the possible spatial impacts of local city council policy we can look at specific examples such as the identification of food deserts (also briefly discussed in Chapter 1) or the decision to invest in social housing in particular areas of a city or to reconsider local tax bands. Again, there is a combination of socio-economic/demographic factors (e.g. numbers of low-income households) with geographical factors (where do they live in the city? what is the level of accessibility that they have to local council services?).
Question 4, pertaining to national government, also relates to socio-economic factors associated with the likelihood of social exclusion and of lacking access to (or being deprived of) what are considered to be basic necessities in society (such as not having access to a car or living on income below the poverty line), but at the same time geographical factors such as distance from the delivery points of public services (e.g. schools, health centres).
2 Use the basic spatial concepts discussed above to frame your questions as this will help when it comes to operationalising the analysis in a GIS setting.
All issues and questions are related to distance, density, accessibility, coverage and colocation, discussed in Chapter 1.
3 What are your data requirements? This means identifying the spatial units you need information for, as well as their characteristics.
First, with regard to the appropriate spatial data model, the spatial units that we need to operationalise include points (for features such as retail outlets, schools, hospitals, etc.), lines (for features such as the road network that can be used to estimate ‘accessibility’) and polygons (e.g. administrative boundaries for local council districts and electoral wards and smaller areas for which population data might be available). Therefore, the vector model described in Chapter 1 is the most appropriate here (and this is also generally the case for most social science applications), as applied throughout the accompanying practicals.
The next step is to identify the characteristics (or attributes) that need to be joined to the spatial units. For example, for retail store units (point data) this information can include floor-space, brand, opening hours, number of employees, number of parking spaces, etc. The road network line data can be enriched with additional characteristics regarding the type and capacity of road, traffic levels, etc. Finally, the area boundary (polygon) data can be joined with demographic and socio-economic data such as total number of residents, population by age-group, social class, car ownership, etc.
4 Do your data already exist in a GIS-ready format? If not, consider how you will get your data into the GIS.
There is a wide range of sources of digital spatial data as well as secondary social survey data that can be used to add characteristics (attributes) to the spatial data.
It is worth noting that there is a rapidly increasing number of open data sources that can be used to obtain free digital geographical data. A good example is the Ordnance Survey in the UK which offers open digital map data for a number of geographical features including rivers, street and road networks as well as administrative and electoral boundaries. There are similar open data resources worldwide (see Appendix 2.1 for more details). Another excellent resource for open data is OpenStreetMap, which can also be used to obtain data on the location of retail outlets and other features relevant to the issues discussed in this chapter.
Similarly, there are several suitable sources for data on characteristics or attributes that can be joined with digital map data. It should be noted that one of the key sources of data on demographic and socio-economic characteristics are the censuses of population, which record demographic and socio-economic information at a single point in time and are normally carried out every five or ten years (Rees et al., 2002). Census data sets describe the state of the whole national population and are extremely relevant for the analysis of a wide range of socio-economic issues and related policies. In addition to the census there is a wide range of administrative and private sector sources of suitable socio-economic data. A good example of a resource that brought together socio-economic and demographic data was the Neighbourhood Statistics service in the UK (see Figure 2.1). Neighbourhood Statistics offered free access to a wide range of social and economic data, which included census small-area data as well as data provided by local government authorities and other providers such as the Home Office (crime data) and the Land Registry (house prices). These data included information on the socio-economic characteristics of the people living in the area, as well as information on housing and crime. Neighbourhood Statistics was discontinued in 2017 but all the data previously obtained via this portal are available from other sources, many of which are listed in Appendix 2.1.
Figure 2.1 Neighbourhood Statistics topics from the UK Office for National Statistics
In addition, there are ongoing developments leading to new methods of geographic data collection, such as Voluntary Geographical Information (VGI) provided by ‘citizens as sensors’ (Goodchild, 2007) and crowdsourcing (Sui et al., 2013), involving non-expert people (the ‘crowd’) in data production with the use of smartphones and other mobile devices (Brovelli et al., 2016). There is also an increasing amount of geographical data generated via social media and great potential exists to integrate and analyse with the use of GIS (Sui and Goodchild, 2011; Croitoru et al., 2013; Huang and Xu, 2014; Zhai et al., 2015; Kim and Koh, 2016).
Using GIS to perform attribute (aspatial) queries
As briefly discussed in the introductory section of this chapter, GIS queries can be distinguished between aspatial attribute queries, which do not require knowledge of topological features (i.e. information on the location of spatial units and also where they are in relation to each other) and spatial, which need to take distance into account and/or involve the combination of different geographical layers. The following are examples of attribute queries that can also be described as aspatial queries:
▪ What are the top ten and bottom ten regions in Europe in terms of university degree holders as a percentage of the total population aged 25–64?
▪ Which areas in a city have unemployment rates that are above the national average?
▪ Which are the five most and five least affluent neighbourhoods in a city?
Although these types of questions can be addressed using information systems and computer programs such as spreadsheet software and statistics packages, the use of GIS enables tabular summaries in tandem with visual analysis and mapping (as will also be discussed and explained in more detail in the next chapter). The first question posed above can be addressed with the use of any spreadsheet-based system, just by obtaining the relevant data from a suitable statistical source such as EUROSTAT and then sorting the regions in descending order of the variable in question to create Tables 2.1 and 2.2.
Table 2.1 Top ten regions: total number of 25-to 64-year-olds having completed tertiary education as a percentage of all population aged 25–64
Region |
% |
Inner London (UK) |
60.7 |
Oslo og Akershus (Norway) |
53.4 |
Prov. Brabant Wallon (Belgium) |
51.9 |
Berkshire, Buckinghamshire and Oxfordshire (UK) |
51.0 |
Eastern Scotland (UK) |
50.4 |
Helsinki-Uusimaa (Finland) |
50.2 |
Outer London (UK) |
48.7 |
Hovedstaden (Denmark) |
48.1 |
Zurich (Switzerland) |
47.7 |
Stockholm (Sweden) |
47.6 |
Source: http://ec.europa.eu/eurostat
Table 2.2 Bottom ten regions: total number of 25-to 64-year-olds having completed tertiary education as a percentage of all population aged 25–64
Region |
% |
Campania (Italy) |
14.3 |
Nord-Vest (Romania) |
14.2 |
Puglia (Italy) |
14.0 |
Vest (Romania) |
13.5 |
Sicilia (Italy) |
13.3 |
Sardegna (Italy) |
13.1 |
Regiao Autonoma dos Acores (Portugal) |
13.0 |
Nord-Est (Romania) |
12.0 |
Sud-Est (Romania) |
12.0 |
Sud-Muntenia (Romania) |
11.4 |
Source: http://ec.europa.eu/eurostat
However, these data can be integrated into GIS for mapping and further analysis. As discussed in Chapter 1, this type of attribute/tabular data can be joined with suitable geographical data (in this case that would be European region digital boundary data) in a GIS system. This would enable us to produce tables such as the above but to also provide spatial information by showing where these regions are and what type of geographical patterns might exist. This can be achieved by creating a thematic map of higher education graduates across all regions (see Figure 2.2).
The second and third questions posed above are also very relevant to the wider issues and example questions discussed in the previous sections. For example, it would be generally reasonable to expect the likely demand for retail products is going to be higher in more affluent areas. Similarly, knowing which areas have the highest unemployment rates can inform discussions pertaining to local and national government policies.
Figure 2.2 Total number of 25-to 64-year-olds having completed tertiary education as a percentage of all population aged 25–64
Source: Constructed by the authors using data from http://ec.europa.eu/eurostat
Figure 2.3 The city of Sheffield, UK, electoral wards
Looking at the data sources briefly discussed in the previous section, we can identify relevant variables that can be used to address these attribute queries. In particular, from the publicly and freely available online data resources (see Appendix 2.1) it is possible to obtain socio-economic and demographic data from the census of population and other sources. For instance, it is possible to obtain information that could be used to address the attribute queries about unemployment, poverty and wealth. We will now give some examples of this type of attribute queries, using the city of Sheffield in the UK as an example. As we will be using the city of Sheffield as an example study area in other chapters of this book it is useful to also provide a map of the city here. Figure 2.3 shows a map of the city of Sheffield and the areas within it, according to its electoral ward geography, a UK local administrative geographical unit for which there is a wide range of data publicly available.
Table 2.3 Electoral wards in the city of Sheffield, UK, with unemployment rates more than the national UK average (8.3%)
Electoral ward |
Unemployment rate (%) |
Manor |
15.05 |
Burngreave |
14.61 |
Castle |
14.34 |
Southey Green |
12.48 |
Firth Park |
11.83 |
Park |
11.48 |
Sharrow |
11.01 |
Norton |
9.79 |
Netherthorpe |
9.77 |
Nether Shire |
9.48 |
Darnall |
9.28 |
Figure 2.4 Screenshot showing the selection of areas in the city of Sheffield, UK, with unemployment rates more than the national UK average (8.3%), 2011
Figure 2.5 Spatial distribution of professional and managerial occupations in Sheffield, UK, 2011
Table 2.4 Top five electoral wards with highest percentages of professional and managerial occupations in the city of Sheffield, UK
Electoral ward |
Percentage of professional and managerial |
Ecclesall |
28.3 |
Broomhill |
25.1 |
Hallam |
25.1 |
Nether Edge |
19.6 |
Dore |
19.1 |
So, using the city of Sheffield as an example, Table 2.3 uses data from the census of UK population to address the unemployment question, whereas Table 2.4 utilises census data on socio-economic class to help address the question regarding the most affluent areas in the city.
Digital boundary data enable us to display this form of information on the map (you can find out more information on how attribute data can be joined with digital boundary data throughout the linked practicals that accompany this textbook). Using the query tools described in Practical B it is possible to identify and highlight neighbourhoods in Sheffield that meet criteria of interest (Figure 2.4) or in order to explore spatial patterns (Figure 2.5).
Spatial queries: buffers and overlay operations
We can now move on to examples of spatial queries that can only be answered by processing information on the actual location and topographic relationships of geographical features. For example, and with regard to the tertiary students example briefly discussed in the previous section, we could consider how far European populations live from their nearest university. Figure 2.6 addresses such a spatial query and is the output of spatial analysis involving a GIS-based calculation of how far populations in different parts of Europe live from a university in terms of travel time. This calculation also involves a consideration of the road network and relevant analysis which is discussed in more detail in Chapter 4.
Figure 2.6 Population living more than 60 minutes from the nearest university in Europe (% of total population)
Source: Constructed by the authors using data from Annoni and Kozovska (2010)
We can also consider spatial queries in relation to the issues of retail demand analysis and service accessibility, building on the previous section’s discussion of attribute (aspatial) queries. Using a function known as a spatial join, it is possible to combine the characteristics associated with individual grocery stores with the charac-teristics associated with the neighbourhoods that they serve. Table 2.5 gives an extract of the output of such a spatial join. Using this information it is also possible to produce summary data on the average unemployment rate and social class profile of the immediate neighbourhood served by each grocery outlet.
It is also possible to use an overlay operation known as point-in-polygon in order to determine which (and calculate how many) grocery stores fall within each neighbourhood (see Figure 2.7).
Table 2.5 Spatial join of grocery stores with electoral ward data
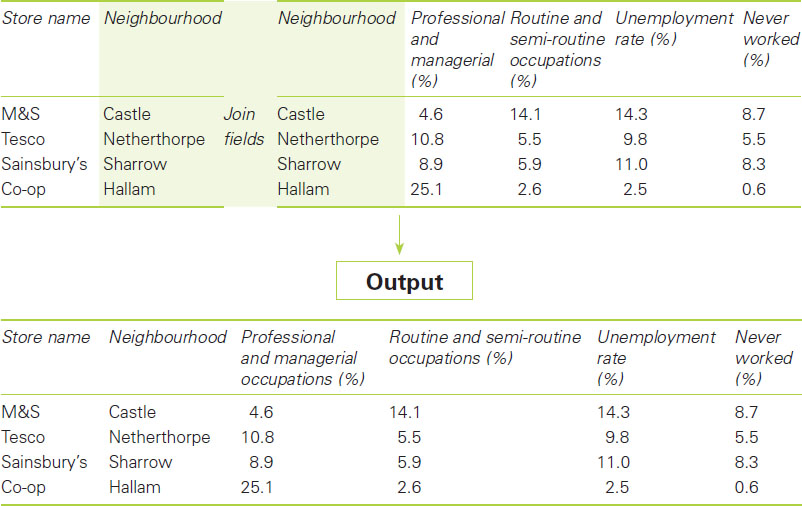
Figure 2.7 Point-in-polygon overlay
Source: http://support.esri.com/other-resources/gis-dictionary/term/point-in-polygon%20overlay
This analysis and discussion is also very relevant to the issues of food deserts which was briefly discussed in the introductory chapter. Table 2.5 gives an indication of the types of areas and accessibility (from a socio-economic affordability view point) in relation to different supermarkets. This analysis can be further enhanced by considering the actual distance between each area and a grocery outlet in order to provide a proxy for geographical accessibility (these issues are discussed in greater detail in Chapters 8, 9, 10 and 11).
It is also possible to use spatial overlay techniques in order to analyse and map the distance between each neighbourhood and its nearest grocery store. We give an example here using a layer of geographical units in the UK known as Lower Layer Super Output Areas (LSOAs). Using the ArcGIS ArcTool Box overlay and spatial join this layer was combined with the groceries store layer in order to calculate the distance to the nearest grocery from each geographical area. The output of this operation is shown in Figure 2.8. Nevertheless, it is useful to highlight that there are alternative (and conceptually equivalent) software approaches to buffer and distance computation. For instance, if there is no need to visualise buffers then the ArcGIS ‘compute distances’ function might be a faster alternative to the ‘buffer distance’ approach. The accompanying practical of this chapter (Practical B) illustrates the ‘select by distance’ approach in ArcGIS, which involves a relatively simpler series of steps to implement, compared to alternative approaches.
Such analysis can provide the basis for a more sophisticated investigation involving more complex buffer and overlays (Cheng et al., 2007; Benoit and Clarke, 1997). For example, Cheng et al. (2007) considered a similar but more extensive set of layers (see Table 2.6) in order to identify the best locations for the development of new shopping malls in Hong Kong. Using spatial overlay they estimated the average distance from potential major demand points (see Table 2.7) as well as demand and total household income for existing shopping malls (see Table 2.8).
Figure 2.8 Distance to nearest grocery stores in Sheffield, UK, from each LSOA
Table 2.6 Geographical layers considered in a GIS approach to shopping mall selection
Layer and sub-layer |
Description of the features |
Symbolisation |
City map |
Draw an outline of the city |
Coastlines covering the whole city |
District areas |
Divide the city into ten district areas |
Ten different colours representing the 10 districts |
Roads |
Draw roads on the city map |
Lines with brown colour |
Streets |
Draw streets on the city map |
Lines with red colour |
Railways |
Draw railways on the city map |
Lines with dark green colour |
Existing shopping malls |
Locate the existing shopping malls on the city map |
Points with labels in alphabet and number as E1, E2, etc. |
Potential locations |
Locate the potential sites on the city map |
Points with labels in alphabet and number as S1, S2, etc. |
Household incomes in each district |
Add up the average monthly household incomes generated in each district |
Points at the centres of districts with labels in alphabet and number as H1, H2, etc. |
Demand size in each district |
Add up the average monthly demands (spending) in each district |
Points at the centres of districts with labels in alphabet and number as A1, A2, etc. |
Household incomes in each estate |
Add up the average monthly household incomes generated in each estate point |
Points with labels in alphabet and number as M1, M2, etc. |
Demand size in each density point (demand point) |
Add up the average monthly demands (spending) in each density point |
Points with labels in alphabet and number as D1, D2, etc. |
Source: Cheng et al. (2007)
Table 2.7 Average distance from major demand points
Potential location |
Total distance (kilometre) |
Average distance (kilometre) |
Aberdeen |
258 |
11.73 |
Central |
210 |
9.54 |
Causeway Bay |
219 |
9.96 |
Kennedy Town |
232 |
10.54 |
Tsimshatsui |
192 |
8.72 |
Tseung Kwan O |
256 |
11.64 |
Tai Po |
340 |
15.47 |
Tuen Mun |
455 |
20.70 |
Source: Cheng et al. (2007)
Table 2.8 Estimating potential demand and household income by shopping mall coverage area
Potential location |
Coverage demand area |
Existing super mall |
Coverage demand (mean population) |
Coverage (mean household income) |
Aberdeen |
Aberdeen, Kennedy Town, Central, Wanchai. |
None |
179,817 |
28,400 |
Central |
Central, Kennedy Town, Aberdeen, Wanchai, Tsimshatsui. |
Admiralty (1) |
200,258 |
25,661 |
Causeway Bay |
Wanchai, Central, Aberdeen, Tsimshatsui, North Point. |
Causeway Bay (1) |
289,890 |
27,929 |
Kennedy Town |
Kennedy Town, Central, Aberdeen. |
None |
184,041 |
29,201 |
Tsimshatsui |
Tsimshatsui, Kowloon City, Shamshuipo, Kwun Tong, Central, Wanchai, North Point. |
Tsimshatsui (3) |
87,733 |
23,600 |
Tseung Kwan O |
Tseung Kwan O, Wong Tai Sin, Kowloon City, Kwun Tong |
None |
429,024 |
18,163 |
Tai Po |
Tai Po, Northern District, Shatin |
None |
412,723 |
18,877 |
Tuen Mun |
Tuen Mun, Yuen Long |
None |
468,951 |
16,500 |
Note: Number in parenthesis denotes the number of existing super mall(s) close to the potential location.
Source: Cheng et al. (2007)
Figure 2.9 Point, line and polygon features and buffers around these features
Source: ArcGIS help system
In the discussion below we summarise some of the types of GIS operations that can be employed to address spatial queries as shown in the remainder of this section (more sophisticated approaches that involve network analysis are discussed in more detail in Chapter 4). These are all core GIS and spatial analysis techniques and feature heavily in the accompanying practicals.
Buffering
Buffering creates a polygon surrounding a feature (such as a point or line) at a specified distance. The top side of Figure 2.9 shows the features point, line and polygon, respectively. The middle part of Figure 2.9 shows the shape of the buffers associated with each in turn, and the bottom part describes the shape of the resulting buffers when the ‘dissolve’ option is selected. These buffers can be useful in identifying feature space that falls within a set distance threshold (proximity) of the point, line or polygon of interest, such as a catchment area around a retail store (point feature), or an area likely to be affected by a particular pollutant (line or polygon). They can also be combined with spatial queries in order to select and identify all features that fall within or outside the boundary of the buffer.
Intersect
Intersect is used to identify features or areas that intersect (overlap) each other. It is similar to ‘select by location’ in that it identifies all features that fall within the intersection of two or more layers, such as all properties falling within a buffer around a hazardous location. Intersect produces a new output layer containing only the features falling within the intersection. Figure 2.10 gives an illustrative example of the intersect function when applied on polygon layers.
Figure 2.10 The intersect procedure
Source: ArcGIS help system
Figure 2.11 The union procedure
Source: ArcGIS help system
Union
This function combines two or more layers or sets of features to create an output layer containing both sets of features. For example, this might be used to combine a layer containing major roads with a layer that represents minor roads, thus producing an output layer containing all roads (see Figure 2.11).
The Modifiable Areal Unit Problem (MAUP) and ecological fallacy
One of the issues arising from the use of GIS and spatial analysis is the so-called MAUP, arising from the use of arbitrary or artificial units of spatial reporting on continuous geographical phenomena. For example, the spatial patterns of professional and managerial occupations shown in Figure 2.3 and discussed earlier in this chapter are based on the use of the electoral ward geography of Sheffield. However, the occupational classification refers to individuals in unique residential locations within each electoral ward, which were then aggregated up to the ward level and divided by the total population in each area in order to compute the percentages. The summary values (e.g. whether an area has a percentage of less than 15%) are affected by the choice of geographical boundaries. For example, if instead of electoral wards, we used postal sectors, the geographical patterns shown in Figure 2.3 might have been different. In other words, by modifying the boundaries of the area unit there might be different geographical patterns as well as results when undertaking further quantitative or statistical analysis. In particular, the MAUP could introduce considerable statistical bias when the summary values are used in statistical analysis to explore geographical associations between different variables. These issues were first identified by Gehlke and Biehl (1934) but the term MAUP was coined by Openshaw and Taylor (1979), who evaluated systematically the variability of statistical analysis results with different sets of geographical boundaries (Wong, 2009; also see Openshaw, 1984a; Openshaw and Rao, 1995; Taylor et al., 2003).
Another relevant issue and concept is that of the ecological fallacy which refers to the inappropriate assignment to an individual of a property or value that has been calculated or estimated for a group. It also applies when inferences about the relationships between individual characteristics are made based on data about geographical areas (Openshaw, 1984b; Jargowsky, 2005). For example, there have been reports following the UK referendum on EU membership that there has been an increase in anti-immigrant hate crime in areas that voted to leave the EU (Stone, 2016). While it might be appropriate to suggest, based on these statistics and reports, that areas with high percentages of ‘leave votes’ are also likely to have relatively higher anti-immigrant hate crime rates, it would be ecological fallacy to suggest that individual people who voted ‘leave’ in the referendum in these areas commit these crimes.
More advanced forms of spatial analysis in GIS
The MAUP and ecological fallacy are issues that always need to be acknowledged, and if possible, addressed in GIS analysis. There are a number of advanced and sophisticated forms of spatial analysis that can be employed to that end. These include kernel density estimation, where a circular area (the kernel) of a set bandwidth is created around a geographical feature (e.g. a building or the location of a crime or health-related incident) and then the density within this area is calculated and analysed. Such advanced forms of spatial analysis are increasingly available in GIS software packages including ArcGIS (for an example of how kernel density surfaces can be created in ArcGIS using John Snow’s cholera data that we also discussed in the introductory chapter see Goranson (2012)). In addition, more sophisticated approaches (which are not typically part of standard GIS software packages) include Geographically Weighted Regression (Brunsdon et al., 1996; Fotheringham et al., 2002; Paez et al., 2002), the Local Indicators of Spatial Association (Anselin, 1995), zone design (Alvanides and Openshaw, 1999) and spatial microsimulation (Ballas et al., 2005). Some of these methods (and application examples) are discussed in more detail in the second part of this book.
The above spatial analysis examples and outputs give a small flavour of what is possible with GIS. Similar examples can be thought of in a wide range of social science contexts including estimating the catchment areas and performance indicators for schools, estimating likely demand for health services and the use of GIS for hospital planning and health service provision, etc. Part II of the book discusses extensively more sophisticated examples of GIS spatial analysis applications and case studies in a social science context.
|
This chapter is accompanied by Practical B: Spatial queries and attribute data. Continuing our introduction to ArcGIS, the practical gives you the opportunity to work further with the transport data sets introduced in Practical A and relating to the city of Chicago. You will gain experience in carrying out powerful spatial and attribute queries by exploring the relationship between different spatial data layers.
Appendix 2.1 Examples of data resources
United States Census Bureau: www.census.gov
Eurostat: http://ec.europa.eu/eurostat
United States Government Open Data: www.data.gov
European Union Open Data Portal: https://data.europa.eu/euodp/en/data
UK Government Open Data: https://data.gov.uk
Australia Government Open Data: www.data.gov.au/
Canada Open Data Government Portal: http://open.canada.ca
New Zealand Government Open Data: https://data.govt.nz
Japan City Open Data Census: http://jp-city.census.okfn.org/
GB Ordnance Survey: www.ordnancesurvey.co.uk
Open Street Map: www.openstreetmap.org/#map=7/53.041/-1.362
EDINA: www.edina.ac.uk/
ESRI ArcGIS software maps database: www.esri.com
European Regional Yearbook: http://ec.europa.eu/eurostat/statistics-explained/index.php/Eurostat_regional_yearbook
European Values Survey: www.europeanvaluesstudy.eu
ILO: www.ilo.org/global/statistics-and-databases/lang--en/index.htm
NASA MODIS sensor: http://modis.gsfc.nasa.gov
Socioeconomic Data and Applications Center (SEDAC) of the Columbia University, New York: http://sedac.ciesin.columbia.edu/data/collection/gpw-v3
The World Bank: http://data.worldbank.org
WHO: www.who.int/gho/en
Social and Spatial Inequalities group: www.sasi.group.shef.ac.uk
Worldmapper: www.worldmapper.org
GIS ESRI library website: http://training.esri.com/campus/library/index.cfm
National Trust Names: www.nationaltrustnames.org.uk/Surnames.aspx
All website URLs accessed 30 May 2017.
Alvanides, S., & Openshaw, S. (1999) Zone design for planning and policy analysis. Geographical Information and Planning, 299–315.
Annoni, P., & Kozovska, K. (2010) EU Regional Competitiveness Index 2010, JRC Scientific and Technical Report, EUR 24346. Publication Office of the European Union, Luxembourg. Available from: http://publications.jrc.ec.europa.eu/repository/bitstream/JRC58169/rci_eur_report.pdf.
Anselin, L. (1995) Local Indicators of Spatial Association – LISA. Geographical Analysis, 27, 93–115.
Ballas, D., Rossiter, D., Thomas, B., Clarke, G. P., & Dorling, D. (2005) Geography Matters: Simulating the Local Impacts of National Social Policies, Joseph Rowntree Foundation contemporary research issues, Joseph Rowntree Foundation, York, ISBN 1 85935 265 0 (paperback). Free pdf copies available from: www.jrf.org.uk/file/36059/download?token=NkTWwksy&filetype=download.
Benoit, D., & Clarke, G. P. (1997) Assessing GIS for retail location planning. Journal of Retailing and Consumer Services, 4(4), 239–258.
Brovelli, M. A., Minghini, M., & Zamboni, G. (2016) Public participation in GIS via mobile applications. ISPRS Journal of Photogrammetry and Remote Sensing, 114, 306–315.
Brunsdon, C. A., Fotheringham, A. S., & Charlton, M. E. (1996) Geographically weighted regression: a method for exploring spatial non-stationarity. Geographical Analysis, 28, 281–298.
Cheng, E. W., Li, H., & Yu, L. (2007) A GIS approach to shopping mall location selection. Building and Environment, 42(2), 884–892.
Croitoru, A., Crooks, A., Radzikowski, J., & Stefanidis, A. (2013) Geosocial gauge: a system prototype for knowledge discovery from social media. International Journal of Geographical Information Science, 27(12), 2483–2508.
Fotheringham, A. S., Brunsdon, C., & Charlton, M. E. (2002) Geographically Weighted Regression: The Analysis of Spatially Varying Relationships, Wiley, Chichester.
Gehlke, C. E., & Biehl, K. (1934) Certain effects of grouping upon the size of the correlation coefficient in census tract material. Journal of the American Statistical Association, 29, 169–170.
Goodchild, M. F. (2007) Citizens as sensors: the world of volunteered geography. GeoJournal, 69, 211–221.
Goranson, C. (2012) GIS Spatial Analyst Tutorial using John Snow’s Cholera Data, YouTube video. Available from: www.youtube.com/watch?v=isVD8u6WrG4.
Huang, Q., & Xu, C. (2014) A data-driven framework for archiving and exploring social media data. Annals of GIS, 20(4), 265–277.
Jargowsky, P. A. (2005) The ecological fallacy, in K. Kempf-Leonard (ed.) Encyclopaedia of Social Measurement, Academic Press, San Diego, CA, 715–722.
Kim, M. G., & Koh, G. H. (2016) Recent research trends for geospatial information explored by Twitter data. Spatial Information Research, 24(2), 65–73.
Openshaw, S. (1984a) The modifiable areal unit problem. CATMOG 38. GeoBooks, Norwich.
Openshaw, S. (1984b) Ecological fallacies and the analysis of areal census data. Environment and Planning A, 16, 17–31.
Openshaw, S., & Rao, L. (1995) Algorithms for reengineering 1991 census geography. Environment and Planning A, 27, 425–446.
Openshaw, S., & Taylor, P. J. (1979) A million or so correlation coefficients: three experiments on the modifiable areal unit problem. Statistical Applications in the Spatial Sciences, 21, 127–144.
Paez, A., Uchida, T., & Miyamoto, K. (2002) A general framework for estimation and inference of geographically weighted regression models: 2. Spatial association and model specification tests. Environment and Planning A, 34(5), 883–904.
Rees, P., Martin, D., & Williamson, P. (2002) The Census Data System, Wiley, Chichester.
Stone, J. (2016) Brexit: surge in anti-immigrant hate crime in areas that voted to leave EU: police statistics show hate crimes to have tripled in some of the most eurosceptic parts of Britain. The Independent. Available from: www.independent.co.uk/news/uk/crime/brexit-hate-crime-racism-immigration-eu-referendum-result-what-it-means-eurosceptic-areas-a7165056.html.
Sui, D., & Goodchild, M. (2011) The convergence of GIS and social media: challenges for GIScience. International Journal of Geographical Information Science, 25, 1737–1748.
Sui, D., Elwood, S., & Goodchild, M. F. (eds) (2013) Crowdsourcing Geographic Knowledge, Springer, Dordrecht.
Taylor, C., Gorard, S., & Fitz, J. (2003) The modifiable areal unit problem: segregation between schools and levels of analysis. International Journal of Social Research Methodology, 6(1), 41–60.
Wong, D. (2009) The modifiable areal unit problem (MAUP), in A. S. Fotheringham & P. Rogerson (eds) The SAGE Handbook of Spatial Analysis, SAGE, Los Angeles, 105–124.
Zhai, S., Xu, X., Yang, L., Zhou, M., Zhang, L., & Qiu, B. (2015) Mapping the popularity of urban restaurants using social media data. Applied Geography, 63, 113–120.