GIS and the Social Sciences

LEARNING OBJECTIVES

▪ What a GIS is and how it can be used

▪ Basic spatial concepts

▪ What map projections are and why they matter

▪ What a spatial data model is and how it is important

The use of Geographic Information Systems, or GIS, is now longstanding within geography. Over the past few years, its usefulness and popularity have begun to diffuse into other social sciences, where both practitioners and students are increasingly expected to produce and consume information that presumes familiarity with GIS analysis. In many fields, such as health or crime, spatial analysis and GIS-based research have become almost ubiquitous. The teaching of GIS methods, however, often remains firmly lodged inside geography departments, and instruction can be stubbornly divorced from applied topics and research questions. This textbook is not aimed at those proposing to become GIS developers and specialists, as those individuals will require much more in the way of theory and background information. Rather, its purpose is to help those who are experts in a variety of social science disciplines or topical areas to become conversant and capable with common GIS tools and concepts. Its entire point is to enable researchers to use GIS in a range of disciplinary settings.

Geographers often argue that geography is what geographers do. That is, research becomes geographical when performed by someone in that field. This tautology aside, a common thread that runs through most spatial research is a belief in the importance of place and space. How this importance is captured varies – both qualitative and quantitative approaches are common. In this book, we emphasise the utility of a GIS for quantitative analysis, with an emphasis on learning tools and methods in an applied setting. We take frequently used GIS tools and show their applicability across the social sciences and then come at the subject from the other direction, highlighting areas of research and how spatial questions and GIS analysis can contribute to new knowledge creation. Thus, the meat of this book commences with Chapter 2 and continues in the subsequent chapters in Part I, which delve into the range of tools most likely to be of interest to social scientists. Part II of the textbook explores specific GIS applications.

The goals of this first chapter are twofold: first, to show how GIS tools open new windows of opportunity and knowledge and, second, to cover important basic concepts that are fundamental to working with spatial data, as well as structuring and answering spatial questions in the social sciences. In our combined teaching experience, we have found that, naturally, everyone wants the fun part: the analytical tools. Many of the roadblocks encountered in research or in reliability of results, however, stem from inadequate attention to the very basics. So, read on!

Before jumping into the applications – the valuable and interesting things a GIS can do – and the fundamental but important material – the basics of working with spatial data – we should be clear what we mean when we refer to a GIS. A GIS, is a combination of many components, the most prominent of which is the actual piece of software being used for analysis. The GIS software, examples of which are Environmental Systems Research Institute’s (ESRI) ArcGIS, open-source QGIS or MapInfo, is used to make maps but also for what is called ‘spatial analysis’. Spatial analysis takes many forms, from computation of spatial variables, such as the distance from households to the nearest hospital, to measurements of area or density calculations, to more sophisticated statistical and/or mathematical modelling. A GIS can also be used purely for data management and organisation, in particular if one is collecting a variety of types of data on a particular place and wants to be able to query the data based on location.

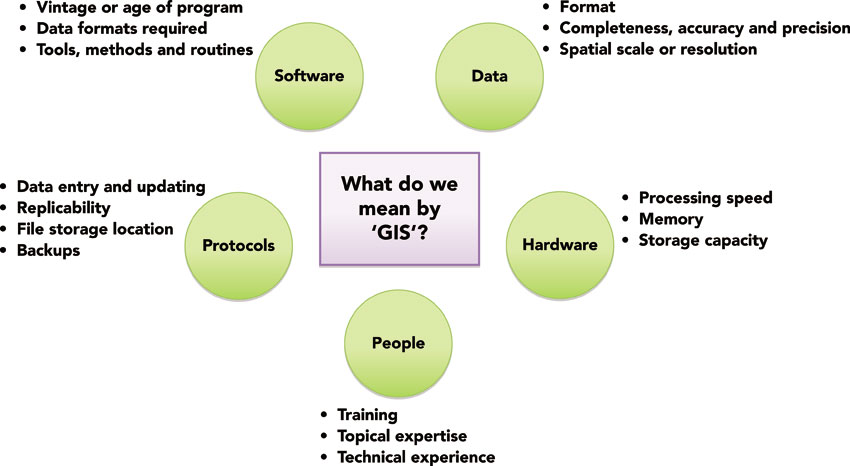
In conversations regarding methods, one will hear phrases such as, ‘I used GIS to create this map’ or ‘I learned GIS last year’ as if the entirety of GIS is contained within a software application. In actuality, the software is but one piece of the GIS puzzle (Figure 1.1). Other key elements are the data being used, the training of the individual working with the software and the computer hardware itself. It might seem as if these are minor points. However, one quickly learns that the quality of the analytical output is only as good as the input data and the training of the user. More importantly, because spatial data can be complex and because analytical procedures tend to be computationally intensive, the processing speed and memory of the computer can matter enormously. As with any technical or methodological subfield, the skills of software developers, GIScientists and computer scientists are indispensable. These are the academics and practitioners who not only implement the algorithms and tools underpinning the software applications, but also develop the very methods and theories that applied researchers depend upon in their own research. Although many researchers use GIS, the majority engages with it at the levels of data, tools and software. For some specialists, though, especially in geography or computer science, GIS is an object of research in itself. Issues to do with development and implementation of methods, as well as more abstract but important questions, such as how space is measured or data organised, all fall increasingly under the rubric of Geographic Information Science, or GISci.

In the mid-19th century, when population growth in London was far outstripping the capacity of existing infrastructure (and when germ theory was still in its infancy), cholera outbreaks were a frequent phenomenon and response was hampered by lack of understanding regarding the mode of transmission. John Snow, a physician today considered the father of modern epidemiology, conceived of mapping cholera deaths along with the locations of water pumps. This map, seen in Figure 1.2, is often considered one of the first examples of ‘spatial analysis’ and even today highlights advantages of visualising data on a map, as well as considering spatial interconnections between multiple types of information (in this case, cholera deaths and water pumps). The innovation is not so much in the underlying data collection process, although Snow was thorough in interviewing affected households and querying their water collection behaviour – after all, mid-19th-century England was good at collecting statistics. The fact remains, though, that evaluating these data in tabular format, versus on a neighbourhood map, allows very different conclusions. The former tells us the typical age and sex of those affected, for example, while the latter gives a clear picture of the spatial clustering in the illness that existed (these are the black bars lining the streets in the map). The innovation that elevates this figure from simply a useful map to an excellent spatial analysis example, however, is the juxtaposition of water pump locations and cholera mortality. This allowed Snow – and subsequent generations of viewers – to hypothesise about possible connections between water quality and cholera spread. In a fitting conclusion to a fascinating tale, Snow was successful in arguing for the pump handle to be removed from the Broad Street pump, which was a common source of water for many of those afflicted.

Many current examples abound of how spatial methods or thinking, and especially GIS, can inform research in the social sciences (see Table 1.1). In general, they share an emphasis on the importance of space in mediating, affecting or determining some outcome. Applications can range from vulnerability research in health care or environmental studies to optimal locations for bus routes or school locations to the identification of food deserts. Climate vulnerability studies combine data on areal footprints of climatic events – sea level rise or the paths of hurricanes, for example – and data on the characteristics of the people or property in those areas affected to draw conclusions about the likely impacts of the event. This is an example of a GIS overlay and it lends itself well to visualisation as well as the generation of variables that then feed into more sophisticated models. In public health research, a common question regarding vulnerability is the extent to which distance from pollution sources can explain a variety of health outcomes, from cardiovascular problems to early childbirth. In these cases, the GIS is used less for visualisation than for calculating distance between individuals and the pollution source of interest.

Spatial optimisation or location theory occupies an important niche in quantitative geography. Its impacts are felt across the social sciences, in any research that investigates coverage or accessibility. These types of analyses might formally address the ideal or best set of locations for public infrastructure – for example, where should primary schools be located if the goal is to build as few schools as possible (as schools are expensive to construct and maintain) but also to allow children to walk as short a distance as possible? Or they might incorporate questions of fairness or equity, which tend to play out spatially in many cases. The recent popularity of food desert research is an excellent example of how a GIS allows one to assess questions of societal inequality in ways no other technology or set of techniques can. The basic idea of a food desert, that some individuals or neighbourhoods have few options nearby for purchasing food, especially fresh fruits and vegetables, is inherently spatial. Similar to vulnerability research, identifying food deserts requires the spatial combination of information about both people and the location of grocery stores. A variety of GIS techniques can be used to compare access to stores across neighbourhoods, but they all share some acknowledgement of the importance of density or distance, both discussed in more depth below. Given the necessary information, it is quick work for the GIS to compute how far away the closest store is, or how many stores lie within a given distance of a particular neighbourhood. You will make use of GIS tools in this context in the linked practical accompanying Chapter 8 where we discuss the application of GIS in retail analysis in more detail.

Another way to approach GIS capability is to consider its most common uses. A GIS can do a lot, but most applications fall into just a few categories: visualisation, data manipulation and creation and spatial analysis. Visualisation includes cartography – the making of maps – as well as other figures or diagrams that help elicit the spatial structure or characteristics of data. All GIS software will be well equipped for the creation and export of all usual types of maps. Maps are powerful communication devices that can be used to illustrate spatial patterns of interest, locations of phenomena of interest or even just study sites. And they are useful in both publications as well as presentations. The value of a good map should never be underestimated. The visualisation of data is also important at the front and back ends of the analysis, for both exploring the data available as well as assessing the results. In sum, a map is helpful at multiple stages of the research process: from exploring data, to developing maps of study site context, to evaluating analytical results. We introduce basic visualisation techniques in the linked practical accompanying Chapter 3, with many of the accompanying practicals providing opportunities to visualise a range of data sets and GIS outputs.

Data manipulation and creation in a GIS is similar to procedures used in other quantitative arenas in the social sciences – baseline data are combined across units or variables to create new information. The difference with a GIS is that information created is extracted from the underlying spatial aspects of the data. For example, in the vulnerability overlay example on page 6, one research product might be a map showing areas under water. A more complex approach would be to generate a variable indicating whether a parcel or area is under water, or perhaps variables showing the depth of water or the speed of winds. The variables can be exported from the GIS and used in a traditional statistical software package. That is, the overall methodological approach has not changed: the GIS has been used to generate new variables. Other standard data manipulation exercises in the social sciences involve calculating distances between types of information (e.g. neighbourhoods and stores or fast food restaurants) or obtaining counts per area of some variable of interest (e.g. reported crimes or playgrounds), many of which are outlined in the accompanying practical activities.

Other common operations take place entirely within the GIS environment. These methods together are often referred to as spatial analysis (or sometimes geoprocessing) and they involve more complicated tools or sets of tools, although the finished product might very well be an intermediate step in creating information to be used in a traditional statistical package. Descriptive spatial statistics, which are used to locate ‘hot spots’ or density measures, which take a set of sample points as input and generate a surface as output are examples of spatial analysis: so are procedures that find potential locations for new businesses or public infrastructure. A researcher hoping to expand access to urban community gardens might use GIS to identify areas of the city without existing gardens (or without sufficient gardening space within a given distance). If she/he then seeks to create new gardens to increase access, though, she/he will need to find locations that meet certain criteria: no existing gardens; available lots or parcels with correct soil and areal characteristics; proximity to public transportation; and zoning that allows for that type of usage. The GIS, with its ability to query both spatial and non-spatial attributes of the data, can easily return a set of potential locations for new gardens. We shall explore GIS and spatial analysis in more detail in Chapter 2.

Across the social sciences, much GIS research leverages insight provided by just a few key spatial concepts. The list of concepts provided below is not intended to be exhaustive, but rather to illustrate a few ways in which a GIS can be used to generate spatial information:

▪ Distance is perhaps the most common spatial characteristic a GIS is prompted to elicit from data. This is partly because the strength of the relationship between a pair of objects is hypothesised to decrease or attenuate as distance increases. This expectation is captured in Tobler’s First Law of Geography (Tobler, 1970), which states that, ‘Everything is related to everything else, but near things are more related than distant things’. Thus research questions across the social sciences – from effects of pollution on pre-term births to disproportionate impacts of hurricanes on sub-populations – carry the weight of Tobler’s Law. Distance is also important because it often serves as a proxy for cost or time. While we might not always observe how much it costs an individual to get from Point A to Point B, if we know how far apart these two points are, we can make an educated guess at cost.

When measuring distance, we distinguish between so-called Manhattan distance and straight-line, ‘Euclidian’ or ‘as the crow flies’ distance. Manhattan distance can be thought of as the actual distance covered when traversing a street network. Although straight-line distance is substantially easier to calculate in a GIS, it does not always give an accurate sense of the true distance or cost of getting from one place to another. On the other hand, some variables, such as air pollution, are better captured with a straight-line distance. Thankfully, a GIS is comfortable with both types of calculation.

▪ Density will already be familiar to many. It is the statistic used to normalise the population of a place by its area. Density, or the count of units found inside some larger area, can act as a proxy for choice or can be used to generate per capita statistics. Standard population density requires no GIS, as counts of people are often tabulated by administrative area as a given. Other times, however, the determination of density requires the marriage of areal, or polygon data, with other types of data: roads or parks or schools, for example.

▪ Proximity is similar to distance but can also combine elements of density discussed above. We might capture proximity via distance but we might also seek to identify the name of the closest facility of some kind. In that case, the distance is less relevant; we simply want the unit for which distance is minimised. On other occasions we might want to know how many facilities or similar fall within a given distance. If we know that people are generally unwilling to walk more than a mile to shop, for example, we might use a GIS to find all shops that lie within a mile of some location.

▪ Accessibility captures a more complex relationship between pairs of objects and in general seeks to answer questions about how far away the closest object is, how many are within a particular distance or how difficult it is to reach the object (this latter could be captured with distance but also with the number of transportation modes required). Accessibility is a trickier concept to handle, though, as it is by nature both spatial and aspatial. If one can conceptualise the spatial component of accessibility, whether density-or distance-based, the GIS can deliver those measurements easily. What the GIS cannot do, though, is contribute an estimate of non-spatial aspects of accessibility: access to information about availability of services driven by opening hours for instance, or willingness to use existing services.

▪ Coverage is complementary to accessibility in the sense that accessibility focuses on the experience of the entity needing access while the other, coverage, can be viewed as the area or population within reach of a particular place. So, while accessibility might measure how many doctors are located within a given neighbourhood or within some distance of the neighbourhood, coverage assesses what share of people or the characteristics of those individuals are within a certain distance of a particular clinic or hospital. Especially for public services and facilities, such as libraries or hospitals, the goal is to ensure that coverage is equitable, related to ‘need’ and within acceptable distance or accessibility thresholds. Again, once the spatial logic of coverage has been defined in a research project, a GIS can make quick work of the analysis.

▪ Colocation is another way of thinking of the overlay illustrations presented above. Although like density it involves the combination of at least two layers, it does not attempt to provide a count or frequency measure for one variable’s occurrence within the other. Rather, colocation seeks to generate new information that is the combination of both layers. Where are the places where both x and y occur? Or, in a given place, do we find both x and y? Colocation is a feature of many types of spatial analysis and is often employed in combination with other types of tools.

Using a combination of these concepts, a GIS can help answer the following types of questions:

▪ How big or long is it? That is, what is its area or the distance of its length?

To get from spatially oriented research question to GIS implementation requires an understanding of how space is conceptualised. As with all quantitative research, a jump must be made from real world to abstract world. Of course, we would like to understand how some phenomenon operates in the real world, but the models we develop must somehow be simplified, lest the model itself become cumbersome and weighed down by our intrinsic inability to put the entire world into a computer. Just as variables in data sets stand in for true characteristics of groups or objects, their location in space must also be somehow abstracted. This abstraction carries with it certain considerations. First, space is considered to be either continuous or discrete. Which it will be depends on some combination of the study topic, how interactions are hypothesised to occur and the type of data available. Continuous space treats the study area as just that: continuous. Every location in the area will have a value and it is not possible to have an absence of value (zero being also a value, of course). Examples of phenomena that operate most logically in continuous space are precipitation and temperature. It is not possible to be somewhere on the surface of the Earth and not have a temperature reading. Discrete space makes more sense if we are locating objects in space. Schools or countries or rivers typically exist in discrete space (i.e. they are not ubiquitous across space). We do not require a data set that registers the presence of a school, yes or no, for every location in an area. Rather, we simply want to record the locations of the objects where they occur and perhaps allow for the possibility that additional future objects might someday also be included.

Whether discrete or continuous, space is also partitioned. This subdivision of space is referred to as spatial scale and it plays an enormous role in how research questions are developed and what sorts of data are required. For example, questions related to the amount of green space in a city can be asked at multiple spatial scales, employing discrete or continuous data. Even if green space is represented in continuous space, rather than assigning a green space value to each parcel or neighbourhood, the scale at which that information is captured will impact the types of questions it can be used to answer. If the purpose is to compare the amount of grass in people’s gardens rather than across a set of cities, the spatial scale will need to reflect this difference. Figure 1.3 shows the distribution of tree canopy, in 30 by 30 metre pixels that measure the percentage of the area covered by trees. This scale of measurement for tree canopy is clearly adequate for even sub-neighbourhood-level analysis: parts of some neighbourhoods are much greener than others. A comparison of front and back garden tree canopy, however, would not be possible: a 30-metre square pixel is likely to have averaged out any variation occurring at that scale.

Similarly, the appropriate spatial scale of roads or cities, for instance, will depend on the type of questions that can be answered. The underlying data about the cities could be the same, but whether the spatial extent of the city is conceptualised as a point in space (appropriate for calculating distances or flows between cities) or an area (invaluable if the end goal is to measure the impact a change in the city has on neighbouring suburbs) will, in the end, dictate the sorts of research that can be accomplished. The best advice, often repeated in GIS and geography, is that the data used should match the hypothesised spatial process at hand.

Hand in hand with considerations of spatial scale or resolution are issues of data accuracy and precision. Accuracy, which refers to the correctness of the data, and precision, which captures how finely measured information is, are important for all sorts of quantitative data. In the context of a GIS, they become important because both concepts relate to spatial characteristics as well as data characteristics. Thus, locations for houses, say, might be accurate to within a few metres or several hundreds of metres. The location of each house, whether accurate or not, might be precise to the tenth of a metre or more. Although in general the preference is, of course, for better data, the extent to which such accuracy matters depends on the research question and the type of analysis. Small amounts of error in accuracy can shift the count of numbers of doctors or food stores in a neighbourhood. Those working in emergency planning might have a much lower tolerance for housing units that are not very accurately or precisely located. In other cases, there is a great deal more flexibility in how accurate the data need to be. The important takeaway message is that one should be aware of the quality of the spatial data used in a project and that this quality should be suited to the purpose for which it will be employed.

Spatial abstraction of reality involves both absolute and relative location – not only where an object is (e.g. its x, y location) but how its location is related to the locations of other objects. For example, for a set of city streets we need to not only locate each street in space but also include the ‘real life details’ an actual street network possesses: which streets intersect and which are overpasses? Or if we are talking about neighbourhoods within the city, and these neighbourhoods are presumed to cover the entire city, we not only want to specify the boundaries of each area, but also that boundaries are shared; that is, it should not be possible to step out of a neighbourhood and not immediately find oneself in the adjacent area. And if we layer our streets and neighbourhoods, we hope that, if a street forms the edge of a neighbourhood, then border and street are coincident in our conceptualisation of the city space. These relationships across objects are what is referred to as topology in a GIS setting. It is unusual for an entry level GIS user to have to work with or adjust topology. However, when issues come up with connectivity or adjacency, faulty topology is often the culprit.

The spatial concepts described above are important first considerations when embarking on work with a GIS. On the whole, the goal is to abstract space in such a way that interactions, connections and locations are represented in ways that capture whatever elements of reality are most important for the type of research being conducted. Two helpful guidelines to keep in mind are those of generalisation and parsimony. Highly accurate data at a fine spatial scale might appear at first glance to be the gold standard of data, but this information will often be difficult to come by, expensive and perhaps more complicated to work with than necessary. Although we want a reasonable abstraction of reality, we do not require a surfeit of information: this is parsimony. Generalisation reflects the idea that although objects have a true geographical footprint in terms of location, area and shape, we do not usually require a perfect representation of the object. All of these aspects of spatial data and space are relevant when it comes to the actual data used in a GIS, as discussed below.

Depending whether our spatial information is continuous or discrete, the GIS will store and handle the data differently. The way information is conceptualised and stored in a GIS is called the spatial data model. The average user will engage with the spatial data model concept at the level of file formats and the types of analysis that are conducted. The two most common spatial data models are the vector and the raster data models. Both have distinct characteristics, along with strengths and weaknesses.

The vector model treats space as discrete, with objects – such as streets or cities – located within space (Figure 1.4a). In the vector model, all of reality is collapsed into points, lines or polygons, and each of these is generated from solitary points or collections of connected points, known as nodes and vertices. Figure 1.5 shows a map of the East Side of Providence, Rhode Island. Information has been captured with a map image; to extract useful information from the map, all features of interest – parks, streets or schools – would need to be translated into points, lines or polygons. Most file formats in current use keep track of the x, y locations of nodes and vertices and the type of geometry of the layer, so whether a collection of connected line segments form a longer line or a closed polygon, in ways that are not immediately visible to the average user. We choose the elements of reality most germane to our research and the spatial layers are then organised together, with the shared underlying location, within the GIS. As discussed above, spatial scale and the research questions being asked will determine whether, for example, cities are best treated as points – with no area – or polygons. Each layer will contain only points or lines or polygons.

Each layer, or slice of reality, is accompanied by a data table, which contains information about the layer, including a unique ID and the type of feature (Figure 1.6). This is the information used to create a map or to conduct analysis. In the vector model, each element of geography is a unit of observation; some file formats will handle multipart units differently, either recognising that a region is comprised of, for example, several islands in one unit or treating each shape as a separate observation. If cities are treated as points, what is visible on the screen is simply an array of dots in space. The data table will contain a row for each observation, or city in this case, and information about that place. Figure 1.6 shows how features and their attribute tables are connected: querying features results in observations selected in both the map and the table. Subsequent analysis with these layers might work with the spatial location of objects, either with regard to other features in the same layer or different layers, but could also involve analysis of the variables in the data, or attribute, table – and usually a combination of both. The linked practical for this chapter uses vector data and explores the link between spatial and attribute data.

Each data model has its strengths and certain types of analysis require a given data type as input. Figure 1.7 provides an example of vector and raster data, the former for administrative characteristics of Rhode Island and the latter for population density. Either type of information could be conceptualised as either raster or vector. We could imagine a raster that, for a given cell size, notes the presence of ‘road’ or ‘no road’. This is virtually nonsensical. Population density could be shown for administrative areas. Indeed this is often the case. However, such visualisations will miss that density does not always follow administrative borders and is characterised by clustering and variation in values.

For data to be spatial, they must contain locational information. Someone, somewhere, had a way of attaching location to the entities for which data were collected. The good news for novice users is that, in many cases, but not all, data in a spatial format will already be georeferenced and the properties of the data will indicate how location is defined. In a few cases – spreadsheets containing latitude and longitude coordinates, for example – the researcher will need to know the spatial properties of the data in order to import them into a GIS. There are two aspects of location that are important in a GIS: coordinate system and projection. An accurate and appealing map, to say nothing of reliable analytical results, requires an understanding of both.

Information is located on the surface of the Earth using a coordinate system. Key words here are ‘location’ and ‘surface of the Earth’. Coordinate systems are used to locate objects somewhere on the round surface of the sphere. The location portion of the problem is handled with an x, y location, usually latitude and longitude, which uniquely identifies that point – there is only one place on the Earth where that intersection of coordinates occurs. The subdivision of the world by latitude and longitude, for example, breaks the globe into sections from North to South called lines of latitude or parallels. Latitude is measured in terms of the degrees north and south of the equator, from 0 at the equator to 90 at the poles. Lines of latitude are parallel slices of the Earth; the distance between the lines is constant. Lines of longitude, also called meridians, are more like slices of an orange: widest in the middle (at the equator) and coming together at the poles (Figure 1.8a). Longitude is measured from East to West, relative to the Prime Meridian, which is 0 degrees and passes through Greenwich, England. The opposite meridian, at 180 degrees, is the theoretical international date line (in practice, national governments around the world will adjust local time to match local political, social and economic needs). Both latitude and longitude are measured in terms of degrees, minutes and seconds, with 60 minutes to a degree and 60 seconds to a minute. This allows for a very good location of points on the surface of the Earth.

The surface of the Earth is a bit trickier to deal with, however, as the shape of the Earth itself is estimated. It is definitely round, but it is not a perfect sphere. Indeed, it is more like a giant beach ball that has been sat on, with the circumference around the equator longer than that going through the poles. The shape of the Earth is referred to as an oblate spheroid. Measurements of the Earth’s shape are now quite decent, but as various estimates have dominated over time and many estimates tend to be more reliable for particular parts of the globe, the shape of the Earth – or the datum – used to locate x, y coordinates is not consistent. Latitude and longitude points in the United States are often collected using the North American Datum of 1983, or NAD 83. Other sets of coordinates use the World Geodetic System 1984, or WGS 1984. You will encounter both during the accompanying practicals.

In order to map geographical information or conduct analysis with it, data are projected. Projection is the process of going from information on a round sphere to information on a flat surface, whether a page or a computer screen. Spatial data are often not projected and must be before they can be used for research. This is a common task, though, and a GIS will either project the data on the fly, not changing the nature of the original information but only displaying it differently, or can create new versions of the data that are projected. To get from round to flat involves a fair amount of mathematics and, if you can imagine flattening an orange or a beach ball, some necessary distortion; it is impossible to go from round to flat without some loss of geographical information. Data are translated from round location to flat location by projecting the information onto a flat surface, either a cylinder, a cone or a plane (see Figure 1.8). The cylinder or cone can then be unrolled and the information is there, on a flat surface.

If one imagines this process of ‘projection’ it is easy to see how some locational information must be lost or distorted. A planar projection offers perfect one-to-one correspondence at the point where the plane touches the surface of the sphere, but information becomes more distorted away from that point of contact. Every projection distorts either shape, area, distance or direction. Especially for larger areas, there is no such thing as a perfect projection, only a good projection for the type of analysis at hand. For example, if the goal is to estimate some measure of density, a priority is an area-preserving, or equal area or equivalent, projection. Other types of projections are conformal, or shape-preserving.

In an ideal world, one searches for GIS data using the internet or a database and finds exactly what is needed immediately. Using keywords such as ‘GIS data’ or ‘shapefile’ (the most common type of vector GIS data) along with other search terms can often isolate spatial data resources. Depending on the scale of analysis and the study site, a great deal of baseline GIS information is available to the public for free. Many larger cities, including London, Chicago, Washington, DC, and San Francisco, have data portals where both spatial and non-spatial information can be accessed. Some countries, such as the United States, make a great deal of data available, but across a variety of government agencies. All US states have websites called ‘GIS Clearinghouses’ where spatial data for the state can be accessed.

Finding required spatial data in a GIS-ready format does occasionally happen. More often, though, intermediate steps are required in order to be able to work with data in a GIS environment. A few of the more common strategies are covered briefly below, including geocoding, tabular joins, importing x, y coordinates, and georeferencing. Geocoding and tabular joins will be covered in deeper detail in Chapter 2. Note that these processes incorporate elements of the GIS background covered above: in particular spatial data models and coordinate systems.

If data include an address (especially with ZIP code/postcode), place name or even latitude/longitude coordinates, this information – spatial in spirit if not in file format – can be used to import a data file into a GIS. The process of locating points in space using an address is referred to as geocoding. Geocoding locates points in space, and creates new spatial data by comparing a spreadsheet with address information to a spatial reference file with street information and address ranges. This procedure is similar to the way in which internet mapping applications locate an address on a map. For a GIS to successfully geocode addresses, the reference file must be of good quality, complete and up-to-date. In practice this means that geocoding is easier in places that have collected, and made publicly available, good street data.

Where geocoding requires access to additional data, in the form of the reference layer, no extra spatial data is required for a GIS to locate x, y locations in space. That is, if a data file contains latitude and longitude information for the spatial units, the GIS can easily locate these in space. Locational accuracy will depend on the accuracy with which data were collected (some handheld GPS units are more accurate than others) but will also depend on the researcher’s ability to identify the underlying coordinate system that was used when the points were collected. Once points have been located in a GIS, locations can be compared to spatial data for which locations are known, to make sure the results are satisfactory.

Other times spatial data are easily found, but they lack the range of variables required for analysis. This is a frequent occurrence when working with administrative or public infrastructure data, such as schools or counties. In many cities in the US, for instance, layers exist that show the locations of primary schools. These data are in GIS format and with a few clicks, one can visualise the entire set of schools for an area. The files do not, however, generally contain much in the way of information about the schools, such as age of building, number of pupils or their characteristics. To bring this sort of additional information into the GIS, one solution is to merge, or join, the attribute table of the spatial data with an external table of data for the same spatial units. To do this, both tables of information must have a common variable that allows the tables to be matched exactly. This common variable must be unique to each observation and its format and content must be identical in both tables. Suppose the goal were a map of EU countries by average income. A layer or shapefile with country locations might be easy to come by but would not contain any information about the countries, just their shape on a map. A separate table with interesting information for each country can then be tied to the attribute table by country name. However, if one table refers to Spain and the other to España, the computer will not recognise the match. For this reason, most administrative data in most countries have numerical codes that are used to uniquely identify areas. These ease the merging of tables considerably. Once the tables are merged in the GIS, variables can be mapped and subsequent analysis completed.

Increase in demand for GIS-compatible data has led to wider availability of spatial data for many parts of the world and for many topics. Often, however, researchers are embarking on projects for which data do not exist. This could be because little or no data have been collected for a study site or because one wishes to make use of historical data, or for some other reason. One strategy is to conduct fieldwork and collect the data oneself. Another is to make use of existing cartographic projects. Researchers, civil servants, explorers and private individuals have been creating maps for centuries. The enormous amount of information contained in printed maps makes them a good resource for information, but one that requires extracting the relevant information from a paper or digital product. For recent map products, it is often worth the time to contact the author to check whether underlying GIS data might be available to be shared. In other cases, the map will be georeferenced. Georeferencing is the process of telling the GIS where locations on the map are in the real world. If not already in digital format, maps are scanned and then added to the GIS. The scanned image of the map, which is simply a picture, is then tagged at several locations to a basemap for which real-world locations are known. The connections between digital map and known locations help to ‘line up’ the map and place it where it should be. The result is mapped information that has been tied to its actual location in the world. It is, however, still only a picture. The next step is to use the scanned image as a base layer along with other data or to manually create new layers by tracing the information on the map, similar to what is seen on the left of Figure 1.5. Digitising features from a georeferenced map is time-consuming but the result is new spatial information that was not previously accessible. You will undertake some basic digitisation in the linked practical accompanying Chapter 12.

The information presented in this chapter is fundamental but might seem a bit abstract. The accompanying practical should help you to begin to understand how basic spatial concepts, data models and even projections are important building blocks for any research project employing a GIS.

Below we have summarised some key ideas that might help in the development of GIS projects:

1 Identify your research question and how it is ‘spatial’. Review existing research in your field that uses a GIS or spatial analysis. This will help give you a better sense of how GIS can be useful to you.

2 Use the basic spatial concepts discussed above to frame your questions as this will help when it comes to operationalising the analysis in a GIS setting.

3 What are your data requirements? This means identifying the spatial units you need information for, as well as their characteristics.

4 Do your data already exist in a GIS-ready format? If not, consider how you will get your data into the GIS.

5 Identify the best projection for your location and spatial scale of analysis and make sure all data are in this projection.

6 Determine what sorts of analysis will be needed to answer your questions. The chapters and practicals that follow will help with that.

The introductory practical (Practical A: Introduction to ArcGIS and spatial data) assumes no prior hands-on experience with a GIS and walks you through the process to launch ArcGIS Desktop, one of the most popular and versatile proprietary GIS software packages. Using exemplar data sets related to transport provision in the US city of Chicago, you will gain familiarity with loading and handling basic vector data sets.

Iliffe, J., & Lott, R. (2008) Datums and Map Projections: For Remote Sensing, GIS and Surveying (2nd edition), Whittles Publishing, Caithness, Scotland. Basic information about projections and coordinate systems.

Longley, P. A., Goodchild, M. F., Maguire, D. J., & Rhind, D. W. (2015) Geographic Information System and Science, Wiley, Chichester. Introductory information regarding GIS (less on applications in the social sciences, but more nuts and bolts of a GIS).

Snow, J. (1854) On the Mode of Communication of Cholera, C.F. Cheffins, London (2nd edition 1855, John Churchill, London).

Tobler, W. (1970) A computer movie simulating urban growth in the Detroit region. Economic Geography, 46(2), 234–240.