You can say it, you can prove it, you can tabulate it, but it is only when you show it that it hits home.
(Dorling, 2007a: 13)
One of the most powerful and creative aspects of GIS is map making and visualisation. We have already given a flavour of GIS capability in the discussion of vector and raster data models in Chapter 1 and of the examples of the outputs of spatial analysis in Chapter 2. In particular, we have already presented examples of one of the most common mapping approaches, the so-called ‘choropleth’ map, where areas are shaded or patterned in proportion to the measurement of a variable being displayed on the map. Most people are familiar with these types of maps as they are often used in media reports to depict the geographical distribution of socio-economic data.1
The creation of thematic maps involves the use of suitable contrasting symbols to portray geographic differences and is underpinned by key principles and a long tradition of cartographic theory and practice (e.g. Bertin, 2011; Brewer, 2005; Dent et al., 2008; Kraak and Ormeling, 2010; MacEachren, 2004; Monmonier, 1996; Perkins, 2003, 2004; Slocum et al., 2008). Table 3.1 summarises what can be described as key elements characterising good mapping practice.
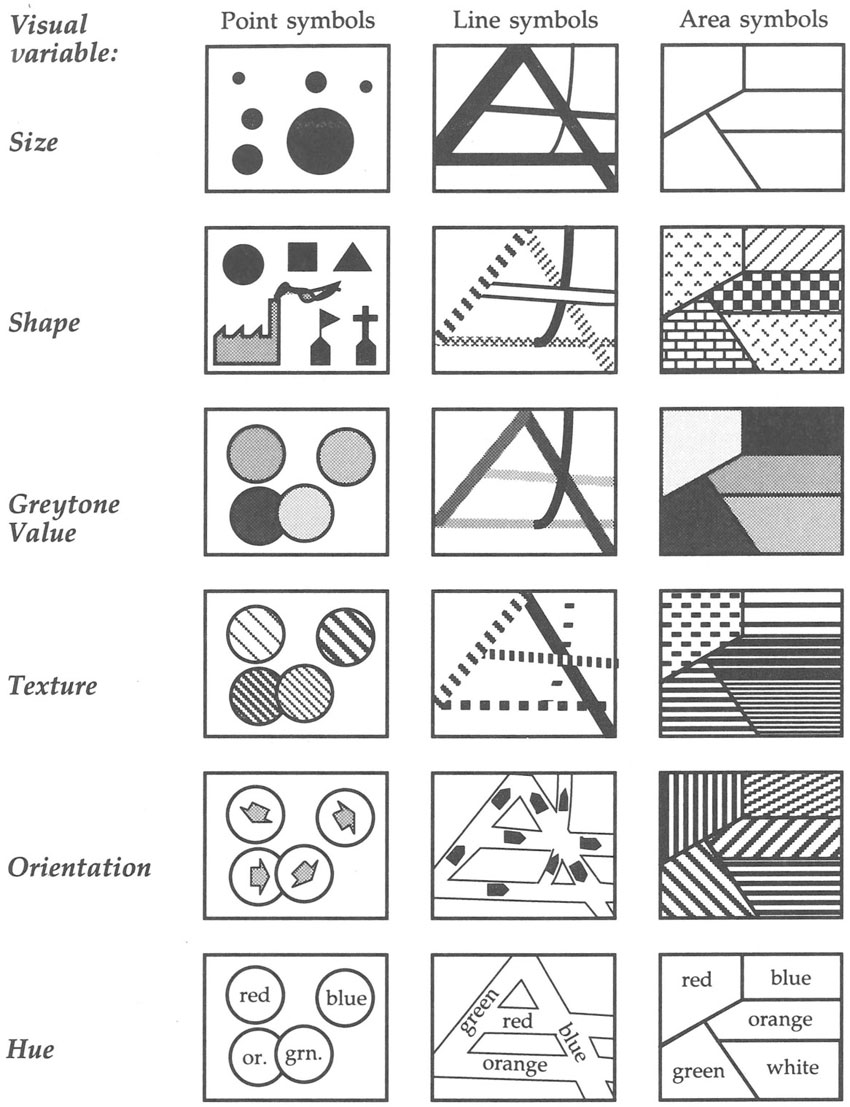
Other issues that need to be considered when designing maps include the levels of measurement of the variables to be mapped, alternative ways of classifying data, colouring schemes, the amount and type of information to display on the map and issues of layout design. In addition key points to be considered are the overall positioning of map elements, the ways they can be perceived by the human eye (and map readers of different backgrounds) and the choice of symbols to represent them. To that end, Jacques Bertin (1967) identified seven main categories of visual variables: position, size, shape, value, colour, orientation and texture (wiki.gis.com, 2016a, 2016b). Bertin’s work has been the basis for further modification and discussion of cartographic principles. For example, Monmonier’s classic and influential work (1996) illustrates how map symbols can differ in size, shape, greytone value, texture, orientation and hue in the form of the six principal visual variables depicted in Figure 3.1. Monmonier suggests that each of these visual variables is important for portraying one kind of geographic difference. In particular, shape, texture and hues are most effective in showing qualitative differences, for example among land uses, dominant religion or most common lifestyle group type in an area. For quantitative differences, size is more suited to showing variation in amount or count, such as the number of television or internet users by market area, or numbers of burglaries by neighbourhood. Greytone value is preferred for displaying difference in rate or intensity. Symbols varying in orientation are most appropriate for representing directional occurrences such as wind direction, migration, travel-to-work or travel-to-shop flows.
Table 3.1 Designing a ‘good map’
Key mapping principles – what makes a good map |
|
Clarity |
The map focuses on its purpose with as little distraction as possible. |
Order |
The elements of the map are organised to guide the map reader to accomplish the intended purpose. |
Balance |
Elements are distributed to give the map a feeling of ‘evenness’. |
Contrast |
Important elements stand out clearly against less important ones. |
Unity |
The various elements come together to make the map appear as a single coherent whole. |
Harmony |
The elements all seem to fit together naturally. |
Source: After wiki.gis.com (2016a, 2016b)
Figure 3.1 The six principal visual variables
Source: After Monmonier (1996)
In this chapter (and accompanying practicals) we consider all these issues in a social science context. We show how thematic maps can be created and we provide an overview and examples of the most common types of mapping used in the social sciences. We begin with a discussion of the different types of socioeconomic and demographic variables and data (known as ‘attribute data’ or ‘associated tabular data’) that can be joined with geographical data. We also consider the latest trends and technologies, including online mapping. Finally, we consider criticisms of these commonly used conventional ways of mapping in the social sciences and we present a case for alternative human-scaled visualisations and cartograms which are increasingly used instead of conventional maps.
Geographic and associated tabular/attribute data
As discussed in Chapter 1 there are two main data types, vector and raster. The choice of the appropriate mapping approach depends on the type of geographical data being used as well as the audience at which the map is aimed. In any case, the first step in building a data set that can be used for mapping is to combine geographical data sets (either raster or vector) with an associated attribute data table containing descriptive information about geographic objects and features, including qualitative and quantitative variables that can be mapped.
For example, a polygon vector layer of administrative electoral wards of a city (such as the one discussed in the previous chapter) or census tracts could be combined with an associated attribute table containing information on the total population in each area, as well as the population by age, sex, economic activity (e.g. whether in full employment, unemployed), rural/urban classification, etc. Similarly, a point vector data layer of supermarkets, other retail outlets or businesses could be joined with an attribute data table containing information on the size of the establishment (e.g. floor-space in squared feet), number of employees, number of parking spaces, total turnover, revenues, etc.; a line vector layer of the road network of a city could be joined to a data table containing information on the road type, capacity, condition and estimated travel time.
In the case of the raster model data, as discussed in Chapter 1, each pixel is assigned one value which might be a categorical or continuous variable. In the social sciences it is much more meaningful and efficient in terms of computational and storage requirements to almost always use vector data for analysis and mapping. Raster data such as satellite imagery are typically used as a background layer to thematic maps of socio-economic data. They can also be used when there is a need to analyse socio-economic data in relation to environmental indicators for which continuous data are available at small-area level (e.g. exploring the relationship between asthma cases, populations at risk and atmospheric pollution). There are also cases when socio-economic or demographic data can be available at small-area grid level, as is the case with the ‘Gridded Population of the World project’ (Center for International Earth Science Information Network, 2015) which provides very small-area grid level estimates of population for the world using data from censuses of housing and population (we show how this data set can be used for mapping and cartogram creation in the last section of this chapter).
Before we describe how attribute data can be mapped using GIS it is important to point out that the choice of a mapping approach depends on the type and measurement scale of each attribute for a spatial entity that is being mapped (as is also the case with statistical analysis). Attribute data are typically distinguished between nominal, ordinal, interval and ratio, following the original work of the American psychologist Stanley Smith Stevens which was published in the journal Science back in 1946 (Stevens, 1946). Nominal attributes have no quantitative value and are typically used to label spatial entities. For example, these can be the names of countries, regions or administrative units within a city (for polygon data), the name of a road (for line data) or the names of the chain to which a supermarket branch belongs (for point data). When the value of the variable being mapped can be ordered, but we do not know the exact differences between the values, then the type of attribute is known as ordinal. For example, regions or cities can be ranked in terms of their perceived quality of life and the area ranked number 1 is considered to be a better place to live compared to that ranked number 2, but we do not know the exact quantitative difference. Attributes are interval when we know not only the order but also the exact difference between the values, but when there is no meaningful value of zero. For example, temperature in Celsius or Fahrenheit is an interval attribute. The distance between 25 and 30 Celsius is the same as that between 30 and 35. However, in interval measurement ratios are not meaningful: we cannot say that 40 degrees Celsius is twice as much as 20. And the value of zero is arbitrary and artificial (zero temperature does not mean that there is no temperature). Attributes are ratio when differences between values make sense and at the same time there is a meaningful value of zero. Total population, gross national product, total government consumption and total grocery floor-space are examples of ratio variables in the social sciences.
These levels of measurement are now well established in the social sciences. However, it should be noted that there have been some concerns with regard to their suitability for use in mapping and cartography (Chrisman, 1998; Forrest, 1999). For example, directional data are numerical but they cannot be ordered in a meaningful sense, due to their cyclic nature. For instance, 355 degrees is not greater or less than 5 degrees: it is just a different direction. Also, with regard to the distinction between ratio and interval scale described above, when it comes to thematic mapping (discussed below), there is not much consensus on how shading intervals might be chosen. Although the levels of measurement described above are widely adopted in geography and cartography, it is important for users of GIS in the social sciences to be aware of these issues. Chrisman (1998) presents a very interesting and comprehensive review of scales of measurement in cartography, highlighting their limitations and making a case for a broader and more suitable (for cartographic use) measurement framework.
In Chapter 2 we provided some examples of data resources for geographic and attribute data (typically socio-economic and demographic data). We now draw on some of these resources to provide examples of attribute data that can be joined with geographic data to be mapped and analysed (it is also possible for such data to be the output of original collection and processing by the GIS user). Table 3.2 shows an example of attribute data extracted for administrative areas in the city of Sheffield in the UK (similar to the data used in the previous chapter) containing information on total population, their mean age and the unemployment rate.
All data layers in a map have a field that can be used as a key in order to join data with associated attribute information (as shown in the practical exercises accompanying this chapter). Similar combinations of geographic and attribute data are possible for point and line data. Once GIS layer and associated attribute data are joined together it is possible to create thematic maps and other visual representations of the characteristics of geographic features. The remainder of this chapter discusses some of these options. We begin with the simplest form of mapping, reference maps.
Mapping location: reference maps
The simplest form of mapping that can be carried out using GIS is that of reference maps where the emphasis is on using suitable graphics to show the location of geographical entities. Reference maps include road maps, tourist maps and guidebooks. In the social sciences reference maps highlight information and the name of geographical features that are of relevance to a social science problem (e.g. names of countries, region, location and name of grocery outlets, schools, hospitals, etc.). In addition, the decision on what and how to display depends on the audience and purpose of the map. For example, and with regard to the social science problems discussed in the previous chapters, a suitable reference map in relation to the likely demand of retail products would show the location of grocery stores, as well as the road network in a city and information on public transport (e.g. bus stops, railway stations). Creating reference maps in GIS is fairly straightforward and we have already used some illustrative examples in the previous chapters (e.g. the map shown in Figure 2.8, showing the location of grocery stores in the city of Sheffield). The emphasis in these maps is on the geographical pattern and labelling of the spatial entities being mapped and on the symbols being used to illustrate them. Proprietary GIS software has excellent capabilities to create high-quality reference maps. A simple example is shown in Figure 3.2.
Table 3.2 Attribute data for a selection of Sheffield, UK, electoral wards
Ward name |
Population |
Mean age |
Unemployment rate (%) |
Arbourthorne |
19,133 |
38.9 |
6.9 |
Beauchief and Greenhill |
18,815 |
41.6 |
6.3 |
Beighton |
17,939 |
40.7 |
3.5 |
Birley |
16,943 |
42.0 |
4.9 |
Broomhill |
16,966 |
30.1 |
2.1 |
Burngreave |
27,481 |
32.6 |
9.1 |
Central |
36,412 |
27.0 |
3.8 |
Walkley |
21,793 |
35.9 |
4.2 |
West Ecclesfield |
17,699 |
43.1 |
3.5 |
Woodhouse |
17,450 |
42.2 |
5.0 |
Figure 3.2 A reference map of Golden Gate, California, US, created using ArcGIS
Source: www.arcgis.com/home/webmap/print.html
The decision about what geographical features to map and which symbols to use depends on the purpose of the map and intended map users. GIS software packages have extensive libraries of symbols that can be used in reference maps.
In addition, such maps are increasingly readily available from online resources such as Google Maps and Bing. Figure 3.3 shows such a map generated via Google Maps for central London (generated by searching for ‘groceries’ in Google Maps). This map shows the location of all grocery stores in central London, as well as information on the road network and rail and underground train stations. The map is the product of a combination of different point, line and polygon layers.
Similarly, a suitable reference map in relation to the local council and national government policy discussed in the previous chapter could include information on the location of organisations related to a particular social policy issue. An example of such a reference map is shown in Figure 3.4, which depicts the location of charity organisations supporting the homeless in central London (again using Google Maps).
There is also a rapidly increasing number of reference maps created via crowd-sourced mapping services such as OpenStreetMap and PublicEarth, which are dynamically updated. We make use of OpenStreetMap throughout the accompanying practicals as a base map.
Figure 3.3 A reference map example: grocery stores in central London
Source: www.google.co.uk/maps/search/groceries/@51.5082749,-0.0985554,14.33z
Figure 3.4 A reference map example: charities and shelters in support of the homeless in central London
Source: www.google.co.uk/maps/search/homeless+shelters/@51.5082749,-0.0985554,14z/data=!3m1!4b1
One of the most powerful and attractive aspects of GIS in the social sciences is the ability to visualise geographic features such as those described in the previous section according to a particular socio-economic or political theme of interest, in order to create thematic maps. This involves a combination of geographic layers with associated attribute data such as those discussed in the second section of this chapter (also see accompanying practicals for examples of how such data can be joined with geographic data and mapped). There are many thematic mapping options and the choice depends on the type of layer file (vector or raster; polygon, line or point) and variable type (e.g. nominal or ratio) being mapped. In this section we present examples of the main types of thematic mapping in the social sciences.
Using graduated colours or patterns: choropleth mapping
One of the most common thematic approaches to representing the quantity of variables being mapped for polygon layers is the so-called choropleth map. The word choropleth is derived from the Greek words choros (meaning area or region) and plethos (meaning multitude). The choropleth approach involves the shading or patterning of polygons according to a categorical variable (such as geodemographic classifications) or continuous data such as an interval or ratio variable (e.g. population or income).
A simple approach involves assigning each value its own colour. This is particularly suitable for nominal or categorical data and in cases when there are only a few values. Figure 3.5 presents an example of a categorical variable being mapped for UK census Output Areas in Sheffield (OAs; areas of an average 125 households). In particular, it presents a map of small areas classified on the basis of a combination of census data in order to label them according to the type of neighbourhood and lifestyle; this is a type of analysis of areas known as geodemographic classification (also see Chapter 5 for more details). There are 1,744 OAs in Sheffield and these are coloured in the map according to their geodemographic classification. For instance, the areas labelled as ‘blue collar communities’ (401 in total) are coloured in blue, whereas the areas labelled as ‘countryside’ (19 in total, but including very large sparsely populated areas that dominate the map) are coloured in green. The method used to create this map is based on the ‘unique values, many fields’ approach. There are seven geodemographic classification groups in total but it is possible for many areas to belong to the same group.
Figure 3.5 Choropleth map with nominal/ordinal data: geodemographic classifications
Figure 3.6 shows another example of categorical data, drawing on the Social Atlas of Europe project (europemapper.org) which we will revisit later in this chapter when discussing human cartographic approaches to mapping in the social sciences. This time the value being mapped is the year of association of European countries with the European Union (ranging from membership to candidate and potential candidates). A rainbow scale is used to determine the colour hue for each state according to the year of association with the European Union. The more recent the formal association the nearer to the red end of the spectrum the hue is. In particular, the countries shown here are shaded using a rainbow colour scheme, starting with shades of dark red to demarcate the countries with the most recent association with the European Union and moving through to a shade of violet for the oldest members of the EU.
Figure 3.6 Choropleth map with nominal/ordinal data: social atlas of Europe rainbow
Source: Ballas et al. (2014)
Figure 3.7 Choropleth map with nominal/ordinal data: Worldmapper regions © Worldmapper.org
Source: www.worldmapper.org/region_map.html
The rainbow colouring scheme is increasingly popular for data visualisations in the social sciences, as it is widely considered to have an attractive display. However, in some cases it can introduce visual confusion and obscure details in the data and there might be other issues with some readers. Eddins (2014) summarises the major relevant themes in the literature about the rainbow colour scheme (but this is also of wider relevance to any colouring scheme) and about the general principles of colour in scientific visualisation. It is also relevant to note here that there are a number of online platforms that can be used to create colour schemes for different types of data and map readers such as Colorbrewer (http://colorbrewer2.org/), Typebrewer (www.typebrewer.org/) and Indiemapper (www.indiemapper.io/).
Figure 3.7 is a map of the world using a similar rainbow colouring scheme and produced in the context of the Worldmapper project (www.worldmapper.org) which we revisit later in the discussion of cartograms. All countries are classified into 12 world regions on the basis of development based on the United Nations Human Development Index. The regions were chosen to be geographically contiguous groups of territories that divided the world into roughly symmetrically balanced population groups, with no region containing fewer than one hundred million people. Hence there are 12 colour ranges on the maps and the shade of the colour within each range helps to identify territories and distinguish them from each other within the regions (five shades of each of the 12 regional colours are used to help differentiate territories within regions). The countries are ordered from poorest to richest by the Human Development Index published in 2004. Shades of dark red are used to demarcate the poorest territories, moving through the rainbow scale to a shade of violet for the best-off.
The choropleth approach can also be adopted to map quantitative variables (including continuous variables) such as ratio or interval. If there are relatively few values being mapped then it might be appropriate to adopt a similar approach to that described above and to assign each value a unique colour. However, in most cases with quantitative continuous variables (e.g. income, unemployment rates) there is a very wide range of values to be mapped and it is more appropriate for these to be grouped into classes. Figure 3.8 shows an example of such a map, depicting the geographical distribution of unemployment rates in the city of Sheffield in England. The particular approach adopted here is that of graduated colours, where the values of the variable being mapped are grouped into classes and each class is identified by a particular colour or shade of the same colour. There are a number of options available with regard to the number of classes and the techniques that can be used to create them. The ArcMap software default number of classes for the map shown in Figure 3.8 is five and the default classification scheme is ‘natural breaks’ (also see the graph in Figure 3.8). The latter is underpinned by a statistical technique that aims to create classes based on natural groups in the data distribution of the variable being mapped. In particular, the technique is aimed at minimising variance within classes and maximising the variance between classes.
The choice of classification scheme and number of classes determines which areas will fall into each class and what the map (and geographical patterns of the variable being mapped) will look like. In other words, by changing the number of classes and classification schemes you can create very different maps providing alternative messages that might inform policy-relevant decisions. For instance, the map shown in Figure 3.8 can be used to make decisions regarding the social policy and area-based priorities of local, regional and national government with regard to where the hot spots of unemployment in the city might be. There are three areas with the darkest shade in the map belonging in the top class (7.5%–9.1%). Figure 3.9 shows what happens if the same variable is mapped on the basis of a different classification method. The classification method used here (also see graph in Figure 3.9) aims to assign the same number of data values (or areas) to each class. Comparing Figures 3.8 and 3.9, we can observe that the lower end value of the top class is 6.9% in Figure 3.9 (compared to 7.5% in Figure 3.8) and there are an additional two areas in the top class coloured with the darker shade in Figure 3.9 (five in total, compared to three in Figure 3.8).
Other classification schemes that can be used to divide the geographical areas mapped include the equal interval method (dividing the range of attribute values into equal-sized sub-ranges). It is also possible to manually define the class breaks and intervals. More sophisticated methods include the geometrical interval (creating class breaks based on class intervals that have a geometrical series) and standard deviation (defining breaks on the basis of how much an area’s values vary from the mean of the variable distribution). In any case, it is important to consider the differences in the geographical pattern of the variable being mapped when using alternative classification schemes and number of classes.
Using graduated/proportional symbol classes
Another approach to mapping quantitative variables is to use graduated symbols. Figure 3.10 shows how the geographical distribution of the variable of unemployment rate mapped in the previous choropleth mapping examples can be depicted using graduated symbols. As with the choropleth map example, the values of unemployment rate are grouped into classes and represented by a symbol (in this example a circle). The symbol is then resized in proportion to the magnitude of the variable being mapped. As is the case with the choro-pleth maps discussed above, there are similar issues regarding the classification techniques and number of classes that need to be considered when using the graduated symbol approach. In addition, a potential difficulty with the graduated symbol mapping option is that when there are too many values then differences between symbols can become indistinguishable. Further, the symbols for high value can become too large and obscure other symbols in neighbouring areas.
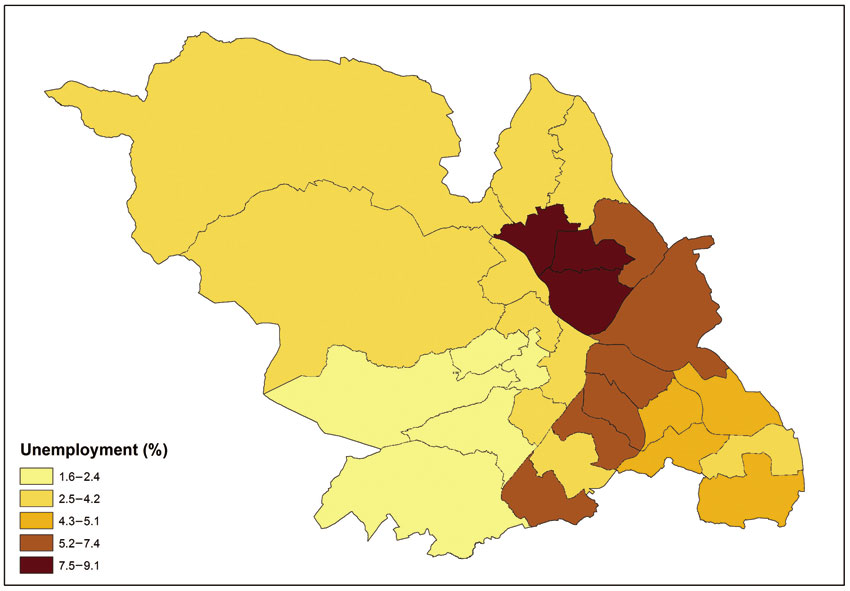
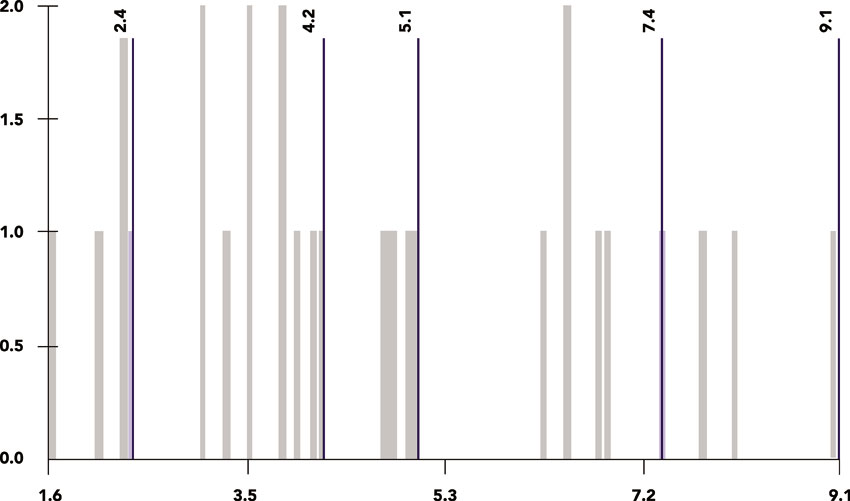
Figure 3 .8 Choropleth map example for unemployment rate in Sheffield, UK, 2011 (natural breaks)
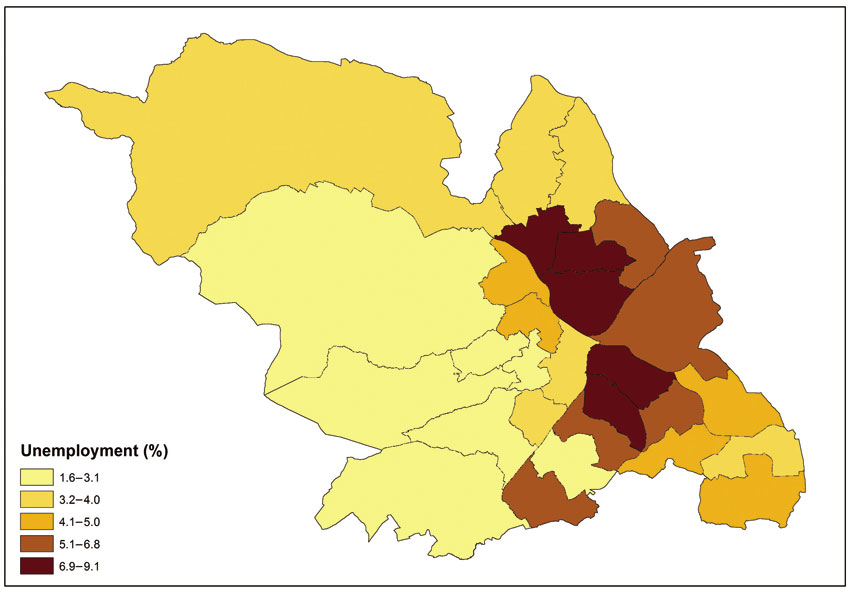
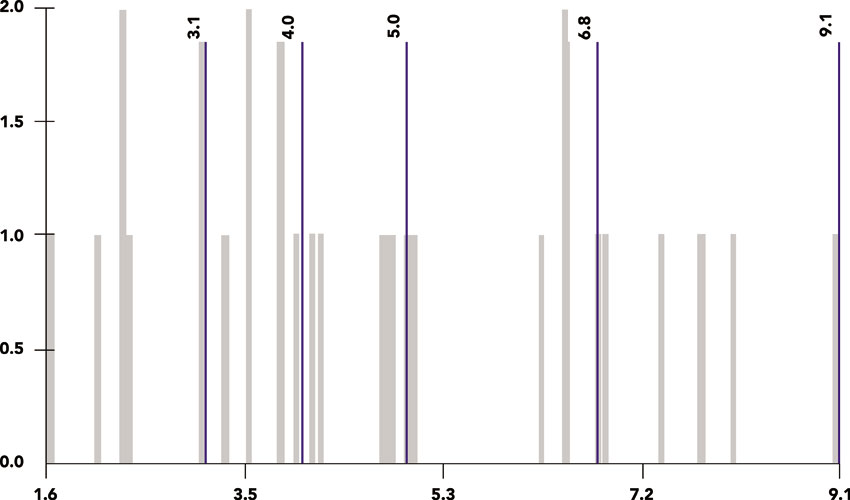
Figure 3.9 Choropleth map example for unemployment rate in Sheffield, UK, 2011 (quantiles)
Figure 3.10 Graduated symbol example: unemployment in Sheffield, UK
Dot density
Another approach to mapping quantities is to use a dot density map. A dot density map can be used to show the amount of an attribute such as total population within an area. Figure 3.11 shows an example using population data for the city of Sheffield for electoral wards within the city.
Each dot represents a specified number of entities or incidents (e.g. number of people, number of burglaries). In the map shown in Figure 3.11 each dot represents 300 people. When creating a dot density map it is necessary to specify how many features each dot represents and how big the dots should be. As is the case with the graduated symbol map, the size of the dots must be carefully specified to ensure that they do not obscure the dots of neighbouring areas. It is also possible to map more than one variable using the dot density approach by using different colours.
Chart-type thematic maps
Another type of thematic mapping involves the use of bar and column charts, stacked bar charts and pie charts. These can be particularly suitable when mapping attributes that are meaningful to compare. For example, a suitable socio-economic variable that can be mapped in this way is occupational classification, which is derived from relevant census variables. Figure 3.12 presents an example of such a map using data on socio-economic occupational grouping obtained from the 2011 UK census of population. Figure 3.12 is a pie chart map, which can be particularly useful for illustrating the distribution of values that add up to a meaningful total. The variables being mapped in Figure 3.12 represent the number of people in each area as a percentage of all working population classified in each of the eight socio-economic occupational groupings. All values add up to 100. Figure 3.13 uses the same data to produce a bar/column chart, while Figure 3.14 shows a stacked bar chart.
Figure 3.11 Dot density map example: population in Sheffield, UK
Figure 3.12 Pie chart map example: occupations in Sheffield, UK
Figure 3.13 Bar chart map example: occupations in Sheffield, UK
Figure 3.14 Stacked bar chart map example: occupations in Sheffield, UK
Figure 3.15 Pie chart (occupations) and choropleth map of unemployment rates in Sheffield, UK
It is also possible to combine chart maps with choropleth maps. For example, Figure 3.15 combines the map shown in Figure 3.12 with the unemployment rate choropleth map shown in Figure 3.8. By combining the two types of maps it is possible to observe geographical patterns and possible associations between variables. For example, as can be seen in Figure 3.15 the three areas with the highest unemployment rates also have relatively high numbers of people in the ‘never worked and long-term unemployed’, ‘routine occupations’ and ‘semi-routine occupations’ social classifications. In contrast, the areas with the lowest unemployment rates have very small numbers of the least well-off social classes and higher percentages of managerial and professional occupations. Such associations and relationships between variables can be quantified and combined into new variables (such as deprivation indexes) that can also be mapped (we will discuss examples of this type of analysis in Chapters 5 and 6).
Mapping point data
We have already presented maps of point data in the previous chapter and in the earlier discussion of reference maps in this chapter. It is possible to add thematic mapping information to such maps. For example, we can revisit the map showing the location of grocery stores in the city of Sheffield that was introduced in the previous chapter. It is possible to add thematic mapping features to this map by using different colour codes to show the chain to which each branch belongs and to also make the size of the point symbol representing each grocery outlet proportional to total floor-space (or other variables such as turnover, number of employees, parking spaces, etc.). Figure 3.16 presents an example of such a map. It is also possible to combine this thematic information with choropleth maps showing the distribution of relevant socio-economic variables such as income or socio-economic classification. For example, it could be argued that the social geography is highly relevant to the potential demand for groceries, with some occupational groups likely to exhibit brand preferences and an overall higher spend. Figure 3.17 combines the groceries point layer with a thematic map of the numbers of managers and professionals by area (as a percentage of the total population).
Figure 3.16 A graduated symbol point map: groceries and floor-space in Sheffield, UK
Figure 3.17 A graduated symbol point map (groceries by floor-space) and choropleth map (distribution of managerial and professional occupations) in Sheffield, UK
Mapping line data
Thematic mapping approaches to line data typically involve displaying line features using different thickness levels and colours to represent different values. Conceptually this approach is similar to the graduated symbol maps presented above. For example, the thickness of roads can vary according to type of road or traffic volume. It is also possible to combine line mapping with choropleth mapping to visualise additional variables and highlight relevant variables. Figure 3.18 shows a mapping example of road data combined with a choropleth map of estimated travel times from different areas in London to the Department of Transport in central London at morning rush hour.
Figure 3.18 A line thematic map example combined with choropleth travel time mapping showing travel time to reach the Department of Transport (SW1) by 9 a.m. using public transport
Mapping flow data
Another type of thematic mapping in the social sciences is that of movement of people, goods and services or money from one place to another. These maps typically use lines to symbolise the flow. The width of the lines can also be drawn in proportion to the size of the flow. In addition, the lines can be colour-coded to visualise further information (e.g. type of goods being transported). Flow maps can be divided into one of three categories (Akella, 2011; Prasad, 2012): radial, network and distributive. Radial maps show the link between one source and many destinations. Network maps show the quantity of the flows in an existing network. Distributive flow maps are typically used to show the distribution of commodities or some other flow that diffuses from origins to multiple destinations (Akella, 2011).
Although most proprietary GIS software packages do not include tools specifically designed to map flows, there are a number of relevant applications and plug-ins. For example, Prasad (2012) presents a flow mapping tool for ArcGIS. Figure 3.19 shows how this tool was used to reproduce a well-known example of a flow map of British coal exports in 1864 by Charles Minard.
Figure 3.19 Mapping flows example: British Coal exports in 1864
Source: https://blogs.esri.com/esri/apl/2012/09/12/generating-distributive-flow-maps-with-arcgis/
Combining different thematic map styles
As we have already seen it is possible to combine different types of mapping approaches to illustrate a wide range of data and their geographical patterns. In this section we present more sophisticated examples of how the spatial distribution of several variables can be mapped simultaneously using a combination of mapping approaches. Figure 3.20 shows a combination of chart map and choropleth mapping, using a bar chart to depict general government balance in European countries as a percentage of their GDP in selected years and choropleth mapping of the countries according to their overall general government gross debt (as a percentage of their GDP).
Cartography and human-scaled geovisualisations
The mapping approaches presented so far in this chapter can be described as conventional. This section draws on a review by Ballas and Dorling (2011) of alternative human-scaled visualisations which includes an argument for human cartograms to be used instead of (or as well as) conventional maps in the social sciences. Most people are used to conventional maps of their regions and countries. Conventional maps appear on television in the weather reports showing geographical regions as they appear from space. However, there have long been arguments for an alternative approach to visualisation that should be used in the social sciences. Conventional maps are very good at showing where oceans lie and rivers run, for example (Ballas and Dorling, 2011). Their projections are calculated to aid navigation by compass or depict the quantity of land under crops. These maps are typically based on area projections such as that of Gerardus Mercator, developed in 1569, which was suitable as an aid for ships to sail across the oceans because it maintains all compass directions as straight lines. As we also discussed in the introductory chapter, all projections inevitably result in a degree of distortion as they transfer the area of the Earth being mapped (or the whole globe) onto a flat surface such as a piece of paper or a display unit such as a computer screen. For instance, the Mercator projection stretches the Earth’s surface to the most extreme of extents and hence introduces considerable visual bias. Areas are drawn in ever expanding proportions depending on how near territory is to the poles and this results in areas such as India appearing much smaller than Greenland (when in reality India has an area more than seven times the size of Greenland). The degree to which such a distortion might be acceptable depends on the intended use of the map. There are a number of alternative projections that correspond to the actual land area size and these are much more suitable for the visualisation and mapping of environmental variables, and for pinpointing the location of physical geographical features of interest, than Mercator’s map ever was (Ballas and Dorling, 2011).
Figure 3.20 A map of government balance and gross debt in Europe
Source: Based on https://tmaps.files.wordpress.com/2010/02/defizit_en.png
However, looking at a city, region or country from space is not the best way to see their human geography. For instance, mapping the distribution of human population on a conventional map means that urban areas with large populations, but small area size, are virtually invisible to the viewer. Conversely, the large rural areas with small populations dominate such a map. When mapping data about people, it is therefore sensible to use a different spatial metaphor, one that reflects population size. Most conventional maps, regardless of the projection method that was adopted to create them, are not designed to show the spatial distributions of humans, although the single spatial distribution of people upon the surface of the globe, at one instance in time, can be shown on them. They cannot illustrate the simplest human geography of population. People are points on the map, clustered into collections of points called homes, into groups of points known as villages, towns or cities. Communities of people are not like fields of crops. The paths through space which they follow are not long or wide rivers of water, and yet, to see anything on maps of people they must be shown as such (Ballas and Dorling, 2011).
In the remainder of this chapter we present alternative ways of mapping data in the social sciences. In particular, we draw on cartographic approaches and arguments that make the case for ‘human cartograms’ to be used for the geovisualisation of data in the social sciences instead of conventional thematic mapping. Such cartograms can be defined as maps in which at least one scalar aspect, such as distance or area, is deliberately distorted to be drawn in proportion to a socio-economic or demographic or any other ‘human’ variable of interest. Human cartograms are similar to conventional maps in that they also involve a degree of visual bias and distortion. However, unlike conventional maps, the distortion introduced by human cartograms is based on a population or social science variable of interest. In particular, the location of boundaries and size of territories of areas is redrawn on the basis of a population variable of interest. In this way the relative values of objects on a map are reflected by the size of the area and this is much easier for the human eye-brain system to assess when compared to trying to translate shades of colour into rates and then to imagine what they imply. Rescaling area to the variation in particular variables is very effective in terms of visual communication and a good example of this is the traditional homunculus used in medical science to portray the human body in terms of the degree of sensitivity: different areas of the skin are rescaled in proportion to the number of nerve endings they contain (also see Dorling, 2007a, 2007b).
Circular cartograms and Universal Data Maps
There are many options and possibilities for creating cartograms and there is a long history in human cartography, both in terms of theoretical debates as well as software development (for recent reviews see Ballas and Dorling, 2011; Hennig, 2013). Figure 3.21 presents the application of a well-used circular cartogram algorithm. This algorithm uses circles to depict electoral wards in Britain. The size of these circles is then drawn in proportion to their total resident population. Further, the circles are colour-coded on the basis of the dominant industry group in the area.
Figure 3.21 A circular (Dorling) cartogram example
Source: www.sasi.group.shef.ac.uk/thesis/small/img023.jpg
Another human cartographic method that is increasingly used in the social sciences is the so-called Universal Data Maps approach. This was originally developed by Durham et al. (2006) to build an online census atlas. This approach is suitable when mapping areas with similar population size (such as parliamentary constituencies in Britain). This approach is similar to the Dorling diagrams discussed above, but in this case all geographical features being mapped have the same size. Each geographical area being mapped is represented by a grid cell (such as a spreadsheet cell) of equal size (see Figure 3.22). Since each geographical unit contains roughly the same population, the cartogram might also be seen as a more ‘democratic’ view of population statistics, effectively according each person the same space on the map (see Dorling, 2006).
This approach was further developed for different spatial units and shapes (using hexagons instead of grid cells) and applied in a wide range of contexts.
Examples of extensive use of this mapping approach include Poverty, Wealth and Place in Britain, 1968 to 2005 (Dorling et al., 2007), The Grim Reaper’s Road Map: An Atlas of Mortality in Britain by Shaw et al. (2008) and People and Places (Dorling and Thomas, 2004).
It is often argued that a disadvantage of these types of cartograms is that they distort the original areas’ real shapes and this affects the degree to which it is familiar and recognisable by a map reader. One of the ways to address this criticism is to present cartograms together with conventional maps and suitable labelling to familiarise the map reader with the cartographic approach to mapping. Figure 3.23 shows a map locator for these cartograms in relation to conventional maps.
Figure 3.22 Change 1971–2001 in percentage of households with access to two or more cars
Source: Durham et al. (2006: 340)
Figure 3.23 A human cartogram map locator example
Source: http://sasi.group.shef.ac.uk/publications/reaper/gr_locator_maps.pdf
Density-equalising cartograms
There are ongoing debates in human geography and cartography regarding the suitability criteria of alternative methods. Overall, the key challenges in human cartography can be summarised as follows (Ballas and Dorling, 2011):
▪ Develop a method that is as simple and easy to understand and implement as possible.
▪ Generate ‘readable’ maps by minimising the distortion of the shape of the geographical areas being mapped, while at the same time preserving accuracy and maintaining topological features.
▪ Determine the cartogram projection uniquely.
▪ Minimise computational speed.
▪ Make the end result independent of the initial projection being used.
▪ Make the end result look aesthetically acceptable.
▪ Have no overlapping regions.
There have been numerous methodological developments aimed at creating cartograms on the basis of automated computer algorithms but there was little success in addressing all the above challenges until the ground-breaking work, in 2004, by two physicists, Mark Newman and Michael Gastner (Gastner and Newman, 2004). Using the diffusion of gas analogy in physics, they developed a cartogram approach that moved the borders of territories with the ‘flow’ of people, until density is equal everywhere. Figure 3.24 illustrates how the method works with a hypothetical example of four areas (Hennig, 2013). The size of the areas (and borders) are changed until the space between the people in each area is the same everywhere (and therefore the population density in all areas is the same). The cartogram is created by ‘diffusing’ the people to give them an even spatial spread of population. As people diffuse, borders are moved with them until all spatial units have equal population density (Ballas and Dorling, 2011; Hennig, 2013; Gastner and Newman, 2004). The people depicted in this cartogram can represent the entire population of the area or other sub-groups such as the unemployed, the elderly, etc. It is also possible, instead of people, to use any other variable (e.g. total income) as long as it adds up to a meaningful total for all areas (in a way this type of cartogram is the geographical equivalent of a pie chart, which also only works if the data used add up to a meaningful total; also see Figure 3.26 and discussion below).
Figure 3.24 An illustration of the Gastner and Newman diffusion-based method for producing density-equalising maps
Source: After Hennig (2013)
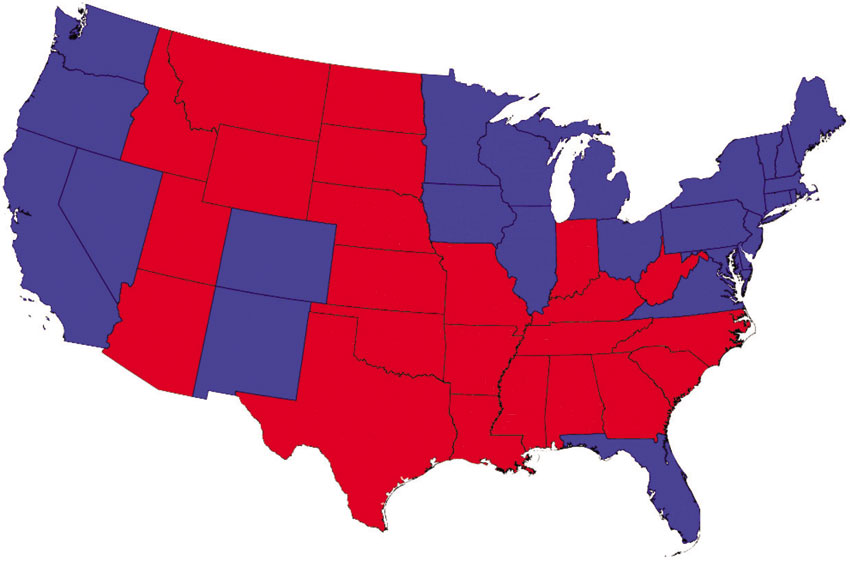
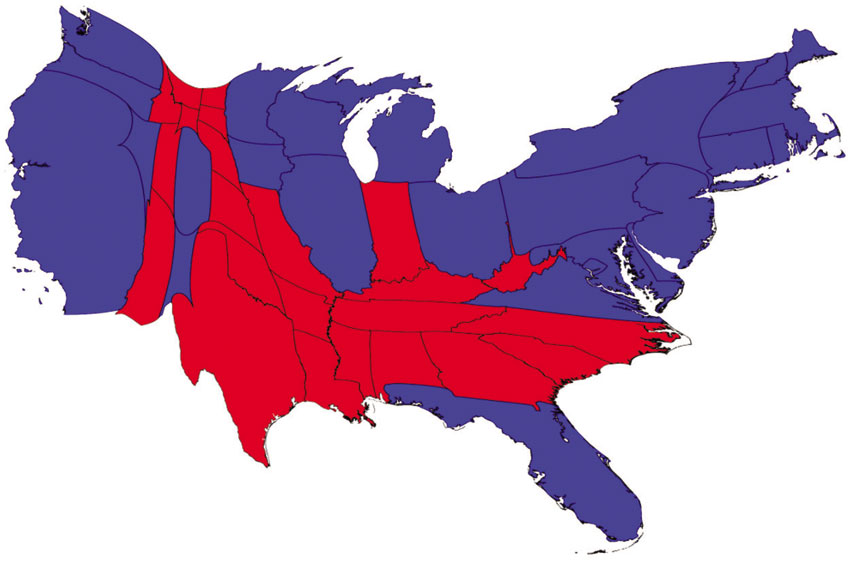
Figure 3.25 Standard versus cartogram mapping of US presidential election results, 2004
Source: Gastner et al. (2004)
One of the first and most popular uses of this approach was to present the US presidential election results. Figure 3.25 presents one of the first applications of the method aimed at challenging the conventional approach to mapping election results. The first map shown in Figure 3.25 is a conventional choropleth thematic map of the 2004 US presidential election results (George W. Bush vs John F. Kerry). In this map each state is coloured red if more of the voters in this state voted for the Republican candidate (George W. Bush) and blue if the majority of the voters voted for the Democrat candidate (John F. Kerry). This map gives the impression that Republican ‘red’ states dominate the country, since they cover significantly more area than the blue ones. However, as is often the case when election results are visualised in this way, this is misleading because the states where Republican voters are the majority tend to have smaller populations (and large rural areas within them), whereas the blue states might be small in area but they are large in terms of the total population (and number of voters) which is what matters in elections. This misleading effect can be corrected by using a cartogram approach that redraws each state with a size proportional to its population rather than area. The second map in Figure 3.25 shows the output of the cartogram method developed by Gastner and Newman (and which is also demonstrated in the practical exercises accompanying this chapter). In this second map the prominence of an area is given on population rather than size. For instance, in this map the state of Rhode Island, which has about a million inhabitants has twice the size of Wyoming, which has half a million inhabitants, even though Wyoming is 60 times bigger than Rhode Island in terms of topographic acreage. Using a cartogram to present the election results paints the true picture of the situation, which is that the US was equally divided in this election.
Over the past ten years the ground-breaking diffusion-based method for producing density-equalising maps has become increasingly popular for mapping in the social sciences and it has been used extensively so far in a number of projects and examples. One of the projects that had a considerable impact in making the method widely known and used is the Worldmapper website (www.worldmapper.org) which was led by Danny Dorling and colleagues at the Social and Spatial Inequalities research group at the University of Sheffield in collaboration with Mark Newman at the University of Michigan. There is also ongoing follow-up work on this project by Benjamin Hennig at the University of Oxford (www.worldmapper.limited). One of the original aims of the Worldmapper project was to map variables in relation to the United Nations Millennium Development Goals (MDGs) using data from the World Bank, the United Nations, the World Health Organization and other sources. We have already presented a map from this project in the choro-pleth map section of this chapter (Figure 3.7). Figure 3.26 depicts the total population of each Worldmapper region as a percentage of the global population. It is often argued that bar charts such as that presented in Figure 3.26 are also conceptually similar to a population cartogram. It can be argued that this bar chart is a very basic and non-continuous cartogram. Every world region is sized according to a variable of interest (total population). The density-equalising cartogram method is conceptually similar to a bar or pie chart, but it maintains topology and the shape of the original territories being mapped, while at the same time it resizes them according to a variable of interest. Figure 3.27 shows a population cartogram from Worldmapper where each country is resized in proportion to each total population. Figure 3.28 shows what is perhaps one of the most influential, impactful and shocking maps of the Worldmapper project. This map was created in relation to the United Nations MDGs and shows the distribution of all people aged 15–49 with HIV (Human Immunodeficiency Virus) worldwide, living in each country. It can be argued that when compared with conventional maps, such cartograms present a much more appropriate and powerful depiction of the magnitude of socio-economic and health issues. In addition, it can be argued that such cartograms (and especially when there is such a huge and shocking spatial disparity, as in the case of the map shown in Figure 3.28) have a much more effective and emotionally powerful visual impact compared to conventional maps or tabular descriptions of the data.
Figure 3.26 Bar chart of total population by Worldmapper region as a percentage of the global population. © Worldmapper.org
Source: www.worldmapper.org
Figure 3.27 Total population (Worldmapper map 002). The size of each territory shows the relative proportion of the world’s population living there. © Worldmapper.org
Source: www.worldmapper.org/display.php?selected=2. Data source: United Nations Development Programme, 2004, Human Development Report
The Worldmapper project has been further refined and extended with the use of smaller area data. In particular, Hennig (2013) used data from the Gridded Population of the World (GPW) project developed by the Socioeconomic Data and Applications Center (SEDAC) of Columbia University, New York (sedac.ciesin.columbia.edu/gpw). This database includes population data and estimates from 1990 to 2015 for all countries of the world in resolutions of up to 2.5 arc minutes, leading to a population grid of 8,640 by 3,432 pixels. The geographical database is available in raster format. Hennig and colleagues (Hennig, 2013; Hennig et al., 2010) developed a method that converted this data to vector polygon format and combined it with further metadata to create a 4,096 by 2,048 pixel-sized lattice and applied the Gastner and Newman density-equalising method to resize each pixel in proportion to the number of people that live there. In particular, the process results in a contiguous gridded population cartogram (known as a Hennig Projection Gridded Population Cartogram), meaning that each new grid cell has an area proportional to the number of people that live there, but still touches only its original eight neighbouring cells. Figure 3.29 shows the output of this method with all the grid cells coloured and shaded according to the Worldmapper colouring scheme discussed earlier.
Figure 3.28 HIV prevalence (Worldmapper map 227). The size of each territory shows the proportion of all people aged 15–49 with HIV worldwide, living there. © Worldmapper.org
Source: www.worldmapper.org/display.php?selected=227
Figure 3.29 A gridded population cartogram of the world
Source: Hennig et al. (2010); www.esri.com/news/arcuser/0110/graphics/cartogram_2-lg.jpg
Figure 3.30 A population cartogram of Europe using Gastner and Newman’s density-equalising method
This gridded population refinement of the Worldmapper project maps has been extensively used to provide so-called human-scaled visualisation of the world in a wide range of contexts. There are hundreds of maps of this type which have also attracted considerable media attention (e.g. the BBC described these as ‘people-powered’ maps; see Brown, 2009 for more details and numerous cartogram examples of individual countries). More examples and stories painted using this approach can be found in Hennig’s original work (Hennig, 2013) as well as the accompanying website (www.viewsoftheworld.net) which is constantly updated with new data and topical themes.
Figure 3.31 Gridded population cartogram of Europe; basemap: Hennig Projection Gridded Population Cartogram
Source: Ballas et al. (2014)
A more recent application of Gastner and Newman’s density-equalising method and of Hennig’s refinement and gridded population cartogram was part of an effort to offer an alternative visualisation of Europe and the European integration project. The Europemapper (www.europemapper.org) project involved the creation of a Social Atlas of Europe (Ballas et al., 2014) with the use of these methods to visualise Europeans living in all the states that have demonstrated a strong commitment to a common European future by being closely associated with the EU, either as current members or as official candidate states (or official potential candidates for EU accession) and/or states that are signed up to any of the following agreements: the European Economic Area, the Schengen Zone and the European Monetary Union. Figure 3.30 shows a population cartogram version of the map shown in Figure 3.6, created with the Gastner and Newman method, using the same rainbow colour scale to determine the colour hue for each state according to the year of association with the European Union. The more recent the formal association the nearer to the red end of the spectrum the hue is (also see the legend in Figure 3.6).
Further, Figure 3.31 shows a map made with the use of the Hennig gridded population cartographic projection on the basis of fine-level spatial information about where people live rather than land mass, showing even more clearly where most people are concentrated. For example, Madrid, Paris, Istanbul and London are huge, while Scandinavia is small, whereas the Rhine-Ruhr metropolitan region in Western Europe, including the areas of Cologne, Dortmund and expanding towards the Netherlands, is much more prominent compared to on a conventional map. In addition, countries and regions that are more densely populated are more visible on the map (e.g. most of the United Kingdom, Italy, Poland, Romania) compared to large rural areas in the north of Europe.
The picture of Europe described above can be enriched further with more information, such as by employing a choropleth mapping approach to shade the gridded population cartograms according to a socio-economic or demographic theme of interest. An example is shown in Figure 3.32, where resized grid cells are coloured on the basis of publicly available data for European statistical regions on higher education attainment of the local workforce. In particular, the shading shows the spatial pattern of the numbers of persons aged 25–64 with a tertiary education degree as a proportion of all people aged 25–64 living there. For example, the cells coloured in the darkest blue are placed within regions where more than 33% of that population has a tertiary education degree (Ballas et al., 2016).
Figure 3.32 Persons aged 25–64 with a tertiary education degree as a proportion of all people aged 25–64 living in Europe; basemap: Hennig Projection Gridded Population Cartogram
Source: Ballas et al. (2016)
It is also possible to combine the population carto-grams with physical and topographical geographical information. Figure 3.33 is the topographic version of the previous two maps, with the area being drawn scaled proportionally to population but coloured by altitude. In this way physical and human geographies can be mixed up on the map. Rather like a traditional physical geography map, upon which cities are drawn, this is a new human geography map, but one upon which mountains and valleys are also depicted.
Figure 3.33 Gridded population cartogram representation of the topography of Europe; basemap: Hennig Projection Gridded Population Cartogram
Source: Ballas et al. (2014)
These cartograms give just a flavour of the geovisualisation potential in the social sciences with the use of GIS and state-of-the-art human cartographic techniques. There are hundreds more examples in relation to this ongoing work (e.g. see www.worldmapper.org, www.europemapper.org and viewsoftheworld.net). One of the practical exercises accompanying this chapter shows how it is possible to create these cartograms.
In this chapter we presented an overview of key cartographic issues and principles pertaining to thematic mapping in the social sciences and we introduced a number of geovisualisation approaches, ranging from so-called conventional thematic mapping (including choropleth maps, graduated symbol and chart-type maps as well as flow maps) to human-scaled visualisations and human cartograms. The latter are increasingly appealing and particularly appropriate in the social sciences. In particular, it is increasingly and convincingly argued that conventional maps that show how cities, regions and countries appear from space, are not an appropriate way to show the spatial distributions of humans and their characteristics. The last section of this chapter provided an overview of key arguments why new innovative human cartographic methods and tools are more suitable and appropriate for the depiction of the spatial distribution of variables pertaining to human societies rather than environmental, geological or meteorological problems (which are the domains for which conventional cartography is more suitable). These methods are increasingly accessible and easy to use due to the availability of free (and user-friendly) software (as is also demonstrated in the practical accompanying this chapter). There are ongoing and exciting developments in social science cartography and geovisualisation aimed at mapping new and sometimes more complex forms of data (including flow data, voluntary geographic information user data and social media data) and involving animation and use of technologies such as OpenStreetMap, Google Earth, Bing and Apple Maps.
This chapter provided an overview of key approaches and methods, but it would have been beyond its scope to offer a comprehensive guide of what is possible and of all the issues and elements of cartographic theory and practice. The cartographic texts briefly referred to in the introductory chapter are among the excellent resources for further reading to complement what we present here in order to create social science maps and geovisualisations that are visually appealing and suitable for different audiences.
|
This chapter is accompanied by two practicals (Practical C(i) and Practical C(ii)). These practicals allow you to practise generating a series of cartographic outputs using your GIS. Practical C(i): Visualisation and thematic mapping, introduces core cartographic visualisation tools in ArcGIS, using data related to small areas in the UK. You also create a human cartogram using an external tool. Practical C(ii): Working with social media data, focuses on point data derived from a novel data source, the social media platform Twitter. You import and visualise this point data using proportional symbols, and also explore how to aggregate point data to geographic zones for subsequent thematic mapping. These skills will be applied across the range of practical activities that follow.
Note
1 E.g. see http://uk.businessinsider.com/state-unemployment-map-january-2016-2016-3.
All website URLs accessed 30 May 2017.
Akella, M. (2011) Creating Radial Flow Maps with GIS. Available from: https://blogs.esri.com/esri/arcgis/2011/09/06/creating-radial-flow-maps-with-arcgis/.
Ballas, D., & Dorling, D. (2011) Human scaled visualisations and society, in T. Nyerges, H. Couclelis, & R. McMaster (eds) Handbook of GIS & Society Research, Sage, London, 177–201.
Ballas, D., Dorling D., & Hennig, B. (2014) The Social Atlas of Europe, Policy Press, Bristol.
Ballas, D., Dorling, D., & Hennig, B. (2016) The Human Atlas of Europe: A Continent United in Diversity, Policy Press, Bristol.
Bertin, J. (1967) Sémiologie graphique, Mouton/Gauthier-Villars, Paris.
Bertin, J. (2011) General theory, from semiology of graphics, in M. Dodge, R. Kitchin, & C. Perkins (eds) The Map Reader, Wiley-Blackwell, Chichester, 8–16.
Brewer, C. (2005) Designing Better Maps: A Guide for GIS Users, ESRI Press, Redlands, CA.
Brown, A. (2009) People-powered maps. BBC Magazine. Available from: http://news.bbc.co.uk/1/hi/magazine/8280657.stm.
Center for International Earth Science Information Network (2015) Socioeconomic Data and Applications Center (SEDAC): Gridded Population of the World (GPW) v3. Available from: http://sedac.ciesin.columbia.edu/data/collection/gpw-v3.
Chrisman, N. R. (1998) Rethinking levels of measurement for cartography. Cartography and Geographic Information Science, 25(4), 231–242.
Dent, B. D., Torguson, J., & Hodler, T. W. (2008) Cartography: Thematic Map Design (6th edition), McGraw-Hill, Dubuque, IA.
Dorling, D. (2006) New maps of the world, its people and their lives. Society of Cartographers Bulletin, 39(1 and 2), 35–40.
Dorling, D. (2007a) Worldmapper: the human anatomy of a small planet. PLoS Medicine, 4(1), 13–18.
Dorling, D. (2007b) Anamorphosis: the geography of physicians, and mortality. International Journal of Epidemiology, 36(4), 745–750.
Dorling, D., & Thomas, B. (2004) People and Places: A Census Atlas of the UK, Policy Press, Bristol.
Dorling, D., Rigby, J., Wheeler, B., Ballas, D., Thomas, B., Fahmy, E., et al. (2007) Poverty, Wealth and Place in Britain, 1968 to 2005, Policy Press, Bristol.
Durham, H., Dorling, D., & Rees, P. (2006) An online census atlas for everyone. Area, 38, 336–341.
Eddins, S. (2014) Rainbow color map critiques: an overview and annotated bibliography, MathWorks: Accelerating the Pace of Engineering and Science. Available from: www.mathworks.com/tagteam/81137_92238v00_RainbowColorMap_57312.pdf.
Forrest, D. (1999) Geographic information: its nature, classification, and cartographic representation. Cartographica, 36, 31–53.
Gastner, M. T., & Newman, M. E. J. (2004) Diffusion-based method for producing density equalizing maps. Proceedings of the National Academy of Sciences of the United States of America, 101, 7499–7504.
Gastner, M., Shalizi, C., & Newman, M. (2004) Maps and Cartograms of the 2004 US Presidential Election Results. Available from: www.personal.umich.edu/~mejn/election.
Hennig, B. D. (2013) Rediscovering the World, Springer Verlag, Berlin.
Hennig, B. D., Pritchard, J., Ramsden, M., & Dorling, D. (2010) Remapping the world’s population visualizing data using cartograms. ArcUser, Winter, 66–69. Available from: www.esri.com/news/arcuser/0110/files/cartogram.pdf.
Kraak, M., & Ormeling, F. (2010) Cartography: Visualization of Spatial Data (3rd edition), Pearson Education, Harlow.
MacEachren, A. M. (2004) How Maps Work, Representation, Visualisation and Design, Guilford Press, New York.
Monmonier, M. (1996) How to Lie with Maps (2nd edition), University of Chicago Press, Chicago, IL.
Perkins, C. (2003) Cartography: mapping theory. Progress in Human Geography, 27(3), 341–351.
Perkins, C. (2004) Cartography: cultures of mapping: power in practice. Progress in Human Geography, 28(3), 381–391.
Prasad, S. (2012) Generating Distributive Flow Maps with ArcGIS. Available from: https://blogs.esri.com/esri/apl/2012/09/12/generating-distributive-flow-maps-with-arcgis/.
Shaw, M., Davey Smith, G., Thomas, B., & Dorling, D. (2008) The Grim Reaper’s Road Map: An Atlas of Mortality in Britain, Policy Press, Bristol.
Slocum, T. A., McMaster, R. B., & Kessler, F. C. (2008) Thematic Cartography and Geovisualisation (3rd edition), Pearson, Harlow.
Stevens, S. S. (1946) On the theory of scales of measurement. Science, 103, 677–680.
wiki.gis.com (2016a) Visual Variables. Available from: http://wiki.gis.com/wiki/index.php/Visual_Variables.
wiki.gis.com (2016b) Cartographic Design. Available from: http://wiki.gis.com/wiki/index.php/Cartographic_Design.